F(a - files.eba.gov.tr

21.7.2017
1
TÜREV KAVRAMI
TANIM: f : A
olmak üzere
lim
x a
f ( x)  f ( a )
xa
R , y=f(x) fonksiyonu ve a  A da sürekli
limiti bir reel sayı ise bu değere f fonksiyonunun
x=a noktasındaki türevi denir. f’(a) veya
gösterilir.
df
(a)
dx
sembolleri ile
h > 0 olmak üzere, x=a+h ise x - a =h dır.
lim
x a
f ( x)  f (a )
=
xa
21.7.2017
lim
h0
f (a  h)  f (a)
h
olur.
2
ÖRNEK: f: R → R
, f(x)=x2 fonksiyonunun x=2
noktasındaki türevini bulalım.
ÇÖZÜM= f(x)=x2 fonksiyonu x=2 de süreklidir
f (2)  lim x 2
f ( x)  f (2)
x2
f ( 2 )  lim x 2
21.7.2017
x2  4
( x  2 )( x  2 )
 lim x 2
4
x2
x2
3
SOLDAN SAĞDAN TÜREV
TANIM:
A  R, a  A
1. lim x  a
varsa
_
f ( x)  f (a)
xa
Limitinin bir reel sayıdeğeri
bu değere f fonksiyonunun a noktasındaki soldan türevi
denir ve f’(a-) şeklinde gösterilir.
2.
f( x ) f( a )
lim
x a
x a 
Limitinin bir reel sayı değeri
varsa bu değere f fonksiyonu, a noktasındaki sağdan
türevi denir ve f’(a+) şeklinde gösterilir.
4
TÜREVİN SÜREKLİLİKLE İLİŞKİSİ
Teorem:
A  R, a  A
olmak üzere;
f : A R
fonksiyonu a
noktasında türevli ise bu noktada süreklidir.
ÖNEMLİ UYARILAR
1. y=f(x) a  A , da türevli ise x=a da süreklidir.
2.f '(a) =f(a) ve f(x) fonksiyonu x=a da sürekli
olmalıdır ki f(x) x =a da türevli olsun
3.Bir fonksiyonun kritik noktalarında türevi araştırılırken
bu noktalarda süreksiz ise türevsizdir. Sürekliyse
sağdan ve soldan türevlerini eşitliğine bakılır.
21.7.2017
5
Örnek:
x  2 hangi noktalarda türevsizdir?
f ( x)  2
x 22
2
Çözüm: f fonksiyonu paydanın 0 olduğu noktalarda tanımsız
dolayısıyla süreksizdir.
x2  2
f ( x)  2
x  x2
x=-1 ve x=2 noktalarında
süreksiz dolayısıyla türevsizdir.
21.7.2017
6
BİR ARALIKTA TÜREVLENEBİLME
TANIM: a,b  R olmak üzere f : (a, b)  R
fonksiyonunun (a,b) aralığının her noktasında
türevi varsa f fonksiyonu (a,b) aralığında
türevlidir. A  R olmak üzere
f : A  R fonksiyonu A tanım kümesinin her
noktasında türevli ise f fonksiyonu tanımlı
kümesinde türevlidir.
21.7.2017
7
TÜREV ALMA KURALLARI
1) f(x)= c
f’(x) = 0
2) f(x) = xn
f’(x) = n . xn-1
3) (c . f (x) )’ = c . f’(x)
4)
5)
 f ( x)  g ( x) 

 f ( x).g ( x)
f ( x)  g ( x)
 f ( x).g ( x)  g ( x). f ( x)



6)  f ( x)   f ( x).g ( x)  g ( x). f ( x)
2
g
(
x
)


g
(
x
)


7) ÖZEL DURUM:
21.7.2017
ax  b
ad  bc
f (x) 
ise f ( x ) 
2
cx  d
(cx  d )
8
MUTLAK DEĞER FONKSİYONUN TÜREVİ
 f ( x) , f ( x)  0 ise
y  f ( x) ise y  
 f ( x) , f ( x)  0 ise
NOT:
Mutlak değer içini sıfır yapan tek
katlı köklerde türev yoktur. Çift katlı
köklerde ise türev vardır.
ÖRNEK:
ÖRNEK:
21.7.2017
f(x)= |x2-4| fonksiyonunun
x= 2 deki türevi varsa
bulunuz
f(x)= |x2| fonksiyonunun x= 0
deki türevini inceleyiniz
9
BİLEŞKE FONKSİYONUN TÜREVİ (zincir kuralı)
h ( x )  (fog )( x ) ise

h ( x )  fog ( x )  f (g( x )).g( x ) dir
h ( x )  fogoh ( x ) ise


h ( x )  (gofoh )( x )  g(f ( h ( x ))f ( h ( x )). h ( x )
SONUÇ:
dir .
y  f (t)
t  g( z )
z  h ( x ) ise
21.7.2017
dy dy dt dz

.
.
dx dt dz dx
dir .
10
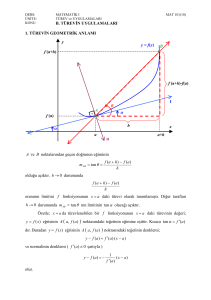
TÜREVİN GEOMETRİK YORUMU
y
T
F(a+h)
A
F(a)

B
C

a
kesen
Y=f(x)
a+h
x
teğet
21.7.2017
11
mAB=tan  =
f ( a  h)  f ( a ) f ( a  h)  f ( a )
BC


AC
( a  h)  a
h
AB kirişinin eğimi h
olacağından
mAT =
lim
h 0
0
için AT teğetinin eğimine eşit
f ( a  h)  f ( a ) f ' ( a )

( a  h)  a
O halde y= f(x) fonksiyonunun grafiğini
x=a noktasındaki teğetinin eğimi f
fonksiyonunun x=a noktasındaki türevine
eşittir. İşte türevin geometrik anlamı da
budur.
21.7.2017
12
TEĞET VE NORMAL DENKLEMLERİ
y
f(a)
Teğet
.
Y=f(x)
Normal
a
21.7.2017
x
13
A (a, f(a)) noktasından çizilen teğet denklemini
bulmak için önce eğim bulunur. Fonksiyonun bu
noktadaki türevi eğimi vereceğinden
y-f(a) =f'(a) . (x- a) teğet denklemi bulunur.
m t .mn  1
Anoktasındaki
normal denklemi ise
şöyle olur:
21.7.2017
1
1
mn  

mt
f ' (a)
1
y  f (a )  
. (x-a)
f ' (a )
14
Örnek: y= f(x)= -x2 +2x –3 parabolünün x=3 apsisli
noktasındaki teğetinin ve normalinin denklemini
bulalım.
Çözüm: x=3, y=-6 olur. f'(x)= -2x +2 olduğundan
teğetin eğimi: MT =f'(3)=(-2 . 3)+2 =-4
normalin eğimi: MN =-1/mT=-1/f'(3) =-1/-4 =1/4
Teğet denklemi: y-(-6)=-4(x-3) ,
y=-4x +6
Normal denklemi : y-(-6)=1/4(x-3) , y=x/4- 27/4
21.7.2017
15
ARTAN ve AZALAN
FONKSİYONLAR
i) Her x1, x2 A için, x1<x2 iken, f(x1)< f(x2) ise,
fonksiyonu, A kümesinde, artandır.
21.7.2017
16
m=tan= f ’(x1)>0 ise, f fonksiyonu (a,b)
aralığında artandır.
21.7.2017
17
ii) Her x1, x2 A için, x1<x2 iken, f(x1)> f(x2) ise, f
fonksiyonu, A kümesinde, azalandır.
21.7.2017
18
m=tan= f ’(x1)<0 ise, f fonksiyonu (a,b)
aralığında azalandır.
21.7.2017
19
f:[a,b]R fonksiyonu,(a,b) aralığında artan ve türevli ise,
fonksiyonun bu aralıktaki türevi pozitiftir
Yani; f fonksiyonu, (a,b) aralığında
- artan bir
fonksiyon ise bu aralığın her elemanı için
f’(x)>0’dır.
b
b
a
f’(x)
+++++
f(x)
artan
SONUÇ
f:[a,b]R, fonksiyonu, (a,b) aralığında azalan
ve türevli ise, fonksiyonun bu aralıktaki türevi
negatiftir.
Yani; f fonksiyonu, (a,b) aralığında azalan
fonksiyon ise bu aralığın her elemanı için,
f’(x)<0’dır.
aa
b
f’(x)
-----
f(x)
azalan
21.7.2017
22
Soru: f(x)=x2-2x fonksiyonunun artan veya
azalan olduğu aralıkları bulunuz?
Çözüm
::
Fonksiyonunun, artan veya azalan olduğu aralıkları
bulabilmek için, türevinin işaretini incelemeliyiz.
-
f’(x)
f(x)=x2-2x  f’(x)= 2x-2
2x-2=0  x=1 olur.
21.7.2017
f(x)
1
-
+
+
azalan artan
23
Soru: R-{-2} için,
mx  1
f(x)=
x 2
fonksiyonu-
nun daima artan olabilmesi için, m ne olmalıdır?
Çözüm :
Fonksiyonun daima artan olabilmesi için, f’(x)>0
olmalıdır.
m.( x  2)  1.(mx  1)
mx  2m  mx  1
2m  1
f’(x)=
=
= ( x  2) 2
( x  2) 2
( x  2) 2
Buradan
21.7.2017
2m  1
0
2
( x  2)

2m  1  0

m
1
2
bulunur.
24
y
-3
-2
Y=f(x)
4
x
Şekilde, y=f(x) fonksiyonunun [-3,4]
aralığındaki grafiğini görmektesiniz.Bu
grafiğe göre, f(x)’in türevinin pozitif veya
negatif olduğu aralıkları bulunuz?
21.7.2017
25
Çözüm :
a) [-3,-2) aralığında,
Fonksiyon azalan olduğundan,f ’(x)< 0 ‘dır.
b) (-2,4)
aralığında,
Fonksiyon artan olduğundan, f ‘(x) > 0’dır.
21.7.2017
26
y
Y=f’(x)
-3
-2 -1
0
1
2
3
4
x
Şekilde, y=f’(x) fonksiyonunun, [-3,4]
aralığındaki türevinin grafiğini
görmektesiniz. Grafiğe bakarak, f(x)’in
artan ve azalan olduğu aralıkları bulunuz?
21.7.2017
27
y
Çözüm :
a) [-3,-2) aralığında:
Y=f’(x)
-3 -2
-1 0 1 2 3 4
x
f’(x) > 0 olduğundan, f(x) bu aralıkta artan’dır.
b) (-2,0) aralığında:
f’(x) < 0 olduğundan, f(x) bu aralıkta azalan’dır.
c) (0,4] aralığında:
x=3 noktası hariç, f’(x) > 0
olduğundan,
f(x) bu aralıkta artan’dır.
21.7.2017
28
MAKSİMUM ve MİNUMUM
NOKTALARININ BULUNMASI
21.7.2017
29
1. YEREL MAKSİMUM NOKTASI:
Tanım: f:[a,b]R, y=f(x) fonksiyonu verilsin. x0(a,b) ve
 > 0 olsun. f fonksiyonu, (x0- ,xo+ ) aralığında en büyük
değerini x0 noktasında alıyorsa, (x0,f(x0)) noktasında bir
yerel maksimumu vardır.
f(x0) değerine, fonksiyonun bir yerel maksimum değeri
denir.
a
f(x0)
f ’(x)
Y=f(x)
a
x0- 
x0
x o+ 
f(x)
b
x0
+
b
-
f(x0)
Maksimum
2. YEREL MİNİMUM NOKTASI:
Tanım:f:[a,b]R, y=f(x) fonksiyonu verilsin. x0(a,b) ve
 > 0 olsun. f fonksiyonu, (x0- ,xo+ ) aralığında en küçük
değerini x0 noktasında alıyorsa, (x0,f(x0)) noktasında bir
yerel minimumu vardır.
f(x0) değerine, fonksiyonun bir
denir.
yerel minimum degeri
a
Y=f(x)
a
f(x0)
x0
x o+ 
f ’(x)
f(x)
x0
-
b
+
f(x0)
b
Minimum
31
Sonuç:
Yerel f(b)
maksimum
a
+
+
+
+++ - +
c
21.7.2017
d
--
f(a) -
-
f(d)
f ’(x)>0
f(c)
-
+
+
+
+
+
+
+
y=f(x)
b
Yerel minimum
f ’(x)<0
f ’(x)>0
32
21.7.2017
33
Soru
:
f(x)= x3-3x2+1 fonksiyonunun yerel maksimum ve
yerel minimum noktalarını bulunuz?
Cözüm:
Önce, f(x)’in türevini alıp, türevin işaretini incelemeliyiz:
f’(x)= 3x2-6x = 0 
-
x1= 0 ve x2= 2
f’(x)
x1= 0  f(0)= 1
x2= 2  f(2)= -3
f(x)
21.7.2017
0
+
0
1
2
-
-
0
+
++
-3
34
Soru : y
-
+
+
+
+++
y=f ’(x)
+
+
-4 -2 –1 0
Cözüm :
f’(x) - -
+
+
+
3
5
x
--
-4
0
Şekilde, y=f(x) fonksiyonunun türevinin grafiğini
görüyorsunuz. Bu grafiğe
bakarak, y=f(x) fonksiyonunun, yerel maksimum ve
yerel minimum noktalarını
bulunuz?
5
++
0
- -
f(x)
21.7.2017
35
. İKİNCİ TÜREVİN
GEOMETRİK ANLAMI
21.7.2017
36
f:[a,b] R fonksiyonu, (a,b) aralığında ikinci mertebeden
türevli olsun:
y=f(x)
y
B
A

a

x1
x2 b
x
Eğrinin çukurluk yönü yukarı doğru
bakmaktadır.
a’dan b’ye, teğetlerin eğim açılarının büyüdüğüne
dikkat ediniz.!
21.7.2017
37
y=f(x)
y
B
A

a

x1
x2
b
x
Bu teğetlerin eğimleri;
m1= tan=f’(x1)
ve
m2=tan=f’(x2)
  tan< tan  f’(x1) < f’(x2) ‘dir.
Yani;
x1< x2 için, f’(x1) < f’(x2) olduğundan, f’ fonksiyonu artan’dır.
f’21.7.2017
fonksiyonu artan olduğundan, türevi, f’’(x) > 0 ‘dır.38
Şimdi de, eğrilik yönü aşağı doğru olan bir eğri inceleyelim:
B
A


a x1
x2
b
a’dan b’ye , teğetlerin eğim açılarının küçüldüğüne dikkat!
Bu teğetlerin eğimleri;
m1= tan=f’(x1) ve m2= tan =f’(x2) ‘dir.
21.7.2017
39
B
A


  tan> tan
a x1

x2
b
f’(x1) > f’(x2) ‘dir.
Yani;
x1< x2 için, f’(x1) > f’(x2) olduğundan, f’ fonksiyonu
azalan’dır. f’ fonksiyonu azalan olduğundan, türevi,
f’’(x) < 0 ‘dır.
40
SONUÇ:
Bir f fonksiyonu için, aralığın her noktasında, f’’(x)< 0
oluyorsa, f fonksiyonunun bu
aralıktaki grafiğinin çukurluk
yönü aşağı doğrudur.
f’’(x)<
0 Konkav
21.7.2017
Bir f fonksiyonu için, aralığın her noktasında, f’’(x)> 0
oluyorsa, f fonksiyonunun bu
aralıktaki grafiğinin çukurluk
yönü yukarı doğrudur.
f’’(x)> 0 Konveks
Soru
:
f:R R, f(x)= x3+x2-2x fonksiyonunun, konveks ve konkav
olduğu aralıkları araştırınız?
Çözüm :
Öncelikle, f’in ikinci türevini alıp, işaretini incelemeliyiz.
f’(x)=3x2+2x-2
f’’(x)=6x+2 = 0
- 
f’’(x)
-- -
-1/3
+
+ + +
f(x)
x= -1/3
21.7.2017
42
Bir önceki örnekte görüldüğü gibi, fonksiyon
eğrisi, eğrilik yönünü bazı noktalarda
değiştirmektedir:
TANIM
Bir f fonksiyonunun grafiğinin, çukurluğunun yön
değiştirdiği ve fonksiyonun sürekli olduğu
noktaya,
Dönüm (büküm)
noktası
denir.
21.7.2017
43
Şekilleri dikkatle inceleyiniz!!!
f(x0)
a
0
f ’’(x)<0
f(x0)
x0
b
f ’’(x)>0
f ’’(x0)=0
Dönüm noktası
0 a
f ’’(x)>0
x0
b
f ’’(x)<0
f ’’(x0)=yok
Dönüm noktası
DİKKAT:
İkinci türevin işaret değiştirdiği nokta DÖNÜM
21.7.2017
noktasıdır.
44
Uygulamalar
21.7.2017
45
1. f: RR, f(x)= x4+x3-2x fonksiyonunun, konveks ve
konkav olduğu aralıkları ve varsa, dönüm noktalarını
bulunuz?
Çözüm :
f’(x)= 4x3+3x2-2
f’’(x)= 12x2+6x
İkinci türevin kökleri:
6x=0
12x2+6x=0
21.7.2017
6x(2x+1) = 0
Tablosunu yaparsak
x1= 0
(2x+1)= 0 x2=-1/2
46
f’’(x)= 12x2+6x
x
f’’(x)
-
+
-1/2
0
-
+
+
f(x)
konveks
konkav
Dönüm
noktası
21.7.2017
konveks
Dönüm
noktası
47
SORU 2.
f: RR, f(x)=(x-3)4 fonksiyonunun, varsa,
dönüm noktasını bulunuz?
Çözüm :
f’(x)=4(x-3)3
f’’(x)= 12(x-3)2
ve
12(x-3)2=0  x1=x2=3
x
f’’(x)
f(x)
21.7.2017
- 
+
3
+
+ 
konveks
konveks
X= 3 de Dönüm noktası varmıdır?
48
x=3 noktası, ikinci türevin kökü olduğu
halde, dönüm noktası değildir
Türev bu noktada, işaret değiştirmemektedir!
Yani; f’’(x0)=0 olması, x0 noktasının DÖNÜM
noktası olmasını gerektirmez!!!!
21.7.2017
49
21.7.2017
50
1.
x 2  7 x  10
lim 2
x 2 x  3x  2
limitinin değerini bulunuz?
Çözüm :
x 2  7 x  10
0
lim 2
=
x 2 x  3x  2
0
belirsizliği var
2x  7
3
2.2  7
x 2  7 x  10
lim
 3
lim 2
=
=
=
x

2
x 2 x  3x  2
2.2  3
2x  3
1
21.7.2017
51
1  cos x
limitinin değerini bulunuz?
xπ
sin x
3. lim
Çözüm :
21.7.2017
1  cos x
=
lim
xπ
sin x
0
belirsizliği var
0
1  cos x
lim
=
xπ
sin x
- sinx
cosx
 sinπ
cosπ
lim
xπ
0
=
=
1
0
52
4.
ln( x  1)
lim x
x e
 cos x
limitinin değerini bulunuz?
Çözüm :
lim
x 
ln( x  1)
e x  cos x
lim
x
21.7.2017
=
ln( x  1)
e x  cos x


=
0
belirsizliği var
1
x1
lim x
x   e - sinx
0

53
5. lim
x0
ln(sin x)
ln(sin 2x)
limitinin değerini bulunuz?
Çözüm :
ln(sin x)
lim
=
x  0 ln(sin 2x )


ln(sin x)
= lim
lim
x  0 ln(sin 2x )
x0
lim
x0
21.7.2017
cosx/sinx
=
2cos2x/sin2x
belirsizliği var
cosx/sinx
2cos2x/sin2x
lim Cosx.sin2x
x 0
2cos2x.sinx
54
6.
1 x
lim  e
x  x
limitinin değerini bulunuz?
Çözüm :
1 x
lim  e = 0
x  x


L’Hospital den
1 x
lim  e
x  x
ex
lim
=
x x
=
ex 
lim
=
x x

x
lim e
x 1
=
e
1
= = 
1
55
Cosx.sin2x
lim
x  0 2cos2x.sinx
lim
x 0
21.7.2017
2.sinx.cos2x
2cos2x.sinx
2sinx.cosx
2. 1
2. cos 2 0
=
=
=1
2. cos( 2.0 )
2. 1
56
7.
lim x. sin  x2  limitinin değerini bulunuz?
x 
Çözüm :
lim x. sin  x2  =  
x 
2
sin( )
0
x
lim
=
x
1
0
x
2
2
2
sin( )
 cos
2
x
x = lim 2. cos( 2 / x)
x
lim
= lim
=2
x


x
1
x
1
21.7.2017
57
2
x
x
8.
1 
 1
lim 


x  1 x  1
ln x 
limitinin değerini bulunuz?
Çözüm :
1 
 1
lim 

 =
x  1 x  1
ln x 
1 
 1
lim 

 =
x  1 x  1
ln x 
21.7.2017
- 
0
 ln x  x  1 
 =
lim 
x  1 ln x  ( x  1)
0


58
L hospital uygularsak
 ln x  x  1 

lim 
x 1 ln x  ( x  1)


lim
x 1
1  x
x
=
( x  1)  x. ln x
x
lim
x 1
1
 1
x
1
 ( x  1)  ln x
x
1 x
= lim
=
x  1 ( x  1)  x. ln x
=
0
0
:
21.7.2017
59
21.7.2017
60
SUNUMUZ BURADA SONA
ERMİŞTİR...
SEYFETTİN KESKİN
Matematik Öğretmeni
21.7.2017
61