θ α α θ θ α α

DERS:
ÜNİTE:
KONU:
MATEMATİK I
TÜREV ve UYGULAMALARI
MAT 101(10)
B. TÜREVİN UYGULAMALARI
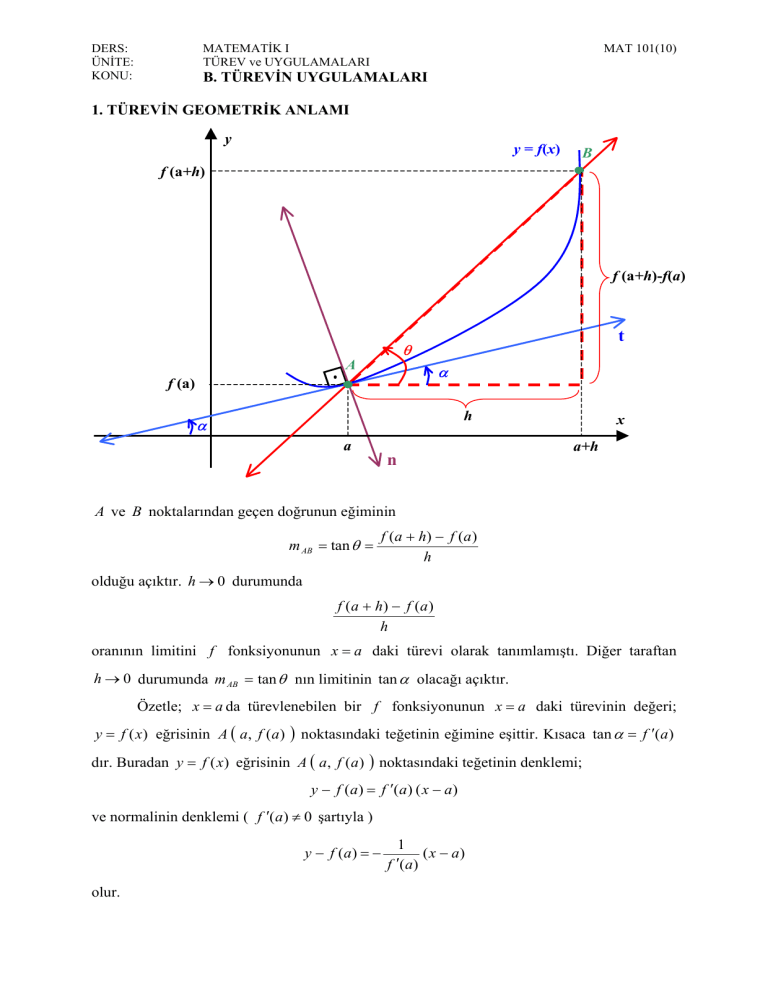
1. TÜREVİN GEOMETRİK ANLAMI
y
y = f(x)
B
f (a+h)
f (a+h)-f(a)
t
θ
A
α
f (a)
h
α
a
n
x
a+h
A ve B noktalarından geçen doğrunun eğiminin
m AB = tan θ =
f ( a + h) − f ( a )
h
olduğu açıktır. h → 0 durumunda
f ( a + h) − f ( a )
h
oranının limitini f fonksiyonunun x = a daki türevi olarak tanımlamıştı. Diğer taraftan
h → 0 durumunda m AB = tan θ nın limitinin tan α olacağı açıktır.
Özetle; x = a da türevlenebilen bir f fonksiyonunun x = a daki türevinin değeri;
y = f (x) eğrisinin A ( a, f (a )
) noktasındaki teğetinin eğimine eşittir. Kısaca
dır. Buradan y = f (x) eğrisinin A ( a, f (a ) ) noktasındaki teğetinin denklemi;
y − f (a) = f ′(a) ( x − a)
ve normalinin denklemi ( f ′(a) ≠ 0 şartıyla )
y − f (a) = −
olur.
1
( x − a)
f ′(a)
tan α = f ′(a)
Örnek: y = x 2 eğrisine, x = 2 apsisli noktasından çizilen teğetin denklemini bulunuz.
Normalin denklemini bulunuz.
Örnek: y = sin x eğrisine
a) x =
π
6
apsisli noktasından çizilen teğet ve normalin denklemini
b) x = π2 apsisli noktasından çizilen teğet ve normalin denklemini yazınız.
Örnek: y = 3 x eğrisine, x = 0 apsisli noktasından çizilen teğeti araştırınız.
NOT: Eğer f , x = a da sürekli ve x → a durumunda
f ′(x) → ∞ ise y = f ( x) eğrisi
A ( a, f (a ) ) noktasında bir düşey teğete sahiptir.
Örnek: y = 2 x 2 + 3 ve y =
3 2 47
x +
eğrileri kaç derecelik açı altında kesişirler?
10
10
y
α1 + θ = α 2
θ = α 2 − α1
y=f(x)
α1
θ
tan θ =
y=g(x)
α2
tan α 2 − tan α1
m − m1
= 2
1 + tan α 2 tan α1 1 + m2 m1
x
Örnek: y = cos x ve y = sin x eğrileri kaç derecelik açı altında kesişirler?
2. TÜREVİN FİZİKSEL ANLAMI
t zamanı göstermek üzere bir hareketlinin t anındaki konumu s = s (t ) ile verilsin. Herhangi
bir t anında hareketlinin hızı;
v(t ) = lim
h →0
s (t + h) − s (t )
h
olur ki türevin tanımından
2
v(t ) = s′(t )
elde edilir. Aynı düşünceyle bu hareketlinin herhangi bir t anında ivmesi;
v(t + h) − v(t )
= v′(t )
h →0
h
a (t ) = lim
dir.
Temel fizikten hatırlayacağınız üzere t = 0 anında s0 = s (0) konumundan v0 ilk hızı
ve a sabit ivmesi ile harekete (düzgün doğrusal hareket) başlayan hareketlinin herhangi bir t
anındaki konumu;
1
s (t ) = s0 + v0 t + at 2
2
dir. Gerçekten s = s (t ) fonksiyonunun t ye göre birinci mertebeden türevi
s ′(t ) = v0 + at
bu hareketlinin herhangi bir t anındaki hızıdır. s = s (t ) nin t ye göre ikinci mertebeden türevi
s ′′(t ) = a
hareketlinin ivmesidir.
Örnek: Bir doğru boyunca hareket eden bir aracın başlangıç noktasına göre t . saniyedeki
konumu s (t ) = 2t 2 + 10 (metre) fonksiyonu ile verilmiştir. Aracın 5 . saniyedeki hızını ve
ivmesini bulunuz.
Örnek: Yerden y0 metre yükseklikten yukarı doğru (dikey) v0 m/s ilk hızı ile fırlatılan bir
cismin herhangi bir t anındaki yerden yüksekliği ( g yer çekim ivmesi olmak üzere)
1
y (t ) = − gt 2 + v0 t + y0
2
metredir. Bu cismin herhangi bir t anındaki hızını veren v(t ) fonksiyonunu bulunuz. v(t ) nin
ne zaman pozitif ne zaman negatif olduğunu tespit ederek yorumlayınız. Bu cisim en fazla kaç
metre yükseğe çıkabilir? Yorumlayınız.
3
3. FONKSİYONLARIN MONOTONLUĞUNUN, MAKSİMUM – MİNİMUM
NOKTALARININ VE KONVEKSLİĞİNİN BELİRLENMESİ
Fonksiyonlar konusunda;
Reel değerli ve reel değişkenli bir f : A → B fonksiyonu verildiğinde
x1 < x2 olmak üzere tüm x1 , x2 ∈ A için f ( x1 ) < f ( x2 ) ise f fonksiyonu A da artandır
demiştik. Ancak bu kriteri kullanmak her zaman kolay olmayabilir. Örneğin bu kriter ile
g ( x) = 2 x + 5 fonksiyonunun monotonluğunu incelemek kolaydır, ancak
f ( x) =
x2 + 1
3x + 5
fonksiyonu için bu yorucu bir işlem olabilir. Öyleyse çok daha kullanışlı ve güçlü bir kriteri
ifade edelim:
Teorem: f fonksiyonu [a, b] de sürekli ve (a, b ) nin her bir noktasında türevli olsun.
∀x ∈ (a, b ) için
f ′( x) > 0 ise f fonksiyonu [a, b] aralığında artan
f ′( x) < 0 ise f fonksiyonu [a, b] aralığında azalandır.
x2 + 1
Örnek: f ( x) =
ile tanımlanan f fonksiyonunun monotonluğunu inceleyiniz.
3x + 5
Örnek: f ( x) = x 2 − 2 x − 3 fonksiyonunun artan-azalan olduğu aralıkları bulunuz.
Örnek: f ( x) = x 3 − 12 x fonksiyonunun yerel ekstremum noktasını bulunuz.
Fermat Teoremi: Verilen bir f : [a, b ] → R fonksiyonunun bir c ∈ (a, b ) de bir yerel
ekstremumu varsa ve f fonksiyonu x = x0 da türevlenebiliyorsa f ′(c) = 0 dır.
Uyarı: Fermat teoreminin karşıtı her zaman doğru değildir. Gerçekten f ( x) = x 3 ile tanımlı
f
fonksiyonunu ele alalım. f ′(0) = 0 olmasına rağmen f
fonksiyonu x = 0 da bir
ekstremum noktasına sahip değildir.
Uyarı: Fermat teoreminin hipotezini iyi anlamak gerekir. Bir fonksiyonun herhangi bir
noktada ekstremuma sahip olması, o fonksiyonun o noktadaki birinci mertebeden türevinin
varlığını garanti etmez. Örneğin g ( x) = x − 1 ile tanımlı g fonksiyonu x = 1 de bir yerel
minimuma sahiptir. Ama f ′(1) yoktur.
4
Bu iki uyarıyı dikkate alarak bir fonksiyonun ekstremum noktalarını tespit etmek için bir
kriter geliştirebiliriz. Reel değerli ve reel değişkenli bir f : A → B fonksiyonunu ele alalım:
1)
f ′( x) = 0
denkleminin köklerini bulalım; bunlar
f
x1 , x2 , K , xn olan noktalara
teoreminin
karşıtının
doğru
x1 , x2 , K , xn
olsun. Apsisleri
fonksiyonunun kritik noktaları diyelim. Fermat
olmadığını
hatırlayarak
şunu
söyleyebiliriz:
f
fonksiyonunun kritik noktaları, ekstremum noktaları olmaya aday noktalardır.
2) Eğer f ′(x) ; x = xi de işaret değiştiriyorsa xi apsisli nokta f fonksiyonunun bir
ekstremum noktasıdır. Daha özel olarak x = xi nin solunda f ′( x) < 0 ve sağında
f ′( x) > 0 ise f fonksiyonunun x = xi bir yerel minimum noktasının var olduğunu
anlarız. Bu durumda A( xi , f ( xi ) ) noktası,
f
fonksiyonunun bir yerel minimum
noktasıdır. Diğer taraftan x = xi nin solunda f ′( x) > 0 ve sağında f ′( x) < 0 ise f
fonksiyonunun x = xi bir yerel maksimum noktasının var olduğunu anlarız.
Örnek:
f : R → R, f ( x ) = x 5 −
20 3
x
3
fonksiyonunun kritik noktalarını bulunuz. Bu
noktalardan hangileri yerel ekstremum noktalarıdır? Varsa f fonksiyonun mutlak ekstremum
noktalarını bulunuz.
Örnek: f ( x) = sin x fonksiyonunun yerel ekstremum noktalarını bulunuz.
Örnek: f ( x) = 2 x 3 − 9 x 2 − 24 x + 45 ile tanımlanan f : [− 5, 5] → R fonksiyonun maksimum
ve minimum değerini hesaplayınız.
Şimdi f fonksiyonunun ekstremum noktaları için verdiğimiz kriterin ikinci adımını
aşağıdaki teoremle geliştirelim.
Teorem: f , (a, b ) aralığında türevli bir fonksiyon, c noktası f fonksiyonunun bir kritik
noktası, f ′′(c) mevcut ve sıfırdan farklı olsun.Eğer
f ′′(c) > 0 ise x = c de f fonksiyonunun bir yerel minumumu,
f ′′(c) < 0 ise x = c de f fonksiyonunun bir yerel maksimumu vardır.
5
Örnek: f : [0, 2π ] → R , f ( x) = 2 sin x + cos 2 x fonksiyonunun yerel ekstremum noktalarını
bulunuz.
Bir fonksiyonun monotonluğuna, fonksiyonun birinci türevinin işaretini inceleyerek karar
verebiliyoruz. Örneğin fonksiyonun artan olduğu durumda fonksiyonun değerindeki artmanın
da giderek arttığını, azaldığını ya da sabit kaldığını görebiliriz.
f
y
y
g
t
h
k
s
x
x
Yukarıda verilen f, g, h fonksiyonları artandır ve birinci mertebeden türevleri pozitiftir. Bu
durumda bir fonksiyonun artan olmasını da sınıflandırmamız gerektiğini anlarız. Benzer
durum t, k, s fonksiyonları için de geçerlidir.
y
y
g ′( x) > 0
f ′′( x) > 0
f ′( x) < 0
f ′( ) 0
g ′′( x) > 0
g ′( x) < 0
f ′( ) 0
f ′( x) > 0
x
x
Şekilde grafiği verilen f fonksiyonu konvekstir (ya da yukarı bükümlüdür) denir. Şekildeki
g fonksiyonu konkavdır (ya da aşağı bükümlüdür) denir.
Teorem: f : [a, b] → R fonksiyonunun (a, b) aralığında ikinci mertebeden türevi var olsun.
∀x ∈ (a, b) için
f ′′( x) > 0 ise f fonksiyonu (a, b) aralığında konveks,
f ′′( x) < 0 ise f fonksiyonu (a, b) aralığında konkavdır.
6
Örnek: f : R → R , f ( x) = x 3 − 2 x 2 − x + 2 fonskiyonunun
a) Artan-azalan olduğu aralıları tespit ediniz.
b) Yerel ekstremum noktalarını bulunuz.
c) Konveks-konkav olduğu aralıkları tespit ediniz.
d) f in grafiğini çiziniz.
Örnekte fonksiyonun konkavlıktan konveksliğe geçtiği noktaya eğrinin dönüm noktası (ya
da büküm noktası) denir. Bu noktada fonksiyonun sürekli olduğuna dikkat ediniz.
UYARI: Bir fonskiyonun dönüm noktasında ikinci mertebeden türevi var olmayabilir.
4. MAKSİMUM – MİNİMUM PROBLEMLERİ
Bir fonksiyonun ekstremum noktalarını bulmak için yukarıda verilen yöntemi
kullanarak bazı özel problemleri çözebiliriz. Örneğin bir otobüsle yolculuk yaparken y = x
eğrisi biçiminde kıvrılan bir yolda A(4,0) noktasında bulunan bir abidenin fotografını
çekmek istiyorsunuz. Abidenin fotografını çekebileceğiniz en kısa mesafe kaç birimdir?
Bu tip problemlerde şu adımları izlemek kolaylık sağlar:
1) Problemi matematiksel olarak ifade ediniz.
2) Problemin içeriğine göre maksimum ya da minimum olması istenilen büyüklüğü, miktarı
ya da uzunluğu problemdeki bir değişkenin fonksiyon olarak yazınız.
3) Problemin içeriğine uygun olarak bu fonksiyonun tanım kümesi tespit edilir.
4) Fonksiyonun maksimum ve minimum değerleri bulunur.
A
Örnek: R cm yarıçaplı bir küre içine yerleştirilebilen
R
3
bir koninin hacmi en fazla kaç cm olabilir?
M
R
B
h-R
r H
C
7
Örnek: Hipotenüsü 6 cm olan dik üçgen biçimindeki
6 cm
bir karton parçası dik kenarlarından birisi etrafında
döndürülüyor. Oluşan dairesel dik koninin hacmi en
h
fazla kaç cm 3 olabilir?
r
Örnek: Çevresi sabit bir C sayısına eşit olan dikdörtgenler içinde alanının değeri en büyük
olanının bir kare olduğunu gösteriniz.
5. TÜREV İLE İLGİLİ BAZI TEOREMLER
Teorem: (Rolle Teoremi) f fonksiyonu [a, b] aralığında sürekli ve ∀x ∈ (a, b) de türevli
olsun. f (a) = f (b) ise f ′(c) = 0 olacak şekilde en az bir x ∈ (a, b) vardır.
Rolle Teoreminde sözedilen c için y = f (x) eğrisinin x = c apsisli noktasındaki teğeti için
ne söyleyebilirsiniz?
Teorem: (Diferensiyel Hesabın Ortalama Değer Teoremi) f fonksiyonu [a, b] aralığında
sürekli ve ∀x ∈ (a, b) de türevli olsun. O taktirde
f ′(c) =
f (b) − f (a)
b−a
olacak şekilde en az bir c ∈ (a, b) vardır.
Bu teoremde sözü edilen c sayısı 0 < θ < 1 olmak üzere c = a + θ (b − a) biçiminde
yazılabilir. Bu durumda teoremin hükmü;
f ′( a + θ (b − a ) ) =
f (b) − f (a)
b−a
olacak şekilde en az bir θ ∈ (0, 1) sayısı vardır biçiminde yazılabilir.
8
Örnek: Ankara – İzmir arası 580 km dir. Bu yolu toplam 8 saatte aldığımızı kabul edelim.
Başlangıç anından ( x = 0 ) herhangi bir x anına kadar aldığımız yolu f ( x) ile gösterelim.
Ortalama Değer Teoremi,
f ′(c) =
f (8) − f (0)
8−0
olacak şekilde en az bir c ∈ (0, 8) sayısının var olduğunu garanti eder. Gerçekten
f (8) − f (0) 580
=
= 72,5
8−0
8
olup, en az bir c ∈ (0, 8) için f ′(c) = 72,5 olmalıdır. Yorumlayınız.
Sonuç: f fonksiyonu [a, b] aralığında sürekli olsun. ∀x ∈ (a, b) için f ′( x) = 0 ise f bir
sabit fonksiyondur.
Problem: Süreklilik ve türev ile ilgili uygun koşullar altında f ′( x) = g ′( x) ise f ( x) ile g ( x)
arasındaki ilişki hakkında ne söyleyebilirsiniz?
Örnek: Bir f fonksiyonu için f ′( x) = 4 x 3 ve f (−1) = 8 olduğuna göre f ( x) = ?
6. LİMİTLERDE BELİRSİZ DURUMLAR
Teorem: (L’Hospital) f ve g x = a da sürekli, x = a nın bir delinmiş komşuluğunda türevli
fonksiyonlar ve bu komşuluktaki her x için g ′( x) ≠ 0 olsun. Eğer
lim f ( x) = lim g ( x) = 0
x →a
x →a
ise
lim
x →a
f ( x)
f ′( x)
= lim
g ( x) x→a g ′( x)
dır.
9
ÖRNEKLER
sin x
x →0
x
(
0
belirsizliği, C: 0)
0
sin x − x
x →0
x2
(
0
1
belirsizliği, C: − )
0
2
(
0
belirsizliği, C: 1)
0
5 x 2 + 3x + 3
x →∞ 4 x 2 − 2 x + 1
(
5
∞
belirsizliği, C: )
∞
4
ln(sin x)
ln(tan x)
(
∞
belirsizliği, C: 1)
∞
1) lim
2) lim
3) lim
cos 1x
x →∞
x
1+ x 2
4) lim
5) lim+
x →0
6) lim(1 − cos x) cot x
( 0 ⋅ ∞ belirsizliği, C: 0)
7) limπ (1 − sin x) tan x
( 0 ⋅ ∞ belirsizliği, C: 0)
8) lim(cot x − 1x )
( ∞ − ∞ belirsizliği, C: 0)
9) lim (1 + 5 x ) x
( 1∞ belirsizliği, C: 20)
x →0
x→ 2
x →0
4
x →0
3 ⎞
⎛
10) lim ⎜1 + ⎟
x →∞
⎝ 4x ⎠
11) lim+ (cot x )
5 x +1
1
ln x
x →0
(
12) lim− 1 − e x
x →0
)
sin x
( 1∞ belirsizliği, C:
15
)
4
( ∞ 0 belirsizliği, C: e −1 )
( 0 0 belirsizliği, C: 1)
10
7. DİFERENSİYEL KAVRAMI VE BİR FONKSİYONA LİNEER YAKLAŞIM
y
y = f (x)
f (x+∆x)
∆y
dy
f (x)
∆x=dx
x
x
x+∆x
Türevin tanımından ve türevin geometrik anlamından
lim
∆x →0
∆y
= f ′( x) = mt
∆x
olduğunu biliyoruz. Buradan
∆y = f ′( x) ∆x + ε
∆x → 0 iken ε → 0 olacak şekilde bir ε sayısı vardır. Diğer bir ifade ile kısaca
∆y ≅ f ′( x) ∆x
yazılabilir. Burada
f ′( x) ∆x
ifadesine f
fonksiyonunun diferensiyeli denir ve dy ile gösterilir. Özetle; y = f ( x)
fonksiyonunun diferensiyeli:
dy = f ′( x) ∆x
dir.
Özel olarak y = f ( x) = x fonksiyonunun diferensiyeli:
dx = x′ ⋅ ∆x = 1 ⋅ ∆x = ∆x
olarak bulunur ki bu eşitlik den
dx = ∆x
olduğu görülür.
dx = ∆x olmasına karşın dy ≠ ∆y dir. Ancak dy ≅ ∆y yazılabilir. Bunları yukarıdaki
grafikte görebilirsiniz.
∆y = f ( x + ∆x) − f ( x)
ve
dy = f ′( x)∆x
olduğundan
11
f ( x + ∆x) − f ( x) ≅ f ′( x)∆x
⇒
f ( x + ∆x) ≅ f ( x) + f ′( x)∆x
elde edilir. Burada x yerine a ve x + ∆x yerine x yazılırsa, ∆x = x − a olup
f ( x) ≅ f (a) + f ′(a) ( x − a)
elde edilir. Burada
L( x) = f (a) + f ′(a) ( x − a)
yazılırsa gerçekten L( x) ≅ f ( x) yaklaşımı elde edilir. Bu L(x) yaklaşımına; x = a civarında
f fonkisyonuna lineer yaklaşım denir.
Örnek: f ( x) = 1 + x fonksiyonu için a = 0 civarında lineer yaklaşımı bulunuz.
1
1
Gerçekten L( x) = 1 + x elde edilir. Yani 1 + x ≅ 1 + x yaklaşımı bulunur.
2
2
1
1 + x ≅ 1 + x lineer yaklaşımından hareketle 1,0201 sayısının değerini yaklaşık olarak
2
1
hesaplayalım. f ( x) = 1,0201 = 1,01 olup, lineer yaklaşımdan L( x) = 1 + x = 1,01005 elde
2
edilir ki gerçek değerle yaklaşık olarak bulduğumuz değer arasındaki fark − 0,00005 olarak
hesaplanır.
1
Şimdi de 1 + x ≅ 1 + x lineer yaklaşımından hareketle 1,1 sayısının değerini yaklaşık
2
olarak hesaplayalım.
1
L( 0,1 ) = 1 + ⋅ 0,1 = 1,05
2
bulunur ki 1,1 ≅ 1,05 dir. Bilgisayar yardımı ile 1,1 ≅ 1,048808848 olduğunu görürüz.
Problem: Acaba 1,1 sayısının değerini daha hassas hesaplamak için ne yapmalıyız?
12
Örnek:
5 sayısını yaklaşık olarak hesaplayınız.
f ( x) = x olsun. Önce f ( x) = x fonksiyonunun a = 4 civarındaki lineer
yaklaşımını bulalım.
L( x) = f (4) + f ′(4) ( x − 4)
⇒
1
L( x) = 2 + ⋅ ( x − 4)
4
olarak bulunur. L(5) = 2,25 aradığımız yaklaşımdır.
Şimdi daha hassas bir yaklaşım bulalım: f ( x) = x fonksiyonunun a = 4,84
civarındaki lineer yaklaşımını bulalım.
L( x) = f (4,84) + f ′(4,84) ( x − 4,84)
⇒
L( x) = 2,2 +
1
⋅ ( x − 4,84)
4,4
olup, L(5) = 2,23636363636364 olarak hesaplanır.
Gerçekten
5 irrasyonel sayısının bilgisayar yardımı ile hesaplanan yaklaşık değeri
5 ≅ 2,23606797749979 olup, a = 4,84 civarında yapılan yaklaşımın daha hassas olduğu
görülür.
Örnek: (Ö.Akın) Yarıçapı 10 br olan yarım küre biçiminde bir kasede x br derinliğinde su
bulunmaktadır. Kasedeki suyun hacmi
V=
π
3
(30 x 2 − x 3 )
ile hesaplanmaktadır. Kasedeki suyun derinliği, en fazla 1/16 br ölçüm hatası ile 5 br olarak
ölçülmüştür.
a) Buna göre suyun hacminin hesaplanmasındaki maksimum hatayı tespit ediniz.
b) Gerçek değerden yaklaşık değer çıkarılarak hesaplanan değere, mutlak hata adı verilir.
Mutlak hatanın gerçek değere oranına da bağıl (göreceli) hata adı verilir. Suyun hacminin
hesabında yapılan mutlak ve bağıl hatayı bulunuz.
(Y.G. ∆y = f ( x + ∆x) − f ( x) ≅ dy = f ′( x)∆x )
Örnek: f ( x) = x 2 −
a) dy
1
ile tanımlı f fonksiyonu veriliyor.
x
b) d 2 y
c) d 3 y
diferensiyellerini hesaplayınız.
13
8. EĞRİ ÇİZİMLERİ
Eğri çizimleri için son aracımızı ele alalım: Asiptotlar. y = f ( x) eğrisinin asimtotları
şöyle bulunur.
Düşey Asimtot: lim− f ( x) = ∞ ya da lim+ f ( x) = ∞ oluyorsa x = a doğrusu, y = f (x)
x→a
x →a
eğrisinin bir düşey asimtotudur.
Yatay Asimtot: lim f ( x) = b ya da lim f ( x) = b oluyorsa y = b doğrusu, y = f (x)
x →−∞
x →∞
eğrisinin bir yatay asimtotudur.
Eğri Asimtot: lim f ( x) − P( x) = 0 ya da lim f ( x) − P ( x) = 0 olacak şekilde bir P
x → −∞
x →∞
polinomu varsa; y = P(x) eğrisi, y = f (x) eğrisinin bir eğri asimtotudur. Eğer y = P(x) bir
doğru ise eğik asimtot adını alır.
Eğer y = f (x) eğrisinin eğik asimtotları varsa; x > 0 için bu asimtot
m = lim
x →∞
f ( x)
x
ve
n = lim( f ( x) − mx )
x →∞
olmak üzere
y = mx + n
dir. x < 0 için eğik asimtot x → −∞ durumundaki limitlerden hesaplanan m ve n için
bulunur. Bu iki eğik asimtot çakışık olabilir.
Örnek: Aşağıda verilen eğrilerin asimtotlarını bulunuz.
a) y =
2x2 +1
3x 2 − 12
b) y =
x +1
x2 − 4
c) y =
x2
x−4
1
d) y = 3 x
e) y = ln x
f) y = e x
14
g) y =
x
ln x
h) y =
ln x
x
ı) y = x 2 − 2 x
Şimdi y = f (x) denklemli bir eğriyi çizmek nasıl bir yol izleneğini özetleyelim:
1) f (x) i reel sayı yapan tüm x ∈ R lerin kümesi tespit edilir. Yani y = f (x) denklemi ile
tanımlanan f fonksiyonunun en geniş tanım kümesi bulunur.
2) Varsa y = f (x) eğrisinin asimtotları bulunur.
3) Eğrinin eksenleri kestiği noktalar bulunur.
4) f fonksiyonunun birinci mertebeden türevi yardımıyla monotonluğu incelenir, ekstremum
noktaları tespit edilir.
5) Gerek duyulursa f fonksiyonunun ikinci mertebeden türevi yardımıyla konveksliğikonkavlığı incelenir.
6) Yukarıda elde edilen bilgiler bir tabloda özetlenir.
7) Çizim yapılır.
Örnek: y = x +
Örnek: y =
1
1
1
1
, y = x+ , y = x + , y = x +
x
x
x
x
eğrilerini çiziniz.
x
eğrisini çiziniz.
1+ x
Örnek: y = ln
Örnek: y = e
x −1
eğrisini çiziniz.
x +1
x +1
x
eğrisini çiziniz.
Örnek: y = x 2 − 2 x − 3 eğrisini çiziniz.
Örnek: y =
1
eğrisini çiziniz.
1 − ex
15