Türev

Türev
Tanım:f:[a,b]
R bir fonksiyon ve x0Є(a,b) olsun.
Lim f ( x)  f ( x ) limitine (varsa) f
0
xx
0
fonksiyonunun x0 noktasına türevi denir ve f’(x0) ile
gösterilir.Bu limitin olması için:
f ( x)  f ( x ) : x  x  lim f ( x)  f ( x ) : x  x
Lim
x x -0
x x +0
Olması gerekir.bu eşitliğin solundaki limite f
fonksiyonunun x=x0 daki soldan türevi, aşağıdaki
limite ise f fonksiyonunun sağdan türevi denir.
0
0
0
0
Türev en basit şekliyle bir eğrinin eğimi olarak
anlatılabilir.
Polinom - yani tamsayılardan oluşan denklemlerin
türevlerinin bulunması çok kolaydır. Peki neden
derslerde tahtalar dolusu işlemler yapılıyor, bunu
açıklayalım.
Türev çok basit bir işlem olmasına rağmen, derslerde
tam da türevin karmaşık olduğu noktalar işlenir fonksiyonun tanımsız olduğu noktada türevinin
incelenmesi gibi.
Tahtalar dolusu yapılan işlemler ise değişik türlerdeki
fonksiyonların türevlerinin bulunmasıdır. Fonksiyon
çeşitleri o kadar fazladır ki bunların türevlerini bulmak
da çok zor olacaktır.
Not:f`(x+0)ile f`(x-0)varsa ve
f`(x+0)=f`(x-0) ise f`(x0) vardır ve
f`(x0)=f`(x+0)=f`(x-0)dir.
Örnek:f(x)=x2+x fonksiyonunu x=2 noktasındaki
türevini bulunuz?
Çözüm:
F`(2)=lim f(x)-f(2):x-2=lim x2+x-6:x-2
İse lim (x+3)=5 olur
Örnek: f(x)=(x-3).Ix-3I ise f fonksiyonunun
x=3 noktasındaki türevini bulunuz?
Çözüm:
f(3)=lim f(x)-f(3):x-3=lim Ix-3I=0 olur x 3
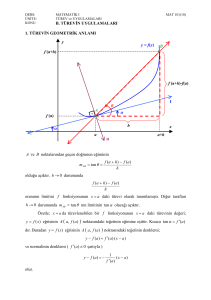
Türevin Geometrik Anlamı:
f'(x) = lim(x-->x0) [f(x)-f(x0)]/[x-x0]
bu bize y=f(x) fonksiyonunun x0 noktasındaki türevini
verir. bu ne demektir, bizim fonksiyonumuzun gösterdiği
eğrinin o noktada (eğer bir limit varsa) eğimi f'(x)'dir.
f'(x) = lim(x-->x0) [f(x)-f(x0)]/[x-x0]
bu bize y=f(x) fonksiyonunun x0 noktasındaki türevini
verir. bu ne demektir, bizim fonksiyonumuzun gösterdiği
eğrinin o noktada (eğer bir limit varsa) eğimi f'(x)'dir
ayrica f(x)=lim(h->0)[f(x+h)-f(x)]/h] seklinde alternatif tanimi
da bulunur
Teğet değme noktasında dik olan doğruyanormal
denir.mteğet.mnormal=-1 dir.
Örnek:f(x)=x2 eğrisinin x=1 noktasındaki teğetinin eğimini
bulunuz.
Çözüm:
mt= f‘(1)=lim f(x)-f(1):x-1
=lim x2-1:x-1=lim (x-1).(x+1):x-1
=lim (x+1)=2 olur.
Örnek:f:R
R f(x)=Ix-2I fonksiyonunun x=2 noktasındaki
türevini bulunuz.
Çözüm: f‘(2+)=lim f(x)-f(2):x-2=lim (x-2)-0:x-2=1
f‘(2-)=lim f(x)-f(2):x-2=lim (x-2)-0:x-2=1
f‘(2+) eşit değildir f‘(2-) olduğundan x=2 noktasında
fonksiyon sürekli halde türevi yoktur.bu noktaya kırılma
noktası denir.
İşaret fonksiyonun türevi:
y=sgnf(x)fonksiyonun türevi varsa sıfırdır.
Örnek:f(x)=sgn(x-5) fonksiyonunun x=5,x=-8 için
türevini bulunuz.
Çözüm:
x=5 için f fonksiyonu süreksiz olduğundan f‘(5)
yoktur.
5>x ise x-5<0 ve f(x =sgn(x-5)=-1 dir
Buradan f‘(x)=0ve f‘(-8)=0 olur.
Türev alma kuralları:Fonksiyonların türevlerini türev
tanımına göre bulmanın uzun işlemler olduğun
gördük.türevleri daha kolay bulmak için :
1.Sabit fonksiyonun türevi sıfırdır.cЄR ise (c)`=0 dır.
2.n Є R için (axn)`=naxn-1
3.toplamın türevi:
[f(x)+g(x)-h(x)]` = f‘(x)+ g‘(x)- h`(x)
bir toplamın türevi,terimlerin türevleri toplamına
eşittir.
4.Çarpımın türevi:
[f(x).g(x)] `=f`(x).g(x)+g`(x).f`(x)
5. [f n(x)]`=n.f n-1 (x).f`(x)
6.Bölümün türevi:
[f(x):g(x)]`=f`(x).g(x)-g`(x).f(x):g2(x)
7. (
) `=1:2 x
x
8.
` =u`(x):2 u(x)
u (x)
Örnek: f(x)=x.g(x),g(2)=4 ve g’(2)=3 olduğuna
göre f’(2)=?
Çözüm:
F(x)=x.g(x) ise f’(x)=1.g(x)+g’(x).x ve
f’(2)=g(2)+g’(2).2=4+6=10 dur.
Uyarı: f fonksiyonu x=-1 de süreksiz olduğundan
türevi yoktur.Bu nedenle f’ fonksiyonu x=-1 de
tanımsızdır.
Mutlak değer fonksiyonunun türevi:y=|g(x)|
fonksiyonunu parçalı biçimde yazdıktan sonra
her dalın ayrı ayrı türevi alınır.g(x)=O için türev
ayrıca araştırılır.
y=|g(x)|={g(x),g(x)0 –g(x),g(x)0
y’={g’(x),g(x)>0 ise -g’(x),g(x)<0 ise
Örnek: f:R R , f(x)=|5-x|+2 olduğuna göre
f(2)+f’(7)’nin değeri nedir?
Çözüm: x>5 için 5-x<0 ise |5-x|=-5+x ve f(x)=5+x+2=x-3 dir.Buradan f’(x)=1 ve f’(7)=1
bulunur.
Diğer taraftan f(2)=|5-2|+2=5 ve f(2)+f’(7)=
5+1=6 olur.
Uyarı:x=a için türevsiz olan bir fonksiyonu başka
bir fonksiyonla çarpımı türevli olabilir.
Bileşke fonksiyonun türevi (zincir kuramı):)
y=f( u)
u=g(x) ise y=f[g(x)]=(fog)(x) dir.
dy:dx=dy:du.du:dx=f’(u).g’(u)
Yani (fog)’(x)=f’[g(x)].g’(x)’dir.
Eğer,
y=f(u),u=g(t),t=h(x) olsaydı;
dy:dx=dy:du.du:dt.dt:dx olurdu.
Örnek:f( x)=g(x3+2),g’(10)=6 ise f’(2) değerini
bulunuz.
Çözüm: f’(x)=g’(x3+2).(x3+2)’
f’(x)=g’(x3+2).3x2 olur.Burada x=2 yazalım.
f’(2)=g’(10).12=6.12=72 bulunur.
Ters fonksiyonun türevi:AR,BR ve f:A
B fonksiyonu birebir örten olsun.f
fonksiyonu x0A noktasında türevli ve
f’(x0)0 ise
f-1:B A fonksiyonu da x0ın f altında olan
y0noktasında türevlidir ve
(f-1)’(y0)=1/f’(x0)dır.
Örnek:f:[2,+)
[3,+),f(x)=x2-4x+7
olduğuna göre f-1fonksiyonunun y1=4
noktasındaki türevini bulunuz.
Çözüm: f,bire bir ve örten olduğundan tersi bir
fonksiyondur.Bu ters fonksiyonu bulmadan da
türevini bulabiliriz.Görüntüsü 4 olan elemanı
bulmak için,
y= f (u)
U = u(x) olmak üzere
1. F(x) = sin u  f ’ (x) = cos u
2. F(x) = cos u  f ’ (x) = -sin u
3. F(x) = tan u  f ’ (x) =(1+tan2u).u ‘ =u ‘ / cos2u = u’
sec2u
4. F(x)=cotan u  f ’(x) = - (1+cotan2u).u=-u’ / sin2u =
u’ cosec2u
ÖRNEK: y=sinx  y’ = cosx.1
y=sin(x2+x)  y’ = cos(x2+x).(2x+1)
y=sin(sin x)=  y’ = cos(sin2x).cos x
TERS TRİGONOMETRİK FONKSİYONLARIN
TÜREVLERİ
1. F(x)=y=arcsinx fonksiyonu
f:[-1,1]  [-/2 , /2], ve arcsinx dir. (f(x) ark sinx
diye okunur ve sinüsü x olan yayın ölçüsü y’dir denir.
f(x) =arcsinx  x=siny dir.
f(x) =arcsinx  f ‘ (x)=1/ 1-x2 dir.
2. F(x) =arccosx fonksiyonu
f(x)=arccosx  x =cosy
f(x) =arccosx  f ‘ (x)=-1/ 1-x2 dir.
3.f(x)=arctanx fonksiyonu
f(x) =arctanx  x=tany dir.
f(x) =arc tanx  f ‘ (x)=1/ 1+x2 dir.
4. 3.f(x)=arccotanx fonksiyonu
f(x) =arccotanx  x=cotany dir.
f(x) =arc cotanx  f ‘ (x)=-1/ 1+x2 dir.
LOGARİTMA FONKSİYONUNUN TÜREVİ
1. (ln x)’ = 1/x, (ln f(x))’ = f ’(x) / f(x)
2. 2. (logax)’ = (1/In a).(1/x), (log a f(x))’ = (1/In a) .
[f’(x)/f(x)]
ÖRNEK: y = ln (x2+5) olduğuna göre, dy/dx türevini
hesaplayınız.
ÇÖZÜM:
dy/dx
(ln (x2+5))’ = (x2+5) / (x2+5) = 2x / (x2+5)
ÖRNEK:
f(x) = log10(x2+1) olduğuna göre f ’(x) türevini
hesaplayınız.
ÇÖZÜM:
f ’(x) = (log10(x2+1))’ = (1 /In 10) [(x2+1)’ /(x2+1)]
= log10 e 2x / x2+1
ÜSTEL FONKSİYONUN TÜREVİ
1. (ex)’ = ex, (e f(x) )’ = e f(x) .(f(x))’
2. (ax)’ = ax . ln a ,
(a f(x) )’ = a f(x) . f ’(x) . ln a
ÖRNEK:
f(x) = e tan x olduğuna göre f ’() değerini hesaplayınız.
ÇÖZÜM:
f ’(x) = (e tan x )’ = (tan x)’ . e tan x = (1+tan2x) . e tan x
olduğundan
f ’() = (1+tan2) . e tan  = (1+02) . e0 = 1.1 = 1’dir
ÖRNEK:
a)(3 x)’, (32x+1 )’ türevlerini hesaplayınız.
ÇÖZÜM:
a)
(3x)’ = 3x . ln3
b)
(32x+1 )’ = (2x+1)’ . 32x+1 . ln 3 = 2 . 32x+1 .ln3
YÜKSEK SIRADAN TÜREVLER (ARDIŞIK
TÜREVLER)
f : A  R , xy = f(x) fonksiyonunun
1. türevi, y’ = f ’(x)
2. türevi, y” = (f ’(x))’ = f ”(x)
3. türevi, y’” = (f ”(x))’ = f ’”(x)
4. türevi, y(4) = (f ’”(x))’ = f (4) (x)
...........................................................
n. türevi, y(n) = (f ( n-1) (x))’ = f ( n) (x)
ÖRNEK:
f(x) = 2x3 – x2 + 5x – 8 olduğuna göre f ”(x) türevini
hesaplayınız
ÇÖZÜM:
f ’(x) = (2x3 – x2 + 5x – 8)’ = 6x2 – 2x + 5
f ”(x) = (6x2 – 2x + 5)’ = 12x –2
KAPALI OLARAK TANIMLI FONKSİYONLARIN
TÜREVİ
f(x,y) = 0 kapalı ifadesinden y = g(x) denklemi ile bir
fonksiyon tanımlanabiliyorsa, bu şekilde tanımlanan
fonksiyona, kapalı olarak tanımlı fonksiyon denir.
f(x,y) = 0 eşitliğinden dy/dx türevi hesaplanırken x
değişken, y de x’in görüntüsü olarak düşünülür. Her
terimin x değişkenine göre türevi hesaplanarak yx’= dy/dx
bulunur.
ÖRNEK:
x3y2 – xy3 – 5x + y + 2 = 0 kapalı ifadesi veriliyor. y’=
dy/dx türevini hesaplayınız.
ÇÖZÜM:
x3y2 – xy3 – 5x + y + 2 = 0 kapalı ifadesinin her teriminin
x’e göre türevi hesaplanarak,
(3x2y2 + x3 .2y.y’) – (y3 + x.3y2y’) – 5 + y’ +0 = 0
y’ = (-3x2y2 + y3 + 5) / (2x3 y – 3xy2 +1) bulunur.
PARAMETRELİ İFADELERİN TÜREVİ
x = f(t) ve y = g(t) ile verilen f ve g fonksiyonlarının ortak
değişkeni (parametre) t olduğuna göre,
dy/dx = (dy/dt) / (dx/dt) dir.
Bu türev ifadesi y’x = y’t / x’t biçiminde de yazılır.
TÜREVİN LİMİT HESABINA UYGULANMASI
(L’HOSPİTAL KURALI)
limx X0 f(x)/g(x)
limitinde 0/0 ya da / 
belirsizliği varsa, genellikle limx X0 f ’(x)/g(x) dir.
(L’Hospital Kuralı)
ÖRNEK:
limx2 (x2 + x – 6) / (x5 – 32) limitini hesaplayınız.
ÇÖZÜM:
0/0 belirsizliği var.  limx2 (x2 + x – 6)’ / (x5 – 32)’ =
limx2 (2x + 1) / 5x4 = (2 . 2 + 1) / (5 . 24) = 1/16
TÜREVİN GEOMETRİK ANLAMI
x0 noktasındaki türevi f fonksiyonunun A=(x0,f(x0))
noktasındaki teğetinin eğimi
m= tan  = f ’(x0) dır.
A=(x0,f(x0)) noktasındaki teğetin denklemi:
y-f(x0)=f ’(x0).(x-x0) olur.
Teğete A=(x0,f(x0)) değme noktasında dik olan doğruya f
fonksiyonunun A noktasındaki normali denir. Buna göre
A=(x0,f(x0)) noktasındaki normalin eğimi –1/ f ’(x0) ve
normalin denklemi y-f(x0) = [-1 / f ’(x0)] (x-x0) olur.
ÖRNEK:
f(x) = -x2+x+6 ile tanımlı f fonksiyonunun apsisi x0=2 olan
teğetinin ve normalinin denklemini yazınız.
ÇÖZÜM:
f fonksiyonunun grafiğine ait ve apsisi x0=2 olan noktanın
ordinatı,
y0 = f(x0) = f(2) = -(2)2+2+6 = 4’tür.
Öyleyse teğetin değme noktası (2,4)= noktasıdır.
f ’(x) =-2x + 1 olduğundan teğetin eğimi; m = f ’(x0) = f
’(2) = -2.2+1 = -3’tür.
Bir noktası ve eğimi bilinen teğetin denklemi,
y- f(x0) = f ’(x0).(x-x0)  y – 4 = -3(x – 2)  y = -3x +
10 olur.
Normalin eğimi –1/f ’(x0) = 1/-3 = 1/3 olduğundan,
normalin denklemi; y – 4 = 1/3 (x – 2)  1/3 x + 10 /3
olur.
ARTAN YADA AZALAN FONKSİYONLAR
TANIM:
A  B olmak üzere f : AR fonksiyonunda
1)
 x1, x2  [a,b] için x1 < x2  f(x1) < f(x2) ise f
fonksiyonu [a,b] aralığında artan fonksiyondur.
2)
 x1, x2  [b,c] için x1 < x2  f(x1) > f(x2) ise f
fonksiyonu [b,c] aralığında azalan fonksiyondur.
3)
 x  [c,d] için f(x) = k (sabit) ise f fonksiyonu [c,d]
aralığında sabit fonksiyondur.
TEOREM:
f fonksiyonu (a,b) , (b,c) , (c,d) arlıklarında türevli olduğuna
göre,
1.  x  (a,b) için f ’(x) > 0  f , (a,b) aralığında artan
2.  x  (b,c) için f ’(x) < 0  f , (b,c) aralığında azalan
3.  x  (c,d) için f ’(x) = 0  f , (c,d) aralığında sabit
ÖRNEK:
f(x) = -x3 + 12x ile tanımlı f : R  R fonksiyonunun artan
yada azalan olduğu aralıkları belirtiniz.
ÇÖZÜM:
f ’(x) = -3x2 + 12 olduğundan f ’(x) = 0  -3x2 + 12 = 0
x = -2 V x = 2
x
-
-2
f’
-
f
azalan
2
+
artan
+
azalan
f ’ türev fonksiyonunun işaret durumu yukarıdaki tabloda
gösterilmiştir.
(- , -2) aralığında f ’ < 0 olduğundan, f fonksiyonu
azalandır.
(-2 , 2) aralığında f ’ > 0 olduğundan f fonksiyonu artandır.
(2 , +) aralığında f ’ < 0 olduğundan f fonksiyonu
azalandır.
TÜREV VE YEREL EKSTREMUM NOKTALARI
TANIM:
f : [a,b]  R fonksiyonunda,
1)
x1  (a,b) ; f(x1) < f(x) olacak biçimde en az bir 
pozitif gerçel sayısı varsa, (x1, f(x1)) noktası f
fonksiyonunun bir yerel minimum noktasıdır. f(x1) değeri,
f fonksiyonunun bir yerel minimum değeridir.
2)
x2  (a,b) ; f(x2) > f(x) olacak biçimde en az bir 
pozitif gerçel sayısı varsa, (x2, f(x2)) noktası f
fonksiyonunun bir yerel maksimum noktasıdır. f(x2)
değeri, f fonksiyonunun bir yerel maksimum değeridir.
Bir fonksiyonun yerel minimum ve yerel maksimum
noktalarına, yerel ekstremum noktaları denir.
TEOREM:
f fonksiyonu (a,b) aralığında türevli ve x0  (a,b) olmak
üzere x0 noktasında bir yerel ekstremum değeri varsa f ’(x0)
= 0’dır.
BİRİNCİ TÜREVLE YEREL EKSTREMUMUN
BELİRTİLMESİ
1. aA ve f ’(a) = 0 olmak üzere:
 x  (a-,a) için f ’(x) > 0 ise f fonksiyonu (a-,a)
aralığında artandır.
 x  (a,a+) için f ’(x) < 0 ise f fonksiyonu (a,a+)
aralığında azalandır.
a noktasında fonksiyonun yerel maksimumu vardır.
2. bA ve f ’(b) = 0 olmak üzere:
 x  (b-,b) için f ’(x) < 0 ise f fonksiyonu (b-,b)
aralığında azalandır.
 x  (b,b+) için f ’(x) > 0 ise f fonksiyonu (b,b+)
aralığında artandır.
b noktasında fonksiyonun yerel minimumu vardır.
ÖRNEK:
f(x) = x3 + 3x2 – 1 ile tanımlı f: RR fonksiyonunun yerel
ekstremum değerlerini bulunuz.
ÇÖZÜM:
f ’(x) = (x3 + 3x2 –1)’ = 3x2 + 6x
f ’(x) = 0  3x2 + 6x = 0
 x = -2 V x = 0
buna göre f ’(-2) = 0 ve f ’(0) = 0 dır.
f ’(x) = 3x2 + 6x birinci türev ifadesinin işareti
aşağıdaki tabloda gösterilmiştir.
x -
f ’(x)=3x2 + 6
-2
+
0
-
+
artan azalan
f ’(-2)=3
+
artan
f(0)= -1
f fonksiyonu (- , -2) aralığında artan, (-2 , 0)
aralığında azalan, (0,+) aralığında artandır.
x = -2 için fonksiyon yerel maksimum değerini alır.
Yerel maksimum değeri f(-2) = (-2)3 + 3(-2)2 – 1 =
3’tür. x = 0 için fonksiyon yerel minimum değerini alır. Yerel
minimum değeri f(0) = 03+3.02 – 1 = -1’dir.
İKİNCİ TÜREVLE YEREL EKSTREMUMUN
BELİRTİLMESİ
f: AR fonksiyonu A kümesinde 1. ve 2. sıradan türevi olan
bir fonksiyon olsun. a, bA olmak üzere:
1. f ’(a) = 0 ve f ”(a) < 0 ise a noktasında f fonksiyonunun
yerel maksimumu vardır.
2. f ’(b) = 0 ve f ”(b) > 0 ise b noktasında f fonksiyonunun
yerel minimumu vardır.
Örneğin, yukarıdaki örnekteki f(x) = x3 + 3x2 – 1 ile
tanımlı f fonksiyonunda:
f ’(x) = 3x2 + 6x
f ”(x) = 6x + 6
f ’(x) = 3x2 + 6x = 0  x = -2 V x = 0’dır.
f ’(-2) = 0 ve f ”(-2) = 6.(-2) + 6 < 0 olduğundan, x = -2
noktasında fonksiyonun yerel maksimumu;
f ’(0) = 0 ve f ”(0) = 6.0 + 6 = 6 < 0 olduğundan x = 0
noktasında fonksiyonun yerel minimumu olduğuna dikkat
ediniz.
ÖRNEK:
f(x) = (x2 – mx – 3) / (x+2) ile tanımlı f fonksiyonunun x = 1
için yerel minimumu olduğuna göre, m’nin değeri nedir?
ÇÖZÜM:
x = -1 için f fonksiyonunun yerel minimumu olduğuna göre
f ’(-1) = 0 olmalıdır.
f ’(x) = [(2x-m)(x+2)-1 . (x2-mx-3)] / (x+2)2 olduğundan
f ’(1) = [(2.1-m)(1+2) - (1-m.1-3)] / (1+2)2 = 0
 (2-m) . 3 – (-m – 2) = 0
 m = 4 olur.
FONKSİYONLARIN DEĞİŞİMLERİNİN
İNCELENMESİ VE GRAFİKLERİN ÇİZİMİ
GRAFİK ÇİZİMİNDE YAPILACAK İŞLEMLER:
1. Eğer fonksiyonun tanım kümesi belirtilmemişse,
fonksiyonun tanımlı olduğu en geniş küme belirtilir.
2. Fonksiyonun türevi hesaplanır. Türevin işaretine göre,
fonksiyonun artan ya da azalan olduğu aralıklar ve
ekstremum noktaları belirtilir.
3. x - ve x + için fonksiyonun limiti bulunur.
4. Grafiğin X ve Y eksenlerini kestiği noktalar bulunur.
5. Asimptotlar (varsa) bulunur.
6. Değişim tablosu düzenlenir.
7. Değişim tablosunda özetlenen bilgiler, koordinat
sisteminde değerlendirilerek fonksiyonun grafiği çizilir.
ÖRNEK:
y = f(x) = [3x – 1] / [x + 2 ] ile tanımlı f: AR
fonksiyonunun değişimini inceleyiniz ve grafiğini çiziniz.
ÇÖZÜM:
Tanım kümesi ve düşey asimptot:
x + 2 = 0  x = -2 olduğundan, fonksiyon x = -2 için
tanımsızdır. Tanım kümesi A=R – {-2} dir.
x = -2 doğrusu düşey asimptottur.
Türev: f ’(x) = [3.(x+2) – 1.(3x-1)] / (x + 2)2 = 7 / (x+2)2
> 0 ’ dır.
ÖRNEKLER
x,
x<2 ise
f(x) =
2,
x=2 ise
x0=2
4-x, x>2 ise
varsa x0 noktasındaki türevini bulunuz. Bu noktada f(x)
sürekli midir?
f ( x )  f ( 2)
x2
lim
 lim
 1 olur.
x2
x2
x2
x2
4 x2
f ( x )  f ( 2)
 1
 lim
x2
x2
x2
olur.
olduğundan türevlenemez.
Şimdi ise sürekliliğini araştıralım
x=2 noktasındaki limitine bakalım
lim f ( x)  lim x  2  f (2)

 olduğundan fonksiyon x0=2
lim f ( x)  lim (4  x)  2  f (2)
lim
x2
x2
x2
x2
x2

noktasında süreklidir.
SORU 2:
f(x)= |x| varsa x0 noktalarındaki türevlerini bulunuz. Bu
3
noktalarda f(x) sürekli midir. x0=2 , x  2
0
x0=2 noktasındaki türevine bakalım.
lim
x 2
f ( x)  f (2)
[| x |]  2
 lim

x2
x2
x2
şimdi bu limitin varlığını araştıralım
lim
x2
[| x |]  2

x2
0 ve
lim
x2
[| x |]  2
 -1
x2
olduğundan x0=2 noktasında türevlenemez.
Şimdi ise x0= noktasındaki türevine bakalım.
3
f ( x)  f ( )
2  lim [| x |]  1  0  f ' ( 3 )
lim
3
3
3
3
2
x
x
x
x
2
2
2
2
olur
x0=2 noktasındaki sürekliliğini araştıralım
lim f ( x)  lim [| x |]  2
x2
x2
ve lim f ( x)  lim[| x |]  1
x2
x2
olduğundan sürekli değildir. x0= 3 / 2 noktasındaki
Sürekliliği
lim f ( x) = lim [| x |]  1 ve
x
3
2
x
3
2
lim f ( x)  lim[| x |]  1
x
3
2
x
3
2
f(3/2)=[|3/2|] = 1 olduğundan x0=3/2 noktasında süreklidir.
SORU 3:
x= y+ arccoty y türevini bulunuz?
ÇÖZÜM:
1-y=y’/1+y2
1-y+y2-y2y=-y
y’ = -(1+y2) / y2
y=1+y-2
SORU 4:
exy-x2+y3=0 eşitliğinden y türevinin x=0 değerini bulunuz?
ÇÖZÜM : exy-x2+y3=0 eşitliğinden
y3=x2+exy
f(x)=y diyelim
y=f(x) olur.
x=0 y=-1
f(0)=-1
3y2.y=2x-(exy)
3y2.y=2x-y.exy
y= (2x-yxy) / 3y2
y= 0 + 1.e0(-1)
y= 1 / 3
SORU 5:
(exy) = y.exy
x=0 y=-1 için