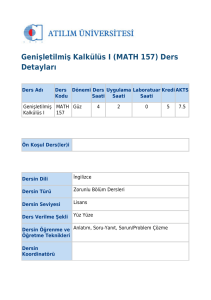
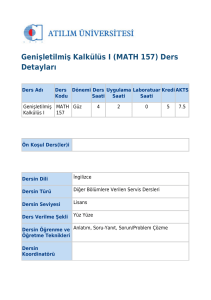
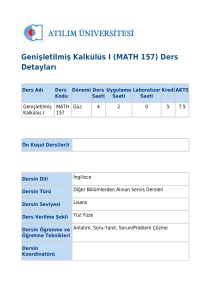
İKTİSADİ
DİNAMİKLİK VE
İNTEGRAL
İŞLEMLERİ
2
İktisat biliminde dinamiklik kavramı, değişkenlerin değişim
süreçlerini, dengeye geliş ya da uzaklaşmalarını içeren bir
analiz tipidir. Daha önce karşılaştırmalı durağanlık analizinde,
dengeden
uzaklaşıldığında
dengeye
yeniden
nasıl
dönüldüğünü ele almıştık. Dinamik analizde ise, dengeye geliş
süreci bir sorun olarak ele alınmaktadır. Diğer önemli nokta,
zamanın
olmasıdır.
sürekli
ya
da
kesikli
biçimde
analize
katılmış
3
Dinamik bir modelde amaç, belirli bir değişim kalıbına bağlı
olarak,
ilgili
değişkenin
zaman
içinde
aldığı
yolun
(ilkel
fonksiyonun) belirlenmesidir. Örneğin nüfusun zaman içinde
şöyle değiştiğini bildiğimizi varsayalım:
dH
= t −1 2
dt
Dinamik analiz, bu şekildeki bir değişim kalıbından hareketle,
H=H(t) ilkel fonksiyonunu bulmak sürecidir. Bu, integral alma
yöntemi ile yapılabilir. Bunu yukarıdaki örnek için yapalım:
H ( t ) = 2t
12
+c
4
İntegral
işlemi,
belirleyebilecek
türev
işleminin
yeterli
bilgi
tersidir.
varsa,
f(x)
İntegral
sabitini
fonksiyonunun
integralini alarak, F(x) ilkel fonksiyonuna ulaşırız. f(x) ‘in x’e
göre integralini şöyle gösterebiliriz:
∫ f ( x )dx
Burada f(x), integrali alınan fonksiyondur. dx integral işleminin x
değişkenine göre yapıldığını söylemektedir.
dF ( x )
= f ( x)
dx
⇒
c rasgele bir integral sabitidir.
∫ f ( x )dx = F ( x ) + c
5
Kural I:
1
n+1
∫ x dx = n + 1 x + c
n
Örnek 1:
1 4
∫ x dx = 4 x + c
3
Örnek 2:
1 2
∫ xdx = 2 x + c
,
( n ≠ −1)
6
Örnek 3:
∫ 1dx = x + c
Örnek 4:
∫
1 52
2
x dx = ∫ x dx =
x +c=
x5 + c
52
5
3
32
Örnek 5:
∫
1
1 −3
1
−4
dx = ∫ x dx = − x + c = − 3 + c
4
x
3
3x
7
Kural II:
∫e
x
dx = e + c
x
Kural IIa:
∫
f ′( x )e f ( x ) dx = e f ( x ) + c
Kural III:
∫
1
dx = ln x + c
x
ya da
∫
1
dx = ln x + c , ( x ≠ 0)
x
Kural IIIa:
∫
f ′( x )
dx = ln f ( x ) + c , f ( x ) > 0
f ( x)
8
Kural IV:
∫ [ f ( x ) + g( x )] dx = ∫ f ( x )dx + ∫ g( x )dx = F ( x ) + G( x ) + c
Örnek 6:
4
2
x
x
3
3
x
+
x
+
1
dx
=
x
) ∫ dx + ∫ xdx + ∫ 1dx = 4 + 2 + x + c
∫(
Örnek 7:
14 x ⎞
14 x
⎛ 2x
2x
∫ ⎜⎝ 2e + 7 x 2 + 5 ⎟⎠ dx = ∫ 2e dx + ∫ 7 x 2 + 5 dx
= e 2 x + ln(7 x 2 + 5) + c
9
Kural V:
∫ kf ( x )dx = k ∫ f ( x )dx = kF ( x ) + c
Örnek 8:
⎛ 2⎞ 3
∫ −2 x dx = −2∫ x dx = ⎜⎝ − 3 ⎟⎠ x + c
2
2
Örnek 9:
1
⎛ x 1 3⎞
x
−2
∫ ⎜⎝ 5e − x 2 + x ⎟⎠ dx = 5∫ e dx − ∫ x dx + 3∫ x dx
1
x
= 5e + + 3 ln x + c
x
10
Kural VI (İkame Kuralı):
∫
du
f ( u) dx = ∫ f ( u)du = F ( u) + c
dx
Bu kural, türevdeki zincir kuralından gelmektedir.
Örnek 10:
2
2
x
(
x
+ 1)dx
∫
Bu problemi iki şekilde çözebiliriz. Birincisinde parantezi
çarpmayla dağıtırız, sonra oluşan ifadenin integralini alırız:
1 4
2
∫ 2 x( x + 1)dx = ∫ (2 x + 2 x )dx = 2 x + x + c
2
3
İkincisinde ikame kuralını kullanırız:
u = x2 + 1
olarak kabul edelim.
du = ( 2 x ) dx
2
u
∫ 2 x( x + 1)dx = ∫ udu = 2 + c1
2
x
(
=
2
+ 1)
2
2
1 4
+ c1 = ( x + 2 x 2 + 1) + c1
2
1 4
2
= x + x +c
2
11
12
Örnek 11:
2
3
99
6
x
(
x
+
2)
dx
∫
u= x +2
3
olarak kabul edelim.
du = 3 x dx
2
2
3
99
2
3
99
x
x
dx
x
x
dx
+
=
+
6
(
2)
2
3
(
2)
∫
∫
1 100
= 2 ∫ u du = u + c
50
99
1 3
100
= ( x + 2) + c
50
13
Örnek 12:
∫ 8e
2 x+3
dx
u = 2x + 3
→
du = 2dx
4∫ 2e 2 x + 3dx = 4∫ e u du = 4e u + c = 4e 2 x + 3 + c
14
Kural VII (Kısmi İntegral):
∫ v du = uv − ∫ u dv
Bu
kural,
türevdeki
temel
çarpımın
türetilmektedir.
d ( uv ) = v du + u dv
∫ d (uv ) = ∫ v du + ∫ u dv
uv = ∫ v du + ∫ u dv
∫ v du = uv − ∫ u dv
türevseli
kuralından
15
Örnek 13:
∫ ln xdx
v = ln x
→
1
dv = dx
x
du = dx
→
u= x
∫ v du = uv − ∫ u dv
1
∫ ln x dx = x ln x − ∫ x x dx
= x ln x − x + c = x (ln x − 1) + c
16
Örnek 14:
∫ x( x + 1)
12
v=x
dx
→
dv = dx
du = ( x + 1) dx
12
→
2
32
u = ( x + 1)
3
∫ v du = uv − ∫ u dv
2
2
32
32
x
x
dx
x
x
x
dx
+
=
+
−
+
(
1)
(
1)
(
1)
∫
∫
3
3
2
4
32
52
= x ( x + 1) − ( x + 1) + c
3
15
12
17
Örnek 15:
xe
dx
∫
x
v=x
→
dv = dx
du = e dx
→
x
u=e
x
∫ v du = uv − ∫ u dv
xe dx = xe − ∫ e dx
x
x
x
= xe − e + c = e ( x − 1) + c
x
x
x
18
Örnek 16:
12
+
+
(
3)(
1)
x
x
dx
∫
v = x+3
→
dv = dx
du = ( x + 1) dx
12
→
2
u = ( x + 1)3 2
3
∫ v du = uv − ∫ u dv
2
2
32
32
∫ ( x + 3)( x + 1) dx = 3 ( x + 1) ( x + 3) − ∫ 3 ( x + 1) dx
2
4
32
= ( x + 1) ( x + 3) − ( x + 1)5 2 + c
3
15
12
Örnek 17:
∫ x ln xdx
1
v = ln x → dv = dx
x
x2
du = xdx → u =
2
∫ v du = uv − ∫ u dv
x2
x2 1
∫ x ln x dx = 2 ln x − ∫ 2 x dx
2
2
2
1⎞
x
x
x ⎛
=
=
ln x −
ln x − ⎟
⎜
2
4
2 ⎝
2⎠
19
20
Şu ana kadar belirsiz integraller üzerinde çalıştık. Belirsiz
integral
herhangi
bir
sayısal
değer
almaz,
yalnızca
bir
fonksiyonla ifade edilir. Buna karşın, şimdi ele alacağımız
belirli integral konusu, integral alma işlemi sonucunda bir
sayısal değer elde etme ile ilgilidir. Belirli integrali şöyle
gösterebiliriz:
∫
b
a
f ( x )dx = F ( x )]a = F (b ) − F (a )
b
21
Örnek 18:
∫
5
1
5
3 x dx = x ⎤⎦ 1 = (5) − (1) = 124
2
3
3
3
Örnek 19:
⎛ 1
⎞
2 4
∫0 ⎜⎝ 1 + x + 2 x ⎟⎠ dx = ⎡⎣ln 1 + x + x ⎤⎦ 0
= (ln 5 + 16) − (ln1 + 0) = ln 5 + 16
4
22
Her belirli integral, belirli bir değere sahiptir. Geometrik
anlamda bu değer, verilen bir eğrinin altında kalan belirli bir
alandır. Örneğin Şekil 4.1a’da y=f(x) fonksiyonu eğrisiyle x
ekseni arasına sıkışmış olan belirli bir A alanını ölçmek
istersek, şunu yapabiliriz. Önce [a,b] aralığını (dikdörtgensel)
parçalara ayırırız. Bu dikdörtgenlerin her birinin taban kenarı
Dx, yüksekliği de f(x) kadardır. Her bir dikdörtgenin alanını
taban kenar çarpı yükseklik ( f(x)Dx ) yoluyla belirler ve
toplarsak, y=f(x) fonksiyonu eğrisiyle x ekseni arasına sıkışmış
olan A alanını yaklaşık olarak hesaplamış oluruz:
23
n
A* = ∑ f ( xi )∆xi
i =1
Eğer dikdörtgen sayısını giderek artırırsak taban alanı daralır,
yaklaşım giderek iyileşir ve sapma azalır. Dikdörtgen sayısı (n)
sonsuza giderken, alan ölçme hatası sıfıra yaklaşır:
n
lim ∑ f ( xi )∆xi = ∫ f ( x )dx = lim A* = A alanı
n →∞
i =1
b
a
n →∞
24
Şekil 4.1a Entegral ve Alan Hesabı
y
C
B
•
•
D
E
•
•
x2
x3
y=f(x)
A
∆x
0
x1
x4
x
25
Şekil 4.1b Entegral ve Alan Hesabı
y
y = f ( x)
0
x1
(=a)
xn
(=b)
x
26
Özellik I :
İntegralin sınırlarının değiştirilmesi, belirli integralin işaretini
değiştirir.
∫
a
∫
a
b
b
b
f ( x )dx = − ∫ f ( x )dx
a
f ( x )dx =F (a ) − F (b ) = − [ F (b ) − F (a )] = − ∫ f ( x )dx
b
a
Özellik II :
İntegral sınırları aynıysa, belirli integral sıfır değerine sahiptir.
∫
a
a
f ( x )dx =F (a ) − F (a ) = 0
27
Özellik III :
Belirli
bir
integral,
sonlu
sayıdaki
belirli
alt
integrallerin
toplamıyla ifade edilebilir.
∫
d
a
b
c
d
a
b
c
f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx + ∫ f ( x )dx , (a < b < c < d )
Özellik IV :
∫
b
a
b
− f ( x )dx = − ∫ f ( x )dx
a
28
Özellik V :
∫
b
a
b
kf ( x )dx =k ∫ f ( x )dx
a
Özellik VI :
∫ [ f ( x ) + g( x )] dx = ∫
b
b
a
a
b
f ( x )dx + ∫ g ( x )dx
a
Özellik VII : (Kısmi İntegral)
∫
x=b
x=a
vdu = [ uv ] x = a − ∫
x=b
x=b
x=a
udv
29
Belirli integralin üst sınırının b gibi sabit bir parametre değil de,
x gibi bir değişken olduğunu düşünelim. Bu durumda integralı
şöyle yazarız:
∫
x
a
f ( x )dx = x − F (a )
Buna göre, f(x) fonksiyonunun altında kalan alan x ’in bir
fonksiyonudur. Sağ yandaki son terim sabit olduğundan, bu tür
bir belirli integral, aslında ilkel fonksiyonlardandır ve belirsiz
bir integrala dönüşmüştür.
30
Örnek 20:
∫
3
1
3
3
3
⎡
⎤
⎡
⎤
⎡
1 2
x
3
1 ⎤ 26
x dx = ⎢ ⎥ = ⎢ ⎥ − ⎢ ⎥ =
= 4.33
2
⎣ 6 ⎦1 ⎣ 6 ⎦ ⎣ 6 ⎦ 6
3
Örnek 21:
∫
4
2
4
4
41
4
⎡x ⎤
⎡x ⎤
⎛1 3
⎞
5
2
x ⎜ x + 1 ⎟ dx = ∫ x dx + ∫ x dx = ⎢ ⎥ + ⎢ ⎥
2 3
2
⎝3
⎠
⎣ 18 ⎦ 2 ⎣ 3 ⎦ 2
6
2
⎡ 46 26 ⎤ ⎡ 4 3 2 3 ⎤
= ⎢ − ⎥ + ⎢ − ⎥ = 242.67
⎣ 18 18 ⎦ ⎣ 3 3 ⎦
3
31
Örnek 22:
∫
2
1
e
−2 x
1 2
1 −2 x 2
−2 x
dx = − ∫ −2e dx = − ⎡⎣ e ⎤⎦ 1
2 1
2
1
1
1
−2(2)
−2(1)
⎡
⎤
⎤⎦ − ⎡⎣ e
⎤⎦ ⎦ = 2 − 4
= − ⎣ ⎡⎣ e
2
2e
2e
Örnek 23:
6 1
6
1 ⎞
1
6
6
⎛1
∫e ⎜⎝ x + 1 + x ⎟⎠ dx = ∫e x dx + ∫e 1 + x dx = [ ln x ] e + [ ln(1 + x )] e
6
= [ ln 6 − ln e ] + [ ln 7 − ln(1 + e )]
32
Sonsuz Sınırlı İntegral
∫
∞
a
f ( x )dx = F (∞ ) − F (a )
ve
∫
b
−∞
f ( x )dx = F (b ) − F ( −∞ )
İntegral sınırlarından bir tanesi olan belirli integrallere, uygun
olmayan integral denir. Bu tür integrallerin değeri belirlenemez.
Bu durumlarda limit kavramına başvururuz.
∫
∞
a
b
f ( x )dx ≡ lim ∫ f ( x )dx
b →∞
a
∫
b
−∞
f ( x )dx ≡ lim
a →−∞
∫
b
a
f ( x )dx
Bu limitler varsa, uygun olmayan integralin yakınsak, yoksa
ıraksak olduğunu söyleriz.
33
Örnek 24:
∫
∞
1
b
1
1
⎡ 1⎤
⎛ −1 ⎞
+ 1⎟ = 1
dx = lim ∫ 2 dx = lim ⎢ − ⎥ = lim ⎜
2
b →∞ 1 x
b →∞
x
⎣ x ⎦ 1 b→∞ ⎝ b
⎠
b
Örnek 25:
∫
∞
1
b 1
1
b
dx = lim ∫ dx = lim [ ln x ] 1 = lim ( ln b ) = ∞
b →∞ 1 x
b →∞
b →∞
x
Örnek 26:
∫
∞
−∞
f ( x )dx = lim
b →+∞
a →−∞
∫
b
a
f ( x )dx
34
Şekil 4.2 Entegralde Yakınsaklık ve Iraksaklık
y
y
1
f ( x) =
x
1
f ( x) = 2
x
x
x
35
Bazı durumlarda alt ve üst sınırlar belirli olsa da, integralı
alınan fonksiyon, [a,b] aralığında sonsuz değerini alabilir. Bu
türden integrallerde de limit kavramına başvururuz.
Örnek 27:
x→0+ iken,
∫
1
0
1
dx
x
1/x→∞ olmaktadır. Bu nedenle tanımsızlaşan alt
limit için a diyelim ve limit kavramını kullanalım.
∫
1
∫
1
a
0
1
1
dx = [ ln x ] a = − ln a
x
1 1
1
dx = lim+ ∫ dx = lim+ ( − ln a ) = −∞
a x
a→0
a→0
x
36
Örnek 28:
∫
9
0
x
−1 2
dx
x→0+ iken, 1/x→∞ olmaktadır.
∫
9
∫
9
a
0
x
−1 2
x
−1 2
9
dx = ⎡⎣ 2 x ⎤⎦ a = 6 − 2 a
12
9
dx = lim+ ∫ x
a→0
a
−1 2
(
)
dx = lim+ 6 − 2 a = 6
a→0
37
Bazı durumlarda integralı
alınan fonksiyon [a,b] alt ve üst
sınırlarında değil, (a,b) açık aralığında sonsuz değere sahip
olabilir. Bu durumlarda, belirli integralin toplama özelliğinden
yararlanarak, alt integrallerin toplamı biçiminde hesaplama
yaparız. Örneğin x→p iken, f(x)→∞ olduğunu varsayalım.
∫
b
a
p
b
f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx
a
p
Eğer her bir toplamdaki belirli integral birer limite sahipse,
toplam integralin yakınsak olduğunu söyleyebiliriz.
38
Örnek 29:
∫
1
−1
1
dx
3
x
Burada x→0 iken, 1/x3→∞ olmaktadır. Bu nedenle integralı iki
toplam biçiminde yazalım.
∫
1
−1
0
1
x dx = ∫ x dx + ∫ x −3 dx
−3
−3
−1
0
b
⎡ − 1 −2 ⎤
⎛ −1 1 ⎞
lim ∫ x dx = lim ⎢ x ⎥ = lim ⎜ 2 + ⎟ = −∞
b → 0 −1
b→ 0
2⎠
⎣ 2
⎦ − 1 b → 0 ⎝ 2b
b
−3
Toplam integralin birinci parçası ıraksak olduğundan, ikincisini
incelemeden,
söyleyebiliriz.
bunun
ıraksak
bir
integral
olduğunu
39
Marjinal Fonksiyondan Toplam Fonksiyonun Elde Edilişi
Toplam fayda, gelir ya da maliyet fonksiyonlarının birinci
türevleri, bunların marjinal fonksiyonlarına eşittir. Dolayısıyla
integral
alma
süreci,
marjinal
bir
fonksiyondan,
toplam
fonksiyona ulaşmamızı sağlar.
Örneğin bir firmanın marjinal maliyet fonksiyonu MC=2e0.2Q ve
toplam sabit maliyeti de 90 birimdir. Buna göre firmanın toplam
maliyet fonksiyonunu belirleyelim.
40
dTC
= MC → dTC = ( MC ) dQ
dQ
∫ dTC = ∫ ( MC ) dQ
TC = ∫ 2e
0.2 Q
→ TC = ∫ ( MC ) dQ
1
0.2 Q
dQ =
2(0.2)e dQ
∫
0.2
1 0.2Q
TC = 2
e
+ c = 10e 0.2Q + c
0.2
41
integral sabiti c ’nin değerini belirlemek için, toplam sabit
maliyetin 90 olduğu bilgisinden yararlanırız. Üretim miktarı
sıfırken
oluşan
toplam
maliyet
yalnızca
sabit
maliyettir.
Yukarıda bulduğumuz integralda Q yerine sıfır yazarak ve 90’a
eşitleyerek, c sabitini belirleriz.
TFC = 10e
0.2(0)
TC (Q ) = 10e
+ c = 90
0.2 Q
+ 80
→
c = 80
42
Marjinal
Tasarruf
Fonksiyonundan
Toplam
Tasarruf
Fonksiyonunun Belirlenmesi
Marjinal tasarruf fonksiyonunun aşağıda verildiği bir ekonomi
varsayalım. Gelir düzeyi (Y) 81 birimken, toplam tasarruf
düzeyi (S) sıfırdır. Buna göre bu ekonominin toplam tasarruf
fonksiyonu nedir?
MPS = 0.3 − 0.1Y
−1 2
dS
= MPS
dY
43
→
∫ dS = ∫ ( MPS ) dY
S = ∫ 0.3 − 0.1Y
−1/ 2
dS = ( MPS ) dY
→ S = ∫ ( MPS ) dY
dY
→ S = 0.3Y − 0.2Y
Y = 81 → S = 0
0 = 0.3(81) − 0.2(81)1/ 2 + c → c = −22.5
S = 0.3Y − 0.2Y
1/ 2
− 22.5
1/ 2
+c
44
Yatırım ve Sermaye Birikimi
dK ( t )
≡ I (t )
dt
→
∫ dK (t ) = ∫ I (t )dt
I ( t ) = 3t
1/ 2
ve
K ( t ) = ∫ 3t dt = 2t
1/ 2
K (0) = K 0 = c →
dK ( t ) = I ( t )dt
→
K ( t ) = ∫ I ( t )dt
t = 0 → K (0) = K 0
3/ 2
+c
K ( t ) = 2t
3/ 2
+ K0
45
Sermaye Stokunun Belirlenmesi
Net yatırım
I ( t ) = 3t 1/ 2
ise, dördüncü yılın sonundaki sermaye
oluşumu nedir?
t
K ( t ) = ∫ I ( t )dt
1
4
K ( t ) = ∫ 3t dt = ⎡⎣ 2t
1/ 2
1
3/ 2
4
⎤⎦ = 14
1
46
Sürekli Birikimdeki Bir Gelirin Bugünkü Değeri
Yıl başına D liralık sabit bir hızla y yıl süren ve yılda r nominal
oranında indirgenen sürekli bir hasılat akımının şimdiki değeri
nedir?
y
y
D
D − rt y
− rt
Π = ∫ De dt = − ∫ − re dt = − ⎡⎣ e ⎤⎦ 0
r 0
r
0
− rt
D
− ry
Π = (1 − e )
r
D = 3000 , r = 0.06 , y = 2 → Π ≅ 5655
47
Pareto Gelir Dağılımı
Pareto’nun gelir dağılımı tanımına göre, nüfusun N kadarının, x
gelirini ya da x’den daha yüksek geliri elde etmesi şöyle
tanımlanmıştır:
dN
−B
= − Ax
dx
Buna göre, a ile b gelir aralığındaki birey sayısını belirleyelim.
b
dN = − Ax − B dx →
N = ∫ − Ax − B dx
a
b
⎡
⎡
x ⎤
b1 − B ⎤ ⎡
a 1− B ⎤
N = ⎢− A
⎥ = ⎢− A
⎥ − ⎢− A
⎥
−
−
−
B
B
B
1
1
1
⎣
⎦a ⎣
⎦ ⎣
⎦
1− B
48
Tüketici Artığı
Tüketici
artığını
entegral
kesin
hesapları
bir
şekilde
kullanırız.
hesaplayabilmek
Örneğin
x
malının
için,
talep
fonksiyonunun ve piyasa fiyatının aşağıdaki gibi olduğunu
varsayalım.
P = a − bQ ,
P=P
∗
Q*
TA =
∫ ( a − bQ )dQ − P Q
*
*
0
Q*
* 2
⎡
bQ ⎤
b(
Q
)
* *
*
* *
= ⎢ aQ −
−P Q
⎥ − P Q = aQ −
2 ⎦0
2
⎣
2
49
Şekil 4.3. Tüketici Artığı
P
a
TA
P
∗
0
•
E
Q
∗
a
b
Q
50
P = 100 − 2Q
P * = 40
Q*
TA = ∫ ( 100 − 2Q)dQ − ( 40 ).( 30 )
P
100 z
0
30
⎡
2Q ⎤
= ⎢100Q −
⎥ − 1200
2 ⎦0
⎣
2
40 z
z
E
D
= ( 100 ).( 30 ) − ( 30 ) − 1200 = 900
2
0
30
z
50
Q
51
P = 100 − Q 2
P * = 36
8
TA = ∫ ( 100 − Q2 )dQ − ( 36 ).( 8 )
P
100z
0
3 8
⎡
Q ⎤
= ⎢100Q − ⎥ − 288
3 ⎦0
⎣
36 z
z
3
(8)
= ( 100 ).( 8 ) −
− 288 = 341.3
3
E
D
0
8
Q
52
Domar Büyüme Modeli
Domar
modeline
göre,
yatırımlar
ekonominin
hem
talep
(çarpan) hem de arz (hızlandıran) yanını etkiler. Çarpanı şöyle
yazabiliriz:
1
Y= I
s
Diğer
yandan
→
dY 1 dI
=
dt
s dt
yatırımlardaki
artış,
kapasite
etkisine
yol
açacaktır. κ yıllık potansiyel çıktı akımını, ρ kapasite-sermaye
oranını göstersin. Buna göre, ekonominin K(t) sermaye stoku
ile, bir yılda üretebileceği miktar:
κ ≡ ρK
Üretimin (arzın) zaman içindeki büyümesi:
53
dκ
dK
=ρ
= ρI
dt
dt
Domar modeline göre ekonominin dengeli bir gelişme süreci
sağlayabilmesi için, arz ve talep eşit olmalıdır.
d κ dY
=
dt
dt
Dolayısıyla modelin temel sorusu şudur: Ekonomide dengeli
gelişme sürecinin sağlanabilmesi için, yatırımlar zaman içinde
nasıl bir seyir izlemelidir?
54
Bu
soruya
demektir.
yanıt
Bunun
vermek
için,
ilk
I(t) fonksiyonunun belirlenmesi
olarak
süreç
içindeki
arz-talep
dengesinden yola çıkalım.
dY d κ
1 dI
1 dI
=
→
= ρI →
= ρs
dt
dt
s dt
I dt
1
∫ I dI = ∫ ρsdt → ln I + c1 = ρst + c2 → ln I = ρst + c
e
ln I
=e
( ρst + c )
→
c ρ st
I =e e
t = 0 iken I (0) = A
→
→ I > 0 için I = Ae
I ( t ) = I (0)e ρst
ρst
55
Şekil 4.3. Domar Büyüme Modelinde Optimal
Yatırım Süreci
I (t )
I ( t ) = I (0)e ρst
I (0)
0
t
56
Yatırımın fiili büyüme oranı (r) , gerekli büyüme oranından (ρs)
büyük ya da küçük olduğu durumlarda ne olacağına bakalım.
Bunun için kapasite kullanım oranını (u) tanımlayalım:
1 dI 1 dI
Y (t )
dY dt s dt
r
I
dt
u = lim
→ u = lim
=
=
=
t →∞ κ ( t )
t →∞ d κ dt
ρI
ρs
ρs
r>ρs ya da r<ρs olmasına bağlı olarak, bir kapasite eksikliği
(u>1) ya da fazlalığı (u<1) oluşur.
57
Fiili yatırım büyüme oranı oranı (r) , gerekli yatırım büyüme
oranından (ρs) büyük olursa, dY/dt>dκ/dt durumu ortaya çıkar,
yani yatırımın talep etkisi, kapasite etkisinden büyük olur,
ortaya bir talep fazlası çıkar. Tersi durumda ise, arz talebi aşar.
Bu durum, ekonomide bir bıçak sırtında denge sürecine neden
olmaktadır.