Çokgenler ve düzlemde kaplamalar

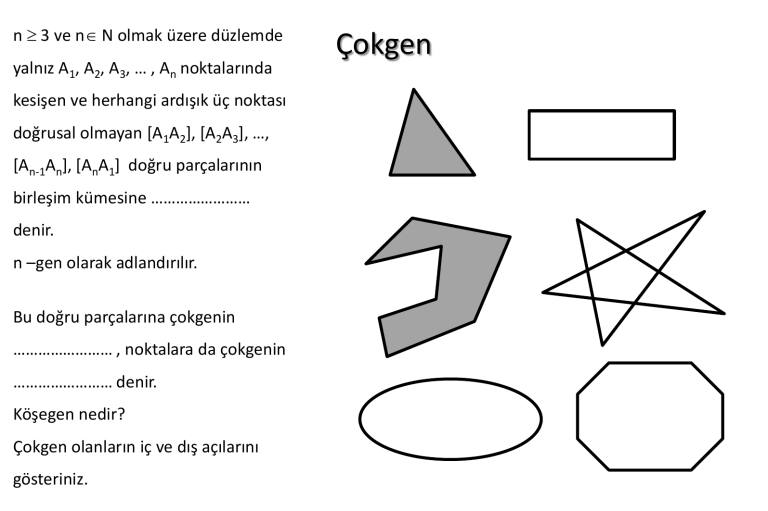
n  3 ve n N olmak üzere düzlemde
yalnız A1, A2, A3, … , An noktalarında
kesişen ve herhangi ardışık üç noktası
doğrusal olmayan [A1A2], [A2A3], …,
[An-1An], [AnA1] doğru parçalarının
birleşim kümesine ……………………
denir.
n –gen olarak adlandırılır.
Bu doğru parçalarına çokgenin
…………………… , noktalara da çokgenin
…………………… denir.
Köşegen nedir?
Çokgen olanların iç ve dış açılarını
gösteriniz.
Çokgen
Çokgensel bölge
Verilen şekillerin içi boş olması ile
dolu olması ne anlama gelir?
Kenarları kesik çizgilerle belirtilmiş
olması ne anlama gelir?
Çokgenler düzlemsel şekillerdir, bir
çokgen düzlemi üç parçaya ayırır;
İç bölge, dış bölge ve çokgen.
Çokgen ile iç bölgesinin oluşturduğu
noktalar kümesine, ……………………….
denir ve (ABCD…) gibi parantez içinde
yazılır.
İç bükey – Dış bükey şekiller
Verilen şekillerde sağ tarafta olanlarla,
sol tarafta olanlar arasında nasıl bir
fark var?
İç bölgede alınan herhangi iki noktayı
birleştiren doğru parçası, yine iç
bölgede kalıyor mu?
İç bölgede kalıyorsa …………………….,
kalmayan en az bir doğru parçası varsa
………………………… şekil denir.
Alıştırma 1
A
d
1) ABC  d = ?
K
2) (ABC)  d = ?
3) (ABC)  (AKLC) = ?
B
L
C
Alıştırma 2
Aşağıda verilen çokgenlerin isimlerini, açı ve kenarlar arasındaki ilişkileri söyleyiniz.
Aşağıdaki tabloyu doldurunuz.
Alıştırma 3
Aşağıdaki tabloyu doldurunuz.
Alıştırma 4
Proje etkinliği 1
Bir kağıdı herhangi bir üçgensel
bölge olacak biçimde kesiniz. İç
açılarına 1, 2, ve 3 yazınız.
1 ve 2 parçalarını koparıp 3.
parçanın yanına şekildeki gibi
ekleyiniz. Çıkan sonucu
tartışınız.
Koparmış olduğunuz 1 ve 2
numaralı parçaları yan yana
getirip 3. parçanın yanına
koyunuz. Çıkan sonucu tartışınız.
Proje etkinliği 2
Alıştırma 4’e göre bulduğunuz
sonuçları yazılı / sözlü ve sembol
kullanarak ifade ediniz.
Sonuç 1:
Sonuç 2:
Proje ödevi
El işi kağıtlarını kullanarak, kare, dikdörtgen, paralelkenar, dik yamuk, ikizkenar yamuk,
eşkenar dörtgensel bölgelerini çizip Alıştırma 4 te yapılan etkinliğe benzer etkinlikler yapınız.
1 – İç açılar toplamı
2 – Dış açılar toplamı
3 – İki iç açının ölçüleri toplamı diğer dış açının ölçüsüne(veya açıların ölçüleri
toplamına) eşittir.
Sonuçlarına ulaşarak bunları sembolik olarak elişi kağıtlarına yazınız.
Etkinlikte gösterdiğiniz sonucu kullanarak geçmiş yıllara ait birer üniversite sorusu
bulup çözümünü gösteriniz.
Ödev teslim süresi 2 haftadır.
Gelmeyen öğrenci numaraları :
Veriliş tarihi
Kontrol tarihi
Çokgenlerde açı özellikleri
1) n kenarlı bir çokgenin iç açılarının ölçüleri toplamı :
2) n kenarlı bir çokgenin dış açılarının ölçüleri toplamı :
3) n kenarlı bir çokgenin iki iç açısının ölçüleri toplamı, diğer köşelerdeki iç açıların
ölçüleri toplamına eşittir.
Alıştırma 1
ABC üçgeninin A köşesine ait
dış açısının ölçüsü kaç derecedir?
Alıştırma 2
a + b + c + d + e + f =?
Alıştırma 3
x =?
Alıştırma 4
x =?
Alıştırma 5
x =?
Alıştırma 6
x =?
Alıştırma 7
x=?
Alıştırma 8
m(BKC) = x = ?
m(BKA) = ?
m(AKC) = ?
m(KBI) = ?
m(KCI) = ?
m(BIC) = ?
Alıştırma 9
a + b = 200o
x=?
Alıştırma 10
a – c = 50o
x=?
Alıştırma 11
b – c = 40o
x =?
Alıştırma 12
a + c = 140o
x =?
İkizkenar üçgen
Eşkenar üçgen
Dik üçgen
DA  = DB= DC
BC  = 2AB
m(BAC)=?
m(C)=?
Paralelkenar
Eşkenar dörtgen
Dikdörtgen
Kare
Dik yamuk
İkizkenar yamuk
Düzgün beşgen
Düzgün altıgen
Ödev 1
Ödev 2
Ödev 3
Ödev 4
Ödev 5
Ödev 6
Ödev 7
EF=?
Ödev 8
Ödev 9
Eşkenar dörtgende
KL=?
Ödev 10
Ödev 11
Dikdörtgen
DE=?
Ödev 12
Ödev 13
Karenin çevresi ?
Ödev 14
Ödev 15
Ödev 16
Ödev 17
AB=?
Ödev 18
Ödev 19
Ödev 20
Ödev 21
Ödev 22
Çokgensel bölgelerin alanı
Kenar uzunluğu 1 birim olan karesel bölgeye birimkare denir.
1 br
1 br
Bir çokgenin sınırladığı bölgedeki birim kare sayısına o çokgensel
bölgenin …………………denir.
Birim karelerden oluşmuş yandaki
şekilde verilen çokgensel bölgelerin
B
A
J
I
alan ve çevrelerini bulunuz.
H
Alanı 9 birimkare olan bir çokgen
çiziniz ve çizdiğiniz çokgenin çevresini
bulunuz.
C
D
F
G
E
Karesel bölgenin alanı
Kenar uzunluğu a birim olan karenin alanını ve çevresini
bulunuz.
a br
Dikdörtgensel bölgenin alanı
Kenar uzunlukları a ve b birim olan dikdörtgenin alanını ve
b br
a br
çevresini bulunuz.
Diküçgensel bölgenin alanı
Dik kenar uzunlukları a ve b birim olan dik üçgenin alanını ve çevresini bulunuz.
b br
b br
a br
a br
b br
a br
Üçgensel bölgenin alanı
Tabanı a birim, yüksekliği h birim olan üçgenin alanını ve çevresini bulunuz.
A
h
B
A
h
C
H
B
a1
H a2
a
A
c
a
B
a
C
C
Dik yamuksal bölgenin alanı
Tabanları a ve c birim, yüksekliği h birim olan dik yamuğun alanını ve çevresini bulunuz.
c
c
S
h
S
h
a
a
c
h
a
S
S
a
c
h
İkizkenar yamuksal bölgenin alanı
Tabanları a ve c birim, yüksekliği h birim olan ikizkenar yamuğun alanını ve çevresini bulunuz.
c
c
h
h
a
a
Paralelkenarsal bölgenin alanı
Kenar uzunlukları a ve b olan paralelkenarın bu kenarlara ait yükseklikleri sırasıyla ha ve hb ise
paralelkenarın alanını ve çevresini bulunuz.
ha
a
b
a
b
Eşkenar dörtgensel bölgenin alanı
Kenar uzunluğu a ve yüksekliği h olan eşkenar dörtgenin alanını ve çevresini bulunuz.
a
h
Düzgün beşgensel bölgenin alanı
Kenar uzunluğu a olan düzgün beşgenin alanını ve çevresini bulunuz.
Düzgün altıgensel bölgenin alanı
Kenar uzunluğu a olan düzgün altıgenin alanını ve çevresini bulunuz.
Alıştırma 1
y
A(0, -2)
B(-5, 0)
C(-2, 0)
Alan(ABC) = ?
O
x
Alıştırma 2
y
A(1, 1)
B(3, 2)
C(4, 4)
Alan(ABC) = ?
O
x
Alıştırma 3
y
A(-4, -1)
B(-2, -3)
C(2, 0)
D(-1, 2)
Alan(ABCD) = ?
O
x
Alıştırma 4
y
C
O(0, 0)
A(2, -2)
B(5, 1)
B
OABC dikdörtgen
Alan(OABC) = ?
Çevre(OABC)=?
O
A
x
Ödev 1
Ödev 2
Ödev 3
Ödev 4
Ödev 5
Ödev 6
Ödev 7
Ödev 8
Ödev 9
Eşlik
I
IV
III
II
Eş üçgenler
y
A(0, 3)
B(2, 0)
C(4, 2)

y

D(0, -3)
E(-2, 0)
F(-4, -2)
z
A

C
x
E
O
x = 3,6 br
y = 4,1 br
z = 2,8 br
ABC ve DEF üçgenleri için1)
yandaki iki koşul
sağlanıyorsa bu iki üçgene
eş üçgenler denir.  ile
gösterilir.
2)
 = 59,0
 = 78,7 
 = 42,3 
A  ...
B  ...
C  ...
AB  .......
BC  .......
AC  .......
B
F
D
x
Eşlik teoremleri
KKK eşliği:
AKA eşliği:
KAK eşliği:
AAA ve KKA eşliği olabilir mi?
Alıştırma 1
Açıortay üzerindeki bir noktadan, açının kenarlarına inilen dikmelerin eşit uzunlukta
olduğunu gösteriniz.
Alıştırma 2
İkizkenar üçgende tabana ait kenarortayın yükseklik ve açıortay olduğunu gösteriniz.
Alıştırma 3
Paralelkenarın karşılıklı kenarlarının eşit uzunlukta olduğunu gösteriniz.
Alıştırma 4
Paralelkenarın köşegenlerinin birbirini ortaladığını gösteriniz.
Alıştırma 5
ABCD eşkenar dörtgeninin alanı
kaç birim karedir?
Alıştırma 6
ABCD ikizkenar yamuğunun
alanı kaç birim karedir?
Alıştırma 7 – Ödev
ABCD kare,
ABC eşkenar üçgen,
DF = AE
AE = DC
m(CKE) =?
m(AFB) =?
Alıştırma 8
AB // DE
AB = BE
x =?
Alıştırma 9
ABCD ikizkenar yamuğunun
alanı x ve y türünden kaç birim
karedir?
Alıştırma 10
ABC eşkenar üçgen
ADE eşkenar üçgen
m(CFD) =?
Benzerlik
Beyin uzunlukları değil, açıları baz alarak,
Şekillerin benzeyip benzemediğine karar veriyor…
Benzerlik oranı (k)
B
A
Karşılıklı elemanların neler
olabileceğini düşününüz.
Benzerlikte büyüme veya
küçülme oranı karşılıklı her
eleman için sabittir.
k  1 ise büyüme, k  1 ise
küçülme olur.
Üçgenlerin benzerliği
AA benzerliği:
KAK benzerliği:
KKK benzerliği:
Çevreler oranı:
Alanlar oranı:
Alıştırma 1
A
A
D
E
B
D
C
B
C
AD
AD
AB

AE
AC

DE
E
DB

AE
EC
BC
temel orantısını gösteriniz.
temel orantısını gösteriniz. Orta taban
olma şartını söyleyiniz.
Alıştırma 2
AE
3

EB
2
A
5
D
A
D
18
x + y =?
E
y
F
F
E
x
B
15
C
C
B
Artış miktarı
Alıştırma 3
Öklit bağıntılarını yazınız ve ispatlayınız.
Alıştırma 4
x =?
AB
AD
?
Alıştırma 5
x =?
Ödev 1
Ödev 2
Ödev 3
Ödev 4
Ödev 5
Ödev 6
Ödev 7
Ödev 8
Ödev 9
Ödev 10
Ödev 11
Ödev 12
Simetri
Noktaya göre simetri
.
Dönüşümler 1
Yansıma
Doğruya göre simetri
AA’ ….. d
AK ….. KA’
Dönüşümler 2
Öteleme
A noktasının u vektörüne göre ötelenmesi.
AA '  u
u
A’
A
Önemli olan A noktasının hangi yönde ve ne kadar kayacağıdır. Şekilde A noktası, u
vektörünün uzunluğu kadar ve u vektörü yönünde paralel olarak kaydırılmıştır.
Dönüşümler 3
Ötelemeli yansıma
Hızlı araba
Arabalı hız
u
Dönüşümler 4
Dönme


A noktası, O noktası etrafında  kadar döndürülürse A’ noktası elde edilir.
Dönme açısının pozitif yönlü olduğuna dikkat ediniz. O noktasına dönme merkezi denir.
Alıştırma 1
…………………..
…………………..
…………………..
…………………..
Alıştırma 2
Düzgün kaplama – Yarı düzgün kaplama
Yansıma, dönme, öteleme ve ötelemeli yansıma olmak üzere dört çeşit dönüşüm kullanılır.
Bir düzlemsel bölgenin, bir figür kullanılarak boşluk kalmayacak ve figürler çakışmayacak
şekilde dönüşümler yardımıyla örtülmesine, …………………………………………….. denir.
Bir düzlemsel bölgenin, birden fazla figür kullanılarak boşluk kalmayacak ve figürler
çakışmayacak şekilde dönüşümler yardımıyla örtülmesine, ……………………………………………..
denir.
Alıştırma 1 – Ödev 1
ABC eşkenar üçgeninde [CH] yüksekliktir.
AOH üçgeninin H noktasına göre simetriği
alınarak taralı olan bir figür alınıyor.
Taralı figür B noktası etrafında negatif yönde
(saat yönünde) 60o döndürülüyor. Oluşan
yeni figür de C noktası etrafında
döndürülüyor. Oluşan diğer figürleri
tarayınız ve yeni bir figür elde ediniz. Bu
figür ile aşağıdaki kaplamanın nasıl elde
edildiğini açıklayınız.
Alıştırma 2
“İçi boyalı bir eşkenar üçgen verilmiş olsun. Bu üçgenin kenar orta noktaları birleştirilerek
merkezde oluşan eşkenar üçgenin içi silinir. Boyalı kalan diğer üçgenler için aynı adımlar tekrar
ettirilir.”
Yukarıdaki örnekte verildiği gibi aynı işlemin sonsuza kadar tekrarı neticesinde meydana gelen
geometrik şekle ……………………………………… denir.
0. adım
1. adım
2. adım
Alıştırma 3 – Ödev 2
Kenar uzunluğu 8 birim olan bir
eşkenar üçgen çizerek 2.
Alıştırmada verilen fraktal
işlemini (ortadaki üçgeni silmek)
5. adıma kadar çiziniz.
(İzometrik noktalı kağıt
kullanarak)
Alıştırma 4 – Ödev 3
3. Alıştırmaya göre tabloyu doldurunuz.