Vektör Uzayları-2

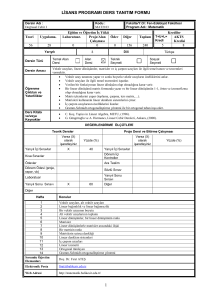
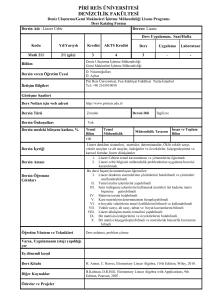
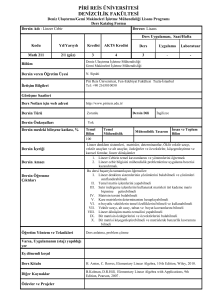
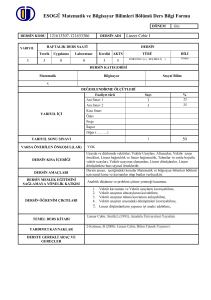
 Teorem 4.28 V bir F ‐ vektör uzayı ve A  v1 , v2 ,..., vn   V olsun. Eğer A kümesi lineer bağımsız ise A nın her alt kümesi de lineer bağımsızdır. Sonuç 4.29 V bir F ‐ vektör uzayı ve A  v1 , v2 ,..., vn   V olsun. Eğer A kümesi lineer bağımlı ise V nin A yı kapsayan her sonlu alt kümesi de lineer bağımlıdır. Önerme 4.30 Bir vektör uzayında sıfır vektörünü içeren her sonlu alt küme lineer bağımlıdır. Önerme 4.31 V bir F ‐ vektör uzayı ve v V  0V  olsun. Bu durumda, v kümesi lineer bağımsızdır, başka bir ifadeyle sıfır vektöründen farklı bir vektör tek başına lineer bağımsızdır. Teorem 4.32 V bir F ‐ vektör uzayı ve A  v1 , v2 ,..., vn   V olsun. A kümesinin F ‐ lineer bağımlı olabilmesi için gerekli ve yeterli koşul v1 , v2 ,..., vn vektörlerinden birisinin diğerlerinin bir F ‐ lineer birleşimi biçiminde yazılabilmesidir. Örnek 4.33 V   3 vektör uzayında A  1,1, 1 ,  2,3,1 ,  4,5, 1 kümesi  ‐ lineer bağımlıdır. Sonuç 4.34 V bir F ‐ vektör uzayı ve v, w  V olsun. v, w vektörlerinin F ‐ lineer bağımlı olması için gerekli ve yeterli koşul v   w veya w   v olacak biçimde   F elemanının bulunmasıdır(yani birinin diğerinin bir skaler katı olmasıdır) Örnek 4.35 Katsayıları reel sayı tüm tek değişkenli polinomların oluşturduğu küme [ x] olmak üzere, V : [ x] kümesi polinomların toplanması ve aşağıdaki gibi tanımlanan bir polinomla bir skalerin çarpılması işlemlerine göre  üzerinde bir vektör uzayı oluşturur: Her   , her f ( x )  a0  a1 x    an x n  [ x] için  a0 , a1 ,..., an     . f ( x) :  a0    a1  x     an  x n İspat. Ödev Bir vektör uzayında sonlu bir kümenin lineer bağımsızlığını ve lineer birleşimini tanımlamıştık. Şimdi de bu kavramları sonlu olması gerekmeyen kümeler için tanımlayalım: Tanım 4.36 V bir F ‐ vektör uzayı ve A  V olsun. Bu durumda A kümesinin bir sonlu alt kümesinin bir lineer birleşimine A nın bir F ‐ lineer birleşimi denir. Örnek 4.37 V  [ x] kümesinin  üzerinde oluşturduğu vektör uzayının A   x 2 k : k     x 2 , x 4 x 6 ,... alt kümesinin bir lineer birleşimi f ( x )  3 x 2  4 x 4  5 x10 dur. Tanım 4.38 V bir F ‐ vektör uzayı ve A, V nin sonsuz elemanlı bir alt kümesi olsun. Eğer A kümesinin her sonlu alt kümesi F ‐ lineer bağımsızsa A kümesi F ‐ lineer bağımsızdır denir. Aksi takdirde, yani A kümesinin F ‐ lineer bağımlı olan bir sonlu alt kümesi varsa A kümesine F  lineer bağımlıdır denir. Örnek 4.39 V  [ x] kümesinin  üzerinde oluşturduğu vektör uzayında A   x k : 0  k    1, x, x 2 , x3 ,... kümesi  ‐ lineer bağımsızdır. Teorem 4.40 V bir F ‐ vektör uzayı ve A  v1 , v2 ,..., vn   V olsun. Bu durumda A kümesinin tüm F ‐ lineer birleşimlerinden oluşan küme yani W : 1v1   2 v2     n vn : 1 , 2 ,..., n   kümesi V nin, A  v1 , v2 ,..., vn  kümesini kapsayan bir alt F ‐ vektör uzayıdır. Ayrıca A  U ve U , V nin bir alt vektör uzayı ise W  U dur. Başka bir ifadeyle W : 1v1   2 v2     n vn : 1 , 2 ,..., n   , V nin A kümesini kapsayan en küçük alt vektör uzayıdır. İspat. Tanım 4.41 Teorem 4.34 ün notasyonu geçerli olmak üzere, V nin 1v1   2 v2     n vn : 1 , 2 ,..., n   alt vektör uzayına v1 , v2 ,..., vn vektörlerinin (veya A  v1 , v2 ,..., vn  kümesinin) gerdiği (veya ürettiği) alt uzay denir ve bu alt uzay v1 , v2 ,..., vn veya Sp  v1 , v2 ,..., vn  ile gösterilir. Not 4.42 V bir F ‐ vektör uzayı ve A  v1 , v2 ,..., vn   V olsun. Bu durumda, v1 , v2 ,..., vn ile ilgili şunlar geçerlidir: i)
v1 , v2 ,..., vn , V nin bir alt vektör uzayıdır. ii)
A  v1 , v2 ,..., vn   v1 , v2 ,..., vn iii)
A  U ve U , V nin bir alt vektör uzayı ise v1 , v2 ,..., vn  U dur. Teorem 4.43 V bir F ‐ vektör uzayı ve A  v1 , v2 ,..., vn   V olsun. Eğer, vn  v1 ,..., vn 1 ise v1 ,..., vn 1  v1 ,..., vn 1 , vn Örnek 4.44 V   3 vektör uzayında A  1,0,0  ,  0,1,0  kümesinin gerdiği alt uzayı bulunuz. Örnek 4.45 V   3 vektör uzayında A  1,0,0  ,  0,1,0  ,  0,0,1 kümesinin gerdiği alt uzayı bulunuz. Çözüm. 1,0,0  ,  0,1,0  ,  0,0,1  a 1,0,0   b  0,1,0   c  0,0,1 : a, b, c     a, b, c  : a, b, c     3 dür yani A  1,0,0  ,  0,1,0  ,  0,0,1 kümesi  3 ü gerer. Örnek 4.46 V   2 uzayını geren bir küme bulunuz. Çözüm. Örnek 4.47 V  [ x] vektör uzayında A  1, x, x 2  kümesi hangi alt vektör uzayını gerer? Tanım 4.48 V bir F ‐ vektör uzayı ve B  V olsun. Eğer aşağıdaki iki koşul gerçeklenirse B kümesine V nin bir F ‐ tabanı denir. i)
ii)
V nin her elemanı B kümesinin bir F ‐ lineer birleşimi olarak yazılabilir. B kümesi F ‐ lineer bağımsızdır. Not 4.49 V bir F ‐ vektör uzayı ve B  v1 , v2 ,..., vn   V olsun. Bu durumda, yani B nin sonlu olması durumunda, taban olmanın koşulları aşağıdaki gibidir: i)
V  v1 , v2 ,..., vn dir yani B  v1 , v2 ,..., vn  kümesi V yi gerer. ii)
B  v1 , v2 ,..., vn  kümesi F ‐ lineer bağımsızdır. Örnek 4.50 B  1,0,0  ,  0,1,0  ,  0,0,1 kümesi V   3 vektör uzayının bir  ‐ tabanıdır. Uyarı 4.51 Bir vektör uzayının tabanı 1 den fazla olabilir. Mesela, B  1,0,0  , 1,1,0  , 1,1,1 kümesi de V   3 vektör uzayının bir  ‐ tabanıdır. Örnek 4.52 Her i  1,..., n için  n de i. bileşeni 1 diğer bileşenleri sıfır olan vektör ei olmak üzere, B  e1 ,..., en  kümesi V   n vektör uzayının bir  ‐ tabanıdır. Örnek 4.53 B   x k : 0  k    1, x, x 2 , x 3 ,... kümesi , V  [ x] vektör uzayının bir  ‐ tabanıdır.  1 0   0 1   0 0   0 0  
Örnek 4.54 B  
,
,
,
  kümesi , V  Mat  2,   vektör uzayının bir  ‐  0 0   0 0   1 0   0 1  
tabanıdır. Teorem 4.55 V bir F ‐ vektör uzayı ve B  v1 , v2 ,..., vn   V olsun. Bu durumda, B kümesinin V nin bir F ‐ tabanı olabilmesi için gerekli ve yeterli koşul her v V için v  1v1   2 v2     n vn
olacak biçimde tek türlü bir yazılışın var olmasıdır. Teorem 4.56 V bir F ‐ vektör uzayı ve B  v1 , v2 ,..., vm  kümesi V nin bir F ‐ tabanı olsun. m  n   olmak üzere, V nin n elemanlı her alt kümesi lineer bağımlıdır. İspat. w1 ,..., wn   V olsun. Amacımız bu kümenin lineer bağımlı olduğunu göstermektir. B  v1 , v2 ,..., vm  kümesi V nin bir F ‐ tabanı olduğundan V nin her elemanı B  v1 , v2 ,..., vm 
kümesinin F ‐ lineer birleşimi olarak yazılabilir. Özel olarak w1 ,..., wn elemanları da bu şekilde yazılabilir. O halde, w1  c11v1  c21v2    cm1vm
w2  c12 v1  c22 v2    cm 2 vm

wn  c1n v1  c2 n v2    cmn vm
olacak biçimde cij  F
 i  1,..., m;
j  1,..., n  elemanları vardır. n
1 , 2 ,..., n  F olmak üzere  i wi  1w1   2 w2     n wn toplamına bakalım: i 1
n
 w
i 1
i
i
 1  c11v1  c21v2    cm1vm    2  c12 v1  c22 v2    cm 2 vm      n  c1n v1  c2 n v2    cmn vm 
 1c11v1  1c21v2    1cm1vm    2 c12 v1   2 c22 v2     2 cm 2 vm      n c1n v1   n c2 n v2     n cmn vm   1c11   2 c12     n c1n  v1  1c21   2 c22     n c2 n  v2    1cm1   2 cm 2     n cmn  vm
dir. B  v1 , v2 ,..., vm  kümesinin lineer bağımsız olduğu da göz önüne alındığında n
 w   w   w
i 1
i
i
1
1
2
2
    n wn  0V olması için gerekli ve yeterli koşulun 1c11   2 c12     n c1n  0 F
1c21   2 c22     n c2 n  0 F 1cm1   2 cm 2     n cmn  0 F
olduğu anlaşılır. Bu ise 1 , 2 ,..., n   F n nin n bilinmeyen ve m denklemden oluşan c11 x1  c12 x2    c1n xn  0 F
c21 x1  c22 x2    c2 n xn  0 F

cm1 x1  cm 2 x1    cmn xn  0 F
lineer homojen denklem sisteminin bir çözümü olması anlamına gelir. Bu lineer denklem sisteminin katsayılar matrisinin rankı r olmak üzere r  m  n olduğundan sistemin  0 F ,...,0 F  dışında başka çözümleri de vardır. O halde w1 ,..., wn  kümesi lineer bağımlıdır. Sonuç 4.57. V bir F ‐ vektör uzayı ve B  v1 , v2 ,..., vm  kümesi V nin bir F ‐ tabanı olsun. Bu durumda, V nin lineer bağımsız bir alt kümesinin eleman sayısı en fazla m olabilir. Sonuç 4.58 V bir F ‐ vektör uzayı ve B  v1 , v2 ,..., vm  kümesi V nin bir F ‐ tabanı olsun. Bu durumda, V nin her F ‐ tabanında tam m tane eleman vardır. Sonuç 4.59 V bir F ‐ vektör uzayı ve B kümesi V nin sosuz elemanlı bir F ‐ tabanı olsun. Bu durumda, V nin her F ‐ tabanında sonsuz sayıda eleman vardır. Tanım 4.60 V bir F ‐ vektör uzayı olsun. Eğer V nin her sonsuz elemanlı alt kümesi lineer bağımlı ise V ye bir sonlu boyutlu vektör uzayı denir. Örnek 4.61 V    x  vektör uzayı sonlu boyutlu değildir. Önerme 4.62 V bir F ‐ vektör uzayı ve A  v1 , v2 ,..., vn  , V nin bir lineer bağımsız alt kümesi ve vn 1 V olsun. Eğer vn 1  v1 , v2 ,..., vn ise v1 , v2 ,..., vn , vn 1 kümesi de lineer bağımsızdır. Teorem 4.63 V  0V  bir sonlu boyutlu F ‐ vektör uzayı olsun. Bu durumda, V nin en az bir F ‐ tabanı vardır ve bu taban zorunlu olarak sonlu elemanlıdır. İspat. V nin hiç F ‐ tabanının bulunmadığını varsayalım. Bu varsayım altında tümevarımla şu önermeyi ispat edelim: Her n pozitif tam sayısı için V nin n  s ( An ) koşuluna uyan bir An lineer bağımsız alt kümesi vardır. … Tanım 4.64 V bir F ‐ vektör uzayı ve B kümesi V nin bir F ‐ tabanı olsun. Bu durumda, B kümesinin eleman sayısına V nin F ‐ üzerindeki boyutu denir ve bu boyut boyFV (veya dim F V ) ile gösterilir. Sadece sıfır vektöründen oluşan vektör uzayının boyutu ise sıfır olarak tanımlanır. Örnek 4.65 boy  2  ?, boy  3  ?, boy  n  ?, boy Mat  2,    ?, boy Mat  n,    ?,
boy Mat  2,    ?, boy [ x]  ? Not 4.66. Boyut kavramı iyi tanımlıdır. Örnek 4.67 V  [ x] vektör uzayının W  a  bx  cx 2  alt vektör uzayı için boyW  ? Örnek 4.68 V   3 vektör uzayının W  1, 2,3 ,  2,1, 4  ,  4,5,10  alt vektör uzayı için boyW  ? Teorem 4.69 V bir F ‐ vektör uzayı ve A  v1 , v2 ,..., vn   V olsun. Eğer, V  v1 , v2 ,..., vn ise V nin A  v1 , v2 ,..., vn  tarafından kapsanan bir F ‐ tabanı vardır ve dolayısıyla boyF V  n dir. Teorem 4.70 V bir sonlu boyutlu F ‐ vektör uzayı ve A  v1 , v2 ,..., vn  , V nin bir lineer bağımsız alt kümesi olsun. Bu durumda, V nin A kümesini kapsayan bir F ‐ tabanı vardır. Teorem 4.71 Sonlu boyutlu bir vektör uzayının her alt vektör uzayı da sonlu boyutludur. Teorem 4.72 V bir F ‐ vektör uzayı ve W da V nin bir alt vektör uzayı olsun. Bu durumda, boyF W  boyFV dir. Başka bir ifadeyle alt vektör uzayının boyutu üst vektör uzayının boyutunu geçemez.