Öteleme

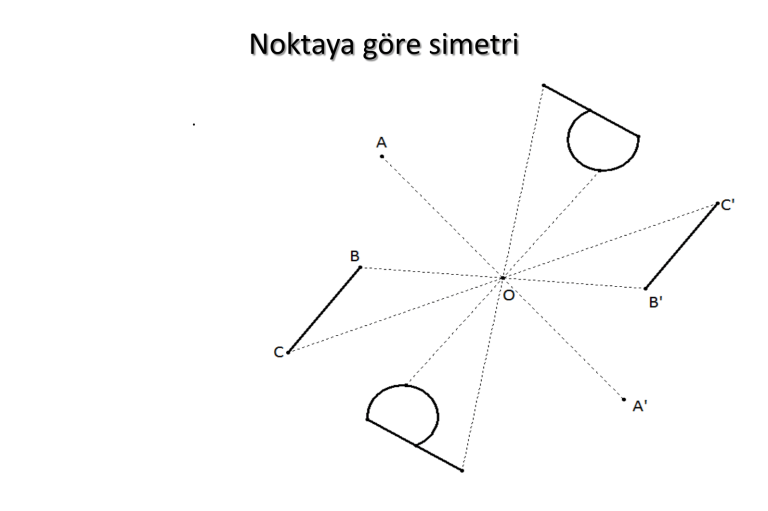
Noktaya göre simetri
.
Doğruya göre simetri
Yansıma
AA’ ….. d
AK ….. KA’
Öteleme
Öteleme
A noktasının u vektörüne göre ötelenmesi.
AA '  u
u
A’
A
Önemli olan A noktasının hangi yönde ve ne kadar kayacağıdır. Şekilde A noktası, u
vektörünün uzunluğu kadar ve u vektörü yönünde paralel olarak kaydırılmıştır.
Ötelemeli yansıma
u
Hızlı araba
Arabalı hız
Dönme
Dönme


A noktası, O noktası etrafında  kadar döndürülürse A’ noktası elde edilir.
Dönme açısının pozitif yönlü olduğuna dikkat ediniz. O noktasına dönme merkezi denir.
Alıştırma
…………………..
…………………..
…………………..
…………………..
Dönüşümler
Düzlemin noktalarını düzlemin noktalarına eşleyen bire bir ve örten fonksiyonlara düzlemin bir
dönüşümü denir.
Noktaya göre simetri, doğruya göre simetri (yansıma), öteleme ve dönme simetrileri birer
dönüşümdür. Bu ve bu dönüşümlerin bileşkelerinden oluşan dönüşümlerde uzaklık ve açı ölçüleri
değişmez.
Öteleme, dönme, yansıma veya bunların bileşke dönüşümlerine düzlemde izometri dönüşümleri
de denir. Bu dönüşümler altında bir şeklin görüntüsüne de bu şeklin simetriği (eşi) denir.
1) Öteleme dönüşümü
Bir P(x, y) noktası verilen u  (a,b) vektörü kadar ötelenirse P'(x',y') elde edilsin;
P'  u  P
(x',y')  (a,b)  (x,y)
P’
(x',y')  (a  x,b  y)
x'  a  x ve y'  b  y
u
P
Tu : R2  R2
Tu (P)  u  P
Tu (P)  P'
P'  u  P
biçiminde tanımlanan Tu fonksiyonu bir öteleme dönüşümüdür.
Çünkü düzlemin her P noktasını öteleyerek P' gibi bir nokta elde edilmesi mümkündür.
(Öteleme:Translation)
Alıştırma 1
Köşeleri A(-6, 3), B(-6, 1) ve C(-3, 3)
olan üçgen Ötelenerek A’B’C’ üçgeni
elde ediliyor. A’(3,5) olduğuna göre
y
A(-6, 3)
a) B’ ve C’ noktalarının koordinatlarını
bulunuz.
b) Öteleme vektörünü bulunuz.
c) Öteleme dönüşümünde elde edilen
üçgen ile ilk üçgeni kıyaslayınız.
ABC üçgeni
u(
,
)
C(-3, 3)
B(-6, 1)
x
O
A'B'C' üçgeni
A(-6,3)

A'(3,5)
B(-6,1)

B'(
,
)
C(-3,3)

C'(
,
)
A’(3, 5)
Alıştırma 2
d: x – 2y + 4 = 0 doğrusu (3, -2) vektörü kadar
ötelenirse elde edilen d’ doğrusunun
denklemini bulunuz ve analitik düzlemde
grafiklerini inceleyiniz.
y
d
(0,2)
P'  T(u) (P)  P  u
P'(x',y') , u  (3, 2) ve P(x,y) için
(x',y')  T(3,2) (x,y)  (x  y)  (3, 2)
(x',y')  (x  3,y  2)
d doğrusu
u  (3, 2)
d'
(-4,0)
x
P(x, y)
O
u
(3,0)
u  (3, 2)
d' doğrusu
(0,2)

(3,0)
(4,0)

(-1, -2)
(x,y)

(x',y')  (x  3, y  2)
x  2y  4  0

x' 2y' 4  0
 (x  3)  2(y  2)  4  0
 x  2y  3  0
P’(x’, y’)
Sonuç:
Öteleme dönüşümlerinde doğruların eğimleri
değişmez.
Ödev
d1: 2x -3y + 1 = 0 doğrusu (1,3) vektörü kadar ötelendiğinde d2 doğrusu elde ediliyor. d2
doğrusu da u vektörü kadar ötelendiğinde 2x -3y – 12 = 0 doğrusu elde edildiğine göre u
vektörünün koordinatlarını bulunuz.
2) Dönme dönüşümü
Bir P(x, y) noktasının orijin etrafında  kadar pozitif yönde döndürülmesiyle elde edilen nokta
P’(x’, y’) olsun;
P vektörünün e1 vektörüyle arasındaki açı  olsun,
P' vektörünün e1 vektörüyle arasındaki açı    ,
P vektörünün e2 vektörüyle arasındaki açı 90o  
P' vektörünün e2 vektörüyle arasındaki açı 90o  (  ) olur.
P  e1  P . e1  cos   x  P  cos 

P  e2  P . e2  cos(90o  )  y  P  sin 
P'  e1  P' . e1  cos(  )  x'  P  cos(  )  x'  x  cos   y  sin 
cos  cos sin  sin 
Dönme: Rotation
P'  e2  P' . e2  cos(90o  (  ))  y'  P  sin(  )  y'  x  sin   y  cos 
sin  cos sin  cos 
R  : R2  R 2
P'  R (P)
(x',y')  (x  cos   y  sin  ,x  sin   y  cos )
Alıştırma 1
ABC üçgeni orijin etrafında 90o
döndürüldüğünde A’B’C’ üçgeni elde
ediliyor.
a) A’, B’ ve C’ noktalarının
koordinatlarını bulunuz.
b) Dönme merkezini söyleyiniz.
c) Dönme dönüşümünde elde edilen
üçgen ile ilk üçgeni kıyaslayınız.
ABC üçgeni
R90o
A'B'C' üçgeni
A(3,1)

A'
B(6,1)

B'
C(3,5)

C'
P(x,y)

P'
Alıştırma 2
Analitik düzlemde verilen d doğrusu orijin etrafında
135o döndürüldüğünde d’ doğrusu elde edilmiştir.
a) doğruların denklemlerini yazınız.
b) Bu iki doğru arasındaki dar ve geniş açıların
ölçülerini söyleyiniz.
P(x, y)
d doğrusu
P(x,y)
x y
+ =1
3 5
R135o


d' doğrusu
P’(x’, y’)
P'(x',y')
x' y'
+ =1
3 5
d
d'
Ödev 1
d : y = x + 1 olmak üzere
d'  R60o (d)
d‘ : ?
d'
d
Ödev 2
Alıştırma 3
A(8, 8) noktası, B(6,5) noktası etrafında 60o
döndürüldüğünde elde edilen K noktasının
koordinatlarını bulunuz.
y
A'  T( 6,5) (A)
K'  R60o (A')
K  T(6,5) (K')
x
Simetriler
Öteleme veya dönme dönüşümlerinden de elde edilebilen diğer dönüşümlere özel dönüşümler
(simetri) denir.
İki çeşit simetri vardır.
1) Noktaya göre simetri
P'  TPM (P)  R180o (P)
P'  2M  P
2) Doğruya göre simetri (yansıma)
d: A noktasından geçen doğrultmanı u olan doğru
AH  H  A 
P'  2H  P
u
A
AP  u
 u,
u u
P'  2A  P  2 
H
AP  u
u
u u
Alıştırma 1
P(5, 1) noktasının, y=2x + 1 doğrusuna göre simetriğini bulunuz.
Çözüm:
d:A(0,1) ve u  (1,2)
Alıştırma 2
 4y  3x  4 4x  3y  2 
,
P(x, y) noktasının, y=2x + 1 doğrusuna göre simetriğini P’ ise P'  

5
5


olduğunu gösteriniz.
Çözüm:
d:A(0,1) ve u  (1,2)
Alıştırma 3
5x + 5y = 1 doğrusunun , y=2x + 1 doğrusuna göre simetriğini bulunuz.
Çözüm:
2. Alıştırmada y =2x+1 doğrusuna göre simetri kuralını bulmuştuk;
 4y  3x  4 4x  3y  2 
P(x,y) y  2x  1 P'  
,

5
5


Sık kullanılan simetriler
(x,y) (a,b)
y
(x,y) (0,0)
(x,y) x  0
(x,y) y  0
(x,y) x  a
(x,y) y  b
(x,y) y  x
(x,y) y  x
x
Alıştırma 1
Alıştırma 2 - Ödev
x2 +2y = 1 eğrisinin,
a) orijine göre simetriğini
b) x eksenine göre simetriğini
c) y eksenine göre simetriğini
d) 1. açıortay doğrusuna göre simetriğini
e) 2. açıortay doğrusuna göre simetriğini
f) x = 1 doğrusuna göre simetriğini
g) y = -3 doğrusuna göre simetriğini
h) (1, 2) noktasına göre simetriğini
i) y = x -1 doğrusuna göre simetriğini
bulunuz.
Ödev 1
a) P(x,y) y  x  1
b) P(x,y) y  x  1
c) P(x,y) y  x  1
d) P(x,y) y  x  1
Ödev 2
a) y = 3x + 6 doğrusunun K(-1, 3) noktasına göre simetriğini bulunuz.
b) y = 3x + 6 doğrusunun x + 3y – 5 = 0 doğrusuna göre simetriğini bulunuz.
Ödev 3
Ödev 4
Ödev 5
Ödev 6
Ödev 7
Ödev 8
Ödev 9
Ödev 10
Ödev 11
Ödev 12
Ödev 13
Ödev 13
Ödev 14
Ödev 15
Ödev 16
Ödev 17
Şerit süslemeler
Bir motifin belirli bir doğrultu boyunca ötelenmesiyle oluşan süslemelere şerit süslemeler denir.
Motifler
Motiflerle elde edilen şerit süslemeler
Öteleme
Yatay yansıma
Dikey yansıma
Ötelemeli yansıma
180o lik dönme
(yarı dönme)
Kaplamalar
Bir düzlemsel bölgenin, bir motif kullanılarak boşluk kalmayacak ve motifler çakışmayacak şekilde
dönüşümler (yansıma, dönme, öteleme, ötelemeli yansıma) yardımıyla örtülmesine düzgün
kaplama denir. Birden çok motif kullanılmışsa yarı düzgün kaplama denir.
Eş şekiller
Eş üçgenler
y
A(0, 3)
B(2, 0)
C(4, 2)

y

D(0, -3)
E(-2, 0)
F(-4, -2)
z
A

C
x
E
O
x = 3,6 br
y = 4,1 br
z = 2,8 br
 = 59,0
 = 78,7 
 = 42,3 
x
B
F
ABC ve DEF üçgenleri için yandaki iki koşul sağlanıyorsa bu iki üçgene eş
üçgenler denir.  ile gösterilir.
D
1) A  ...
B  ...
C  ...
2) AB  .......
BC  .......
AC  .......
Eşlik teoremleri
KKK eşliği:
AKA eşliği:
KAK eşliği:
AAA ve KKA eşliği olabilir mi?
Ödev 1
Açıortay üzerindeki bir noktadan, açının kenarlarına inilen dikmelerin eşit uzunlukta
olduğunu gösteriniz.
Ödev 2
İkizkenar üçgende tabana ait kenarortayın yükseklik ve açıortay olduğunu gösteriniz.
Ödev 3
Paralelkenarın karşılıklı kenarlarının eşit uzunlukta olduğunu gösteriniz.
Ödev 4
Paralelkenarın köşegenlerinin birbirini ortaladığını gösteriniz.
Ödev 5
ABCD eşkenar dörtgeninin alanı
kaç birim karedir?
Ödev 6
ABCD ikizkenar yamuğunun
alanı kaç birim karedir?
Ödev 7
ABCD kare,
ABC eşkenar üçgen,
DF = AE
AE = DC
m(CKE) =?
m(AFB) =?
Ödev 8
AB // DE
AB = BE
x =?
Ödev 9
ABCD ikizkenar yamuğunun
alanı x ve y türünden kaç birim
karedir?
Ödev 10
ABC eşkenar üçgen
ADE eşkenar üçgen
m(CFD) =?
Homoteti dönüşümü
P'M  k  MP
M sabit bir nokta ve k sabit bir reel sayı olmak üzere;
P'  M  k(P  M)
olacak biçimde P’ noktasına P nin M merkezli, k oranlı homotetiği denir.
H: R2  R2
P'  H(P)  M  k(P  M)
dönüşümüne M merkezli k oranlı homoteti dönüşümü denir.
M noktası ve k sayısı sabit kalmak üzere, değişen P noktalarının meydana getirdiği şekil ile
P’ noktalarının meydana getirdiği şekile homotetik şekiller (benzer şekiller) denir.
Alıştırma 1
M merkezli k = 3 oranlı homoteti verilmiştir.
MP'
3
MP
MA'
 ...
MA
MB'
 ...
MB
MC'
 ...
MC
A  ...
ABC üçgeni ile A’B’C’ üçgeni homotetik (benzer)dir.
Homoteti dönüşümünde açılar korunur,
şekildeki uzunluklar ise orantılıdır (yani
karşılıklı uzunluklar oranı sabittir, bu oran
homoteti oranına eşittir.)
B  ...
C  ...
A'B'
A'C'
B'C'
P'A'
 ....,
 ....,
 ...,
 ...
AB
AC
BC
PA
Alıştırma 2
M merkezli k1 = 2, ve k2 = 3 oranlı iki ardışık homoteti verilmiştir. Yani; |MA’|=2|MA|, |MA’’|=3|MA’|
ABC üçgeni ile A’B’C’ üçgeninin benzerlik oranı k1 = 2,
A’B’C’ üçgeni ile A’’B’’C’’ üçgeninin benzerlik oranı k2 = 3
ABC üçgeni ile A’’B’’C’’ üçgeninin benzerlik oranı ……………………dır.
Benzerlik
Beyin uzunlukları değil, açıları baz alarak,
Şekillerin benzeyip benzemediğine karar veriyor…
Üçgenlerin benzerliği
AA benzerliği:
KAK benzerliği:
KKK benzerliği:
Çevreler oranı:
Alanlar oranı:
Temel orantı
A
A
D
E
B
D
C
B
C
AD
AD
AB

AE
AC

DE
BC
E
DB

AE
EC
Alıştırma
A
A
3
3
D
9
E
D
2
B
2
x
C
B
12
E
x
C
Tales teoremleri
A
E
B
D
B
A
F
E
C
C
F
D
Alıştırma
AE
3

EB
2
A
5
D
A
D
18
x + y =?
E
y
F
F
E
x
B
15
C
C
B
Artış miktarı
Dik üçgende metrik bağıntılar
Öklit bağıntılarını yazınız ve ispatlayınız.
Alıştırma 4
x =?
AB
AD
?
Alıştırma 5
x =?
Ödev 1
Ödev 2
Ödev 3
Ödev 4
Ödev 5
Ödev 6
Ödev 7
Ödev 8
Ödev 9
Ödev 10
Ödev 11
Ödev 12
Ödev 12
Menelaus teoremi
1) A, B, C doğrusaldır
2) C, D, E doğrusaldır
3) E, F, B doğrusaldır
4) A, F, D doğrusaldır
Alıştırma
|AF| = |FD|
1
|ED| = 2|CD|
x
Alıştırma
|AF| = |FD|
2
|ED| = 2|CD|
1
x + y =?
x
y
Seva teoremi
Sonuç: |BD| = |DC|  FE // BC
Sonuç : ABC üçgeninin kenarortayları seva teoremi gereği tek noktada kesişir.
Alıştırma 1
G, (ABC) nin ağırlık merkezidir.
A(ABC) = 48
|GK|=3
|AK|=?
3
|GE|=?
A(GFK)=?
A(ADK)=?
Alıştırma 2
x =?
y =?
Fraktal
Uzunluğu 1 birim olan doğru parçası veriliyor. Bu doğru parçası 1/3 oranında
küçültülüp 120o saat yönünde döndürülüp dikey yansıması alınarak bir motif
oluşturuluyor.
Motifi oluşturan her doğru parçasına aynı kural uygulanarak aşağıdaki fraktal görüntü
elde ediliyor. Bu fraktala “Korş (Korch) eğrisi” denilir.
Alıştırma
Temel geometrik çizimler 1
1) Verilen bir doğru parçasına eşit uzunlukta bir doğru parçası çizmek
Temel geometrik çizimler 2
2) Verilen bir açıya eş açı çizmek
Temel geometrik çizimler 3
3) Verilen bir açının açıortayını çizmek
Temel geometrik çizimler 4
4) Verilen bir doğru parçasının orta dikme doğrusunu çizmek
Temel geometrik çizimler 5
5) Doğru üzerindeki bir noktadan dik çıkma
Temel geometrik çizimler 6
6) Bir noktadan bir doğruya dik inme
Temel geometrik çizimler 7
7) Verilen bir üçgenin iç teğet çemberini çizme
Temel geometrik çizimler 8
8) Verilen bir üçgenin istenilen kenarına teğet olan dış teğet çemberini çizme
Temel geometrik çizimler 9
9) Verilen bir üçgenin çevrel çemberini çizme
Alıştırma 1
a = 3 br
b = 5 br
c = 7 br
olan ABC üçgenini çiziniz.
Alıştırma 2
a = 3 br
b = 5 br
m(C) = 45o
olan ABC üçgenini çiziniz.
Alıştırma 3
a = 8 br
c = 7 br
m(C) = 60o
olan ABC üçgenlerini çiziniz.
Alıştırma 4
a = 8 br
c = 7 br
m(C) = 120o
olan ABC üçgenini çiziniz.