YER MANYETİK ALANI
Manyetik Moment (M)
Bir cismin Manyetik momenti veya manyetik dipol momenti bir manyetik
alan karşısında o cismin yöneliminin bir ölçüsüdür. Manyetik moment bir
vektör olup, cisim kendini manyetik alan doğrultusu na paralel gelecek
Mıknatıslanabilme
şekilde yönlendirmek ister.
özelliği
olan
her
cisim,
eşit
büyüklükte, biri (+) diğeri (-)
iki
kutbu
olduğundan,
mağnetik moment göz önüne
alınan
cismin
mağnetik
özelliğini
yansıtan
temel
fiziksel büyüklüktür. Aynı
mağnetik
momente
sahip
mıknatıslar birbirinden çok
farklı uzunluklarda olabilir. V
hacmindeki bir cismin net
mağnetik momenti;
Şekil (a) loop şeklindeki bir telin etrafında manyetik moment ve manyetik kuvvet çizgileri (b) V
hacmindeki bir cismin manyetik momenti, cisim içerisindeki herbir atom etrafındaki elektronun
meydana getirdiği manyetik momentlerin toplamıdır.
Mağnetik moment a) bir çift mağnetik kutup (Şekil 2.4) göz
önüne alınarak tanımlanabilir. +P ve –P şiddetinde kutuplara
sahip ve kutuplar arasındaki uzaklık
“L” olan bir çubuk
mıknatısı mağnetik momenti ; Mağnetik momentin birimi; Am2
(SI) ve M=LxP
Şekil Bir çift mağnetik kutuptan
meydana gelen mağnetik dipol. Mağnetik
moment (+) P kutbu ile kutuplar
arasındaki “L” uzaklığının çarpımıdır.
b) Bir elektrik akımının telin etrafında bir mağnetik alan
oluşturdu bilinmektedir. Eğer teli bir loop şeklinde r2 alanı
olacak şekilde bükürsek o zaman loop un oluşturduğu mağnetik
moment (Şekil 2.5).
M=r2i
Şekil 2.5. Bir elektrik akımının telin etrafında meydana
getirdiği manyetik alan sonucu loop’un taradığı alan ve elektrik
akımına bağlı olarak bir manyetik moment oluşmaktadır.
2.4. Mıknatıslanma Şiddeti
Mıknatıslanma özelliği olan bir malzeme dış alan içine
konulduğunda indiksiyon mıknatıslanma (etki ile mıknatıslanma)
adı
verilen
bir
mıknatıslanma
kazanır.
İndiksiyon
mıknatıslanmanın yönü dış alanın yönü ile aynıdır. Dış alanın
şiddeti, o malzemeye ait belirli bir alan şiddetine doğru
arttırıldıkça indiksiyon mıknatıslanmanın şiddeti de artar. Dış
alan, maddenin içinde var olduğunu düşünebileceğimiz yönlenme
bakımından farklı direnme gücüne sahip dipollerin kendi
yönünde dizilmelerini sağlar.
Mıknatıslanma şiddeti J vektörü ile gösterilir. J vektörünün
büyüklüğü,cismin birim hacim başına düşen mağnetik momentin
büyüklüğüdür.
Mıknatıslanma şiddeti (J)– birim hacim başına düşen manyetik
moment olup; J=Mtoplam/v
Manyetik Kutup
=1 dyn
İki manyetik monopol arasındaki kuvvet Coulomb kanunu ile tanımlanır.
r= iki yük arasındaki mesafe, k =sabit SI birim sisteminde = 1/40
Bir elektrik yük bir kynaktan bir elektrik alan üretir. Elektrik alan dışarı doğru
Radyal olarak yayılmaktadır. . E0 (örnekte pozitif diverjans vardır).
Manyetik akanlar zıt yönlü iki kutuptan oluştuğundan, bir manyetik kutuptan
Çıkan kuvvet çizgisi zıt yönlü diğer kutba geri gider. O yüzden artan veya azalan
Net akı yoktur. .H=0
Manyetik alan skaler alanın gradyanı yani manyetik potansiyelin gradyanı
olarak yazılabilir. Bu durum elektrik akımların veya manyetik kaynağın
Uzakta olması durumunda göz önüne alınabilir.
B=H durumunda; o zaman H =-V yazılabilir.
Normal şartlarda B ve birbiriyle yakın ilişki içerisindedir. Hem B hem H
manyetik alan için kullanılmaktadır. B indiksiyon H ise alanı
tanımlamaktadır. B ve H arasındaki ilişki ise;
ile verilmektedir. Μ manyetik geçirgenlik olup, SI
sistemde Henry/m ‘dir. μo =4π × 10-7H ⋅ m-1 dir. Eğer mıknatıslanan cismin
dışında bir bölge söz konusu ise o zaman M = 0 ve B = μoH’dir.
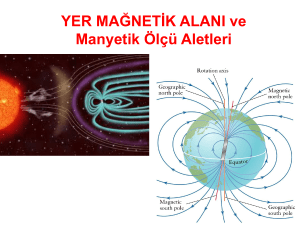
Yer Manyetik Alan
Manyetik alan bir vektördür (B).
Yerin gravite alanı zaman göre sabit olmasına karşın,
yermanyetik alanı hem doğrultu hem şiddetinde saniye veya
bin yıllık dönemlerde değişime uğrar.
Yer Manyetik Alan kuvvetinin birimi SI’de Tesla ‘dır
Yeryüzeyinde Doğrultusunu
ölçmek için eğim açısı ve
sapma açısı kullanılır. Manyetik
vektör üç ortogonal ksene
paralel kartezyen bileşenler
şeklinde ifade edilir.
Bv=BsinI
BH=BcosI
BN=BcosIcosD
BE=BcosIsinD
KÜÇÜK BİR ÇUBUK MIKNATISIN OLUŞTURDUĞU MANYETİK
ALAN
1. Bir Mıknatısın Mağnetik Ekseni Üzerinde Bir Noktada Oluşturduğu Alan (1. Gauss
Durumu).
Boyu 2l ve kutup şiddeti P olan bir çubuk mıknatısın mağnetik ekseni izerinde ve (d >> 1)
olmak üzere, d uzaklığında bir A noktasında oluşturduğu alanı bulmak için; önce, K kutbunun
A noktasında oluşturduğu alan için
HK=
ve G kutbunun A noktasında oluşturduğu alan için de
HG=
P
(d l ) 2
P
(d l ) 2
Bağıntıları yazılır. Buradan A noktasında oluşan toplam alan için;
H=
P
P
2
(d l )
(d l ) 2
H=
4 Pdl
(d l 2 ) 2
2
Bağıntısına ulaşılır. d >> 1 olduğundan l4 , d4 e göre ihmal edilebileceğinden
H=
2M
d3
Böylece 2l boyundaki çubuk mıknatısın d uzaklığında bir A noktasında oluşturduğu alan
ifadesine ulaşılır.
2. Bir Mıknatısın Orta Yerinde Mağnetik Eksene Dik Doğrultuda Bir Noktada Oluşturduğu
Alan (II. Gauss Durumu)
Boyu 2l ve kutup şiddeti P olan bir çubuk mıknatısın mağnetik eksenine dik doğrultuda ve
merkezinden d uzaklığındaki bir A noktasında oluşturduğu alan için,
H A 2l
HK
r
HA=
2 Pl
r3
Yazılabilir. Ayrıca HK=P/r olduğundan
Bağıntısına ulaşılır. Buradan
r2=d2+l2 ve
M=2Pl olduğundan
HA=
M
(l 2 d 2 )3
2
Bağıntısı elde edilir. d2 >> 12 olduğundan, bir çubuk mıknatısın eksenine dik doğrultuda ve
merkezinden d uzaklığında bir A noktasında oluşturduğu mağnetik alan
HA=
M
elde edilir.
d3
3. Bir Mıknatısın Orta Yerinde, Eksenle Açısı Yapan Herhangi Bir Doğrultu Üzerinde Bir
Noktada Oluşturduğu Mağnetik Alan
Boyu 2l olan bir çubuk mıknatısın mağnetik ekseni ile açısı yapan bir doğrultuda ve
mıknatısın O orta noktasından d kadar uzakta bir A noktasında oluşturduğu H A alanı bulmak
için önce M1 ve bu doğrultuya dik doğrultudaki izdüşümünü de M2 ile gösterirsek bu
durumda,
M1=M cos
M2=Msin
Yazılabilir. M1 momentli mıknatısın A noktasında
oluşturduğu mağnetik alan I. Gauss durumuna göre
H1=
2M 1
d3
ve M2 momentli mıknatısın A noktasında oluşturduğu mağnetik alan II. Gauss durumuna göre,
H2=
M2
d3
M1 ve M2 momentlerini M momenti cinsinden yazarsak;
H1=
2M cos
M sin
ve H2=
bağıntılarına ulaşılır. 2l boyundaki bir çubuk mıknatısın
3
d
d3
ekseniyle açısı yapan bir doğrultu üzerinde ve d uzaklığında bir A noktasında oluşturduğu
toplam alan;
HA2=H12+ H22 olduğundan
HA=
M
4 cos 2 sin 2 bağıntısı elde edilir. Alanın doğrultusu ise,
3
d
tan=
H2 1
= tan bağıntısı ile belirlenir.
H1 2
Yer Manyetik Alanı
Manyetik alan bir vektördür (B).
Yerin gravite alanı zaman göre sabit olmasına karşın, yermanyetik alanı hem
doğrultu hem şiddetinde saniye veya bin yıllık dönemlerde değişime uğrar.
Yer Manyetik Alan kuvvetinin birimi SI’de Tesla ‘dır
Yeryüzeyinde Doğrultusunu ölçmek için eğim açısı ve sapma açısı kullanılır. Manyetik vektör
üç ortogonal eksene paralel kartezyen bileşenler şeklinde ifade edilir.
Bv=BsinI
BH=BcosI BN=BcosIcosD
BE=BcosIsinD
Veya küresel koordinatlarda enlem, boylam ve yarıçapa bağlı olarak ifade edilebilir. Küresel
koordinatlarda Kartezyen koordinatlara ait x,y,z bileşenleri hesaplanabilir.