integral

İNTEGRAL
İNTEGRAL HESABI-ALAN HESABI
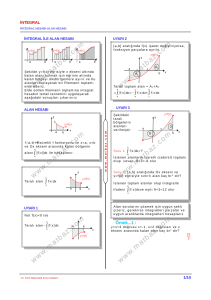
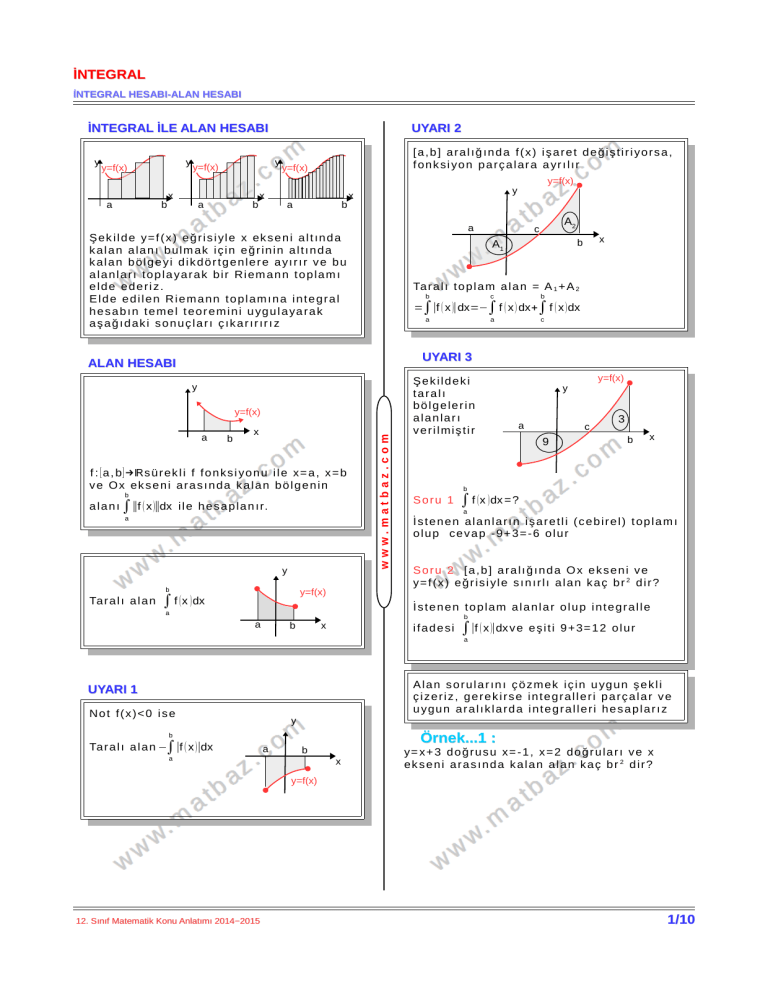
İNTEGRAL İLE ALAN HESABI
y
y
y=f(x)
b
a
y
y=f(x)
x
UYARI 2
b
a
x
[ a , b ] a r a l ığ ın d a f ( x ) i ş a r e t d e ğ i ş t i r i yo r s a ,
f on k s i yo n p a r ç a l a r a a yr ı l ı r
y=f(x)
b
a
a
Ş ek i l d e y= f ( x ) e ğ r i s i yl e x ek s e n i a l t ı n d a
k a l a n a l a n ı b u l m ak i ç i n e ğ r i n i n a l t ı n d a
k a l a n b ö l g e yi d i k d ö r t g e n l e r e a yı r ı r v e b u
a l a n l a r ı t o p l a ya r a k b i r R i em a n n t o p l am ı
e l d e e d e r i z.
E l d e e d i l e n R i e m a n n t o p l am ı n a i n t e g r a l
h e s a b ı n t e m e l t e o r e m i n i u yg u l a ya r ak
a ş a ğ ı d ak i s o n u ç l a r ı ç ı k a r ı r ı r ı z
A2
c
x
b
A1
Ta r a l ı t o p l a m a l a n = A 1 + A 2
b
c
b
=∫|f ( x )|dx=−∫ f ( x ) dx+∫ f ( x ) dx
a
a
c
UYARI 3
ALAN HESABI
y
a
b
x
f : [ a , b ] →ℝs ü r ek l i f f o n k s i yo n u i l e x = a , x = b
v e O x ek s e n i a r a s ı n d a k a l a n b ö l g e n i n
b
a l a n ı ∫||f ( x )||dx i l e h e s a p l a n ı r.
a
y
b
y=f(x)
∫ f (x )dx
www.matbaz.com
y=f(x)
Ta r a l ı a l a n
y=f(x)
y
x
Şekildeki
taralı
bölgelerin
alanları
verilmiştir
y=f(x)
y
a
c
9
3
b
x
b
Soru 1
∫ f (x )dx = ?
a
İstenen alanların işaretli (cebirel) toplamı
o l u p c e v a p - 9+ 3 = - 6 o l u r
Soru 2 [a,b] aralığında Ox ekseni ve
y= f ( x ) e ğ r i s i yl e s ın ı r l ı a l a n k a ç b r 2 d i r ?
İ s t e n e n t o p l am a l a n l a r o l u p i n t e g r a l l e
a
a
b
x
b
ifadesi
∫∣f ( x )∣dx v e
e ş i t i 9 + 3= 1 2 o l u r
a
A l a n s o r u l a r ın ı ç ö zm ek i ç i n u yg u n ş e k l i
ç i ze r i z , g e r e k i r s e i n t e g r a l l e r i p a r ç a l a r v e
u yg u n a r a l ık l a r d a i n t e g r a l l e r i h e s a p l a r ı z
UYARI 1
N o t f ( x )< 0 i s e
y
Örnek...1 :
b
Ta r a l ı a l a n −∫∣f ( x )∣dx
a
a
b
x
y= x + 3 d o ğ r u s u x = - 1 , x = 2 d o ğ r u l a r ı v e x
ek s e n i a r a s ın d a k a l a n a l a n k a ç b r 2 d i r ?
y=f(x)
12. Sınıf Matematik Konu Anlatımı 2014−2015
1/10
İNTEGRAL
İNTEGRAL HESABI-ALAN HESABI
Örnek...2 :
Örnek...6 :
y = x2 parabolü, y =0 ve x =2 doğrularının
sınırladığı kapalı bölgenin alanı kaç br 2 ?
G r af i ğ i v e r i l e n
y= f ( x ) f o nk s i yo n u
y=f(x)
y
2
için
∫ x.f ( x2 +3) dx = ?
0
4
6
2
3
x
5
Örnek...3 :
2
y=3− x e ğ r i s i i l e o x e k s e n i a r a s ı n d a k a l a n
3
k ap a l ı b ö l g e n i n a l a n ı k aç b r 2 d i r ?
Örnek...7 :
Örnek...4 :
www.matbaz.com
y = 9x - x2 eğrisi x = - 1 ve x=1 doğruları ve
o x ek s e n i a r a s ın d a k a l a n b ö l g e n i n a l a n ı k a ç
b r 2 d i r.
y
Ş e k i l d e k i y= f ( x )
y=f(x)
p a r a b o l ü v e x ek s e n i
arasında kalan taralı
a l a n k a ç b i r im k a r e d i r ?
-1
1
x
-1
Örnek...8 :
8
v e x = 5 d o ğ r u s u v e x ek s e n i
x
a r a s ı n d a k al a n a l a n ı h e s a p l a yın ı z
y= x ² , y=
Örnek...5 :
Ş e k i l d e k i t e p e n ok t a s ı A
o l a n y= f ( x ) p a r a b o l ü i l e
x ekseni arasında kalan
a l a n k a ç b i r im k a r e d i r ?
y
4
A(2,4)
x
2
y=f(x)
12. Sınıf Matematik Konu Anlatımı 2014−2015
7
2/10
İNTEGRAL
İNTEGRAL HESABI-ALAN HESABI
DEĞERLENDİRME 1
1) y=x+1 doğrusu x=0, x=3 doğruları ve x ekseni
arasında kalan alan kaç br2 dir?
y=f(x)
5) Grafiği
verilen y=f(x)
fonksiyonu için
2
∫ x.f ' (x ) dx
y
4
9
2
3
7
x
8
0
2) Şekildeki y=f(x) parabolü ve x ekseni
arasında kalan alan kaç
y=f(x)
birim karedir?
y
8
x
-2
6) y=x²-2x parabolü x=1 ve x=5 doğruları ve x
ekseni arasında kalan alanı hesaplayınız.
y
3) Şekildeki tepe noktası
T(r,6) olan y=f(x)
parabolü ile x=2 ve x=4
ve x ekseni arasında
kalan alan kaç birim
karedir?
y=f(x)
7
T
2
x
4
7) y= 5 , x=e ve x=e19 doğruları ve x ekseni
x
arasında kalan alanı hesaplayınız
4) y = 4 - x2 eğrisi x = 1 ve x=3 doğruları ve Ox
ekseni arasında kalan bölgenin alanı kaç br2
dir
12. Sınıf Matematik Konu Anlatımı 2014−2015
3/10
İNTEGRAL
İNTEGRAL HESABI-ALAN HESABI
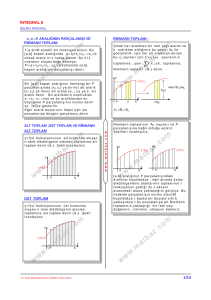
İKİ EĞRİ ARASINDA KALAN ALAN
y
Örnek...9 :
y = x 2 e ğ r i s i i l e y = x + 1 2 d o ğ r u s u a r a s ın d a
k a l a n k ap a l ı b ö l g e n i n a l a n ı k aç b r 2 d i r ?
y
y=g(x)
y=f(x)
y=g(x)
y=f(x)
A
x
a
xx
a
b
b
İ k i e ğ r i a r a s ı a l a n b u l u n u r k e n g r af i k l e r
a r a s ı n d ak i a l a n yi n e d ik d ö r t g e n l e r e
b ö l ü n e r ek a l a n R i em a n n t o p l am ı n a
d ö n ü ş t ü r ü l ü r.
y
K
y=g(x)
Örnek...10 :
y=f(x)
x
L
a
y = x2 -14 ve y = 4- x2 parabolleri arasında
k a l a n k ap a l ı b ö l g e n i n a l a n ı k aç b r 2 d i r
b
Genel olarak eğriler arasındaki alanı
b u lm a k i ç i n g r a f i k l e r ç i zi l d ik t e n s o n r a O y
ek s e n i n e p a r a l e l K L ş e r i d i ç i zi l i r. B u
ş e r i d i k e n d i s i n e p a r a l e l o l a r ak k a yd ı r a r ak
b ö l g e yi t a r a d ı ğ ı m ı z d a ü s t v e h e p y = f ( x )
eğrisi üzerinde alt ucu da hep g(x) eğrisi
ü ze r i n d e d e ğ i ş m e s i g e r ek i r. Ş ek l i
i n c e l e yi n i z
b
B u d u r um d a a l a n A =
∫∣f ( x )−g (x )∣dxo l u r.
a
A k s i t ak d i r d e i n t e g r a l i p a r ç a l a m ak g e r ek i r
y
y=g(x)
K
a
L
c
Örnek...11 :
y= x 2 v e y= x 4 e ğ r i l e r i a r a s ın d a k a l a n a l a n ı
bulunuz.
x
b
y=f(x)
Ta r a l ı a l a n l a r t o p l a m ı
b
c
b
∫∣f ( x )−g (x )∣dx=∫ ( f ( x )−g (x ) )dx +∫ ( g( x )−f ( x ) )dx
a
a
12. Sınıf Matematik Konu Anlatımı 2014−2015
c
4/10
İNTEGRAL
İNTEGRAL HESABI-ALAN HESABI
Örnek...12 :
Örnek...14 :
y= x 3 v e b u e ğ r i ye x = 1 d e ç i zi l e n t e ğ e t i
arasında kalan bölgenin alanını
4
∫ √ 16−x2 dx
i n t e g r a l i n i h e s a p l a yı n ı z.
0
√2
Örnek...15 :
2
Örnek...13 :
∫ ( √ 1−x 2−x ) dx
0
y= √ x v e y= x - 2 d o ğ r u s u v e x ek s e n i
a r a s ı n d a k a l a n a l a n ı b u l u n u z.
Örnek...16 :
Ş ek i l d ek i m er k e zc i l d a i r e n i n n
ç a p ı 1 2 b i r i m d i r. t a r a l ı a l a n ı
integralle ifade ediniz
y
x
Hatırlatma
S t a n d a r t ç e m b e r d e n k l em i n i k u l l a n a r ak
a ş a ğ ı d ak i b a ğ ı n t ı l a r ı e l d e e d e r i z
y
y
y=√ r 2−x 2
x=−√ r − y
2
2
x
x
y
y
x=√ r − y
2
x
2
x
y=−√ r −x
2
2
12. Sınıf Matematik Konu Anlatımı 2014−2015
5/10
İNTEGRAL
İNTEGRAL HESABI-ALAN HESABI
X=F(Y) VE Y EKSENİYLE SINIRLANDIRILMIŞ
ALANLAR
Örnek...1 :
y
b
Ta r a l ı a l a n =
x = f ( y) f o n k s i yo n l a r ı p a r a b o l d e nk l em l e r i n i
ya z ı n ı z
x=f(y)
y
Y EKSENİNDE ALAN HESABI
x=f(y)
a
a
U YA R I 1
N o t x = f ( y) < 0 i s e
x
x=f(y)
A(3,18)
x
1)
b
∫ f ( y ) dy
y
b
b
t a r a l ı a l a n = - ∫ f ( y ) dy
x
a
a
UYARI 2
y
y
x
-4
2)
[ a , b ] a r a l ığ ın d a f ( y) i ş a r e t d e ğ i ş t i r i yo r s a ,
f on k s i yo n p a r ç a l a r a a yr ı l ı r
x=f(y)
2
-2
b
x
Ta r a l ı t o p l a m a l a n
b
c
b
a
a
c
= ∫|f ( y )|dy=∫ f ( y ) dy−∫ f ( y ) dy c
3)
x=f(y)
x=f(y)
a
y
3
27 x
İKİ EĞRİ ARASINDA KALAN ALAN
-3
y
x=g(y)
b
taralı alan
∫|g ( y )−f ( y )|dy
b
a
c
∫ ( f ( y )−g ( y )) dy+∫ (g ( y )−f ( y ) )dy
x=f(y)
y
4)
b
a
x
c
L
K
x
T(2,-7)
c
a
x=f(y)
5)
UYARI
y
x=f(y)
2
A(5,1)
y= f ( x ) e ğ r i s i v e r i l i p y e k s e n i i l e s ın ır l ı
b ö l g e n i n a l a n ı s o r u l d u ğ u n d a s ık l ık l a
v e r i l e n f o nk s i yo n u n t e r s i yl e i ş l e m
ya p a r ı z.
x
12. Sınıf Matematik Konu Anlatımı 2014−2015
6/10
İNTEGRAL
İNTEGRAL HESABI-ALAN HESABI
Örnek...2 :
Örnek...4 :
Ve r i l e n p a r a b o l l e r v e y e k s e n i yl e
sınırlandırılmış taralı alanları bulunuz
y = lnx eğrisi, y = 1 ve y = 3 doğruları ve oy
ek s e n i a r a s ın d a k a l a n k a p a l ı b ö l g e n i n a l a n ı
kaç br2 dir?
y
A(1,3)
2
1)
x
x=f(y)
Örnek...5 :
y
Grafiği verilen y=f(x) fonksiyonuna göre
−2
2
∫ f ( x ) dx +∫ f −1 (x ) dx kaçtır?
−3
y
1
y=f(x)
2
1
A(4,32)
x
2)
-3
-2
x=f(y)
-2
Örnek...6 :
x=f(y)
3)
y
1
4
x
G r a f i ğ i v e r i l e n y= 2 x v e y= 8 / x
f on k s i yo n l a r ı v e y ek s e n i
a r a s ın d a k a l a n t a r a l ı
8
b ö l g e n i n a l a n ı k aç b i r i m
k ar e d i r ?
y
y=2x
y=8/x
x
-1
Örnek...3 :
y= e x e ğ r i s i y= 1 , y= e v e y e k s e n i a r a s ı n d a
k al a n a l a n k a ç b i r im k a r e d i r ?
12. Sınıf Matematik Konu Anlatımı 2014−2015
Örnek...7 :
Ş ek i l d ek i m er k e zc i l d a i r e n i n n
çapı 14 birimse taralı alanı
integralle ifade ediniz
y
x
7/10
İNTEGRAL
İNTEGRAL HESABI-ALAN HESABI
DEĞERLENDİRME 2
1) y=x2 vey=2x+8 doğrusu arasında kalan alanı
bulunuz.
2
5)
∫ √ 4−x 2 dx=?
−2
6) y=ex fonksiyonu y=e ile y
ekseni arasında kalan taralı
bölgenin alanı kaç birim
karedir?
y
y=ex
e
x
2) y=x2 vey=4x-x2 arasında kalan alanı bulunuz.
3) y=x3 vey=x4 arasında kalan alanı bulunuz.
7) x = -y2 +6 parabolü ile x = y doğrusu
tarafından sınırlanan kapalı bölgenin alanı kaç
br2 dir?
y
4) f(x)=x2 ve g(x)=(x-2)2 ile x ekseni arasında
sınırlı bölgenin alanı kaç br2 dir.
12. Sınıf Matematik Konu Anlatımı 2014−2015
8) Şekilde doğru ile merkezcil
daire arasındaki taralı
bölgenin alanını integralle
-4
ifade ediniz
2
x
8/10
İNTEGRAL
İNTEGRAL HESABI-ALAN HESABI
9)
y=
27
ve y=x2 eğrileri ve y=10 doğrusu
x
arasında sınırlı bölgenin alanı kaç birim
karedir?
12)
√ x+ √ y=1 bağıntısıyla birinci
bölgede sınırlı bölgenin alanı
kaç birim karedir?
y
√ x+ √ y=1
x
10) y=-x²+x+6 ile y=x+2 doğrusu arasında kalan
alanı bulunuz.
y
13) Şekilde y=f(x)
fonksiyonunun türevinin
grafiği verilmiştir. f(0)=3
ise f(3) kaçtır?
1
1
-1
3
x
y=fı(x)
11) y=x3 fonksiyonu x=1 noktasındaki normali ve
x=0 doğrusu ile sınırlandırılmış bölgenin alanı
kaç birim karedir?
12. Sınıf Matematik Konu Anlatımı 2014−2015
14) f ( x )= √ x−2 , g ( x )=x2 +2 fonkiyonları ve x=18 ile
y=18 doğruları ve eksenler arasında kalan
bölgenin alanı kaç birim karedir?
9/10
İNTEGRAL
İNTEGRAL HESABI-ALAN HESABI
y
15) Şekilde y=f(x)
fonksiyonunun grafiği
verilmiştir. Buna göre
7
∫∣f ' ( x )∣dx kaçtır?
18) x=y 2−4 ile y=3 doğrusu ve y ekseni ile
düzlemin 1. bölgelsinde sınırlandırılmış
bölgenin alanı kaç birim karedir?
y=f(x)
4
5
-2
7
x
−2
y
19)
16) x=y2 parabolü ile x = 0 ve y = 2 doğruları
arasında kalan bölgenin alanı kaç br2 dir?
Şekilde merkezi orjin olan dörtte
bir çember yayı veriliyor. Doğru ile
daire arasında kalan taralı bölgenin
alanını integralle ifade ediniz
-1
x
-2
17) y = ex eğrisi ile y = 6 doğrusu ve oy ekseni
arasında kalan kapalı bölgenin alanı kaç br2
dir?
12. Sınıf Matematik Konu Anlatımı 2014−2015
20) Şekildeki merkezcil elips
ve doğru ile sınırlandırılmış
bölgeyi integralle ifade
ediniz.
y
x
-4
-2
-3
10/
10/10