Hemen indir (188 KB.)

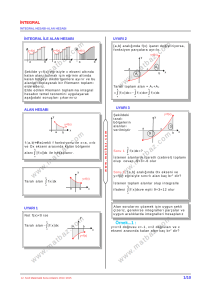
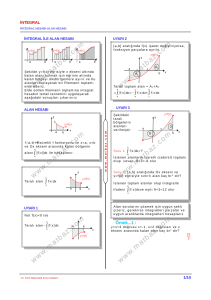
slayt6
Teorem: f:[a,b]  R , g:[a,b]  R fonksiyonları [a,b] aralığında
integrallenebilir iki fonksiyon olsun. c  [a,b] ve k  R olmak
üzere:
b
c
b
a
a
c
1. f(x).dx   f(x).dx   f(x).dx tir.
b
b
a
a
2. k.f(x).dx  k. f(x).dx tir.
b
b
b
a
a
c
3. f(x)  g(x) .dx   f(x).dx   g(x).dx tir.
slayt7
Örnek:
a-)
2

x .dx
-1
b-)
3
 x.sgn(x
 2).dx
-1
c-)
4

2
9  x 2 .dx
slayt8
Çözüm:
a-)
2
0
1
2
1
1
0
1
0
2
1
1
 x .dx   x .dx   x .dx   x .dx  x |  x |  1  1  0 bulunur.
b-)
3
2
3
x2 2 x2 3
1 x.sgn(x - 2).dx  1 x.dx  2 x.dx   2 |1 2 2|  1 bulunur.
c-)
4
3
4
8 64
2 9 - x .dx  2 (9 - x ).dx  3 (9 - x ).dx  27  9 18  3  3  36  9  27  6 bulunur.
2
2
2
Alan Hesabı
Dönel Cisimlerin Hacimleri
slayt1
Alan Hesabı
Eğrilerle sınırlı düzlemsel bölgelerin alan hesabını
yaparken, aşağıdaki teoremi kullanacağız.
Teorem: f:[a,b]  R , f(x) fonksiyonu pozitif ve
integrallenebilen bir fonksiyon olsun. y=f(x) eğrisi, x=a , x=b ve
y=0 doğruları tarafından sınırlanan bölgenin alanı,
b
S   f(x).dx
a
slayt2
1.Sonuç: y=f(x) fonksiyonu [a,b] aralığında negatif değer
alıyorsa,
b
S    f(x).dx
a
slayt3
2.Sonuç: f:[a,b] R ,y=f(x) fonksiyonu, aralığın bir parçasında
negatif değerli, bir parçasında pozitif değerli ise,
d
S   | f(x) | .dx
a
slayt4
Örnek1: f(x)=3x2+6x eğrisi ve Ox ekseni arasında kalan kapalı
bölgenin alanını hesaplayalım.
slayt5
Çözüm1:
Şekilden görülebileceği gibi, f(x)=3x2 +6x=0
denkleminin kökleri 3x(x+2)=0  x1=-2 ve x2=0 dır. Kökler
arasında f(x)<0 olduğundan; aranan alan;
0
0
0
S    f(x).dx    (3x  6x).dx  -(x  3x ) |
2
-2
3
2
-2
2
S  (x  3x ) |  (2) 2  3.(2) 2  (03  3.02 )
3
2
0
S  8  12  0  4 birimkare bulunur.
2
Slayt6
Örnek2: Aşağıdaki grafik, f(x)=lnx fonksiyonuna aittir. Buna
göre, taralı alanlar toplamı S ise, S değeri nedir?
Slayt7
Çözüm2:
Fonksiyon [1/e,1] arasında negatif, [1,e2] arasında pozitif
değerler aldığı dikkate alınırsa, aranan alan;
1
e2
1
e2
1
e
1
1
e
1
S    f(x).dx   f(x).dx    lnx.dx   lnx.dx
2
1
e
1
e
1
1
e
e2
1
1
S  (x.lnx  x) |  (x.lnx  x) |  (x.lnx  x) |  (x.lnx  x) |
1 1 1
S   ln    (0  1)  (e 2 lne 2  e 2 )  (ln1  1)
e e e
2
2 2
e3  2e  2
2
2
S    1  2e  e  1    e  2  S 
birimkare bulunur.
e
e
e
Slayt8
3.Sonuç: f:[a,b]R
fonksiyon olsun.
,
g:[a,b]R
integranellenebilen
iki
Slayt9
b
S1 
 f(x).dx
b
, S2 
 g(x).dx
a
a
Bu durumda, iki eğri arasında kalan taralı alan;
b
b
b
a
a
a
S  S1  S2   f(x).dx   g(x).dx   (f(x)  g(x)).dx bulunur.
Slayt10
4.Sonuç:
x2
x3
x1
x2
S  S1  S2   (f(x) - g(x)).dx   (g(x) - f(x)).dx
slayt11
Örnek1: f(x)=sinx ve g(x)=cosx fonksiyonları veriliyor:
a. İki fonksiyonun grafikleri arasında kalan ve x=0 , x=/6
doğruları ile sınırlı bölgenin alanını bulunuz.
b. İki eğri arasındaki kapalı bölgelerinden birisinin alanını
hesaplayınız.
slayt12
Çözüm1:
a. f(x)=sinx , g(x)=cos(x) fonksiyonlarının grafikleri şekildeki
görülmektedir.
x[0,/6] aralığında cosx>sinx olduğundan;
S 
π
6
 (cosx  sinx).dx
π
6
 (sinx  cosx) |
0
0
π
π
1
3

S   sin
 cos   (sin0  cos0  
 0 1
6
6
2
2

S
3 1
2
birimkare bulunur.
slayt13
b. f(x) = g(x)  sinx = cosx  cos (/2-x) = cosx  x1= /4 ,
x2= 5/4 .
O halde, f(x)=sinx , g(x)=cosx eğrileri arasındaki sınırlı
bölgelerden birinin alanı,
S 
5π
4
 (sinx
 cosx).dx  (-cosx  sinx)
π
4
5π
4
|
π
4
5π
5π  
π
π

S   - cos
- sin
- sin
   - cos

4
4
4
4

 

S
2

2
S 2

2



2

2 birimkare
2

2
2
2
bulunur.




slayt14
Teorem: g:[c,d]  R , x=g(y) fonksiyonu [c,d] aralığında pozitif
ve integrallenebilen bir fonksiyon olsun.
x=g(y) eğrisi, y=c , y=d ve x=0 doğruları tarafından
sınırlanan bölgenin alanı,
d
S   g(y).dy dir.
c
slayt15
Örnek: Aşağıdaki şekilde, x = y2+1 eğrisinin x=1 ile x=5
aralığındaki parçası çizilmiştir. Buna göre, taralı alan kaç br2
dir?
Çözüm:
Önce integralin sınırlarını
bulalım.
x=1 için, 1=y2+1 y=0
x=5 için, 5=y2+1 y0
olduğundan, y=2 bulunur.
2
2
y3
A   (y  1).dy 
y|
3
0
0
2
14
A
br 2 bulunur.
3
slayt16
5.Sonuç: x=g(y) fonksiyonu [c,d] aralığında negatif değerler
alan integrallenebilen bir fonksiyon olsun. Bu durumda; x=g(y)
eğrisi, y=c , y=d , ve x=0 doğruları ile sınırlı bölgenin alanı;
d
S    g(y).dy dir.
c
slayt17
Örnek: Aşağıdaki şekilde görülen parabolün denklemi , x=y22y dir. Taralı bölgenin alanının kaç birim kare olduğunu bulalım.
Çözüm:
y2-2y=0  y1=0  y2=2 bulunur.
Buna göre taralı alan;
2
2
0
0
A    (y 2  2y).dy   (2y  y 2 ).dy
3 2
y
A  y2 
|
3 0
4
A
br 2 bulunur.
3
slayt18
6.Sonuç: Eğer x=g(y) fonksiyonu [c,d] aralığında hem negatif
hem de pozitif değerler alıyorsa, x=g(y) eğrisi, y=c , y=d ve x=0
doğruları ile sınırlı bölgenin alanı,
e
d
d
c
c
c
S  S1  S2    g(y).dy   g(y).dy   | g(y) | .dy
slayt19
Örnek: Aşağıdaki şekilde görülen eğrinin denklemi ,
x= -y.(y+1).(y-2) dir. Buna göre,taralı alanların toplamı kaç
birim karedir?
Çözüm:
x= -y.(y+1).(y-2)=0
 y1=-1 , y2=0 ,
y3=2 bulunur. Verilen
bağıntı denkleminde;
-1<y<0 için, f(y)>0
olduğundan aranan
alanlar toplamı;
slayt20
0
2
0
2
A    f(y).dy   f(y).dy    (-y  y  2y).dy   (-y3  y 2  2y).dy
3
-1
0
-1
2
0
0
2
 y 4 y3
 y 4 y3
5 8 37
2
2
A  

 y  |   

 y  | 
 
birimkare bulunur.
3
3
 4
 1  4
 0 12 3 12
7.Sonuç: x=g(y) , x=f(y)
eğrileri arasında kalan
y=c , y=d doğruları ile
sınırlı alan;
d
S
 | f(y) - g(y) | .dy
c
slayt21
Örnek: x=y2 parabolü ile x+y=6 doğrusu arasında kalan sınırlı
bölgenin alanını bulunuz.
Çözüm:
y2=6-y  y2+y-6=0
 y1 =-3  y2 =2 bulunur.
2
A
-3
A


2
3 2
y
y
(6  y )  y 2 .dy  6 y 

|
2
3 -3
125
br 2 bulunur.
6
slayt22
Dönel Cisimlerin Hacimleri
Teorem: y=f(x) fonksiyonu [a,b] aralığında integrallenebilen bir
fonksiyon olmak üzere, y=f(x) eğrisi etrafında, x=a , x=b ve Ox
ekseni etrafında 360o döndürülmesi ile oluşan dönel cismin
hacmi;
b
b
V  π. y 2 .dx  π. f(x)  .dx tir.
2
a
a
slayt23
1.Sonuç: [a,b] aralığında integrallenebilen iki fonksiyon, y=f(x)
ve y=g(x)olsun. x[a,b] için f(x)g(x)0 ise; y=f(x) ve y=f(x)
eğrileri, x=a ve x=b doğruları arasında kalan bölgenin Ox ekseni
etrafında 360o döndürülmesiyle oluşan dönel cismin hacmi;
b


V  π. f 2 (x) - g 2 (x) .dx tir.
a
Örnek: f(x)=x2 eğrisi, x=0 , x=2 doğruları ve Ox ekseni
etrafından sınırlanan kapalı bölgenin Ox ekseni etrafında 360o
döndürülmesiyle oluşan dönel cismin hacmini bulunuz.
slayt24
Çözüm:
Elde edilen cisim, yukarıdaki şekilde görülmektedir.
2
2
1 5 2 32π 3
V  π. (x ) .dx  π. x .dx  π. x | 
br olur.
5 0
5
0
0
2 2
4
slayt25
2.Sonuç: x=f(y) fonksiyonunun eğrisi, y=c , y=d doğruları ve
Oy ekseni ile sınırlanan düzlemsel bölgenin Oy etrafında 360o
döndürülmesiyle oluşan dönel cismin hacmi;
d
V  π. x 2 .dy dir.
c
slayt26
3.Sonuç: y[c,d] için f(y)g(y)0 ise; x=f(y) ve x=g(y)
eğrileri ile y=a ve y=b doğruları arasında kalan bölgenin y
ekseni etrafında 360o döndürülmesiyle oluşan yeni cismin
hacmi;
d


V  π. f 2 (y)  g 2 (y) .dy dir.
c
slayt27
Örnek1: y=x2 parabolü, x=0 , y=2 doğruları arasında kalan
bölgenin Oy ekseni etrafında 360o döndürülmesiyle elde edilen
dönel cismin hacmini bulunuz.
Çözüm1:
y=x2  x=y (x0= dır. Oluşan cismin hacmi;
2
2
y2 2
V  π. ( y ) .dy  π. y.dy  π.
|  2π br 3olur.
2 0
0
0
2
slayt28
Örnek2: x=y2 eğrisi ve y=x2 eğrisi arasında kalan düzlemsel
bölgenin Oy ekseni etrafında 360o döndürülmesiyle elde edilen
dönel cismin hacmini bulunuz.
slayt29
Çözüm2:
y=x2  y=(y2)2  y=y4  y-y4 =0  y=0 ve y=1 bulunur.
O halde, oluşan dönel cismin hacmi; y[0,1] da y=x2
parabolünün oluşturduğu hacimden, x=y2 parabolünün
oluşturduğu hacim çıkartılarak bulunur.


 y 2 y5  1
1 1


V  π. ( y ) - (y ) .dy  π. (y - y ).dy  π.

|  π.  

5 0
 2 5
 2
0
0
3π 3
V
br bulunur.
10
1
2
2 2
1
4
slayt30
Örnek3: x+y=1 eğrisinin koordinat eksenleri arasında kalan
bölgenin, Ox ekseni etrafında 360o döndürülmesiyle elde edilen
dönel cismin hacmini bulunuz.
slayt31
Çözüm3:
y=1-x  y=1-2x+x dir. Eğri, eksenleri x=1 ve y=1 de keser.
1
1
0
0
V  π. (1 - 2 x  x).dx  π. (1  4x  x 2  4 x  2x  4 x ).dx
3
1
3
5 1




1
8
8
2
2
3
2
2 
2
2 


V  π. 1  6x  x  4x  4x .dx  π. x  3x  x  x  x  |
3
3
5 0


0
1 8 8 π

V  π.1  3     
br 3 bulunur.
3 3 5  15

1
Bitir