= = »10

BÖLÜM 3:
NÜKLEONLAR ARASI KUVVET- NÜKLEER KUVVET
Atomdaki elektronların hareketini kontrol eden kuvvetler elektromanyetik kuvvettir.
Elektromanyetik kuvvet atomları ve molekülleri bir arada tutar.
Çekirdekteki kuvvetler şunlardır:
1- Elektriksel kuvvetler (Coulomb kuvveti). Uzun menzilli, 1/r2 ile orantılı kuvvetlerdir.
Çekirdekte bu kuvvetler sadece protonlar arasında mevcuttur (nötronlar yüksüzdür). İtici
kuvvetlerdir. Bu kuvvetler çekirdeğin kararlılığını kesinlikle açıklamazlar. Bağlanma enerjisini
azaltmaya katkıda bulunurlar.
2- Nükleer kuvvetler: Çekirdeği bir arada tutan kuvvetlerdir, tüm nükleon tipleri arasında
çekici bir kuvvettir. Çok kuvvetlidir, nükleonlar birbirine değer değmez etkili olur.
Bir atomda elektronları yörüngede tutan kuvvet negatif elektronlarla pozitif çekirdek arasındaki
bildiğimiz elektrostatik çekim kuvvetidir. Ancak çekirdek içinde nükleonları bir arada tutan
kuvvet elektrostatik çekim kuvveti değildir. Nötronlar yüksüz olduğundan elektrostatik kuvveti
görmezler. Protonlar da pozitif yüklü olduğundan elektrostatik kuvvet çekici değil iticidir.
Yüklü ya da yüksüz tüm maddelere etkiyen kütle çekim kuvveti (gravitational force) daima
çekici olduğundan nükleonların kütle çekim kuvveti ile bağlandığı düşünülebilir. Basit bir
hesaplama ile kütle çekim kuvvetinin çok küçük ve yetersiz olduğu gösterilebilir.
Felek 
Elektrostatik itme kuvveti
FG 
Kütle çekim kuvveti
Fkütleçekimi
Felek
=
Gmp2
k e2
=
k q2
r2
G mp2
r2
G evrensel çekim sabiti
(6,67x10  11Nm2kg 2 )(1,67x10
 27
(9x109 Nm2C 2)(1,6x10 19 C) 2
kg) 2
»10 36
Buradan kütle çekim kuvvetinin elektrostatik kuvveti yenemeyecek kadar zayıf olduğu yani
çekirdeği bir arada tutamayacağı anlaşılır. Kararlı çekirdekler mevcut olduğundan, Bu durumda
çekirdek içinde başka bir çekici kuvvetin var olduğu anlaşılmaktadır.
1
Böylece çekirdeği bir arada tutan yeni bir kuvvet tanımlamamız gerekir, çekirdek kuvveti (veya
nükleer kuvvet). Bu kuvvetli (güçlü, strong) nükleer kuvvet çok küçük bir nükleer hacimde bir
arada bulunan nötronlar ve protonları bir arada tutacak ve protonlar arasındaki itme kuvvetinin
yenecek kadar güçlü bir kuvvet olmalıdır. Başka bir deyişle yükten bağımsız kuvvetli bir çekici
kuvvet olmalıdır. Bu nedenle çekirdek kuvvetine kuvvetli (strong) etkileşme denir. Nükleer
kuvvet kısa menzillidir, 10-15 m veya daha kısa menzillerde etkilidir. Çünkü bu etki nükleer
“yüzeyin” çok ötesine uzanmayacaktır. Bu etkileşme tüm nükleonlar arasındadır, p-p; p-n; n-n.
Çekirdeği bir arada tutan çekici bir kuvvet olmasına rağmen, nükleonlar birbirlerine 0,5fm
civarında yaklaştıklarında bu kuvvet itici bir kuvvet olur. Nükleonlar temel olarak birbirlerine
daha yakın olamazlar. Yukawa bu kuvvetli etkileşmeyi, karşılıklı bir yer değiştirme kuvveti
olarak modellemiştir. Burada karşılıklı yer değiştirme parçacıkları pionlar ve diğer ağır
parçacıklardır. Dört temel kuvvetin en kuvvetlisidir. Nükleonun yük ve spin durumuna bağlıdır.
Termonükleer reaksiyonlarda örneğin güneşin çekirdeğinde gerçekleşen reaksiyonlarda
önemlidir.
Kararlı atomlarda çekirdek içinde çekici ve itici kuvvetler dengede olur. Eğer bu kuvvetler
dengede değilse, atom kararlı olamaz ve çekirdek daha kararlı bir duruma ulaşmak için
radyasyon yayınlar.
Kuvvetli etkileşmeyi biraz daha ayrıntılı inceleyelim. Proton ve nötronlar kuarklardan
oluşmuştur ve kuarklar arasında karşılıklı olarak yer değiştiren gluonlar tarafından oluşturulan
kuvvetli (strong) bir nükleer kuvvet ile bir arada tutulurlar. Glonlar hem renk hem anti renk
taşırlar. Kuark ve antikuark çiftleri ise mezonları oluşturur. Çok sayıda nükleona sahip olan
çekirdekte etkin kuvvetli kuvvetler mesonların karşılıklı yer değiştirmesi ile açıklanabilir.
Nükleonların kuarklardan oluştuğunun bilinmesine karşın henüz deneysel olarak tek bir kuark
ve antikuark izole edilememiştir.
Günümüzde standart model her bir nükleonun 3 tane kuarktan oluştuğunu ve nükleer
kuvvetlerin kuarklar arasındaki etkileşmelerin bir sonucu olduğunu ileri sürmektedir. Proton
pozitif yüklü olduğundan iki tane +2/3 yüklü yukarı kuark (up) ve -1/3 yüklü aşağı (down)
kuarktan oluşmuştur (uud). Nötron ise bir adet +2/3 yüklü yukarı kuark ile iki adet -1/3 yüklü
aşağı kuarktan (udd) oluşan yüksüz bir parçacıktır.
2
Zayıf etkileşme ise çekirdek veya daha küçük mertebede önemlidir. Bir nötronun elektron ve
anti nötriono salarak bir protona dönüştüğü beta bozunumundan sorumludur. Antinötrino ve
madde arasındaki zayıf etkileşme o kadar zayıftır ki, antinötrino kilometrelerce kalınlıktaki bir
kurşun duvardan kolaylıklar geçebilir. Dolayısıyla büyük bir patlamayla bir süpernova
oluştuğunda, enerjisinin çoğu zayıf etkileşme yolu ile açığa çıkar. Yani zayıf kuvvetler yıldız
patlamalarında önemli bir rol oynar.
İki nükleon arasındaki kuvveti incelemek için deneysel hiçbir sonuca değinmeden, nükleonnükleon kuvvetinin bazı özelliklerini önceden tahmin edebiliriz:
1. Bu kuvvet kısa uzaklıklarda, Coulomb kuvvetinden daha güçlüdür. Nükleer kuvvet
çekirdekteki proonların Coulomb itmesinden çok daha fazla güçlü olabilir. (protonların
birbirlerini itmeleri sistemi dağıtmaya yetmiyor.)
2. Nükleer kuvvet uzun mesafelerde, atomik boyut mertebesinde, ihmal edilebilir derecede
zayıfıtr. Bir molekülde çekirdekler arasındaki etkileşmeler ancak Coulomb kuvvetine
dayanarak anlaşılabilir. Yani kısa menzillidir. (Nükleonlar sadece en yakın
komşularıyla etkileşirler.)
3. Bazı parçacıklar nükleer kuvvetten etkilenmezler; örneğin atomik yapıda elektronların
nükleer kuvvetten etkilendiklerini gösteren hiçbir kanıt yoktur.
Nükleer kuvvetin özelliklerini özel olarak incelemek için deneyler yapmaya başlarken
başka birçok önemli özellikleri buluruz:
4. Nükleon-nükleon kuvveti nükleonların proton veya nötron olup olmamasından hemen
hemen bağımsız gibi görünür. Bu özelliğe yük bağımsızlığı denir.
5. Nükleon-nükleon kuvveti nükleonların spinlerinin paralel veya antiparalel olup
olmamalarına bağlıdır. Yani spin bağımlıdır.
6. Nükleon-nükleon kuvveti, nükleonları belli bir ortalama uzaklıkta tutan itici bir terim
içerir. (Bunun dışında çekicidir.)
7. Nükleon-nükleon kuvvetinin merkezi olmayan veya tensör bir bileşeni vardır. Kuvvetin
bu bileşeni, merkezi kuvvetlerde bir hareket sabiti olan yörüngesel açısal momentumu
korumaz.
8. Yük
simetrilidir.
7
7
3𝐿𝑖4 , 4𝐵𝑒3
(Ayna
simetrisine
sahip
iki
çekirdek
incelendiğinde,
ç𝑒𝑘𝑖𝑟𝑑𝑒𝑘𝑙𝑒𝑟𝑖𝑛𝑒 bakılırsa bunların birbirlerine çok yakın sistemler olduğu
görülür.)
3
3.1. DÖTERON
Bir döteron ( 2He çekirdeği ) bir nötron ve bir protondan ibarettir. ( bir nötr 2He atomuna
döteryum denir. ) Döteron, nükleonların en basit bağlı halidir ve bu yüzden nükleon-nükleon
etkileşmesini incelemek için ideal bir system oluşturur. Atom fizikçileri için hidrojen atomu
neyse çekirdek fizikçileri içinde döteron odur. Hidrojenin uyarılmış durumları arasındaki
elektromanyetik geçişlerin ölçülen Balmer serilerinin hidrojenin yapısını anlamayı sağladığı
gibi, döteronun uyarılmış durumları arasındaki elektromanyetik geçişlerde onun yapısını
anlamayı sağlamalıdır. Ancak, ne yazık ki, döteronun hiçbir uyarılmış durumu yoktur. Döteron
öyle zayıf bağlı bir sistemdir ki yalnız “uyarılmış durumlar” serbest bir proton ve serbest bir
nötrondan ibaret olan bağlı olmayan sistemlerdir.
Bağlanma Enerjisi
Döteronun bağlanma enerjisi çok hassas ölçülmüş bir niceliktir ve üç farklı yolla belirlenebilir.
Döteronun kütlesini spektroskopiyle doğrudan belirleyebilir ve buradan bağlanma enerjisi
hesaplanabilir:
Döteryum atomunun kütlesi M(2,1)=2.014102u olarak bulunmuştur. Döteronun bağlanma
enerjisi,
𝐵𝐸( 21𝐻 ) = [𝑚(1𝐻 ) + 𝑚𝑛 − 𝑚( 21𝐻 )]𝑐 2
𝑚( 1𝐻 ) = 1.007825𝑢
𝑚𝑛 = 1.00866501𝑢
𝐵𝐸( 21𝐻 ) = 0.0023880𝑢 = 2.224 𝑀𝑒𝑉
𝐵𝐸⁄ = 1.112 𝑀𝑒𝑉
𝐴
Yani zayıf bağlı çekirdektir.
Spin ve parite
Döteronun 𝐼⃗ toplam açısal momentumunun, nötron ve protonun sn ve sp özgün spinleri ve
nükleonların ortak kütle merkezleri etrafındaki ℓ yörünge açısal momentum olmak üzere üç
bileşeni vardır:
𝐼⃗ = 𝑠𝑛 + 𝑠𝑝 + ℓ
𝐼⃗ = ⃗⃗⃗⃗
𝐽𝑝 + 𝐽⃗𝑛
𝐼⃗ = 𝑠⃗𝑛 + 𝑠⃗𝑝 + ⃗⃗
ℓ𝑃 + ⃗⃗
ℓ𝑛
4
1
2
𝑠𝑛 = 𝑠𝑝 =
,
𝑠⃗ = 𝑠⃗𝑛 + 𝑠⃗𝑝 = 0,1
Döteronun ölçülen spin ve paritesi = 𝐼 𝜋 = 1+ ’dır.
⃗⃗
ℓ = ⃗⃗
ℓ𝑃 + ⃗⃗
ℓ𝑛
𝐼⃗ = ⃗⃗
ℓ + 𝑠⃗
𝑠⃗ = 𝑠⃗𝑛 + 𝑠⃗𝑝
𝐼𝜋
Parite (−1)ℓ
ℓ=0
𝑠=1
1
1+
ℓ=0
𝑠=0
0
0
ℓ=1
𝑠=0
1
1−
ℓ=1
𝑠=1
2
0− , 1− , 2−
ℓ=2
𝑠=0
2
2+
ℓ=2
𝑠=1
3
1+ , 3,2
ℓ = 0, 1, 2, 3
s, p, d, f
2𝑠+1
ℓ𝐼
(1) = 3𝑆1
(2) = 3𝐷1
Döteron %96 (1) durumunda ve %4 (2) durumunda bulunur.
𝐼 = 1, ℓ = 0, 𝑠 = 1
3
𝑆1 , ℓ = 0, ℓ𝑛 , ℓ𝑝 = 0 ], proton ve nötron aynı kuantum durumundalar. Pauli dışarlama
1
𝑠 = 1, 𝑠𝑛 , 𝑠𝑝 = 2
ilkesine göre 2 proton ve 2 nötron aynı kuantum durumunda olamayacaklarıd. Bu sebeple n-n,
p-p sistemlerinin olamayacağını görüyoruz.
Manyetik dipol moment
Eğer ℓ = 0 varsayımı doğruysa manyetik momente hiçbir yörüngesel katkı olmaması gerekir
ve bu durumda toplam manyetik momentin sadece nötron ve protonun manyetik momentlerinin
toplamı olduğu kabul edilebilir:
𝜇 = 𝜇𝑛 + 𝜇𝑝
=
𝑔𝑠𝑝 𝜇𝑛
𝑔𝑠𝑛 𝜇𝑛
𝑠𝑛 +
𝑠𝑝
ℏ
ℏ
5
Burada 𝑔𝑠𝑛 = −3,826084 ve 𝑔𝑠𝑝 = 5,585691’dir. Gözlenen manyetik moment, spinleri en
1
büyük değerine (+ 2 ℏ) sahip olduğu zaman, 𝜇’nün z bileşeni olarak alınır.
𝜇=
1
𝜇 (𝑔 + 𝑔𝑠𝑝 ) = 0,879804𝜇𝑛 ∗∗∗∗
2 𝑛 𝑠𝑛
Gözlenen değer (0,8574376 ± 0,0000004)𝜇𝑛 ’dir ve hesaplanan değerle tam olarak
uyuşmamaktadır. Aradaki ufak fark, proton ve nötron arasındaki mezon değiş tokuşundan gelen
katkılar gibi başka nedenlere atfedilebilir. Burada, bu uyumsuzluğun, döteronun dalga
fonksiyonundaki d durumunun (ℓ = 2) küçük karışımından ileri geldiğini varsayacağız:
𝜓 = 𝑎𝑠 𝜓(ℓ = 0) + 𝑎𝑑 𝜓(ℓ = 2)
Manyetik momentin bu dalga fonksiyonu ile hesaplanması,
𝜇 = 𝑎𝑠 2 𝜇(ℓ = 0) + 𝑎𝑑 2 𝜇(ℓ = 2)
Değerini verir, burada 𝜇(ℓ = 0) **** denkleminde hesaplanan değer ve (ℓ = 2) =
1
4
(3 − 𝑔𝑠𝑝 − 𝑔𝑠𝑛 )𝜇𝑛 , bir d durumu için hesaplanan değerleridir. Gözlenen değer 𝑎𝑠 2 = 0,96
ve 𝑎𝑑 2 = 0,04 ile uyumludur; bu demektir ki döteron %96 olasılıkla ℓ = 0 ve %4 olasılıkla
ℓ = 2 durumunda bulunur.

Spin bağımlılığı:
Döteronda iki durum söz konusudur;
3
𝑆1 ve 3𝐷1
3
𝑆1 : ℓ = 0, 𝑠 = 1, 𝐼 = 1
1
𝑆0 : ℓ = 0, 𝑠 = 0, , 𝑠 = 0 bulunamıyor. Bunun için de nükleer kuvvet spin bağımlıdır.

Nükleon-nükleon arası potansiyel merkezi olmayan bir tensör potansiyel terim içerir:
Döteronun dalga fonksiyonu
3
𝑆1 ve
3
𝐷1 durumlarının karışımıdır. Bu karışımı sağlayan
merkezi bir potansiyel olamaz. O yüzden tensor potansiyel terimi vardır.
Bir s durumunun ℓ = 0 dalga fonksiyonu küresel simetriktir; elektrik kuadrapol moment sıfır
olur. Farklı ℓ durumlarının karışımı olan dalga fonksiyonları merkezi olmayan potansiyellerden
kaynaklanmaktadır.
6
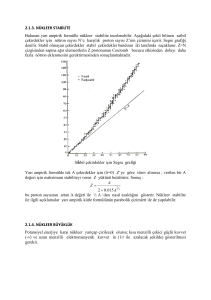
Kararlılık Eğrisi
Çekirdeklerin pek çoğu, nükleer bir reaksiyonla kararsız hale getirilmediği sürece, kararlıdır.
Nükleer kararlılık çekirdek içindeki kuvvetlerin dengesi ile belirlenir. Protonlar pozitif yüklü
parçacıklar olduğundan birbirini iterler. Çekirdek içindeki nükleer kuvvetler ise nükleonları bir
arara tutmaya çalışır. Bu iç kuvvetler arasındaki dengeyi belirlemek en önemli faktördür.
Dünyada 267 adet kararlı çekirdek, 19 tane neredeyse kararlı çekirdek vardır. Dolayısıyla
nükleer karalılık çekirdek içindeki nötron ve proton sayılarının oranı ile belirlenir. Bizmuttan
(Z=83) sonraki tüm elementler radyoaktiftir. Nükleer reaksiyonlar sonucunda insan yapımı pek
çok çekirdek oluşturulmuştur ve hepsi radyoaktiftir. Başka bir deyişle tüm olası kararlı
çekirdekler doğada bulunurlar. Nötron sayısının proton sayısına göre grafiği kararlılık eğrisi
olarak adlandırılır. N=Z civarındaki çekirdekler kararlı çekirdeklerdir.
40
20𝐶𝑎 ’e
kadar olan
çekirdekler kararlıdır ve nötron/proton oranı yaklaşık olarak bire eşittir. Kalsiyum’un
üzerindeki çekirdekler (Z=20) daha fazla nötron sayısına sahiptir. Dolayısıyla kütle numarası
büyük olan atomlar için bu değer değişir. Hafif çekirdeklerde A<20, N/Z oranı 1’e yakındır.
Kütle numarası küçük olan çekirdeklerin kararlı olabilmesi için nötron/proton oranının bir veya
bire yakın olması gerekir. Örneğin
13 14
12
6𝐶, 6𝐶, 6𝐶
izotoplarının nötron/proton oranı sırasıyla
1,00, 1,16 ve 1,33’dür. Bu nedenle doğal karbon izotopları arasında
karşılık
14
6𝐶
13
12
6𝐶, 6𝐶
kararlı olmasına
kararsız radyoaktif bir elementtir. Ağır çekirdeklerde ise A>20, N/Z oranı nötron
sayısındaki artışa bağlı olarak 1 ile 1,6 arasında değişir, çekirdeğin kararlı olabilmesi için bu
değerin yaklaşık olarak 1,5 civarında olması gerekir. Kararlılık bölgesi dışında kalan
çekirdekler ise kararsız çekirdeklerdir. N/Z oranı 1–1,6 arasında değişir. Kararsız çekirdekler
alfa, beta veya gamalar yayınlayarak kararlı hale gelmeye çalışırlar. Bu parçalanma süreci
çekirdek kararlılık bölgesine ulaşıncaya dek devam eder.
286 tane kararlı veya nerdeyse kararlı çekirdeğe ek olarak:
— 167 tane çift sayıda proton ve nötron içeren çekirdek vardır (% 58),
— 57 tane çift sayıda proton, tek sayıda nötron içeren çekirdek vardır (% 20),
— 53 tane tek sayıda protona, çift sayıda nötrona sahip çekirdek vardır (% 19).
— Yalnızca 9 tane tek sayıda proton ve nötrona sahip çekirdek vardır (% 3).
Tek-çift kuralı olarak bilinen bir kurala göre nötron veya proton sayıları çift olan çekirdeklerin
kararlı oldukları gözlenmiştir. (Tek-çift denilirken dikkat etmek gerekir, Z-N yani proton sayısınötron sayısı sırası ile söylenir. Tek-çift deniliyorsa tek sayıda proton çift sayıda nötron; çift7
tek çekirdek deniliyor ise çift sayıda proton, tek sayıda nötrondan oluşan çekirdekten söz
ediliyor demektir.) Sihirli sayılar kuralına göre ise nötron ve/veya proton sayıları 2, 8, 20, 50,
82 ve 126 olan çekirdekler kararlıdır. Bu nedenle bu sayılara sihirli sayılar denir. Hem proton
208
hem de nötron sayıları sihirli sayılardan birine eşit olan 24𝐻𝑒, 168𝑂, 40
20𝐶𝑎, 82𝑃𝑏 gibi çekirdekler
bolluk dereceleri (doğal dağılım oranları) yüksek olan kararlı çekirdeklerdir. A>209 ve Z>83
değerlerinden sonraki çekirdekler kararsızdır. En büyük atom numarasına sahip çekirdek 209
83𝐵𝑖
çekirdeğidir.
Bu eğride N=Z bölgesinde çekirdekler yaklaşık olarak kararlılık eğrisi civarında dağılmıştır.
Proton sayısı ve nötron sayısının büyük (fazla) olduğu üst bölgede alfa bozunması gerçekleşir.
Buradaki çekirdeklerin kütle numaraları çok büyüktür, ağır çekirdekler olarak adlandırılırlar.
Bu durumda çekirdek bir alfa parçacığı (  ) – yani helyum çekirdeği yayınlayarak başka bir
elemente dönüşür. Reaksiyon
A
ZX

A-4
4
Z-2 X + 2 He
212
şeklindedir. Örneğin
84
4
Po  208
82 Pb + 2 He
.
Proton sayısı 83’den, nükleon sayısı ise 209’dan büyük çekirdeklerde gözlenir. Alfa bozunması
(parçalanması) bir ana çekirdeğin ardışık, zincirleme parçalanmalarla başka çekirdeklere
dönüştüğü radyoaktif serilerde de (bozunma kümeleri) sıkça gözlenir.
Şekil 3.1 Kararlılık eğrisi
8