Bankacılar Dergisi, Sayı 58, 2006
Operasyonel Risk İleri Ölçüm Modelleri
Giriş
Çalışma iki bölümden oluşmaktadır. İlk bölümde operasyonel risklerin ölçülmesi kapsamında hangi ileri ölçüm modellerinin kullanılması gerektiği, söz konusu ölçüm modellerinin özellikleri, karşılaşılabilecek sorunlar, ölçüm modellerinin zayıf ve güçlü yönlerinin neler
olduğu üzerinde durulmuştur. Bu bölümde tanıtılan ölçüm yaklaşımları şunlardır:
Kayıp Dağılımı Yaklaşımı
Stres Testleri / Senaryo Analizi
Skorkart Yaklaşımı
Bayesgil Metodlar
İkinci bölümde banka ismi verilmeden Türk bankacılık sisteminde operasyonel risk
ölçümünde kullanılan ileri ölçüm modelleri incelenmiş olup söz konusu incelemede toplam
12 bankanın verileri kullanılmıştır. Çalışma, bankacılık sektöründe operasyonel risklerin
ölçülmesi konusunda Türk bankacılık sisteminin bulunduğu noktanın belirlenmesi hedeflenmiştir.
I. Operasyonel Risklerin Ölçümünde Hangi İleri Ölçüm Modelleri Kullanılmalı,
Özellikleri, Karşılaşılabilecek Sorunlar, Zayıf/Güçlü Yönleri
A. Kayıp Dağılımı Yaklaşımı
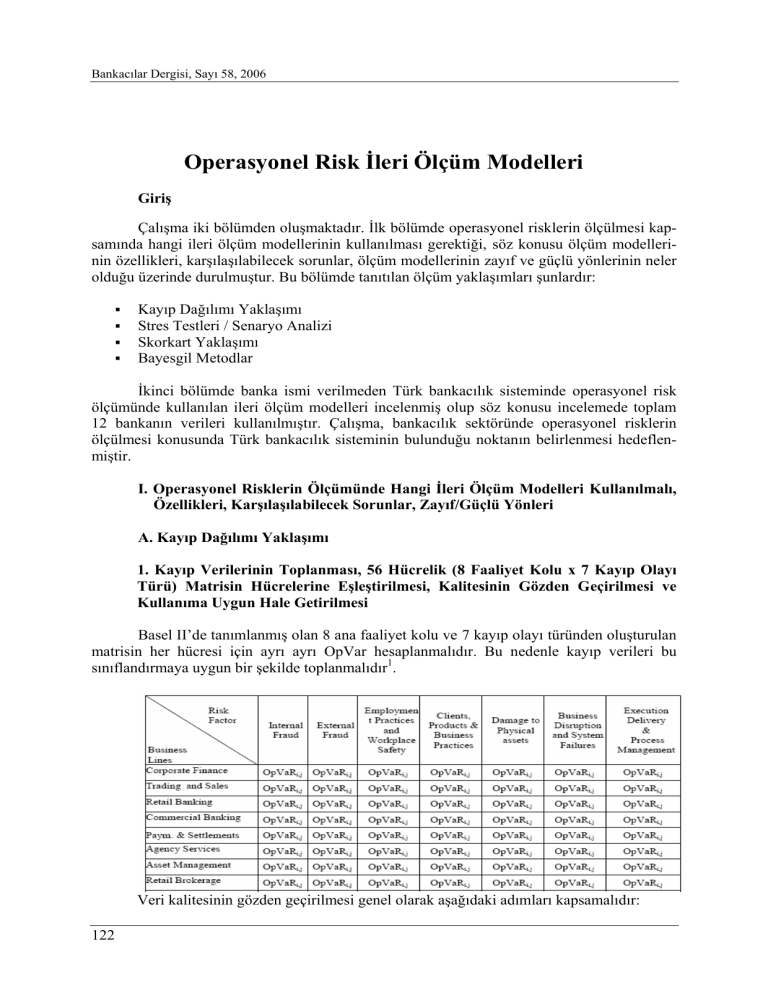
1. Kayıp Verilerinin Toplanması, 56 Hücrelik (8 Faaliyet Kolu x 7 Kayıp Olayı
Türü) Matrisin Hücrelerine Eşleştirilmesi, Kalitesinin Gözden Geçirilmesi ve
Kullanıma Uygun Hale Getirilmesi
Basel II’de tanımlanmış olan 8 ana faaliyet kolu ve 7 kayıp olayı türünden oluşturulan
matrisin her hücresi için ayrı ayrı OpVar hesaplanmalıdır. Bu nedenle kayıp verileri bu
sınıflandırmaya uygun bir şekilde toplanmalıdır1.
Veri kalitesinin gözden geçirilmesi genel olarak aşağıdaki adımları kapsamalıdır:
122
Bankacılar Dergisi
Bankanın veritabanı kullanılarak tespit edilen toplam kayıp tutarı ile dahili veri toplanan kaynaklardan gelen verilere ilişkin toplam kayıp tutarı karşılaştırılarak eksiklik
olup olmadığı veya birden fazla kez raporlanan olay olup olmadığı kontrol edilir.
Verilerin sınıflandırılmasında herhangi bir yanlışlık olup olmadığı kontrol edilir.
Sınıflandırmada hata yapılması sermaye hesaplamalarını etkileyeceğinden, bu tür hataların düzeltilmesi büyük önem taşır.
Eğer bankanın ileri ölçüm yaklaşımları (İÖY) kapsamına almış olduğu hücrelerden2
birinde veya birkaçında yetersiz veri gözlemlenmişse, söz konusu verilerin senaryo
analizi veya dış veriler ile desteklenmesi seçeneği üzerinde durulmalıdır.
Son olarak, toplanan verilerin kalitesinin gözden geçirilmesi ve potansiyel sorunların
tespit edilebilmesi için histogramlardan faydalanılabilir.
Şekil 1: Yasal zarar olaylarına ilişkin kayıp verilerinden faydalanılarak oluşturulmuş
histogram3 (Ek: 1)
Şekil 1:
3.800.000
3.400.000
3.600.000
3.200.000
3.000.000
2.600.000
2.800.000
2.400.000
2.000.000
2.200.000
1.800.000
1.600.000
1.200.000
1.400.000
800.000
1.000.000
Zarar tutarları kullanılarak oluşturulan
yandaki histogramda, belli aralıktaki
zarar tutarlarının kaç kez gözlemlendiği
gösteril-mektedir. Buna göre, zarar
tutarlarına ilişkin alt eşik değeri
yaklaşık, 100.000 dolardır.
400.000
600.000
50
45
40
35
30
25
20
15
10
5
0
200.000
Olay sayısı
Tutar Bazında Gerçekleşen Olay Sayısı
Veri setinden oluşturulan histogram,
beklentilere uygun bir şekle sahiptir.
Daha düşük zarar tutarlarına ilişkin daha
çok olay gözlemlenmiştir. Ayrıca
kuyruk alanında yer alan büyük zarar
olayları da mevcuttur.
Zarar Tutarı (USD)
Basel II ileri ölçüm yaklaşımını kullanmayı amaçlayan bir banka, son yıllarda dahili
veri toplama konusunda daha fazla çaba göstermeye başlamış olabilir. Bu durumun raporlanan kayıp olayı sıklığına nasıl yansıdığı bir histogram yardımıyla görülebilir. ( Şekil 2)
Şekil 2:
Yıllar İtibariyle Raporlanan Kayıp Olayı Sayısı
140
100
80
60
40
20
0
H az .00
E y l.00
A ra.00
M ar.01
H az .01
E y l.01
A ra.01
M ar.02
H az .02
E y l.02
A ra.02
M ar.03
H az .03
E y l.03
A ra.03
M ar.04
H az .04
E y l.04
A ra.04
M ar.05
H az .05
E y l.05
Olay Say ısı
120
Çeyrek yıl
Bu histogramda, özellikle 2005 yılının 2.
ve 3. çeyreklerinde veri toplama konusuna
ağırlık verildiği gözlemlenmektedir. Bu
durumda tüm yılları dikkate alarak, zarar
olaylarının yıllık ortalama sıklığının (56)
bulunması gerçekçi olmayacaktır. Bu
ortalama, gerçek ortalamadan uzak
olacaktır. Çünkü zarar olayı verisinin az
olması, zarar olayının gerçekleşmemesinden değil, raporlanmamış olmasından
kaynaklanmaktadır. Böyle bir histograma
bakılarak, daha sağlıklı veri toplandığı
gözlemlenen son 4 çeyreğin yıllık zarar
olayı sıklığını (255) dikkate alma kararı
verilebilir.
123
Operasyonel Risk Çalışma Grubu
2. İstatistiksel Testler Uygulanarak En Uygun Sıklık ve Şiddet Dağılımlarının
Tespit Edilmesi
Aktüeryal modele dayanan Kayıp Dağılımları Yaklaşımı kapsamında risklerin
ölçümü, kayıpların sıklık ve şiddet olmak üzere iki bağımsız stokastik süreçte incelenmesi ve
modellenmesi gerekliliğini doğurmaktadır. Toplanan kayıp verilerine hangi sıklık ve şiddet
dağılımlarının uygun olacağının belirlenebilmesi için verilere ilişkin birtakım özelliklerin
görsel ve sayısal olarak incelenmesi, veri setine belirli istatistiksel testlerin uygulanması
gerekmektedir. Bu işlemler, Basel II’de tanımlanan 8 faaliyet kolu ve 7 kayıp olay türünden
oluşan matrisin her hücresi için ayrı ayrı gerçekleştirilmelidir.
Varsayımlar:
Sıklık ve şiddet dağılımları birbirinden bağımsızdır.
Bir hücredeki kayıp tutarları rassal değişkendir (random variable), birbirinden bağımsız ve benzer dağılıma sahiptir (independent identically distributed).
Bir hücredeki kayıp olaylarının sayısı rassal bir değişkendir.
Kayıp şiddetinin modellemesinde, sürekli dağılımlar (continuous distributions), kayıp
sıklığının modellemesinde ise kesikli dağılımlar (discrete distributions) kullanılır. Kayıp
şiddeti ile sıklığı negatif değerler alamayacağından, bu dağılımların 0’a eşit ve 0’dan büyük
olan bölümleri dikkate alınır.
Şiddet ve Sıklık Dağılımlarını Belirleme Adımları:
2.1. Normalite Testleri
Verilerin normal dağılım özelliği taşıyıp taşımadığı araştırılır.
H0: Veri seti, normal dağılımdan gelmektedir.
Karşıt hipotez: H1: Veri seti, normal dağılımdan gelmemektedir.
Verilerin normalite kontrolü için incelenecek istatistikler ve uygulanabilecek yöntemler
şunlardır:
i) Momentlerin incelenmesi
Verilerin 3. ve 4. moment (central moments) incelenir. Standart normal dağılımın momentleriyle karşılaştırılarak bir yorum yapılır.
1. moment = Ortalama
E [( X )] = µ
2. moment = Varyans
[
σ 2 = E ( X − µ)2
3. moment = Çarpıklık (skewness)
s=
[
E ( X − µ )3
σ
]
]
3
Kayıp tutarı verilerine hangi istatistiksel dağılımların uygun olabileceği düşünülürken,
göz önünde bulundurulması gereken bir nokta, çarpıklık katsayısıdır. Normal dağılımın
124
Bankacılar Dergisi
çarpıklık katsayısı 0’dır ve dağılım simetriktir. Çarpıklık katsayısının 0’dan büyük olduğu
durumlarda dağılım sola yatık, 0’dan küçük olduğu durumlarda ise sağa yatıktır. (Şekil 3)
Örneğin, Şekil.1’deki örnekleme ilişkin çarpıklık katsayısı 4,42’dir. Verilerin çarpıklık
katsayısı istatistiksel açıdan anlamlı ölçüde sıfırdan farklı ise söz konusu verilerin normal
dağıldığını varsaymak doğru olmayacaktır.
Şekil 3: Normal olmayan dağılımların çarpıklık katsayısına göre örnek görünümleri
4. moment = Basıklık (kurtosis) Normal dağılımın basıklık katsayısı 3’dür.
κ=
[
E ( X − µ )4
]
σ4
Normal dağılımın basıklık katsayısı 3’dür. Basıklık katsayısının 3’ten büyük olduğu
durumlarda dağılım kalın kuyruklu, küçük olduğu durumlarda ise ince kuyrukludur. (Şekil 4)
Şekil 4: Basıklık katsayısına göre dağılımların örnek görünümleri
Çok yüksek tutarlarda kayıpların gözlemlenmesi, şiddet dağılımının kuyruk alanının
genişlemesine yol açar. Kalın kuyruk alanlarına sahip olduklarından dolayı şiddet dağılımları
için uygun olabilen dağılımların bazıları şunlardır: Weibull, Üssel, Pearson, Lognormal,
Pareto, Gamma.
125
Operasyonel Risk Çalışma Grubu
ii) Grafik ve Histogramlar
Normal Olasılık Grafiği (Normal Probability Plot): Bir eksen gözlenen değerler, diğer
eksen ise normal dağılım varsayımına göre beklenen değerler eksenidir. Veriler normal
dağılım gösteriyorsa, noktaların bir doğru üzerinde yer alması ya da etrafında belirli bir desen
göstermeden dağılması gerekir.
Örnek:
Şekil 5, normal dağılıma sahip bir veri setinin grafiğine bir örnek iken, Şekil 6 ise
normal dağılımdan gelmeyen verilerin grafiğine bir örnektir.
Şekil 5: Normal dağılıma sahip örnek verilerin Normal Olasılık Grafiği
Şekil 6: Normal olmayan dağılıma sahip örnek verilerin Normal Olasılık Grafiği
126
Bankacılar Dergisi
Histogram: Yatay eksen gözlenen değerleri, dikey eksen ise frekansı, yani gözlemlenme sayısını gösterir. Normal dağılıma sahip bir veri setinin histogramı simetrik olur.
Normal olmayan verilerin histogramı ise simetrik olmaz. (Şekil 7 ve 8)
Şekil 7: Yaklaşık olarak Normal dağılıma sahip örnek verilerin histogramı
Şekil 8: Normal dağılıma sahip olmayan örnek verilerin histogramı
iii) Lilliefors Normalite Testi
Ortalama ve varyans önemli olmaksızın, veri setinin birikimli dağılım fonksiyonu ile
standart normal dağılımın birikimli dağılım fonksiyonu arasındaki en yüksek dikey farkı
ölçer. Aradaki fark belirginse dağılımın normal olmadığı anlaşılır. Kolmogorov-Smirnov
testinin normal dağılım için özelleşmiş bir biçimidir.
iv) Shapiro-Wilk Testi
Shapiro-Wilk test, normal dağılımdan çeşitli yönlerden sapmaları tespit etmekte kullanılan varyans analiz testidir. Örneklemin sıralı istatistikleri ile, standart normal dağılımın
sıralı istatistiklerinin beklenen değer, varyans ve kovaryanslarından oluşan matris dikkate
alınarak hesaplanan Shapiro-Wilk test istatistiğinin tablo değerlerinden küçük olduğu
durumlarda, veri setinin normal dağılımdan geldiğine ilişkin hipotez reddedilir. Hipotezin
reddedilmesi, dağılımın normal olmadığını göstermesine karşın, test istatistiğinin tablo
değerinden büyük olması verilerin normal dağılımdan geldiğine ilişkin bir kanıt oluşturmaz.
Shapiro-Wilk testi, örneklemde çok sayıda aynı değere sahip verinin yer aldığı durumlarda
çok doğru sonuçlar vermez. Ancak küçük ve orta büyüklükte (veri sayısı<3000) örneklemler
için en güvenilir sonuçları veren normalite testidir.
127
Operasyonel Risk Çalışma Grubu
2.2. Şiddet Dağılımlarının Parametrelerinin Belirlenmesi
Weibull, Gamma, Lognormal, Üssel, Pareto, Pearson gibi dağılımlar, kayıp şiddetini
ifade etmeye uygun olabilecek dağılımlardır. Bu dağılımların parametreleri, veri setine uygun
olacak şekilde belirlenir. Dağılım parametrelerini belirlemek için uygulanabilecek yöntemler
şunlardır:
i) Momentler Yöntemi (Method of Moments-MM)
Örneklemin momentleri dağılımın teorik momentlerine eşitlenerek bir denklem sistemi oluşturulur. Bu denklem sistemi çözülerek parametreler tahmin edilir.
Örnek:
Gamma dağılımının olasılık yoğunluk fonksiyonu aşağıdaki gibidir:
x
−
1
f ( x;α , β ) = α
xα −1.e β
β Γ(α )
Gamma dağılımının ilk momenti, yani ortalaması:
E (x) = αβ
Örneklemin ilk momenti, yani ortalaması:
n
X = ∑ Xi /n
i =1
İki moment birbirine eşitlenirse:
n
αβ = ∑ X i / n
i =1
(1)
Gamma dağılımının ikinci momenti:
E ( x 2 ) = β 2α (α + 1)
Örneklemin ikinci momenti:
n
∑ X i2 / n
i =1
İki moment birbirine eşitlenirse:
n
β α (α + 1) = ∑ X i2 / n
2
i =1
(2)
(1) ve (2) denklemleri birlikte çözülürse:
α=
128
n
∑ X i / n
i =1
2
n 2 n
∑ X i / n ∑ X i / n
i =1
i =1
2
n 2 n
∑ X i / n − ∑ X i / n
i =1
β = i =1
n
∑ X i / n
i =1
2
Bankacılar Dergisi
olarak bulunur. Örneklemdeki veriler formüllerde yerine koyularak parametreler tahmin
edilmiş olur.
Momentler yöntemi, kolay hesaplanma avantajına karşın yaklaşık sonuçlar vermesi,
doğruluk yüzdesinin tahmin edilememesi gibi dezavantajları nedeniyle tek başına kullanılması
her zaman güvenilir sonuçlar vermeyen bir yaklaşımdır.
ii) En Çok Olabilirlik Yöntemi (Maximum Likelihood Estimation-MLE)
Bir sürekli rassal değişkene ait olasılık yoğunluk fonksiyonu biliniyorsa ve parametreleri tahmin edilecekse bunun için en güvenilir yöntemlerden biri MLE’dir. Parametrelerin
olabilirlik fonksiyonunun maksimize edilmesi yoluyla en muhtemel sonuçlar elde edilir.
x, olasılık dağılım fonksiyonu f ( x; θ1 , θ 2 ,..., θ k ) olan bir sürekli rassal değişkendir.
Tahmin edilmek istenen k adet parametre (θ1 , θ 2 ,..., θ k ) biçiminde gösterilirse, R adet
birbirinden bağımsız veri için maksimize edilmesi gereken olabilirlik fonksiyonu şu şekilde
gösterilir:
R
L(θ1 , θ 2 ,..., θ k | x1 , x 2 ,..., x R ) = L = ∏ f ( xi ;θ1 , θ 2 ,..., θ k )
,
i = 1,2,..., R
i =1
Olabilirlik fonksiyonunun maksimize edilmesinin zorluğu nedeniyle logaritması alınarak işlemler kolaylaştırılır ve 0’a eşitlenerek maksimize edilir:
R
ln L = ∑ ln f ( xi ;θ1 , θ 2 ,..., θ k )
i =1
∂ ln L
=0
∂θ j
,
j = 1,2,..., k
Örnek:
Gamma dağılımının olasılık yoğunluk fonksiyonu:
x
−
1
f ( x;α , β ) = α
xα −1.e β
β Γ(α )
Gamma dağılımı için logaritması alınmış olabilirlik fonksiyonu (log-likelihood
function):
R
1
x
ln L = ∑ − ln(Γ(α i ) ) + α i ln + (α i − 1) ln( xi ) − i
βi
β i
i =1
Bu fonksiyonun α ve β parametrelerine göre türevleri sıfıra eşitlenerek örneklem verileri yerine koyulduğunda parametreler tahmin edilmiş olur.
∂ ln L
∂ ln L
=0
=0
∂β
∂α
,
129
Operasyonel Risk Çalışma Grubu
MLE yönteminde, veri seti büyüdükçe tahminler gerçek değere yakınsar, yani tahminin doğruluğu artar. Buna karşılık, en yüksek olabilirlik tahmin edicisi her zaman var
olmayabilir ya da birden fazla olabilir. Bundan dolayı Momentler Yönteminin (MM)
yönteminin çıktıları En Çok Olabilirlik Yöntemi (MLE) yöntemi için başlangıç değeri
oluşturma amacıyla kullanılarak tahmin güvenilirliği artırılabilir.
Örnek:
Üssel Dağılımın Parametresinin Hesaplanması:
Üssel dağılımın olasılık dağılım fonksiyonu f ( x ) =
e
−
x
λ
λ
. Kayıp verilerinin şiddeti-
nin bu dağılımı izlediği varsayılıyorsa, örneklemdeki veriler ve MLE (maximum likelihood
estimator) kullanılarak λ parametresi tahmin edilmelidir. λ’nın en çok olabilirlik yöntemi ile
hesaplanan tahmin edicisi 1 / (Σ Xj / n)’dir; yani örneklemin ortalamasının çarpmaya göre
tersine eşittir.
Şekil 1’e ilişkin kayıp tutarı verilerini içeren örneklemin ortalaması 439.726’dır. Dolayısıyla “bu verilere dayanılarak hesaplanan tahmin edici 1/439.726 = 0,00000227’dir ve bu
örneklemdeki veriler olasılık dağılım fonksiyonu f(x) = e (-x/0,00000227)/0,00000227 olan bir
popülasyondan geliyor olabilir,” diyebiliriz.
Bu yöntemle, şiddet dağılımı için uygun olabilecek diğer olasılık dağılımlarının parametreleri de hesaplanır ve bir sonraki aşamada istatistiksel testler uygulanarak, en uygun
şiddet dağılımı tespit edilir.
2.3. Sıklık Dağılımlarının Parametrelerinin Belirlenmesi
Basel II’ye göre bankalar 1 yıllık zaman zarfında karşı karşıya kalabilecekleri kayıp
olaylarına ilişkin sermaye ayırmalıdırlar. Dolayısıyla, bir yıl içinde bankanın hangi sıklıkta
kayıp olayı ile karşılaştığının takibi ileriki yıllar için tahmin yapılabilmesi için gereklidir. Bu
nedenle, herbir hücre için, toplanan kayıp verilerine ilişkin sıklık dağılımının oluşturulması
gerekmektedir. Poisson, Binom ve Negatif Binom gibi dağılımlar, kayıp sıklığını ifade
etmeye uygun olabilecek dağılımlardır. Bu dağılımların parametreleri, veri setine uygun
olacak şekilde yukarıda anlatılan Momentler Yöntemi (MM) veya En Çok Olabilirlik
Yöntemi (MLE) yöntemleriyle belirlenir. MLE daha güvenilir sonuçlar vermesi nedeniyle
tercih edilebilir. Bir yıl içinde gerçekleşmesi beklenen kayıp sıklığına λ denirse, λ, o yıl içinde
gerçekleşmesi beklenen toplam olay (kayba yol açmayan olaylar dahil) sayısı (N) ile
beklenen kayıp olasılığının (θ) çarpımına eşittir.
λ = N* θ
Binom Dağılım
N
h(n) = θ n (1 − θ ) N −n , n = 0,1,2,..., N
n
130
Bankacılar Dergisi
Binom dağılımdaki n değeri, bir yılda meydana gelen kayıp olayı sayısını ifade eder.
Binom dağılımın dezavantajı, kullanılabilmesi için N değerinin bilinmesi veya öngörülebilmesi gerekmesidir. Çünkü θ parametresinin tahmin edicisi n/N’dir ve bu yüzden N bilinmediği (ya da öngörülemediği) takdirde model kurulamaz.
Poisson Dağılımı
Eğer binom dağılımdaki N değeri büyük ise ve θ küçük ise, (özellikle N≥ 20 ve θ ≤ 0,05
ise) Poisson dağılımı binom dağılım için iyi bir yaklaşım (approximation)’dır. Eğer N≥100 ve
N θ≤10 ise yaklaşım kusursuza yakındır. Poisson dağılımının olasılık dağılım fonksiyonu:
λ.e − λ
h( n) =
, n = 0,1,2,...
n!
Kayıplara ilişkin verilerin sıklık dağılımının bir Poisson dağılımı olduğu varsayılıyorsa,
λ’nın tahmin edilmesi gerekmektedir. λ ’nın tahmin edicisi (MLE) ise örneklemdeki n
değerlerinin ortalamasıdır.
Ek.1’de yer alan yasal yaptırımlara ilişkin kayıp olaylarının 25 aylık veriye dayandığını ve aylar itibariyle aşağıdaki sıklıkta gerçekleştiğini varsayalım. 25 ayda toplam 75 kayıp
olayı gerçekleşmiştir, yani λ’nın tahmin edicisi 75/25=3’tür. Bu değer, bir aylık ortalama
kayıp sıklığı beklentisidir. Ancak Basel II’ye göre, bankalar 1 yıllık zaman zarfında karşı
karşıya kalabilecekleri kayıp olayları için sermaye ayırmalıdırlar. Dolayısıyla, yıllık sıklık
dağılımı olarak, lambdası 3*12=36’ya eşit olan bir Poisson dağılımı kullanılabilir.
Ay
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Kayıp
olaylarının
sayısı
3
1
4
8
0
2
0
7
1
0
2
1
2
4
10 1
5
2
4
1
5
3
3
Şekil 9:
0,3
Olasılık
5
0,25
0,2
0,15
0,1
0,05
0
0
1
2
3
4
5
6
7
8
9
10
Yandaki grafik, yukarıdaki tablodaki
veriler kullanılarak oluşturulmuştur ve bir
ayda belli bir sayıda kayıp olayı meydana
gelmesine ilişkin olasılıkları göstermektedir. Bu grafiğe lambda’sı 3 olan bir
poisson dağılımı oturtularak, (aylık) sıklık
dağılımının elde edilmesi mümkündür.
Aylık kayıp olayı sıklığı
Şekil 10:
Poisson - Gerçek Veri Karşılaştırması
Şekil 10’da gerçek veriye dayanılarak
oluşturulan grafik ile, poisson (λ=3)
dağılımının olasılık değerleri karşılaştırılmaktadır.
Olasılık
0,3
0,25
0,2
0,15
0,1
0,05
Negatif0 Binom
0 1
Dağılım
2
3
Poisson (lambda=3)
4
5
6
7
8
9
10
Aylık kayıp olayı sıklığı
Örneklemden elde edilen veri
131
1
Operasyonel Risk Çalışma Grubu
Negatif binom dağılımın olasılık dağılım fonksiyonu:
α + n − 1 n
θ (1 − θ )α
h( n) =
n −1
Şekil 10’te yer alan örneklemdeki gibi uç değerlerin gözlemlendiği, yani kuyruk alanı
kalın olan örneklemler için kimi zaman negatif binom dağılım tercih edilebilir.
2.4. Uyum İyiliği Testleri (Goodness of Fit Tests)
Önceki adımlarda veri setine uygun parametreleri belirlenen sıklık ve şiddet modellerinin uygunluğu grafiksel ve niceliksel çeşitli Uyum İyiliği (Goodness of Fit) testleri ile
sınanır.
H0=Veri seti, test edilen dağılıma uygun bir popülasyondan gelir.
H1= Veri seti, test edilen dağılıma uygun bir popülasyondan gelmez.
Non-Parametrik testler (Kolmogorov-Smirnov testi, Ki-kare testi, Anderson-Darling
testi)
i) Kolmogorov-Smirnov Testi
Örneklem ile uygunluğu test edilen dağılımın birikimli dağılım fonksiyonları arasındaki en yüksek dikey farkı ölçer. Test istatistiği tablo değerinden büyükse, seçilen dağılımın
örnekleme uygun olmadığı sonucuna varılır.
D = max Fo ( y i ) − Fe ( y i )
1≤i ≤ n
Fo : Örneklemin birikimli yoğunluk fonksiyonu
Fe : Uygunluğu test edilen dağılımın birikimli yoğunluk fonksiyonu
n : Örneklemdeki gözlem sayısı
K-S testi yalnızca sürekli dağılımlara uygulanır (sıklık dağılımının uyum iyiliği testi
için uygun değildir). Test istatistiğinin karşılaştırılacağı kritik tablo değerleri dağılımsal bir
varsayıma dayanmaz, tüm dağılımlar için aynıdır. Ancak bu test, dağılımın kuyruklarında,
merkezine oranla daha az hassastır. Ayrıca, dağılımın parametrelerinin örneklemden tahmin
edilmesi, testin güven düzeyini azaltır.
ii) Ki-kare (Chi-square) Testi
Gözlemlenen frekans değerleri ile uygunluğu test edilen dağılımın beklenen frekans
değerleri arasındaki farkın büyüklüğünü ölçer. Test istatistiğinin tablo değerinden büyük
olduğu durumlarda, seçilen dağılımın örnekleme uygun olmadığı sonucuna varılır.
( o i − ei ) 2
χ =∑
ei
i =1
2
k
oi : Gözlenen frekans değerleri
ei : Uygunluğu test edilen dağılımın beklenen frekans değerleri
k : n adet veride küme sayısı
132
Bankacılar Dergisi
Ki-kare testi, Kolmogorov-Smirnov ve Anderson-Darling testlerinin aksine kesikli dağılımlar için de uygulanabilir.
iii) Anderson-Darling Testi
Kolmogorov-Smirnov testinin farklılaştırılmış biçimidir, kuyruklara daha çok ağırlık vererek
bir örneklemin belirli bir dağılıma uygunluğunu test eder. Test istatistiğinin tablo değerinden
büyük olduğu durumlarda, seçilen dağılımın örnekleme uygun olmadığı sonucuna varılır.
n
A = −n − ∑
2
i =1
(2i − 1)[ln F ( y i ) + ln F ( y n −i +1 )]
n
F (y): Dağılımın birikimli fonksiyonu
n: Örneklemdeki gözlem sayısı
Testin kritik tablo değerleri dağılımdan dağılıma farklılık gösterir, bu nedenle farklı
dağılımlar için farklı tablolar kullanılmalıdır.
Grafiksel Uyum İyiliği Testi
Probability-Probability Plot
Verilerin belirli bir dağılımdan gelip gelmediğine ilişkin görsel fikir veren bir grafiksel uyum iyiliği testidir. Bir eksen sıralı gözlenen değerler, diğer eksen ise dağılım varsayımına göre sıralı beklenen değerler eksenidir. Veriler test edilen dağılımdan geliyorsa, grafikte
noktaların yaklaşık olarak bir doğru üzerinde yer alması gerekir.
2.5. En Uygun Sıklık ve Şiddet Modellerinin Seçilmesi
Grafiksel ve niceliksel uyum iyiliği (Goodness of fit) testleri en iyi sonuçları veren
sıklık ve şiddet modelleri belirlenir.
Seçilen hiçbir dağılımın tek başına kuyruk bölümünün operasyonel risk kayıplarının
ekstrem değerlerini açıklamak için yeterli olmadığının öngörüldüğü durumlarda, dağılımın
gövdesi ve kuyruğu için farklı dağılımların kullanılması tercih edilebilir.
3. Sigortanın Dikkate Alınması
Basel II’ye göre, ileri ölçüm yöntemleri kullanıldığı takdirde, sigortanın risk azaltıcı etkisi operasyonel risk sermaye yükümlülüğü hesaplamalarında dikkate alınabilecektir. Ancak
bankalar sigorta yaptırarak, sigortanın etkisini dikkate almadan hesaplamış oldukları
ekonomik sermayenin en fazla yüzde 20’si oranında sermaye tasarrufu sağlayabileceklerdir.
Buna ek olarak, Basel II’de sigortayı sağlayan kuruluşun ve sigorta poliçesinin sağlaması
gereken bazı koşullar belirlenmiştir.
Kayıp dağılımı yaklaşımında sigortanın etkisi hesaplanırken, öncelikle sigorta poliçelerinin hangi olay türü/faaliyet kolu kategorilerini kapsamına aldığı saptanacak ve eşleştirme
yapılacaktır. Daha sonra, herbir olay türü/faaliyet kolu kategorisi için sigorta muhafiyeti,
sigorta kapsamına girecek en yüksek tutar ve bir olayın sigorta kapsamına girme olasılığı
belirlenmelidir. Bu unsurlardan ve daha önce oluşturulmuş olan sıklık ve şiddet dağılımların133
Operasyonel Risk Çalışma Grubu
dan faydalanılarak Monte Carlo simülasyonu yapılmalı ve böylece sigortanın ekonomik
sermayeye etkisi bulunmalıdır.
4. Monte Carlo Simülasyonu ile Toplam Kayıp Dağılımının Oluşturulması ve
Belirlenmiş Güven Aralığında (Basel II’ye Göre Yüzde 99.9) Operasyonel Risk
Sermaye Gereksiniminin Her Hücre İçin Hesaplanması
Birbirinden bağımsız iki stokastik süreci temsil eden şiddet ve sıklık modelleri, toplam
kayıp modelini oluşturulmak üzere birleştirilir.
∞
i*
∑ p (i ).F ( x), x > 0
G ( x) = i =1
p (0), x = 0
G(x): Toplam kayıp modeli
Fn*(x): Sıklık dağılımının n kat konvolüsyonu
p : Sıklık dağılımının olasılık fonksiyonu
Şiddet ve sıklık modellerinin birleştirilmesinde, Hızlı Fourier dönüşümü ve ardışık
metod yöntemleri ile Monte Carlo simülasyonu kullanılabilir. Monte Carlo simülasyonu,
özellikle dağılımların normal ve olaylar arası ilişkilerin doğrusal olmasını gerektirmemesinden ve mümkün olan birçok durumu kapsayacak şekilde rassal süreç simülasyonu sağlamasından dolayı tercih edilmektedir.
Monte Carlo simülasyonu, birçok değişkeni dikkate alarak çok sayıda iterasyonla, bilinen bir birikimli dağılım fonksiyonuna uygun veri örneklemesine olanak sağlayan bir
metoddur. Monte Carlo simülasyonunda yapılan örneklemeler toplam kayıp modelini
oluşturur. Böylece bir yılda meydana gelebilecek olayların toplam şiddetine ilişkin olasılık
değerleri hesaplanmış olur.
Şekil 11: Sıklık ve Şiddet modellerinden Toplam kayıp modelinin oluşturulması
Geliştirilmiş birçok yazılım aracılığıyla, yüzbinlerce iterasyon ile Monte Carlo hesaplaması yapılabilmektedir. Kayıp verilerine uygun olan şiddet ve sıklık modelleri belirlendik134
Bankacılar Dergisi
ten sonra, kullanılan sistemin elverdiği büyüklükte iterasyon sayısına karar verilir. İterasyon
sayısı artıkça ölçümün hassaslığı artacaktır, çünkü rassal olarak yaratılacak örneklemin
büyüklüğü iterasyon sayısı ile orantılıdır.
Monte Carlo simülasyonu kapsamında yapılan hesaplamanın adımları şu şekilde özetlenebilir:
− İterasyon sayısı kadar (n defa) aşağıdaki işlemler tekrarlanır:
Rassal sayı üreteci ile 0 ile 1 arasında sayı türetilir.
Bu sayı, sıklık modelinin birikimli dağılım fonksiyonundaki güven düzeyi (quantile)
olarak alınır ve bu güven düzeyine denk gelen olay sayısı frekans (f) olarak bulunur.
Frekans olarak elde edilen sayı kadar olay için şiddet dağılımından değer üretilmelidir.
Bunun için f defa aşağıdaki işlem tekrarlanır:
o Rassal sayı üreteci ile 0 ile 1 arasında sayı türetilir.
o Bu sayı, şiddet modelinin birikimli dağılım fonksiyonundaki güven düzeyi
(quantile) olarak alınır ve buna denk gelen olay şiddeti (s) bulunur.
si , i=1,...,f değerleri toplanarak toplam kayıp tutarı bulunur. S =
f
∑ si
i =1
− n defa iterasyon sonucu elde edilen n adet S değerinin oluşturduğu örneklemin biçimlendirmiş olduğu dağılım, toplam kayıp dağılım modelini oluşturur.
Şekil 12: Sıklık dağılımının şiddet dağılımı ile Monte Carlo simulasyonu metoduyla birleştirilmesi
Basel II’de tanımlanan 8 faaliyet kolu ve 7 kayıp olay türünden oluşturulan matrisin bir
hücresi için Monte Carlo simülasyonu ile oluşturulmuş olan bu toplam kayıp dağılımının
ortalaması Beklenen kayıp (EL), yüzde 99.9’luk güven aralığına (quantile) denk gelen değer
ile beklenen değer arasındaki fark Beklenmeyen kayıp(UL), bu iki değerin toplamı ise o
faaliyet kolu ve kayıp olay türüne ilişkin operayonel risk sermaye gereksinimini (OpVaR)
verir.
Bankanın faaliyet gösterdiği Basel faaliyet kollarından her birinde ortaya çıkabilecek
her kayıp olay türü için yapılması gereken bu hesaplama sonucunda matrisin bütün hücreleri
için OpVaR değerleri elde edilmelidir.
135
Operasyonel Risk Çalışma Grubu
5.
Herbir Hücre İçin Hesaplanmış Olan Operasyonel Risk Sermaye
Gereksiniminin, Hücreler Arasında Var Olabilecek Korelasyona İlişkin
Varsayımlar Dikkate Alınarak Toplanması ve Toplam Operasyonel Risk
Sermaye Gereksinimine Ulaşılması
Basel II’de tanımlanan 8 faaliyet kolu ve 7 kayıp olay türünden oluşturulan matrisin
her hücresi için ayrı ayrı hesaplanmış olan OpVaR tutarları, bankanın toplam operasyonel risk
sermaye gereksiniminin bulunması amacıyla birleştirilmelidir.
Bu aşamada, tüm OpVaR değerlerini toplayarak sonuca ulaşmak alternatiflerden biridir. Bu yaklaşım, her hücreye ilişkin operasyonel risk verilerinin birbirlerine istatistiksel
olarak tam bağımlı (perfectly correlated) olduklarını, yani aralarındaki korelasyonun 1
olduğunu (ρ=1) varsaymak anlamına gelir. Dolayısıyla, tüm olayların aynı anda olacağı
anlamını taşır ve çok muhafazakar bir bakış açısı olacaktır. Bu nedenle, bu yaklaşım gerçekçi
bir sonuç vermeyecek ve sermayenin yüksek belirlenmesine neden olacaktır.
Her faaliyet kolu-kayıp olayı türü hücresine ilişkin operasyonel risk verilerinin tam olarak bağımlı (perfectly correlated) olduklarını varsaymak gibi, birbirinden bağımsız
(statistically independent) olduklarını varsaymak da anlamlı olmayabilir. Bu yaklaşım,
olaylar arasındaki korelasyonun 0 olduğunu (ρ=0) kabul eder ve olayların birbirini belirli
ölçüde tetikleme ihtimalini hesaba katmayarak düşük bir sermaye toplamına ulaşmaya neden
olur.
Örnek:
Korelasyonun 1 olduğu durum için toplam sermayenin durumu aşağıdaki gibi gösterilebilir:
8
7
ρ = 1 → OpVaRtoplam = ∑∑ OpVaRi j = OpVaR11 + OpVaR12 + ... + OpVaR78
i =1 j =1
Korelasyonun 0 olduğu durum için toplam sermayenin hesaplanmasına ilişkin örnek
bir yöntem aşağıdaki gibi gösterilebilir:
ρ = 0 → OpVaRtoplam =
8
7
∑∑ OpVaRij2 =
i =1 j =1
2
OpVaR112 + OpVaR122 + ... + OpVaR78
Her iki varsayım da gerçek koşullara uyum göstermez. Bu nedenle, hücreler arasındaki
korelasyonun belirlenerek toplam operasyonel risk sermayesi hesabına yansıtılması gerekmektedir. Korelasyonun etkisi hesaba katılarak oluşturulan yıllık toplam kayıp, korelasyonun
1’e eşit olduğu durumdan küçük, 0 olduğu durumdan büyük bir değere ulaşılmasını sağlayacaktır.
Örnek:
Hücreler arası korelasyonun hesaba katılmasına ilişkin örnek bir yöntem:
136
Bankacılar Dergisi
Hücrelerarası bağımlılığın ölçüsü olan korelasyonun hesaba katılması için kullanılabilecek yöntemlerden biri, Copula fonksiyonudur.
Copula fonksiyonunun uygulanışı kısaca şöyle özetlenebilir:
− i Basel faaliyet kolunu, j kayıp olay türünü belirtmek üzere, Basel faaliyet kolları ve
kayıp olay türleri matrisindeki hücrelerden her biri için yıllık kayıp tutarı Xij rassal değişkenleriyle ifade edilsin.
Xij rassal değişkeninin marjinal yoğunluk fonksiyonu f(Xij) olsun.
Bu durumda matriste yıllık kayıp tutarlarını ifade eden X11, X12, ..., X17, X21,...,X87 olmak
üzere 56 rassal değişken ile f1(X11), f2(X12), ..., f7(X17), f8(X21),...,f56(X87) olmak üzere 56
marjinal yoğunluk fonksiyonu olacaktır.
Xij: yıllık kayıp rassal değişkeni
f(Xij): yıllık kayıp değişkeninin marjinal yoğunluk fonksiyonu
i: 1,...,8 Basel faaliyet kolu
j: 1,...,7 Kayıp olay türü
− Matrisin ilk iki hücresine ait marjinal yoğunluk fonksiyonlarının bileşik yoğunluğu
h(X11,X12) olsun. Eğer X11 ve X12 değişkenleri birbirinden bağımsız olsaydı, h(X11,X12) =
f1(X11).f2(X12) olurdu. Ancak aralarındaki bağımlılığı ifade etmek için bileşik yoğunluk
formülü şu şekilde değiştirilir:
h(X11,X12) = f(X11).f(X12).c(X11,X12)
Burada c(X11,X12), X11 ve X12 değişkenleri arasındaki bağımlılığı belirlemek üzere kullanılacak olan Copula’dır.
X11 ve X12 değişkenlerinin korelasyon hesaba katılmış olarak toplamını bulmak için
h(X11,X12) içinden (X11+X12) dağılımı çekilir:
Y1 = X 11 + X 12
k (Y1 ) =
∫ h( X 11 ,Y1 − X 11 )dX 11 = ∫ h(Y1 − X 12 , X 12 )dX 12
X 11
X 12
(X11 + X12) + X13 + X14 +...+ X87
(Y1 + X13) + X14 +...+ X87
(Y2 + X14) +...+ X87
(Y3 +...) + X87
Yukarıda görüldüğü biçimde birer birer tüm matris hücreleri için aynı adımlar tekrarlanır:
Y2 = Y1 + X 13
k (Y2 ) =
∫ h( X 13 ,Y2 − X 13 )dX 13 = ∫ h(Y2 − Y1 ,Y1 )dY1
X 13
Y3 = Y2 + X 14
Y1
137
Operasyonel Risk Çalışma Grubu
k (Y3 ) =
∫ h( X 14 ,Y2 − X 14 )dX 14 = ∫ h(Y3 − Y2 ,Y2 )dY2
X 14
Y2
Böylece son hücre de toplama eklenmiş ve korelasyonun etkisi hesaba katılarak yıllık
toplam kaybın bileşik dağılımı elde edilmiş olur. Ortaya çıkan sonuç, korelasyonun 1’e eşit
olduğu durumdan küçük, 0 olduğu durumdan büyük bir değere ulaşılmasını sağlayacaktır.
6. Kayıp Dağılımı Yaklaşımının Avantaj ve Dezavantajları
6.1. Kayıp Dağılımı Yaklaşımının Avantajları
Kayıp dağılımı yaklaşımı kapsamında, sermaye gereksinimi iç verileri temel alarak
hesaplanmaktadır. Bu nedenle, hesaplanan sermaye gereksinimi, ilgili bankanın kendine has özelliklerini yansıtır ve riske daha duyarlıdır.
İstatistiksel bir yöntemdir ve objektiftir.
Operasyonel riske maruz değer, 1 yıllık zaman zarfında ve belirli bir güven aralığında
maruz kalınabilecek toplam kayıp miktarını ifade eder. Bu ölçüt, kredi riski ve piyasa
riskinin ölçümünde kullanılan yöntemlerle uyumludur. Kayıp dağılımı yaklaşımının
kullanılması, operasyonel risk, piyasa riski ve kredi riski için hesaplanan sermaye gereksinimlerini istatistiksel olarak anlamlı bir şekilde biraraya getirmeyi mümkün kılar.
Yapılan bir değişikliğin kayıp sıklığına ve şiddetine ne yönde ve ne derecede etki
edeceği tahmin edilerek, söz konusu değişikliğin beklenen ve beklenmeyen kayıp tutarlarına etkisi tahmin edilebilir. Böylece, risk azaltıcı kontrollerin artırılması/azaltılması kararlarının alınması öncesinde, fayda-maliyet analizlerinin yapılması
mümkün olur.
Sigortanın risk azaltıcı etkisi, sermaye gereksinimini hesaplamalarında dikkate alınabilir.
6.2. Kayıp Dağılımı Yaklaşımının Dezavantajları
Sermaye gereksinimi, sadece geçmiş verilere dayanılarak hesaplandığı için geriye
dönük bir bakış açısı söz konusudur. Kayıp dağılımı yaklaşımına ileriye dönük bir yapı kazandırabilmek için, senaryo analizleri, skorkart verilerinden faydalanılmalıdır.
Veri kıtlığı, kayıp dağılımı yaklaşımının önündeki en büyük engeldir. Bankaların
birçoğu, özellikle bazı faaliyet kolları/olay türleri için güvenilir bir iç veritabanına sahip olmayacaktır. Bu sorun, kayıp dağılımı yaklaşımı ile elde edilen sonuçların güvenilirliğini olumsuz yönde etkileyecektir. Veri sorununu azaltmak için, iç veri tabanındaki veriler, nitel yaklaşımlardan elde edilen veriler ile desteklenebilir.
Kayıp dağılımı yaklaşımının uygulanması, yetişmiş insan kaynağı ve yazılım yatırımı
ihtiyacını doğurmaktadır. Bu nedenle, söz konusu yaklaşımı yüksek bir maliyete sahiptir.
138
Bankacılar Dergisi
B. Stres Testleri ve Senaryo Analizi
Stres altında tahmin edilen kayıp, bankanın en kötü durum senaryosu çerçevesinde tanımlanan ve sayısal hale getirilen riskinin ortaya çıkaracağı nihai maliyeti ifade eder.
Operasyonel riske maruz değer (OpVaR) hesaplaması, normal koşullar altında ne kadar riske maruz kalınabileceğine ilişkin istatistiksel ölçümler sağlamasına karşın, en uç
noktalarda gerçekleşebilecek olaylara ve olağanüstü koşul değişikliklerine bankanın duyarlılığı hakkında bilgi vermez. Bu nedenle, OpVaR yönteminin stres testleri ve senaryo analizi ile
desteklenmesi gerekir.
Stres testleri, olağan dışı büyüklükteki kayıplara neden olabilecek koşulların belirlenmesi, bunların gerçekleştiği durumların simüle edilmesi ve sonuçlarının tahmin ve tespit
edilmesi sürecidir. Senaryo analizi ise stres testi yöntemlerinden biridir.
1. Kullanım Alanları
Bankanın risk profilini daha iyi anlamak ve üst yönetime aktarmakta bir araçtır.
Bankanın risk sınırlarının ve limitlerinin tespiti için kullanılır.
Anormal koşullar göz önünde bulundularak acil durum planlarının geliştirilmesine
yardımcı olur.
Riske dayalı sermaye tahsisinde, riske maruz değer hesabına katkıda bulunmak amacıyla kullanılır.
Bir yılda yaşanacak kaybın OpVaR’ı aşması durumunda ne büyüklükte bir kayıpla
karşı karşıya kalınabileceğine ilişkin fikir verir.
Operasyonel riske maruz değer (OpVaR) tutarı yüzde 99,9’luk güven aralığı kullanılarak hesaplandığında ortaya çıkacak OpVaR tutarı, 1000 yıldan birinde (yüzde 0,1 olasılıkla)
aşılacağı tahmin edilen toplam kayıp tutarını verir. Elde edilen bu kayıp tutarı, normal
koşullar altında hesaplanan bir en kötü değer olacaktır. Stres testleri ise, toplam kayıp tutarı
OpVaR'ı aştığı takdirde yaşanacak kaybın olası büyüklüğü hakkında fikir verir.
Stres testleri, kısa dönemli ve yukarı yönlü yaklaşımlardır. Yani, iç süreçlerin incelenmesi ve risklerin nedenlerinin belirlenmesinden yola çıkılarak bankanın maruz olduğu
riskin boyutu belirlenir. Bu aşamada, hem niteliksel hem de niceliksel yöntemler kullanılır.
Bankalar, düzenli ve ayrıntılı olarak stres testi ve senaryo analizi programları uygulamalıdır.
En kötü durum senaryosu çerçevesinde tanımlanan ve sayısallaştırılan riskin ortaya çıkarabileceği kayıpları karşılayabilecek tutarda özkaynak ayrılmalıdır.
2. Senaryo Analizi
Senaryo analizi, koşullar normalin dışına çıktığı takdirde risk etkenlerinin değerlerindeki değişimlerin ne olacağını ve bunların bankaya ne gibi olumsuz etkilerde bulunabileceğini
sınamak için kullanılan bir stres testi yöntemidir. Risk etkenlerinin normal olarak değerlendirilebilecek sınırlar içerisinde değişebilecekleri varsayımıyla yapılan hesaplamalarda gözden
kaçırılabilecek olan olağanüstü durumların etkilerini inceleyebilme olanağı sağlar.
Senaryo analizi kapsamında, bir veya birkaç risk etkeninin değerinde belli oranlarda değişmeleri içerecek şekilde tasarlanmış senaryoların yanısıra deprem, terörist saldırısı vb.
olağandışı/nadir olayların olması durumunda bunun banka üzerindeki etkilerinin ne olacağı
139
Operasyonel Risk Çalışma Grubu
incelenir. Kullanılacak senaryolar belirlendikten sonra bunların olası etkileri sayısallaştırılmalıdır. Sayısallaştırma kapsamında, değerlerinde varsayımsal değişmeler öngörülen risk
etkenlerine duyarlılık belirlenir ve bu senaryoların bankaya toplam etkisi hesaplanır.
Varsayımsal değişiklik uygulanacak olan risk etkenlerini tespit etmek, risk yöneticilerinin dikkatle üzerinde durması gereken, uzmanlık gerektiren, zorlu bir süreçtir. Kayıp
verilerinin ayrıntılı ve eksiksiz olarak toplanabilmesi, değerlendirilebilmesi ve sistemin
işleyişine aşinalık, bu süreçte avantaj sağlar. Çünkü, tarihi verilerin risk etkenleri ile ilişkisini
aylar, hatta günler bazında değerlendirebilmek, senaryo analizinin ve stres testlerinin
güvenilirliğini artıracaktır. Ancak, kayıplara ve risk etkenlerine ilişkin verilerin özellikle
başlangıç aşamasında tam olmasının beklenemeyeceği, bu nedenle kullanılacak olan
varsayımların ve belirsizliklerin sağlam temeller üzerine dayandırılması gerekliliği unutulmamalıdır.4
Kayıp senaryolarının oluşturulması için öz değerlendirme yaklaşımı kullanılabilir. Öz
değerlendirme yöntemi, iş birimi yöneticilerinin kendi iş birimlerindeki risk profilini
belirlemesi, bu risklere ilişkin kontrollerin güçlü ve zayıf yönlerini değerlendirmesi ve öznel
tahminler oluşturması yoluyla Banka’nın maruz olduğu risklerin ölçülmesi ve yönetilmesi için
kullanılan bir risk yönetim sürecidir. Bu yaklaşım, bankanın risk profilini belirleme ve analiz
etme sürecine iş birimi yöneticilerini dahil ettiğinden, senaryoların uzman görüşü ile
detaylandırılmasını sağlar.
Örnek:
Bir iş kolunda gerçekleşen operasyonel risk kayıplarının ve olası risk etkenlerine ilişkin verilerin gün bazında sayısal olarak izlenebildiğini varsayalım. Elde edilen verilere ve risk
yöneticilerinin sistemin işleyişi hakkındaki birikimlerine dayanarak riskin temel etkenleri ve
kaybın büyüklüğüne ilişkin fikir verecek göstergeler tespit edilir. Bu aşamada, öz değerlendirme yöntemiyle iş birimi yöneticilerinin görüşlerinden de yararlanılabilir. Bilgi toplanacak
risk etkenleri, o gün gerçekleşen işlem sayısı, sistem aksaklıklarının sayısı veya personel
sayısı gibi birçok faktör olabilir. Bu faktörlerin, iş kolundaki kayıplar üzerindeki etkisinin
sayısallaştırılması gerekir.
Risk etkenlerinin kayıplar üzerindeki etkisini formüle etmek için kullanılabilecek yöntemlerden biri regresyon analizidir. Regresyon analiziyle kaybın risk etkenleri cinsinden bir
denklemi elde edilir. Bu denklemin değişkenleri olan risk etkenlerine verilecek değişik
değerler, hesaplanan toplam kayıp tutarını değiştirecektir. Yaratılacak türlü senaryolarla risk
etkenlerinin alabileceği değerler normalin dışına çıkarılarak toplam kaybın bu değişimlere
bağlı olarak aldığı değerler gözlemlenir ve sistemin risk etkenlerine karşı hassaslığı değerlendirilir. Böylece gerçek hayatta karşılaşılabilecek olağandışı olayların sistem üzerinde
simülasyonu yoluyla olası sonuçların öngörülmesi sağlanmış olur.
Risk etkenlerinin kayıplar üzerindeki etkisini formüle etmek için kullanılabilecek
yöntemlerden bir diğeri de Bayes ağları yaklaşımıdır. Bayes ağları, bir riskin ortaya çıkmasına
yol açan faktörler ile risk arasında ilişki kurmak için kullanılan istatistiksel bir modeldir.
Uzman görüşlerinden yararlanılarak değişkenler ve aralarındaki neden-sonuç ilişkisi formüle
edilerek risk analizi gerçekleştirilir. (Bkz. Bayesgil metodlar-Bayes ağları)
140
Bankacılar Dergisi
3. Stres Testleri ve Senaryo Analizinde Karşılaşılabilecek Sorunlar
Stres testi uygulanırken izlenen standart bir süreç veya etkileri tespit edilebilecek standart senaryolar yoktur. Ayrıca, risklerin gerçek nedenlerinin ve risklere etki eden temel
faktörlerin belirlenmesi, uzun ve zorlu bir süreçtir. Bu faktörlerin yaratacağı toplam kaybın
doğru bir şekilde formüle edilmesi ise yoğun istatistiksel çalışmalar gerektirir. İstatistiksel
çalışmaların doğru sonuçlar vermesi ise kayıp verilerinin kalitesi ve detayların çeşitliliğiyle
doğrudan bağlantılıdır. Kayıplara ve risk etkenlerine ilişkin verilerin özellikle başlangıç
aşamasında tam olması beklenemeyeceğinden, kullanılacak olan varsayımların ve yöntemlerin
sağlam olması gerekir. Dış veri kaynaklarından yararlanılması, yüksek şiddet-düşük sıklık
gösteren olaylara ilşkin veri eksikliğinin giderilmesi ve başka kurumların başına gelen
olayların yarattığı etkilerin gözlemlenmesi olanağı sağlaması nedeniyle gereklidir.
Tüm bu nedenlerle stres testi ve senaryo analizi süreci, risk yöneticilerinin bilgi ve tecrübelerine dayanan, nesnel ve öznel verilerin hassas bir şekilde entegre edilmesini gerektiren,
ancak, etkin kullanıldığında kurumun risk profili hakkında önemli fikir sağlayan bir yönetim
aracıdır.
C. Skorkart Yaklaşımı
Skorkart yaklaşımı, riskleri tanımlamaya, yönetmeye ve azaltmaya yönelik kullanılan
kalitatif yöntemlerden biridir. Pek çok finansal kurum, risk ve kontrol özdeğerlendirme
çalışmaları doğrultusunda anahtar risk göstergelerini ve kontrol noktalarını belirlemektedir.
1. Skorkart Yaklaşımının Uygulama Kapsamı
i) Risk Tanımlama:
Riski yönetmek üzere operasyonel riski sayısallaştırmadan önce organizasyonun maruz olduğu yüksek riskler tanımlanmalı ve bu riskleri izlemek ve kontrol etmek üzere bir
yöntem geliştirilmelidir. Bir kurumun risk profili tarif edilebildiğinde ve izlenebildiğinde üst
yönetim riski azaltmaya yönelik bir programı hayata geçirebilir. Bunun için çok çeşitli
yöntemler izlenebilir. Yaygın olarak kullanılan yöntem, üst yönetimle görüşmeler aracılığıyla
kurumun hedeflerinin belirlenmesi ve bu hedeflere ulaşmaya engel olabilecek durumların
tespit edilmesidir. Buna alternatif olarak, süreçlerin ve süreçleri bilen yöneticiler aracılığıyla
bu süreçlerdeki risklerin tanımlanması olabilir. Hedef veya süreç gibi bir bağlam olmazsa
riskin hangi seviyede analiz edileceği belirsizleşecektir. Bir riskin analizi, riskin sahibinin
belirlenmesi, kuruma etkisinin ve olabilirliğinin değerlendirilmesi ile sağlanır.
Riskin sahibinin belirlenmesi belirli bir kişinin sorumluluk alarak riski yönetmesini
ve risk azaltıcı faaliyetleri yürütmesini sağlar.
Riskin etkisi genel olarak yüksek, orta, düşük olarak tarif edilir. Fakat çoğunlukla,
ileri safhalarda bu, sayısal bir değere dönüşür ve bu şekilde izlenir.
Benzer şekilde frekans da yüksek, orta, düşük olarak tarif edilir. Fakat yüzde veya
zaman olarak ifade edilmeye yönelinir.
Risk özdeğerlendirme çalışmasının başarısı, üst yönetimin sürece destek verme derecesine, eylem planlarının anahtar operasyonel zayıflıkları işaret etmesine ve üst/orta kademe
yöneticilerin riski sahiplenerek yönetme istekliliğine bağlıdır.
141
Operasyonel Risk Çalışma Grubu
ii) Kontrollerin Tanımlanması:
Benzer bir süreç kontroller için de uygulanır. Kontrolün düzgün yürütülmesi için
kontrol sorumlusu tanımlanır. Kontrolün önemi ve verimliliği görüşmeler aracılığıyla
değerlendirilir. Kontrolün verimliliği, kontrolün riski azaltmak için kendiliğinden ne kadar
etkili olduğuna ve ne şekilde uygulandığına göre değerlendirilmelidir. Böyle bir değerlendirme süreci, eylem planlarının net olmasına olanak sağlar.
iii) Risk-Kontrol İlişkisinin Kurulması:
Risk ve kontrol değerlendirmelerinin sonucunun kullanıldığı ve çeşitli senaryolar
aracılığıyla simülasyonların yapıldığı bir modelleme yaklaşımı, organizasyona kontrollerden
önce ve sonraki risk düzeyini belirleme olanağı sağlar.
Organizasyonda risk bilincini artırmak üzere çoğunlukla riskler ve kontrollerin tanımlanmasının ardından anahtar risk göstergeleri belirlenir. Anahtar risk göstergeleri, mevcut
risk yönetiminin ne şekilde yürütüldüğünün, riskin şiddetinin, sıklığının ve kontrolün
verimliliğinin gözden geçirilmesini sağlar. Benzer şekilde operasyonel kayıp ile ilgili
içveriler de riskin yeniden değerlendirilmesi ve kontrolün yeterliliğini ölçmek için
kullanılabilir.
vi) Skorkart Yaklaşımı:
Skorkart yaklaşımı bir kurumun tanımladığı riskler ve kontrollere bağlı olarak esnek
bir yaklaşımla sermayenin hesaplanabilmesini sağlar. İç/dış verinin toplanabilmesi için bir
veritabanı oluşturmadan önce, süreç risk öz değerlendirme çalışmalarıyla başlatılabileceği
için risk yönetimi hakkında kurum içi bilgi, becerinin artmasına ve risk kültünün gelişmesine
olanak sağlar.
Skorkart, basit olarak bir kurumun risk ve kontrollerine ilişkin bir liste olarak tanımlanabilir. Risk, riskin sahibi, olabilirliği, etkisi, kontrolü, kontrolün sahibi, kontrolün tarifi
ve kontrolün etkisi gibi detayları içerir. Yargısal bir yaklaşım olmasına rağmen, geçmiş
istatistiki bilgiler yerine işkollarının gelecek hakkındaki beklentilerine göre şekillenir.
Bir skorkart en azından riskin tarifi, riskin frekansı ve riskin etkisi bilgilerini içermelidir. Ancak bu durumda kontrolün risk azaltıcı etkisi değerlendirilemeyecek ve kaynak
tahsisi buna göre planlanamayacaktır.
Bir skorkart kontrolleri geliştirmeyi hedefleyen eylem planlarını ve çeşitli tanımlayıcı bilgileri içerebilir. İleri versiyonlarında riskin mevcut durumunu izlemek üzere anahtar
risk göstergeleri eklenebilir.
Kayıp verileri toplandıkça, riskler ile ilişkilendirilerek bu bilgiler skorkartlarda yer
alabilir. Kayıplar skorkartta yer alan etki ve olabilirlik değerlerini gözden geçirmek üzere
kullanılabilir ve üst yönetime organizasyonun riskleri ve kontrolleri hakkında güncel bilgi
sunarlar.
Toplanan veriler operasyonel risk için sermaye miktarını hesaplamak üzere kullanılacaksa risklerin gerçekleştiği ve kontrollerin başarısız olduğu durumlar simüle edilir ve
142
Bankacılar Dergisi
simülasyon sonucunda elde edilen dağılım analiz edilir. Bu piyasa riski modellemesine
benzer bir süreçtir.
Skorkart listesinde yer alan riskleri sermaye yeterliliği için kullanımı için skorkartta
yer alan kalemlerin sayısal değerler olması gerekir. (örneğin olabilirlik için gerçekleşme
yüzdesi ,etki için parasal bir değer, kontrol başarısı için yüzdesel bir ifade). Risk ve kontrolün sahipleri için de bir korelasyon değeri verilebilir. (ilişkisiz ise 0 korelasyon, -1 ise zıt
korelasyon, +1 ise tam korelasyon)
iv) Model Simülasyonları
Model Simülasyonları, kullanılan teknoloji, simülasyonun verimliliği, risk ve kontrol
verilerinin tam olmasına bağlı olarak 3 şekilde yapılabilir.
1-Kontrol odaklı: Öncelikle kontrollerin simülasyonu, bir kontrolün başarısız olması
halinde risklerin simülasyonu
2-Risk odaklı: Öncelikle risklerin simülasyonu, bir riskin gerçekleşmesi halinde kontrollerin simülasyonu
3- Risk ve kontrol odaklı: Risklerin ve kontrollerin birlikte simülasyonu
İleri ölçüm yaklaşımlarında riskler için farklı dağılım modelleri kullanılarak analizler
yapılabilmektedir. Ancak risklerin etki ve olabilirliğinin saptanmasının öznel bir süreç
olduğu düşünülürse, simülasyonda kullanılacak dağılım türünün istatistiksel yöntemlerle
tahmin edilmesi gerekli olmayacak ve aslında sonuçların kalitesine de çok etki etmeyecektir.
Bu nedenle “normal dağılım” varsayımı yapılabilir.
Riskler genelde başka risklerle ilişkilidir. Bu durum skorkartlara yansıtılmalıdır.
Risklerin veya kontrollerin korelasyonu saptanarak bağımlılık ilişkisi simülasyonda yer
alabilir ve gerçeğe daha yakın bir sonuç elde edilir.
Bazı simülasyon modellerinde tüm kontrollerin yapılmasına rağmen riskin gerçekleşmesi durumu da simülasyonun içinde yer alabilir.
v) Brüt ve Net Riskin Sayısallaştırılması:
Kurumların brüt riski ve kontrolün değerini parasal değerler üzerinden sayısallaştırabilmeleri kontrol kaynaklarının daha verimli bir şekilde planlanmasına olanak sağlar. Brüt
riskin bilinmesi durumunda kurumlar risklerini yüksek/orta/düşük gibi ifadelerle değerlendirmek yerine parasal etkisine göre sıralayabilir. Bir kontrol aracılığıyla riskin azaltılma
derecesi yine parasal değerlerle veya yüzdesel olarak ifade edilebilir. Böyle bir değerlendirmenin sonucunda yüksek bir risk için aşırı kontrol söz konusu ise kontrol kaynaklarının bir
kısmı daha küçük risklere kaydırılabilir. Kontrolden önceki kayıpların miktarı kontrol sonrası
kayıpların miktarı ile karşılaştırılarak kontrolün net etkisi mutlak ve oransal olarak hesaplanabilir.
vii)
Risk İştahı:
Bir organizasyonun operasyonel risk iştahını parasal değerlerle ifade edilebilmek zordur. Bunun için genellikle “muhafazakar”, “agresif” gibi ifadeler kullanılır. Sayısal olarak
143
Operasyonel Risk Çalışma Grubu
risk iştahı ise organizasyonun kabul ettiği risk seviyesini muhtemel kayıp miktarı ve
frekansın ölçümü ile belirlenebilir.
viii)
Stres Testi ve Senaryo Analizi:
Risk ve kontrollerinin sayısallaştırılmasının bir avantajı da risk envanteri üzerinde
analize imkan verebilmesidir. Böylelikle bir kontrolün kaldırılması ile riskin ne kadar
artacağı veya kontrol kalitesinin artırılarak riskin ne kadar azalacağı senaryo analizleri ile
belirlenebilir.
2. Skorkart Yaklaşımının Zayıf ve Güçlü Yönleri
Risk ve kontrol değerlendirilmesinin yapılması bir organizasyona önemli ölçüde değer katar. Kayıp verilerinin kullanıldığı modellerle karşılaştırıldığında riskin daha erken
sayısallaştırılması olanağını sunar. Bir organizasyonun maruz olduğu risklerin sayısallaştırılması ve bu riskleri azaltmaya yönelik kontrollerin belirlenmesi risk ve kontrol arasındaki
karşılıklı etkileşimi ortaya koymayı sağlar. Bu yöntem, riski azaltmaya yönelik kontrollerin
verimliliğinin hızlıca tespitini sağlar; zayıf kontrollerin belirlenmesi ve kontrollerin iyileştirilmesi için kaynakların en doğru şekilde tahsisini sağlar. Sayısallaştırılmış bir risk envanterinin olması, risklerin ve kontrollerin “eğer (what-if) analizleri” aracılığı ile stres testlerinin
yapılmasını sağlar.
Risk öz değerlendirme çalışmaları kayıp veritabanlarındaki bilgilere dayanan
modellemeler kadar gelişkin olmasa da kurum içi “risk farkındalığı” yaratmak ve kontrolü
sağlamak üzere ileri bir risk yönetim çerçevesi ve kültürü oluşturulmasını sağlar. Kayıp
verilerine dayanan modellemelerden üstün yanı operasyonel risk sermayesinin hesaplanmasında sadece geçmiş veriler üzerine odaklanmak yerine gelecekteki riskleri öngörmeye
olanak sunmasıdır. Çoğunlukla tecrübe edilen riskler için yeterli kontrol sağlanmaktadır oysa
gelecekteki risklerin belirlenmesi ve gerekli kontrollerin tarifi için riski azaltmaya yönelik
bir yöntem daha işlevseldir. Bu yöntemin en zayıf yönü faaliyet kolu yöneticileri tarafından
doldurulacak olan skorkartların göreceli olarak öznel olması ve sorulacak soruların, ölçüm ve
puanlama yönteminin sık sık gözden geçirilmesi gerekliliğidir. Yaklaşımın öznel olmasının
getirdiği olumsuzluğu azaltmak için geçmiş kayıp tutarları ile öz değerlendirme sonuçları
skorkart yaklaşımının sonuçlarının doğrulanmasında kullanılmalıdır.
D. Operasyonel Risk Ölçümünde Bayesgil Yöntemler
Gelişmiş ölçüm yaklaşımlarının kullanılmaya başlanılmasının ilk aşamalarında,
bankaların birçoğu, özellikle bazı faaliyet kolları/olay türleri için güvenilir bir iç veritabanına
sahip olmayacaktır. Bu nedenle, iç veritabanındaki verilerin, nitel yaklaşımlardan elde edilen
veriler ile desteklenmesi gerekecektir. Bayesgil yöntemler, bu soruna iyi bir çözüm sunmaktadır. Çünkü Bayesgil yöntemler, nitel ve nicel bilgileri, istatistiksel temellere dayanarak,
birleştirebilmektedir.
Bu bölümde, Bayesgil yöntemlerin operasyonel risk ölçüm ve yönetimindeki iki
kullanım alanına yer verilecektir. Bunlar;
•
•
144
Bayesgil çıkarsama ve
Bayes ağlarıdır.
Bankacılar Dergisi
Söz konusu kullanım alanlarının her ikisinin de istatistiksel dayanağı Bayes kuralı olduğundan, öncelikle Bayes kuralı kısaca açıklanacaktır.
1. Bayes Kuralı
Bayesgil metotların dayanak noktası, X ve Y olaylarının koşullu olasılıklarına ilişkin
teoremdir. Bu teoreme göre;
P(X, Y) = P(X|Y)*P(Y) = P(Y|X)*P(X)
Yukarıda yer verilen denklem aşağıdaki gibi yeniden düzenlendiğinde Bayes kuralına ulaşılır:
P(X|Y) = P(Y|X)*P(X) / P(Y)
Bu kurala göre X’in olasılık dağılımı, Y hakkında elde edilen bilgiler ışığında güncellenir.
2. Bayesgil Çıkarsama (Bayesian Inference)
Klasik istatistikte, bir modelin parametrelerinin sabit olduğu fakat bilinmediği
varsayılır. Ancak, Bayesgil yaklaşımda, modelin parametrelerinin de rassal değişken olduğu
varsayılmaktadır. X’in gözlemlenmiş verileri (ör. operasyonel riskten kaynaklanan kayıpları),
θ’nın ise modelin parametrelerini ifade ettiğini varsayalım. Bayes teoremi, X verilerinin
gözlemlenmesinden sonra, θ’nın X’e bağlı koşullu olasılık dağılımının bulunmasında
kullanılır. Bayes teoremi kullanılarak, söz konusu dağılıma şu şekilde ulaşılabilir:
p(θ | X) =
p(θ )p(X | θ )
p(θ )p(X | θ )
=
p(X)
∫ p(θ ) p(X | θ )∂θ
Yukarıdaki denklemde p(X) bir ölçeklendirme sabiti olarak görev yaptığından, Bayes
teoremi yaygın olarak şu şekilde ifade edilmektedir:
p(θ|X) α p(θ) * p(X|θ) yani;
Son dağılım α Ön dağılım * Olabilirlik fonksiyonu
•
Operasyonel risk yönetimi açısından bakıldığında Bayesgil tahmin, objektif veriler ile
sübjektif verileri bir araya getiren bir parametre tahmin yöntemidir. “Objektif” veriler
bankanın iç verileridir. “Sübjektif” veriler ise, bir dış veritabanından elde edilen (dolayısıyla bankaya tam olarak uygun olmayan) veriler, uzman görüşleri ile oluşturulan risk
skorları veya yapılan senaryo analizleri olabilir.
•
Ön olasılık dağılımı, verinin gözlemlenmesinden önce parametre değerlerine (θ) ilişkin
var olan kanılar ile oluşturulan olasılık dağılımıdır. Diğer bir deyişle ön olasılık dağılımı,
θ hakkındaki bilgi birikimini (ya da tahmini) yansıtır. Sübjektif veriler, ön olasılık dağılımının oluşturulmasında kullanılır.
•
Olabilirlik fonksiyonu, parametreler veri iken örneklemin olabilirliğini ifade eder.
Objektif veriler kullanılarak olabilirlik fonksiyonu oluşturulur.
145
Operasyonel Risk Çalışma Grubu
•
Son dağılım ise, ön olasılık dağılımı ve olabilirlik fonksiyonunun çarpımı ile ifade edilir.
Yani ön kanıları ve örneklemden elde edilen bilgiyi bir araya getiren bir dağılımdır. Bayes
teoremi ön olasılıkların revizyonunu sağlar.
Ön Olasılık
Dağılımı
•
Ek (Yeni) Bilgi
Bayes Teoremi
Son Olasılık
Dağılımı
Eğer gerek duyuluyorsa, son dağılım kullanılarak parametrenin değerinin tahmin edilmesi
mümkündür, buna Bayesgil tahmin denir.
Örnek 1’de yukarıda yer verilen süreç açıklanmaktadır.5:
C Bankasında, dolandırıcılık olaylarına ilişkin skorkart çalışması yapılmıştır. Bu çalışmada elde edilen
verilere göre, bankadaki uzmanlar ortalama dolandırıcılık olasılığının yüzde 5 seviyesinde oluşmasını
beklemektedirler. Uzmanlara göre, en kötü senaryo, (yüzde 99’luk yüzdelik dilimde) dolandırıcılık olasılığının
yüzde 10 seviyesine çıkmasıdır. Ortalama olasılığa ek olarak, en kötü senaryonun belirlenmesi, uzman
görüşünün ne derece kesin olduğunun (yani varyansının) ifade edilmesi açısından önemlidir. Bu bilgiler
doğrultusunda bir ön dağılım oluşturulacaktır. Aşağıda yer verilen beta dağılımı, ortalaması ve varyansıyla
uzman görüşünü yansıtmaktadır:
f1(p) α p4(1-p)94
Bankada toplanan dolandırıcılık verisine göre, veri gözlem süresinde gerçekleştirilen 60 işlemden 6’sında
dolandırıcılık olayı meydana gelmiştir. İç veritabanına dayanarak aşağıda yer alan beta dağılımına sahip
olabilirlik fonksiyonu oluşturulacaktır:
f2(p) α p6(1-p)54
İki fonksiyonun çarpımı, son dağılımı verecektir.
f3(p) α p10(1-p)148
Parametrenin Bayesgil tahmini, son dağılımın ortalamasına6 yani 0,0688’e eşittir. Eğer Bayesgil yöntem
kullanılmasa ve sadece iç veritabanından elde edilen bilgi ile bir tahmin yapılsa kayıp olasılığı 6/60=0,10 olarak
tahmin edilecektir. Bayesgil yöntem kullanılarak, uzman görüşünden de faydalanılabilmektedir.
Sübjektif veriler ne kadar kesinse, Bayesgil parametre tahmini uzman görüşüne o kadar yakın olacaktır. Bu,
Bayesgil yöntemin diğer bir güçlü yönüdür. Eğer, uzmanların görüşü daha kesin olsaydı (varyans daha düşük
olsaydı); örneğin uzmanların oluşturduğu en kötü senaryo, (yüzde 99’luk yüzdelik dilimde) dolandırıcılık
olasılığının yüzde 8 seviyesine çıkması olsaydı, ön dağılım ve son dağılımı aşağıdaki gibi olacaktı:
•
f1(p) α p19(1-p)379
•
f3(p) α p25(1-p)433
Parametrenin Bayesgil tahmini ise, 0,0565’e eşit olacaktı. Uzman tahminine göre ortalama dolandırıcılık
olasılığı 0,05 iken iç veritabanında gözlemlenen ortalama dolandırıcılık olasılığı 0,1’dir. Görüldüğü üzere
uzman görüşü kesinleştikçe, parametrenin Bayesgil tahmini 0,0688’den 0,0565’e gerilemiş ve uzman görüşüne
yaklaşmıştır. (Bkz. Şekil 13
3
Şekil: 13
146
Bankacılar Dergisi
Parametre tahmininin sadece objektif verilere dayanılarak yapılması gerektiğini
savunan kişilerce, sübjektif değerlendirmeleri de dikkate alan Bayesgil yöntemlere karşı
çıkılmaktadır. Ancak Bayesgil çıkarsamanın, klasik çıkarsamaya göre bazı önemli üstünlükleri bulunmaktadır:
•
•
•
•
Objektif ve sübjektif verileri -istatistiksel temellere dayandırarak- bir araya getirebilir. Bu
sayede, sadece iç kayıp verileriyle sınırlı kalınmayarak, ileriye dönük bir yapı oluşturulabilir.
Objektif ve sübjektif verilerden hangisi daha güvenilir/kesin ise, parametre tahmini sadece
o veriler kullanılarak elde edilecek sonuca daha yakın olur.
Gelişmiş bankaların pek çoğu, iç verilerini senaryo analizi, skorkart yöntemi gibi
yöntemlerle desteklemektedir. Ancak bu verilerin tahmin sürecine nasıl dahil edildiği
bankadan bankaya değişiklik göstermektedir. Bayesgil metotlarda, sübjektif veriler sürece
sadece ön olasılık dağılımı aracılığı ile dahil edilebilmektedir ve bu sayede süreç kolayca
denetlenebilir.
Ön olasılık dağılımlarının oluşturulabilmesi için süreçler, faaliyetler bazında operasyonel
risklerin belirlenmesi ve değerlendirilmesi gerektiğinden, operasyonel risk yönetimini ve
kültürünü geliştiren bir yöntemdir.
3. Bayes Ağları
Bayes ağları, bir riskin ortaya çıkmasına yol açan faktörlerin olasılık dağılımı ile
riskin çok değişkenli olasılık dağılımı arasındaki ilişkiyi kuran istatistiksel bir modeldir.
Bayes ağları, rassal değişkenleri temsil eden düğümler (nodlar) ve bu değişkenler arasındaki
neden-sonuç ilişkisini temsil eden bağlantılardan oluşur. Şekil 14’te basit bir Bayes ağının
çatısı görülmektedir.
Şekil 14
A ve B düğümleri, C düğümünü etkileyen faktörleri temsil etmektedir. Örneğin, C
personel devir hızını temsil ediyorsa, A ve B, sağlık ve iş güvenliği seviyesini ve ücret
yapısını temsil ediyor olabilir. Operasyonel risk yönetimi açısından bakıldığında, A ve B gibi
riskin gerçekleşme ihtimalinde etkisi olan ve “başlangıç düğümü” adı verilen faktörler, risk
yöneticilerince belirlenmiş olan anahtar risk faktörlerini (key risk drivers) temsil edebilir.
“Hedef düğüm” adı verilen C ise anahtar risk göstergelerini (key risk indicators) temsil
edebilir.
Ağdaki her bir değişken için sübjektif kanılara dayanılarak bir ön olasılık dağılımı belirlenir. Bayesgil analiz sürecinde, ağdaki değişkenlere ilişkin yeni bilgiler edinildikçe
sübjektif tahminler iyileştirilir.
Aşağıda yer alan adımları izleyerek, Bayes ağlarını oluşturmak mümkündür:
147
Operasyonel Risk Çalışma Grubu
•
•
•
Öncelikle ağ topolojisi oluşturulmalıdır. Diğer bir deyişle, uzman görüşlerinden faydalanılarak değişkenler ve bu değişkenler arasında neden-sonuç ilişkisi belirlenmeli ve bir
operayonel kayıp modeli oluşturulmalıdır. Ağ topolojisi, uzmanların ilgili operasyonel
riskin oluşum sürecini nasıl yorumladığını yansıtır, dolayısıyla ağ topolojisini oluşturmanın tek bir yolu yoktur.
Bayes ağında yer alan “başlangıç düğümleri”nin tümü için olasılık dağılımı saptanmalıdır.
Ayrıca hedef düğümlerinin başlangıç düğümlerine bağlı koşullu olasılık dağılımları saptanmalıdır. Sözkonusu olasılık dağılımları, parametreler hakkında sahip olunan ön bilgiler
ışığında oluşturulur. Bu olasılık dağılımlarının oluşturulmasının ardından, bu dağılımlar
kullanılarak hedef düğümlerinin olasılık dağılımları hesaplanabilir.7
Operasyonel risklerin daha etkin yönetilmesi için, oluşturulan bir Bayes ağı karar ve fayda
düğümleri eklenerek geliştirilebilir. Bu sayede, hedef düğümünde yer alan bir operasyonel
riskin azaltılması için uygulanacak kontrolün maliyetinin, sağladığı yarardan daha düşük
olup olmadığı belirlenebilir.
Operasyonel risk yönetimi ve operasyonel riske esas sermaye tahsisinin bir bütün olarak gözönünde bulundurulabilmesini sağlamak için, hedef düğümleri olay türü/faaliyet kolu
bazında kayıp olaylarının sıklığını ve şiddetini temsil eden bir Bayes ağı oluşturulabilir. Diğer
bir deyişle, oluşturulan Bayes ağı, sıklık ve şiddet dağılımlarını, anahtar risk faktörlerinin bir
fonksiyonu olarak modelleyebilecektir. Böylece, operasyonel risk yönetimi ve risk azaltımı,
doğrudan sermaye tahsisi ile ilişkilendirilebilecektir. Ayrıca, kapsamlı bir şekilde oluşturulan
sözkonusu Bayes ağında olay türü/faaliyet kolları arasındaki korelasyonlar da dikkate alınmış
olacaktır.8
Bayes ağları kullanılarak senaryo analizi ve nedensel analiz yapılabilir. Aslında, Bayes
ağlarının en güçlü yönlerinden biri bu analizlerin kolayca yapılabilmesine imkan tanımalarıdır:
•
•
Senaryo analizi: Bayes ağı kullanılarak, risk faktörlerinin olasılıklarının değiştirilmesinin
riskin gerçekleşme olasılığı ve dolayısıyla kayıp tahmini üzerindeki etkisi incelebilir.
Örneğin, bir banka, çalışanları için sağlık sigortası sağlamayı bırakmasının personel devir
hızına etkisini Bayes ağı aracılığıyla inceleyebilir.
Nedensel analiz: Operasyonel kayıp olaylarına ilişkin yeni veriler ışığında, anahtar risk
faktörlerinin (başlangıç düğümlerinin) olasılıklarının güncellenmesidir. Meydana gelen
operasyonel kayıp olaylarının nedenlerinin analiz edilmesi açısından kullanışlı bir yöntemdir.
3.1. Bayes Ağlarının Avantajları ve Dezavantajları
Avantajları:
•
•
•
•
148
Operasyonel riske yol açan sebeplerin analiz edilebilmesine olanak tanır.
Bayes ağları kullanılarak kolaylıkla senaryo analizi yapılabilir. Böylece sadece geçmiş
verilerle sınırlı kalınmayarak, ileriye dönük bir yapı oluşturulabilir.
Kontrol uygulanmasına ilişkin kararların alınmasında yol gösterici olarak kullanılabilirler.
İç ve dış verilerin, senaryo analizinin ve iş ortamını ve iç kontrol sistemlerini yansıtan
başka faktörlerin aynı modelde kullanılmasına imkan verir.
Bankacılar Dergisi
•
Kapsamlı bir şekilde oluşturulan bir Bayes ağında olay türü/faaliyet kolları arasındaki
korelasyonlar dikkate alınmış olacaktır.
Dezavantajları:
•
•
•
Bayes ağlarının topolojisi, uzman görüşleri doğrultusunda oluşturulur; bu nedenle
sübjektiftir.
Bankanın tüm faaliyet kollarını ve tüm olay türlerini yansıtacak bir Bayes ağının
oluşturulması çok güç bir süreçtir.
İş süreçleri dinamik bir yapıya sahip olduğundan, Bayes ağlarının düzenli olarak gözden
geçirilmesi ve halen geçerli olup olmadıklarının sorgulanması gerekmektedir.
II. Türk Bankacılık Sektöründe Kullanılan Operasyonel Risk İleri Ölçüm
Modelleri
1. Operasyonel Risk Kayıp Verilerinin Toplanması
Çalışmaya toplam 12 banka katılmış olup 1 banka hariç çalışmaya katılan bankaların
tamamı operasyonel risk kayıp verilerini toplamaktadır.
2. Operasyonel Kayıp Verisi Toplanıyorsa Ne Şekilde Toplandığı / İş Süreçlerinin
Nasıl Şekillendirildiği
i.. Merkezi veya şubelerin/birimlerin giriş yaptığı dağınık sistemler:
Merkezi Sistemler: 6 banka operasyonel kayıp verilerini merkezi olarak toplamaktadır.
Merkezi sistemlerde şubeler ve birimler kayıp verilerini direkt operasyonel risk yönetimine
raporlamamamaktadır. Merkezi olarak toplanan veriler ağırlıklı olarak İç Kontrol Merkezi,
Teftiş Kurulu, Muhasebe, İnsan Kaynakları vb bölümlerde biriken operasyonel kayıp
verilerinin toplanması şeklinde gerçekleşmektedir. Merkezi sistemlerde Operasyonel Risk
Yönetimi söz konusu bölümlerin tespit ettiği veya kaydettiği verileri belirlemiş olduğu
kriterlere uygun olarak kategorize etmektedir.
Dağıtık Sistemler: 5 banka operasyonel kayıp verilerini dağıtık sistemlerle toplamaktadır. Dağınık sistemlerde şubeler ve birimler günlük bazda kayıp verilerini direkt olarak
operasyonel risk yönetimine bildirmektedir. Söz konusu bildirimler genel olarak banka içinde
kurulmuş olan intranet sistemleri vasıtasıyla veya hazırlanan şablonların sistemden doldurularak gönderilmesi şeklinde gerçekleşmektedir. Operasyonel risk kayıplarının uygun yönetim
kademeleri onayından geçmesi sistem tarafından sağlanmakta ve söz konusu kayıp son onay
mercii olarak operasyonel risk yönetimi bölümüne gelmektedir. Burada dikkat çekici
hususların başında bazı uygulamalarda operasyonel kayıpları operasyonel risk yönetiminin
onayından geçmeksizin giderleşememekte ve işlem yapılmak üzere muhasebe bölümüne
iletilmesi için operasyonel risk yönetiminin onayından geçmesi gerekmektedir. Söz konusu
uygulama Basel II’ye uygun olarak kayıpların muhasebeyle mutabakatı ve kayıpların
toplanması açısından kendi içerisinde bir kontrol mekanizması yaratmaktadır.
ii. Kayıp verisi toplama amacıyla banka bünyesinde geliştirilen veya dış kaynaklardan
satın alınan bir operasyonel risk aracının kullanılıp kullanılmadığı:
149
Operasyonel Risk Çalışma Grubu
Operasyonel risk kayıp verisi toplayan toplam 11 bankadan 7’si excel programını kullanırken 4 adedi web tabanlı programlar kullanmaktadırlar. Web tabanlı programların 3’ü
bankaların kendi geliştirdiği programlar olup, kalan bir tanesi dış kaynaklardan satın alınması
suretiyle ilgili bankaya uyarlanmıştır.
iii. Toplanan operasyonel risk kayıplarının alt sınırının (eşik-threshold) tutarının) ne
olduğu:
Operasyonel kayıp verisi toplayan 11 bankanın 8’i herhangi bir alt sınır uygulamamakta olup tüm operasyonel kayıpları toplamaktadırlar. 3 adet banka ise operasyonel kayıp
verilerinde 2.250.-YTL, 1.000.-YTL ve 100.-YTL tutarında alt sınır (eşik-threshold)
uygulamaktadır.
iv. Operasyonel kayıp verilerinin toplanmasında sigortalanmış kayıpların dikkate alınıp alınmadığı, sigortadan tahsil edilen tutarların sürece dahil edilip edilmediği:
Operasyonel kayıp verisi toplayan 11 bankanın 2’si sigortadan tahsil edilen kayıp tutarlarını dikkate almamaktadır. Diğer tüm bankalar operasyonel kayıpların gerçekleşmesinin
ardından sigortadan tahsil edilen tutarları kayıp veri tabanlarına kaydetmektedirler.
v. Personelden tahsil edilen kayıplara (kasa noksanı vb.) ve operasyonel hata sonucu
elde edilen gelir fazlalarına (kasa fazlası vb.) ilişkin verilerin toplanıp toplanmadığı:
Operasyonel kayıp verisi toplayan 11 bankanın 5’i gelir fazlalarına ilişkin verileri toplamamaktadır. Diğer tüm bankalar ise hem tahsil edilen kayıpları hem de elde edilen gelir
fazlalarını toplamaktadırlar.
vi. Diğer kanallardan tahsil edilen kayıplara yer verilip verilmediği :
Operasyonel kayıp verisi toplayan 11 bankanın 2’si diğer kanallardan tahsil edilen kayıplara kayıp veri tabanlarında yer vermemektedirler. 9 adet banka ise diğer kanallardan tahsil
edilen operasyonel kayıplarını dikkate alarak kayıp veri tabanlarında yer vermektedirler.
vii. Herhangi bir operasyonel risk yönetim aracı kullanılıyorsa söz konusu aracın özelliklerinin neler olduğu:
-
Operasyonel risk yönetim aracının kayıp veri tabanını içerip içermediği,
-
Operasyonel risk yönetim aracının risk ölçümü yapıp yapmadığı,
-
Operasyonel risk yönetim aracının Basel II’nin öngördüğü şekilde ileri ölçüm
yöntemlerine uygun olarak yasal sermaye hesaplaması yapıp yapmadığı,
-
Operasyonel risk yönetim aracının risk yönetimi fonksiyonunun olup olmadığı,
operasyonel risk yönetimi açısından riski gidermeye yönelik alınacak aksiyon
belirlenmesi ve sürecin takibine imkan sağlayıp sağlamadığı.
Operasyonel risk kayıp verisi toplayan 11 banka içerisinde 1 banka Basel II’nin
öngördüğü ileri ölçüm yaklaşımları paralelinde geliştirilmiş operasyonel risk yönetim aracı
kullanmaktadır. Söz konusu bankanın operasyonel risk yönetim aracı operasyonel risk kayıp
150
Bankacılar Dergisi
veri tabanını içermektedir. Kayıp veri tabanında bulunan kayıp verileri ve diğer kalitatif
yöntemler (öz değerlendirme, senaryo analizi vb.) girdi olarak kullanılmakta olup Basel II’nin
öngördüğü şekilde istatistiksel tabanlı risk ölçümleri (yüzde 99,9 güven aralığı kullanılmaktadır.) dikkate alınarak risk ölçümü ve yasal sermaye hesaplaması yapmaktadır. Ayrıca söz
konusu bankanın risk yönetim aracının risk yönetimi fonksiyonları bulunmakta olup
operasyonel risk yönetimi açısından riski gidermeye yönelik alınacak aksiyon belirlenmesine
ve risk yönetim sürecinin takibine imkan vermektedir. Operasyonel kayıp verisi toplayan
diğer bankalar operasyonel risk yönetim aracı kullanmamaktadır.
2. Risk Ölçümü Kapsamında Hangi Yöntemlerden Faydalanıldığı
Operasyonel kayıp verisi toplayan 11 banka içerisinde 1 banka Basel II’nin öngördüğü
ileri ölçüm yaklaşımları kapsamında risk ölçümü yapmakta olup ayrıntılara aşağıda değinilmiştir.
a. Kantitatif Yöntemler (Kayıp Veri Dağılımı, İçsel Ölçüm Yaklaşımı, Frekans ve Şiddet Kapsamında Hangi Dağılım Modellerini Kullandıkları-Normal, Lognormal, Poisson,
Weibull, vb)
İleri Ölçüm Yaklaşımları kapsamındaki Kayıp Dağılım Yaklaşımı yöntemi ile
operasyonel riske maruz değer (OPVAR) hesaplanmaktadır. Sıklık için Poisson dağılımı,
şiddet için Weibull dağılımı kullanılmaktadır. Bu iki dağılım Monte Carlo simülasyonu ile
birleştirilerek toplam kayıp dağılımı oluşturulmaktadır.
b. Kalitatif Yöntemler(Scorecard, Senaryo Analizi, Öz Değerlendirme)
Kalitatif anlamda öz değerlendirme yaklaşımı kullanılmaktadır. Olayların ortalama
sıklığı, ortalama şiddeti ve en kötü değerlerine ilişkin bankanın birimleriyle gerçekleştirilen
çalışmalar sonucunda elde edilen subjektif tahminlerden yararlanılmaktadır. Sonuç olarak öz
değerlendirmeyle elde edilen veriler sayısallaştırılarak öznel bir riske maruz değer rakamı
hesaplanmaktadır.
c. Karma Yöntemler (Kalitatif ve Kantitatif Sonuçların Nasıl Birleştirildiği)
Kayıp dağılımı yaklaşımı ile elde edilen sermaye gereksinimi tahmini ile öz değerlendirme kapsamında oluşturulan sermaye gereksinimi tahmini, ağırlıklı ortalama yöntemiyle
birleştirilerek toplam sermaye gereksinimi rakamına ulaşılmaktadır.
151
Operasyonel Risk Çalışma Grubu
Ek 1:
Yasal Risk Verileri
3.821.987 ,00 630.200,00 360.000,00 250.000,00 200.000,00 160.000,00
2.567 .921,00 600.000,34 350.000,00 248.341,96
200.000,00 157 .083,00
1.415.988,00 556.000,00 350.000,00 239.102,93 193.500,00 153.592,54
1.299.345,00 550.000,00 332.000,00 232.500,00 192.806,7 4 151.000,00
917 .000,00 505.947 ,00 301.527 ,50 230.000,00 191.07 0,31 150.930,39
907 .07 7 ,00 483.7 11,60 297 .035,48 229.368,50 186.330,00 150.411,29
845.000,00 426.000,00 294.835,23 220.357 ,00 185.000,00 146.87 5,00
800.000,00 423.319,62 27 4.509,80 220.07 0,00 182.435,7 2 145.500,50
7 50.000,00 416.562,38 27 0.341,11 220.000,00 180.000,00 143.000,00
7 42.651,56
410.060,7 2 260.000,00 214.634,95 17 6.000,00 142.7 7 4,19
7 34.900,00 406.001,47
255.414,00 210.536,56
17 6.000,00
660.000,00 400.203,01 252.000,00 204.450,00 165.000,00
202.07 7 ,38 165.000,00
650.000,00 394.67 2,11 251.489,59
*Tabloda yer alan yasal risk verileri dolar cinsindendir.
Kaynak: Cruz, Marcelo G. 2002. Modeling, Measuring and Hedging Operational Risk.
Dipnotlar
1
Bankalar, içsel operasyonel risk ölçüm sistemlerinde nasıl bir sınıflandırma izleyeceklerini kendileri
belirleyeceklerdir. Ancak yine de, denetim otoritesinin onay verme sürecini kolaylaştırmak için, bankanın
tarihsel iç kayıp verilerini Basel II’de belirlenmiş olan 8 ana faaliyet koluna ve 7 kayıp olayı türüne eşleyebilmesi ve talep edilmesi halinde ilgili verileri denetim otoritesine sağlayabilmesi gerekmektedir.
2 Basel II’de bir bankanın bazı faaliyetleri ile ilgili olarak İleri Ölçüm Yaklaşımını, bazı faaliyetleri ile ilgili
olarak da Temel Gösterge veya Standart Yaklaşımı kullanmaları belirli koşulların yerine getirilmesi şartıyla
mümkün kılınmıştır.
3 Marcelo G. Cruz, Modeling, Measuring and Hedging Operational Risk, (John Wiley & Sons, Ltd., 2002), 57.
4
Bankaların İç Denetim ve Risk Yönetimi Sistemleri Hakkında Yönetmeliğe göre, stres testleri kapsamında
risklerin risk faktörlerine göre sayısallaştırılmasında, geçmiş deneyimlerden yararlanıldığı takdirde kullanılan
varsayımlar, ölçümün tutarlılığı ve izlenen yöntem, bankanın yönetim kurulunca onaylanmalıdır.
5
Carol Alexander, Bayesian Methods for Measuring Operational Risk
6
Karesel kayıp fonksiyonu (quadratic loss function) varsayımı altında, parametrenin Bayesgil tahmini, son
dağılımın ortalamasıdır.
7
Anahtar risk faktörünün (başlangıç düğümü) olasılık dağılımı P(Y), anahtar risk göstergesinin (hedef düğümü)
koşullu olasılık dağılımı ise P(X|Y) ise, anahtar risk göstergesinin dağılımı P(X), ∫ p(Y) p(X|Y)dy’dir.
8
Örnek için bkz. Paola Giudici, Integration of Qualitative and Quantitative Operational Risk Data: A Bayesian
Approach.
Kaynakça
152
Cruz, Marcelo G. (2002), Modeling, Measuring and Hedging Operational Risk. UK: John Wiley-Sons.
Yasuda, Yuji (2003), “Application of Bayesian Inference to Operational Risk Management.” University of
Tsukuba.
Giudici, Paolo (2004), “Integration of Qualitative and Quantitative Operational Risk Data: A Bayesian
Approach” Operational Risk Modelling and Analysis: Theory and Practice (sf.131-138). Risk Books.
Alexander, Carol, (2003), Operational Risk: Regulation, Analysis and Management. Londra: Financial
Times Prentice Hall.
Ramamurthy, S., Arora, H. - Ghosh, A. (2005), Applying Op Risk and Probabilistic Networks to Corporate
Actions Processing. Operational Risk Magazine, s.36-38.
Alexander, Carol, “Bayesian Methods for Operational Risk”, University of Reading.












