SAKARYA ÜNİVERSİTESİ
İktisadi Matematik
Hafta 6
6. Bölüm Türevler
Yrd. Doç. Dr. Şakir Görmüş
ÖĞRENME HEDEFLERİ:
1. Türev işlemlerini yapar.
2. Fonksiyonların grafiği hakkında bilgi sahibi olur.
3. Kısmi türevleri alabilir.
4. Toplam türev alabilir.
5. Kısmi ve toplam türevleri iktisadi modellere uygulayabilir.
İÇİNDEKİLER:
7.1. TÜREV KAVRAMI
7.2. TÜREV ALMA KURALLARI
7.3 . YÜKSEK DERECEDEN TÜREVLER
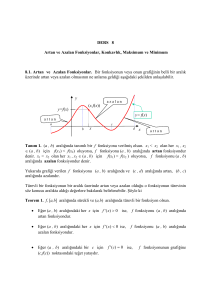
7.4. ARTAN VE AZALAN FONKSİYONLAR
7.5. KISMİ VE TOPLAM TÜREVLER
7.1. Kısmi Türevler
7.2. Toplam Türevler
7.2.1. Kapalı Fonksiyonların Toplam Türevi
7.6. YOUNG’S TEOREMİ
7. Türev
Y = f (x) fonksiyonunda Y değeri x değişkenine bağlı olduğundan x deki değişmeler Y değerini de
değiştirecektir.
X deki değişimi Δx = 𝑥1 − 𝑥0 olarak ifade edebiliriz. 𝑥 = 𝑥0 olduğunda fonksiyonun değeri
Y = f (𝑥0 ) olacaktır. 𝑥 değeri değiştiğinde ise fonksiyonun değeri de f (𝑥0 + ∆𝑥) olacaktır. Buna
göre fonksiyon değerindeki değişimin bağımsız değişkendeki değişime oranını aşağıdaki gibi
yazabiliriz:
∆𝑌
∆𝑋
=
𝑓 (𝑥0 + ∆𝑥)−𝑓 (𝑥0 )
∆𝑥
Buna göre;
𝑑𝑦
𝑑𝑥
= 𝑓 ′ (𝑥 ) = lim
Δ𝑦
∆𝑥→0 Δ𝑥
yazılır ve f’in x’ e göre türevi olarak okunur.
7.1. TÜREV KAVRAMI
Türev en basit tanımı ile bir fonksiyonun belli bir noktadaki anlık değişim oranını ve eğimin bir ölçüsünü verir.
Türev alma diferansiyel yöntemi olarak ta adlandırılır.
Bir fonksiyonun belli bir noktada türevinin alınabilmesi için:
1. Fonksiyon o noktada sürekli bir fonksiyon olmalıdır.
2. Fonksiyonun o noktada tek bir teğeti bulunmalıdır.
Bununla birlikte,
1. Y = f (x) fonksiyonunun türevi de x’in bir fonksiyonudur ve bundan dolayı her bir x değerine karşılık
gelen sadece bir y değeri vardır.
2. Y = f (x) fonksiyonunun x noktasındaki türevi, eğriye bu noktadan çizilen teğetin eğimine eşittir.
3. Y = f (x) fonksiyonunun x noktasındaki türevi, bu noktada x’teki küçük bir değişmenin y’yi hangi yönde
ve ne ölçüde değiştireceğini gösterir.
Bir fonksiyonun türevi matematik kitaplarında aşağıdaki gibi farklı şekillerde gösterilmektedir. y = f (x)
türevi aşağıdaki şekilde gösterilebilir:
f’ (x)
f’
𝑑𝑦
Δ𝑦
𝜕𝑦
𝑑𝑥
Δ𝑥
𝜕𝑥
Örnek:
Y= f(x)= x2 fonksiyonunun türevi,
f’ =
𝑑𝑦
𝑑𝑥
= 2𝑥
bunun anlamı fonksiyonun x noktasındaki
anlık değişimi 2x’tir.
x = 0 için
x = 1 için
x = 2 için
x = 3 için
𝑑𝑦
𝑑𝑥
𝑑𝑦
𝑑𝑥
𝑑𝑦
𝑑𝑥
𝑑𝑦
𝑑𝑥
=0
=2
=4
=6
Görüldüğü üzere fonksiyonun değişim oranı x’in aldığı değere göre değişmektedir. x= 2 noktasında değişim
oranı 4 iken x=3 noktasında değişim oranı 6 olmuştur. Diğer bir ifade ile x’in değeri artıkça türevin değeri yani
fonksiyonun eğimi artmaktadır. x = 1 noktasında x bir birim artarken y 2 birim artarken, x = 2 noktasında x bir
birim artarken y 4 birim artmaktadır.
7.2 TÜREV ALMA KURALLARI
Bir fonksiyonun türevini bulmak için bir kural anlatmış olmamız rağmen, sayısal değer söz konusu olduğunda
bu yöntemin çok basit olmadığı da bir gerçektir. Bu sebeple Y f ( X ) gibi bir fonksiyon varsayarak türev
alma kurallarını yazabiliriz.
1. Üstlü bir ifade için:
f ( X ) kX n
Burada k ve n herhangi reel sayılardır. Böylece f ' ( X ) şu şekilde bulunur:
f ' ( X ) nkX n1
2
Örneğimizi dikkate aldığımızda f ( X ) 5 X fonksiyonu için türevin
f’ (x) = -10 X olduğu görülür.
Örnek :
f ( X ) 18 X 6
f ' ( X ) 108 X 5
f ( X ) 0.4 X 1/2
f ' ( X ) 0.2 X 1/2
f ( X ) 150 X
f ' ( X ) 150
f '(X ) 0
f ( X ) 150
Son iki örnek yorum gerektirmektedir. f ( X ) 150 X eğimi 150 olan lineer bir fonksiyondur. f ( X ) 150
ise X’in bir fonksiyonu değildir. Böylece X eksenine paralel bir doğru ile gösterilir ve eğimi sıfırdır.
2. Üstel Fonksiyonların Farklarının ve Toplamlarının Türevi
Eğer bazı fonksiyonlar diğer fonksiyonların toplamı ve / veya farkından oluşuyorsa, bu fonksiyonların türevleri
bireysel türevlerin toplamı veya farkından oluşur.
Örnek: f ( X ) 1200 300 X 5 X 2
f '(X )
d
d
d
(1200)
(300 X )
( 5 X 2 )
dX
dX
dX
0 300 10 X 300 10 X
3. Çarpım Şeklindeki Fonksiyonların Türevi
Şayet Y bağımlı değişkeni n ve z’nin bir fonksiyonu ise;
Y f ( X ) n( X ) z ( X )
Türev şu şekilde bulunur:
f ' ( X ) n( X ) z ' ( X ) n' ( X ) z ( X )
Örnek: n( X ) 5 X 2 6 X ve z ( X ) 3 X 4 12 bu iki fonksiyonun çarpımı söz konusu ise;
Y f ( X ) (5 X 2 6 X )(3 X 4 12)
Her bir fonksiyonun ayrı ayrı türevini alırsak;
n( X ) 5 X 2 6 X
fonksiyonun türevi:
n' ( X ) 10 X 6
z ( X ) 3 X 4 12
fonksiyonun türevi:
z ' ( X ) 12 X 3
Buradan:
f ' ( X ) (5 X 2 6 X )(12 X 3 ) (10 X 6)(3 X 4 12)
60 X 5 72 X 4 30 X 5 120 X 18 X 4 72
90 X 5 90 X 4 120 X 72
4. Bölüm Şeklindeki Fonksiyonların Türevi
Şayet Y fonksiyonu şu şekilde verilmişse;
Y f (X )
n( X )
z( X )
Fonksiyonun türevi ise;
f '(X )
n' ( X ) z ( X ) n( X ) z ' ( X )
z ( X )2
Daha önceki örneğimizi uygularsak;
Y f (X )
f '(X )
5X 2 6X
şimdi bu fonksiyonun türevini bulursak;
(3 X 4 12)
(10 X 6)(3 X 4 12) (5 X 2 6 X )(12 X 3 )
(3 X 4 12)2
5. İç içe Geçmiş Fonksiyonların Türevi (Zincir Kuralı)
n gibi bir fonksiyon z gibi bir fonksiyonun fonksiyonu ise yani;
n f ( g ( z )) fonksiyonun türevi;
dn dn dg
dz dg dz
Örnek: Varsayalım ki
f ( x, y) x 2 y y 2 verilmiş olsun. Şimdi x ve y ’nin de t ’nin bir
fonksiyonu olduğunu varsayalım:
x(t ) 4t 2 4 ve y (t ) t 3 8 ve F (t ) f ( x(t ), y (t )) ise zincir kuralını kullanarak F ' (2) yi
bulunuz.
F ' (t )
df '
df '
x (t )
y (t )
dx
dy
Şimdi; f1 2 xy, f 2 x 2 2 y ve x' (t ) 8t , y ' (t ) 3t 2 . Böylece
F ' (t ) (2 xy)(8t ) ( x 2 2 y)(3t 2 )
t 2 olduğunda x 18 ve y 0 bulunur. Bu değerleri türevde yerine koyduğumuzda;
F ' (2) 216 bulunur.
Örnek: Ayşe’nin tüketimi babasının gelirine ve babasının geliri ise ücretine bağlıdır.
Tüketim ve gelir fonksiyonları aşağıdaki gibi verilmiştir.
C = 3 + Y1/2 ve Y = 2W2
Ayşe’nin babasının gelirindeki bir artış Ayşe’nin tüketimini nasıl etkileyecektir?
1
1
𝑑𝐶
𝑑𝐶 𝑑𝑌
1
1
1
4𝑊
=
= 𝑌 − 2 4𝑊 = (2𝑊 2 )− 2 4𝑊 = (2𝑊 −1 4𝑊) =
=1
𝑑𝑊
𝑑𝑌 𝑑𝑊 2
2
2
4𝑊
Örnek: Ayşe’nin elde ettiği fayda tüketimine ve tüketimi ise gelirine bağlıdır. Ayşe’nin fayda ve
tüketim fonksiyonları sırasıyla aşağıdaki gibidir.
U = 2Q1/2 ve Q = Y1/2
Ayşe’nin gelirindeki bir artış faydasını nasıl etkileyecektir?
1
𝑑𝑈
𝑑𝑈 𝑑𝑄
=
= 𝑄 −2
𝑑𝑌
𝑑𝑄 𝑑𝑌
1
1
1 −1/2
𝑌
= ( 𝑌 2 )− 2
2
1 1
1
1 −1
1 3
1
𝑌 2 = 𝑌− 4
𝑌 −2 = 𝑌 − 4 = 4
2
2
2
2 √𝑌 3
6. Bir doğal log fonksiyonun türevi:
1
Y f ( X ) ln X
x
f '(X )
1
X
Ekonomik analizde kullanılan logaritmik fonksiyonların yukarıdaki örnekten daha karmaşık olduğu
unutulmamalıdır.
Y f ( X ) ln(4 X 2 6 X 10)
ve
g ( X ) (4 X 2 6 X 10)
f ( X ) ln g ( X )
Logaritmik kuralı ve çarpım kuralını birlikte uyguladığımızda şu sonuca ulaşırız:
f '(X )
1
1
g'(X )
(8 X 6)
2
g( X )
(4 X 6 X 10)
8X 6
(4 X 6 X 10)
2
Örnek: dy / dx ’i hesaplayınız.
(a) y x 2 ln x
(b) y x3 ln x
(c) y
ln x
x
Cevaplar:
(a) y ' 2 x
(c) y '
1
x
(b) y ' 3x ln x x3 (1/ x) 2 x ln x x 2
(1/ x) x (ln x).1 1 ln x
x2
x2
7. Ters Fonksiyon Kuralı
Y f ( X ) X 3 gibi bir fonksiyonumuz olsun. Fonksiyonun türevini bulmak istediğimizde:
dY
f ' ( X ) 3X 2
dX
Ancak, orijinal fonksiyonun tersini bulmak istediğimizde:
X g (Y ) Y 1/3
dX
1
1
dX
1
diğer yandan
olduğundan
g (Y ) Y 2/3
3
dY dY / dX
dY
3
3 Y
dY
3Y 3 sonucu bulunur. Bu sonuç ters fonksiyon kuralı olarak bilinir. Her fonksiyonun tersi
dX
yoktur, ancak monotonik olan fonksiyonların tersi vardır.1
7.3 YÜKSEK DERECEDEN TÜREVLER
f ‘(x) şeklinde gösterilen birinci türev f (x) fonksiyonunun eğimini ve her bir x değerindeki değişim
oranını vermektedir.
f ‘’(x) şeklinde gösterilen ikinci türev f ‘(x) fonksiyonunun eğimini ve her bir x değerindeki değişim
oranını vermektedir.
f ‘’’(x) şeklinde gösterilen üçüncü türev f ‘’(x) fonksiyonunun eğimini ve her bir x değerindeki
değişim oranını vermektedir.
1
X ve Y özellikle sayılara ilişkin olduğunda, birebir eşleşme özelliği fonksiyonlar sınıfına özgü bir durum olarak
gözüktüğünde monotonic fonksiyonlardan söz edilir. Şayet, x1 x2 olduğunda f ( x1 ) f ( x2 ) oluyor ise f ’in
monoton olarak arttığı söylenir.
Örnek:
y = f (x) = x4 + 2x3- 5x2 + 8
f ‘(x) = 4x3 + 6x2- 10x
f ‘’(x) = 12x2 + 12x- 10
f ‘’’(x) = 24x + 12
7.4 ARTAN VE AZALAN FONKSİYONLAR
Bir fonksiyonun birinci türevine bakarak fonksiyonun artan veya azalan olduğuna ve ikinci türevine
bakarak artış ve azalış hızını belirleyebiliriz.
1. Artan oranda artan fonksiyon:
f ‘(x) > 0 ise artan bir fonksiyondur.
f ‘’(x) > 0 ise artan oranda artan bir fonksiyondur.
Örnek:
f (x) = x2 , x > 0
f ‘(x) = 2x > 0 artan bir fonksiyondur.
f ‘’(x) = 2 > 0 artan oranda artan bir fonksiyondur.
2. Azalan oranda artan fonksiyon:
f ‘(x) > 0 ise artan bir fonksiyondur.
f ‘’(x) < 0 ise azalan oranda artan bir fonksiyondur.
Örnek:
f (x) = x1/2 , x > 0
f ‘(x) = ½ x -1/2 > 0 artan bir fonksiyondur.
f ‘’(x) = - ¼ x –3/2 < 0 azalan oranda artan bir fonksiyondur.
3. Azalan oranda azalan fonksiyon:
f ‘(x) < 0 ise azalan bir fonksiyondur.
f ‘’(x) > 0 ise azalan oranda azalan bir fonksiyondur.
Örnek:
f (x) = 2x -1 , x > 0
f ‘(x) = -2 x -2 < 0 azalan bir fonksiyondur.
f ‘’(x) = 4 x –3 > 0 azalan oranda azalan bir fonksiyondur.
4. Azalan oranda azalan fonksiyon:
f ‘(x) < 0 ise azalan bir fonksiyondur.
f ‘’(x) < 0 ise artan oranda azalan bir fonksiyondur.
Örnek:
f (x) = - x2 , x > 0
f ‘(x) = -2 x < 0 azalan bir fonksiyondur.
f ‘’(x) = -2 < 0 artan oranda azalan bir fonksiyondur.
7.5. Kısmi Türevler
Bağımlı bir değişkenin birden fazla bağımsız değişkenin fonksiyonu olması durumunda bağımsız
değişkenlerden diğerlerinin sabit tutularak yalnızca tek bir bağımsız değişkene göre bağımlı
değişkenin türevinin alınması işlemine kısmi türev denir.
Böylece fonksiyonu oluşturan bağımsız değişkenlerden sadece birindeki değişimin, diğer bağımsız
değişkenler sabit kabul edilerek veya değişmedikleri varsayılarak, bağımlı değişken üzerindeki etkisi
incelenir.
Y = f ( 𝑥1 , 𝑥2 , … … … … , 𝑥𝑛 ) şeklindeki birden fazla bağımsız değişkenli fonksiyonlara çok
değişkenli fonksiyon denir. Çok değişkenli fonksiyonun bağımsız değişkenlerinden sadece birine
göre türevine kısmi türev alma işlemi denir ve bu işlemin sonucu kısmi türev değerini verir. Kısmi
türevde, türevi alınan değişkenin değişmesine izin verilirken diğer değişkenlerin sabit kaldığı
varsayılır.
Fonksiyonun kısmi türevleri,
𝜕𝑦
𝜕𝑓(𝑥1 , 𝑥2 … … 𝑥𝑛 )
=
= 𝑓1′
𝜕𝑥1
𝜕𝑥1
𝜕𝑦
𝜕𝑓(𝑥1 , 𝑥2 … … 𝑥𝑛 )
=
= 𝑓2′
𝜕𝑥2
𝜕𝑥2
Örnek: Y = 3𝑥14 + 2𝑥22 − 𝑥3 fonksiyonunun 𝑥1 , 𝑥2 𝑣𝑒 𝑥3 e göre kısmi türevleri:
𝜕𝑦
𝜕𝑥1
𝜕𝑦
𝜕𝑥2
𝜕𝑦
𝜕𝑥3
= 12𝑥13
𝑥2 𝑣𝑒 𝑥3 sabitken Y’nin 𝑥1 e göre kısmi türevi.
= 4𝑥2 𝑥1 𝑣𝑒 𝑥3 sabitken Y’nin 𝑥2 e göre kısmi türevi.
= −1
𝑥1 𝑣𝑒 𝑥2 sabitken Y’nin 𝑥3 e göre kısmi türevi.
Örnek: Y = 3𝑥14 𝑥22 𝑥3 fonksiyonunun 𝑥1 , 𝑥2 𝑣𝑒 𝑥3 e göre kısmi türevleri:
𝜕𝑦
𝜕𝑥1
𝜕𝑦
𝜕𝑥2
𝜕𝑦
𝜕𝑥3
= 12𝑥13 𝑥22 𝑥3
𝑥2 𝑣𝑒 𝑥3 sabitken Y’nin 𝑥1 e göre kısmi türevi.
= 6 𝑥13 𝑥2 𝑥3
𝑥1 𝑣𝑒 𝑥3 sabitken Y’nin 𝑥2 e göre kısmi türevi.
= 3𝑥14 𝑥22
𝑥1 𝑣𝑒 𝑥2 sabitken Y’nin 𝑥3 e göre kısmi türevi.
Kısmi türev sadece x1 in değişmesi ve diğer x lerin sabit kalmasından dolayı y de meydana gelen
değişmeyi ölçmektir. Eğer bütün değişkenlerin (bağımsız) değişmesine izin verilseydi bir bağımsız
değişkendeki değişmenin bağımlı üzerindeki etkisini isole etmek mümkün olmayacaktır.
Kısmi türevler, x ve y nin fonksiyonları olduğundan kısmi türevlerin değerler x ve y nin alacağı
değerlere göre değer alırlar.
Kısmi Türev Uygulamaları
Örnek: İki mal üreten bir firmanın maliyet fonksiyonu
TC = 10 𝑄1 𝑄22 − 5 𝑄12 𝑄2 olarak verilmiştir. 𝑄1 𝑣𝑒 𝑄2 mallarına ait marjinal maliyet
fonksiyonlarını bulunuz.
Birinci mala ait MC fonksiyonu:
𝜕𝑇𝐶
𝜕𝑄1
= 𝑀𝐶1 = 10 𝑄22 − 10 𝑄1 𝑄2
İkinci mala ait MC fonksiyonu:
𝜕𝑇𝐶
𝜕𝑄2
= 𝑀𝐶2 =
20 𝑄1 𝑄2 − 5 𝑄12
Örnek: X malının talep fonksiyonu aşağıdaki gibi verilmiştir.
𝑄𝑥 = 4 − 2 𝑃𝑥 +
1
𝑃 +3𝑌
2 𝑦
a) Talebin Çapraz fiyat esnekliğini bulunuz ve yorumlayınız.
𝜺𝒙𝒚 =
𝜀𝑥𝑦 =
𝝏𝑸𝒙 𝑷𝒚
𝝏𝑷𝒚 𝑸𝒙
𝜕𝑄𝑥 𝑃𝑦
𝜕𝑃𝑦 𝑄𝑥
eğer > 0 ise ikame, < 0 ise tamamlayıcı maldır.
=
1 𝑃𝑦
2 𝑄𝑥
> 0 ikame maldır.
b) Talebin Gelir esnekliğini bulunuz ve yorumlayınız.
𝜺𝒈𝒆𝒍𝒊𝒓 =
𝜀𝑔𝑒𝑙𝑖𝑟 =
𝝏𝑸𝒙
𝒀
𝝏𝒀
𝑸𝒙
𝜕𝑄𝑥
𝑌
𝜕𝑌
𝑄𝑥
eğer > 0 ise normal, < 0 ise düşük maldır.
=3
𝑌
𝑄𝑥
> 0 normal maldır.
7.6. Toplam Türevler
Y = f (x, z) fonksiyonu x ve z olmak üzere iki bağımsız değişkenden oluştuğundan Y bağımlı
değişkeninde meydana gelecek toplam değişim x ve z bağımsız değişkenlerinin yol açtığı toplam
değişime eşit olacaktır. Bu durum Y nin toplam türevi olarak aşağıdaki gibi ifade edilebilir.
𝑑𝑌 = (
𝜕𝑌
𝜕𝑌
) 𝑑𝑥 + ( ) 𝑑𝑧
𝜕𝑥
𝜕𝑧
Yukarıdaki toplam türev daha sade bir şekilde aşağıdaki gibi de ifade gösterilebilir.
𝑑𝑌 = 𝑌𝑥 𝑑𝑥 + 𝑌𝑧 𝑑𝑧
Z sabit iken x in bağımlı değişken üzerindeki etkisini göstermek için
𝜕𝑌
𝑑𝑌
𝜕𝑌 𝜕𝑌 𝜕𝑧
= ( )𝑧 𝑠𝑎𝑏𝑖𝑡 =
+
𝜕𝑥
𝑑𝑥
𝜕𝑥
𝜕𝑧 𝜕𝑥
elde edilir.
Örnek: Y = 3x2 +2xz – 2z2 fonksiyonunun toplam türevini yazınız.
Y’deki toplam değişim x ve z’ deki ayrı ayrı değişimleri Y üzerindeki etkilerinin toplamına eşittir ve
aşağıdaki gibi ifade edilebilir.
𝑑𝑌 = (
𝜕𝑌
𝜕𝑌
) 𝑑𝑥 + ( ) 𝑑𝑧
𝜕𝑥
𝜕𝑧
𝑑𝑌 = (6𝑥 + 2𝑧) 𝑑𝑥 + (2𝑥 − 4𝑧) 𝑑𝑧
Örnek:
Y =
2 𝑥𝑧
𝑥+𝑧
fonksiyonunun toplam türevini yazınız.
𝑑𝑌 = (
𝑑𝑌 =
𝜕𝑌
𝜕𝑌
) 𝑑𝑥 + ( ) 𝑑𝑧
𝜕𝑥
𝜕𝑧
2𝑧 (𝑥 + 𝑧) − 2𝑥𝑧
2𝑥 (𝑥 + 𝑧) − 2𝑥𝑧
𝑑𝑥
+
𝑑𝑧
(𝑥 + 𝑧)2
(𝑥 + 𝑧)2
Örnek: Üç mal tüketen ( x, z, y) bir tüketicinin fayda fonksiyonu
U = 4x3zy2 olarak verilmiştir. Toplam türevini yazınız.
𝑑𝑈 =
𝜕𝑈
𝜕𝑈
𝜕𝑈
𝑑𝑥 +
𝑑𝑧 +
𝑑𝑦
𝜕𝑥
𝜕𝑧
𝜕𝑦
dU = (12x2zy2) dx + (4x3y2) dz + (8x3zy) dy
Örnek: Üretim fonksiyonu 𝑄 = 𝑓 (𝐿, 𝐾) = 𝐴 𝐿𝛼 𝐾 1−𝛼
olarak verilmiştir. Toplam türevini yazınız.
𝑑𝑄 = 𝐴𝛼𝐿𝛼−1 𝑑𝐿 + 𝐴(1 − 𝛼)𝐾 −𝛼 𝑑𝐾
7.6.1. KAPALI FONKSİYONLAR TOPLAM TÜREVLERİ
Burada kapalı türev kavramı çeşitli özel durumlar için geliştirilecektir.
Durum 1: Birbirleriyle ilişkilenmiş bağımsız değişkenler
z f x, y
dz
y g x
f
f
dz f d f dy f f dy
d dy
y
d d y dx x y d
dz
: z’in x’e göre toplam türevi
d
f
: Dolaysız etki x z
x
f
: Dolaylı etki x y z
y
Fonksiyonel durumda sadece bir tane bağımsız değişkende değişiklik görülmüştür, normal türevdeki
durum budur. Fakat Toplam türevde iki bağımsız değişken (yada hepsi) in y de sebep olduğu toplam
değişme söz konusu olmakta ve ölçülmektedir.
Genel olarak z f x, y1 , y 2 , y n ve y1 g x , y 2 hx , , y n k x . BU durumda z’nin x’e
göre toplam türevi
dx f f dy1 f dy 2
f dy n
dir.
dz x y1 dx y 2 dx
y n dx
Örnek:
Y = 4x – z2 x = 3z2 + z + 5 fonksiyonunun z’ye göre toplam türevini alınız.
𝑑𝑌 = (
𝜕𝑌 𝜕𝑥
𝜕𝑌
)𝑑𝑧 +
𝑑𝑧
𝜕𝑥 𝜕𝑧
𝜕𝑧
𝜕𝑌
𝜕𝑌 𝜕𝑥
𝜕𝑌
=(
)+
𝜕𝑧
𝜕𝑥 𝜕𝑧
𝜕𝑧
dY = 4 ( 6z + 1) dz + (- 2z) dz
𝑑𝑌
= 24𝑧 + 4 − 2𝑧 = 22𝑧 + 4 olarak bulunur.
𝑑𝑧
Durum 2: Bağımsız değişkenlerin her ikisininde bağımsız diğer bir değişkenin fonksiyonu
olması hali
z f x, y , x g t , y ht
z f g t , ht
dz
f
f
f d f dy
dx dy dz
x
y
x dt y dt
t karşın gelen z deki değişme x ve y aracılığıyla z transfer edilir.
birden fazla bağımsız değişken için kullanıldı.
d bir bağımsız değişkenli fonksiyonlar için kullanıldı.
Genel olarak z f 1 , 2 ,, n ve 1 g t , 2 ht , , n k t ve z’nin t’ye karşın toplam
türevi
dz f1
d
d 1
d
f2 2 fn n
dt
dt
dt
Örnekler:
1. z 2 y 3 ,
1 2
t , y 3t 3
2
dz
d
dy
3
f
fy
2 y t 3 2 y 2 9t 2 2 y 3 t 27 2 y 2 t 2
dt
dt
dt
2. Q AL K 1 , K 2M 2 , L 4M
dQ
dL
dK
fL
fK
AL 1 K 1 4 1 AL K 4M
dM
dM
dM
K
4 A
L
1
L
4 AM 1
K
10. 3. 2. YOUNG’S TEOREMİ
YoungTeore mi : Bir fonksiyonun iki değişkene göre birinci dereceden türevlerinin çapraz türevleri eşittir.
Z=f(x,y) gibi bir fonksiyonun x’e göre türevinin y’ye göre türevi, bu fonksiyonun y’ye göre türevinin x’e
göre türevleri eşittir. Yani
2 f
2 z
f xy
f yx
xy
yx
Verilen bir f x, y fonksiyonunun ikinci dereceden olağan türevleri ve karşıt türevleri sürekli ise
f xy f yx sağlanır.
Örnek:
1. z x 2 2 xy y 2
z x 2 x 2 y 2x y
z y 2 x 2 y 2 x y
z xx 2
z yy 2
z xy 2 z yx
z yx 2