17.Basit Har.Hark czm

BAS‹T HARMON‹K HAREKET
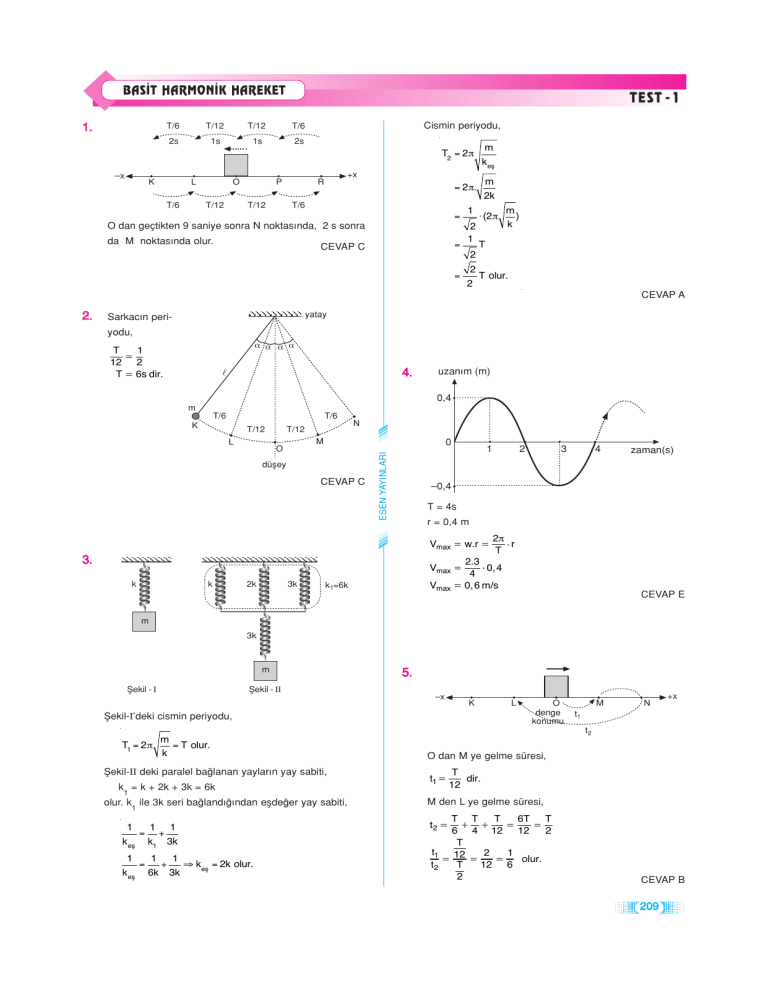
1.
–x
TEST - 1
T/6
T/12
T/12
T/6
2s
1s
1s
2s
K
L
T/6
O
T/12
P
T/12
Cismin periyodu,
T2 = 2 π
m
k eş
= 2 π.
m
2k
+x
R
T/6
=
O dan geçtikten 9 saniye sonra N noktas›nda, 2 s sonra
da M noktas›nda olur.
=
CEVAP C
1
2
1
⋅ (2 π
m
)
k
T
2
=
2
T olur.
2
CEVAP A
2.
yatay
Sarkac›n periyodu,
α α α α
T
1
=
12 2
T = 6s dir.
l
4.
uzan›m (m)
0,4
m
T/6
T/6
T/12
L
T/12
N
M
O
0
düfley
CEVAP C
ESEN YAYINLARI
K
1
2
3
4
zaman(s)
–0,4
T = 4s
r = 0,4 m
Vmax = w.r =
3.
2π .
r
T
2.3 .
0, 4
4
Vmax = 0, 6 m/s
Vmax =
k
k
2k
3k
k1=6k
CEVAP E
m
3k
m
fiekil - I
fiekil - II
5.
–x
K
fiekil-I’deki cismin periyodu,
T1 = 2 π
m
= T olur.
k
fiekil-II deki paralel ba¤lanan yaylar›n yay sabiti,
k1 = k + 2k + 3k = 6k
olur. k1 ile 3k seri ba¤land›¤›ndan eflde¤er yay sabiti,
1
1 1
= +
k eş k1 3k
1
1
1
=
+
⇒ k eş = 2k olur.
k eş 6k 3k
L
O
denge
konumu
M
N
+x
t1
t2
O dan M ye gelme süresi,
t1 =
T
dir.
12
M den L ye gelme süresi,
T T
T
6T T
+ +
=
=
6 4 12 12
2
T
t1 12
2
1
olur.
=
=
=
t2
T
12 6
2
t2 =
CEVAP B
209
Basit Harmonik Hareket
6.
9.
Cisim K den O ya 3 saniyede
geldi¤ine göre cismin periyodu
T = 3 . 4 = 12 saniyedir. Yay sabiti,
düfley
duvar
I. yarg› yanl›flt›r.
m
k
2
12 = 2 . 3 .
k
2
2 =
(
k
L
•K
T = 2π .
x
2kg
k=
3s
1
N/m dir.
2
eflitli¤inden bulunur.
•L
Cismin periyodunu art›rmak için m kütlesi art›r›lmal›, k
yay sabiti azalt›lmal›d›r.
Periyot genli¤e ba¤l› de¤ildir.
P - L aras›ndaki uzakl›¤a ba¤l› de¤ildir.
III. yarg› yanl›flt›r.
T/6
T/12
T/12
T/6
2s
1s
1s
2s
m
–x
O
T/12
P
T/12
m
k
,
g
2π
T
=
2T
2π
1 mg
=
4
k,
k,
mg =
olur.
4
+x
CEVAP A
R
11.
T/6
Cisim denge noktas›na ulaflt›¤›nda h›z› maksimumdur.
H›z› O noktas›nda maksimum, K ve R noktalar›nda ise
minimumdur.
I. yarg› do¤rudur.
Cismin aralar› geçme süreleri flekilde gösterilmifltir. 3.
saniyede cisim O noktas›ndad›r.
Sal›n›mlar aras›ndaki faz fark›,
t
T
1 2
=
6 T
T = 12 s olur.
ESEN YAYINLARI
L
T/6
CEVAP B
CEVAP E
10.
K
yatay
yer
P
m
k
T = 2π .
3s
II. yarg› yanl›flt›r.
7.
O
Kütle - yay sisteminin periyodu,
•O
x
m
k
p=
k
k
K
L
Cismin periyodundan,
m
k
2
12 = 2 . 3
k
2
4 =
k
1
k = N/m olur.
2
T = 2π
II. yarg› yanl›flt›r.
Cisim 2. saniyede P de,
8. saniyede L dedir.
H›z vektörel büyüklük oldu¤undan, 2. ve 8. saniyede h›zlar›n büyüklükleri eflittir. H›zlar› eflit de¤ildir.
III. yarg› yanl›flt›r.
CEVAP C
CEVAP A
12.
k
8.
k
k
k
V
3m
k
–x
K
O
denge konumu
L
+x
T2
2m
›
V = Vmax cos w.t
2π T
›
V = V . cos
.
T 8
π
›
V = V . cos
4
2
›
V =V.
olur.
2
T1
fiekil- I
2π
T1
=
T2
CEVAP D
210
fiekil- II
2π
2m
k
2
3m
3k
= 2 olur.
CEVAP D
BAS‹T HARMON‹K HAREKET
1.
TEST - 2
5.
Basit sarkac›n periyodu,
,
Tb = 2π.
g
Yay sarkac›n periyodu,
m
Ty = 2π.
d›r.
k
K
–x
O
L
V = Vmax cos w.t
π
t
2
Vmax = 24 cm/s
V = 24 cos
Basit sarkaç ve yay sarkac› Ay’a götürüldü¤ünde çekim
ivmesi azald›¤›ndan; basit sarkac›n frekans› azal›r, yay
sarkac›n›n frekans› de¤iflmez.
π
rad/s
2
Vmax = w.r
w=
I. yarg› yanl›flt›r.
π
.r
2
3
24 = . r
2
r = 16 cm
24 =
Kütleler art›r›ld›¤›nda, basit sarkac›n frekans› de¤iflmez,
yay sarkac›n›n frekans› azal›r.
II. yarg› yanl›flt›r.
olur.
CEVAP A
Basit sarkac›n periyodu kütleden ba¤›ms›z, yay sarkac›n
periyodu ise yerçekim ivmesinden ba¤›ms›zd›r.
III. yarg› do¤rudur.
2.
CEVAP C
6.
F=k.x
20 = k . 0,1
m
k
ı
m = 2kg
4
400
6
3
T=
s olur.
=
10 5
T = 2.3
ESEN YAYINLARI
k› = 2k = 400 N / m
T1
=
T2
4,
g
,
g
2π
2π
α α α α
T1 2
=
T2
1
T1 = 12 s
T2 = 6 s olsun.
k = 200 N / m
T = 2π
+x
denge
konumu
4l
1s
0,5s 0,5s
l
II
1s
4m
I
fiekilde görüldü¤ü m
K
2s
gibi 1. karfl›laflma
L do¤rultusu üzerinde olur.
N
L
2s
1s
O
1s
M
düfley
CEVAP B
CEVAP A
3.
X
–x
+x
K
L
O
P
R
7.
düfley
duvar
Cisim R noktas›ndan O noktas›na giderken h›z› artar
dolay›s›yla kinetik enerjisi artar.
I. yarg› yanl›fl, III. yarg› do¤rudur.
Cisim denge noktas›na yaklaflt›¤›nda cismin ivmesi azal›r.
II. yarg› yanl›flt›r.
CEVAP C
m
k
P
yatay
yer
x
O
x
K
Cismin O noktas›ndaki momentumu (P) ve kütlesi (m)
bilindi¤ine göre O noktas›nda cismin maksimum kinetik
enerjisi,
2
4.
Cisim T noktas›ndan ikin-
Ek =
ci kez geçerken –y yö-
2
1
1 2
P
2
mV =
= k.x
2
2m 2
nünde hareket eder. Bu
durumda yay cismi ken-
1
P
2
mV =
den bulunabilir.
2
2m
R
dine çeker. Kuvvet +y yö-
k
+y
nündedir. Kuvvet ile ivme
F
ayn› yönlüdür.
O
H›z – y yönündedir.
T
a
denge
noktas›
m
eflitli¤inden x bilindi¤ine göre k yay sabiti bulunur. Cismin periyodu,
T = 2π.
–y
P
V
CEVAP B
m
da bulunur.
k
Cismin K noktas›ndaki ivmesi,
F = k x = m.a
eflitli¤inde, k, x ve m bilindi¤inden a bulunur.
CEVAP E
211
Basit Harmonik Hareket
8.
10.
6
=
8
3l
2π
2π
4l
3
4
k2
k1
1
k eş
1
k eş
çivi
m
l
K
hK
P
hL
O
Basit sarkac›n periyodu,
T = 2π .
,
g
2π
6
T
4,
o=2
g
,
o =2
g
,
2π .
= 4 olur.
g
=
ı
2π
6
T
=
ı
k1
k2
m
m
k2
9
16
1 1
=
+
16 9
25
=
144
144
=
25
=
k eş
1
t 1 = . e 2π .
4
1
. 2 . e 2π .
4
k1
k2
k1
=
eflitli¤inden bulunur.
Cismin K den O ya gelme süresi 2 saniye oldu¤undan,
m
k1
m
k2
T1 = 6s
T2 = 8s
fiekil- I
m
T›
fiekil - II
m
16
m
144
25
12
4.5
ı
T = 10 s olur.
CEVAP D
Cismin O dan P ye gelme süresi,
t2 =
1
. e 2π .
4
,
1
o = . 4 = 1 s olur.
g
4
ESEN YAYINLARI
I. yarg› do¤rudur.
Cismin periyodu,
T = 2t1 + 2t2
= 2.2 + 2.1
= 6 s olur.
11.
m kütleli cismin periyodu,
,
a
T = 2π .
α
l
eflitli¤inden bulunur.
II. yarg› do¤rudur.
Gezegenin çekim ivmesi
(a) y› bulabilmek için periyot ve ipin boyu bilinmelidir.
Cismin K noktas›ndaki enerjisi P noktas›ndaki enerjisine eflittir.
E =E
K
P
m . g . hK = m . g . hL
m
CEVAP C
hK = hL dir.
III. yarg› do¤rudur.
9.
kütle(m)
CEVAP E
periyot(T)
periyot(T)
12.
periyot(T)
fiekil - I
uzunluk(l)
fiekil- II
çekim
ivmesi(g)
fiekil- III
T = 2π.
3s
,
oldu¤undan periyot
g
x (cm)
K
, ile orant›d›r.
II. grafik do¤rudur. III. grafik yanl›flt›r.
L
O
M
N
1s
CEVAP D
212
K noktas›nda göründükten 6 s sonra K de görülür. 3 s
sonra N de, 1 s sonra M noktas›nda görülür.
Sarkac›n periyodu kütleye ba¤l› de¤ildir.
I. grafik do¤rudur.
Sarkac›n periyodu,
π
rad/s
3
2π
w=
T
π
2π
=
3
T
T=6s
w=
CEVAP B
BAS‹T HARMON‹K HAREKET
1.
TEST - 3
Yaylar›n periyotlar›,
düfley
duvar
m
k
K
–r
yatay
L düzlem
+r
O
T1 = 2 π
m
k
T2 = 2 π
m
4m
= 2π
k
k
4
denge
konumu
T1
Cismin L noktas›ndaki ivmesi
➞
T2
➞
a = – w2 r
=
1
olur.
2
CEVAP B
2
a=
4π
T
2
. r ba¤›nt›s›ndan T bulunur.
F = k.x
m.a = k.x
ba¤›nt›s›nda m bilinmedi¤inden k bulunamaz.
Cismin O noktas›ndaki h›z›,
V = w.r =
2π
. r ba¤›nt›s›nda T ve r bilindi¤inden V buluT
nur.
2.
CEVAP C
H›z - uzan›m grafi-
h›z
¤ine göre, I. yarg›
Vmak
–r
+r
uzan›m
–Vmak
‹vme - uzan›m grafi-
ivme
¤ine göre, II. yarg›
Cisme K noktas›nda
etki
➞
eden
+r
–r
uzan›m
kuvvet
2F , M noktas›nda
4.
T/6
T/12
L
x
L’den P’ye
CEVAP B
R’den S’ye
Yaylar ayn› yaydan kesil-
seri ba¤l› 4 yay›n seri
m
ba¤lanmas› gibi düflüne-
fiekil- I
k
1 4
= ⇒ k 2 = olur.
k2 k
4
cismin periyodu
k2
K
1 1 1 1 1
= + + +
k2 k k k k
6
R
x
S
saniyede,
T
12
saniyede
e,
T
12
T
6
saniyede,
saniyyede gelir.
k
k1
sabiti k1= k ise, boyu 4l
¤er yay sabiti,
T
L den S ye gelme süresi
di¤inden özdefltir. Boyu
olan yay› boylar› l olan
x
O
Cisim serbest b›rak›ld›¤›nda noktalar aras›ndaki uzakl›k-
O’den R’ye
III. yarg› yanl›flt›r.
biliriz. Bu durumda eflde-
x
P
P’den O’ya
–amak
– F dir.
l1= l olan yay›n eflde¤er
T/6
m
➞
3.
T/12
lar eflit oldu¤undan,
amak
do¤rudur.
ESEN YAYINLARI
do¤rudur.
k
K
k
T
= 6 ⇒ T = 2.6 = 12 s olur.
2
Cismin L den P ye gelme süresi,
TLP =
m
T 12
=
= 2 s olur.
6
6
I. yarg› yanl›flt›r.
Cismin frekans›, f =
fiekil- II
T
saniye oldu¤undan,
2
k
1
1 -1
=
s
olur.
T 12
II. yarg› do¤rudur.
m
Cisim b›rak›ld›ktan 6 s sonra S noktas›nda 12 saniye sonra L de, 18 s sonra tekrar S noktas›ndad›r ve h›z› s›f›rd›r.
III. yarg› do¤rudur.
CEVAP D
213
Basit Harmonik Hareket
5.
7.
Sarkaçlar›n uzunluklar›
eflit oldu¤undan periyodlar›,
θ
,
g
T = 2π.
θ
l
θ
l
eflit olur. Bu durumda
sarkaçlar M noktas›nda
çarp›fl›rlar.
K
I. yarg› do¤rudur.
m kütlesi K den L ye
gelirken potansiyel
enerji kaybeder. Bu
enerji kinetik enerjiye
dönüflerek cismin h›z›n› art›r›r. Cismin h›z›n›n artmas› demek
çizgisel h›z›n›n artmas› demektir.
l
m
P
K
L
Aç›sal h›z, V = ω . l
eflitli¤inde l sabit oldu¤undan çizgisel h›z (V) artt›¤›ndan aç›sal h›z (ω) da artar.
düfley
N
M
rak›l›yorlar. K den b›rak›lan sarkaç daha fazla
Merkezcil ivmenin büyüklü¤ü,
yükseklikten b›rak›ld›¤›ndan h›z› daha büyüktür.
2
II. yarg› do¤rudur.
a=
M noktas›nda iplerdeki gerilmeler,
m.V
r
θ θ
düfley
L
Sarkaçlar ayn› anda b›-
T = m.g +
tavan
V
2
= ω .l
l
eflitli¤inden l sabit oldu¤undan V veya ω artt›¤›ndan
merkezcil ivme artar.
CEVAP E
2
dir.
V ler farkl› oldu¤undan ip gerilmeleri de farkl›d›r.
III. yarg› yanl›flt›r.
ESEN YAYINLARI
CEVAP C
6.
F(N)
8.
12
X
Y
8
Z
4
1
m=2kg
2
3
fiekil - I
X
4
x(m)
düfley
duvar
Y
Z
6kg
yatay
düzlem
yatay
fiekil - II
Yaylar özdefl ve birbirlerine paralel ba¤l› olduklar›nda sis-
Kuvvet - uzan›m grafi¤inin e¤imi bize yaylar›n yay sabitini
temin yay sabiti,
verir.
X in yay sabiti,
kefl = k + k + k + k + k
kX =
= 5k
= 5.10
= 50 N/m olur.
Kütle yay sistemin periyodu,
T = 2π
= 2.3.
=
Y nin yay sabiti, k Y =
8
= 4 N/m
2
Z nin yay sabiti, k Z =
4
= 2 N/m olur.
2
Yaylar fiekil - II deki gibi seri ba¤lan›rsa yaylar›n eflde¤er
m
k eş
yay sabiti,
2
50
6
s olur.
5
CEVAP C
1
1
1
1
+
+
=
k X k Y k Z k efl
1
1 1
1
+ + =
12 4 2 kefl
10
1
6
=
( kefl = N/m olur.
12
k efl
5
Sistemin periyodu,
214
12
= 12 N/m
1
Basit Harmonik Hareket
T = 2π .
12.
m
k efl
6
6
5
= 6 5 s olarak bulunur.
Cisim O dan geçerken
ipteki gerilme kuvveti,
α α
2
= 2.3.
m.V
Tip =
+ mg
r
l
2
38 = 2.
CEVAP E
V
+ 2.10
4
2
V
2
V = 6 m/s olur.
18 =
T
Cismin periyodu,
9.
–x (cm)
K
O
–20
L
2
mg Fmk
V=
denge
konumu
2
V = w R –x
2π
2
2
R –x
=
T
2.3
400 – 256
=
8
6
= .12
8
= 9 cm/s olur.
O
2πr
T
2.3.,
6=
T
6.4
6=
( T = 4 s olur.
T
+x (cm)
+20
16
L
K
Cismin O dan L ye gelme süresi,
T 4
t = = = 1 s olur.
4
4
CEVAP E
CEVAP D
k
k
k
m
k
k
m
m
yatay düzlem
fiekil - I
k
fiekil- II
yer
ESEN YAYINLARI
10.
fiekil- III
Yaylar özdefl ve üçüde paralel oldu¤undan,
kefl = k + k = 2k olur.
Cisimlerin periyotlar›,
T1 = T2 = T3 = 2π.
11.
m
olur.
k
CEVAP A
Asansör duruyorken veya
sabit h›zla gidiyorken cismin periyodu,
T = 2π.
Cismin periyodu de¤iflmez.
I. yarg› do¤rudur.
Asansör ivmeli hareket yaparken periyot,
T = 2π.
α
,
dir.
g
,
g›
l
K
P
olur.
›
›
g = g ± a olur. Asansörün hareket yönü bilinmeden g
ivmesi bilinemez.
II. ve III. yarg›lar için kesin birfley söylenemez.
CEVAP A
215
BAS‹T HARMON‹K HAREKET
1.
T = 4s
TEST - 4
5.
r = 0,4 m
α α
3. saniye sonunda ivme maksimum olur.
2
2
amax = w r =
4π
T
2
4l
.r
l
K
K
2
amax = 0, 9 m/s olur.
CEVAP E
Cismin periyodu,
T = 2π.
,
dir.
g
›
T
=
T2
α
l
‹pin boyu ve cismin kütlesi
2 kat›na ç›kart›l›rsa sarkac›n periyodu,
T = 2π.
L
2,
= 2T
g
K
T›
fiekil - I
fiekil - II
4,
g
,
g
2π
2π
fiekil - II deki sistemin periyodu,
ı
T =
,
1
= . e2π.
4g
2
,
1
o = T olur.
g
2
II. yarg› do¤rudur.
Aç› 10° den küçükse periyot aç›ya ba¤l› de¤ildir.
III. yarg› do¤rudur.
CEVAP D
ESEN YAYINLARI
Sarkaç, çekim ivmesi Dünya’n›n 4 kat› olan bir gezegene götürüldü¤ünde periyot,
›
T
T
2
=
T2 1
T
T2 =
olur.
2
olur. I. yarg› yanl›flt›r.
T = 2π.
3l
4l
çivi
4.9
amax =
. 0, 4
16
2.
α
6.
T T 3
+ =
T olur.
2 4 4
Yay sarkac›n›n periyodu,
T = 2π
m
d›r.
k
Yay sarkac›n›n periyodu yerçekimi ivmesine, asansörün
ivmesine ba¤l› olmad›¤›ndan de¤iflmez.
Asansör yukar› yönde düzgün h›zlan›rken basit sarkac›n
periyodu,
3.
➞
a
➞
F➞
V
T = 2π
k
,
olur. ‹lk duruma göre periyodu azal›r.
g+a
CEVAP A
N
K
x
O
x
P
Cismin N noktas›ndan 2. kez geçerken hareket yönü K
den O ya do¤rudur. Yay aç›ld›¤› için cismi çeker. Kuvvet
➞
➞
ile ivme ayn› yöndedir. Bu durumda h›z (V), kuvvet (F) ve
➞
ivme (a) +x yönünde olur.
CEVAP C
4.
CEVAP D
mX
= 2π
k
m
=T
k
mY
= 2π
k
16m
= 4T
k
Y kütlesinin ilk kez denge konumuna gelme süresi,
Tdenge =
TY 4T
=
= T dir.
4
4
Bu sürede X cismi bir sal›n›m yapar ve ilk hareket noktas›na gelir.
CEVAP C
216
x = 2 x o .cos
π
⋅ 0 = 2 x o .cos 0 = 2 x o
6
olur. Bu durumda cisim P noktas›ndan harekete geçmifltir.
t = 20. saniyede cisim,
π
⋅ 20
6
10 π
= 2 xo .cos
3
= 2 xo .cos(2 π +
Y cisminin periyodu,
TY = 2π
Cisim t = 0 an›ndaki konumu,
x'=2 xo .cos
X cisminin periyodu,
TX = 2π
7.
4π
)
3
4π
3
= 2 xo .cos 240°
= 2 xo .cos
1
= 2 xo .(− )
2
= −xo olur..
Bu da cismin L noktas›nda oldu¤unu gösterir.
Basit Harmonik Hareket
I I. yol
10.
2π
ω=
T
Fnet
m
mg – Fk
=
m
V .d .g
=g– b s
Vb . d c
1. g
=g–
4
3
= g olur.
4
CEVAP B
m1
k
m2
k
T
ı
3
T
ı
2π
=
su
,
a
ı
T = 2π
,
3
g
4
= 2π
9
k
25
k
2
=
mg
Cismin periyodu,
m1
9
=
m 2 16
2π
Fk l
olur.
a=
ye gelir. 2 s de K den P ye gelir.
3 2π
=
4
2π
3s
Cisim su içinde iken ivmesi,
Cisim 12 s sonra tekrar P noktas›na gelir. 6 s de P den K
3
,
=
g
T = 2π
π
2π
=
⇒ T = 12 s olur.
6
T
8.
Cismin havadaki periyodu,
2
.T
3
2
=
. 3
3
=
3
5 2
= 2 s olur.
ı
T =5 2s
olur.
CEVAP E
ESEN YAYINLARI
CEVAP D
9.
α
α α
α
11.
l
yavafllad›¤›nda
l
m
T/6
2t
T/6
K
2t
T/4
T/12 T/12
L t
t
M
N
P
K
m.g
Araban›n h›z› sabit iken periyot,
,
dir.
g
T = 2π.
Araba ivmeli hareket yapt›¤›nda periyot,
ı
T = 2π .
I. yarg› yanl›flt›r.
ı
g =
T
oldu¤undan,
12
12t
T
=
= t olur.
12
12
II. yarg› do¤rudur.
P
T/4
T
( T = 12t olur.
6
L den M ye gelme süresi
›
m.a
Parça盤›n K den L ye gelme süresi T/6, L den M ye
gelme süresi T/12 dir. L den M ye gelme süresi M den N
ye gelme süresine, K den L ye gelme süresi de N den P
ye gelme süresine eflittir. III. yarg› do¤rudur.
K den L ye gelme süresi 2t ise;
2t =
T
CEVAP E
2
,
g
g +a
ı
2
dir.
Periyot ve frekans de¤iflir. Periyot azal›r, frekans artar.
Cisim ivmelenece¤inden cisme etki eden net kuvvet artaca¤›ndan ipteki T› gerilme kuvveti artar.
CEVAP A
217
ESEN YAYINLARI
Basit Harmonik Hareket
218