mühendislikte olasılık, istatistik, risk ve güvenilirlik

Bölüm 3
RASGELE DEĞİŞKENLERİN DAĞILIMLARI
Bir rasgele değişkene ait rasgele olayların dağılımlarını toplu bir şekilde dağılım
fonksiyonu ile ifade edebiliriz. Bu fonksiyonun gösterilişi değişkenin kesikli yada
sürekli oluşuna göre farklıdır. Basit rasgele olayların olasılıklarının tanımlanması
açısından rasgele değişkenleri iki sınıfa ayırarak incelemek gerekir.
Kesikli rasgele değişkenler; Örnek uzayındaki eleman sayısı (basit olay) sonlu olan
(bir kavşağa 1 dakikada gelen araba sayısı, 1 yıldaki yağışlı günlerin sayısı gibi)
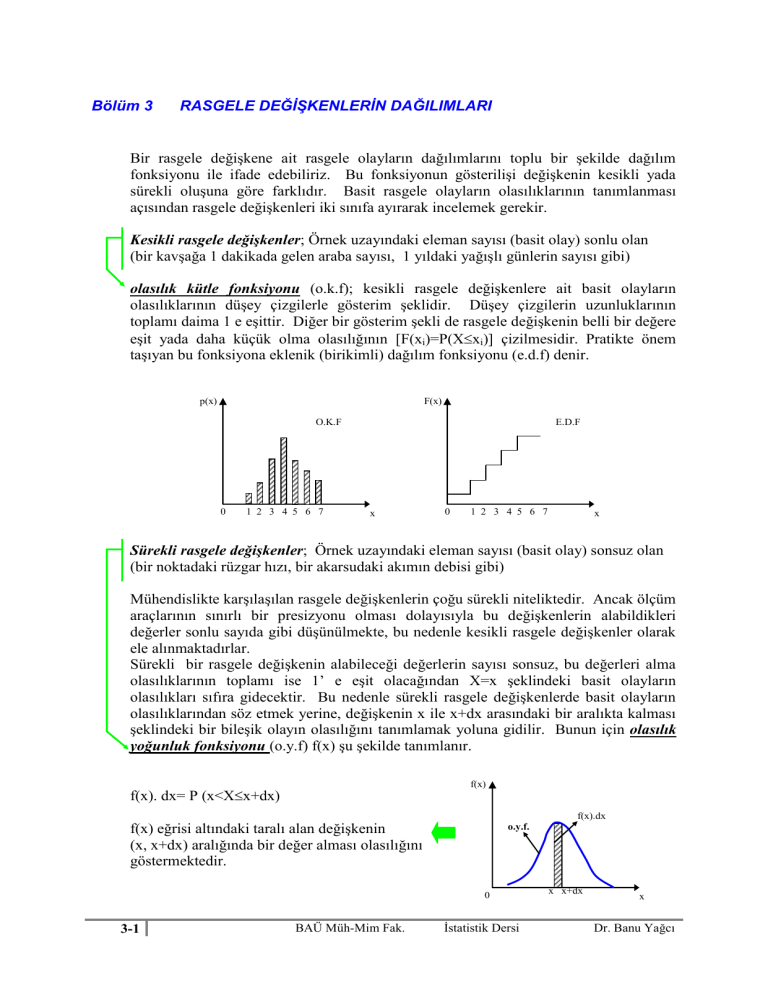
olasılık kütle fonksiyonu (o.k.f); kesikli rasgele değişkenlere ait basit olayların
olasılıklarının düşey çizgilerle gösterim şeklidir. Düşey çizgilerin uzunluklarının
toplamı daima 1 e eşittir. Diğer bir gösterim şekli de rasgele değişkenin belli bir değere
eşit yada daha küçük olma olasılığının [F(xi)=P(Xxi)] çizilmesidir. Pratikte önem
taşıyan bu fonksiyona eklenik (birikimli) dağılım fonksiyonu (e.d.f) denir.
p(x)
F(x)
O.K.F
0
1 2 3 4 5 6 7
E.D.F
x
0
1 2 3 4 5 6 7
x
Sürekli rasgele değişkenler; Örnek uzayındaki eleman sayısı (basit olay) sonsuz olan
(bir noktadaki rüzgar hızı, bir akarsudaki akımın debisi gibi)
Mühendislikte karşılaşılan rasgele değişkenlerin çoğu sürekli niteliktedir. Ancak ölçüm
araçlarının sınırlı bir presizyonu olması dolayısıyla bu değişkenlerin alabildikleri
değerler sonlu sayıda gibi düşünülmekte, bu nedenle kesikli rasgele değişkenler olarak
ele alınmaktadırlar.
Sürekli bir rasgele değişkenin alabileceği değerlerin sayısı sonsuz, bu değerleri alma
olasılıklarının toplamı ise 1’ e eşit olacağından X=x şeklindeki basit olayların
olasılıkları sıfıra gidecektir. Bu nedenle sürekli rasgele değişkenlerde basit olayların
olasılıklarından söz etmek yerine, değişkenin x ile x+dx arasındaki bir aralıkta kalması
şeklindeki bir bileşik olayın olasılığını tanımlamak yoluna gidilir. Bunun için olasılık
yoğunluk fonksiyonu (o.y.f) f(x) şu şekilde tanımlanır.
f(x)
f(x). dx= P (x<Xx+dx)
f(x).dx
f(x) eğrisi altındaki taralı alan değişkenin
(x, x+dx) aralığında bir değer alması olasılığını
göstermektedir.
o.y.f.
0
3-1
BAÜ Müh-Mim Fak.
İstatistik Dersi
x x+dx
x
Dr. Banu Yağcı
Sürekli değişken halinde de birikimli dağılım fonksiyonunun tanımı değişmez. Bağıntı
(F(x)) rasgele değişkenin belirli bir değere eşit olması ya da ondan küçük olması
olasılığını belirtir
Bir X rasgele değişkenine ilişkin olasılık dağılımı çoğunlukla birikimli olasılık dağılım
fonksiyonu yada kısaca dağılım fonksiyonu ile tanımlanabilir.
X kesikli rasgele değişken ise;
F ( x)  P( X  x) 
dağılım fonksiyonu;
 P( X  x )
tümxi ler  x
i
X sürekli rasgele değişken ise;
x
dağılım fonksiyonu;
F ( x)  P( X  x) 
 f (u)du

Bir rasgele değişkenin temel tanımlayıcıları – Dağılımların Parametreleri
Bir rasgele değişkenin olasılıksal özellikleri (karakteristikleri); dağılım fonksiyonunun
yada eşdeğer şekilde olasılık yoğunluk ya da kütle fonksiyonunun biçimi ile
parametreleri kesinlikle belirlenebiliyorsa tam olarak tanımlanabilir. Olasılıksal
özellikleri tanımlayan temel büyüklüklerin en önemlileri; rasgele değişkenin merkezsel
değeri ve değerlerin dağılımının ölçüsüdür. Dağılımın simetrik olmadığı biliniyorsa,
kaykılmanın ölçüsü de önem kazanır ve bilinmesi yararlı olur.
Ayrıca dağılım fonksiyonu bilinse bile, pratik uygulamalar için önemli olan bilgileri
sağlamaları nedeniyle, temel büyüklüklerin bilinmesi gereklidir. Değişkenin dağılım
fonksiyonunun belli özelliklerini yansıtan bu büyüklüklere dağılımın parametreleri
denir. Parametrelerin eldeki verilerden tahmin edilmesi ve kullanılması dağılım
fonksiyonunun tahmin edilip kullanılmasına göre çok daha kolay olur. Bu nedenle
yaklaşık ta olsa çabuk cevapların elde edilmesi gereken mühendislik problemlerinde
parametreleri kullanmak gerekir.
Yukarıda da ifade edilmiş olduğu gibi parametreler dağılımın şu gibi özelliklerini belirtirler;
 Dağılımın merkezini, yani rasgele değişkenin çeşitli gözlemlerde alabileceği değerlerin
çevresinde kümelendiği değeri
 Çeşitli gözlemlerde rasgele değişkenin alacağı değerlerin, bu merkez çevresindeki
yayılmasının büyüklüğünü
 Dağılımın çarpıklığını
 Dağılımın sivriliğini
Bir rasgele değişkenin dağılımının bu gibi özelliklerinden herhangi birinin ölçüsü olan bir
parametreyi çeşitli şekillerde tanımlamak mümkündür. Ancak bunların arasında en çok
kullanılan istatistik moment tipindeki parametrelerdir (ortalama değer, varyans).
3-2
BAÜ Müh-Mim Fak.
İstatistik Dersi
Dr. Banu Yağcı
Ortalama değer (beklenen değer, merkezsel değer); Bir rasgele değişkenin olabilir değerleri
bir dizi oluşturur. Dolayısıyla bu dizinin merkezsel değeri ile ilgilenmemiz doğaldır
(ortalama değer gibi). Özellikle rasgele değişkenin farklı değerleri farklı olasılıklara yada
olasılık yoğunluklarına sahip olduğu için “ağırlıklı ortalama” ile ilgileniriz. Olasılık
teorisinde ağırlıklı ortalama, ortalama değer yada beklenen değer terimiyle adlandırılır ve
çoğunlukla mx yada E(X) simgesiyle belirtilir. Diğer taraftan bazı kitaplarda x simgesiyle de
gösterilmektedir.
X, olasılık kütle fonksiyonu p(xi) olan bir kesikli rasgele değişken ise;
E ( X )  mx 
 x . p( x )
i
i
tümxi ler
X, olasılık yoğunluk fonksiyonu f(x) olan sürekli bir rasgele değişken ise;

E ( X )  mx 
 x. f ( x).dx

bağıntılarından görüldüğü gibi, ortalama değer yada beklenen değer: kesikli rasgele
değişkenler için değişkenin her değeri ile bu değerin karşılığı olasılığın çarpılması ve böylece
belirlenen çarpım sonuçlarının toplanmasıyla elde edilir; sürekli değişkenler için ise toplamlar
yerine entegral alınır.
Bu tanımlardan görüleceği gibi, kesikli rasgele değişkenlerde ortalama, xi noktalarına
yerleştirilen p(xi) kütlelerinin ağırlık merkezinin absisidir. Sürekli rasgele değişkenlerde ise
ortalama, o.y.f. ile x ekseni arasında kalan alanın ağırlık merkezinin absisidir.
Bir rasgele değişkenin merkezsel değerini belirten öteki büyüklükler de mod ve medyandır.
Mod, ~
x , bir X rasgele değişkeninin en muhtemel; başka bir deyişle, olasılığı yada olasılık
yoğunluğu en fazla olan değeridir. Medyan, xm, bir X rasgele değişkeninin, altındaki ve
üstündeki değerlerinin olasılığı eşit olan değeridir (F(xm)=0.50 ).
Bir X rasgele değişkenine ilişkin ortalama değer, mod ve medyan genelde farklıdır. Ancak
olasılık yoğunluk fonksiyonunun simetrik olması halinde bu üç değer birbiriyle çakışır;
x =xm
mx = ~
Varyans ve standart sapma (dağılımın ölçüsü); Merkezsel değerden sonra bir rasgele
değişkene ilişkin en önemli büyüklük dağılımın ölçüsü ya da değişkenliğidir. Bu rasgele
değişken değerlerinin merkezsel değer dolayında ne ölçüde kümelendiği ya da dağıldığı
anlamına gelir. Böyle bir ölçünün ise merkezsel değerden sapmaları belirten bir fonksiyon
olacağı açıktır. Buna bağlamda ortalama değere göre karesel sapmaların ağırlıklı ortalaması
varyans [Var(X)] terimiyle adlandırılır.
3-3
BAÜ Müh-Mim Fak.
İstatistik Dersi
Dr. Banu Yağcı
X, kesikli rasgele değişken ise;
 ( x  m ) . p( x )
Var ( X ) 
2
i
x
i
tümxi ler

X, sürekli rasgele değişken ise;
Var ( X )   ( x  mx ) 2 . f ( x)dx

Tanımlardan varyansın, rasgele değişkenin olasılık yoğunluk fonksiyonu ile x ekseni arasında
kalan alanın ağırlık merkezinden geçen düşey bir eksene göre atalet momenti (ikinci
merkezsel moment) olduğu görülmektedir. Yukarıdaki ifadelere göre varyans; rasgele
değişkenin ortalamasından farkının karesinin beklenen değeridir;
Var ( X )  E (( X  mx )2 )
Varyansın büyük olması değişkenin ortalama çevresindeki yayılmasının büyük olduğunu
gösterir. Alttaki şekilde X1 ve X2 değişkenlerinin ortalamaları aynı olmakla birlikte X1 in
varyansı daha büyüktür. Bu durum çeşitli gözlemlerde ortalamadan uzak değerler alma
olasılığının X1 için daha büyük olduğunu göstermektedir.
f(x)
Var(X1)>Var(X2)
2
1
0
mx1=mx2
x
Yukarıdaki varyans bağıntısındaki entegralin kareli terimi açılırsa, varyans için şu kullanışlı
bağıntı elde edilir;
Var ( X )  E ( X 2 )  mx2
Bu bağıntıdaki E(X2) terimi X in karesel ortalama değerini belirtir.
Boyut bakımından fiziksel bir anlamı olabilmesi için dağılımın ölçüsü bağlamında varyansın
karekökü ile tanımlanan standart sapmanın () kullanılması uygundur.
 x  [Var ( X )]1 / 2
3-4
BAÜ Müh-Mim Fak.
İstatistik Dersi
Dr. Banu Yağcı
Varyasyon (değişim) katsayısı; Daha önceki bölümde de belirtildiği gibi, bir dağılımın
kapsamı (yayılma alanı) hakkında yalnızca varyans ya da standart sapma ile bilgi edinemeyiz.
Bu nedenle, dağılım kapsamı ölçüsünün merkezsel değere göre bağıl şekilde belirtilmesi; ve
standart sapmanın ortalama değere bölünmesiyle elde edilen varyasyon katsayısının (V)
kullanılması daha anlamlı ve yararlı olur;
Vx   x / mx (Bazı kitaplarda Cx ile gösterilir)
Varyasyon katsayısı ortalamaları farklı olan iki rasgele değişkenin yayılımlarını
karşılaştırmamıza imkan verir. Hangi değişkenin varyasyon katsayısı daha büyük ise o
değişkenin yayılması ortalamasının daha büyük bir yüzdesine eşit demektir.
Kaykılmanın ölçüsü (Çarpıklık katsayısı); Bir rasgele değişkenin başka bir özelliği de
olasılık dağılımının simetrik olması yada olmamasıdır. Düşey bir eksene göre simetrik
olmayan bir dağılım için asimetrinin derecesi ve yönü bağlamındaki özelliğidir. Bir
asimetrinin yada kaykılmanın ölçüsü üçüncü merkezsel moment ile tanımlanır.
X kesikliyse;
E ( X  mx )3 
 ( x  m ) . p( x )
3
x
i
tümxi ler

X sürekli ise;
E ( X  mx )3   ( x  mx )3. f ( x)dx

Olasılık dağılımının ortalamaya göre simetrik olması halinde E=(X-mx)3=0 olacağı hemen
görülebilir. Çarpılmanın boyutsuz ölçüsü bir çarpıklık (kaykılma) katsayısı ile tanımlanır.
 = E(X-mx)3 / x3
(bazı kitaplarda CsX ile gösterilir)
f (x)
f (x)
=0
<0
0
f (x)
x
0
>0
x
0
x
 nın pozitif olması dağılımın pozitif çarpık olduğunu (sağa doğru uzayan bir kuyruğu
bulunduğunu), negatif olması ise dağılımın negatif çarpık olduğunu (sola doğru uzayan bir
kuyruğu bulunduğunu) gösterir.
Kurtosis katsayısı; 4. mertebeden merkezsel momente dayalı olarak dağılımın sivriliğini
gösteren bir katsayıdır. Katsayının değeri dağılımın o.y.f. nun sivriliği ile birlikte artar.
kx = E(X-mx)4 / x4
3-5
BAÜ Müh-Mim Fak.
İstatistik Dersi
Dr. Banu Yağcı
Çok Değişkenli Dağılımların Parametreleri;
X ve Y gibi iki rasgele değişkenin ortak dağılımında, X ve Y nin marjinal dağılımlarının
ortalama, varyans gibi parametrelerinden başka X ve Y nin merkezsel çarpım momentini de
göz önüne almak gerekir. Bu momente kovaryans adı verilir.
Cov(X,Y)= E[(X-mx) (Y-my)]

Cov( X , Y ) 
 ( x  m ).( y  m ). f ( x, y)dxdy
x
y

Kovaryansın boyutu X ve Y değişkenlerinim boyutlarının çarpımı gibi olduğundan, boyutsuz
bir katsayı elde etmek için kovaryans X ve Y nin standart sapmalarının çarpımına bölünerek
korelasyon katsayısı tanımlanır.
 X ,Y 
Cov( X , Y )
 x . y
Bu katsayının değeri -1 ile 1 arasında değişebilir. X,Y nin mutlak değerinin 1 e yaklaşması,
ileride gösterileceği gibi, X ile Y arasındaki doğrusal bağımlılığın kuvvetlenmesini ifade eder.
X ve Y nin bağımsız olması halinde ise kovaryansın 0 a eşit olduğu kolayca gösterilebilir.
Kovaryansın 0 a eşit olmayıp pozitif değer alması, X in ortalamadan büyük değerlerine
genellikle Y nin ortalamadan büyük değerlerinin, X in ortalamadan küçük değerlerine de Y
nin ortalamadan küçük değerlerinin karşı geldiğini gösterir. Bu durumda X ve Y bağımsız
olmayıp aralarında bir bağımlılık vardır. Kovaryansın negatif değer alması da rasgele
değişkenlerin bağımlı olduğunu gösterir, ancak bu durumda değişkenlerden biri artarken
diğeri azalmaktadır.
Korelasyon katsayısının mutlak değerinin 1 e eşit olması X ile Y arasında y=a+bx şeklinde
doğrusal fonksiyonel bir bağımlılık olduğunu gösterir. Bağımlılığın fonksiyonel olmakla
birlikte doğrusal olmaması halinde ise korelasyon katsayısı 1 e eşit olmayabilir. Örneğin
y=ax2 fonksiyonel bağıntısı X ile Y arasında sıfıra yakın bir korelasyon katsayısı verir. Buna
göre korelasyon katsayısı iki rasgele değişken arasındaki doğrusal bağımlılığın bir ölçüsüdür.
3-6
BAÜ Müh-Mim Fak.
İstatistik Dersi
Dr. Banu Yağcı
[Uygulama 1] Bir X rasgele değişkeninin olasılık yoğunluk fonksiyonu aşağıdaki gibi
verilmiş olsun;
f(x) = ax2
0 x 10
f(x) = 0
başka yerde
(a) Bu fonksiyonun a’ nın hangi değeri için geçerli olabileceğini araştırınız ve X’ in 5 ten
büyük olma olasılığını hesaplayınız.
(b) X rasgele değişkeninin ortalama değerini, varyansını, standart sapmasını ve varyasyon
katsayısını, mod ve medyanını belirleyiniz.
10
 ax dx  1.0
2
(a)
ve dolayısıyla
a (10)3 / 3=1.0
ve a=3/1000
olmalıdır.
0
5
P(X>5) = 1- P(X5) = 1-  (3x 2 / 1000)dx =1 – (53 / 1000) = 0.875
0
10
E ( X )   x(3x 2 / 1000)dx  7.5
(b)
f(x)
0
3/10
10
Var ( X )   ( x  7.5) (3x / 1000)dx  3.75
2
f(x)=3x2/1000
2
0
X=(3.75)1/2 =1.94,
Vx=1.94/7.5=0.26
0
x
10
Yukarıda çizilen dağılım fonksiyonunun şekline göre mod değeri ~
x =10 olur.
xm
 (3x
2
/ 1000)dx  0.50 , dolayısıyla
xm3=500,
xm=7.94 (medyan)
0
[Uygulama 2]
50 km uzunluğundaki bir yol üzerinde trafik kazalarının üniform olarak
dağıldığı (f(x)=C) kabul ediliyor. Yolun 20 km si ile 30 km si arasında bir kaza meydana
gelmesi olasılığı nedir?
50
 Cdx  50.C  1
C=0.02
0
x
x
0
0
F ( x)   f ( x)dx   0.02dx  0.02 x
P(20<X30) = F(30) – F(20) = 0.02*30 – 0.02*20 = 0.20
3-7
BAÜ Müh-Mim Fak.
İstatistik Dersi
Dr. Banu Yağcı
OLASILIK DAĞILIMLARI / OLASILIK MODELLERI
Mühendislik alanında karşılaşılan fiziksel yada fiziksel olmayan rasgele değişken
büyüklüklerin olasılık dağılımları için model alınabilecek çok sayıda sürekli ve kesikli
fonksiyon bulunmaktadır. Ne var ki seçilen fonksiyon yani teorik dağılım ilgili rasgele
değişkene ilişkin deneysel dağılımı (histogram) olabildiğince gerçekçi biçimde yansıtmalıdır
(betimlemelidir).
Bu bağlamda, örneğin bir sürekli X rasgele değişkenine ilişkin f(x) fonksiyonunun yalnızca
biçiminin tahmin edilmiş olmasının, fonksiyona ilişkin eğrinin altında kalan alanlarla
belirlenen olasılıkların hesaplanmasını sağlamayacağı göz önünde bulundurulmalıdır. Çünkü
söz konusu alanların hesaplanabilmesi için anılan eğrinin denkleminin de belirlenmiş olması
gerekir.
Olasılıksal problemlerin çözümünde ise, model (fonksiyon) belirlendikten sonra, modele
ilişkin parametreler, örnekleme sonucu sağlanan istatistiksel verilerle tahmin edilir; örnek
ortalama değeri, örneğin standart sapması gibi. Bu bağlamda en uygun modelin seçimi,
varolan fonksiyonların özelliklerinin çok yakından bilinmesini gerektirir. Özetle model
konusunda en uygun kararın verilmesi, mühendisin bu konudaki bilgisine, deneyimine ve
mühendislik sezgisine bağlıdır.
Mühendislik alanında karşılaşılan rasgele değişkenlerin deneysel dağılımlarının çoğunu çok
yakından betimleyen çözümsel modellerin başlıcaları;
-
Normal dağılım
Lognormal dağılım
Binom dağılımı
Poisson dağılımı
Üssel dağılım
Gamma dağılımı
Khi-kare dağılımı
Geometrik dağılım
t tağılımı
F dağılımı
Üniform dağılım
Beta dağılım
Weibull dağılımı
Normal dağılım (Gauss dağılımı)
İstatistiğin tüm alanlarında rastlanan geniş ölçüde kullanılan en önemli sürekli olasılık
dağılımı normal dağılımdır. Doğada, sanayide, bilimsel araştırmalarda ve tüm mühendislik
alanlarında karşılaşılan rasgele değişkenlerin deneysel dağılımlarının pek çoğunun yapısına
uyar. Dağılımın normal eğri terimiyle adlandırılan grafiği çan biçimindedir.


3-8
f ( x) 
x
 1  x   2 
exp  
 
 2
 2    
BAÜ Müh-Mim Fak.
1
İstatistik Dersi
Dr. Banu Yağcı
Normal değişkenin olasılık dağılımını tanımlayan matematiksel bağıntı iki parametreye bağlı
değişir; ortalama değer (), standart sapma ().
Normal dağılımın özellikleri;
→ X ekseni ile normal eğri arasında kalan alan bire eşittir.

 f ( x)d
x
1

→ Normal dağılım ortalamaya göre simetriktir.



f ( x)d x 

 f ( x)d
x
 0.50
→ Normal dağılımda; değerlerin % 68.26 sı 1 aralığında, % 95.44 ü 2 aralığında
ve % 99.74 ü 3 aralığında yer almaktadır.

E
- ( +
+
u
+
2
→ Normal dağılım
s 2 3çarpıklık katsayısı sıfırdır
) olduğundan
3 s simetrik
→ Normal dağılımın basıklık katsayısı 3 dür.
=
s
s
→ Eklenik dağılım fonksiyonu doğrusal bir çizgidir.
0
s
s
-
-2
-3
% 68,26 +
% 95.44
% 99.74
+2
+3
→ Dağılım simetrik olduğundan ortalama, mod ve medyan değerleri eşittir.
3-9
BAÜ Müh-Mim Fak.
İstatistik Dersi
Dr. Banu Yağcı
Normal dağılımın parametreleri olan  ve  değerlerinin tanım aralıklarının gereği olarak,
teorik olarak, sonsuz sayıda normal dağılım düşünülebilir. İstatistikte normal dağılıma sahip
bir X değişkeninin belirli bir değere eşit veya daha küçük, belirli bir değere eşit veya daha
büyük yada belirli iki değer arasındaki değerleri alma olasılıklarının hesaplanması sık
gereksinim duyulan bir durumdur. Sözü edilen bu olasılıkların hesaplanması için integral
işlemi gereklidir. Ancak teorik olarak sonsuz sayıda olan normal dağılımlardan sadece bir
tanesi için integral değerlerinden bazıları hesaplanarak tablo halinde yayınlanmıştır. Bu
tablolar ortalaması sıfır ve standart sapması bir olan normal dağılım için hazırlanmıştır. =0
ve =1 olan normal dağılım standart normal dağılım olarak bilinir.
Standart normal dağılmış olan Z sürekli değişkenine ait olasılıkların standart normal
dağılım tablosundan bulunması;
Örnek 1; Z standart normal değişkeninin 1.06 ya eşit veya daha küçük değerler alma olasılığı
nedir?
Tablodan;
1.06
0
P(Z1.06)= 0.8554
E
Örnek 2; Z standart normal değişkeninin 3.25 değerine eşit veya daha büyük değerler alma
(
olasılığı nedir?
u
Tablodan;
)
P(Z3.25) = 1 – P(Z3.25) = 1 – 0.9994 = 0.0006
=
E
Örnek 3; Z standart normal değişkeninin -0.19 değerine eşit veya daha küçük değerler alma
(0
olasılığı nedir?
u
Tablodan;
)
P(Z-0.19) = 1 – P(Z0.19) = 1- 0.5713 = 0.4287
=
E
Örnek 4; Z standart normal değişkeninin 1.02 ve 2.12 veya bu aralıktaki değerleri alması
olasılığı nedir ?
3
0(
u
Tablodan;
)
s
P(1.02  Z 2.12) = P(Z  2.12) – P(Z  1.02)
= 0.9830 – 0.8461
=
= 0.136
E
BAÜ Müh-Mim Fak.
İstatistik Dersi
Dr. Banu Yağcı
3-10(0
3
u
3.25
0
-0.19
0
0.19
0 1.02
2.12
Standart normal dağılım Tablosu
Z
A
 f (Z )dz

A
Z
,0
3-11
,00
,01
,02
,03
,04
,5000
,5040
,5080
,5120
,5160
,5199
,05
,1
,5398
,5438
,5478
,5517
,5557
,5596
,2
,5793
,5832
,5871
,5910
,5948
,5987
,3
,6179
,6217
,6255
,6293
,6331
,6368
,4
,6554
,6591
,6628
,6664
,6700
,6736
,5
,6915
,6950
,6985
,7019
,7054
,7088
,6
,7257
,7291
,7324
,7357
,7389
,7422
,7
,7580
,7611
,7642
,7673
,7704
,8
,7881
,7910
,7939
,7967
E
(
u
)
=
Z
,06
,07
,O8
,09
,5239
,5279
,5319
,5359
,5636
,5675
,5714
,5743
,6026
,6064
6103
,6141
,6406
,6443
,6480
,6517
,6772
,6808
,6844
,6879
,7123
,7157
,7190
,7224
,7454
,7486
,7517
,7549
,7734
,7764
,7794
,7823
,7852
,7995
,8023
,8051
,8078
,8106
,8133
,9
,8159
,8186
,8212
,8238
,8264
,8289
1,0
,8413
,8438
,8461
,8485
,8508
,8531
1,1
,8643
,8665
,8686
,8708
,8729
1,2
,8849
,8869
,8888
,8907
,8925
1,3
,9032
,9049
,9066
,9082
1,4
,9192
,9207
,9222
1,5
,9332
,9345
1,6
,9452
,9463
1,7
,9554
,9564
,9573
1,8
,9641
,9649
,9656
1,9
,9713
,9719
,9726
0
,8315
,8340
,8365
,8389
,8554
,8577
,8599
,8621
,8749
,8770
,8790
,8810
,8830
,8944
,8962
,8980
,8997
,9015
,9099
,9115
,9131
,9147
,9162
,9177
,9236
,9251
,9265
,9279
,9292
,9306
,9319
,9357
,9370
,9382
,9394
,9406
,9418
,9429
,9441
,9474
,9484
,9495
,9505
,9515
,9525
,9535
,9545
,9582
,9591
,9599
,9608
,9616
,9625
,9633
,9664
,9671
,9678
,9686
,9693
,9699
,9706
,9732
,9738
,9744
,9750
,9756
,9761
,9767
2,0
,9772
,9778
,9783
,9788
,9793
,9798
,9803
,9808
,9812
,9817
2,1
,9821
,9826
,9830
,9834
,9838
,9842
,9846
,9850
,9854
,9857
2,2
,9861
,9864
,9868
,9871
,9875
,9878
,9881
,9884
,9887
,9890
2,3
,9893
,9896
,9898
,9901
,9904
,9906
,9909
,9911
,9913
,9916
2,4
,9918
,9920
,9922
,9925
,9927
,9929
,9931
,9932
,9934
,9936
2,5
,9938
,9940
,9941
,9943
,9945
,9946
,9948
,9949
,9951
,9952
2,6
,9953
,9955
,9956
,9957
,9959
,9960
,9961
,9962
,9963
,9964
2,7
,9965
,9966
,9967
,9968
,9969
,9970
,9971
,9972
,9973
,9974
2,8
,9974
,9975
,9976
,9977
,9977
,9978
,9979
,9979
,9980
,9981
2,9
,9981
,9982
,9982
,9983
,9984
,9984
,9985
,9985
,9986
,9986
3,0
,9987
,9987
,9987
,9988
,9988
,9989
,9989
,9989
,9990
,9990
3,1
,9990
,9991
,9991
,9991
,9992
,9992
,9992
,9992
,9993
,9993
3,2
,9993
,9993
,9994
,9994
,9994
,9994
,9994
,9995
,9995
,9995
3,3
,9995
,9995
,9995
,9996
,9996
,9996
,9996
,9996
,9996
,9997
3,4
,9997
,9997
,9997
,9997
,9997
,9997
,9997
,9997
,9997
,9998
BAÜ Müh-Mim Fak.
İstatistik Dersi
Dr. Banu Yağcı
Standart normal dağılım dışındaki normal dağılımlar için alan hesaplamalarında
kullanılacak hazır tablolar yoktur. Ancak her normal dağılım,
X 

doğrusal dönüştürmesi ile standart normal dağılıma dönüşür. Bu dönüştürmeden sonra
olasılık hesaplarında standart normal dağılım tablosundan faydalanılır.
Örnek 5; X değişkeni ortalaması 100 ve varyansı 144 olan bir normal dağılım göstermektedir.
Rassal olarak seçilecek bir birimin değerinin 112 yada daha küçük olma olasılığı nedir ?
Tablodan;
P(X112) = P(Z  112  100 ) = P(Z  1) = 0.8413
100
112
144
E
(
Örnek 6; Bir beton toplumunu göz önüne alalım. X betonun basınç mukavemeti olsun.
İstatistiksel deneyler sonucu normal dağılım parametreleri m=32 MPa ve =3 MPa tahmin
u
edilmiş bulunsun. Bu bilgilere göre aşağıdaki soruları cevaplandıralım.
)
a) Beton basınç mukavemetinin 25 MPa ile 40 MPa arasında değer alması olasılığı ne
olur?
=
P(25 X  40) = P(Z  (40-32)/3) - P(Z  (25-32)/3) = P(Z  2.67) - P(Z  -2.33)
0
Tablodan;
P(Z  2.67) – [1- P(Z  2.33)]
P(25 X  40) = 0.0062 -[1- 0.9900] = 0.9863
b) mukavemetin en az 20 MPa olması ihtimali nedir?
P(X 20) = 1 – P(Z (20 -32)/3) = 1 – P(Z -4) = 1- [1- P(Z4)]= 0.9999
Örnek 7; Bir kabuk çatı A, B ve C gibi üç mesnede oturmaktadır. Mesnetlere gelen yükler
duyarlılıkla tahmin edilebilmekte; fakat mesnetlerin altındaki zemin koşulları tam
kestirilememektedir. A, B ve C mesnetlerinde oluşan A, B ve C oturmalarının sırayla,
ortalama değerleri 20 mm, 25 mm, 30 mm; ve varyasyon katsayıları 0.20, 0,20, 0,25 olan
bağımsız normal değişkenler olduğunu kabul edelim ve şu soruları cevaplandırmak isteyelim;
a) Maksimum oturmanın 40 mm yi aşması olasılığı ne olur ?
b) A ve B mesnedinin sırayla 25 mm ve 35 mm oturduğu biliniyorsa; maksimum oturma
farkının 8 mm yi aşmaması olasılığı nedir? Maksimum oturma farkının 15 mm yi
aşmaması olasılığı nedir?
C
A
3-12
BAÜ Müh-Mim Fak.
B
İstatistik Dersi
Dr. Banu Yağcı
(a) P(max > 40 mm) = 1- P(max  40 mm) = 1-P(A40  B 40  C40)
= 1- P(A40) . P(B40) . P(C40)
= 1- P[Z  (40-20)/4] . P[Z  (40-25)/5] . P[Z  (40-30)/7.5]
= 1- P[Z  5] . P[Z  3] . P[Z  1.333]
= 1 – (1) . (0.9986) . (0.9087) = 0.092
(b) A ve B mesnetlerinin oturmaları arasındaki fark AB=35-25= 10 mm > 8 mm olduğu için
C ne olursa olsun, P(max 8 mm) = 0 olur. Yani max 8 mm oluşması olayı mutlak
imkansız olaydır.
C < 10 mm yada C > 40 mm olması durumunda AC> 15 mm (A=25 mm olduğu için)
C < 20 mm yada C > 50 mm olması durumunda BC> 15 mm (B=35 mm olduğu için)
olacaktır. Bu iki koşula göre;
C oturmasına ilişkin kabul edilebilir bölge (20mm  C  40 mm) olur. Bu bölgenin dışında
kalan C değerleri için maksimum oturma farkı 15 mm yi aşar. O halde;
P(max  15 mm) = P( 20 mm  C  40 mm) = P[Z (40-30)/7.5] - P[Z (20-30)/7.5]
= P(Z 1.333) – P(Z -1.333) = P(Z 1.333) – [1- P(Z1.333)]
= 0.9087 – (1- 0.9087) = 0.8174
Formüller
F ( x)  P( X  x) 
x
 P( X  xi )
F ( x)  P( X  x) 
ve
tümxi ler  x
E ( X )  mx 

 xi . p( xi )
E ( X )  mx 
ve
 ( x  m ) . p( x )
2
i
x
 x. f ( x).dx

tümxi ler
Var ( X ) 
 f (u)du

i

ve
Var ( X )   ( x  mx ) 2 . f ( x)dx

tümxi ler
Var ( X )  E (( X  mx ) 2 )
/
Var ( X )  E ( X 2 )  mx2
 x  [Var ( X )]1/ 2
/
Vx   x / mx
 = E[(X-mx)3] / x3
/
kx = E[(X-mx)4] / x4
3-13
BAÜ Müh-Mim Fak.
İstatistik Dersi
Dr. Banu Yağcı