Işıma ile ısı transferinin üç yolu vardır: taşınım

ISI DİNAMİĞİNİN İKİNCİ YASASINA BİR İSTİSNA:
ENTROPİNİN AZALMASI VE ISIL IŞIMA YOLUYLA GÜÇ ÇEVRİMLERİNDE
VERİM ARTIŞI
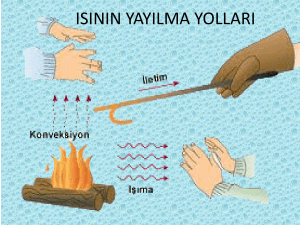
Işıma ile ısı transferinin üç yolu vardır: taşınım, iletim ve ışınım. İlk iki yolda ısı
transferinin gerçekleşmesi sıcaklık farkına ve fiziksel temasa bağlıdır. Işınım ile ısı
transferinde başka bir ortama gerek yoktur. Isıl ışınım elektromağnetik ışıma bandının belli
bir aralığını kapsar. Görünen ışıma bu bandın küçük bir kısmını oluşturur. Bütün cisimler
sıcaklıklarına göre belli dalga boyunda ışınım yoluyla ısı enerjisi yayarlar ve aynı yolla alırlar.
Yayılan ışınım yüzey sıcaklığına ve dalga boyuna bağlıdır. Aldıkları veya verdikleri ısı
enerjisi arasında ki farka göre sıcaklıkları artar veya azalır. İki ortam veya yüzey arasındaki ısı
alışverişini ortamların veya yüzeylerin sıcaklıkların, ışıma özellikleri ve geometrileri belirler.
Sıvı veya gaz cisimler arası ısı transferi hacimsel bir olaydır. Katı cisimler veya bazen sıvı
yüzler arası ısı transferi yüzeysel özelliklere bağlıdır. Bu çalışmada cisimlerin yüzeysel
özellikleri kullanılacaktır. Cisimlerin yüzeysel özellikleri ideal yüzeye göre tanımlanır.
Cisimler üzerinden yansıyan ışınım yoluyla görülür. Üzerinden ışınım yansımayan cisimler
göze siyah görünürler. Buradan hareketle bütün dalga boyunda üzerine gelen ışımayı yutan
yüzey siyah cisim olarak adlandırılır. Siyah cisim aşağıdaki özelliklere sahip ideal yüzey
olarak tanımlanır:
1- Belli sıcaklık ve dalga boyunda en fazla ışıma yayar. Aynı sıcaklık ve dalga boyunda
hiçbir yüzey daha fazla ışıma yapamaz.
2- Üzerine düşen bütün ışımayı dalga boyu ve yönden bağımsız olarak yutar.
3- Siyah yüzey ışıması sıcaklık ve dalga boyuna bağlı olarak yönden bağımsız
gerçekleşir.
Bir yüzeyin yaydığı toplam ışıma Stefan-Boltzman kanunu olarak bilinen aşağıdaki eşitlik ile
bulunur:
Eb = σT4
i ve j olarak tanımlanan iki yüzey arasındaki ışıma ile ısı transferi aşağıdaki gibi hesaplanır:
i yüzeyinden j yüzeyine ulaşan ışıma:
qi→j =Ai*Fij*Ebi
j yüzeyinden i yüzeyine ulaşan ışıma:
qj→i =Aj*Fji*Ebj
A yüzey alanı, Fij ve Fji
yüzey faktörleri, Ebi ve Ebj her iki yüzeyin yaptığı ışıma
iki yüzey arasındaki net ısı alışverişi:
qij=qi→j - qj→i ve Eb = σT4
ısıl denge için
qij=0
ve
qi→j = qj→i
Ai*Fij* σ Ti4 = Aj*Fji* σ Tj4
Ti = ( Aj*Fji / Ai*Fij )1/4 Tj
Parantez içindeki
Aj*Fji / Ai*Fij ifadesi karşılıklılık eşitliği gereği her zaman
bire eşittir. Bu sebeple ısıl denge durumunda yüzeylerin sıcaklıkları aynı olur. Daha açık bir
ifade ile yüzeylerin alıp verdikleri ısı miktarı ile sıcaklıkları birbirine eşittir. Bu eşitlik iki
yüzey birbiri ile herhangi bir yansıtıcı vasıtası ile ısı transferi yaptıkları durumda da değişmez.
Yukarıdaki hesaplama yüzeylerin düz ve ışımanın yönden bağımsız olduğu
varsayılmıştır. Gerçekte yüzey ışıması yönden bağımsız değil ve/veya yansıtıcı yüzeyler düz
olmayıp içbükey veya dışbükey olabilmektedir. Güneş ışınlarının yoğunlaştırılmasında
içbükey ayna kullanılmaktadır.
1-İçbükey ayna yoluyla iki yüzey arasında ısı transferi:
İki yüzeyin içbükey ayna yoluyla ısı alıverişi yaptığı bir düzeneğimiz olsun. i yüzeyini
ab olarak, j yüzeyini cd olarak gösterelim. i yüzeyinin alanı Aab j yüzeyinin alanı Acd olsun.
Yüzeyler siyah (ε=1) ve birbiriyle ısı transferinin içbükey ayna yoluyla gerçekleşir. Aynanın
yarıçapı 60 mm ve yüzeyler ayna yüzeyinden 90 mm uzaklıkta merkezin 30 mm önündedir.
Yansıma kurallarını kullanarak elde edilen görüntü aşağıdaki gibidir. Konumu şekilde
gösterilen görüntü gerçek ters ve gerçek görüntüsünden küçüktür.
Şeklin incelenmesinden anlaşılacağı gibi ab yüzeyinden cd yüzeyine giden ışınlar c`d`
görüntüsünden, yine cd yüzeyinden ab yüzeyine giden ışınlar a`b` görüntüsünden geçmek
zorundalar. Bu sebeple Aab* Fab→cd bulmak için Aab* Fab→c’d’ ‘nin hesaplanması, Acd*
Fcd→ab ‘yi bulmak için Aab* Fab→c’d’ ‘nin bulunması gerekir. Ayrıca içbükey aynanın xy yayı
şeklinde olması gerekir.
ac`=((40-5)2+452)1/2=57,00877125
ad`=((40-10)2+452)1/2=54,08326913
bd`=45
bc`=((10-5)2+452)1/2=45,27692569
Aab* Fab→c’d’ =((57,00877125+45)-( 54,08326913+45,27692569)/2)
=1,324288215
ca`=((10-20)2+452)1/2=46,09772229
cb`=((10-5)2+452)1/2=45,27692569
db`=((20-5)2+452)1/2=47,4341649
da`=45
Acd* Fcd→a’b’ =((46,09772229+47,4341649)-( 45,27692569+45)/2)
=1,62748075
Elde edilen verileri baştaki eşitliğe yerleştirirsek
Tab / Tcd = (Acd* Fcd→a’b’ / Aab* Fab→c’d’ )1/4
=(1,62748075/1,324288215)1/4
= (1,228947544 )1/4
=1,052890814
Bu sonuç içbükey ayna yoluyla biri biriyle ısı transferi yapan yüzeyler alıp verdikleri ısı
enerjisinin eşit yani net ısı transferinin sıfır olduğu durumda yüzey sıcaklıklarını farklı
olduğunu gösterir. Yine buradan böyle konumlanmış iki yüzey arasında ısı dinamiğinin ikinci
kanununa bir istisna olarak düşük sıcaklıktan yüksek sıcaklığa ısı transferi
gerçekleşebileceğini çıkarabiliriz.
2- Yöne bağlı değişimin iki yüzey arasındaki ısı transferine etkisi:
Işımanın yöne bağlı olarak ısı transferine etkisi daha çok düzlemsel olmayan yüzeylerde
gözlemlenebilir. Bu sebeple bu etkisi iç içe geçmiş silindirik yüzeyler arasındaki ısı transferini
incelemek gerekir. Yüzeylerin yaptığı ışımanın yöne bağlı değişimi aşağıda daha önce şekil
1’de görüldüğü gibi yönden bağımsız değil, şekil 2’de görüldüğü gibi yöne bağlı değişim
gösterdiğini kabul edelim.
Yöne bağlı ışımada bir noktadan yayılan ışıma normalden 80 derecelik açıya kadar sabit, 80
ila 90 derece arasında sıfır olsun. iç içe geçmiş silindirlerimizden iç silindirin çapı dış
silindirin çapından öyle küçük olsun ki dış silindirdeki bir noktadan yatayla 10 derece açı
yaparak çıkan ışıma iç silindire teğet geçsin. Bu şartlardaki bir düzenek aşağıdaki gibidir:
Yönden bağımsız ışımalı ısı transferinde iç yüzeydeki ışımanın tümü dış yüzey tarafından
yutulduğu için şekil faktörü 1’dir. Dış yüzeyden yayılan ışımanın 10 derecelik açı aralığındaki
kısmı tekrar aynı yüzeye geri döner. Işımanın yukarıda verilen profile bağlı olarak
gerçekleştiğini var sayarsak 10 derece aralığında ışıma olmadığı için aynı miktar ışıma geri
dönmez. Dış yüzeydeki her noktanın yatayla 10 derece açıdan sonra ışıma yapacağı ve aynı
profile bağlı olarak iç yüzeye gelen ışımanın geliş açısı 10 derece olana kadar ışımayı
yansıtacağı görülür. Bu durumda geri dönen ışıma yapılan hesaplamaya göre 4.16 derecelik
bir açı aralığında olduğundan ilk duruma göre geri dönen ışımanın daha az olduğu ve karşı
yüzeye giden ışıma artacağı görülür. Bu durum aşağıdaki şekilde özetlenebilir:
Yukarıda içbükey ayna vasıtasıyla ısı transferi yapan iki yüzeyde oluşan sıcaklık farkı
gibi iç içe geçmiş silindirik yüzeyler arasında ışıma yöne bağlı olarak gerçekleştiğinde ısı alış
veriş miktarı eşit olmasına rağmen yüzey sıcaklıklarının eşit olmayabileceğini görülür. Net ısı
transferini sıfır olabilmesi için bu düzenekte düşük sıcaklıktan yüksek sıcaklığa ısı transferi
gerçekleşir. Bu sonuç yine ısı dinamiğinin ikinci kanununa bir istisnanın mümkün olduğunu
gösterir.
Yukarıda tarif edilen iki durum genel düşüncenin aksine ısı dinamiğinin ikinci
yasasının istisnası olabileceğini, izole bir sistemde entropinin azalabileceği süreçlerin
mümkün olduğunu gösterir. Yine bu sonuç ısıl güç çevrimlerinde termal ışıma yoluyla
verimin artırılarak atık ısının azaltılabileceğini gösterir. Bu yol ile toplam verim yüzde yirmi
oranında artırılabilir. Atık ısının termal ışıma yoluyla tekrar geri kazanıldığı güneş enerjisini
buhar çevrimi yoluyla elektrik enerjisine çevirmede yüzde 50 verime ulaşılabilir.