Ticaret Matematiği - Bingöl Üniversitesi

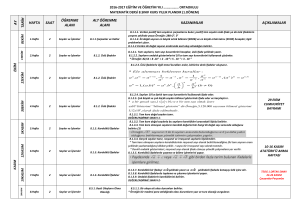
BİNGÖL ÜNİVERSİTESİ SOSYAL BİLİMLER MESLEK YÜKSEK
BÜRO YÖNETİMİ UZAKTAN EĞİTİM MÜFREDAT PROGRAMI
Dersin Adı:
Matematik
Dersin Sorumlusu:
Öğr. Gör. Mustafa ALTIN
İletişim Bilgileri:
[email protected]
Dersin Kredisi:
3 KREDİ
Ders AKTS:
3 AKTS
BİNGÖL ÜNİVERSİTESİ MATEMATİK DERSİ 1.HAFTA DERS NOTLARI
TEMEL KAVRAMLAR
A. SAYI
1. Rakam
Sayıları yazmaya yarayan sembollere rakam denir.
2. Sayı
Rakamların çokluk belirten ifadesine sayı denir.
Üç basamaklı abc sayısı a, b, c rakamlarından oluşmuştur.
Her rakam bir sayıdır. Fakat her sayı bir rakam olmayabilir.
B. SAYI KÜMELERİ
1. Sayma Sayıları
{1, 2, 3, 4, ... , n , ...} kümesinin her bir elemanına sayma sayısı denir.
2. Doğal Sayılar
={0, 1, 2, 3, 4, ... , n , ...} kümesinin her bir elemanına doğal sayı denir.
3. Pozitif Doğal Sayılar
= {1, 2, 3, 4, ... , n , ...} kümesinin her bir elemanına pozitif doğal sayı denir.
4. Tam Sayılar
= {... , – n , ... – 3, – 2, – 1, 0, 1, 2, 3, ... , n , ...} kümesinin her bir elemanına tam sayı denir.
Tam sayılar kümesi; negatif tam sayılar kümesi:
, pozitif tam sayılar kümesi:
ve sıfırı eleman
kabul eden: {0} kümenin birleşim kümesidir.
Buna göre,
5. Rasyonal Sayılar
a ve b birer tam sayı ve b  0 olmak koşuluyla
a
biçiminde yazılabilen sayılara rasyonel sayılar
b
denir.
biçiminde gösterilir.
6. İrrasyonel Sayılar
Virgülden sonraki kısmı tahmin edilemeyen sayılara irrasyonel sayılar denir.
biçiminde yazılamayan sayılar: a, b 
ve b  0} biçiminde gösterilir.
Hem rasyonel hem de irrasyonel olan bir sayı yoktur.
sayıları birer irrasyonel sayıdır.
7. Reel (Gerçel) Sayılar
Rasyonel sayılar kümesiyle irrasyonel sayılar kümesinin birleşimi olan kümeye reel (gerçel) sayılar
kümesi denir.
biçiminde gösterilir.
8. Karmaşık (Kompleks) Sayılar
kümesinin her bir elemanına karmaşık sayı denir.
C. SAYI ÇEŞİTLERİ
1. Çift Sayı
olmak koşuluyla 2n ifadesi ile belirtilen tam sayılara çift sayı denir.
Ç = {... , – 2n , ... , – 4, – 2, 0, 2, 4, ... , 2n , ...}
biçiminde gösterilir.
2. Tek Sayı
olmak koşuluyla 2n + 1 ifadesi ile belirtilen tam sayılara tek sayı denir.
T = {... , – (2n + 1), ... , –3, –1, 1, 3, ... , (2n + 1), ...} biçiminde gösterilir.
T : Tek sayı
Ç : Çift sayıyı göstersin.
Bölme işlemi için yukarıdaki biçimde bir genelleme yapılamaz.
• Tek sayılar ve çift sayılar tam sayılardan oluşur.
• Hem tek hem de çift olan bir sayı yoktur.
• Sıfır (0) çift sayıdır.
3. Pozitif Sayılar, Negatif Sayılar
Sıfırdan büyük her reel (gerçel) sayıya pozitif sayı, sıfırdan küçük her reel (gerçel) sayıya negatif sayı
denir.
• a, b birer negatif sayıdır.
• c, d birer pozitif sayıdır.
• İki pozitif sayının toplamı pozitiftir. (c + d > 0)
• İki negatif sayının toplamı negatiftir. (a + b < 0)
• Çıkarma işleminde eksilen çıkandan büyük ise sonuç (fark) pozitif, eksilen çıkandan küçük ise fark
negatif olur.
m – n ifadesinde m eksilen, n çıkandır.
• Zıt işaretli iki sayıyı toplamak için; işaretine bakılmaksızın büyük sayıdan küçük sayı çıkarılır ve
büyük sayının işareti sonuca verilir.
• Aynı işaretli iki sayının çarpımı (ya da bölümü) pozitiftir.
• Zıt işaretli iki sayının toplamı; negatif, pozitif veya sıfırdır.
• Zıt işaretli iki sayının çarpımı (ya da bölümü) negatiftir.
• Pozitif sayının bütün kuvvetleri pozitiftir.
• Negatif sayının tek kuvvetleri negatif, çift kuvvetleri pozitiftir.
4. Asal Sayı
Kendisinden ve 1 den başka pozitif tam sayılara tam bölünmeyen 1 den büyük doğal sayılara asal sayı
denir.
2, 3, 5, 7, 11, 13, 17, 19, 23 sayıları birer asal sayıdır.
• En küçük asal sayı 2 dir. 2 den başka çift asal sayı yoktur.
• Asal sayıların çarpımı asal değildir.
5. Aralarında Asal
Ortak bölenlerinin en büyüğü 1 olan tam sayılara aralarında asal sayılar denir.
a ile b aralarında asal ise,
a
oranı en sade biçimdedir.
b
D. ARDIŞIK SAYILAR
Belirli bir kurala göre art arda gelen sayı dizilerine ardışık sayılar denir.
n bir tam sayı olmak üzere,
• Ardışık dört tam sayı sırasıyla;
n, n + 1, n + 2, n + 3 tür.
• Ardışık dört çift sayı sırasıyla;
2n, 2n + 2, 2n + 4, 2n + 6 dır.
• Ardışık dört tek sayı sırasıyla;
2n + 1, 2n + 3, 2n + 5, 2n + 7 dir.
• Üçün katı olan ardışık dört tam sayı sırasıyla;
3n, 3n + 3, 3n + 6, 3n + 9 dur.
Ardışık Sayıların Toplamı
n bir sayma sayısı olmak üzere,
• Ardışık sayma sayılarının toplamı
• Ardışık çift doğal sayıların toplamı
2 + 4 + 6 + ... + (2n) = n(n + 1)
• Ardışık tek doğal sayıların toplamı
1 + 3 + 5 + ... + (2n – 1) = n2
• Artış miktarı eşit olan ardışık tam sayıların toplamı
r : İlk terim
n : Son terim
x : Artış miktarı olmak üzere,
Ardışık sayıların toplamı, sayı adedine bölünürse ortanca terim bulunur. Eğer sayı adedi
çift ise, ortanca terim sayı dizisine ait değildir.
SAYI SİSTEMLERİ
A. SAYI BASAMAĞI
Bir sayıyı oluşturan rakamlardan her birine bu sayının basamağı denir.
Bir doğal sayıda kaç tane rakam varsa sayı o kadar basamaklıdır. 243 üç basamaklı bir sayıdır.
B. ÇÖZÜMLEME
Doğal sayıyı oluşturan rakamların bulunduğu yerdeki değerine basamak değeri denir.
Basamak değerlerinin toplamına o sayının çözümlenmiş biçimi denir. Üç basamaklı abc sayısı aşağıda
çözümlenmiştir.
• ab = 10 . a + b
• abc = 100 . a + 10 . b + c
• aaa = 111 . a
• ab + ba = 11 . (a + b)
• ab – ba = 9 . (a – b)
• abc – cba = 99 . (a – c)
C. TABAN
Bir sayı sisteminde sayının basamak değerlerini göstermek için kullanılan düzene taban denir.
T taban olmak üzere,
(abcd)T = a . T3 + b . T2 + c . T + d dir.
Burada,
• T, 1 den büyük doğal sayıdır.
• a, b, c, d rakamları T den küçüktür.
• Taban belirtmeden kullandığımız sayılar 10 luk tabana göredir.
• (abc, de)T = a . T 2 + b . T + c . T0 + d . T – 1 + e . T – 2
= a . T 2 + b . T + c + d . T – 1 + e . T – 2 dir.
1. Onluk Tabanda Verilen Sayının Herhangi Bir Tabana Çevrilmesi
Onluk tabanda verilen sayı, hangi tabana çevrilmek isteniyorsa, o tabana bölünür. Bölüm tekrar tabana
bölünür. Bu işleme bölüm 0 olana kadar devam edilir.
Ardışık olarak yapılan bu bölmelerden kalanlar sondan başlayarak (ilk kalan son rakam olacak şekilde)
sıralanmasıyla istenen sayı oluşturulur.
2. Herhangi Bir Tabanda Verilen Sayının 10 luk Tabana Çevrilmesi
Herhangi bir tabandan 10 luk tabana geçirilirken verilen sayı, ait olduğu tabana göre çözümlenir.
3. Herhangi Bir Tabanda Verilen Sayının Başka Bir Tabanda Yazılması
Herhangi bir tabanda verilen sayı önce 10 tabanına çevrilir. Bulunan değer istenen tabana
dönüştürülür.
4. Taban Aritmetiğinde Toplama, Çıkarma, Çarpma İşlemleri
Değişik tabanlarda yapılacak işlemler 10 luk sistemdekine benzer biçimde yapılır.
T tabanında verilen sayılarda toplama ve çarpma işlemleri bilinen cebirsel işlem gibi yapılır, ancak
sonuç T den büyük çıkarsa içinden T ler atılıp kalan alınır. Atılan T adedi elde olarak bir sonraki
basamağa ilave edilir.
Çıkarma işlemi yapılırken 10 luk sistemdekine benzer biçimde, bir soldaki basamaktan 1 (bir)
almak gerektiğinde, bu 1 in aktarıldığı basamağa katkısı tabanın sayı değeri kadardır. Fakat alındığı
basamaktaki rakam 1 azalır.
BÖLME ve BÖLÜNEBİLME
A. BÖLME
A, B, C, K birer doğal sayı olmak üzere:
bölme işleminde,
• A ya bölünen, B ye bölen, C ye bölüm, K ya kalan denir.
• A = B . C + K dır.
• Kalan, bölenden küçüktür. (K < B)
• Kalan, bölümden (C den) küçük ise, bölen (B) ile bölümün (C) yeri değiştirilebilir. Bu durumda K
ile A değişmez.
• K = 0 ise, A sayısı B ile tam bölünebiliyor denir.
B. BÖLÜNEBİLME KURALLARI
1. 2 İle Bölünebilme
Birler basamağındaki rakamı çift olan sayılar 2 ile tam bölünür.
Tek sayıların 2 ile bölümünden kalan 1 dir.
2. 3 İle Bölünebilme
Rakamlarının sayısal değerleri toplamı 3 ün katı olan sayılar 3 ile tam bölünür.
Bir sayının 3 ile bölümünden kalan, rakamlarının toplamının 3 ile bölümünden kalana eşittir.
3. 4 İle Bölünebilme
Bir sayının onlar basamağındaki rakam ile birler basamağındaki rakamın (son iki basamak) belirttiği
sayı, 4 ün katı olan sayılar 4 ile tam bölünür.
... abc sayısının 4 ile bölümünden kalan bc nin (son iki basamak) 4 ile bölümünden kalana eşittir.
• ... abc sayısının 4 ile bölümünden kalan
c + 2 . b nin 4 ile bölümünden kalana eşittir.
4. 5 İle Bölünebilme
Birler basamağındaki rakam 0 veya 5 olan sayılar 5 ile tam bölünür.
Bir sayının 5 ile bölümünden kalan, o sayının birler basamağındaki rakamın 5 ile bölümünden kalana
eşittir.
5. 7 İle Bölünebilme
(n + 1) basamaklı anan-1 ... a4a3a2a1a0 sayısının 7 ile tam bölünebilmesi için,
k  Z olmak üzere,
(a0 + 3a1 + 2a2) – (a3 + 3a4 + 2a5) + ... = 7k
olmalıdır.
Birler basamağı a0, onlar basamağı a1, yüzler basamağı a2, ... olan sayının (...a5a4a3a2a1a0 sayısının)
7 ile bölümünden kalan
(a0 + 3a1 + 2a2) – (a3 + 3a4 + 2a5) + ...
işleminin sonucunun 7 ile bölümünden kalana eşittir.
6. 8 İle Bölünebilme
Yüzler basamağındaki, onlar basamağındaki ve birler basamağındaki rakamların (son üç rakamın)
belirttiği sayı 8 in katı olan sayılar 8 ile tam bölünür.
3000, 3432, 65104 sayıları 8 ile tam bölünür.
Birler basamağı c, onlar basamağı b, yüzler basamağı a, ... olan sayının (...abc sayısının) 8 ile
bölümünden kalan c + 2 . b + 4 . a toplamının 8 ile bölümünden kalana eşittir.
7. 9 İle Bölünebilme
Rakamlarının toplamı 9 un katı olan sayılar 9 ile tam bölünür.
Bir sayının 9 ile bölümünden kalan, o sayının rakamlarının toplamının 9 ile bölümünden kalana eşittir.
8. 10 İle Bölünebilme
Birler basamağındaki rakamı 0 (sıfır) olan sayılar 10 ile tam bölünebilir. Bir sayının birler
basamağındaki rakam o sayının 10 ile bölümünden kalandır.
9. 11 İle Bölünebilme
(n + 1) basamaklı anan–1 ... a4a3a2a1a0 sayısının 11 ile tam bölünebilmesi için
(a0 + a2 + a4 + ...) – (a1 + a3 + a5 + ...)... = 11 . k
ve k  Z olmalıdır.
(n + 1) basamaklı anan–1 ... a4a3a2a1a0 sayısının 11 ile bölümünden kalan
(a0 + a2 + a4 + ...) – (a1 + a3 + a5 + ...)... işleminin sonucunun 11 ile bölümünden kalana eşittir.
Aralarında asal iki sayıya bölünebilen bir sayı, bu iki sayının çarpımına da tam bölünür.
• 2 ve 3 ile tam bölünen sayılar 6 ile de bölünür.
• 3 ve 4 ile tam bölünen sayılar 12 ile de bölünür.
C. BÖLEN KALAN İLİŞKİSİ
A, B, C, D, E, K1, K2 uygun koşullarda birer doğal sayı olmak üzere,
A nın C ile bölümünden kalan K1 ve
B nin C ile bölümünden kalan K2 olsun.
Buna göre,
• A . B nin C ile bölümünden kalan K1 . K2 dir.
• A ± B nin C ile bölümünden kalan K1 ± K2 dir.
• D . A nın C ile bölümünden kalan D . K1 dir.
• AE nin C ile bölümünden kalan K1E dir.
Burada kalan değerler bölenden (C den) büyük ise, tekrar C ile bölünerek kalan bulunur.
D. ÇARPANLAR İLE BÖLÜM
Bir A doğal sayısı B . C ile tam bölünüyorsa A sayısı B ve C doğal sayılarıyla da bölünebilir.
Fakat bu ifadenin karşıtı (A sayısı B ile ve C ile tam bölünüyorsa A sayısı B . C ile tam bölünür.) her
zaman doğru değildir.
144 sayısı 2 . 6 = 12 ile tam bölünür ve 144 sayısı 2 ile ve 6 ile de tam bölünür.
6 sayısı 2 ile ve 6 ile tam bölünür. Fakat 6 sayısı 2 . 6 = 12 ile tam bölünemez.
BİNGÖL ÜNİVERSİTESİ MATEMATİK DERSİ 2. HAFTA DERS NOTLARI
BİR TAM SAYININ TAM BÖLENLERİ
Bir tam sayının, asal sayıların çarpımı biçiminde yazılmasına bu sayının asal çarpanlarına
ayrılması denir.
a, b, c birbirinden farklı asal sayılar ve m, n, k pozitif tam sayılar olmak üzere,
A = am . bn . ck olsun.
• A yı tam bölen asal sayılar a, b, c dir.
• A sayısının pozitif tam bölenlerinin sayısı:
(m + 1) . (n + 1) . (k + 1) dir.
• A sayısının pozitif tam sayı bölenlerinin ters işaretlileri de negatif tam sayı bölenidir.
• A sayısının tam sayı bölenleri sayısı:
2 . (m + 1) . (n + 1) . (k + 1) dir.
• A sayısının tam sayı bölenleri toplamı 0 (sıfır) dır.
• A sayısının pozitif tam sayı bölenlerinin toplamı:
• A sayısının asal olmayan tam sayı bölenlerinin sayısı, A nın tam sayı bölenlerinin sayısından A nın
asal bölenlerinin sayısı çıkarılarak bulunur.
• A nın asal olmayan tam sayı bölenleri toplamı
– (a + b + c) dir.
• A sayısından küçük A ile aralarında asal olan sayıların sayısı:
• A sayısınının pozitif tam sayı bölenlerinin çarpımı:
RASYONEL SAYILAR
A. TANIM
şeklinde ifade edilen sayılara rasyonel sayı veya kesir denir.
B. KESİR ÇEŞİTLERİ
1. Basit Kesir
İşaretine bakılmaksızın payı paydasından küçük olan kesirlere basit kesir denir.
2. Bileşik Kesir
İşaretine bakılmaksızın payı paydasından küçük olmayan (büyük veya eşit olan) kesirlere bileşik kesir
denir.
3. Tam Sayılı Kesir
Herhangi bir sayma sayısı ile birlikte yazılabilen kesirlere tam sayılı kesir denir.
birer tam sayılı kesirdir.
Her bileşik kesir bir tam sayılı kesir biçiminde yazılabilir.
C. RASYONEL SAYILARDA İŞLEMLER
1. Genişletme ve Sadeleştirme
k  0 olmak üzere,
2. Toplama - Çıkarma
Toplama ve çıkarma işleminde payda eşitlenecek biçimde kesirler genişletilir ya da sadeleştirilir.
Oluşan kesirlerin payları toplanır (ya da çıkarılır) ortak payda alınır.
3. Çarpma - Bölme
4. İşlem Önceliği
Toplama, çıkarma, çarpma, bölme ve üs alma işlemlerinden bir kaçının birlikte bulunduğu rasyonel
sayılarda işlemler, aşağıdaki sıraya göre yapılır.
1) Parantezler ve kesir çizgisi işleme yön verir.
2) Üslü işlemler varsa sonuçlandırılır.
3) Çarpma - bölme yapılır.
4) Toplama - çıkarma yapılır.
Toplama ile çıkarma ve çarpma ile bölme kendi arasında öncelik taşımaz. Özellikle
çarpma ile bölmede öncelik söz konusu ise bu, parantezle belirlenir.
D. ONDALIK KESİR
1. Ondalık Kesir
Bir rasyonel sayının payını paydasına böldüğümüzde bu rasyonel sayının ondalık açılımını buluruz.
Bu ondalık açılıma ondalık kesir denir.
Burada a ya tam kısım, bcd ye de ondalıklı kısım denir.
2. Devirli (Periyodik) Ondalık Kesir
Bir ondalık kesirde ondalıklı kısım belli bir kurala göre tekrarlanıyorsa bu sayıya devirli ondalık kesir
denir.
Devreden kısım üzerine (—) işareti konulur.
3. Ondalık Sayılarda İşlemler
a. Toplama - Çıkarma: Ondalık kesirler toplanırken, virgüller alt alta gelecek şekilde yazılır ve
doğal sayılarda toplama - çıkarma işleminde olduğu gibi toplama - çıkarma işlemi yapılır. Sonuç,
virgüllerin hizasından virgülle ayrılır.
b. Çarpma: Ondalık kesirlerin çarpımı yapılırken, virgül yokmuş gibi çarpma işlemi yapılır. Sonuç,
çarpılan sayıların virgülden sonraki basamak sayılarının toplamı kadar, sağdan sola doğru virgülle
ayrılır.
c. Bölme: Ondalık kesirlerin bölme işlemi yapılırken, bölen virgülden kurtulacak biçimde 10 un
kuvveti ile çarpılır. Bölünen de aynı 10 un kuvveti ile çarpılarak normal bölme işlemi yapılır.
4. Devirli Ondalıklı Sayının Rasyonel Sayıya Dönüştürülmesi
Devreden 9 ise bir önceki rakam 1 artırılır.
E. RASYONEL SAYILARDA SIRALAMA
Pozitif kesirlerde sıralama yapılırken aşağıdaki yollardan biri kullanılır.
I. Yol:
Paydaları eşit olan (eşitlenen) kesirlerden payı en büyük olan diğerlerinden daha büyüktür.
II. Yol:
Payları eşit olan (eşitlenen) kesirlerden paydası en küçük olan diğerlerinden daha büyüktür.
III. Yol:
Payı ile paydası arasındaki farkı eşit olan, basit kesirlerde, payı en büyük olan diğerlerinden daha
büyüktür.
Payı ile paydası arasındaki farkı eşit olan, bileşik kesirlerde, payı en büyük olan diğerlerinden daha
küçüktür.
Yukarıda verilen yöntemler pozitif kesirlerde geçerlidir. Negatif kesirlerde ise durum tersinedir.
F. İKİ RASYONEL SAYI ARASINDAKİ SAYILAR
a
c
ile arasında sayılamıyacak çoklukta rasyonel sayı vardır.
b
d
Bunlardan bazılarını bulmak için b ile d nin OKEK i bulunur. Verilen kesirlerin paydaları bulunan
OKEK inde eşitlenir. İstenen koşuldaki sayıyı bulmak için kesirler genişletilebilir.
x,
a
c
ile kesirlerinin ortasındaki bir sayı ise,
b
d
VİZE KONULARI BURAYA KADAR
BİNGÖL ÜNİVERSİTESİ MATEMATİK DERSİ 3. HAFTA DERS NOTLARI
ÜSLÜ İFADELER
1.1. Üslü İfade
A bir reel (gerçel) sayı ve n pozitif tam sayı olsun.
a.a.a....a = an
n tane
olacak şekilde n tane a’nın çarpımı olan an’ye üslü ifade denir.
Örnek 1.1.1: a)
3.3.3.3 = 34
4 tane
1 1 1 1
   
5 5 5 5
b)
3
Uyarı 1.1.1: a bir reel sayı ve n pozitif tam sayı olmak üzere;
a + a + a + ... + a = n.a
n tane
olduğu için, an ile n.a ifadeleri birbirine karıştırılmamalıdır. Yani,
an  n.a’dır.
Örnek 1.1.2: 2 + 2 + 2 + 2 + 2 = 5.2 = 10 dur.
5 tane
Tanım 1.1.1: 1. a sıfırdan farklı bir reel sayı olmak üzere,
a0 = 1 dir.
2. 00 ifadesi tanımsızdır.
3. 1n = 1’dir. n  IR
Örnek 1.1.3: a) 80 = 1

b)  3  2

0
1
c) 115 = 1
Tanım 1.1.2: Bir üslü ifadenin üssü, üslerin çarpımıdır.
a 
 a m.n dır.
 
 5 2.3  56 dır.
m n
Örnek 1.1.4: 5 2
3
n
Uyarı 1.1.2: 1) a m ifadesi bilinemez. Çünkü n sayısının; m’nin üssü mü
yoksa am’nin üssü mü olduğu belli değildir.
 
2) a m
n
n
 a m 
üslerin parantezlerle neyin üssü olduğu belirtilmelidir.
Tanım 1.1.3:
a 
m n
 a m. n
   a 
Olduğu için a m
a 
n m
n
n m
dir.
 a n.m
Örnek 1.1.5: 2x = y
olduğuna göre,
Çözüm:
8x’in y türünden eşitini bulalım.
8x = (23)x = (2x)3 = y3 tür.
Örnek 1.1.6: 3a = b
olduğuna göre,
Çözüm :
5.(81)a nın b türünden eşitini bulalım.
5.(81)a = 5.(34)a = 5.(3a)4 = 5.b4 tür.
Tanım 1.1.4: a bir reel sayı olmak üzere,
a n 
1
dir.
an
benzer şekilde a ve b sıfırdan farklı reel sayılar olmak üzere
a
 
b
n
n
b
   dir.
a
Örnek 1.1.7: 5-1 + 5-2
İşleminin sonucunu bulalım.
Çözüm:
5 1  5  2 
1 1
1 1 5 1 6
 2  


dir.
5 5
5 25
25
25
5 
(1)
Tanım 1.1.5: Pozitif sayıların bütün kuvvetlerini pozitiftir.
a > 0  an > 0 dır.
Örnek 1.1.8: a) 4-2 = 16 > 0’dır.
b) 4-2 =
1
1

0
2
16
4
Tanım 1.1.6: Negatif sayıların çift kuvvetleri pozitiftir.
a > 0 ve n çift sayı ise (-a)n = an < 0’dır.
Örnek 1.1.9: a) (-4)2 = 42 = 16 > 0 dır.
b) (-4)-2 = 4-2 =
1
1

 0 dır.
2
16
4
Tanım 1.1.7: Negatif sayıların tek kuvvetleri negatiftir.
A > 0 ve n tek sayı ise (-a)n = -an < 0’dır.
Örnek 1.1.10: a) (-4)3 = -43 = -64 < 0’dır.
b) (-4)-3 = -4-3 = 
1
1

 0 dır.
3
64
4
Uyarı 1.1.4: a > 0 ve n çift sayı ise, (-a)n  -an dir.
Örnek 1.1.11. (-2)4  -24 tür. Çünkü,
(-2)4 = 24 = 16 ve -24 = -16 dır.
Örnek 1.1.12: (-3)3 + (-52) + (-4)2
İşleminin sonucunu bulalım.
Çözüm:
(-3)3 + (-52) + (42)
= -33 + (-52) + 42
= -27 – 25 + 16
= 36
Tanım 1.1.8: Tabanları ve üsleri aynı olan ifadelerin toplamı,
katsayıların toplamı ile üslü ifadenin çarpımına eşittir.
a . xn + b.xn = (a+b)n dir.
Örnek 1.1.13: 8 .103 + 4.103 = (8+4) . 103 = 12.103
Uyarı 1.1.5: a5 + a2 toplamı yapılamaz. Çünkü, bu iki sayının tabanları
aynıdır. Fakat üsleri aynı değildir.
İki üslü sayının toplamının yapılabilmesi için, bu sayıların
tabanları ve üsleri aynı olmalıdır.
Tanım 1.1.9: Tabanları ve üsleri aynı olan ifadelerin farkı, katsayılar
farkı ile üslü ifadenin çarpımına eşittir.
a.xn – b.xn (a-b)xn
Örnek 1.1.14: 5 . 104 – 2 . 104 = (5-2)104 = 3 . 104
Tanım 1.1.10: Tabanları eşit olan üslü ifadelerin çarpımını bulmak
için; üsler toplamı, ortak tabanın üssü olarak yazılır.
am . an = am+n
Örnek 1.1.15: 103 . 105 = 103+5 = 108
Tanım 1.1.11: Üsleri eşit olan üslü ifadelerin çarpımını bulmak için
tabanlar çarpımı ortak üssün tabanı olarak yazılır.
an . bn = (a.b)n
Örnek 1.1.16: 28 . 58 = (2.5)8 = 108
Örnek 1.1.17: 3x = p
Olduğuna göre,
Çözüm:
9x+1
9x+1 ifadesinin p türünden eşitini bulalım.
= 9x . 91
= (32)x . 9
= (3x)2 . 9
= p2 . 9
= 9 . p2
(Tabanları aynı olan ifadelerin üsleri toplanıyordu. Burada
bu işlemin tersi yapılıyor. )
Tanım 1.1.12: Tabanları eşit olan üslü ifadelerin bölümünü bulmak
için; paydaki sayının üssünden paydadaki sayının üssü çıkarılır,
ortak tabanın üssü olarak yazılır.
am
 a mn
n
a
Örnek 1.1.18:
713
 7138  7 5
8
7
Tanım 1.1.13: Üsleri eşit olan ifadelerin bölümünü bulmak için; payın
tabanı paydanın tabanına bölünür, ortak üs bölümün üssü olarak
yazılır.
am  a 
 
bm  b 
m
5
Örnek 1.1.19:
12 5  2 
    2 5  32
5
6
1
a
Örnek 1.1.20:
b
m
 bn
m
 an


m
n
İşleminin sonucu a ve b türünden bulalım.
Çözüm
a
:
b
m
 bn
m
 an


a   b 

b   a 
m
n
m m
n m
m n
n n
2
a m   b mn

2
b mn  a n 
= am
2
n2
 b nmmn
= am
2
n2
 b m n  m n
= am
2
n2
 b0
= am
= am
2
2
n 2
1
n2
1.2. ÜSLÜ DENKLEMLER
Tanım 1.1.2: Tabanları eşit olan üslü denklemlerin üsleri de eşittir.
a 0, a  -1, a 1 olmak üzere
am = an  m = n dir.
Örnek 1.2.1:
5 x 1
 125 x 3
2 x
5
Eşitliğini sağlayan x değerini bulalım.
Çözüm:
5 x 1
 125 x 3
5 2 x
 
5x+1 . 5 (2-x) = 5 3
5x+1 . 5 –2+x) = 5 3(
x 3
x 3)
5 x+1 – 2 + x = 5 3x-9
5 2x-1 = 5 3x-9 dur.
5 2x-1 = 5 3x-9  2x – 1 = 3x – 9
2x – 3x = -9 + 1
-x = -8
x=8
Tanım 1.2.2: Üsleri eşit olan denklemlerde üs tek sayı ise tabanları
eşit, üs çift sayı ise tabanlar eşit ya da tabanların biri diğerinin ters
işaretine eşittir.
n tek sayı ve an = bn  a = b dir.
n çift sayı ve an = bn  a = b veya a = -b’dir.
Örnek 1.2.2: x3 = 53  x = 5 tir.
Örnek 1.2.3: (x + 7)3 = (3x - 11)3
Eşitliğini sağlayan x değerini bulalım.
Çözüm:
3 tek sayı olduğu için, tabanlar eşittir. Buna göre,
(x + 7)3 = (3x - 11)3  x + 7 = 3x – 11
7 + 11 = 3x – x
18 = 2x
x
18
2
x=9
bulunur.
Tanım 1.2.3: xn = 1 denkleminin çözümünde 3 durum vardır.
X = 1 .................................. 1. Durum
Veya
xn = 1 
N = 0 ve x  0 ..................... 2. Durum
Veya
X = -1 1 ve n çift sayı ......... 3. Durum
Örnek 1.2.4: a) 18 = 1 dir. Çünkü 1’in tüm reel kuvvetleri 1’dir.
b) 50 = 1’dır. Çünkü –1’in tüm çift kuvvetleri 1’dir.
c) (-1)6 = 1’dir. Çünkü –1’in tüm çift kuvvetleri 1’dir.
Örnek 1.2.5: (x+3)x-2 = 1
Eşitliğini sağlayan x değerini bulalım.
Çözüm:
(x+3)x-2 = 1  x + 3 = 1 ..........................1. Durum
veya
x – 2 = 0 ve x + 3  0 ................ 2. Durum
veya
x + 3 = -1 ve x – 2 çift sayıdır ...... 3. Durum
1. Durum : x + 3 = 1  x = 1 – 3  x = -2
2. Durum : x – 2 = 0  x = 2
Bu kök üssü sıfır yapmadığı için, alınır.
3. Durum : x + 3 = -1  x = -4
Bu kök yazıldığına üs çift sayı olacağı için, bu kök de alınır.
O halde denklemi sağlayan x değeri : -4, -2, 2’dir.
1.3. ÇÖZÜMLÜ ÖRNEKLER
Örnek 1.3.1:
 22   3 2 
2
5 2   4 
işleminin sonucu kaçtır?
Çözüm :
 22   32    8   9
2
25  4 2
5 2   4
Örnek 1.3.2:
x 
a a b
 
 xb
a b

89
25  16

1
9
işleminin sonucunu bulalım.
Çözüm:
x   x 
a a b
b a b
 x a  a b  x b  a  b 
 xa
2
 ab
 x bab
 xa
2
 ab abb 2
 xa
2
b 2
2
Örnek 1.3.3:
 m2   m 4   m3
işleminin sonucunu bulalım.
 m2   m 4   m3   m 5   m 4   m 3 
 m 5  m 4  m 3
  m 5 4 3
 m 6
Örnek 1.3.4:
0,0256 4 10 4
3
işleminin sonucu kaçtır?
Çözüm:
0,0256 4  10 4  256  10 4 4  10 4
3
3

 2 8  10  4

3
4
 10 4
   10 
3
4
3
4 4
 3
8 
 4
 3
 4 
 4
 28
2
 10
 2 6  10 3  10 4
 64  10 3 4
 10 4
 10 4
 6410
 640
Örnek 1.3.5:
3a = 4 olduğuna göre,
3a + 1 – 2 . 9a nın değeri kaçtır?
Çözüm:
3a = 4 olduğuna göre
3a + 1 – 2.9a
= 3a . 31 – 2 . (32)a
= 3a . 3 – 2 . (3a)2
= 4 . 3 – 2 . 42
= 12 – 2 . 16
= 12 – 32
= -20
Örnek 1.3.6:
a, b tam sayı ve a < 5 olmak üzere,
1
 
a
b 1
 27
olduğuna göre, a + b kaçtır?
Çözüm :
1
 
a
b 1
a 
1 b 1
 27
 33
a b 1  33
a, b tam sayı ve a < 5 olduğu için
a = 3 ve -b-1 = 3 tür. Buradan,
-b=3+1
olur.
b = 4 tür.
O halde, a + b = 3-4 = 1
olur.
Örnek 1.3.7:
x  2x  4  1
2
eşitliğini sağlayan x değeri kaç tanedir?
Çözüm :
x  2x  4  1
2
eşitliğinin sağlandığı üç durum olabilir.
1. Durum:
x  2x  4  1  x + 2 = 1
2
x=1–2
x = -1
2. Durum :
 x  2  x  4  1  x2 – 4 = 0
2
x2 – 4 = 0
 x2 = 4
x=2
Ayrıca,
x+20
ve x + 2  0 dır.
veya x = -2 dir.
 x  -2 dir.
(x = 2 veya x = -2)
(x  -2)  x = 2
ve
dir.
(Yani, üssü sıfır değerlerden, tabanı sıfır yapmayanlar alınır.)
3. Durum :
x  2x 4  1  x + 2 = -1
2
ve
x2 – 4 çift sayıdır.
x+2=-1
 x = -3
Bu değer için x2 – 4 ün çift sayı olup olmadığına bakalım.
(-3)2 – 4 = 9 – 4 = 5
5 tek sayıdır. O halde, buradan eşitliği sağlayacak değer bulamaz.
Demek ki, denklemi sağlayan değer 2 tanedir.
Bu değer: x = -1 ve x = 2
dir.
BİNGÖL ÜNİVERSİTESİ MATEMATİK DERSİ 4. HAFTA DERS NOTLARI
KÖKLÜ İFADELER
n, 1’den büyük bir doğal sayı olmak üzere, xn = a eşitliğini
sağlayan x sayısına a nın n. Dereceden kökü denir.
a nın n. Dereceden kökü
n
a şeklinde gösterilir.
2
a a
: karekök a
3
a
: küpkök a
4
a
: dördüncü dereceden kök a şeklinde okunur.
Uyarı: Bazı köklü sayılar reel sayı değildir.
n
a ifadesinin bir reel sayı belirtmesi için :
a  0 veya n tek sayı olmalıdır.
Örnek:
Sonuç:
3 , 4 5 , 6 2 , 10 4
sayıları reeldir.
3
3 , 5 5 , 7 7 , 15 4
sayıları reeldir.
3
3 , 5  5 , 7  2 , 15  4
sayıları reeldir.
 3 , 4  5 , 6  2 , 10  4
sayıları reel değildir.
n pozitif çift sayı ve a negatif reel sayı ise
n
a ifadesi reel
sayı değildir.
Örnek:
4
8  x köklü ifadesinin reel sayı belirtmesi için, x hangi
şartı sağlamalıdır?
Çözüm:
4
8 x  R  8 – x  0
8x
x8
n
a n  a m dir.
Tanım :
m
Örnek :
1)
3
3
52  5 2
8 2 2
3
2
2)
Tanım:
a  0 ise
Örnek:
1)
5
3
2
a n  a dır.
m
75  7
2) 3 125  3 53  5
Tanım:
m tek sayı ile ise
Örnek:
1)
3
m
a n  a dır.
27  3 33  3
2) 3  8  3  2  2
3
Tanım:
m çift sayı ise
Örnek:
1)
Örnek:
4
 54
  5   5  5
n
1  1 dir.
n
0  0 dır.
x2  x
Olduğuna göre,
Çözüm:
a n  a dır.
9  3 33  3  3
2)
Sonuç :
m
9  3 8  5  32  4  4 işleminin sonucu kaçtır?
4
9  3 8  5  32  4  4 =
4
2
32  3 23  5  25  4  4
= 3  2   2  4
= 3 + 2 + 2 – (-4)
4
=7+4
= 11
Tanım :
k bir doğal sayı ve a > 0 olmak üzere
a n  k m a k n dir.
m
5  2 51  32 531  6 53  6 125
Örnek:
Tanım: k bir doğal sayı ve a > 0 olmak üzere
6
2
 5
10
2
m
an 
Tanım:
t > 0 olmak üzere, t  n a  n t n  a dır.
5
n
a k dır.
 3 55
Örnek:
6
10
m
k
Örnek: 2 5  2 2  5  4  5  20
Tanım:
Toplama, çıkarma
Köklerinin dereceleri ve içi eşit olan ifadeler, toplanırken ya
da çıkarılırken; kat sayılar toplanır ya da çıkarılır, sonuç
köklü ifadeye sayı olarak yazılır.
a n x  b n x  c n x  a  b  c n x dir.
Örnek: 1) 83 5  33 5  8  33 5
2)
0,08  0,32 

0,042  0,162
0,22  2  0,42  2
 0,2  2  0,4  2
 0,2  0,4  2
 0,6   2
Tanım: Çarpma
Köklerinin dereceleri aynı olan sayılar çarpılırken, aynı kök içinde
çarpma yapılır.
n
x  n y  n x  y dir. (n çift sayı ise x, y  R+ olmalıdır.)
köklerinin dereceleri aynı olmayan sayılar çarpılmadan önce, köklerinin
dereceleri eşitlenir. Sonra çarpma yapılır.
Örnek: 1)
4  3 2  3 5  3 4  2  5  3 40  3 8  5
3
 3 2 2  5  23 5
2)  2  3   5  12   2   5  3  12
 10  3  12
 10 36
= 10 . 6
= 60
Tanım: Bölme
Köklerinin dereceleri aynı olan sayılar bölünürken; kök
aynen kalır, sayıların bölümü kökün içine yazılır.
n
x
n
y
n
x
, y  0 (n çift sayı ise x, y  R+ olmalıdır)
y
köklerinin dereceleri aynı olmayan sayılar bölünmeden
önce, köklerinin dereceleri eşitlenir.
3
Örnek: 1)
3
24
3
3
24 3
 8  3 23  2
3
a3  b5
2)
a 5  b3
a 3  b5
b2
b
b

   
5
3
2
a
a b
a
a
2

Tanım: Paydayı Rasyonel Yapma
Paydasında köklü terim bulunan bir kesrin paydasını kökten
kurtarma işlemine paydayı rasyonel yapma denir.
Tanım:
a
Örnek:
2
Tanım:
Uyarı:

Örnek:
b
3

a b
dir.
b

2 3
x

3 3
a b

a b 
2
3 1


2 3
 3
2



x a b
dir.
a b

a  b  a  b dir.


2 3 1

2 3
3

3 1

311



2 3 1
3 1



2 3 1
 3 1
2
İÇ İÇE KÖKLER
Tanım:
m n
Örnek:
1)
a  mn a
3 6
23
2)
Tanım:
n
Örnek:
1)
2  36 2  18 2
1

2
3
23 
1 2

2
3
2 2  32 2 21  3 2
a n a n a ...  n 1 a
4
84 84 8...  41 8  3 2 3  2
2)
3
53 53 5...  31 5  2 5  5
a : n a : n a ...  n 1 a
Tanım:
n
Örnek:
1) 3 16 : 3 16 : 16...  31 16  4 2 4  2
2)
Tanım:
3 : 3 : 3...  21 3  3 3
a ardışık iki pozitif tam sayının çarpımı olsun
a  a  a  ...  ardışık iki sayının büyüğü
a  a  a  ...  ardışık iki sayının küçüğü
Örnek:
6 = 3 . 2 olduğu için,
6  6  6  ...  3
6  6  6  ...  2 dir.
Tanım:
x = a + b, y = a.b ve a>b ise,
x2 y  a  b
x  2 y  a  b dir.
Örnek:
2  1  2
1)
3 2 2 
2)
8 4 3  8 22 3
2 1  2  1  2  1
 8  2 22  3
 8  2 12

6  2  2
62
 6 2
Tanım:
ab  n a  n b dir.
1)
2)
Örnek:
3
3 < 3 10 < 3 25
1
5
>
1
8
Sayıların köklerinin dereceleri farklı olduğu için, köklerin derecelerini
eşitleyelim
2  2 21  23 213  6 23  6 8
Çözüm:
3
3  3 31  32 312  6 32  6 9
8 < 9 olduğuna göre
Demek ki,
2<
3
6
8<
3 tür.
6
9 dır.
ÇÖZÜMLÜ ÖRNEKLER
Örnek:
4
3 x  x  4
Toplamının reel sayı belirtmesi için x hangi aralıkta olmalıdır?
Çözüm:
4
3  x  x  4 toplamının bir reel sayı belirtmesi için,
4
3  x  IR ve
4
3  x  IR  3 – x  0
x  4  IR olmalıdır.
3x
x  3 ........(1)
x  4  IR  x + 4  0
x  -4 .....(2)
(1) ve (2) sonuçları birlikte göz önüne alınırsa,
x  3 ve x  -4  - 4  x  3 tür.
Buna göre; x,[-4,3] aralığında olmalıdır.
Örnek:
4,24
6
işleminin sonucu kaçtır?

2
1,06
Çözüm:
4,24
6


2
1,06

4  1,06
6

2
1,06
2 1,06  6
2 1,06
=6
Örnek:
3
28  1  3
28  1
Çözüm :
3
28  1  3
28  1  3
işleminin sonucu kaçtır?

3

28  1 
 28 
2
 12

28  1
 3 28  1
 3 27
3 3
=3
Örnek:
2a
3  b olduğuna göre,
54 ün eşiti nedir?
54  2  33
Çözüm :
 2  33
 2
 3
3
= a . b3
Örnek: Hangisinin yaklaşık değerleri bilinirse
288 sayısının yaklaşık değeri
hesaplanabilir?
Çözüm:
288
2
144
2
72
2
36
2
18
2
9
3
3
3
1
288  2 2  2 2  32  2
 2.2.3. 2
 12 2
olduğuna göre,
288 in yaklaşık değeri hesaplanabilmesi için
yaklaşık değerinin bilinmesi gerekir.
Örnek:
x 1,2  0,2 olduğuna göre x kaçtır?
Çözüm :
x 1,2  0,2
2 nin
x
Örnek:
12
2
2 10
2 10
1

x



10
10
10 12
10 12
6
21

2 4a
2 a  3  214 a 

1 6

6
 6

6
6
6 6
2
2
2 
a 4
2
34
2
9
a < b < 0 olduğuna göre,
a  b2  3 a 3  4 b 4
Çözüm:

6
21 4 a ifadesinin eşiti nedir?

Örnek:
1
2a = 3
Olduğuna göre
Çözüm :

ifadesinin eşiti nedir?
n çift sayı ise
n
xn  x
n tek sayı ise
n
x n  x tir.
a < b  a – b ve a < b < 0 olduğuna göre,
a  b2
 3 a3  4 b4  a  b  a  b
 a  b  a  b
 a  b  a  b
=0
Örnek: x  3 , y  3 2 , z  4 6 olduğuna göre; x, y, z arasındaki sıralama nedir?
Çözüm :
x  3  2 31  26 316  12 36  12 729
y  3 2  3 21  3.4 21.4  12 2 4  12 16
z  4 6  4 61  3.4 61.3  12 63  12 216
729 > 216 > 16 olduğu için, x > z > y dir.
BASİT EŞİTSİZLİKLER
Devirli bir ondalık açılımı olan rasyonel sayılar kümesi ile devirli bir ondalık açılımı
olmayan irrasyonel sayılar kümesinin birleşimi Reel sayılar kümesini oluşturur.
a < a + 1 < a + 2 şeklindeki ifadelere eşitsizlik ya da reel sayıların
sıralaması adı verilir.
a ve b iki reel sayı olsun , a ile b arasında ;
a < b , a = b , a < b gibi üç farklı durum söz konusudur.
a sayısı , b sayısından küçük ise a < b , a sayısı b sayısından büyük ise a > b şeklinde
gösterilir.
REEL SAYILARDA EŞİTSİZLİĞİN ÖZELLİKLERİ
1.
Bir eşitsizliğin her iki yanına aynı sayı eklenirse , ya da her iki yanından aynı sayı
çıkarılırsa yön değişmez.
a<b
a+c< b+c
a–c< b–c
a>b
a+c> b+c
a–c> b– c
Örneğin ; - 13 < 4 eşitsizliğinin her iki yanından 5 çıkarırsak :
-13 – 5 < 4 – 5
- 18 < - 1 sıralaması elde edilir.
a) Bir eşitsizliğin her iki yanı pozitif bir reel sayı ile çarpılırsa ya da bölünürse
2.
eşitsizlik yön değiştirmez.
b) Eşitsizliğin her iki yanı negatif bir reel sayı ile çarpılırsa ya da bölünürse eşitsizlik
yön değiştirir.
a > b ve c < 0 ise
a . c < b . c ve
a < b
dir.
Örneğin ; - 6 < - 2 iken her iki taraf ( - 3 ) ile çarpılırsa :
(-6).(-3)>(-2).(-3)
18 > 6 şeklinde yön
değiştireceğine dikkat ediniz.
Aynı şekilde 18 > 4 eşitsizliğinin her iki yanı ( - 2 ) ile bölünürse yön
değişir.
18 > 4
18 < 4
-2
-2
-9 < -2
3.
a ve b aynı işaretli iki reel sayı ve a > b ise
b
< a
Yani ; eşitsizliğin her iki yanı ters çevrilirse eşitsizlik yön değiştirir. a ve b ters işaretli
ise bu sayıların ters
çevrilmesi eşitsizliğin yönünü değiştirmez.
ÖRNEK :
a)
8>3
8 < 3
b)
2<5
2 > 5
4.
n pozitif tam sayı olmak üzere
0 < a < b ise an < bn
.
Örneğin ;
23 < 53
2<5
3 < 2
1
8 < 125
2
3
<
2
1
2
5. n pozitif tam sayı olmak üzere
I. n çift iken an > bn
a < b < 0 ise
II n tek iken an < bn
Örneğin ;
6.
-4<-2
-4
-5<-3
-5
2
3
> -2
2
< -3
3
n € Z n ≥ 2 olmak üzere
dir.
0 < a < 1 ise an < a
dır.
( 0, 1 ) aralığındaki sayıların ( basit kesirlerin ) pozitif artan kuvvetleri arttıkça sayı
küçülür.
NOT :
0 < a < 1 ve n € Z+ ise a n < a n-1 dir.
ÖRNEK :
a)
1
3
<
2
b)
3
2
< 1
2
2
>
7
c)
2
1
2
3
3
7
a >
5
2
b
a < b
5
7.
a < b ve b < c
a<c
dir.
8.
a < b
+
c <+ d
a+c< b+d
dir.
(aynı yönlü eşitsizlikler alt alta toplanabilirler . )
ÖRNEK :
a)
x < 5 ve 5 < y ise x < y dir.
b)
- 11 <
+
2 <
-9 <
c)
2
+
5
7
a ve b reel sayı olmak üzere
a < b < 8 ise
a < 8
+
b < 8
a + b < 16
9.
olur.
a , b , c , d pozitif reel sayılar olmak üzere ;
a > b
c > d ise a . c > b . d dir.
REEL (GERÇEL) SAYI ARALIKLARI :
1.
Kapalı Aralık :
a ve b reel sayılar olsun.
a ≤ b x ≤ b eşitsizliğini sağlayan x reel sayıları içine alan küme [ a , b ] şeklinde
gösterilir ve böyle aralıklara kapalı
R
a
2.
b
Açık Aralık :
a,b € R
ve a < b olsun
aralık denir.
a < x < b eşitsizliğini sağlayan x reel sayılarının kümesi ( a , b ) şeklinde gösterilir ve
böyle aralıklara açık aralık denir.
( a , b ) açık aralığında a ve b uç noktalarının kümeye ait olmadığına dikkat ediniz.
R
a
b
[ a , b ) ve ( a , b ] şeklinde gösterilen aralıklara yarı açık aralıklar denir.
ÖRNEK :
x ve y reel sayılardır.
-5<x<3
- 2 < y < 9 olduğuna göre
a)
4x – 3y ifadesinin alabileceği en küçük ve en büyük tamsayı değerleri kaçtır?
b)
x2 ile y2 nin en geniş değerler aralığı nedir?
c)
x . y nin alabileceği en küçük ve en büyük tam sayı değerleri nelerdir?
ÇÖZÜM:
x ve y nin reel sayılar olarak verildiğine dikkat edilmelidir.
a)
4x – 3y ifadesini elde edebilmek için ;
-5 < x < 3 eşitsizliğinin her üç yanını 4 ile
-2 < y < 9 eşitsizliğini de -3 ile çarpalım ve alt alta toplayalım.
-5 < x < 3
-20 < 4x < 12
-2 < y < 9
6 > -3y > -27
-27 < -3y < 6
-20 < 4x < 12
+
-27 < -3y < 6
-47 < 4x-3y < 18
olur.
O halde 4x - 3y nin alabileceği en küçük tamsayı değeri -46, en büyük tamsayı
değeri 17 olur.
b)
-5 < x < 3
0 ≤ x2 < ( -5 )2
0 ≤ x2 < 25
-2 < y < 9
0 ≤ y2 < 92
0 < y2 < 81
olur.
UYARI :
a, b ve c pozitif sayılar iken
a<b<c
a2 < b2 < c2
2<x<5
4 < x2 < 25 gibi.
olur.
c)
-5 < x < 3
-2 < y < 9 eşitsizlikleri alt alta çarpılmaz . Çünkü dört sınırında pozitif sayı olması
gerekir.
Böyle hallerde x . y nin alt ve üst sınırlarını bulmak için alt alta ve çapraz olarak
çarpmalar yapılır. Elde
edilen sonuçların en küçüğü alt sınır , en büyüğü de üst sınır olarak alınır.
( -5 ) . ( -2 ) = 10
3 . 9 = 27 *
-45 < x . y < 27 olur.
( -5 ) . 9 = -45 *
( 3 ) . -2 = -6
O halde x . y nin en küçük tamsayı değeri -44 , en büyük tamsayı değeri 26 olur
ÖRNEKLER :
Örnek :
2 < x < 3 ve -1 < y < 2 olmak üzere , 2x – y ifadesinin alabileceği tamsayı değerlerin
toplamını bulalım.
Çözüm :
2<x<3
2.(2<x<3)
-1 < y < 2
-1 . ( -1 < y < 2 )
4 < 2x < 6
+
-2 < -y < -1
2 < 2x < -y < 7
olur.
2x –y sayısı 3 , 4 , 5 , 6 tamsayı değerlerini alabilir.
Bunların toplamı , 3 + 4 + 5 + 6 = 18 dir.
Örnek :
a . b2 < 0 , a . c > 0 ve b3 < 0 olduğuna göre , sırasıyla a , b , c sayılarının işaretlerini
bulunuz.
c5
Çözüm :
a . b2 < 0 ise a ile b2 ters işaretlidir.
b2 > 0 olduğuna göre, a < 0 dır ……..*
a . c > 0 ise a ile c aynı işaretlidir.
a < 0 olduğuna göre, c < 0 dır…..*
b3 ile c5 ters işaretlidir.
b3 < 0 ise
c5
c < 0 olduğu için c5 < 0 olacağından b3 > 0 olmalıdır.
b3 > 0 olduğuna göre , b >0 dır …….*
O halde a , b , c sayılarının işaretleri sırasıyla - , + ,- dir.
MUTLAK DEĞERLİ BASİT EŞİTSİZLİKLER
1 ) a > 0 ,│x│ ≤ a
- a ≤ x ≤ a dır.
x
R
-a
2 ) │x │ ≥ a
0
a
x ≥ a veya x ≤ - a dır.
X
X
R
-a
0
3 ) a < │f ( x ) │ < b ise
I )
a < f ( x ) < b veya
II )
a < - f ( x) < b dir.
UYARI :
a )
│x │ ≥ 0 , (
b )
│x │ = │y│
x2 = y2
c )
│x │ > │y│
x2 > y2
d )
│x │ = │y│
x = y veya x = -y
X
€ R için )
a
ÖRNEK
:
│2x – 3│ = 2002 ise x in alabileceği değerlerin toplamı kaçtır ?
ÇÖZÜM
:
2x – 3 =0 ise x = 3
2
x in alabileceği değerlerin toplamı 2 . 3 = 3 bulunur.
2
ÖRNEK
:
│X – 2│ + │2 – X │ = 10 denkleminin çözüm kümesi nedir ?
ÇÖZÜM
:
│X – 2│ = │2 – X │ olduğundan
│X – 2│ + │2 – X │ = 10
ise 2│ x – 2│ = 10
│X – 2│ = 5
A)
x–2 = 5
ise
x=7
B)
x - 2 = -5
ise
x = -3
Ç. K. = { -3 , 7 }
bulunur.