11.03.2014
DEVAM
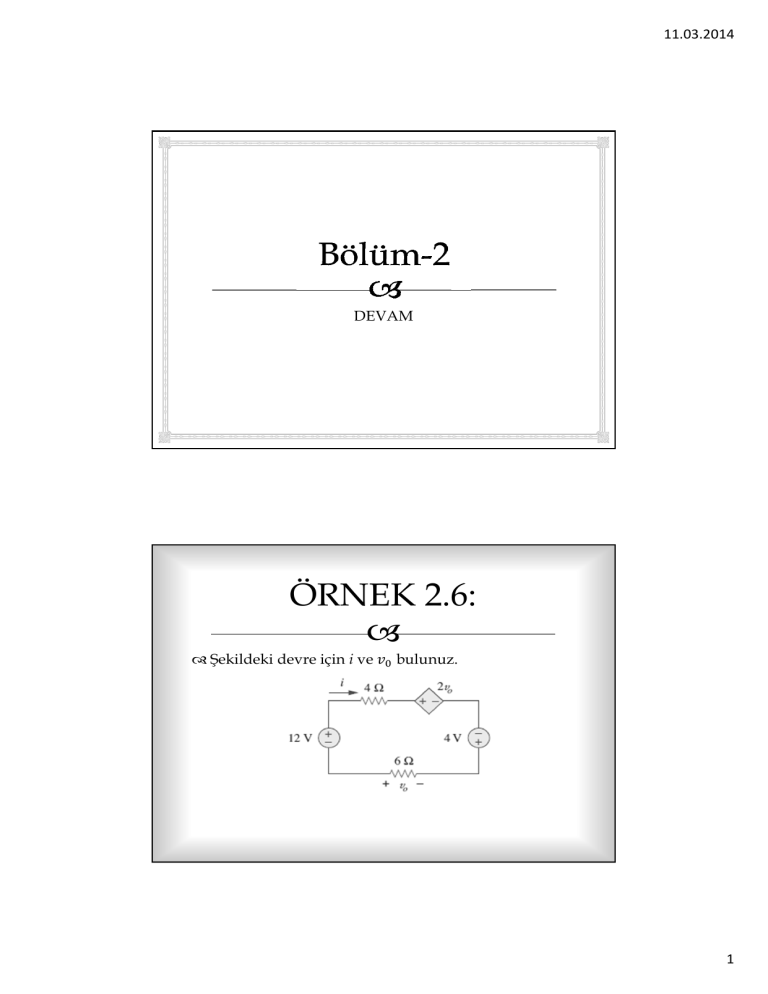
ÖRNEK 2.6:
Şekildeki devre için i ve ݒ bulunuz.
1
11.03.2014
Örnek 2.7:
Şekildeki devre için ݅ ve ݒ bulunuz.
Örnek 2.8:
Şekildeki devre için gerilim ve akımları bulunuz.
2
11.03.2014
2.5. Seri direnç ve Gerilim
bölme
Kirchoff’un Gerilim Kanunu çevrede
uygulanırsa;
2.5. Seri direnç ve Gerilim
bölme
Bu denklem devrenin eşdeğer direnci ile de yazılabili
3
11.03.2014
2.5. Seri direnç ve Gerilim
bölme
Buradan şu sonuç çıkarılabilir;
Seri bağlı dirençlerin eş değer direnci her bir direncin
toplamı ile bulunur.
Devredeki her bir direnç üzerindeki gerilim;
2.5. Seri direnç ve Gerilim
bölme
Dikkat edilirse, gerilim dirençler arasında direnç
büyüklükleri ile doğru orantılı olarak paylaşılmıştır.
Daha büyük direnç değerli eleman daha fazla
gerilim çekmiştir.
N elemanlı bir devre için bu olay;
Gerilim bölme kuralı olarak adlandırılır.
4
11.03.2014
2.6. Paralel Dirençler ve Akım
Bölme
• Devredeki dirençler a-b düğümleri
arasına paralel bağlanmışlar.
• Dolayısı ile aynı gerilim farkına
sahiptirler.
veya
• a noktasında Kirchoff’un akım kanunu yazarsak;
2.6. Paralel Dirençler ve Akım
Bölme
ܴ paralel bağlı dirençlerin eş değeri ise;
Özel olarak paralel bağlı
iki direncin eş değeri;
N adet bağlanmış paralel
direncin eş değeri;
5
11.03.2014
2.6. Paralel Dirençler ve Akım
Bölme
N adet paralel bağlanmış direncin ܴ değeri paralel bağlı
en küçük dirençten daha küçüktür.
Eğer paralel bağlı dirençler eşit ise
Paralel bağlı dirençler ile çalışırken bazen direnç yerine iletkenlik
ile alışmak daha uygundur.
2.6. Paralel Dirençler ve Akım
Bölme
Şekildeki devrede a düğümüne
giren toplam akım i biliniyor ise ݅ଵ
ve ݅ଶ akımları nasıl bulunur?
a
Devre hakkında bildiğimiz bir şey
var o da paralel dalların
gerilimlerinin aynı olması. Bu
durumda;
Akım Bölme Kuralı dır.
6
11.03.2014
2.6. Paralel Dirençler ve Akım
Bölme
Paralel bağlı devrelerde özel iki durumdan bahsedilirse;
Dallardan biri kısa devre ise;
a
Dallardan biri açık devre ise;
Örnekler
7
11.03.2014
2.7. Y- Dönüşümleri
Şekildeki devrenin eş değer
direncini bulmak için ne serilik ne
de paralellik kullanılamıyor.
Bu ve benzeri durumlar için Y-
dönüşümleri kullanılır.
Her ikisi de Ybağlantısıdır.
2.7. Y- Dönüşümleri
Her ikisi de
bağlantısıdır.
dan Y bağlantısı elde etmek:
8
11.03.2014
2.7. Y- Dönüşümleri
Y den bağlantısı elde etmek:
Örnekler
9
11.03.2014
2.8. Uygulamalar
ÖRNEK: Şekildeki devrede 9 V luk pil,
lambalara bağlanmıştır. a) Pilden çıkan
toplam akım, b) her bir lambadan geçen
akım, c) her bir lambanın direnci.
ÇÖZÜM: a) Pilin ürettiği enerji, lambaların harcadığı enerjiye eşittir.
b) Devredeki lambalar dirençler olarak
şekildeki gibi modellenebilir.
b) R1 direnci üzerinden geçen akım;
KAK üst düğümde uygulanırsa;
c) Her bir lambanın gücü biliniyor öyle ise direnci için;
10
11.03.2014
DC-Metre
Voltaj regülatörü olarak TV, radyo
gibi yerlerde sıklıkla kullanılır.
11