Uploaded by
common.user6608
Geometri Formülleri: Üçgenler, Dörtgenler, Çemberler
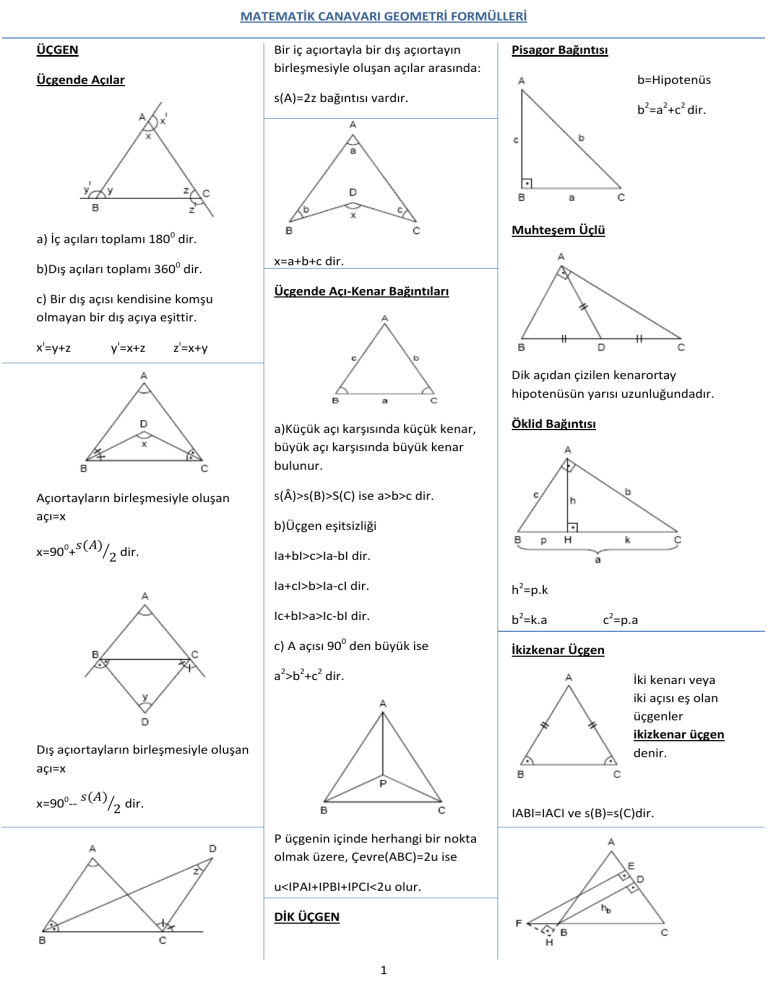
MATEMATİK CANAVARI GEOMETRİ FORMÜLLERİ Bir iç açıortayla bir dış açıortayın birleşmesiyle oluşan açılar arasında: ÜÇGEN Üçgende Açılar Pisagor Bağıntısı b=Hipotenüs s(A)=2z bağıntısı vardır. Muhteşem Üçlü a) İç açıları toplamı 1800 dir. b)Dış açıları toplamı 3600 dir. c) Bir dış açısı kendisine komşu olmayan bir dış açıya eşittir. xı=y+z yı=x+z b2=a2+c2 dir. x=a+b+c dir. Üçgende Açı-Kenar Bağıntıları zı=x+y Dik açıdan çizilen kenarortay hipotenüsün yarısı uzunluğundadır. a)Küçük açı karşısında küçük kenar, büyük açı karşısında büyük kenar bulunur. Açıortayların birleşmesiyle oluşan açı=x x=900+ 𝑠(𝐴)� 2 dir. s(Â)>s(B)>S(C) ise a>b>c dir. b)Üçgen eşitsizliği Ia+bI>c>Ia-bI dir. Ia+cI>b>Ia-cI dir. h2=p.k Ic+bI>a>Ic-bI dir. b2=k.a c) A açısı 900 den büyük ise İkizkenar Üçgen a2>b2+c2 dir. 𝑠(𝐴)� 2 dir. c2=p.a İki kenarı veya iki açısı eş olan üçgenler ikizkenar üçgen denir. Dış açıortayların birleşmesiyle oluşan açı=x x=900-- Öklid Bağıntısı IABI=IACI ve s(B)=s(C)dir. P üçgenin içinde herhangi bir nokta olmak üzere, Çevre(ABC)=2u ise u<IPAI+IPBI+IPCI<2u olur. DİK ÜÇGEN 1 MATEMATİK CANAVARI GEOMETRİ FORMÜLLERİ D dış teğet çemberinin merkezi olmak üzere, A,B,H noktaları doğrusal; F,B,C noktaları doğrusal [FH] ⊥ [HB] IABI=IACI ise IFEI-IFHI=hb-hc dir. Üçgende Kenarortay Bağıntıları Kenarortay ların kesiştiği noktaya ağırlık merkezi denir. c) P eşkenar üçgen üzerinde olmak üzere, P noktasından kenarları çizilen paralellerin toplamı üçgenin bir kenar uzunluğuna eşittir. P herhangi bir nokta, [PR]//[AB], [PS]//[AC] ve IABI=IACI olmak üzere, Üçgende Açıortay Bağlantıları G, ağırlık merkezi ise IANI iç açıortay, IPRI+IPSI= IABI=IACI IAGI=2IGFI ve IBGI=2IGDI ve Eşkenar Üçgen IGCI=2IGEI dir. İç açıları ve kenarları eşit üçgene eşkenar üçgen denir. a) Eşkenar üçgende yükseklik, kenarortay ve açıortay uzunlukları eşittir. IABI IBNI = IACI INCI ve IANI2=a.b-p.k dir. IANI dış açıortay, Kenarortay Teoremi: 2Va2+(a2/2)=b2+c2 dir. Va=hb=na IABI IBNI = IACI INCI ve IANI2=p.k-a.b dir. *Bir üçgende iki dış açıortay ile bir iç açıortay bir noktada kesişirler. Bu nokta üçgenin dış teğet çemberinin merkezidir. G, ağırlık merkezi ve s(A)=900 ise 5Va2= Vb2+ Vc2dir. [BD] ⊥ [CE] b)P eşkenar üçgen üzerinde olmak üzere, İse Va2= Vb2+ Vc2 olur. P noktasından kenarları çizilen dikmelerin toplamı üçgenin yüksekliğine eşittir. 2 MATEMATİK CANAVARI GEOMETRİ FORMÜLLERİ Çevrel Çemberinin Yarıçapı ve Kenar Uzunlukları Verilen Üçgenin Alanı Üçgende ALAN ABC ile DEF üçgeni benzer ise İki Kenar ve Bu Kenarlar Arasındaki Açı Biliniyorsa Alan: 𝐼𝐴𝐵𝐼 𝐼𝐵𝐶𝐼 𝐼𝐴𝐶𝐼 = = 𝐼𝐷𝐸𝐼 𝐼𝐸𝐹𝐼 𝐼𝐷𝐹𝐼 = 𝑘 𝑜𝑟𝑎𝑛𝚤𝑛𝑎 𝐛𝐞𝐧𝐳𝐞𝐫𝐥𝐢𝐤 𝐨𝐫𝐚𝐧ı 𝑑𝑒𝑛𝑖𝑟. Benzerlik oranı IOCI=R 𝑎.𝑏.𝑐 Alan= 4𝑅 Üçgende Alanla İlgili Özellikler 1.Yükseklikleri eşit olan üçgenlerin alanları oranı tabanları oranına eşittir. 𝐼𝐴𝐵𝐼 𝐼𝐵𝐶𝐼 𝐼𝐴𝐶𝐼 ℎ𝑎 ℎ𝑏 = = = = 𝐼𝐷𝐸𝐼 𝐼𝐸𝐹𝐼 𝐼𝐷𝐹𝐼 ℎ𝑑 ℎ𝑒 ℎ𝑐 = =𝑘 ℎ𝑓 Ayrıca, olup ha=hb olursa 1 2 Alan= . a.b.sinC 1 2 (Alanlar oranı benzerlik oranının karesine eşittir.) Alan= . b.c.sinA Alanların oranının oranı olduğu basit bir şekilde anlaşılabilir. 1 2 Alan= . a.c.sinB Üç Kenar Uzunluğu Bilinen Üçgenin Alanı (U Kuralı): Çevre=a+b+c olsun u= a+b+c 2 Temel Benzerlik Teoremi 2. Taban uzunlukları eşit olan üçgenlerin alanları oranı yükseklikleri oranına eşittir. (a=b ise) olsun. Alan=�𝑢. (𝑢 − 𝑎). (𝑢 − 𝑏). (𝑢 − 𝑐) Çevresi ve İç Teğet Çemberinin Yarıçapı Verilen Üçgenin Alanı ED//BC ise 𝐼𝐴𝐸𝐼 𝐼𝐴𝐷𝐼 𝐼𝐸𝐷𝐼 = = 𝐼𝐴𝐵𝐼 𝐼𝐴𝐶𝐼 𝐼𝐵𝐶𝐼 3. Oranına temel benzerlik teoremi denir. Thales Teoremi u= a+b+c 2 Alan=u.r 𝐴(𝐴𝐵𝐶) 𝐼𝐴𝐵𝐼. 𝐼𝐴𝐶𝐼. 𝐼𝐵𝐶𝐼 = 𝑎. 𝑐. 𝑒 + 𝑏. 𝑑. 𝑓 𝐴(𝐷𝐸𝐹) BENZERLİK ORANI olsun. (r:yarıçap) 3 AD//BE//CF MATEMATİK CANAVARI GEOMETRİ FORMÜLLERİ İç teğet çemberinin yarıçapı = r 𝐼𝐴𝐶𝐼 𝐼𝐴𝐵𝐼 𝐼𝐵𝐶𝐼 = = 𝐼𝐷𝐸𝐼 𝐼𝐵𝐸𝐼 𝐼𝐵𝐷𝐼 Menelaus Teoremi P herhangi bir nokta olmak üzere, A= a2+c2+e2=b2+d2+f2 𝑛.𝑎.𝑟 2 ÇOKGENLER Dışbükey (Konveks) Çokgenler *İç açılar toplamı: (n -2) . 180° *Dış açılar toplamı =360° 𝐼𝑃𝐶𝐼 𝐼𝐵𝑆𝐼 𝐼𝐴𝑅𝐼 . . =1 𝐼𝑃𝐵𝐼 𝐼𝐴𝑆𝐼 𝐼𝑅𝐶𝐼 Seva Teoremi 𝐼𝐴𝑆𝐼 𝐼𝐵𝑇𝐼 𝐼𝐶𝑅 . . =1 𝐼𝐵𝑆𝐼 𝐼𝐶𝑇𝐼 𝐼𝐴𝑅𝐼 Stewart Teoremi *Bir köşeden (n – 3) tane köşegen çizilebilir. *Köşegen sayısı=n(n-3)/2 * n kenarlı dışbükey bir çokgenin içerisinde, bir köşeden köşegenler çizilerek (n – 2) adet üçgen elde edilebilir. *Kenar sayısı n olan bir konveks çokgenin çizilebilmesi için (2n-3)tane elemanı bilinmelidir. Bu elemanların en az (n-2) tanesi uzunluk, en çok (n-1) tanesi açı olmalıdır. Çevrel çemberin yarıçapı= R n kenarlı düzgün çokgenin alanı, 1 2 A= . 𝑛.R2.sinα 360 ) 𝑛 (α= DÖRTGENLER Konveks Dörtgenler *İç açıları toplamı:3600 dır. *Dış açıları toplamı:3600 dır. Alan Düzgün Çokgenler Tüm kenarları ve tüm açıları eşit olan çokgenlere düzgün çokgenler denir. * n kenarlı düzgün bir çokgenin bir dış açısının ölçüsü: *Bir iç açısı ise 360 𝑛 180- (n−2)180 n 360 𝑛 ile bulunur. 1 2 A(ABCD)= . IACI. IBDI. sina a2+c2=b2+d2 veya ile bulunur. Düzgün Çokgenin Alanı Carnot Teoremi 4 Alan= IACI. IBDI 2 MATEMATİK CANAVARI GEOMETRİ FORMÜLLERİ Dikdörtgen 2. *Açıları 900dir. *Karşılıklı kenarları eşit ve paraleldir. [AC] [BD] köşegen olmak üzere, Alan=a.b.sinα S1.S3=S2.S4 PARALELKENAR Çevre=2a+2b=2(a+b) Karşılıklı kenarları paralel ve eşit olan dörtgene paralelkenar denir. *Paralelkenarın karşılıklı açılarının ölçüleri eşittir. Alan= a.b K kenarlar üzerinde herhangi bir nokta olmak üzere, A(ABCD)=2.(S1+S2) dir. Köşegenler alanı 4 eşit parçaya böler. [AB]//[DC] ve [AD]//[BC] ve α+θ=1800 dir. P paralelkenar içinde bir nokta olmak üzere, S1+S3= S2+S4 P içerde herhangi bir nokta olmak üzere, IBPI2+IDPI2=IAPI2+ICPI2 dir. Köşegenlerin kesişimi “E” ağırlık merkezidir. Köşegenler birbirini ortalar ve alanı 4 eşit parçaya ayırır. Alan 𝑆 8 A(ABCD)=S ise A(DEF)= A(ABE)=A(BCF)= 𝑆 4 A(BEF)= 3𝑆 8 P dışarda herhangi bir nokta olmak üzere, IBPI2+IDPI2=IAPI2+ICPI2 dir. Kare *Açıları 900dir. *Bütün kenarları eşit ve paraleldir. 1. Alan=a.ha=b.hb dir. IBHI2=IHFI.IHEI dir. (Benzerlikten) 5 *Köşegenler açıortaydır. MATEMATİK CANAVARI GEOMETRİ FORMÜLLERİ [AB]//[DC]//[EF] olmak üzere, [AD]nin orta noktası “E” ve [BC]nin orta noktası “F” ise [DC] ye orta taban denir. Eğer S1=S2 ise x= Çevre=4a Alan=a2 dir. İkizkenar Yamuk IACI.IBDI 2 Alan= Yan kenarları eşit uzunlukta olan yamuğa ikizkenar yamuk denir. dir. IACI=IBDI=a√2 dir. [AB]//[DC] ise DELTOİD s(A)+s(D)=s(B)+s(C)=1800 dir. *Taban açıları eşittir. *Köşegenleri eşit uzunluktadır. Taban uzunlukları eşit iki ikizkenar üçgenin tabanlarının birleştirilmesiyle oluşan şekle denir. *Tepe açılarını birleştiren köşegenler açıortaydır. [EF] orta taban, [EF]= 𝑎+𝑐 2 Yamuğun Alanı *Köşegenler dik kesişir. Alan= IACI.IBDI 2 dir. * Yamuk IAHI=IKBI=I 𝑎+𝑐 ]. ℎ 2 Alan=[ Yalnızca iki kenarı paralel olan dörtgene yamuk denir. *Paralel olan yamuğun kenarlarına yamuğun tabanları, diğer kenarlara ise yan kenarlar denir. ise a−c 2 I ABCD ikizkenar yamuk IKCI=IKBI ise A(ABCD)=2.A(AKD) A(ABCD)=IKHI.IADI dir. ve yamuğun yüksekliği h= 6 𝑎+𝑐 2 ve Alan=h2 dir. MATEMATİK CANAVARI GEOMETRİ FORMÜLLERİ Dik Yamuk Yan kenarlarından biri tabana dik ise bu yamuğa dik yamuk denir. Bir dik yamukta köşegenler dik kesişiyorsa, h2=√𝑎. 𝑐 dir. a)Merkez Açı=İki yarıçapın oluşturduğu açıya merkez açı denir. *Merkez açının ölçüsü gördüğü yayın ölçüsüne eşittir. b)Çevre Açı: Bir ucu ortak olan iki kiriş arasındaki açıya çevre açı denir. *Çevre açı gördüğü yayın ölçüsünün yarısına eşittir. ÇEMBER Çember, düzlemde sabit bir noktaya eşit uzaklıkta bulunan noktaların kümesinin oluşturduğu yuvarlak, geometrik şekil. *Çapı gören çevre açının ölçüsü 900dir. *Çember dışındaki bir P noktasından teğetler çizilirse bu uzunluklar birbirine eşittir. *Bir kesenin, çember içerisinde kalan parçasına kiriş denir. *Çemberi iki eş parçaya ayıran doğru parçasına çap denir. Merkezden geçen kiriş, çaptır. *Çember üzerinde herhangi iki nokta arasında kalan parçaya yay denir. c)Teğet-Kiriş Açı: Çemberde bir teğet ile bir kirişin oluşturduğu açıya denir. *Teğet-kiriş açı gördüğü yayın ölçüsünün yarısına eşittir. [AP]=[BP] *Çember ile iki ortak noktası olan doğruya kesen denir. *Çember dışındaki bir noktadan sonsuz sayıda kesen çizilir. *Çember ile bir ortak noktası olan doğruya teğet denir. AB yayı Ölçüsü ise şeklinde gösterilir. ile gösterilir. *Merkezle teğet noktasını birleştiren yarıçap, teğete diktir(900). 7 MATEMATİK CANAVARI GEOMETRİ FORMÜLLERİ Bu kesenler arasındaki bağıntı, IPAI.IPBI=IPCI.IPDI=IPKI.IPLI dir. *A noktası teğet ise Dairenin Alanı ve Çevresi İçi dolu çembere daire denir. Dairenin Alanı=π.r2 Kuvvet şöyle alınır. Çember veya direnin çevresi= 2.π.r IPAI2=IPBI.IPCI=IPDI.IPEI dir. Daire diliminin alanı= Çember yayının uzunluğu= P çemberin içinde herhangi bir nokta olmak üzere, IPAI.IPEI=ICPI.IPHI=IDPI.IPKI * *Merkezden uzunlukları eşit kirişlere çizilen dikmelerin uzunlukları eşittir. 8







