Uploaded by
common.user6322
Kinematik Ders Notları
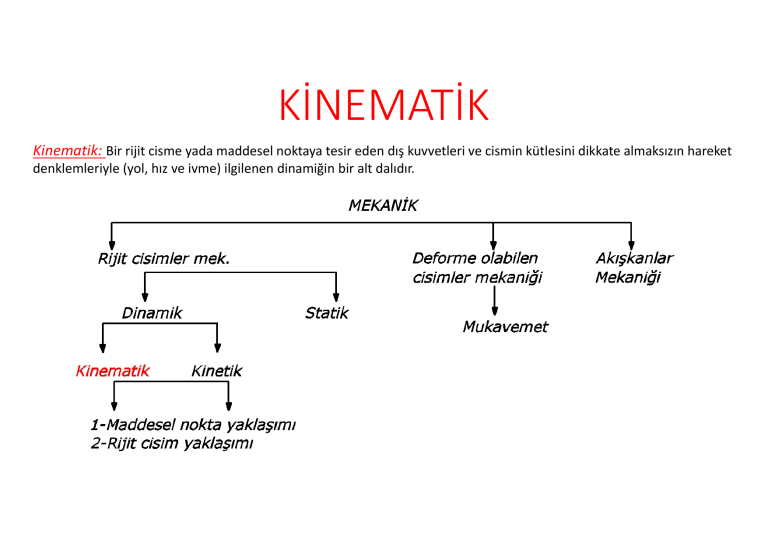
KİNEMATİK Kinematik: Bir rijit cisme yada maddesel noktaya tesir eden dış kuvvetleri ve cismin kütlesini dikkate almaksızın hareket denklemleriyle (yol, hız ve ivme) ilgilenen dinamiğin bir alt dalıdır. 1-Maddesel Noktalar Kinematiği 1. Doğrusal hareket 2. Düzlem Eğrisel hareket a. Dik koordinatlar (Kartezyen) b. Normal, teğetsel koordinatlar c. Kutupsal koordinatlar 3. Uzayda eğrisel hareket 4. İzafi hareket a. Eksenlerin ötelenmesi b. Eksenlerin dönmesi 5. Sınırlandırılmış hareket 2-Rijit Cisimler Kinematiği 1. 2. 3. 4. 5. Dönme (Rotasyon) Mutlak hareket İzafi hız Ani dönme merkezi İzafi ivme 3-Üç boyutlu rijit cisimlerin kinematiği 1. 2. 3. 4. 5. Kaynaklar: 1. Engineering Mechanics DYNAMICS JL Meriam, LG Kraige 2.Mechanics for Engineers FP Beer, ER Johnston 3. Engineering Mechanics:Dynamics Russell C. Hibbeler Öteleme hareketi Sabit eksen etrafında dönme Paralel düzlem hareketi Sabit nokta etrafında dönme Genel hareket TEMEL KAVRAMLAR • Uzay: Cisimler tarafından işgal edilen geometrik bölgedir. • Zaman: Birbirini izleyen olayların bir ölçüsüdür ve Newton mekaniğinde mutlak bir değer olarak kabul edilir. • Kütle: Ataletin sayısal bir ölçüsüdür diğer bir ifadeyle hareketin değişimine gösterilen dirençtir. • Kuvvet: Bir cismin diğer bir cisim üzerindeki vektörel etkisidir. • Maddesel Nokta: İhmal edilebilir boyutlara sahip bir cisimdir. Hareketin tanımlanmasında veya üzerindeki kuvvetlerin etkimesinde cismin boyutlarının bir önemi yok ise cisim maddesel bir nokta olarak kabul edilebilir. • Rijit Cisim: Cismin tüm boyutlarıyla karşılaştırıldığında şeklindeki veya cismin bütün olarak konumundaki değişikliklerin ihmal edilebilir seviyede olduğu bir cisimdir. • Skaler büyüklük: Tek bir şiddetle ifade edilen büyüklüklerdir. (Zaman,enerji,yoğunluk,kütle) • Vektörel büyüklük: Şiddetleri yanında yönlerinin de belirtilmesi gereken büyüklüklerdir. (yer vektörü, hız, ivme, moment, ağırlık, momentum BİRİMLER NEWTON KANUNLARI Newton’un 1.Kanunu (Eylemsizlik): Üzerine bir kuvvet etkimiyorsa bir maddesel nokta duruyor ise durmaya, hareket ediyor ise üniform hız ile hareket etmeye devam eder. Newton’un 2.Kanunu (F=m.a): Bir maddesel noktanın ivmesi üzerine etkiyen bileşke kuvvet ile orantılıdır ve bu kuvvet yönündedir. Newton’un 3.Kanunu (Etki-Tepki Prensibi): Temas eden cisimler arasındaki etki ve tepki kuvvetleri birbirine şiddetçe eşit, yönce ters ve aynı doğru üzerindedir. ÇEKİM KANUNU MADDESEL NOKTALAR KİNEMATİĞİ Fiziksel boyutları yörüngesinin eğrilik yarıçapına kıyasla çok küçük P maddesel noktasının herhangi bir t anındaki konumu dik koordinatlar (x,y,z), silindirik koordinatlar (r,θ,z) ve kutupsal koordinatlar (R,θ,φ) belirtilerek tanımlanabilir. Ayrıca P’nin hareketi eğriye teğet (t) ve normal (n) eksen takımı ile de tanımlanabilir. Maddesel noktaların (veya rijit cisimlerin) hareketi, sabit referans eksenlerden (mutlak hareket analizi) ölçülen koordinatları kullanılarak veya hareketli referans eksenlerden (izafi hareket analizi) ölçülen koordinatları kullanılarak tanımlanabilir. Mühendislikteki makinaların ve yapıların hareketlerinin önemli bir kısmı düzlemsel hareket ile temsil edilebilir. Düz bir doğru boyunca hareket olan doğrusal hareket ile düzlemsel hareket konumuza başlıyoruz ve düzlemsel bir eğri boyunca hareket tanımı ile devam ediyoruz. DOĞRUSAL HAREKET Düz bir hat boyunca hareket eden P maddesel noktası dikkate alındığında herhangi bir t anında P'nin konumu, hat üzerindeki uygun sabit bir O referans noktasından ölçülen s mesafesiyle belirlenebilir. t+Δt anında maddesel nokta P` noktasına hareket etmekte ve koordinatları s+Δs olmaktadır. Δt zamanı boyunca konum koordinatındaki değişim, maddesel noktanın Δs yer değiştirmesi olarak adlandırılır. Maddesel noktanın P’den P` noktasına Δt zaman aralığı hareketi esnasındaki ortalama hızı 𝜈 Δt zaman aralığı azaltılıp limitte sıfıra yaklaşırken, ortalama hız 𝜈 = 𝑙𝑖𝑚 → Anlık hız= 𝑣 = anlık hızına yaklaşır. = 𝑠̇ (1) ile ifade edilir Maddesel noktanın P’den P` noktasına Δt zaman aralığı hareketi esnasındaki ortalama ivmesi 𝑎 Δt zaman aralığı azaltılıp limitte sıfıra yaklaşırken, ortalama ivme a= 𝑙𝑖𝑚 → Anlık ivme= 𝑎 = = = 𝑣̇ veya 𝑎 = = 𝑠̈ (2) ile ifade edilir. = anlık ivmeye yaklaşır. DOĞRUSAL HAREKET (1) ve (2) denklemlerinde 𝑑𝑡 yok edilir ise; 𝑣𝑑𝑣 = 𝑎𝑑𝑠 (3) denklemi elde edilir. Hareket değişkenlerindeki sonlu değişimleri içeren doğrusal hareket problemleri bu temel diferansiyel bağıntıların integrasyonu ile çözülür. Doğrusal hareketi yöneten diferansiyel denklemlerin yorumuna 𝒔, 𝒗, 𝒂 ve 𝒕 arasındaki bağıntılarının grafik olarak gösterimi ile önemli ölçüde açıklık kazandırılmaktadır. Yanda verilen şekil, bir doğrusal hareket için 𝑡 anından 𝑡 anına kadar s değişiminin şematik çizimidir. Herhangi bir t anında eğriye teğet çizerek, 𝜈 = 𝑑𝑠/𝑑𝑡 hızını veren eğimi elde edilir. Böylece hız eğrinin tüm noktalarında belirlenebilir. DOĞRUSAL HAREKET Herhangi bir anda 𝒔 − 𝒕 eğrisinin eğimini veren 𝜈 = 𝑑𝑠/𝑑𝑡 eşitliğinden faydalanılarak hız(𝝂)-zaman(𝒕 ) eğrisi elde edilebilir. Benzer şekilde 𝝂- 𝒕 eğrisinin herhangi bir andaki 𝑑𝜈/𝑑𝑡 eğimi o andaki ivmeyi verir ve 𝒂- 𝒕 eğrisi buna bağlı olarak elde edilebilir. DOĞRUSAL HAREKET Denklem (1) 𝑣 = idi Denklem (2) 𝑎 = idi ∫ 𝑑𝑠 = ∫ 𝑣𝑑𝑡 veya 𝑠 − 𝑠 = 𝑣 − 𝑡 eğrisi altında ∫ 𝑑𝑣 = ∫ 𝑎𝑑𝑡 veya 𝑣 − 𝑣 = (a-t) eğrisi altında kalan alan. kalan alan. DOĞRUSAL HAREKET Denklem (3) 𝑣𝑑𝑣 = 𝑎𝑑𝑠 idi ∫ 𝑣𝑑𝑣 = ∫ 𝑎𝑑𝑠 (𝑎-𝑠) eğrisi altındaki alan = (𝑣 − 𝑣 ) 𝑣 hızı 𝑠 konum koordinatının bir fonksiyonu olarak çizildiğinde, herhangi bir A noktasındaki eğrinin eğimi d𝑣/ds dir. Bu noktada eğriye AB normalini çizerek benzer üçgenlerden 𝐶𝐵/𝑣 = 𝑑𝑣/𝑑𝑠 olduğu görülebilir. Böylece ivme(𝑎) = 𝐶𝐵 = 𝑣( ) elde edilmiş olur. DOĞRUSAL HAREKET 𝒔, konum koordinatı, 𝒕’nin tüm değerleri için biliniyorsa zamana göre ardışık matematiksel veya grafiksel türevler 𝒗 hızını ve 𝒂 ivmesini vermektedir. Pek çok problemde, konum koordinatları ve zaman arasındaki fonksiyonel bağıntı bilinmemektedir. Bu bağıntının ivmeden ardışık integrasyon ile belirlenmesi gerekmektedir. İvme hareket eden cisimler üzerine etkiyen kuvvetlerden belirlenmekte olup ivmenin kuvvetlerden elde edilmesi KİNETİK dersinde anlatılacaktır. Kuvvetlerin doğasına bağlı olarak, ivme zamanın, hızın, veya konum koordinatlarının fonksiyonu veya bu büyüklüklerin birleşiminden oluşan bir fonksiyon olarak belirtilebilir. a) İVMENİN SABİT OLMASI HALİ: (𝑎=sabit) Başlangıç şartları; 𝑠 = 𝑠 , 𝑣 = 𝑣 ve 𝑡 = 0 𝑎= ∫ 𝑑𝑣 = 𝑎 ∫ 𝑑𝑡 𝑣 − 𝑣 = 𝑎𝑡 𝑣 = 𝑣 + 𝑎𝑡 𝑣= ∫ 𝑑𝑠 = ∫ 𝑣 𝑑𝑡 𝑠 − 𝑠 = ∫ (𝑣 + 𝑎𝑡)𝑑𝑡 𝑠 = 𝑠 + 𝑣 𝑡 + 𝑎𝑡 DOĞRUSAL HAREKET b) İVMENİN ZAMANIN FONKSİYONU OLMASI HALİ: (𝑎= 𝑓(t)) Başlangıç şartları; 𝑠 = 𝑠 , 𝑣 = 𝑣 ve 𝑎 = 𝑎 𝑎= = 𝑎(t) 𝑣= ∫ 𝑑𝑣 = ∫ 𝑎(t)𝑑𝑡 ∫ 𝑑𝑠 = ∫ 𝑣 𝑑𝑡 𝑣 = 𝑣 + ∫ 𝑎(t)𝑑𝑡 𝑠=𝑠 + (𝑣 + ∫ 𝑎(t)𝑑𝑡)𝑑𝑡 c) İVMENİN HIZIN FONKSİYONU OLMASI HALİ: (𝑎= 𝑓(𝑣)) Başlangıç şartları; 𝑠 = 𝑠 , 𝑣 = 𝑣 ve 𝑎 = 𝑎 𝑎= =𝑓 𝑣 𝑣𝑑𝑣 = 𝑎𝑑𝑠 ∫ 𝑑𝑣 = ∫ 𝑓(𝑣)𝑑𝑡 𝑣𝑑𝑣 = 𝑓(𝑣)𝑑𝑠 ( ) ∫ 𝑑𝑠 = = ∫ 𝑑𝑡 ( ) 𝑡= ( ) 𝑠=𝑠 + ( ) DOĞRUSAL HAREKET d) İVMENİN YOLUN FONKSİYONU OLMASI HALİ: (𝑎= 𝑓(s)) 𝑣𝑑𝑣 = 𝑎𝑑𝑠 ∫ 𝑣𝑑𝑣 = ∫ 𝑓(𝑠)𝑑𝑠 𝑣 = 𝑣 + 2 ∫ 𝑓(𝑠)𝑑𝑠 Hız, yer değiştirmenin bir fonksiyonu olarak bulunur 𝑣 = 𝑓(𝑠) 𝑣= 𝑣=𝑔 𝑠 = 𝑣=𝑔 𝑠 𝑔(𝑠) = (𝑣 + 2 ∫ 𝑓(𝑠)𝑑𝑠) ∫ 𝑑𝑡 = ( ) ÖRNEK DOĞRUSAL HAREKET Düz bir doğru boyunca harekete zorlanan bir maddesel noktanın konum koordinatı 𝑠 = 2𝑡 − 24𝑡 + 6 denklemi ile tariflenmektedir. Burada s uygun bir orjinden ölçülmekte olup birimi metre, t’nin birimi saniyedir. a)maddesel noktanın t=0’daki başlangıç koşulundan 72m/s hıza erişmesi için gereken zamanı b) 𝑣=30 m/s iken maddesel noktanın ivmesini ve c) t=1 s’den t=4 s’ye olan zaman aralığı boyunca maddesel noktanın net yer değiştirmesini belirleyiniz. Çözüm 𝑣= 𝑑𝑠 = 6𝑡 − 24 𝑚/𝑠 𝑑𝑡 𝑎= a) 𝑣 = 6𝑡 − 24=72 t= 4sn b) 𝑣 = 6𝑡 − 24 = 30 t= 3sn 𝑎 = 12𝑡 c) Δ𝑠 = 𝑠 − 𝑠 𝑑𝑣 = 12𝑡 𝑚/𝑠 𝑑𝑡 12.3 = 36𝑚/𝑠 Δ𝑠 = 2 4 − 24 4 + 6 − 2 1 − 24 1 + 6 = 54𝑚 ÖRNEK Çözüm DOĞRUSAL HAREKET Bir doğru boyunca hareket eden maddesel noktanın yeri s = 𝑡 − 6𝑡 − 15𝑡 + 40 bağıntısıyla tanımlanmaktadır. s metre ve t saniye ile ifade edilmek üzere; a)Hızın 0 olduğu zamanı bulunuz b)Bu andaki yeri ve gidilen uzaklığı bulunuz c)Bu andaki ivmeyi bulunuz d)t= 4sn’den t=6sn’ye kadar maddesel noktanın gittiği yolu bulunuz. s = 𝑡 − 6𝑡 − 15𝑡 + 40 a)𝑣 = 3𝑡 − 12𝑡 − 15 = 0 𝑣= c) 𝑎 = 6𝑡 − 12 𝑎= = 6𝑡 − 12 𝑡 = −1𝑠 ve 𝑡 = +5𝑠 b) 𝑠 = (5) − 6(5) − 15(5) + 40 t=0 için = 3𝑡 − 12𝑡 − 15 𝑠 = −60𝑚 𝑠 = 40𝑚 𝑎 = 6(5) − 12 𝑎 = +18𝑚/𝑠 t=0 ile t=5sn aralığında gidilen yol Δs=-60-40=-100m Negatif yönde 100m DOĞRUSAL HAREKET d) 𝑠 = (4) − 6(4) − 15(4) + 40 = −52𝑚 𝑠 = (5) − 6(5) − 15(5) + 40 = −60𝑚 𝑠 = (6) − 6(6) − 15(6) + 40 = −50𝑚 4. ve 5. saniyeler arasında gidilen yol; 𝑠 −𝑠 = −60𝑚 − (−52𝑚) = −8𝑚 Negatif yönde 8m 5. ve 6. saniyeler arasında gidilen yol; 𝑠 − 𝑠 = −50𝑚 − (−60𝑚) = +10𝑚 Pozitif yönde 10m DOĞRUSAL HAREKET ÖRNEK Bir top, binanın 18m yükseklikteki bir penceresinden 12m/s hızla düşey olarak yukarı doğru atılmıştır. Topun ivmesi aşağı doğru 9,81 𝑚/ 𝑠 ’dir. a)Herhangi bir t zamanında topun hızını ve yerden yüksekliğini bulunuz b)Topun ulaşabileceği maksimum yüksekliği ve buna karşılık gelen t süresini bulunuz c)Topun yere değeceği zamanı ve buna karşılık gelen v hızını bulunuz. Çözüm 𝑎= = =sabit ∫ / 𝑑𝑣 = ∫ 𝑎𝑑𝑡 = −9,81 ∫ 𝑑𝑡 18 a) 𝑣 − 𝑣 = −9,81𝑡 𝑣 = 12 − 9,81𝑡 𝑠 = 18 + 12𝑡 − 4,905𝑡 𝑚 ; b) Maksimum yükseklikte 𝑣 = 0 olur. 𝑣 = 12 − 9,81𝑡 = 0 𝑠 = 18 + 12(1,223) − 4,905(1,223) 𝑣= ∫ 𝑠 = 25,74 𝑚 c) Top yere değdiğinde 𝑠 = 0 olur. 𝑠 = 18 + 12𝑡 − 4,905𝑡 =0 𝑡 = 3,496𝑠 𝑣 = 12 − 9,81𝑡 𝑣 = 12 − 9,81 3,496 = −22,3 𝑚/𝑠 𝑑𝑠 = ∫ 12 − 9,81𝑡 𝑑𝑡 𝑡= , s − 𝑠 = 12𝑡 − 9,81 𝑡 = 1,223 𝑠 DOĞRUSAL HAREKET ÖRNEK Bir maddesel nokta 𝑡 = 0 iken orijinde 𝑣 = 50 𝑚/𝑠 başlangıç hızı ile x-ekseni boyunca hareket etmektedir. İlk 4 saniye ivmesiz olarak hareket etmektedir. Daha sonra 𝑎 = −10 𝑚/𝑠 ’lik ivmeye maruz kalır. Maddesel noktanın ivmesini ve yer değiştirmesini 𝑡 = 8𝑠 𝑣𝑒 𝑡 = 12𝑠 için bulunuz. Ayrıca maddesel noktanın ulaşacağı maksimum yer değiştirmeyi bulunuz. Çözüm 𝑎 = = −10 ∫ 𝑑𝑣 = −10 ∫ 𝑑𝑡 𝑣 − 50 = −10(𝑡 − 4) 𝑣= ∫ 𝑣 = 90 − 10𝑡 𝑑𝑠 = ∫ (90 − 10𝑡)𝑑𝑡 𝑠 = 50(4) + ∫ (90 − 10𝑡) 𝑑𝑡 = −5𝑡 + 90𝑡 − 80𝑚 𝑡 = 8𝑠 𝑖ç𝑖𝑛 𝑡 = 12𝑠 𝑖ç𝑖𝑛 𝑥 = −5(8 ) + 90(8) − 80 = 320𝑚 𝑥 = −5(12 ) + 90(12) − 80 = 280𝑚 t = 9 s' den sonra, hareket negatif x- doğrultusunda olduğundan, t = 12 s anındaki x-koordinatı t = 8 s anındakinda en küçüktür. Maksimum pozitif x-koordinatı bu nedenle t = 9 s anındaki x değeridir. 𝑠 = −5(9 ) + 90(9) − 80 = 325𝑚 DOĞRUSAL HAREKET ÖRNEK Yüklü bir vagon, yay ve damperli bir tamponla birleştiği sırada sabit bir hızla hareket ediyor. Birleşmeden sonra 𝑥 𝑣𝑒 𝑡 𝑠𝚤𝑟𝑎𝑠𝚤𝑦𝑙𝑎 mm ve saniye(s) cinsinden ifade edilmek üzere 𝑥 = 60𝑒 . sin 16𝑡 bağıntısıyla tanımlanmaktadır. 𝑡 = 0,3𝑠 iken vagonun konumunu, hızını ve ivmesini bulunuz. Çözüm . 𝑥 = 60𝑒 𝑣= 𝑎= sin 16𝑡 𝑑𝑥 = 60(−4.8)𝑒 𝑑𝑡 𝑑𝑣 = 1382.4𝑒 𝑑𝑡 . 𝑎 = −13977.6𝑒 . si n 16 𝑡 + 60(16)𝑒 sin 16𝑡 − 4608𝑒 . . si n 16 𝑡 − 9216𝑒 . co s 16 𝑡 cos 16𝑡 − 4608𝑒 . co s 16 𝑡 . co s 16 𝑡 − 15360𝑒 . si n 16 𝑡 DOĞRUSAL HAREKET Çözüm 𝑒 . =𝑒 . ( . ) =𝑒 . = 0.23692 si n 16 𝑡 = si n 16 (0.3) = si n 4.8 = −0.99616 co s 16 𝑡 = co s 16 0.3 = co s 4.8 = 0.08750 𝑥 𝑎 . = 60 0.23692 −0.99616 = −14.16mm = − 288 0.23692 −0.99616 + 960 0.23692 0.08750 = 87.9𝑚 𝑚⁄𝑠 𝑣 . . = −(13977.6)(0.23692)(−0.99616) − (9216)(0.23692)(0.08750) = 3108𝑚 𝑚⁄𝑠 DOĞRUSAL HAREKET ÖRNEK Dairesel hareketi gidip-gelme hareketine çeviren Scotch-yoke mekanizması üzerindeki A noktasının ivmesi 𝑎 = −1.8sin(𝑘𝑡) bağıntısıyla tanımlanmaktadır. 𝑎 𝑣𝑒 𝑡 sırasıyla 𝑚⁄𝑠 ve saniye(𝑠) ve k=3rad/s olarak verilmektedir. t = 0’da x = 0 ve 𝑣 = 0,6𝑚/𝑠 olduğuna göre t = 0,5𝑠 iken A noktasının hız ve konumunu bulunuz. Çözüm 𝑎= 𝑎 = −1.8si n 𝑘 𝑡 𝑣 = 0,6 m/s 𝑑𝑣 ⇒ 𝑑𝑣 = 𝑎𝑑𝑡 𝑑𝑡 𝑣−𝑣 = 𝑎𝑑𝑡 = −1.8 𝑣 − 0.6 = 𝑥 =0 𝑑𝑣 = si n(𝑘 𝑡)𝑑𝑡 = 𝑎𝑑𝑡 1.8 co s(𝑘 𝑡)| 𝑘 1.8 (co s(𝑘 𝑡) − 1) = 0.6co s(𝑘 𝑡) − 0.6 3 𝑣 = 0.6 cos(𝑘𝑡) 𝑚 ⁄𝑠 𝑘 = 3𝑟𝑎 𝑑⁄𝑠 DOĞRUSAL HAREKET Çözüm 𝑣= 𝑑𝑥 ⇒ 𝑑𝑥 = 𝑣𝑑𝑡 ⇒ 𝑑𝑡 𝑥−𝑥 = 𝑥−0= 𝑣𝑑𝑡 = 0.6 𝑑𝑥 = 𝑣𝑑𝑡 co s(𝑘 𝑡)𝑑𝑡 = 0.6 si n(𝑘 𝑡)| 𝑘 0.6 (si n(𝑘 𝑡) − 0) = 0.2si n(𝑘 𝑡) 3 𝑥 = 0.2𝑠𝑖 𝑛(𝑘 𝑡) 𝑚 𝑘𝑡 = (3)(0.5) = 1.5𝑟𝑎𝑑 𝑣 = 0.6𝑐𝑜 𝑠 1.5 = 0.0424𝑚/𝑠 𝑥 = 0.2𝑠𝑖 𝑛(1.5) = 0.1995𝑚 DOĞRUSAL HAREKET ÖRNEK Yandaki Scotch-yoke mekanizmasında A noktasının ivmesi 𝑎 = −1.08sin(𝑘𝑡) − 1.44cos(𝑘𝑡) bağıntısıyla verilmektedir. İvme(𝑎) birimi 𝑚⁄𝑠 - zaman(t) birimi ise saniye(s) ve k=3rad/s şeklinde olduğuna göre 𝑥 = 0.16𝑚 ve 𝑣 = 0.36 𝑚/𝑠 olduğuna göre 𝑡 = 0,5 𝑠’de A noktasının konumunu ve yerini belirleyiniz. Çözüm 𝑎= 𝑎 = −1.08si n( 𝑘 𝑡) − 1.44co s( 𝑘 𝑡) 𝑚⁄𝑠 𝑑𝑣 ⇒ 𝑑𝑣 = 𝑎𝑑𝑡 ⇒ 𝑑𝑡 𝑣 − 0.36 = 𝑑𝑣 = 𝑎𝑑𝑡 𝑣 = 0.36 𝑚⁄𝑠 𝑣 − 𝑣 = −1.08 𝑥 = 0.16 m 𝑘 = 3𝑟𝑎 𝑑⁄𝑠 sin(𝑘𝑡)𝑑𝑡 − 1.44 1.08 1.44 1.08 1.44 co s(𝑘 𝑡)| − si n(𝑘 𝑡)| = (cos3𝑡 − 1) − (sin3𝑡 − 0) 𝑘 𝑘 3 3 𝑣 = 0.36cos3𝑡 − 0.48sin3𝑡 𝑡 = 0.5𝑠 için 0.36 cos 1.5 − 0.48 sin 1.5 𝑣 = −0,453𝑚/𝑠 cos(𝑘𝑡)𝑑𝑡 DOĞRUSAL HAREKET Çözüm 𝑑𝑥 ⇒ 𝑑𝑥 = 𝑣𝑑𝑡 ⇒ 𝑑𝑡 𝑣= 𝑥−𝑥 = 𝑥 − 0.16 = 𝑣𝑑𝑡 = 0.36 𝑑𝑥 = 𝑣𝑑𝑡 co s(𝑘 𝑡)𝑑𝑡 − 0.48 si n(𝑘 𝑡)𝑑𝑡 0.36 0.48 0.36 0.48 si n(𝑘 𝑡)| + co s(𝑘 𝑡)| = (sin(3𝑡) − 0) + (cos(3𝑡) − 1) 𝑘 𝑘 3 3 𝑥 = 0.12si n(3 𝑡) + 0.16co s(3 𝑡) 𝑚 𝑡 = 0.5𝑠 𝑖ç𝑖𝑛 𝑥 = 0.12si n(1.5) + 0.16co s(1.5) = 0.1310 𝑚 DOĞRUSAL HAREKET ÖRNEK Çözüm Bir şilep motorları aniden durduğunda 𝑣 =8 deniz mili hızına sahiptir. Şilebin 𝑣=4 deniz mili hızına erişebilmesi için 𝑡 = 10 𝑑𝑘 geçmektedir. Bu süre içerisinde şilebin aldığı yolu ve hızını zaman cinsinden ifade ediniz. Denizin şilebe uyguladığı kuvvetten dirençten dolayı şilep 𝑎 = −𝑘𝑣 şeklinde bir ivmeye sahiptir. 𝑎 = −𝑘𝑣 = 𝑣 𝑣= 1 + 𝑣 𝑘𝑡 𝑑𝑠 8 𝑣= = 𝑑𝑡 1 + 6𝑡 𝑠= 8 6 𝑑𝑢 𝑢 𝑑𝑣 = −𝑘 𝑣 𝑑𝑣 𝑑𝑡 10 1 𝑡= = 𝑠𝑎𝑎𝑡 60 6 𝑑𝑠 = 4 𝑠 = ln 𝑢 3 4= 8 𝑑𝑡 1 + 6𝑡 1 1 − + = −𝑘𝑡 𝑣 𝑣 𝑑𝑡 ( ⁄ ) 𝑠= ise k=3/4 𝑚𝑖𝑙 8 𝑑𝑡 1 + 6𝑡 4 𝑡 𝑠 = ln(1 + 6𝑡) 0 3 1 1 + 𝑣 𝑘𝑡 = 𝑣 𝑣 𝑣= 1 + 6𝑡 = 𝑢 𝑠 = ln(1 + 6𝑡) 𝑣 8 = 1 + 𝑣 𝑘𝑡 1 + 8 3 𝑡 4 6𝑑𝑡 = 𝑑𝑢 𝑑𝑡 = 𝑑𝑢 6 DOĞRUSAL HAREKET ÖRNEK Bir aerodinamik test neticesinde arabanın hareketine araba fren yaptığı zaman 𝑎 = −𝐶 − 𝐶 𝑣 Şeklinde bir ivme kazandırdığı tespit edilmiştir. Gerçek harekette 𝑡 = 0 anında araba 𝑣 = 𝑣 hızına sahipse motor devreden çıkartıldığı zaman arabanın durabilmesi için gereken mesafeyi beren ifadeyi bulunuz. Çözüm 𝑎𝑑𝑠 = 𝑣𝑑𝑣 𝑠= 𝑠=− − 𝑑𝑢 2𝐶 𝑢 −𝐶 − 𝐶 𝑣 . 𝑑𝑠 = 𝑣𝑑𝑣 1 𝑠=− ln 𝑢 2𝐶 1 𝐶 +𝐶 𝑣 ln 2𝐶 𝐶 +𝐶 𝑣 𝑣=0 𝑠= 𝑠= 𝑠=− 𝑑𝑠 = 1 ln 𝐶 + 𝐶 𝑣 2𝐶 1 𝐶 +𝐶 𝑣 ln 2𝐶 𝐶 +𝐶 𝑣 1 𝐶 +𝐶 𝑣 ln 2𝐶 𝐶 𝑣𝑑𝑣 − 𝐶 +𝐶 𝑣 𝑣 𝑣 𝑢 =𝐶 +𝐶 𝑣 𝑑𝑢 = 2𝐶 𝑣𝑑𝑣 𝑑𝑢 𝑣𝑑𝑣 = 2𝐶 DOĞRUSAL HAREKET ÖRNEK Bir sıvı tankının içerisine bir mermi 𝑣 hızı ile ateşleniyor. Sıvı mermiye bir direnç göstererek 𝑎 = −𝑘𝑣 şeklinde bir ivme kazanmasına neden oluyor. Merminin sıvı içerisinde başlangıç hızının yarısı hıza sahip olduğu anda almış olduğu yolu ve bu yol için gereken 𝑡 zamanını bulunuz Çözüm 𝑎 = −𝑘𝑣 1 𝑣 /2 𝑠 = − ln 𝑣 𝑣 𝑘 𝑑𝑣 𝑎= 𝑑𝑡 𝑣𝑑𝑣 = 𝑎𝑑𝑠 1 𝑣 𝑠 = − ln 𝑘 2𝑣 𝑑𝑣 −𝑘𝑣 = 𝑑𝑡 𝑡= 1 2 1 − 𝑘 𝑣 𝑣 𝑡= 1 𝑘𝑣 −𝑘𝑣 𝑑𝑠 = 𝑣𝑑𝑣 𝑠= 1 𝑑𝑡 = − 𝑘 1 𝑑𝑠 = − 𝑘 / 1 ln 2 𝑘 𝑑𝑣 𝑣 𝑠= 0,693 𝑘 𝑡=− 1 1 − 𝑘 𝑣 𝑣 /2 𝑣 / 𝑑𝑣 𝑣 DOĞRUSAL HAREKET ÖRNEK Aeorodinamik direnç etkisi hesaba katıldığında bir topun ivmesi yukarı doğru hareket ederken 𝑎 aşağı doğru hareket ederken 𝑎 ’dir. Burada k bir sabit olup değeri k=0,0066 (1/m)’dir. Topun fırlatma hızı 𝑣 = 30 𝑚/𝑠’dir. Maksimum h yüksekliğini ve yere çarpma hızını bulunuz. Çözüm 𝑎𝑑𝑠 = 𝑣𝑑𝑣 𝑑𝑢 = 2𝑘𝑣𝑑𝑣 𝑢 = 𝑔 + 𝑘𝑣 ℎ=− 1 ln 𝑔 + 𝑘𝑣 2𝑘 0 𝑣 −𝑔 − 𝑘𝑣 𝑑𝑠 = 𝑣𝑑𝑣 𝑎 𝑑𝑠 = 𝑣𝑑𝑣 𝑣𝑑𝑣 = 𝑑𝑢 2𝑘 1 𝑔 ℎ = − ln 2𝑘 𝑔 + 𝑘𝑣 ℎ=− ℎ=− 𝑑𝑠 = 1 2𝑘 − 𝑣𝑑𝑣 𝑔 + 𝑘𝑣 𝑑𝑢 1 = − ln 𝑢 𝑢 2𝑘 1 9,81 ln 2(0,0066) 9,81 + 0,0066.30 ℎ = 35,87 𝑚 DOĞRUSAL HAREKET Çözüm 𝑎𝑑𝑠 = 𝑣𝑑𝑣 1 −ℎ = ln −𝑔 + 𝑘𝑣 2𝑘 −𝑔𝑒 = −𝑔 + 𝑘𝑣 𝑑𝑠 = 𝑣𝑑𝑣 −𝑔 + 𝑘𝑣 −𝑔 + 𝑘𝑣 1 −ℎ = ln 2𝑘 −𝑔 𝑣 0 𝑣 = 𝑔 − 𝑔𝑒 1 𝑘 −2𝑘ℎ = ln −𝑔 + 𝑘𝑣 −𝑔 𝑣 = 23,68 𝑚/𝑠 DOĞRUSAL HAREKET ÖRNEK Bisikletlerin bazılarında şok emilimini sağlamak için yağ dolu bir silindirde hareket eden bir piston kullanılır. Ön tekerlek bir tümsekten geçtiğinde silindir 𝑣 hızıyla hareket eder. Gidon çatalına takılan piston daha sonra silindire göre hareket eder ve yağ pistonlardaki deliklerden akmaya zorlanır. Bu da piston’un 𝑎 = −kv olacak şekilde yavaşlamasına sebep olur. a) 𝑣 𝑦𝑖 𝑡 𝑐𝑖𝑛𝑠𝑖𝑛𝑑𝑒𝑛 b) 𝑥 𝑖 𝑡 𝑐𝑖𝑛𝑠𝑖𝑛𝑑𝑒𝑛 c)𝑣 𝑦𝑖 𝑥 𝑐𝑖𝑛𝑠𝑖𝑛𝑑𝑒𝑛 ifade ediniz. Çözüm a) b) 𝑎 = 𝑑 𝑣 ⁄𝑑 𝑡 𝑣 𝑒 𝑑𝑥 = 𝑑𝑡 𝑑𝑣 = −𝑘 𝑣 𝑑𝑣 −𝑘𝑣 = 𝑑𝑡 𝑑𝑥 = 𝑣 𝑒 𝑑𝑡 ln 𝑑𝑡 𝑥=− [𝑒 𝑣 = −𝑘𝑡 𝑣 𝑡 ] =− 0 (𝑒 𝑣=𝑣 𝑒 − 1) 𝑥= 𝑣 (1 − 𝑒 𝑘 DOĞRUSAL HAREKET Çözüm c) 𝑎 = 𝑣𝑑 𝑣⁄𝑑 𝑥 −𝑘𝑣 = 𝑣 𝑑𝑣 𝑑𝑥 𝑑𝑣 = −𝑘𝑑𝑥 𝑑𝑣 = −𝑘 𝑣 − 𝑣 = −𝑘𝑥 𝑑𝑥 𝑣 = 𝑣 − 𝑘𝑥 DOĞRUSAL HAREKET ÖRNEK Çözüm İki yay ile zemine tutturulmuş kayar eleman, sürtünmesi ihmal edilebilir yatay kılavuz içinde hareket etmekte ve 𝑠 = 0 𝑣𝑒 𝑡 = 0’da ortadaki konumdan geçerken 𝑠 yönünde 𝑣 hızına sahiptir. İki yay birlikte kayar elemanın hareketine, yer değiştirme ile orantılı fakat ters yönde ve 𝑎 = −𝑘 𝑠 'e eşit ivme veren bir geciktirme kuvveti uygulamaktadır, burada k sabittir. 𝑠 yer değiştirme ve 𝑣 hız bağıntılarını 𝑡'nin fonksiyonu olarak belirleyiniz. 𝑣𝑑𝑣 = 𝑎𝑑𝑠 𝑣= 𝑣𝑑𝑣 = ∫ −𝑘 𝑠𝑑𝑠 𝑣 −𝑘 𝑠 = ∫ 𝑑𝑡 = =− 𝑠 𝑣= 𝑡=∫ 𝑎 −𝑥 x=a. sin 𝝧 𝑏𝑖ç𝑖𝑚𝑖𝑛𝑑𝑒 𝑠= . sin 𝑢 𝑑𝑠 = . cos 𝑢 . du 𝑣 −𝑘 𝑠 DOĞRUSAL HAREKET Çözüm . 𝑡=∫ 𝑠= 𝑡= . . sin 𝑢 1 sin 𝑘 𝑘 𝑠 𝑣 𝑠= . sin 𝑘𝑡 𝑣= 𝑣 −𝑘 𝑠 . 𝑡=∫ 𝑢 = sin 𝑠 𝑘𝑡 = sin 𝑘 𝑠 𝑣 𝑣= 𝑣 𝑣 −𝑘 sin (𝑘𝑡) 𝑘 𝑡= sin 𝑘𝑡 = 𝑘𝑠 𝑣 𝑣 = 𝑣 . cos(𝑘𝑡) DOĞRUSAL HAREKET ÖRNEK 𝑣 hızı ile düşen cisim yaylarla desteklenmiş platforma çarpmakta ve temasını korumaktadır. Çarpmadan sonra cismin İvmesi 𝑎 = 𝑔 − 𝑐𝑦 olup burada c pozitif bir sabittir ve y platformun orijinal konumundan ölçülmektedir. Yayların maksimum sıkışması 𝑦 olarak gözlemleniyorsa c sabitini belirleyiniz. Çözüm 𝑎 = 𝑔 − 𝑐𝑦 = 𝑣 𝑑𝑣 𝑑𝑦 (𝑔 − 𝑐𝑦)𝑑𝑦 = (𝑔𝑦 − 𝑐 𝑔𝑦 − 𝑐 𝑦 )| 2 𝑦 𝑣 =− 2 2 = 𝑣𝑑𝑣 𝑣 | 2 𝑐= 𝑣 + 2𝑔𝑦 𝑦 DOĞRUSAL HAREKET ÖRNEK 𝑣 hızı ile düşen koni, paketlenen malzeme kütlesine çarpmakta ve içine girmektedir. Çarpmadan sonra koninin ivmesi 𝑎 = 𝑔 − 𝑐𝑦 olup 𝑐 pozitif bir sabit ve 𝑦 batma mesafesidir. Maksimum batma derinliği 𝑦 olarak gözlemleniyorsa 𝑐 sabitini belirleyiniz. 𝑎 = 𝑔 − 𝑐𝑦 = 𝑣 (𝑔 − 𝑐𝑦 )𝑑𝑦 = (𝑔𝑦 − 𝑐 𝑔y − 𝑐 𝑦 )| 3 𝑦 𝑣 =− 3 2 = 𝑑𝑣 𝑑𝑦 𝑣 𝑑𝑣 𝑣 | 2 𝑐= 3𝑣 + 6𝑔𝑦 2𝑦