Basınç Ve Akışkan Statiği

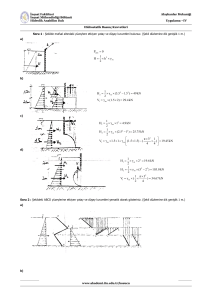
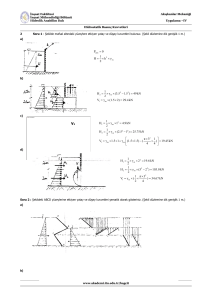
BÖLÜM 3:
BASINÇ VE AKIŞKAN STATİĞİ
BASINÇ NEDİR?
 Bir
akışkan tarafından birim alana
uygulanan normal kuvvete basınç denir
 Basınç birimi N/m2 olup buna pascal (Pa)
denir.
 1 kPa = 103 Pa 1 MPa = 106 Pa
 1 bar = 105 Pa
 1 psi = 0.069 bar
 Binek otomobil lastiği yaklaşık 30 psi = 2
bar
Etkin, mutlak ve vakum basıncı
Bir Noktadaki Basınç
 Akışkan
içerisinde herhangi bir noktadaki
basınç her yönde aynıdır.
 Basıncın büyüklüğü var, ancak yönü
yoktur. Dolayısıyla skaler bir büyüklüktür.
Basınç derinlikle nasıl değişir?
Basınç, akışkan ağırlığının bir sonucudur ve
yerçekimi bulunan bir ortamda sadece düşey
yönde değişir. Basıncın derinlikle değişimi
için yandaki akışkan kütlesine denge şartı
uygulanırsa,
F
z
 maz  0
P2 x  P1x   g xz  0
P  P2  P1   gz   s z
O halde basınç derinlikle doğrusal olarak artar.
Basınç yatay yönde değişmez.
Basıncın derinlikle değişimi

Bir sıvı içerisindeki basınç kabın şeklinden
bağımsızdır.
Pascal İlkesi


Kapalı bir kaptaki
akışkana uygulanan dış
basınç, akışkan
içerisinden her noktadaki
basıncı o oranda artırır.
Pistonları aynı seviyede
alırsak:
F1 F2
F2 A2
P1  P2  


A1 A2
F1 A1

Burada A2/A1 oranına
ideal mekanik fayda adı
verilir.
Manometreler




P1  P2
P2  Patm   gh
Akışkan içerisinde z
kadarlık bir yükseklik farkı
P/g büyüklüğüne
karşılık gelir.
Bu ilkeye göre
tasarlanmış düzenek
veya cihazlara
manometre denir.
Tipik bir manometre
yandaki gibidir.
Büyük basınçlar için
yükseklikten tasarruf
etmek amacıyla civa gibi
yoğun akışkanlar
kullanılır.
Çok Tabakalı Akışkanlar




Her bir sütunun basıncı P = gh
ifadesinden hesaplanır.
Basınç aşağı inildikçe artar (+), yukarı
çıkıldıkça azalır (-).
Aynı akışkanın iki noktası aynı
seviyedeyse, bu iki noktanın
basınçları aynıdır.
Böylece bir noktadan başlayıp gh
terimini aşağı inildikçe ekleyerek,
yukarı çıkıldıkça çıkararak istenen
noktanın basıncı hesaplanabilir:
P2  1gh1  2 gh2  3 gh3  P1
Basınç Düşüşünün Hesaplanması



Basınç düşüşünün
ölçümü en iyi manometre
ile yapılır.
1 noktasından başlanarak
manometre içinden 2
noktasına gelinir. Bu
esnada inerken (+)
çıkarken (-) işaret
kullanılarak P1-P2
hesaplanır.
Borudaki akışkan gaz ise,
2>>1 ve P1-P2= gh
olur.
Barometre
 Barometreler
kullanılır.
açık hava basıncını ölçmede



PC   gh  Patm
Patm   gh
Bu yüzden barometre
basıncına atmosfer basıncı da
denir.
C noktasındaki civa buharının
basıncı çok küçüktür ve sıfır
alınabilir. Dolayısıyla akışkan
sütununun ağırlığı alttan
etkiyen atmosferik basınç
kuvveti ile dengelenmelidir.
Atmosfer basıncı yükseklere
çıkıldıkça düşer ve bunun
birçok etkisi olur: pişirme
süresi, burun kanaması, motor
performansı, uçakların
performansı vb..
YÜZEYLERE GELEN HİDROSTATİK
KUVVETLER
Atatürk Barajı (Şanlıurfa)
DÜZ YÜZEYLER

Düz yüzeye gelen hidrostatik
kuvvetler bir paralel kuvvetler
sistemi oluşturur.

Amacımız bu tür yüzeylere gelen
hidrostatik kuvvetleri ve etki
noktalarını (basınç merkezi BM)
belirlemektir.

Yüzeyin her iki yanına da etkimesi
halinde atmosfer basıncının etkisi
dikkate alınmaz. Böylece sadece
etkin basınçla çalışmış oluruz.
Şekil 3-24
Düz Yüzeye Gelen Kuvvet

Plaka üzerinde herhangi bir noktadaki basınç
P  P0   gh  P0   gy sin 
FR   PdA   ( P0   gy sin  )dA  P0 A   g sin   ydA
A
A
Ağırlık merkezinin tanımından:
1
yc   ydA
AA
A
Bileşke Kuvvet
FR  ( P0   gyc sin  ) A  ( P0   ghc ) A  Pc A  Port A
Homojen (sabit yoğunluğa sahip) bir sıvıya tamamen
daldırılan düz bir yüzey üzerine etki eden bileşke kuvvet,
yüzeyin kütle merkezindeki basınç ile yüzeyin alanının
çarpımına eşittir (Şekil 3–27).
Bileşke Kuvvetin Yeri



Bileşke kuvvetin etki çizgisi ile yüzeyin
kesişme noktasına BM denir.
Yüzeyin kütle merkezi ile BM, alan yatay
olmadıkça üst üste çakışmaz.
BM, moment alınarak bulunur:
y p FR   yPdA   y ( P0   gy sin  )dA
A
A
 P0  ydA   g sin   y 2 dA
A
A
 P0 yc A   g sin  I xx ,O
Alan 2. momenti veya alan
atalet momenti
BM’nin hesabı
Çeşitli kaynaklarda verilen atalet momentleri alanın kütle
merkezinden geçen eksene göre tanımlıdır (burada ise
eksen takımı alanın kütle merkezinden geçmemektedir)
 Ancak Paralel Eksen Teoremi ile bu sorun da kolaylıkla
aşılabilir:

I xx,O  I xx,c  yc A
2
Böylece BM:
y p  yc 
Ancak
I xx,c
 yc  P0 /(  g sin  ) A
P0  0
ise;
y p  yc 
I xx ,c
yc A
Bazı düz yüzeyler ve özellikleri
Basınç Prizması: Geometrik yol

Düz bir yüzey üzerine etki eden
kuvvetler, tabanı (sol yüz)
yüzeyin alanı, yüksekliği de
basınç olan bir hacim meydana
getirir.

Bu prizmanın hacmi, istenen
bileşke kuvveti, kütle merkezinin
yüzey üzerindeki izdüşümü ise bu
kuvvetin etki noktasını verir.
Bazı Özel Durumlar
Örnek: Batmış Bir Arabanın Kapısına
Etkiyen Hidrostatik Kuvvet
Ağır bir araba, kaza sonucu göle uçarak
tekerlekleri üzerinde gölün tabanına
çökmüştür (Şekil 3–31). Arabanın
kapısı 1.2 m yüksekliğinde ve 1 m
eninde olup üst kenarı suyun serbest
yüzeyinden 8 m aşağıdadır. Kapı
üzerindeki hidrostatik kuvveti ve
basınç merkezinin konumunu
belirleyerek sürücünün kapıyı açıp
açamayacağını tartışınız.
Kabuller
1 Göl tabanı yataydır.
 2 Yolcu kabini içeri su sızdırmayacak şekilde iyi
yalıtılmıştır.
 3 Arabanın kapısı dik bir dikdörtgensel plaka olarak
düşünülebilir.
 4 İçeri su girmediği için kabin içerisindeki basınç
atmosferik olarak kalmakta ve dolayısıyla içerdeki
havanın sıkışması söz konusu değildir. Bu yüzden,
kapının her iki tarafına da etkimesinden ötürü atmosferik
basınç hesaplamalarda dikkate alınmaz.
 5 Arabanın ağırlığı, üzerine etkiyen kaldırma kuvvetinden
daha fazladır.

Çözüm
Port  Pc   ghc   g (s  b / 2)


1kN
2
 (1000 kg/m )(9.81m/s )(8  1.2 / 2 m) 

84.4
kN/m

2 
1000
kg.m/s


3
2
FR  Port A  (84.4kN/m2 )(1m 1.2m)  101.3kN
b
b2
1.2
1.22
yp  s  
 8

 8.61m
2 12( s  b / 2)
2 12(8  1.2 / 2)
EĞRİSEL YÜZEYLER
FH  Fx
FV  Fy  W
FR  FH2  FV2


Eğrisel yüzey üzerine etkiyen hidrostatik kuvvetin yatay
bileşeni, yüzeyin düşey izdüşümüne etki eden hidrostatik
kuvvete eşittir (hem büyüklük hem de etki çizgisi olarak).
Eğrisel yüzey üzerine etkiyen hidrostatik kuvvetin düşey
bileşeni, yüzeyin yatay izdüşümüne etki eden hidrostatik
kuvvet ile akışkan bloğunun ağırlığının toplamına (zıt
yönde etkiyorsa, farkına) eşittir.
Eğrisel Yüzeyler

Eğrisel yüzey sıvı üzerinde
kalıyorsa, sıvı ağırlığı ve
hidrostatik kuvvetin düşey
bileşeni zıt yönlerde etkir
FH  Fx
FV  Fy  W
Basınç kuvvetlerinin yüzeye dik
olması ve hepsinin de
merkezden geçmesinden ötürü,
dairesel bir yüzey üzerine etki
eden hidrostatik kuvvet daima
dairenin merkezinden geçer.
Çok tabakalı akışkanların düz
yüzey üzerine etkisi
FR   FR,i   Pc,i Ai
Çok tabakalı bir akışkan içerisinde dalmış bir yüzey üzerindeki
hidrostatik kuvvet, farklı akışkanlar içerisinde kalan yüzeyleri ayrı
ayrı göz önüne almak suretiyle belirlenebilir
Örnek 3-9

A noktasından mafsallı 0.8 m yarıçapında uzun bir silindir, Şekil 3–
36’da görüldüğü gibi otomatik kapak olarak kullanılmakta olup su
seviyesi 5 m’ye ulaştığında kapak A noktasındaki mafsal etrafında
açılmaktadır. (a) Kapak açıldığında silindir üzerindeki hidrostatik
kuvveti ve etki çizgisini ve (b) silindirin 1 metre uzunluğunun
ağırlığını belirleyiniz.
Örnek 3-9: ÇÖZÜM
Yatay kuvvet:
FH  Fx  Port A   ghc A   g (s  R / 2) A


1kN
 (1000 kg/m )(9.81m/s )(4.2  0.8 / 2 m)(0.8m 1m) 
 36.1 kN
2 

 1000 kg.m/s 
3
2
Düşey kuvvet:
Fy  Pave A   ghc A   ghtaban A


1kN
 (1000 kg/m3 )(9.81m/s 2 )(5m)(0.8m 1m) 
 39.2 kN
2 

 1000 kg.m/s 
Örnek 3-9: ÇÖZÜM
Akışkan bloğunun 1 m uzunluğunun ağırlığı (aşağı yönlü):
W  mg   g (hacim)   g ( R2 -  R2 / 4)(1m)  1.3 kN
Düşey yöndeki net kuvvet:
FV  Fy  W  39.2 1.3  37.9kN
Bileşke kuvvet:
FR 
FH 2  FV 2 
36.12  37.92  52.3kN
Kapak açılmak üzereyken tabanda tepki kuvveti
yoktur. Mafsala göre moment alınarak;
FR R sin  - Wsilindir R  0
Wsilindir  FR sin   (52.3kN)sin 46.40  37.9kN
Kaldırma Kuvveti
ARCHIMEDES İLKESİ
Bir akışkan içerisinde daldırılan cisim üzerine etki
eden kaldırma kuvveti, cisim tarafından yeri
değiştirilen akışkanın ağırlığına eşittir ve bu
kuvvet, yer değiştiren hacmin kütle merkezi
boyunca etkir.
FK  Falt - Füst  a g (s  h) A - a gsA  a ghA  a g ( Hacim)
Yüzen Cisimler:
FK  W
Örnek 3-40: Hidrometre
(a) Bir sıvının bağıl yoğunluğunu, saf suya karşılık
gelen işaretten itibaren ∆z mesafesinin
fonksiyonu olarak veren bir bağıntı elde ediniz.
(b) 1 cm çapında ve 20 cm boyunda olan bir
hidrometrenin saf su içerisinde yarısı batmış
olarak yüzmesi için (10 cm çizgisinde) içerisine
konulması gereken kurşun kütlesini belirleyiniz.
Önce suda sonra da sudan daha hafif bir
sıvıda yüzme şartı yazılır ve birbirine
eşitlenirse:
Whidro  FK , su   su g (hacim)bat   su gAz0
Whidro  FK ,a   su g (hacim)bat   su gA( z0  z )
b , a 
 akışkan
 su

z0
z0  z
RİJİT CİSİM HAREKETİ
Bu tür bir harekette kayma gerilmesi
oluşmaz. Dolayıyla akışkana
etkiyen yalnızca kütle ve basınç
kuvvetleridir. Sadece z yönü için bu
kuvvetlerin gösterildiği diferansiyel
hacim elemanı alalım ve Newton’un
2. yasasını uygulayalım:
 F   m  a   (dx dy dz)  a
 Fs, z
P dz 
P dz 
P


 P
 dxdy   P 
 dxdy   dxdydz
z 2 
z 2 
z


 Fs , x
P

dxdydz
x
 Fs , y
P
  dxdydz
y
Rijit Cisim Hareketi
Toplam yüzey (basınç) kuvveti:




 F s   Fs, x i   Fs, y j   Fs, z k

 P  P  P  
 
i
j
k  dxdydz    P dxdydz
y
z 
 x
Kütle kuvveti:



 F B , z   g m k    g dxdydz k





 F   F S   F B  ( P   g k ) dxdydz 


 m  a   (dx dy dz )  a

 P   g k   a
TEMEL DENKLEM
Özel Durumlar:
Denklemin açık hali:




P  P  P 
i
j
k   g k    (a x i  a y j  a z k )
x
y
z
Özel Durum 1: Statik haldeki akışkanlar
P
   ax  0
x
P
  ay  0
y
Özel Durum 2: Serbest düşme
P P P


0
x y z
az   g
P
  g
z
Doğrusal Yörünge Üzerinde Sabit
İvmeli Hareket
Doğrusal bir yörünge üzerindeki hareketi xzdüzleminde inceleyeceğiz P=P(x, z)=?:
P
   ax
x
P
   ( g  az )
z
P
P
dP ( x, z ) 
dx 
dz
x
z
dP    ax dx   ( g  az )dz
P
0
y
Doğrusal hareket
Sonlu büyüklükler cinsinden iki nokta arasındaki basınç farkı:
P    ax x   ( g  az )z
Veya;
P2  P1    ax ( x2  x1 )   ( g  az )( z2  z1 )
Orijin (z= 0 ve x = 0) noktasındaki basınç
P0
alınırsa, herhangi bir noktadaki basınç;
P  P0   ax x   ( g  az ) z
Yüzeyin eğiminin belirlenmesi
1 ve 2 noktalarının her ikisi de serbest
yüzeyde seçilirse dP = 0 olacaktır.
dP    ax dx   ( g  az )dz  0
Buradan,
dzizobar
ax

  tan   sabit
dx
g  az
Bu tür hareketlerde de sıvı kütlesinin korunduğu unutulmamalıdır.
Örnek 3-12
80 cm yüksekliğinde ve 2 m  0.6
m kesit alanında kısmen suyla
doldurulmuş bulunan bir balık
tankı bir kamyonun arkasında
taşınacaktır (Şekil 3–52). Tank
0 km/h’den 90 km/h hıza 10
saniyede ivmelenmektedir. Bu
ivmelenme sırasında tanktan
su boşalması istenmemesi
halinde, tanktaki başlangıç su
yüksekliğini belirleyiniz. Tankın
uzun veya kısa kenarının
hangisinin hareket
doğrultusuyla paralel olarak
hizalanmasını önerirsiniz?
Çözüm
Tanker sadece x-yönünde ivmelenmektedir.
V
(90  0) km/h  1m/s 
2
ax 
=

  2.5 m/s
t
10s
 3.6 km/h 
ax
2.5
tan  

 0  0.255
g  az 9.81
Durum 1: Uzun kenar hareket doğrultusunda:
zs1  (b1 / 2) tan = (2m) / 2  0.255  0.255m
Durum 2: Kısa kenar hareket doğrultusunda:
zs 2  (b2 / 2) tan = (0.6m)/2  0.255  0.076m
Silindirik Kapta Dönme
ar  r , az  a  0  P  P(r, z)
2
P
P
dP(r , z ) 
dr  dz
r
z
P
   ar
r
P
   ( g  az )    g
z
dP(r, z)   r dr   gdz
2
Yüzeyin şekli
Serbest yüzeyde dP = 0 alınırsa:
dP(r, z)   r dr   gdz  0
2
2
2 2
dzizobar
r
 r

z
 C1
dr
g
2g
Serbest yüzey paraboliktir !.. Şekilde r = 0 için z = h c= C 1olduğundan,
zs 

2
2g
r  hc
2
Oluşan hacim ve özellikleri
Taşma olmaması halinde (son hacim) = (ilk hacim) olacağından;
2 2
 2 2




R
2
   2 zs rdr  2  
r  hc rdr   R 
 hc    R 2 h0
2g

 4g

r 0
r 0 
R
R
Böylece en düşük derinlik:
Yüzeyin denklemi:
hc  h0 
zs  h0 
2
4g
 2 R2
4g
( R 2  2r 2 )
Maksimum yükseklik farkı:
zs,maks  zs ( R)  zs (0) 
2
2g
R2
Basınç dağılımı
r2
2
 dP(r, z)    r
1
r1
P2  P1 
 2
2
z2
2
dr    gdz
z1
(r22  r12 )   g ( z2  z1 )
Eğer (r, z) = (0, 0) noktasındaki basınç P0 alınır ve 2 noktası herhangi
bir nokta olarak düşünülürse;
P  P0 

2
2
r   gz
2
ÖRNEK 3-13 Bir sıvının dönme sırasında
yükselmesi
Şekil 355’te gösterilen 20 cm çapında, 60
cm yüksekliğindeki düşey silindir,
yoğunluğu 850 kg/m3 olan bir sıvıyla 50
cm yüksekliğine kadar kısmen
doldurulmuştur. Silindir sabit bir hızla
döndürülmektedir. Sıvının kap
kenarlarından taşmaya başlayacağı
dönme hızını belirleyiniz
ÇÖZÜM
Dönen düşey silindir tabanının merkezini orijin (r = 0, z = 0)
alındığında sıvı serbest yüzeyinin denklemi;
zs  h0 
2
4g
( R 2  2r 2 )
Buna göre kap çeperindeki su yükselmesi r = R alınarak,
zs  h0 
 2 R2
4g
Su dökülme seviyesine ulaştığında z = 60 cm = 0.60 m
olacağından;
0.60  0.50 
 2 0.12
4  9.81
   19.8 rad/s = 189 devir/dakika
Kap tabanının orta noktasının kuru kalması için devir sayısı ne olmalı dersiniz?
EES Ne İşe Yarar?
Örnek 2-72
T, K
273.15
278.15
283.15
293.15
303.15
313.15
333.15
353.15
373.15
µ, Pa · s
1.787  10-3
1.519  10-3
1.307  10-3
1.002  10-3
7.975  10-4
6.529  10-4
4.665  10-4
3.547  10-4
2.828  10-4
Suyun dinamik viskozitesinin mutlak sıcaklık ile değişimi yukarıdaki
tabloda verilmiştir. Tablodaki değerleri kullanarak viskozite için
 = (T) = A + BT + CT2 + DT3 + ET4 formunda bir bağıntı geliştiriniz.
Geliştirdiğiniz bağıntıyı kullanarak suyun 50C’de 5.468  10-4 Pa  s
olması gerektiği bildirilen viskozitesini hesaplayınız. Elde ettiğiniz sonucu
 = D  eB/T ile verilen Andreas denkleminin sonucuyla karşılaştırınız (bu
ifadedeki D ve B değerleri, tablodan verilen viskozite verileri kullanılarak,
bulunacak olan sabitlerdir).
ÇÖZÜM
Adım 1: EES ekranında mu = a+T şeklinde rastgele bir fonksiyon
tanımla (mu=viskozite, a=katsayılar, T = sıcaklık)
Adım 2: Tables menüsünden “new parametric table” seç ve verilen
tablo değerlerini iki sütun halinde gir.
0.0018
0.0016
Adım 3: “Plot” menüsünden “X-Y plot” seç.
0.0014
0.0012
0.001
Adım 4: “Plot” menüsünden “curve-fit” seç
0.0008
0.0006
0.0004
0.0002
270
292
314
336
T
= 0.489291758 - 0.00568904387T + 0.0000249152104T2 - 4.8615574510-8T3 + 3.5619807910-11T4
 = 0.000001475*EXP(1926.5/T)
Andreas denklemi
358
380
Eksenleri belirliyoruz.