1. BÖLÜM
VEKTÖRLER
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
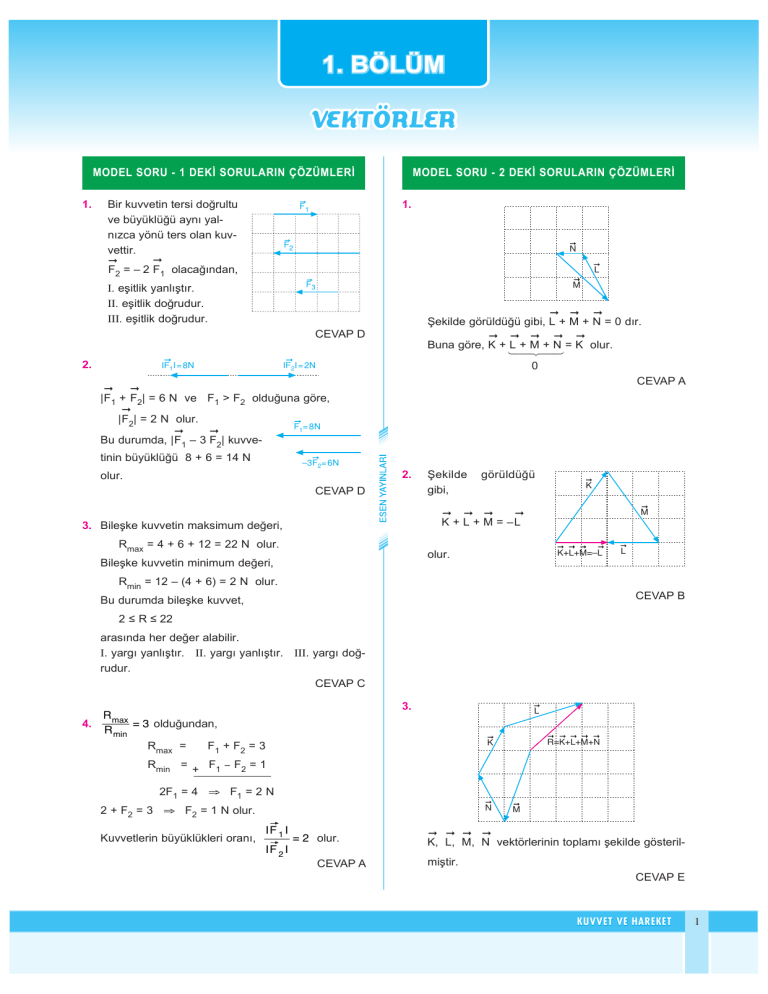
Bir kuvvetin tersi doğrultu
ve büyüklüğü aynı yalnızca yönü ters olan kuvvettir.
F2 = – 2 F1 olacağından,
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
1.
F1
F2
N
L
M
F3
I. eşitlik yanlıştır.
II. eşitlik doğrudur.
III. eşitlik doğrudur.
Şekilde görüldüğü gibi, L + M + N = 0 dır.
Buna göre, K + L + M + N = K olur.
14243
0
CEVAP A
CEVAP D
2.
IF1I= 8N
IF2I= 2N
| F1 + F2| = 6 N ve F1 > F2 olduğuna göre,
| F2| = 2 N olur.
F1= 8N
Bu durumda, | F1 – 3 F2| kuvvetinin büyüklüğü 8 + 6 = 14 N
–3F2= 6N
olur.
2.
CEVAP D
Şekilde
gibi,
görüldüğü
K
M
K + L + M = –L
3. Bileşke kuvvetin maksimum değeri,
Rmax = 4 + 6 + 12 = 22 N olur.
K+L+M=–L
olur.
Bileşke kuvvetin minimum değeri,
Rmin = 12 – (4 + 6) = 2 N olur.
L
CEVAP B
Bu durumda bileşke kuvvet,
2 ≤ R ≤ 22
arasında her değer alabilir.
I. yargı yanlıştır. II. yargı yanlıştır. III. yargı doğrudur.
CEVAP C
3.
R max
= 3 olduğundan,
4.
R min
Rmax =
L
R=K+L+M+N
K
F1 + F2 = 3
Rmin = + F1 − F2 = 1
2F1 = 4 ⇒ F1 = 2 N
N
2 + F2 = 3 ⇒ F2 = 1 N olur.
Kuvvetlerin büyüklükleri oranı,
IF 1 I
IF 2 I
= 2 olur.
CEVAP A
M
K, L, M, N vektörlerinin toplamı şekilde gösterilmiştir.
CEVAP E
KUVVET VE HAREKET
1
4. Şekilde görüldüğü gibi,
K+L+N+P+M=M
14243
0
8.
K
N
M
Şekilde görüldüğü
gibi, K noktasal
cismi +y yönünde
hareket eder.
+y
–x
+x
F1 R
•
olur.
F2
P
L
CEVAP D
F3
F4
–y
CEVAP C
5.
Şekilde
görüldüğü
M
gibi, I ve II eşitlikleri
K+M=N
K
doğru, III eşitliği yan-
L
lıştır.
+y
K
K+L=–2M
9.
N
L
Şekilde görüldüğü gibi, K noktasal cismi +x
yönünde hareket
eder.
F4
F3
•
K
–x
R
+x
F2
N+L=–M
F1
CEVAP C
–y
CEVAP A
10. K + L = M dir.
6.
K
I. eşitlik doğrudur.
M + P = – N dir.
K
L
II. eşitlik doğrudur.
K + L + N + P = 0 dır.
R=K+L+M+N+P
P
M
N
M
P
L
III. eşitlik doğrudur.
N
CEVAP E
11.
F4
K, L, M, N, P vektörlerinin toplamı şekilde gös-
R
F2
terilmiştir.
CEVAP B
•
K
Fd
F1
F3
7.
K
Şekilde görüldüğü gibi, F4 kuvveti kesikli çizgilerle
gösterilen kuvvetlerden 2 numaralı kuvvettir.
CEVAP B
L
K+L=–M
|K+L|=|M|
K
K+L+M=0
–L
L
KUVVET VE HAREKET
F3
F1
F2
K
K
Şekilde görüldüğü gibi; I, II ve III eşitlikleri doğrudur.
CEVAP E
2
12. F4 kuvveti şekilde gösterildiği gibidir.
F4
CEVAP A
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
1.
RK =
2F =
2 .4
RM =
3F =
3 . 8 olur.
4.
4
IF2I = 12v2 N
45°
4
IF3I = 7v3 N
60°
RK ve RM taraf tarafa oranlanırsa,
RK
=
RM
4
IF1I = 15N
37°
O
4
2 .4
2
6
1
=
=
=
olur.
6
3 .8 2 3
6
IF4I = 7v3 N
F1 ve F2 kuvvetlerini bileşenlerine ayıralım.
CEVAP A
F1x = 15 . cos37°
12N
9N
= 15 . 0,8
2.
= 12 N
3F
4F
F1y = 15 . sin37°
R
12N
12N
4
= 15 . 0,6
45°
F
K
F1 +F2 =21N
=9N
v2F
F
4
3F
3F
F2x = 12 2 .
2
= 12 N
2
F2y = 12 2 .
2
= 12 N
2
F
Önce 2 F kuvvetini bileşenlerine ayıralım. Daha
sonra zıt kuvvetler çıkarılır.
Bileşke kuvvetin büyüklüğü,
daki açı 60° olduğundan bu
21N
F3 ve F4 kuvvetleri eşit ve ara-
iki kuvvetin bileşkesi,
R2 = (3F)2 + (4F)2 ⇒ R = 5F olur.
CEVAP D
3 . ^7 3 h = 21N olur.
R34 =
•
30°
Şekildeki kuvvetler eşit ve
21N
aradaki açı 120° olduğundan
3.
Fx= 5N
İlk olarak 5v2 N luk kuv-
45°
45°
veti dik bileşenlerine ayıralım.
Fy= 5N
F1 , F2 , F3 ve F4 kuvvetlerinin bileşkesi, R = 21 N
olur.
CEVAP E
|F|= 5 2N
5.
F1x = F1 . cos37° = 5 . 0,8 = 4 N
2
= 5N
2
2
Fy = F . sin45° = 5 2 .
= 5N
2
Fx = F . cos45° = 5 2 .
F1y = F1 . sin37° = 5.0,6 = 3 N
F2 = 5v2 N ise, açı 45° olduğundan,
Şimdi tüm kuvvetlerin toplamını kolaylıkla bulabiliriz.
8N
3N
Bileşke kuvveti bulmak için önce 5 N ve 5v2 N luk
kuvvetleri bileşenlerine ayırmak gerekir.
F2x = 5 N ve
F2y = 5 N olarak yazılabilir.
3N
R
7N
1N
2N
4N 5N
5N
2N
4N
5N
5N
Bileşke kuvvetin büyüklüğü,
4N
R
Bileşke kuvvet,
R2 = 32 + 42 ⇒ | R| = 5 N olur.
CEVAP C
R2 = 22 + 42 ⇒ R = 2v5 N olur.
CEVAP C
KUVVET VE HAREKET
3
6.
10.
k
4N
F1
F
Fk=5N
F3x
60°
F2x
4N
53° 53°
60°
30°
4N
F2y
F
3N
F2
F3
Bir kuvvetin bileşenleri alınırken, kuvvetin ucundan
eksenlere paraleller çizilir. Bu paralellerin eksenleri kestiği noktalar kuvvetin bileşenleridir.
3N
F3y
F2 ve F3 bileşenlerine ayrılırsa, bileşke kuvvet, 2N
olarak bulunur.
CEVAP C
Buna göre,
30, 60, 90 üçgeninden 30° → Fk = 5 N ise,
90° → F, = 10 N
60° → F = 5v3 N olur.
11.
F3
CEVAP E
7.
IF1I = 8N
M
α
K cisminin y doğrultusunda hareket edebilmesi
için F kuvvetinin Fx bileşeni,
F1 =8 N
M
α
α
Fx = 4 – 1 = 3 N olmalıdır.
F kuvvetinin büyüklüğü,
Fx = F . sin37°
3 = F . 0,6
F = 5 N olur.
8.
CEVAP D
y
•
18N
•
x
K
x
10N
| F3| = | R| = 10 N olur.
Şekil-II de F3 kuvveti ters çevrildiğinde M cismine
etki eden bileşke kuvvet,
| RM| = F1 + F2 + F3
= 10 + 10
= 20 N olur.
20N
fiekil-I
fiekil - ΙΙ
Şekil-I de M cismi hareketsiz kaldığından,
R=10 2N olur.
10N
6N
F3 = 10 N
F1 ve F2 kuvvetlerinin bileşkesi,
R2 = (8)2 + (6)2
R2 = 100 ⇒ R = 10 N olur.
24N
K
F2 =6 N
fiekil - Ι
y
8N
IRI = 10 N
IF2I = 6N
fiekil-II
Şekil-II de görüldüğü gibi, K noktasal cismine etki
CEVAP C
eden bileşke kuvvetin büyüklüğü 10 2 N olur.
CEVAP C
12.
9.
Şekilde görüldüğü
gibi, K noktasal
cismine etki eden
bileşke
10N
10N
olur.
5F
|F1|=10N
30°30°
kuvvetin
büyüklüğü
60°
|F3|=10N
K•
R=10N
CEVAP B
KUVVET VE HAREKET
60°
•
K
60°
3F
60°
x
60°
30°
2F
2F
60°
R=2F
60°
|F2|=20N
4
2F
y
4F
Şekilde görüldüğü gibi, K noktasal cismine etki
eden bileşke kuvvetin büyüklüğü R = 2F dir.
CEVAP A
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
1.
4.
K + L – M = 2K
123
K
4
IF1I = 3f
4
R12
37°
2K
K
olur.
IF3I = 6f
127°
53°
4
Şekilde görüldüğü gibi,
L
153°
–M
4
IF2I = 4f
F1 ve F2 kuvvetlerinin bileşkesi,
CEVAP D
2 = (3f)2 + (4f)2
R12
4
IF3I = 6f
R12 = 5f dir.
4
R nin büyüklüğü,
| R| = F3 – F1 – F2
| R| = 5f + 6f
| R| = 11f olur.
4
I–F1 – F2I = 5f
CEVAP E
2.
5.
|F1+F2|=r
|F1|=r
|F2|=r
30°
60° 60°
Şekilde görüldüğü gibi, M
vektörü Şekil-II de gösterilen vektörlerden 2 numaralı vektöre eşittir.
–L
K
K–L
L
L–M
30°
–M
|F3|=r
CEVAP B
Önce kuvvetler arasındaki açıyı bulalım.
α + 2α + 2α + α = 180°
6α = 180°
α = 30° olur.
| F1+ F2| = | F3| = r dir.
R nin büyüklüğü,
R = F1 + F2 − 3 F3
R = r − (−3r)
R = 4r olur.
3.
CEVAP E
6.
K
K–R
R
K
–N
L
L
R1=K+L
R2=M–N
M+R
M
R
L
R3=L–M
P
–M
Şekilde görüldüğü gibi, |R2| = |R3| > |R1|
CEVAP A
N
M–N
M
Şekilde görüldüğü gibi, II ve III vektörleri M – N
vektörüne eşittir.
CEVAP D
KUVVET VE HAREKET
5
5.
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
1.
Küpün kenar uzunluğu a ise hacmi V = a3 olur. Bu
durumda bir kenarın uzunluğu,
V = a3
A vektörünün büyüklüğü,
2
2
2
64 = a3 ⇒ a = 4 cm
2
olur. Bu değer bir vektörün ( Rw) bileşenlerine eşit
| A | = k + , = 3 + 4 = 5 br olur.
B vektörünün büyüklüğü,
| B |=
2
2
2
2
k +, +m =
2
olduğundan bu vektörün büyüklüğü,
| R|2 = a2 + a2 + a2
| R|2 = 42 + 42 + 42
| R| = 4v3 cm olur.
2
3 + 4 + 5 = 5 2 br
olur. Taraf tarafa oranlandığında,
|A |
5
1
=
=
olur.
5
2
2
|B|
CEVAP C
CEVAP A
2.
A vektörü A = 2 a + b + c şeklinde tanımlandığından büyüklüğü,
|A |=
=
2
2
(2a) + b + c
2
2
2
(2.2) + 3 + 5
2
= 50
= 5 2 br olur.
CEVAP C
3.
A vektörünün büyüklüğü
| A|2 = A2x +A2y +A2z
| A|2 = 62 +82 + 102
| A|2 = 200
| A| = 10v2 br olur.
6.
y
c
8br
6br
x
c
c
x
c
z
z
a , b ve c vektörleri küpün kenar uzunlukları olduğundan büyüklükleri birbirine eşittir.
| a| = | b| = | c|
II. ifade doğrudur.
a + b ≠ c olduğundan III. eşitlik yanlıştır.
CEVAP D
KUVVET VE HAREKET
B
c
x
I. ifade doğrudur.
Şekilde a, b ve c vektörleri üç boyutlu olduğundan
üçüde birbirine diktir.
a⊥b⊥c
6
A
10br
CEVAP B
4.
y
y
A ve B vektörlerinin tüm bileşenlerinin büyüklük
leri birbirine eşit olduğundan A ve B vektörlerinin
büyüklükleri,
|A |=
| B |=
2
2
2
2
c +c =
2c
2
c +c +c =
3c
eşitlikleri taraf tarafa oranlanırsa,
|A |
=
|B|
2c
=
3c
2
olur.
3
CEVAP B
TEST
1.
1
ÇÖZÜMLER
K = – M dir.
5.
VEKTÖRLER
K
I. eşitlik doğrudur.
|N| = |2 L| dir.
–L
M–L
II. eşitlik doğrudur.
M – L ! K dır.
M
–L
III. eşitlik yanlıştır.
K–L+M=5br
CEVAP C
2.
M
L+N=2M
1birim
M–K=L
L
K
–K
K+L=M
Şekilde görüldüğü gibi, K – L + M vektörünün
büyüklüğü 5 birimdir.
CEVAP A
N
L
1birim
M
N–M=K
–M
6.
L
L–M=–K
N
K
K–2L=–M
–M
Şekilde görüldüğü gibi, L – M = – K dır.
2L
CEVAP B
M
–N
3.
K
M
M
M–N=K
N
M–N=–2K
2L
L
+M=
L
N+2L=–2K
K
Şekilde görüldüğü gibi; I, II ve III eşitlikleri doğrudur.
CEVAP E
–N
K+L=N
K
Şekilde görüldüğü gibi; I, II ve III eşitlikleri doğrudur.
CEVAP E
7.
➞
F5
➞
4.
F4
L
K
➞
K
L+N=–M
L
➞
➞
N
K+L=N
R
F3
F1
➞
F2
K
–M
K–M=2N
Şekilde görüldüğü gibi; I, II ve III eşitlikleri doğrudur.
CEVAP E
Şekilde görüldüğü gibi, K noktasal cismi F3 kuvveti
doğrultusunda hareket eder.
CEVAP C
KUVVET VE HAREKET
7
8.
12.
➞
F1
➞
F3
➞
F2
➞
F2
➞
F4
K
➞
➞
F1
F3
K
➞
➞
R
➞
F4
F5
Şekilde görüldüğü gibi, F4 kuvveti kesikli çizgiler-
Şekilde görüldüğü gibi, K noktasal cismi F2, F4
le gösterilen kuvvetlerden 5 numaralı kuvvettir.
kuvvetlerinin bileşkesi yönünde hareket eder.
CEVAP E
CEVAP C
9.
13.
➞
F5
➞
F1
➞
➞
F2
F4
➞
➞
K
R
➞
F3
F2
➞
➞
R
K
F1
➞
F3
Şekilde görüldüğü gibi, F4 kuvveti kaldırılırsa, K
noktasal cisminin hareket yönü değişmez.
CEVAP D
10. F1 ve F3 kuvvetleri-
le gösterilen kuvvetlerden IV numaralı kuvvettir.
CEVAP D
➞
IF2I=2F
nin bileşkesi F olur.
➞
Bu durumda bileşke
F
➞
IF1I= F
kuvvet,
Şekilde görüldüğü gibi, F3 kuvveti kesikli çizgiler-
α
R = 2 F = 20 N olur.
2α
14. 2 N luk kuvvet bileα
➞
IF3I=F
F2 kuvveti,
IF4I= F
6v2N
ayrıldıktan
sonra zıt yönde olan
2N
kuvvetler çıkarılır.
➞
| F2| = 2F = 20N olur.
şenlere
v2N
CEVAP A
11.
➞
L
F3
Bileşke kuvvet,
➞
F2
2
R2 = (3 2 ) + (4 2 )
Ι
➞
➞
F4
F1
K
le gösterilen kuvvetlerden I numaralı kuvvettir.
CEVAP A
KUVVET VE HAREKET
R2
= 18 + 32
R2
= 50
4v2N
K
3v2N
2
4v2N
➞
R
R = 5 2 N olur.
Şekilde görüldüğü gibi, F4 kuvveti kesikli çizgiler-
8
v2N
45°
45°
3v2N
CEVAP B
TEST
1.
2
VEKTÖRLER
ÇÖZÜMLER
3.
Üç kuvvetin minimum değeri,
➞
F1
Rmin = 8 – (3 + 4)
=8–7
= 1 N olur.
➞
F2
K
➞
Üç kuvvetin maksimum değeri,
R
➞
Rmax = 8 + 3 + 4
= 15 N olur.
F3
Şekilde görüldüğü gibi, F3 kuvveti kesikli çizgiler-
Bileşke kuvvet,
le gösterilen kuvvetlerden 2 numaralı kuvvettir.
Rmin ≤ R ≤ Rmax
CEVAP B
1 ≤ R ≤ 15
arasında olacağından 0 olamaz.
CEVAP A
4.
➞
F4
➞
F1
➞
K
➞
F3
2.
Verilen kuvvetlerin doğruluğunu
uç uca ekleme metodunu kulla-
Şekilde
F1
F2
➞
F2
görüldüğü
gibi, F4 kuvveti Şekil II de
gösterilen kuvvetlerden 3 numaralı kuvvettir.
F4
narak inceleyelim.
P
R
CEVAP C
F3
F5
I.
F1 + F3 = F2
F1 + F2 + F3 = 2 F2
4
4
F1
I. yargı yanlıştır.
F2
4
F3
II.
F1 + F3 + F4 + F5 = 0
F1 + F2 + F3 + F4 + F5 = F2
5.
kuzey
700m
400m
bat›
II. yargı yanlıştır.
400m
güney
4
III. F1 + F4 + F5 = – F3
F1
III. yargı doğrudur.
4
4
F4
F3
4
F5
Bu durumda yalnız III. yargı doğrudur.
do¤u
Yer değiştirmeleri vektörel olarak gösterecek olursak,
(∆x)2 = (700 - 400)2 + (400)2
∆x2 = (300)2 + (400)2
∆x2 = 250000 ⇒ ∆x = 500 m olur.
CEVAP C
CEVAP D
KUVVET VE HAREKET
9
6.
9.
➞
F2
➞
➞
➞
➞
F3
F1
F3
F1
➞
➞
F3
F1
R
➞
K
➞
➞
0
F2
–R
F2
➞
0
F4
➞
R
➞
F4
fiekil-Ι
Şekilde görüldüğü gibi; F1, F2, F3, F4 kuvvetleri
fiekil-ΙΙ
Şekil II de görüldüğü gibi, F4 kuvveti 5 numaralı
kuvvettir.
nin bileşkesi R dir. Bu kuvvetlerden F1 ve F4 kuvvetleri kaldırılırsa cisim yine aynı yönde hareket
CEVAP E
eder.
CEVAP D
10. F5 kaldırıldığında cismin hızının ve yönün
nasıl
F2
F1
değişeceğini
görebilmek için bileş
ke kuvveti bulup F5
F5
R
F3
F4
ile kıyaslamak gerekir. Bileşke kuvveti uç
7.
uca ekleme metodu ile +x yönünde 1 birim olarak
bulunur. F5 kaldırılırsa bileşke kuvvet +x yönünde
➞
F3
2 birim olur. Bu da cismin hareket yönünün değişmeyip, hızının artacağını gösterir.
➞
CEVAP E
F5
K
➞
F4
➞
F1
Şekilde görüldüğü gibi; F1, F3, F4, F5 kuvvetleri
nin bileşkesi sıfırdır. Buna göre, F2 kuvveti kaldırıldığında cisim sabit hızla harekete devam eder.
CEVAP B
11.
8.
➞
F3
x+ y
Tanımlanan x ve y vektörlerini z =
vektö4
➞
ründe yerine yazarsak,
z=
➞
F2
➞
F1
( F 1 + 2 F 2 + F 3) + ( F 1 + 2 F 2 + 3 F 3)
4
➞
➞
F2+F3
➞
F1+F2
➞
F2
➞
➞
F2+F3
➞
F1
F
z = 1 + F 3 vektörü bulunur.
2
Bu durumda z vektörü Şekil - II
de gösterilen I nolu vektördür.
F1
2
z
F3
KUVVET VE HAREKET
Şekilde görüldüğü gibi, F1 + F3 kuvveti Şekil II deki
kesikli çizgilerle gösterilen II vektörünün doğrultu-
CEVAP A
10
➞
F3
sundadır.
CEVAP B
12. K noktasal cismi
dengede olduğundan
cisme
4
14.
4
F3
F2
z
IF2I = 4N
etki
eden net kuvvet
α β
sıfırdır. Kuvvet vek-
K
yatay
törel büyüklük oldu-
y
ğundan,
F2 + F3 = – F1
IF3I = 12N
4
x
F1
olur.
I. yargı doğrudur.
IF1I = 3N
F1 + F2 + F3 toplamının büyüklüğü,
F2 . sinβ = F3 . sinα tür.
II. yargı yanlştır.
α > β ise bileşke kuvvet büyük kuvvete daha yakın
olduğundan | F2| > | F3| tür.
2
2
2
2
2
R=
F1 + F2 + F3
=
3 + 4 + 12
2
= 9 + 16 + 144
III. yargı doğrudur.
CEVAP D
= 169
= 13 N olur.
CEVAP A
13.
kuzey
F1
K
bat›
do¤u
F2
F3
güney
F2 ve F3 kuvvetleri şekildeki kuvvetler seçildiğinde cisme etki eden net kuvvet sıfır olur ve cisim
kuzey - doğu yönünde sabit hızla hareket edebilir.
F2 ve F3 kuvvetlerinin bileşkesi – F1 eşittir.
I. yargı doğrudur.
F2 ve F3 kuvvetlerinin bileşkesinin x bileşeni –1
birimdir.
II. yargı doğrudur.
F1 kuvveti kaldırıldığında cisim güney - batı yönünde hareket etmez.
III. yargı yanlıştır.
CEVAP C
KUVVET VE HAREKET
11
TEST
1.
3
VEKTÖRLER
ÇÖZÜMLER
Bileşke kuvvet
v 3F olduğuna
p
4.
F
m
3f
göre aralarındaki
açı 60° dır. Aradaki
açı
30°
60°
120°
k
olduğunda bileş-
f
60°
ke kuvvet,
3f
K
•
F
60°
l
30° 30°
R
F
R = F olur.
n
2f
120°
Önce zıt olan 3f ile f nin bileşkesi alınır. 2f kuvvet-
F
leri arasındaki açı 120° olduğundan bileşke kuvvet
CEVAP A
m yönünde,
3f – 2f = f olur.
CEVAP C
2.
y
4
4
F1
F2
2
4
F3
1
K
x
4
F4
5
4
5.
3
F1
F1y
Cismin y doğrultusunda ha- reket edebilmesi için
bileşke kuvvetin x bileşeni sıfır olmalıdır.
30°
Bu koşulu sağlayan kuvvet, kesikli çizgilerle gösterilen kuvvetlerden 4 numaralı kuvvettir.
CEVAP D
F2
F1x
F1 in iki bileşeni vardır. Birisi F1x, diğeri ise F1y dir.
Bu durumda bileşke kuvvet F1y ye eşit olur.
F1y = R
F1 . cos30° = 20
F1.
3.
3
40
N
= 20 ⇒ F1 =
2
3
➞
F1
F2 kuvvetinin büyüklüğü,
➞
F3
➞
F2
F2 = F1x
➞
F4
K
= F1 . sin30°
Şekilde görüldüğü gibi F4 kuvveti kesikli çizgilerle
=
40 . 1
3 2
gösterilen kuvvetlerden III numaralı kuvvettir.
=
20
N olur.
3
CEVAP C
12
KUVVET VE HAREKET
CEVAP B
6.
9.
➞
+y
F4
➞
F2
F5
➞
R
R
➞
m
F1
➞
–x
➞
F3
F2
m kütleli noktasal cisim şekildeki R bileşke vektörü
yönünde hareket eder.
F1 ve F3 kuvvetleri kaldırıldığında cismin hareket
yönü değişmez.
+x
F3
F5
F4
–y
F1, F2, F3, F4, F5 kuvvetleri etkisinde K cismi +y
yönünde hareket eder.
Bir süre sonra F1 kuvveti kaldırılırsa, cisim +y
yönünde harekete devam eder, hareket yönü
değişmez.
CEVAP A
CEVAP B
7.
•
K
F1
K
L
M
–N
10.
Şekilde görüldüğü gibi,
➞
➞
F2
F1
0
K + L – N + M = M olur.
123
➞
K
0
CEVAP C
➞
F3
➞
L
8.
3F ile 4F kuvvetlerinin bi-
4F
5F
leşkesi, 5F olur. Bileşke
Şekilde görüldüğü gibi, öteki iki kuvvet Şekil-II de
verilen kuvvetlerden K ve L kuvvetleridir.
3F
kuvvetin 4F ile yaptığı açı
CEVAP A
37°, 3F ile yaptığı açı 53°
olur. 3F ile 5F aynı yönlü
37°
53°
olduğundan bu iki kuvvetin
67°
3F
bileşkesi 8F olur.
11.
K
60°
|F1| = 20N
3 0°
F2
3 0°
8F
F3 60°
8F
Bu kuvvetin diğer 8F ile
Verilen kuvvetler eşkenar üçgen oluşturduğundan,
| F1| = | F3| = |2 F2| olur.
arasındaki açı,
53° + 67° = 120°
olduğundan, bileşke kuv-
60°
R
60°
vet, R = 8F olur.
K
8F
CEVAP D
Bu durumda,
| F3| = 20 N, | F2| = 10 N olur.
F1 + F3 = 2 F2 ⇒ | F1 + F3| = 20 N olur.
| F1 + F2 + F3| = 20 + 10 = 30 N olur.
CEVAP D
KUVVET VE HAREKET
13
12.
14. Şekildeki tüm kuvvetler arasındaki açı 90°
dir. 6 N ile 8 N kuvvetlerinin bileşkesi 10 N
dur. 10 N ile 24 N kuvvetleri birbirine diktir.
F1
F2
F4
R
•
F3
K
2
fS
6N
8N
24N
R2 = (10)2 + (24)2
R2 = 100 + 576
R2 = 676
Şekilde görüldüğü gibi, cisme etki eden sürtünme
kuvveti 2 numaralı kuvvettir.
CEVAP B
13.
F3
F1
F1–F2
F1
F1+F3
F2
F4
F2
F1
F3
R
Fd
I. yol:
Dengeleyici kuvvet bileşkeye eşit ve zıt yöndeki
kuvvettir.
Şekilde görüldüğü gibi, F4 kuvveti kesikli çizgilerle
gösterilen 5 numaralı kuvvetir.
II. yol:
x
____
y
____
R = F1 + F2 + F3 + F4:
–2
2
F1 + F3 :
2
1
+
F2 :
–2
0
___________________________________
Son iki eşitlik (–) ile çarpılıp toplandığında F4 kuvveti elde edilir.
x
y
____
____
F1 + F2 + F3 + F4 :
–2
2
– F1 + F3 :
–2
–1
+
– F2 :
+2
0
___________________________________
F4 :
–2
1
olur. Buda 5 nolu kuvvettir.
CEVAP E
14
KUVVET VE HAREKET
R = 26 N olur.
CEVAP E
Adı ve Soyadı : .....................................
1.
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
Bölüm
Yazılı Soruları
(Vektörler)
Önce F3 vektörünü bileşenlerine ayıralım.
F
3x
= 8 2 . cos45°
F3 = 8v2N
2
=8 2.
2
= 8N
F
3y
= 8 2 . sin45°
=8 2.
= 8N
➞
➞
b) F3 ile F4 arasındaki açı 90°
ve büyüklükleri eşit olduğundan,
F3y =8N
➞
➞
R = 16 N olur.
b) R =
➞
–
➞
F2
8N
R=16N
8N
8N
c) F1 ile F4y birbirini götürür.
F1 + F4 = F4x
| F1 + F4| = | F4x| = 3 N
➞
8N
8N
8N
➞
F2
+
➞
F3
R=16v2N 16N
8N
olur.
c) R =
8N
+ F3
R = 16v2 N
➞
–
d) R =
➞
+
➞
F2
F4y =3N
–
d) | F3 + F4 − F2| = 6 + 4
8N
F3
F4
= 10 N
R=16N
R = 16 N olur.
F4=3v2N
8N
8N
➞
F3
F4x =3N
8N
➞
F1
8N
➞
F1
|F1|=3N
olur.
16N
R = 0 olur.
➞
F4
= 6 N olur.
➞
➞
F1
F3 +F4
| F3 + F4| = v2 . 3v2
F3x = 8N
a) R = F1 + F2 + F3
➞
F3
F3 + F4 vektörünün büyüklüğü;
45°
45°
2
2
ÇÖZÜMLER
–F2
F3 + F 4
olur.
8N
8N
|F3 + F4|=6N
|–F2|=4
8N
2.
a) F1 ile F2 arasındaki açı 90° olduğundan Pisagor teoremi kullanılarak bileşke bulunabilir.
| F1 + F2|2 = F12 + F22
F1 =3N
| F1 + F2|2 = 32 + 42
| F1 + F2|2 = 9 + 16
F 1 +F 2
2
| F1 + F2| = 25
F2 = 4 N
| F1 + F2| = 5 N olur.
3.
Kuvvetler arasındaki açı 3θ = 360° ⇒ θ = 120° dir.
a)
F3
F1+ F3
60°
60°
F2
F1
F1 + F3 = − F2 ⇒ F1 + F2 + F3 = 0 olur.
KUVVET VE HAREKET
15
b)
4.
F3
20v2 N luk kuvvetlerin
y
R=40N
arasındaki açı 90° oldu–F2
60°
ğundan bileşke kuvvetin
F2
60°
20v2N
20v2N
büyüklüğü 40 N olup, +y
–F3
F1
45°
yönündedir.
45°
30N
x
θ
4
Çizimden de görüldüğü gibi,
F
− F2 + (− F3) = F1
a) Görüldüğü gibi F kuv-
F1 + (− F2 − F3) = 2 F1 olduğundan
–F2
2F1 -F2
b) tani =
30N
θ
4
F
30 3
= & i = 37° olur.
40 4
2F1
2 F1 ile − F2 kuvvetleri arasındaki açı 60° dir.
|2 F1 − F2|2 = (2F)2 + (F)2 + 2.(2F).(F).cosθ
|2 F1 − F2|2 = (2.4)2 + (4)2 + 2.(2.4).4.cos60°
= 64 + 16 + 64 .
5.
1
2
60°
➞
F1
➞
F4
➞
➞
F3
F2
Şekilde görüldüğü gibi, F4 kuvveti kesikli çizgilerle
gösterilen kuvvetlerden 2 numaralı kuvvettir.
= 112 ⇒ |2 F1 − F2| = 4v7 N olur.
d)
➞
R
K
= 80 + 32
–
θ
yüklüğü 50 N a eşittir.
| F| = 50 N olur.
F2
60°
R=50N
veti dengeleyici kuvvet olduğundan bü-
| F1 − F2 − F3| = |2 F1| = 8 N olur.
c)
40N
F2
F3
2
F 2–
F3
2
F
F
F
I F2 − 3 I2 = (F2)2 + ( 3 )2 + 2.F2. 3 cos60°
2
2
2
= (4)2 + (2)2 + 2 . 4 . 2 .
= 16 + 4 + 8
6.
➞
F1
1
2
➞
F2
0
➞
➞
K
F4
F3
= 28
F
I F2 − 3 I = 2v7 N olur.
2
16
KUVVET VE HAREKET
Şekilde görüldüğü gibi, F4 kuvveti kesikli çizgilerle
gösterilen kuvvetlerden 5 numaralı kuvvettir.
7.
–R
K
K
R
F4
F3
F1
F1
F3
F2
F2
fiekil-Ι
fiekil-ΙΙ
Şekil-II de görüldüğü gibi, F4 kuvveti kesikli çizgilerle gösterilen kuvvetlerden 1 numaralı kuvvettir.
10. F2 ve F4 kuvvetleri zıt yönlü
ol duk la rın dan
ikisinin bileşkesi
5 N, F1 ve F3
kuv vet le ri zıt
yönlü olduklarından bu ikisinin bileşkesi de
5 N olur.
4
y
IF3I=5N
4
IF4I=5N
4
IF2I=10N
x
z
4
IF1I=10N
8.
Önce zıt yönlü kuvvetlerin
30N
20N
Eğer θ açısı 0° olursa,
=
2
(20) + (15)
•
R = 5 2 N olur.
bileşkesini bulalım.
R=
5N
Bu iki kuvvet arasındaki açı 90°
olduğundan bileşke kuvvet,
5N
4
R
10N
2
20
R
625
= 25 N olur.
15
Eğer θ açısı 90° olursa,
20
15
R = 20 + 15 = 35 N olur.
Öyleyse bileşke kuvvetin büyüklüğü 25 < R < 35
değerleri arasındadır.
9.
4
F1
4
F2
M
1
2
3
4
Cismin +x yönünde hareket
edebilmesi için y doğrultusundaki net kuvvetin sıfır olması gerekir. 1 nolu kuvvet
uygulandığında cisim –x yönünde hareket edebiliceğinden 1 nolu kuvvet üçüncü
kuvvet olamaz.
5
2
2
3
2
1
KUVVET VE HAREKET
17
18
KUVVET VE HAREKET
2. BÖLÜM
BAĞIL HAREKET
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
3.
I. yol:
kuzey
VL=5m/s
kuzey
VLK
45°
5m/s 15m/s
L
bat›
VLK=10m/s
VML=20m/s
VKy=15m/s
do¤u
K
VKx=20m/s
37°
bat›
do¤u
VK=25m/s
güney
M
L aracının yere göre hızı 5 m/s dir.
II. yol:
güney
20m/s
K aracı L aracını kuzey
batıya gidiyormuş gibi
gördüğüne göre, L ye
göre K nin kuzey ve batı
hız bileşenleri eşittir. Bu
durumda L nin hızı,
20 = VL + 15
VL = 5 m/s olur.
K aracındaki gözlemci L aracını kuzeye doğru
10 m/s hızla hareket ediyormuş gibi görür.
CEVAP B
53°
VK=25m/s
15m/s
15m/s
.
VL
20m/s
25m/s
CEVAP A
4.
bat›
K
2.
do¤u
•
L
2V
kuzey
yatay
yol
L
K
V
V
bat›
M
M
V
do¤u
VML = VM – VL
3V = VM – 2V
VM = 5V, doğuya doğru
VKM = VK – VM
–6V = VK – 5V
VK = –V, batıya doğru
güney
K aracının hızı doğuya doğru V dir.
VKM = VK – VM
K aracındaki gözlemci L aracını,
VLK = VL – VK
=V–V
= 2V – (–V)
=0
= 2V + V
M aracındaki gözlemci K yi duruyormuş gibi görür.
CEVAP E
= 3V, doğuya doğru gidiyormuş gibi görür.
CEVAP C
KUVVET VE HAREKET
19
5.
(–) bat›
8.
do¤u (+)
•
K
kuzey
Vo=20m/s
Vç=5m/s
VM VMK
yatay yol
VK
VML
bat›
do¤u
VL
Çocuğun yere göre hızı,
VLK
Vçyer = Vo + Vç
= 20 + 5
güney
= 25 m/s olur.
Şekilde görüldüğü gibi,
L aracındaki yolcu çocuğu 10 m/s hızla batıya doğ-
K deki gözlemci L yi güneybatıya doğru gidiyor-
ru gidiyormuş gibi gördüğüne göre, kendi hızı,
muş gibi görmez.
VçyerL = Vçyer – VL
I. yargı yanlıştır.
–10 = (5 + 20) – VL
L deki gözlemci M yi kuzeye doğru gidiyormuş gibi
VL = 25 + 10
görür.
VL = 35 m/s, doğuya doğru olur.
II. yargı doğrudur.
CEVAP E
M deki gözlemci K yi doğuya doğru gidiyormuş gibi
6.
görür.
kuzey
III. yargı doğrudur.
CEVAP D
bat›
do¤u
•
VL=V
VK=Vv2
VLK=V
güney
K aracındaki gözlemci L yi batıya doğru V hızıyla
gidiyormuş gibi görür.
CEVAP A
9.
VK
7.
VM
kuzey
VML
VK=V
VLK
VL
VLK= 2V
VL=V
bat›
do¤u
VML=V
Şekilde görüldüğü gibi, M aracının yere göre hız
vektörü VM Şekil-II de gösterilen vektörlerden 1
VM= 2V
güney
Şekilde görüldüğü gibi, L deki gözlemci M yi güneye doğru V hızıyla gidiyormuş gibi görür.
CEVAP B
20
KUVVET VE HAREKET
numaralı vektöre eşittir.
CEVAP A
10.
kuzey
VK
VLK
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
VL
1.
VKN
konum
VN
bat›
do¤u
VML
2x
K
VM
x
güney
L
0•
Şekilde görüldüğü gibi,
K deki gözlemci L yi doğuya doğru gidiyormuş gibi
t
2t
zaman
3t
–x
görür.
Konum-zaman grafiğinde doğrunun eğimi hızı
verir. K ve L nin hızları,
I. yargı doğrudur.
L deki gözlemci M yi güneye doğru gidiyormuş gibi
görür.
VK =
2x – (–x) 3x x
Tx
=
=
= & VK = 3V, doğuya
3t – 0
3t
t
Tt
VL =
Tx
0 – x –x
=
=
& VL = –V, bat›ya olur.
3t – 0 3t
Tt
II. yargı doğrudur.
N deki gözlemci K yi kuzeydoğuya doğru gidiyormuş gibi görür.
K aracındaki gözlemciye göre L aracının hızı,
III. yargı doğrudur.
VLK = VL – VK
CEVAP E
= –V – 3V
= –4V
batıya doğru olur.
CEVAP E
2.
Araçların üçü de aynı
yönde ve aynı hızla
hareket etmektedir.
Üçünün de t süredeki
yer
değiştirme
miktarları eşittir.
∆x K = ∆x L = ∆x M = x
tir.
konum
2x
K
x
L
zaman
0•
–x
t
M
I. yargı doğrudur.
II. yargı yanlıştır.
VKL = VL – VK = 0
olduğundan, K aracındaki gözlemci L yi duruyor
görür. III. yargı doğrudur.
CEVAP C
KUVVET VE HAREKET
21
3.
5.
x(m)
hız
2V •
80 •
K
V• L
0•
L
•t
•
2t
K
K
•
zaman
3t
0•
•4
L
0-t zaman aralığında K ve L araçları arasındaki
t(s)
–40 •
uzaklık artmaktadır. K aracı L den uzaklaşmakta
dır.
I. yargı doğrudur.
Dx
V =
eşitliğinden K ve L araçlarının hızlarının
Dt
t-2t zaman aralığında K ve L araçları arasındaki
büyüklüğü,
uzaklık azalmaktadır. L deki gözlemci K yi yaklaşı-
80 – 0
80
=
= 20 m/s
4–0
4
0 – (–40)
40
VL =
=
= 10 m/s olur.
4
4–0
VK =
yor görür.
II. yargı doğrudur.
2t-3t zaman aralığında K ve L araçları arasındaki
K aracındaki gözlemciye göre L nin hızı,
VLK = VL – VK
uzaklık artmaktadır. L aracı K den uzaklaşmaktadır. K deki gözlemci L yi uzaklaşıyor görür.
= 10 – 20
III. yargı doğrudur.
= –10 m/s olur.
CEVAP E
K deki gözlemci L yi batıya doğru 10 m/s hızla
hareket ediyormuş gibi görür.
CEVAP B
6.
hız
2V •
K
4.
Araçlar +x yönünde
hareket etmektedir.
I. yargı doğrudur.
∆xK = x – 0 = x
K
0-t aralığında K ve
t
K
•t
•
2t
•
3t
zaman
uzaklık artmaktadır. K aracı L den uzaklaşmaktadır. L deki gözlemci K yi uzaklaşıyor görür.
I. yargı doğrudur.
L
olur.
L
0-t zaman aralığında K ve L araçları arasındaki
zaman
0
∆xL = x – (–x) = 2x
II. yargı yanlıştır.
0•
x
0-t aralığında,
L
V•
konum
t-2t zaman aralığında K ve L araçları arasındaki
uzaklık artmaktadır. K aracı L den uzaklaşmakta-
–x
dır. L deki gözlemci K yi uzaklaşıyor görür.
L araçları arasındaki
uzaklık azalmaktadır. K aracındaki gözlemci L yi
II. yargı yanlıştır.
2t-3t zaman aralığında K ve L araçları arasındaki
yaklaşıyor görür.
uzaklık azalmaktadır. L aracı K ye yaklaşmaktadır.
III. yargı doğrudur.
CEVAP C
K deki gözlemci L yi yaklaşıyor görür.
III. yargı yanlıştır.
CEVAP A
22
KUVVET VE HAREKET
3.
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
1.
k›y›
L
k›y›
5V
K•
•
Va=3m/s
•M
.
d2
V
B
A
37°
•
K
k›y›
d1
∆x
V
120m
Va=V
L
•.
xB
xA
Motorların suya göre hızları,
k›y›
tA =
Yüzücünün K den M ye gidiş süresi, M den L ye
dönüş süresine eşit olduğundan,
12 =
d 1 + d 2 (5V + V) .t
=
d2
(5V – V) .t
d
V
120
V
V = 10 m/s olur.
B motorunun karşı kıyıya ulaşma süresi,
d1 + d2 6 3
= =
d2
4 2
tB =
2d 1 + 2d 2 = 3d 2
d
120
120
=
=
= 20 s olur.
V. sin 37°
10.0, 6
6
Motorlar karşı kıyıya ulaştıklarında aralarındaki
2d 1 = d 2
uzaklık,
d1 1
= olur.
d2 2
∆x = xB – xA
= (V.cos37° + Va).tB – Va.tA
CEVAP B
= (10.0,8 + 3).20 – 3.12
= 220 – 36
= 184 m olur.
CEVAP D
4.
2.
sol
sa¤
V=5m/s
Vy
37°
Vx
Va
37°
.
K
k›y›
d
120
120
=
=
= 40 s olur.
V. sin 37° 5.0, 6
3
Yüzücünün karşı kıyıya çıktığı noktanın L noktasına uzaklığı,
k›y›
Yüzücünün hızı,
t=
Yüzücünün karşı kıyıya çıkma süresi,
t=
V
Va=3m/s
.
k›y›
40m
60m
K
P
.
k›y›
L
.
120m
L
20 =
d
V. sin 37°
60
V.0, 6
V = 5 m/s olur.
Yüzücü yatayda |LP| = 40 m lik yolu alacağından,
x = (V.cos37° – Va).t
ILPI = (Va – V.cos37°).t
= (5.0,8 – 3).40
40 = (Va – 5.0,8).20
= (4 – 3).40
2 = Va – 4
= 40 m olur.
Va = 6 m/s olur.
Yüzücü L nin 40 m soluna çıkar.
CEVAP D
CEVAP D
KUVVET VE HAREKET
23
5.
L
k›y›
.
8.
Va=5m/s
VA
A
.
37°
4m/s
37°
➞
Va=3m/s
4m/s
3m/s
k›y›
4m/s
K
4m/s
5m/s
B
k›y›
.
5m/s
100m
VB=5m/s
3m/s 3m/s
L
3m/s
V2=5m/s
K
k›y›
M
I. motorun K noktasından L noktasına gidiş ve
dönüş süresi eşit olup,
A yüzücüsünün suya göre yataydaki hızı akıntının
hızından küçük olduğundan L nin sağına çıkar.
100
= 25 s olur.
4
I. motorunun aynı noktaya geliş süresi 50 s olur.
xA = (5 – 4).20 = 20 m olur.
t=
B yüzücüsünün yere göre yatay hızı 4 m/s olur.
Yüzücünün yere göre hızı verildiğinden akıntının
hızı dikkate alınmaz.
ı
II. motor K den M ye t sürede giderse dönüş süreı
si (50 – t ) saniye olur.
B yüzücüsünün yatayda aldığı yol,
IKMI uzaklığı,
xB = 4.20 = 80 m olur.
ı
IKMI = (5 + 3).t = 8tı
İki yüzücü arasındaki uzaklık,
ı
8t = (5 – 3)(50 – tı)
∆x = xB – xA
ı
ı
8t = 2.(50 – t )
= 80 – 20
ı
4t = 50 – t
= 60 m olur.
ı
ı
5t = 50
CEVAP A
ı
t = 10 s
6.
L
IKMI = 8tı = 8.10 = 80 m olur.
k›y›
M
CEVAP E
B
VB=6m/s
9.
VA
M
Va
A
L
N
V2
P
R
S k›y›
Va
53°
k›y›
K
V1
İki yüzücünün de yatayda aldıkları yollar eşit olduğundan,
2
Va
1
6 + Va = VA.0,6 + Va
Şekilde görüldüğü gibi, 2 motoru karşı kıyıya R
noktasında çıkar.
CEVAP D
6 = 0,6 VA
VA = 10 m/s olur.
CEVAP C
10.
L
k›y›
k›y›
K
(VB + Va).t = (VA.cos53° + Va).t
7.
Vb2
Vb1
kuzey
M
2V
2v2V
bat›
A
VB
2V
motor
do¤u
B
k›y›
K
N
P
R
S
T
Akıntının hızı şekilde görüldüğü gibi yatayda
| Va| = 3 br olur. A motoru M noktasında karşı kıyıya çıktığı anda B motoru P noktasında bulunur.
CEVAP B
24
araç
Va
VA
KUVVET VE HAREKET
güney
Motorun yere göre hızı batıya doğru 2V dir.
Araçtaki gözlemci motoru güneybatı yönünde
2v2V hızıyla gidiyor gibi görür.
CEVAP D
11.
k›y›
L
M
.
N
Va=2m/s
60m
VM=5m/s
Vy
37°
.
k›y›
Vx
K
Motorun karşı kıyıya çıkma süresi,
t=
d
60
60
=
=
= 20 s olur.
VM . sin 37°
5.0, 6
3
|KM| uzaklığı,
IKMI = VM.t = 5.20 = 100 m olur.
|LN| uzaklığı,
ILNI = (VM.cos37° + Va).t
= (5.0,8 + 2).20
= 6.20
= 120 m olur.
|KM| ve |LN| taraf tarafa oranlanırsa,
IKMI 100 5
=
=
olur.
ILNI 120 6
CEVAP E
12.
R
S
N
T
k›y›
P
M
V2
Va
Vb2
Va
Vb1
V1
2
1
K
L
k›y›
Şekilde görüldüğü gibi, 1 motoru M noktasına geldiği anda, 2 motoru S noktasında bulunur.
CEVAP D
KUVVET VE HAREKET
25
TEST
1
BAĞIL HAREKET
ÇÖZÜMLER
1.
M
4.
kuzey
L
VK=v2V
VMK
VM=V
bat›
Va
120m
VL=V
V
V.sin37°
do¤u
VML=2V
.
37°
V.cos37°
güney
t=
ediyormuş gibi görür.
20 =
CEVAP C
V=
d
V. sin 37°
120
V.0, 6
6
= 10 m/s olur.
0, 6
Yüzücü karşıda L noktasına çıktığına göre, yatay
hızının bileşkesi sıfır olmalıdır.
Va – V.cos37° = 0
Va – 10.0,8 = 0
Va = 8 m/s olur.
CEVAP B
M nin yere göre hız vektörü Şekil-II deki vektörV2
lerden 5 tir.
V1
VL
5.
x1
k›y›
x3
L
x2
VK
VM
V3
Va
V2
CEVAP E
Va
Va
•
K
x 1 = 4 br _b
b
x 2 = 2 br ` x 1 = x 3 > x 2 olur.
b
x 3 = 4 br b
a
3.
kuzey
6.
VK
VM
bat›
VML
VLK
VK
VL
do¤u
VL
CEVAP B
kuzey
VLK
VML
Va
V1
k›y›
VM
k›y›
K
Motorun suya göre hızı,
L hareketlisi M yi 2V hızıyla batıya doğru hareket
2.
k›y›
.
bat›
do¤u
güney
güney
Şekilde görüldüğü gibi, M deki gözlemci yalnız L
ye bakarak kendisini kuzeye doğru gidiyormuş gibi
algılar.
CEVAP A
26
KUVVET VE HAREKET
Şekilde görüldüğü gibi, M deki gözlemci yalnız L
ye bakarak kendisini batıya doğru gidiyormuş gibi
algılar.
CEVAP A
7.
10.
x2
x1
L
k›y›
VKL=V
VL=V
Va
V2
L
II
Va
kuzey
Va
K
60°
60°
V1
VK=V
60°
bat›
do¤u
I
•
K
k›y›
güney
x1 = 2 br
L aracındaki gözlemci K yi doğuya doğru V hızıyla
x2 = 4 br olduğundan,
gidiyor gibi görür.
x1
2 1
= =
olur.
4 2
x2
CEVAP C
CEVAP D
8.
k›y›
Va=3m/s
A
V
V
B
M
K
•
11. Motorun karşı kıyıya
ulaşma süresi,
d
t=
VM
bağıntısından bulu-
L
k›y›
K
t artınca, motorun karşı kıyıya ulaştığı noktanın L
ye uzaklığı artar.
II. yargı doğrudur.
VM azalınca, şekle göre motorun yere göre hızının
büyüklüğü azalır.
A motorundaki gözlemciye göre B nin hızı,
V = VB – V A
BA
V = –15 – 15 = –30 m/s
BA
I VBAI = 30 m/s olur.
CEVAP E
M
k›y›
Va=3m/s
120m
III. yargı yanlıştır.
CEVAP B
L
12.
x
.
P
k›y›
Va
4x
VM=10m/s
8m/s
53°
V
Vb
.
ILPI = Va.t dir.
3V – 9 = 2V + 6
V = 15 m/s olur.
60m
Va
➞
I. yargı doğrudur.
V+3 3
=
V–3 2
L
.
k›y›
VM
VM azalırsa, motorun karşı kıyıya
ulaşma süresi artar.
Motorlar M noktasında karşılaştığına göre motorların hızı,
(V + Va) .t x A
=
(V – Va) .t x B
P
.
d
nur.
k›y›
9.
L
6m/s
.
k›y›
K
|KL| ve |LP| uzaklıklarını oranlarsak, akıntının hızı;
.
k›y›
K
Motorun karşı kıyıya çıkma süresi,
ILMI = Va.t
60 = 3.t
t = 20 s olur.
10.0, 8
4
=
1 Va – 10.0, 6
4
8
=
1 Va – 6
Motorun suya göre hızı,
V=
d
120
=
= 6 m/s olur.
t
20
VM . sin 53°.t
4x
=
(Va – VM . cos 53°) .t
x
Va – 6 = 2
CEVAP A
Va = 8 m/s olur.
CEVAP D
KUVVET VE HAREKET
27
TEST
1.
2
BAĞIL HAREKET
ÇÖZÜMLER
K aracına bakan L aracındaki gözlemci, kendi aracını batıya doğru gidiyormuş gibi algıladığına göre
gözlenen kendisidir.
VLK = VL – VK
VLK = 0 – 2V = –2V olur.
4.
kuzey
bat›
do¤u
O
VK=V
güney
Şekilde görüldüğü gibi, L aracındaki gözlemci M
aracını doğuya doğru V hızı ile gidiyor gibi görür.
II. yargı yanlıştır.
VLK = –V – 2V = –3V olur.
CEVAP A
III. yargı doğru olabilir.
CEVAP D
5.
k›y›
L
IVaI=3m/s
|Va|=3m/s
80m
|Vb1|=4m/s
|V1|=5m/s
|V2|=4m/s
53°
M
L
N
P
R
k›y›
M
K
k›y›
1 motorunun karşıya çıkma süresi,
d
80
t=
=
= 20 s olur.
Vb1
4
Va
Va
VM=Vv2
VL=V
I. yargı doğru olabilir.
VLK = 3V – 2V = V olur.
2.
VML=V
VLK=Vv2
VM
VM
Bu sürede 2 motorunun yatayda aldığı yol,
|KM| = (V2 + Va).t
k›y›
K
= (4 + 3).20
Motor suya göre aynı hızla K den L ye doğru hare-
= 140 m olur.
CEVAP C
ket ederse, karşı kıyıya NP arasında çıkar.
CEVAP B
6.
M
L
k›y›
Va
X
(Vs)yer Y
Z
kuzey
3.
VK=V
VLK=V
K
O
do¤u
VM=V
X, Y ve Z yüzücüleri karşı kıyıya ayna anda çıkarlar.
I. yargı doğrudur.
Y ve Z yüzücüleri karşı kıyıya aynı noktada çıkarlar.
II. yargı doğrudur.
VMK=Vv2
güney
Şekle göre, I., II. ve III. yargılar doğrudur.
CEVAP E
KUVVET VE HAREKET
k›y›
VL=Vv2
VML=V
bat›
28
Va
X ve Z yüzücülerinin yere göre hızlarının büyüklükleri eşittir.
III. yargı doğrudur.
CEVAP E
7.
M
N
P
R
10.
k›y›
konum
3x
K
2x
L
Va
➞
VA
➞
VB
A
zaman
0•
Va
t
M
–x
B
K
–2x
k›y›
L
N
Araçların yere göre hızları,
L motoru P noktasında karşı kıyıya çıkar.
3x
⇒ VK = 3Vo
t
2x
VL =
⇒ VL = 2Vo
t
x
VM =
⇒ VM = Vo
t
2x
VN = –
⇒ VN = –2Vo olur.
t
CEVAP C
VK =
M aracındaki gözlemci L yi V hızı ile doğuya gidiyormuş gibi görür. Bu durumda,
8.
L
Motorun karşı kıyıya
ulaşma süresi,
t=
d
dir.
VM
P
.
k›y›
VLM = VL – VM = 2Vo – Vo = Vo = V olur.
VMK = VM – VK = V – 3V = –2V olur.
Va
VM
I. yargı doğrudur.
VM yarıya indirilirse,
t iki katına çıkar.
VMN = VM – VN = V – (–2V) = 3V olur.
.
I. yargı doğrudur.
II. yargı yanlıştır.
k›y›
K
VLM = VL – VM = 2V – V = V olur.
Motor karşı kıyıya yine P noktasında çıkar.
III. yargı yanlıştır.
CEVAP A
II. yargı doğrudur.
Motorun suya göre hızı ve akıntı hızı yarıya indirilirse, motorun yere göre hızı yarıya düşer.
III. yargı doğrudur.
CEVAP E
L
11.
M
V
120m
9.
k›y›
Va
A
E
Va
B Va
k›y›
Va
|Va|=7m/s
Vyer
k›y›
120
tan53° =
| LM |
4
120
=
3
| LM |
Va
C
K
N
37°
53°
Va
|LM| = 90 m olur.
D
•
K
•
L
•
M
•
N
•
P k›y›
B ve C motorları karşı kıyıya aynı noktada çıkar.
CEVAP D
120
| LN |
3
120
=
4
| LN |
tan37° =
|LN| = 160 m olur.
KUVVET VE HAREKET
29
|MN| uzunluğu,
|MN| = |LN| – |LM|
= 160 – 90
= 70 m olur.
|MN| uzunluğunu akıntı hızı aldırmıştır.
Motorun nehri geçme süresi,
70
| MN |
=
= 10 s olur.
7
Va
t=
|KN| uzunluğu ise,
sin37° =
120
| KN |
3
120
=
5
| KN |
|KN| = 200 m olur.
Motorun yere göre hızı,
Vyer =
200
| KN |
=
= 20 m/s olur.
10
t
CEVAP D
12.
M
k›y›
S
➞
VA
Va
N
➞
VB
A
P
T
R
Va
B
K
L
k›y›
A motoru M noktasında karşı kıyıya ulaştığı anda,
B motoru P noktasında bulunur.
30
KUVVET VE HAREKET
CEVAP B
TEST
1.
3
BAĞIL HAREKET
ÇÖZÜMLER
3.
Araçlar doğuya hareket ederse,
bat›
VK=3V
VM=V
M
.
N
.
VA
VKM=2V
VB
A
B
.
VKM=2V
k›y›
do¤u
Araçlar batıya hareket ederse,
bat›
P
do¤u
VK=V
.
VM=3V
IMPI = Va.tA = Va.
d
VA
INPI = Va.tB = Va.
d
dir.
VB
olur.
Araçlar aynı yönde doğuya ya da batıya hareket
edebilir.
k›y›
L
K
IMPI > INPI olduğundan,
I. yargı için kesin birşey söylenemez.
tA > tB dir.
K ya da M aracının hızı en büyük olabilir.
VB > VA dır.
II. yargı için kesin birşey söylenemez.
I. ve II. yargılar doğrudur.
L ye göre K nin hızı V ise,
V = VK – VL ... '
A nın yere göre hızı B ninkinden küçüktür.
L ye göre M nin hızı –V ise,
III. yargı yanlıştır.
–V = VM – VL ... ( olur.
CEVAP D
Denklem ' ve ( ortak çözülürse,
2V = VK – VL olur.
M aracındaki gözlemciye göre, K aracının hızı
doğuya 2V olur.
III. yargı kesinlikle doğrudur.
CEVAP C
➞
2.
VML
➞
VKL
➞
VMK
L aracındaki gözlemciye göre K nin hız vektörü,
V1 = V K – V L
K aracındaki gözlemciye göre M nin hız vektörü,
V2 = VM – VK olur.
V1 ve V2 toplanacak olursa,
V1 + V2 = VM – VL vektörü elde edilir.
4.
L
•.
M
N
P
R
k›y›
Va
Va
VM
.
K
k›y›
M aracındaki gözlemciye göre L nin hız vektörü
Motor suya göre aynı hızla KL doğrultusunda
Şekil-II deki vektörlerden 1 dir.
hareket ederse, karşı kıyıya LN arasında çıkar.
CEVAP A
CEVAP A
KUVVET VE HAREKET
31
5.
Araçların yere göre hızları,
7.
konum
2x
K
VK =
2x
& VK = 2V
t
x
L
VL =
x
& VL = V
t
0•
VM =
–x
& VM = –V
t
zaman
t
–x
kuzey
VLK=10v2m/s
VL=10m/s
O
bat›
do¤u
VML=10m/s
M
VM=10v2m/s
VK=10m/s
olur. M aracındaki gözlemciye göre L nin hızı,
VLM = VL – VM
VLM = V – (–V) = 2V olur.
VMK=10m/s
güney
I. yargı doğrudur.
K aracındaki gözlemci M aracını 10 m/s hızla
K aracındaki gözlemciye göre L nin hızı,
VLK = VL – VK
doğuya gidiyor gibi görür.
CEVAP C
VLK = V – 2V = –V olur.
II. yargı doğrudur.
K ve L araçları arasındaki uzaklık arttığından,
L aracındaki gözlemci K yi uzaklaşıyor görür.
III. yargı doğrudur.
CEVAP E
8.
L
6.
(–)
k›y›
M
•
•
N
•
P
R
•
•
S
•
(+)
K
VL
L
Va
VK
M
VM
V2
V1
yatay yol
Va
II
I
VKL = VK – VL = 5V
•
k›y›
K
VK – (–VL) = 5V
VK + VL = 5V
VK > VL
VK < VL
II motoru karşı kıyıya R noktasında çıkar.
CEVAP D
4 olabilir.
I. yargı için kesin birşey söylenemez.
VKM = VK – VM = –V
9.
VK – VM = –V olur.
M
M
k›y›
VM > VK dır.
II. yargı kesinlikle doğrudur.
VA
VK + VL = 5V
B
– VK + VM = V
________________
A
VL + VM = 6V olur.
VL > VM
VL < VM
4 olabilir.
C
k›y›
A ve B yüzücüleri için akıntı hızı aynı olduğundan,
A yüzücüsüne göre B nin hızı değişmez.
CEVAP B
KUVVET VE HAREKET
VC
K
III. yargı için kesin birşey söylenemez.
32
VB
I. yargı yanlıştır.
C yüzücüsünün akıntı doğrutusunda aldığı yol:
11.
1
I. durumda,
•
3
2
L
k›y›
x1 = (V + V).t
x1 = 2Vt olur.
II. durumda,
x2 = (V + 2V).t
x2 = 3Vt olur.
•
K
II. yargı yanlıştır.
k›y›
Akıntı hızı iki katına çıkartılırsa, B yüzücüsü M
x1 > x3 olduğuna göre, V1 > V3 tür.
noktasına çıkar.
x2 > x3 olduğuna göre, V3 > V2 dir.
III. yargı doğrudur.
Buna göre, V1 > V3 > V2 olur.
CEVAP C
CEVAP B
12.
konum
10. Nehrin genişliği:
k›y›
M
L
2x •
K
x•
d
Va=3m/s
VM=5m/s
L
•
0•
Vb
M
k›y›
K
Nehrin genişliği
zaman
t
–x •
0-t zaman aralığında,
d = VM.t1
L ve M aynı yönde, K zıt yönde hareket etmektedir.
= 5.20
I. yargı doğrudur.
= 100 m olur.
L ve M araçlarının hızları eşit olduğundan, L deki
gözlemci M yi duruyormuş gibi görür.
Motorun nehri en kısa yoldan geçiş süresi:
k›y›
L
Va=3m/s
d=100m
II. yargı doğrudur.
K ve L araçları zıt yönde hareket ettiklerinden, K
daki gözlemci L yi uzaklaşıyormuş gibi görür.
Vb=4m/s
VM=5m/s
K
III. yargı doğrudur.
k›y›
CEVAP E
Motorun nehrin karşı kıyısına en kısa yoldan
geçme süresi,
t2 =
d
100
=
= 25 s olur.
Vb
4
CEVAP A
KUVVET VE HAREKET
33
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
Bölüm
Yazılı Soruları
(Bağıl Hareket)
3.
kuzey
1.
ÇÖZÜMLER
konum
3V •
K (bat›)
V•
L (bat›)
VMK
VML L
M
K
bat›
VKL
0•
do¤u
–2V •
(+) bat›
M (do¤u)
VL =V
do¤u (–)
güney
a) L aracındaki gözlemci K yi doğuya doğru gidiyor gibi görür.
b) K aracındaki gözlemci M yi batıya doğru gidiyor gibi görür.
c) M aracındaki gözlemci L yi doğuya doğru gidiyor gibi görür.
2.
(–) bat›
•
= V – 3V
= – 2V
doğuya doğru 2V hızıyla gidiyor görür.
b) L aracındaki gözlemci M aracını,
Vbağıl = VM – VL
do¤u (+)
Vo=30m/s
Vö=5m/s
a) K aracındaki gözlemci L aracını,
Vbağıl = VL – VK
= (–2V) – V
= – 3V
•
VA=10m/s
yatay yol
a) Vbağıl = Vgözlenen – Vgözlemci
Öğrencinin yere göre hızı,
Vöyer = 5 + 30 = 35 m/s
olur. Atlete göre öğrencinin hızı,
VÖA = VÖyer – VA = 35 – 10 = 25 m/s
olur. Doğuya doğrudur.
b) Atlete göre otobüsün hızı,
VOA = VO – VA = 30 – 10 = 20 m/s
olur. Doğuya doğrudur.
c) Öğrenciye göre otobüsün hızı,
VOÖ = VO – VOyer = 30 – 35 = –5 m/s
olur.
34
KUVVET VE HAREKET
doğuya doğru 3V hızıyla gidiyor görür.
c) M aracındaki gözlemci K aracını,
Vbağıl = VK – VM
= 3V – (–2V)
= 5V
batıya doğru 5V hızıyla gidiyor görür.
4.
6.
x(m)
L
k›y›
.
K
40
Va=6m/s
120m
20
V
t(s)
0•
4
M
40m
–20
–40
.
K
k›y›
Motor K den M ye t = 10 saniyede geldiğine göre,
L
IKM| = (VM – Va).t
Konum-zaman grafiğinin eğimi hızı verir. K ve L
araçlarının hızı,
40 – (–20) 60
Tx
=
= 15 m/s (doğu)
VK =
⇒ VK =
4–0
4
Tt
Va=6m/s
.
40 = (V – 6).10
4=V–6
Vy=8m/s
V=10m/s
V = 10 m/s olur.
Tx
–40 – (–20) –20
=
= –5 m/s (batı)
VL =
⇒VL=
4–t
4
Tt
•
K
Yüzücünün K noktasından L noktasına çıkabilmesi
L ye göre K nin hızı,
VKL = VK – VL
için şekildeki yönde yüzmesi gerekir.
|KL| = Vy.t
= 15 – (–5)
ı
ı
ı
120 = 8. t ⇒ t = 15 s olur.
= 15 + 5
= 20 m/s olur.
Doğuya doğrudur.
bat›
5.
K
L
L
7.
do¤u
Va=4m/s
M
2V
120m
yatay yol
L
aracındaki gözlemci
k›y›
.
M
3V = VM – 2V
la gidiyor gördüğüne göre,
VKM = VK – VM
–4V = VK – 5V
VK = V, doğuya doğru
K aracındaki gözlemci L aracını,
VLK = VL – VK
VLK = 2V – V
VLK = V, doğuya gidiyor görür.
V
B
53°
.
37°
Vx=4m/s
3m/s
K
k›y›
A yüzücüsü karşı kıyıya L noktasında çıktığına göre,
V.cos37° = Va
V.0,8 = 4
VM = 5V, doğuya doğru
M aracındaki gözlemci K aracını batıya 4V hızıy-
Vy=3m/s 4m/s
A
aracını doğuya 3V
hızıyla gidiyor gördüğüne göre,
VML = VM – VL
V
V = 5 m/s olur.
B yüzücüsünün karşı kıyıya çıkma süresi,
tB =
d
120
120
=
=
= 30 s
V. sin 53° 5.0, 8
4
olur ve karşıya çıktığında yatayda aldığı yol,
ILMI = (V.cos53° + Va).tB
= (5.0,6 + 4).30
= 7.30
= 210 m olur.
KUVVET VE HAREKET
35
8.
M
L
2x
•.
k›y›
N
10.
M
.
N
.
VB
VA=5m/s
4x
VM.sin53°
VM=10m/s
53°
.
VM.cos53°
K
A
B
.
K
k›y›
Yüzücü yatayda x, düşeyde 4x yolunu almıştır. Bu
durumda,
VM . sin 53°.t
4x
=
2x (Va – VM . cos 53°) .t
k›y›
Va=3m/s
100m
Va
P
30m
.
L
k›y›
A yüzücüsünün karşıya çıkma süresi,
tA =
| KM | 100
=
= 20s olur.
VA
5
A yüzücüsünün yatayda aldığı yol,
IMPI = Va.tA = 3.20 = 60 m olur.
10.0, 8
4
=
2 Va – 10.0, 6
B yüzücüsünün yatayda alacağı yol,
4
8
=
2 Va – 6
INPI = IMPI – 30 = 60 – 30 = 30 m olur.
Va – 6 = 4
B yüzücüsü karşıya çıktığında yatayda,
Va = 10 m/s olur.
|NP| = 30 m yol alacağından karşıya çıkma süresi,
|NP| = Va.tB
30 = 3.tB ⇒ tB = 10 s olur.
B yüzücüsünün karşıya çıktığında düşeyde aldığı
yol,
|LN| = 100 m olacağından,
|LN| = VB.tB
100 = VB.10 ⇒ VB = 10 m/s olur.
9.
L
M
.
k›y›
Va=4m/s
120m
Vy=8m/s
VM=10m/s
.
53°
K
Vx=6m/s
k›y›
Motorun karşı kıyıya çıkma süresi,
t=
120
120
120
=
=
= 15 s olur.
VM . sin 53° 10.0, 8
8
Yüzücünün yatayda aldığı yol,
ILMI = (VM.cos53° + Va).t
= (10.0,6 + 4).15
= (6 + 4).15
= 10.15
= 150 m olur.
36
KUVVET VE HAREKET
3. BÖLÜM
DİNAMİK
Şekil-II deki cisme etki eden sürtünme kuvveti,
fs = k . N = 0,2 . (100 + 60)
= 0,2 . 160
= 32 N olur.
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
(–)
20 N
(+)
6 m/s
20N
6 m/s
Cismin ivmesi,
60°
53°
K
K
2N
•
10 N
•
10N
a2 =
12N
L
cismi uygulanan net kuvvet cismi önce
Fnet 80 – 32 48
2
=
=
= 4, 8 m/s olur.
m
10
10
Cisimlerin ivmeleri oranı,
a 1 7, 2 3
olur.
=
=
a 2 4, 8 2
(+)
yönde yavaşlatır. Cisim durduktan sonra (–) yönde
CEVAP D
hızlanır. Cismin ivmesi,
aK =
Fnet 10 – 2 8
2
=
= = 4 m/s olur.
mK
2
2
3.
a(m/s2)
L cismine uygulanan net kuvvet cismi önce (–)
yönde yavaşlatır. Cisim durduktan sonra (+) yön-
5
de hızlanır. Cismin ivmesi,
aL =
Fnet 12 – 10 2
2
=
= = 1m/s olur.
mL
2
2
İvmelerin büyüklükleri oranı,
aK 4
= =4
aL 1
fs=5
İvme-kuvvet grafiğinin eğimi
olur.
F(N)
α
0
15
1
değerine eşittir.
kütle
Bu durumda kütle,
15 – 5 10
m=
=
= 2 kg olur.
5
5
CEVAP D
Grafikten sürtünme kuvveti 5N, yüzeyin sürtünme
katsayısı ise,
2.
60N
100N
37°
fs = kmg
5 = k.2.10
1
k=
= 0,25 olur.
4
80N
fs
CEVAP C
G=100N
fiekil- I
Şekil-I deki cisme etki eden sürtünme kuvveti,
fs = k . N = 0,2 . (100 – 60)
= 0,2 . 40
= 8 N olur.
m=5kg
.
4
|F|=30N
yatay
düzlem
k=0,2
Cismin ivmesi,
a1 =
4.
Fnet 80 – 8 72
2
=
=
= 7, 2 m/s olur.
m
10
10
Cisme etki eden sürtünme kuvveti,
fs = k.mg = 0,2.5.10 = 10 N olur.
80N
37°
Cismin ivmesi,
F – fs
30 – 10
20
a=
=
=
= 4 m/s2 olur.
5
5
m
fs
6 saniye sonra cismin hızı,
60N
G=100N
fiekil- II
V = a.t = 4.6 = 24 m/s olur.
CEVAP D
KUVVET VE HAREKET
37
5.
m=5kg
.
K
L
M
KL arasında,
a1 =
F
m
4=
F
5
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
yatay
düzlem
➞
F
1.
3kg
LM arasında,
T
K
F – fs
m
20 – fs
2=
5
•
a2 =
F = 20 N olur.
ip
2kg
L
.
4
IFI=20N
yatay düzlem
Sistemin ivmesi;
a=
fs = 10 N olur.
LM arasında cisim ile yatay düzlem arasındaki
Fnet
2
F
20
20
=
=
=
= 4 m/s olur.
/m m K + m L 3 + 2
5
T gerilme kuvvetinin büyüklüğü,
sürtünme katsayısı,
T = m K .a = 3.4 = 12 N olur.
fs = k.m.g
CEVAP D
10 = k.5.10
k = 0,2 olur.
CEVAP B
2.
Sistemin ivmesi,
düfley
T – GL = mL.a
F
24 – 20 = 2.a
.
4 = 2a
6.
h›z
•
+a
j
0
•
•
–j
•
t
–a
I
II
III
•t
•2t
ip
GK=30N
F – (GK + GL) = (mK + mL).a
•3t zaman
F – (30 + 20) = (3 + 2).2
•
mK=3kg
H.Y
F kuvvetinin büyüklüğü,
•
•3t zaman 0•
•2t
K
a = 2 m/s2 olur.
ivme
T
L
mL=2kg
F – 50 = 10
F = 60 N olur.
Aracın ivme-zaman grafiği şekildeki gibidir. İvme
GL=20N
CEVAP C
ile kuvvet doğru orantılı olduğundan ivme-zaman
grafiğini kuvvet-zaman grafiği gibi düşünebiliriz.
I ve II zaman aralıklarında araca etkiyen net kuv-
3.
1kg
T
4kg .
vet aynı yönlüdür.
yatay düzlem
I
I. yargı doğrudur.
I ve III zaman aralıklarında araca etkiyen net kuv-
4kg
T
1kg .
vet hareket yönüne zıt yöndedir.
II zaman aralığında net kuvvet, hız ve yer değiştir-
2kg
me vektörleri aynı yönlüdür.
T
III
III. yargı doğrudur.
CEVAP E
➞
F2
yatay düzlem
II
II. yargı doğrudur.
➞
F1
3kg .
➞
F3
yatay düzlem
İplerdeki gerilme kuvvetleri eşit olduğundan cisimlerin ivmeleri ve kuvvetler,
Şekil-I de,
Sistemin ivmesi ve ipteki T gerilme kuvveti,
a1 =
F1
5
T = 1.a1 = 1.
38
KUVVET VE HAREKET
F1
olur.
5
5.
Şekil-II de,
tavan
.
Sistemin ivmesi ve ipteki T gerilme kuvveti,
a2 =
F2
5
T = 4.a2 = 4.
F2
olur.
5
T2
m L
Şekil-III te,
T1
a
Sistemin ivmesi ve ipteki T gerilme kuvveti,
M
a
m.g
m K
F
a3 = 3
5
3m
3m.g
m.g
F
T = 2.a3 = 2. 3 olur.
5
Sistemin ivmesi,
T gerilme kuvvetleri eşit olduğuna göre, kuvvetle-
a=
FNET G M – (G L + G K)
=
mK + mL + mM
Rm
a=
3mg – (mg + mg) mg g
olur.
=
=
m + m + 3m
5m 5
rin büyüklükleri arasındaki ilişki,
F1 4F2 2F3
=
=
5
5
5
K cismine dinamiğin temel prensibi uygulandığında,
F1 = 4F2 = 2F3
T1 – GK = mK . a
F1 > F3 > F2 olur.
CEVAP E
T1 – mg = m .
T1 =
g
5
6
mg olur.
5
M cismine dinamiğin temel prensibi uygulandığında,
GM – T2 = mM . a
4.
2m
K
ip
m
L
3mg – T2 = 3m
3m
ip
M
.
4
F
T2 = 3mg –
yatay düzlem
I. durumda sistemin ivmesinin büyüklüğü:
a=
FNET
F
F
F
=
=
=
Rm
m K + m L + m M 2m + m + 3m 6m
olur.
II. durumda sistemin ivmesinin büyüklüğü :
›
a =
g
5
T2 =
3
mg
5
12
mg olur.
5
T1 ve T2 gerilme kuvvetleri taraf tarafa oranlanırsa,
6
mg
T1
1
= 5
=
olur.
T2 12
2
mg
5
CEVAP C
F
F
F
=
=
olur.
m L + m M m + 3m 4m
Bulduğumuz ivmeler taraf tarafa oranlanacak olursa,
F
›
›
a
3
3
= 4m =
& a = a olur.
a
F
2
2
6m
CEVAP D
KUVVET VE HAREKET
39
6.
tavan
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
tavan
.
1.
ip
T
a1
T
a1
L •
ip
T
3m
3mg
3m
mg
fiekil-I
a2
2
➞
FKL
FLK
Sistemin ivmesi,
L
a=
3mg
fiekil-II
Fnet
2
F
28
28
=
=
=
= 4 m/s olur.
7
Rm m K + m L 3 + 4
K nin L ye uyguladığı kuvvet,
FKL = mL.a = 4.4 = 16 N olur.
Şekil-I deki sistemin ivmesi,
a1 =
L
K
yatay düzlem
mg
•
➞
K • m
m
m • K
.
➞
IFI=28N
a2
mL=4kg
mK=3kg
g
3mg – mg
2mg
=
=
olur.
2
4m
4m
CEVAP D
Şekil-II de K cismine dinamiğin temel prensibi
uygulandığında,
2.
T = ma2 + mg olur.
F
K
L
. .
FLK
FKL
yatay düzlem
Sistemin ivmesi,
a=
3ma 2
2
F net
F
F
F
olur.
=
=
=
Rm m K + m L 2m + 3m 5m
L nin K ye uyguladığı kuvvetin büyüklüğü, K nin L
7a 2
g=
2
ye uyguladığı kuvvete eşit olduğundan,
I FKLI = I FLKI
2g
a2 =
olur.
7
a1 ve a2 taraf tarafa oranlanırsa,
g
a1
7
= 2 =
olur.
4
a2
2g
7
.
➞
L cismine dinamiğin temel prensibi uygulandığında,
a
3mg – 2T = 3m. 2
2
3mg – 2ma2 – 2mg =
mL=3m
mK=2m
T – mg = m.a2
FKL = mL.a = 3m.
FLK =
F
3
= F
5m 5
3
F olur.
5
CEVAP C
CEVAP A
3.
4
F
.
mK=3m
L
K
4
FKL
mL=5m
mM=2m
M
4
4
FLK FLM
4
FML
yatay düzlem
Sistemin ivmesi ile cisimlerin ivmeleri aynı olacağından, K nin L ye uyguladığı kuvvetin büyüklüğünün, M nin L ye uyguladığı kuvvetin büyüklüğüne
oranı,
FKL ^m L + m M h .a 5m + 2m 7m 7
olur.
=
=
=
=
FML
m M .a
2m
2m 2
CEVAP E
40
KUVVET VE HAREKET
4.
mK=6kg
mL=4kg
K
. . L
|F1|=30N .
.
FKL
FLK
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
|F2|=10N
1.
yatay düzlem
K
Sistemin ivmesi,
F
F – F2
a = NET = 1
Rm
mK + mL
a=
mL=6kg
mL=2kg
4
|F|=20N .
4
FLM
mK.amak = k.mK.g
amak = 0,4.10
amak = 4 m/s2 olur.
Cisimler birlikte hareket ettiğinden, F kuvvetinin
büyüklüğü,
M
4
amak =
FML
yatay düzlem
4=
Sistemin ivmesi,
a=
a=
FNET
∑m
=
F
4+6
F = 40 N olur.
F
CEVAP B
20
4+2+4
=
20
10
= 2 m/s 2
mL=6kg
mK=4kg
L
K . .
|F|=40N .
FKL
FLK
fsK
fsL
yatay düzlem
➞
F
mK=4kg
.
fs
K
L
fs
mL=6kg
yatay düzlem
Cisimler arasındaki sürtünme kuvvetinin büyüklüğü,
= 0,3.4.10
= 12 N olur.
K ve L cisimlerinin ortak hareket edebilecekleri en
fsK = k.mK.g = 0,2.4.10 = 8 N
büyük ivme,
fsL = k.mL.g = 0,2.6.10 = 12 N olur.
fs = mL.amak
Sistemin ivmesi,
F – (fsK + fsL)
F
a = NET =
mK + mL
Rm
12 = 6.amak
amak = 2 m/s2 olur.
40 – (8 + 12)
40 – 20
20
=
=
= 2 m/s2
10
10
4+6
olur. K nin L ye uyguladığı kuvvetin büyüklüğü,
FKL – fsL = mL.a
Cisimleri birlikte hareket ettirebilecek F kuvveti,
amak =
2=
FKL – 12 = 6.2
FKL = 24 N olur.
2.
fs = k.mK.g
Cisimlere etki eden sürtünme kuvvetleri,
a=
Fnet
F
=
Rm m K + m L
mK + mL + mM
olur. M nin L ye uyguladığı kuvvetin büyüklüğü L
nin M ye uyguladığı kuvvetin büyüklüğüne eşit olacağından,
FLM = FML = mM . a
FML = 4.2 = 8N olur.
CEVAP A
6.
➞
F
Fey = fs
mM=4kg
. .
L
K
.
L
K cisminin maksimum ivmesi,
K nin L ye uyguladığı kuvvetin büyüklüğü,
FKL – F2 = mL.a
FKL – 10 = 4.2
FKL = 18 N olur.
CEVAP A
mK=4kg
fs
yatay düzlem
30 – 10
20
=
= 2 m/s2 olur.
6+4
10
5.
mK=4kg
Fey=mK.amak
CEVAP D
Fnet
F
=
Rm m K + m L
F
4+6
F = 20 N olur.
CEVAP B
KUVVET VE HAREKET
41
3.
4
IFI=20N .
fs
K ve L cisimlerinin ortak hareket edebilecekleri en
büyük ivme,
mK=2kg
fs
K
•
L
fs = mL.amak
mL=4kg
k=0
12 = 8.amak & amak =
yatay düzlem
K ve L cisimleri arasındaki sürtünme kuvveti,
K ve L cisimlerini ortak hareket ettirebilecek en
büyük kuvvet,
fs = k.mK.g = 0,4.2.10 = 8N olur.
Fmak = (mK + mL).amak
K ve L cisimlerinin ivmelerinin büyüklükleri,
aK =
3
m/s2 olur.
2
F – fs 20 – 8 12
2
=
=
= 6 m/s olur.
mK
2
2
= (4 + 8).
3
2
= 6.3
f
2
8
a L = s = = 2 m/s olur.
mL 4
= 18 N olur.
CEVAP B
CEVAP D
4.
Fey
.
6.
mK=2kg
K
|F|=18N .
L
fs
k=0,4
k=0,4
mL=3kg
.
fs
F
K cisminin düşmeden taşınabilmesi için sistemin
ortak maksimum ivmesi,
mK.amak = k.mK.g
= 8 N olur.
amak = 0,4.10
amak = 4 m/s2 olur.
K cisminin düşmeden taşınabilmesi için F kuvvetinin en büyük değeri,
Fmak = (mK + mL).amak
Cisimlerin ortak hareket edebilecekleri maksimum
kuvvet,
f
8
amak = s =
= 2 m/s2
4
mL
Fmak = (mK + mL).amak = (2 + 4).2 = 12N
olur.
= (2 + 3).4
= 20 N olur.
CEVAP C
F > Fmak olduğundan cisimler ayrı ayrı hareket
ederler.
F – fs
18 – 8
10
aK =
=
=
= 5 m/s2,
2
2
mK
aL =
.
K
L
mK=4kg
fs
mL=8kg
yatay düzlem
K ve L cisimlerine etki eden sürtünme kuvveti,
fs = k.mK.g
= 0,3.4.10
= 12 N olur.
42
KUVVET VE HAREKET
mL=4kg
fs = k.mK.g
= 0,4.2.10
fs
fs
L
K ve L cisimlerine etki eden sürtünme kuvveti,
Fey = fs
F
K
yatay düzlem
yatay düzlem
5.
mK=2kg
fs
8
=
= 2 m/s2 olur.
4
mL
CEVAP C
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
1.
3.
fs=10N
T
k=0
yatay
düzlem
T
L
yatay
düzlem
mL=3kg
L
mL=5kg
k=0,2
.
T
K
.
mK=5kg
GK=50N
K
mK=2kg
L cismine etki eden sürtünme kuvveti,
GK=20N
fs = k.mL.g = 0,2.5.10 = 10 N olur.
Sistemin ivmesi,
Dinamiğin temel prensibi sisteme uygulanırsa,
a=
F
mK g
a = net =
Rm m K + m L
=
2
2.10 20
a=
=
= 4 m/s olur.
2+3
5
Fnet
G –f
= K s
Rm m K + m L
2
50 – 10 40
=
= 4 m/s olur.
5+5
10
K cismine dinamiğin temel prensibi uygulandığında,
L cismine dinamiğin temel prensibi uygulanırsa,
GK – T = mK.a
50 – T = 5.4
T = mL.a = 3.4 = 12 N olur.
T = 30 N olur.
CEVAP C
2.
fs
2m
L
2m
K
yatay düzlem
CEVAP B
mL
4.
L
.
➞
V
M
yatay düzlem
K
m
Cisimler sabit hızla gidebilmesi için, net kuvvetin
sıfır olması gerekir. Bu durumda,
fs = GM
k.4mg = mg
k=
1
olur.
4
İlk durumda ivme 2 m/s2 ise kütleler arasındaki ilişki,
F
a1 = net
Rm
2=
m K .g
mK + mL
2=
m K .10
mK + mL
5mK = mK + mL
4mK = mL dir.
II.
durumda,
__________
Kütleler yer değiştirildiğinde sistemin ivmesi,
m L .g
a2 =
mK + mL
L cismi alındığında sistemin ivmesi,
Fnet mg – k2mg
=
Rm
3m
1
10 – .2.10
4
=
3
10 – 5
=
3
5
=
m/s2 olur.
3
mK
mK.g
GM
I.
durumda,
_________
.
a=
=
4m K .g
m K + 4m K
=
4.10
5
= 8 m/s2 olur.
CEVAP D
CEVAP E
KUVVET VE HAREKET
43
5.
mK
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
ip
K
.
1.
mK=2kg
mL=2kg
L
4
h=2m
fs = k1.mK.g = 0,2.2.10 = 4N
1
42 = 2.a. 2
fs = k .(m + m ).g = 0,2 (2 + 3).10 = 10N
2
K
L
2
a = 4m / s2 olur.
olur. L cisminin ivmesi,
F – _ fs + fs i
aL =
mL
K cisminin kütlesi,
m L .g
a=
mK + mL
1
2. 10
mK + 2
mK + 2 = 5
20 – ^4 + 10 h
3
=
6
3
2.
olur.
CEVAP A
mK=m
mK=1,5kg
fs
T
mL=2m
.
k=0
2
CEVAP B
2a
K
2
=
= 2m/s
mK = 3 kg olur.
yatay
düzlem
.
fs2
kuvveti,
ϑ2 = 2a x
6.
L
K ile L ve L ile yatay düzlem arasındaki sürtünme
Sistemin ivmesi,
4=
.
fs1
mL=3kg
•
yatay düzlem
20N
yatay düzlem
•
.
|F|=20N
T
.
K
fs1
k=0,5
L
.
yatay düzlem
T
T
2x
K
M
2T
x
L
mL=4kg
mM.g
a
K ve L cisimleri arasındaki sürtünme kuvveti,
mL.g
t saniyede K cismi 2x yol alırsa L cismi x kadar yol
alır. Bu durumda K nin ivmesi 2a, L nin ivmesi a
olur.
T = mK . 2a
T = 1,5 . 2a = 3a
cekleri maksimum ivme,
fs
2
5m
=
= 5 m/s olur.
mK
m
Dinamiğin temel prensibi sisteme uygulandığında,
4 . 10 – 2.3a = 4 . a
40 = 10a
amak =
a = 4 m/s2
T = 3a
5=
=3.4
= 12 N olur.
CEVAP C
KUVVET VE HAREKET
K nin L nin üzerinden düşmeden hareket edebile-
amak =
mL . g – 2T = mL . a
44
fs = k.mK.g = 0,5.m.10 = 5 m olur.
m M .g
mK + mL + mM
m M .10
3m + m M
3m + mM = 2mM ⇒ mM = 3m olur.
CEVAP C
3.
5.
mK=2kg
➞
K
fs
IFI=50N
.
mL=4kg
.
T
fs
L
k=0
.
.
T
ip
.
T
•f
sür
mL=6m
mK=4m
K
L
fsür
yatay
düzlem
yatay düzlem
.
ip
K ve L cisimleri arasındaki sürtünme kuvveti,
fsür = k.mK.g = 0,5.2.10 = 10 N olur.
M
mM=4m
K cismine dinamiğin temel prensibi uygulandığında sistemin ivmesi,
4mg
Sistemin ivmesi eşitliğinden
G M – fs
F
a = NET =
mL + mM
Rm
T – fs = mK.a
T – 10 = 2.a
T – 10
a=
olur.
2
4mg – fs
g
=
4
6m + 4m
L cismine dinamiğin temel prensibi uygulandığında,
10mg = 16mg – 4fs
F – (fs + T) = mL.a
T – 10
)
50 – (10 + T) = 4.(
2
50 – 10 – T = 2T – 20
4fs = 6 mg
3mg
olur.
fs =
2
İpteki T gerilme kuvveti,
3
T = fs =
mg olur.
2
40 – T = 2T – 20
60 = 3T ⇒ T = 20 N olur.
CEVAP D
CEVAP B
6.
4.
mK=1kg
K
fs
4
F
1
.
yatay düzlem
•
L
•
T=4N
mK=2kg
fs
K
mL=3kg
L
yatay düzlem
ip
fs
T=4N
1
mL=4kg
.
M
2
Cisimler birlikte hareket edebilmesi için sistem ivmesi,
a=
fs = k1.mK.g = 0,2.1.10 = 2N
1
fs = k2.(mK + mL) . g = 0,2.5.10 = 10N olur.
2
Sistemin ivmesi,
T – fs = mK.a
1
fs
f
= s olmal›d›r.
mL 3
K ve L cisimlerine dinamiğin temel prensibi uygulanırsa,
m g – fs
a= M
mK + mM
a=
4 – 2 = 1.a
a = 2 m/s2 olur.
10 – fs
olur.
3
fs
10 – fs
=
3
3
L cismini çeken F kuvvetinin büyüklüğü,
F – _ fs + fs + T i
1
2
mL
2fs = 10
fs = 5 N olur.
F – ^2 + 10 + 4 h
4
Sürtünme katsayısı,
fs = k.mK.g
8 = F – 16
F = 24N olur.
mM=1kg
mM.g
tünme kuvveti;
2=
.
fs
K ile L cismi ve L ile yatay düzlem arasındaki sür-
a=
fs
CEVAP D
5 = k.2.10
1
k=
= 0,25 olmalıdır.
4
CEVAP C
KUVVET VE HAREKET
45
MODEL SORU - 7 DEKİ SORULARIN ÇÖZÜMLERİ
1.
3.
➞
Eğik düzlem üzerinde hareket
a
fs
eden cismin ivmesi,
K
G . sin a – fs
a= K
m
mg sin a – mg cos a.k
=
m
GK.sinα
mL=10kg
L
fs
GXL
α GK.cosα
53°
GK
mK=5kg
K
k
a=1m/s2
GK=50N
.
yatay düzlem
.
a
➞
= g.(sinα – kcosα) eşitliği
GXL = mL.g.sin53° = 10.10.0,8 = 80 N
ile bulunur.
Dinamiğin temel prensibi sisteme uygulanırsa,
İvme eğik düzlemin yapıldığı maddenin cinsine (k)
ve eğim açısına (α) bağıdır.
a=
Fnet G XL – (fs + G K)
=
Rm
mK + mL
1=
80 – (fs + 50)
5 + 10
CEVAP D
15 = 80 – fs – 50
fs = 15 N olur.
Sürtünme kat sayısı,
fs = kmL.g.cos53°
2.
15 = k.10.10.0,6
h›z
k=
VB=6t
tBC
tAB
0
Cismin hız-zaman grafiği şekildeki gibi olur.
4.
AB yolunda cismin ivmesi,
mgsina
mgcosa
mg
Cismin B noktasındaki hızı,
•
VB = aAB.t = 6.t = 6t olur.
Cisim aşağı doğru kayarken oluşan sürtünme kuvfs = (mgcosα).k eşitliği ile bulunur.
VC = VB – ay.tBC
Sürtünme kuvveti, m, g, α ve k değerlerine bağlı-
0 = 6t – ay.2t
dır. Eğim açısı (α) artarsa cosα azalır. Sürtünme
6t = ay.2t ⇒ ay = 3 m/s2 olur.
kuvveti de azalır.
CEVAP A
Sürtünme kat sayısı,
fsür = m.a
V
kmg = m.a
fs
k.10 = 3
B
m
C
CEVAP C
KUVVET VE HAREKET
a
vetinin değeri,
BC bölümünde cismin yavaşlama ivmesi,
46
fs
K
aAB = g . sin37° = 10 . 0,6 = 6 m/s2 olur.
k = 0,3 olur.
CEVAP B
t(s)
3t
t
15 1
= = 0, 25 olur.
60 4
5. Sistemin ivmesi,
1
.a.t2
2
1
4 = .a.22
2
T
H.Y
x=
GKx
a = 2 m/s2
mK K
•
T
L • mL=3kg
1.
GL=30N
h=4m
37°
olur.
MODEL SORU - 8 DEKİ SORULARIN ÇÖZÜMLERİ
H.Y
Asansör aşağı yönde hızlanırken, dinamometrenin
gösterdiği değer,
halat
Gı = mg – ma
.
= 2.10 – 2.4
yatay düzlem
= 12 N
K cisminin kütlesi,
olur.
G – Gx K
a= L
mK + mL
m.a
a=
m L .g – m K .g. sin 37°
mK + mL
2=
30 – m K .10.0, 6
mK + 3
a=4m/s2
m.a
m=2kg
mg
2mK + 6 = 30 – 6mK
8mK = 24
mK = 3 kg olur.
CEVAP B
CEVAP E
2.
halat
halat
H.Y
6.
kg
fs1
T1
T2
m
mg
m
mg
m.a
H.Y
T1 = m.g olur.
k=0,1
mLgsin37°
Asansör yukarı yönde hızlanırken:
.
37°
m.a ip
T3
Asansör yukarı yönde sabit hızla hareket ederken:
fs2
L
ip
mg
=2
mL
K
H.Y
ip
m
fs1
mK=1kg
halat
T2 = mg + ma olur.
yatay düzlem
K ile L arasındaki sürtünme kuvveti,
Asansör aşağı yönde hızlanırken:
fs1 = k1.mK.g.cos37°
T3 = mg – ma olur.
= 0,2.1.10.0,8
Buna göre,
= 1,6 N
T2 > T1 > T3 olur.
L ile eğik düzlem arasındaki sürtünme kuvveti,
CEVAP A
fs2 = k2(mK + mL).g.cos37°
= 0,1.3.10.0,8
3.
= 2,4 N
a sis =
L cisminin ivmesi,
aL =
=
m L .g. sin 37° – (fs1 + fs2)
mL
2mg – mg g
=
2m + m
3
olur. K cismine dinamiğin temel prensibi uygulandığında
2.10.0, 6 – (1, 6 + 2, 4)
2
12 – 4
2
= 4 m/s2 olur.
Asansör sabit hızla hareket ederken:
=
T = 2mg – 2m
CEVAP B
T=
4
mg olur.
3
T
ip
2mg – T = 2m.asis
g
3
asistem
T
K 2m
L m
asistem
2mg
mg
KUVVET VE HAREKET
47
Asansör aA ivmesi ile aşağı doğru düzgün olarak
yavaşlarken:
›
2m ^g + a A h – m ^g + a A h
2m + m
›
g + aA
olur.
3
a sis =
a sis =
5.
halat
a=5m/s2
T
ip
T K
ı
a > a olduğundan ivme artar.
GıK=45N
L •
mL=2kg
GıL=25N
Dinamiğin temel prensibi K cismine uygulandığında,
ı
ı
Asansör
2m.(g + aA) – T = 2m.asis
T = 2m c g + a A –
ı
mK=3kg
•
g + aA
m
3
K ve L cisimlerine etki eden net kuvvetler,
GıK = mK.(g + a) = 3.(10 + 5) = 45 N
4
T =
m (g + aA) olur.
3
ı
GıL = mL.(g + a) = 2.(10 + 5) = 30 N olur.
ı
T > T olacağından gerilme kuvveti artar.
Sistemin ivmesi,
CEVAP A
ı
ı
a =
ı
GK – GL
45 – 30
15
=
=
= 3 m/s2 olur.
3+2
5
mK + mL
İpte oluşan T gerilme kuvvetinin büyüklüğü,
GıK – T = mK.aı
45 – T = 3.3
T = 36 N olur.
CEVAP D
4.
halat
h›zlan›yor
g
2
6.
h›zlan›y
TK
K
m
mg
L
ma
mgsin30°
30°
g
2
TL
ma
a=2m/s2
masin30°
Fey=ma
30°
GK=mg
GL=mg
fiekil-I
fiekil-II
g
ivmesi ile yukarı doğru hız2
landığından ipteki gerilme kuvveti,
Şekil-I deki asansör
Asansör yukarı doğru a ivmesi ile hızlanırken
içindeki cisme yer çekim ivmesinin yanı sıra asansörün a ivmeside etki eder. Bu durumda cismin
ivmesi,
F
aı = net
Rm
mg sin 30° + ma sin 30°
=
m
TK = ma + mg = m
Şekil-II deki asansör
g
3
+ mg =
mg olur.
2
2
g
ivmesi ile aşağı doğru hız2
landığından ipteki gerilme kuvveti,
TL = mg – ma = mg –
mg mg
=
olur.
2
2
= 10 . 0,5 + 2 . 0,5
Gerilme kuvvetlerinin oranı ise;
= 6 m/s2 olur.
CEVAP C
48
KUVVET VE HAREKET
3
TK 2 mg
=
= 3 olur.
TL
mg
2
CEVAP E
TEST
1
ÇÖZÜMLER
Şekil-III te,
V(m/s)
1.
DİNAMİK
Toplam kuvvet sıfır olduğundan ivme sıfır olur.
16
İpteki gerilme kuvveti,
32m
0
48m
4
T3 = F olur.
t(s)
Buna göre,
7
T2 > T1 = T3 olur.
Cismin ivmesi,
F
20
a=
=
= 4 m/s2 olur.
m
5
CEVAP E
4 saniye sonra cismin hızı,
V = a.t = 4.4 = 16 m/s olur.
3.
7 saniyede aldığı yol,
➞
Σ∆x = 32 + 48 = 80 m olur.
mL=3m
mK=2m
F
.
mM=m
L
K
M
CEVAP A
yatay düzlem
Sistemin ivmesi,
F
F
F
a=
olur.
=
=
m K + m L + m M 2m + 3m + m 6m
2.
T1
m
m
T2
m
m
.
T3
m
III
K nin L ye uyguladığı kuvvet,
.
FKL = (mL + mM).a = (3m + m).
m
.
2F
F
=
olur.
3
6m
M nin L ye uyguladığı kuvvet,
2F
FML = mM.a = m.
yatay düzlem
II
F
2F
yatay düzlem
I
F
.
F
F
=
olur.
6
6m
Kuvvetler taraf tarafa oranlanırsa,
F
FKL
=
FML
yatay düzlem
2F
3
F
6
= 4 olur.
CEVAP D
Şekil-I de,
Sistemin ivmesi,
a1 =
2F
F
=
2m m
İpteki gerilme kuvveti,
F
= F olur.
T1 = m.a1 = m.
m
Şekil-II de,
2F – F
F
=
2m
2m
İpteki gerilme kuvveti,
T2 – F = m.a2
T2 – F = m.
T2 =
Cisme etki eden sür-
fs
tünme kuvveti,
fs = k.F
= 0,3.40
m=2kg
k=0,3
.
➞
IFI=40N
düfley
duvar
yukar›
= 12 N olur.
Sistemin ivmesi,
a2 =
4.
F
2m
3
F olur.
2
➞
Cismin ivmesi,
G – fs
m
20 – 12
=
2
8
=
2
= 4 m/s2 olur.
a
G=20N
afla¤›
a=
CEVAP C
KUVVET VE HAREKET
49
5.
7.
h›z
3V •
2V •
L
2x
K
2V •
M
2x
t
•
•
2x
•
t
2t
•
zaman
3t
Kuvvet ile ivme doğru orantılı olduğundan, kuvvet-zaman grafiğini ivme-zaman grafiği gibi düşünebiliriz. Bu durumda cismin hız-zaman grafiği
şekildeki gibi olur.
zaman
3t
2t
2x
•
0
•
x
V•
V•
0•
hız
K, L, M cisimlerinin ivmeleri,
V
aK =
,
2t
V
aL = ,
t
2V
aM =
olur.
3t
Cismin 0-t zaman aralığında aldığı yol, 2x olduğuna göre 0-3t aralığında aldığı yol,
Rx = 2x + 2x + 2x + x + 2x = 9x olur.
CEVAP D
K, L, M cisimlerinin kütleleri,
2Ft
F
F
=
=
,
V
aK
V
2t
F
Ft
F
=
=
,
mL =
V
V
aL
t
F
F
3Ft
=
=
olur.
mM =
2V
aM
2V
3t
mK =
8.
K
fs
Buna göre mK > mM > mL olur.
6.
mK=2kg
CEVAP E
T=12N
yatay k=0,2
düzlem
a
L
yatay
düzlem
GL=mL.g
.
Sürtünme kuvveti,
T=12N
mK=3kg
a
GK=30N
K cismi için dinamiğin temel prensibini uygularsak,
GK – T = mK.a
fs = k mK g
= 0,2 2.10
= 4N olur.
Sistemin ivmesi,
T – fs = mK.a
30 – 12 = 3.a
18 = 3a
a = 6 m/s2 olur.
L cismine dinamiğin temel prensibi uygulanırsa,
T – fs = mL.a
12 – fs = 1.6
fs = 6 N
L cismi ile yatay düzlem arasındaki sürtünme katsayısı,
fs = k.mL.g
6 = k.1.10
12 – 4 = 2.a
8 = 2a
a = 4m/s2 olur.
L cisminin kütlesi,
mL.g – T = mL.a
mL.10 – 12 = mL.4
6 mL = 12
mL = 2 kg olur.
CEVAP C
k = 0,6 olur.
CEVAP E
KUVVET VE HAREKET
mL
T=12N
K
50
T=12N
L
mL=1kg
fs
.
9.
Cismin AB yolunda
ivmesi,
a = g.sin53°
11.
V(m/s)
h›z
8
V•
= 10.0,8
16
= 8 m/s2
Cismin B noktasında hızı,
0•
4
0
1
t(s)
3
–V•
•
•
t
I
•
2t
II
3t zaman
III
V = a.t = 8.1 = 8 m/s
Grafikte görüldüğü gibi,
Hız-zaman grafiğinde doğrunun eğimi ivmeyi verir.
Net kuvvet ivme ile doğru orantılıdır.
IBCI = 2.8 = 16 m olur.
CEVAP D
ivme
net kuvvet
a•
F•
zaman
0•
t
2t
3t
–a•
0•
zaman
t
2t
3t
–F•
Net kuvvet, hız ve yer değiştirme vektörleri II.
zaman aralığında aynı yönlüdür.
10.
m
fs
CEVAP B
m
M
fs
L
yatay düzlem
.
m
K
mg
12.
I.
durumda,
_________
a
L
Cisimler 2 m/s2 lik ivme ile hızlandıklarına göre,
F
mg – k2mg
a1 = net =
Rm
3m
2=
yatay düzlem
T1
10 – 20k
3
T2
K
6 = 10 – 20k
M
GK
20k = 4
GM
Sistemin ivmesi,
k = 0,2 olur.
a=
GM – GK
dir.
mK + mL + mM
II.
durumda,
__________
L cisminin kütlesi artarsa ivme azalır.
K ve L cisimlerinin yeni durumda ivmeleri,
T1 – GK = mKa
a2 =
.
Fnet mg – kmg
=
Rm
2m
T1 = GK + mKa olur.
GM – T2 = mM.a
10 – 0, 2.10
2
8
=
2
Sistemdeki L cisminin kütlesi artırılırsa sistemin
= 4 m/s2 olur.
ivmesi azalır. Yukarıdaki bağıntılara göre,
=
T2 = GM – mM.a olur.
CEVAP B
T1 : azalır
T2 : artar.
CEVAP A
KUVVET VE HAREKET
51
TEST
2
1.
DİNAMİK
ÇÖZÜMLER
3.
m=4kg
.
fs
2
1
mL=2m
➞
L
IFI=20N
k=?
.
yatay düzlem
Cisim durmakta olduğundan cismin ivmesi,
V = a.t
yatay düzlem
T1
mK=3m
30°
K
T2
15 = a.5
a = 3 m/s2 olur.
M
3mg
mM=5m
Ortam sürtünmeli olduğundan sürtünme kuvveti,
F – fs
m
20 – fs
3=
4
5mg
a=
Sistem 1 yönünde hareket eder.
Sistemin ivmesi,
Fnet
5mg – 3mg
2
2.10
=
=
= 2 m/s olur.
Rm 3m + 2m + 5m
10
a=
12 = 20 – fs
fs = 8 N olur.
2 saniye sonra L cisminin hızı,
V = a.t = 2.2 = 4 m/s olur.
Sürtünme kat sayısı,
CEVAP C
fs = kmg
8 = k.4.10
1
k=
= 0,2 olur.
5
4.
CEVAP A
a=
2.
H.Y.
H.Y.
mL=4kg
L
T
mK=6kg
GxK=48N
53°
.
GM=50N
3mg – mg
4m
=
2g
4
Cisimlere etki eden kuvvetler şekilde gösterilmiştir. Sistemin ivmesi,
G + G xL – G M
a = xK
mK + mL + mM
fs
GxK – T = mK.a
KUVVET VE HAREKET
mg
CEVAP C
K
L
k=0,3
mL=3kg
Sistemin maksimum ivmesi,
CEVAP A
yatay
düzlem
K ile L cisimleri arasındaki sürtünme kuvveti,
fs = k.mK.g = 0,3.2.10 = 6 N olur.
48 – T = 6.2
52
2mg
mK=m K
mK=2kg
IFI=8N
K cismine dinamiğin temel prensibi uygulanırsa,
T
M mM=2m
.
➞
= 2 m/s2 olur.
T = 48 – 12 = 36 N olur.
mg
5.
=
mL=m
L
GM – T = mM.a
g
2mg – T = 2m.
2
T = mg olur.
yatay düzlem
48 + 32 – 50
6+4+5
30
=
15
=
M cismine dinamiğin temel
prensibi uygulanırsa,
M
K
Fnet
Rm
g
=
olur.
2
mM=5kg
GxL=32N
Sistemin ivmesi,
amak =
fs
2
6
= = 2 m/s olur.
mL 3
K ve L cisimlerini ortak hareket ettirebilecek en
büyük kuvvet,
Fmak = (mK + mL).amak
= (2 + 3).2
= 10 N olur.
K cismine uygulanan 8 N luk kuvvet, cisimleri ortak
hareket ettirir.
2
F
8
8
a=
=
= m/s olur.
mK + mL 2 + 3 5
8.
2V•
V•
0•
halat
–a
9.
N
.
fs
➞
Cisim sabit hızla hareket ettiğine göre,
fsür = F = 8 N olur.
Sürtünme kuvvetinden,
fsür = k(mg – ma)
8 = 0,4.(40 – 4.a)
20 = 40 – 4a
mL=6kg
L
CEVAP E
2a
T
T
.
yatay düzlem
T
10.
2T
K
mK=6kg
a
mK.a
•
ip
.
fs T
L
ivme
.
kuvvet
2a•
2F•
K cisminin ivmesi, aK = a ⇒ aL = 2a olur.
L cismine dinamiğin temel prensibi uygulanırsa,
T
K
Sürtünme kuvveti,
fs = k.mK.g
= 0,5.2.10
= 10 N olur.
K cismine dinamiğin temel prensibi uygulanırsa,
T – fs = mK.a
T – 10 = 2a
T = 2a + 10 olur.
L cismine dinamiğin temel prensibi uygulanırsa,
F – (T + fs) = mL.a
30 – (2a + 10 + 10) = 3.a
10 = 5a
a = 2 m/s2 olur.
T gerilme kuvveti,
T = 2.2 + 10 = 14 N olur.
CEVAP B
mg
7.
•
3t zaman
mL=3kg
yatay düzlem
IFI=8N
20 = 4a ⇒ a = 5 m/s2 olur.
•
2t
mK=2kg
k=0,5
fs
|F|=30N .
Fey.=ma
m=4kg
•t
Kuvvet ile ivme doğru orantılı olduğundan, kuvvet-zaman grafiğini ivme-zaman grafiği gibi düşünebiliriz. Bu durumda cismin hız-zaman grafiği
şekildeki gibi olur.
CEVAP D
CEVAP B
6.
hız
0•
T = mL.2a
•t
2t
•
3t
•
zaman
0•
•t
2t
•
3t
•
zaman
T = 6.2a = 12a olur.
K cismine dinamiğin temel prensibi uygulanırsa,
mK.g – 2T = mK.a
–3F•
fiekil-I
6.10 – 2.12a = 6a
60 = 30a
a = 2 m/s2 olur.
T gerilme kuvveti,
T = 12a = 12.2 = 24 N olur.
–3a•
CEVAP D
fiekil-II
Hız-zaman grafiğinde doğrunun eğimi ivmeyi vereceğinden cismin ivme-zaman grafiği Şekil-I deki
gibi olur. Bu durumda cisme etkiyen yatay kuvvetin
zamanla değişim grafiği Şekil-II deki gibi olur.
CEVAP E
KUVVET VE HAREKET
53
TEST
1.
3
DİNAMİK
ÇÖZÜMLER
4.
Sistemin ivmesi,
V(m/s)
F
F – F2
2
40 – 10 30
a = net = 1
=
=
= 6 m/s
3+2
5
Rm m K + m L
olur.
12
mL=2kg
.
FKL
L
4
.
➞
IF2I=10N
0
yatay düzlem
K nin L ye uyguladığı kuvvet,
t(s)
4
Cismin yavaşlama ivmesi,
FKL – F2 = mL.a
TV 4 – 12 –8
2
a=
=
=
= –2 m/s olur.
4–0
4
Tt
FKL – 10 = 2.6
FKL = 22 N olur.
Cisme etki eden sürtünme kuvveti,
CEVAP D
Fnet
a=
Rm
10 – Fs
–2 =
5
–10 = 10 – Fs
2.
mK=3m
L
K
fs = 20 N olur.
mL=m
Sürtünme kat sayısı,
mL.g.sin37°
mK.g.sin37°
fs = kmg
37°
20 = k.5.10
2
= 0,4 olur.
k=
5
.
yatay düzlem
CEVAP C
Sistemin ivmesi,
F net
a=
Rm
m K g sin 37° – m L g sin 37°
=
mK + mL
=
=
➞
5.
(–)
yatay
= 5.10.0,6
•
Sistemin ivmesi,
(+)
m X
m
2α
= 30 N olur.
m
mgsinα
α
GxK=30N
37°
GxK = mK.g.sin37°
CEVAP C
mgsin2α
T
miştir.
= 3 m/s2 olur.
K
➞
a
şekilde gösteril-
6.2
4
.
mK=5kg
eden kuvvetler
10.0, 6 (3m – m)
4m
3.
IFI=40N
Cisimlere etki
T
mL=7kg
L
GL=70N
a=
Fnet (G L + G xK) – F
=
Rm
mK + mL
a=
(70 + 30) – 40 60
2
=
= 5 m/s olur.
5+7
12
L cismine dinamiğin temel prensibi uygulanırsa,
GL – T = mL.a
mgsin2α > mgsinα olduğundan
70 – T = 7.5
X cismi (–) yönde düzgün hızlanır.
CEVAP E
54
KUVVET VE HAREKET
T = 35 N olur.
CEVAP B
6.
8.
Fsür=k.mg.cosi
m
•
30°
yatay
•
T
L
fs
mgsini
A
2a
mL=4kg
j
yatay düzlem
.
k=0,25
T
B
2T
K
60°
C
•
yatay
düzlem
a
mK.g
K cisminin ivmesi,
Cisim sabit hızla hareket edebilmesi için net kuvvetin sıfır olması gerekir.
aK = a ⇒ aL = 2a olur.
L cismine etki eden sürtünme kuvveti,
k.mgcosθ = mg.sinθ
fs = k.mL.g
k.cosθ = sinθ
sin i
k=
= tanθ olur.
cos i
= 0,25.4.10
= 10 N olur.
AB bölümünde:
k = tan30° =
mK=4kg
L cismine dinamiğin temel prensibi uygulanırsa,
1
olur.
3
T – fs = mL.aL
T – 10 = 4.2a
BC bölümünde:
T = 8a + 10
kı = tan 60° = v3 olur.
K cismine dinamiğin temel prensibi uygulanırsa,
kı ve k sürtüme katsayıları oranlandığında,
GK – 2T = mK.a
›
k
3
=
= 3 ⇒ kı = 3k olur.
k
1
3
mK.g – 2T = mK.a
4.10 – 2(8a + 10) = 4.a
CEVAP D
40 – 16a – 20 = 4a
20 = 20a
düfley
7.
a = 1 m/s2 olur.
➞
F
H.Y.
K
K cisminin ivmesi 1 m/s2 olur.
mK=1kg
T=42N
GK=10N
CEVAP B
9.
T2
a
L
m
=2
mL=3kg
mL
2m.g.sin30°
T2
L
GL=30N
M mM=m
30°
L cismi için dinamiğin temel prensibini uygularsak,
T – GL = mL.a
a
mg
T1=12N
a m =2m K
K
42 – 30 = 3.a
2mg
12 = 3a
Sistemin ivmesi,
2mg + 2mg sin 30° – mg
a=
5m
2g
=
5
20
=
5
a = 4 m/s2 olur.
Sistemi harekete geçiren kuvvet,
F – (GK + GL) = (mK + mL).a
F – 40 = 4.4
F = 56 N olur.
CEVAP A
= 4m/s2 olur.
KUVVET VE HAREKET
55
K cismine dinamiğin temel prensibi uygulanırsa,
11.
mK=m
GK – T1 = mK.a
2mg – T1 = 2m.a
K
ip
.
•
fs
fs
L
2m.10 – 12 = 2m.4
yatay
düzlem
mL=2m
12m = 12
.
m = 1 kg olur.
M
M cismine dinamiğin temel prensibi uygulanırsa,
mM=m
T2 – mM.g = mM.a
GM=m.g
T2 – mg = ma
Sistemin ivmesi,
T2 – 1.10 = 1.4
T2 = 14 N olur.
CEVAP A
a mak =
fs
f
= s
m L 2m
a mak =
m M .g – fs
mK + mM
a mak =
mg – fs
m+m
olur. İki eşitlikten,
fs
m.g – fs
=
2m
2m
2fs = mg
10.
mK=2kg
k=0,3
mL=3kg
fs =
K
L
fs
.
mg
2
olur. K ve L cisimleri arasındaki sürtünme katsayısı
➞
F
fs = k mK g
yatay düzlem
mg
= kmg
2
Sürtünme kuvveti,
fs = k.mK.g = 0,3.2.10 = 6 N olur.
k = 0,5 olur.
CEVAP D
Maksimum ivme,
amak =
fs
2
6
= = 3 m/s olur.
mK 2
F kuvvetinin en büyük değeri,
12.
Fmak = (mK + mL).amak
2V
= (2 + 3).3
= 15 N olur.
h›z
CEVAP B
x
V
x
0
2x
t
2x
2t
3t
zaman
Cismin hız-zaman grafiği şekildeki gibidir.
Grafiğe göre, I., II. ve III. yargılar doğrudur.
CEVAP E
56
KUVVET VE HAREKET
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
Bölüm
Yazılı Soruları
(Dinamik)
1.
ÇÖZÜMLER
3.
mL=5kg
T
a
T
3
sin
.g.
m L 37°
T
mL=2kg
L
GXL=10N
mK=3kg
K
.
30°
GXL = mL.g.sin30° = 2.10.
GK=30N
yatay
a
mK=5kg
yatay
düzlem
53°
yatay düzlem
Sistemin ivmesi,
m K .g sin 53° + m L g sin 37°
a=
mK + mL
F
G – G XL
a = net = K
Rm
mK + mL
5.10.0, 8 + 5.10.0, 6
5+5
40 + 30
=
10
2
30 – 10 20
=
= 4 m/s olur.
2+3
5
=
b) K cismine dinamiğin temel prensibi uygulanırsa,
GK – T = mK.a
= 7 m/s2 olur.
30 – T = 3.4 ⇒ T = 18 N olur.
K cismine dinamiğin temel prensibi uygulanırsa,
2.
mK.g.sin53° – T = mK.a
m
5.10.0,8 – T = 5.7
A
m
10
8m
k=0,5
53°
B
T = 40 – 35 ⇒ T = 5 N olur.
4.
x=
V
K
mK.g.sin53°
1
= 10 N
2
a) Sistemin ivmesi,
a=
L
7°
.
mK=3kg
fsK=3N
T
K
yatay k=0,1
düzlem
T
yatay düzlem
a) Cismin ivmesi,
a = g.(sinα – k.cosα)
= g.(sin53° – k.cos53°)
= 10.(0,8 – 0,5.0,6)
= 10.(0,8 – 0,3)
= 10.0,5
= 5 m/s2 olur.
b) Cismin aldığı yoldan,
1
x = .at2
2
1
.5.t2
2
t2 = 4
10 =
t = 2s olur.
c) Cismin B noktasına geldiği anda hızı,
V = a.t = 5.2 = 10 m/s olur.
mL=2kg
fsL=3N
L
mLg.sin53°
k=0,25
.
53°
yatay düzlem
a) K ve L cisimlerine etki eden sürtünme kuvvetleri,
fsK = k.mK.g = 0,1.3.10 = 3 N
fsL = k.mL.g.cos53° = 0,25.2.10.0,6 = 3 N
olur. Sistemin ivmesi,
F
a = net
Rm
m L .g. sin 53° – (fsK + fsL)
=
mK + mL
=
2.10.0, 8 – (3 + 3)
⇒ a = 2 m/s2 olur.
3+2
b) K cismine dinamiğin temel prensibi uygulanırsa,
T – fsK = mK.a
T – 3 = 3.2 ⇒ T = 9 N olur.
KUVVET VE HAREKET
57
5.
8.
➞
IFI=20N
yatay
N=46N
mK=2kg
➞
m=3,4kg
37°
O
fs
16m
Fy=12N
K ve L cisimlerine etki eden sürtünme kuvveti,
fs = k(mK + mL).g
G=34N
= 0,2.(2 + 3).10
a) Sürtünme kuvveti, fs = k.N = 0,2.46 = 9,2 N
= 10 N olur.
Cismin ivmesi,
Sistemin ivmesi 2 m/s2 olduğuna göre,
F – fs
a=
mK + mL
F
F –f
a = net = x s
Rm
m
=
16 – 9, 2 6, 8
2
=
= 2 m/s olur.
3, 4
3, 4
10 = F – 10
F = 20 N olur.
9.
Sistemin ivmesi,
F
a = net
Rm
=
F – (G K + G L)
mK + mL
=
60 – 50
2+3
=
10
5
düfley
a=5m/s2
halat
ı
GK=20N
= 3.(10 + 5)
= 45 N
mK=2kg
K
ı
GL
= mL.(g + a)
= 2.(10 + 5)
= 30 N olur.
T
L
= 2 m/s2 olur.
K ve L cisimlerine
etki eden kuvvetler,
G K = mK.(g + a)
IFI=60N
H.Y.
F – 10
2+3
2=
b) Cismin B noktasındaki hızı,
V2 = 2ax
V2 = 2.2.16
V2 = 64
V = 8 m/s olur.
6.
yatay düzlem
k=0,2
yatay
düzlem
B
L
K
fs
Fx=16N
A
k=0,2
.
F
mL=3kg
mL=3kg
a›
mL=2kg L
›
aı =
L cismine dinamiğin temel prensibi uygulanırsa,
T – GL = mL.a
T – 30 = 3.2
T = 36 N olur.
K mK=3kg a›
G›K=45N
G›L=30N
Sistemin ivmesi,
GL=30N
T
T
›
G K – G L 45 – 30 15
2
=
=
= 3 m/s olur.
mK + mL
3+2
5
T gerilme kuvveti,
ı
G K – T = mK.aı
45 – T = 3.3
T = 36 N olur.
7.
T=38N
m=5kg
Fey=ma
10.
➞
a
37°
➞
IFI=40N
fs
GX
37°
.
KUVVET VE HAREKET
K
L
yatay
düzlem
İpteki gerilme kuvveti T = 38 N olduğuna göre
arabanın ivmesi,
T = mgsin37° + ma.cos37°
T = 5.10.0,6 + 5.a.0,8
38 = 30 + 4a
8 = 4a
a = 2 m/s2 olur.
58
.
mK=4kg
fs
mL=8kg
k=0
yatay
düzlem
Cisimler ayrı ayrı düşünüldüğünde,
fs = k.mK.g = 0,4.4.10 = 16 N
aK =
F – fs 40 – 16 24
2
=
=
= 6 m/s olur.
mK
4
4
aL =
fs
2
16
=
= 2 m/s olur.
mL
8
4. BÖLÜM
HAREKET
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
4.
hız
V•
1.
0
h›z
•
2t
•
zaman
•
zaman
3t
–V •
V•
•
•
0
• 3t
2t
t
ivme
zaman
a•
–V•
0
Araç, (0-t) aralığında +x yönünde hızlanmakta,
(t-2t) aralığında +x yönünde yavaşlamakta, (2t-3t)
aralığında ise -x yönünde hızlanmaktadır. Aracın
hız-zaman grafiği şekildeki gibidir.
CEVAP A
2.
t•
konum
t•
•
2t
3t
–a •
0-3t aralığında aracın hız-zaman ve ivme-zaman
grafikleri şekildeki gibi olur.
Araç t = 0 anında x kadar öndedir. t sürede –x
kadar yol alıp başlangıç noktasına geri dönmüştür.
x•
Bu süreden sonra hareketli yine (–) yönde hareket
etmektedir. 2t anında hareketlinin hızı sıfır olup
K
•
0
t
zaman
L
(+) yönde yön değiştirmiştir. Araç, 2t anında yön
değiştirmiştir.
I. yargı doğrudur.
–x •
Aracın 0-t zaman aralığındaki ivme vektörü ile
0-t zaman aralığında:
t-2t zaman aralığındaki ivme vektörü zıt işaretlidir.
K ile L araçları +x yönünde eşit ve sabit hızlarla hareket etmektedir.
II. yargı doğrudur.
I. yargı doğrudur.
2t-3t zaman aralığındaki ivme vektörü aynı işaret-
II. yargı yanlıştır.
lidir.
K ile L araçları arasındaki uzaklık sabit kalmaktadır.
III. yargı yanlıştır.
III. yargı doğrudur.
Aracın t-2t zaman aralığındaki ivme vektörü ile
CEVAP C
CEVAP D
3.
hız
V•
•
0
t
•
•
2t
3t
zaman
ivme
a•
0
•
t
• 2t
• 3t
zaman
–a •
0-3t zaman aralığında aracın hız-zaman ve ivmezaman grafikleri şekildeki gibi olur.
CEVAP D
KUVVET VE HAREKET
59
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
5.
h›z
K
V•
1.
konum
•
0
•
t
2t
•
3t
hız
0
II
III
III zaman aralığında araçlar arasındaki uzaklık
azalmaktadır.
CEVAP D
V•
K
+x
K
+x
•t
L
•
+x
•
0
2t zaman
+x
L
•
2t zaman
t
hız
2V •
M
+x
0
•
•
V•
–x 2t zaman
M
t
4x•
L
•
• 3t
2t
x
–x
• 4t
zaman
–V •
Yalnız M aracı 2t anında, t = 0 anındaki konumuna
dönmüştür.
CEVAP C
0-3t zaman aralığında aracın konum-zaman grafiği
şekildeki gibi olur.
K
x
•t
0
–V•
Şekildeki hız-zaman grafiğinde görüldüğü gibi, 4t
anında K ile L araçları arasındaki uzaklık 2x tir.
konum
CEVAP B
2x•
x•
0•
•t
•
2t
•
7.
V(m/s)
3t zaman
CEVAP B
4.
h›z
6.
V•
3.
I
I ve II zaman aralıklarında araçlar arasındaki
uzaklık artmaktadır.
hız
V•
zaman
zaman
Aracın konum-zaman grafiği şekildeki gibidir.
CEVAP C
2.
• 3t
2t
L
–V •
x•
•
t•
0
2x •
K
30 •
V(m/s)
30
20 •
•
20
•
L
10
•
K
L
10 •
0
•
5
•
10
•
15
•
20
t(s)
K ve L araçlarının aldıkları yollar,
•
0
•
2
•
4
•
6
•
8
K ve L araçlarının aldıkları yollar,
∆xK = 120 m
xK = 10 + 120 = 130 m
∆xL = 140 m
xL = 140 m
xL – xK = 140 – 130 = 10 m olur.
Buna göre; L aracı K den 10 m öndedir.
60
KUVVET VE HAREKET
t(s)
∆xK = ( 10 + 20 ) .30 = 450 m
2
∆xL = ( 10 + 30 ) .15 + 5.10
2
= 300 + 50
= 350 m olur.
CEVAP B
Buna göre, t = 0 anında K aracı L den 100 m geridedir.
CEVAP D
8.
0-t zaman aralığında,
K aracı +x yönünde
yavaşlayıp durmakta,
L aracı ise –x yönünde hızlanmaktadır.
hız
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
V•
K
DxK= +x
0
DxL= –x
K ile L araçları birbirine zıt yönde hareket
etmektedir.
•t
t(s)
L
h›z
1. 0-3t zaman aralığında
aracın hız-zaman grafiği
şekildeki gibi olur.
2V•
V•
•t
0
–V•
•
•
3t zaman
2t
I. yargı doğrudur.
CEVAP C
V
olur.
2
–V
=
olur.
2
VortK =
VortL
2.
h›z
II. yargı doğrudur.
3V•
0–V
V
=–
olur.
t–0
t
–V – 0
V
aL =
=–
olur.
t–0
t
aK =
2V•
V•
III. yargı doğrudur.
CEVAP E
•t
0
•
•
2t
zaman
3t
Aracın hız-zaman grafiği şekildeki gibidir.
9.
∆xK = 125 m
Grafiğe göre;
V(m/s)
xK = 125 m
I. yargı yanlıştır.
20 •
∆xL = 100 m
L
xL = 25+100 = 125 m
10
Buna göre, L aracı durduğu anda araçlar yan
yanadırlar.
II. ve III. yargılar doğrudur.
25m
25m
K
25m
50m
0
CEVAP E
25m
•
5
•
10 t(s)
3.
CEVAP E
10.
0-3t zaman aralığında
aracın hız-zaman grafiği şekildeki gibi olur.
h›z
2V•
V•
h›z
V•
•
•
3t zaman
2t
K
CEVAP A
•
0
–V •
•t
0
t
•
2t
• 3t
zaman
4.
L
h›z
h›z
2V•
K ile L araçları t anında yön değiştirmişlerdir.
I. yargı kesinlikle doğrudur.
x
V•
0
x
K ile L araçlarının t = 0 anındaki konumları bilinmediğinden, 2t anındaki konumları için kesin birşey
söylenemez.
•t
2x
•
2t
2x
V•
•
3t zaman
0
x
•t
2x
•
x
2t
K
L
fiekil-I
fiekil-II
•
3t zaman
II. yargı için kesin birşey söylenemez.
K ve L araçlarının hız-zaman grafikleri Şekil-I ve
2t anında cisimlerin konumları t=0 anındaki konumdur. Bu konum bilinmediğinden 2t-3t aralığında araçlar arasındaki uzaklıkların nasıl değişeceği
bilinemez.
Şekil-II deki gibidir.
III. yargı için kesin birşey söylenemez.
CEVAP A
∆xK = 6x, ∆xL = 4x tir.
Buna göre, t = 0 anında K aracı L den 2x kadar geridedir.
CEVAP D
KUVVET VE HAREKET
61
5.
8.
h›z
hız
3V•
2V•
2x
V•
2x
I
0
x
2x
II
•t
•
2x
III
2t
2V•
•
V• Dx
I
zaman
3t
DxII
DxIII
Aracın 0-3t zaman aralığında hız-zaman grafiği şekildeki gibidir. Hareketlinin yer değiştirmeleri,
0
I
•t
II
•
•
zaman
2t III 3t
(0-3t) zaman aralığında aracın hız-zaman grafiği
şekildeki gibi olur.
∆x1 = 2x
∆x2 = 4x
Şekilde görüldüğü gibi, DxI = DxII > DxIII olur.
∆x3 = 3x
CEVAP C
∆x2 > ∆x3 > ∆x1 olur.
CEVAP E
9.
Kuvvet
ile
ivme
h›z
doğru orantılı oldu-
2V
ğundan kuvvet-zaV
man grafiği ivme-
6.
V(m/s)
x
zaman grafiği ola0
rak düşünülebilir.
20•
3
x
2
2x
t
zaman
3t
2t
Hız-zaman grafiğinde doğrunun altındaki alan
10•
50m 100m
•
0
•
5
hareketlinin yer değiştirmesini verir. Bu durumda
75m
•
10
15
cismin hız-zaman grafiği şekildeki gibidir.
t(s)
2V.t
V.t
+ 2V.t + V.t +
2
2
x
= x + 2x + x +
2
9x
=
olur.
2
∆x =
Aracın hız-zaman grafiği şekildeki gibidir.
Aracın (0-15) s aralığındaki yer değiştirmesi,
∆x = 50 + 100 + 75 = 225 m olur.
CEVAP D
10.
7.
V(m/s)
Vo+8•
V(m/s)
22•
Vo •
20•
18•
4•
CEVAP E
0
•
4
48m
0
76m
•4
•
12
t(s)
Aracın (0-12) s aralığındaki hız-zaman grafiği şekildeki gibidir.
80m
•8
•
8
•
12
Hareketli (0-12)s aralığında ∆x = 120 m yer değiştirdiğinden,
t(s)
Aracın (0 – 12) s aralığında hız-zaman grafiği
şekildeki gibi olur.
D x = 48 + 76 + 80 = 204 m olur.
∆x = 120 m
(Vo + Vo + 8)
Vo.4 +
.4 + (Vo + 8).4 = 120
2
4Vo + (2Vo + 8).2 + (Vo + 8).4 = 120
Aracın (0 – 12) s aralığında ortalama hızı,
Dx
204
=
= 17 m/s olur.
Vort =
12
Dt
12Vo + 48 = 120
12 Vo = 72
CEVAP D
Vo = 6 m/s olur.
CEVAP B
62
KUVVET VE HAREKET
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
5.
Aracın ivmesi,
V s2 = V o2 + 2a.x
122 = 82 + 2a.20
1. Araç a sabit ivmesi ile hızlandığına göre hız-zaman
144 = 64 + 40a
grafiği şekildeki gibi olur. İvmesi,
80 = 40a ⇒ a = 2 m/s2 olur.
V(m/s)
11a
(10a + 11a)
42 =
.1
2
Hızı 20 m/s iken aracın harekete geçtiği noktadan
uzaklığı,
10a
84 = 21. a
V s2 = V o2 + 2a.x
42m
2
a = 4 m/s olur.
0
10
11
V2 = 0 + 2a.x
t(s)
V2 = 2a.x
CEVAP D
2.
Aracın ivmesi,
1
x = .a.t2
2
1
50 = .a.52
2
202 = 2.2.x
400 = 4.x & x = 100 m olur.
6.
a = 4 m/s2 olur.
3.
Aracın hız-zaman grafiği şekildeki gibi olur.
CEVAP D
V(m/s)
20•
18•
16•
Aracın 4. saniye içerisinde yaptığı yer değiştirme,
∆x = :
Araçlar eşit yol aldıklarından birbirlerini yakalarlar.
Bu sürede geçen zaman,
xK = xL
1
. a . t2 = VL . t
2
1
. 5 . t2 = 30 . t
2
t = 12 s olur.
Alınan yol ise,
Aracın 10. saniye sonunda hızı,
V= a.t = 4.10 = 40 m/s olur.
xK = xL = 30 . 12 = 360 m olur.
7.
Tx
10•
16 + 18
D .1
2
0
CEVAP C
•
1
•
2
•
3
•
4
•
5 t(s)
= 17 m olur.
CEVAP C
Yolcunun otobüse yetişme süresi,
Vo = a . t
6 = 2 . t ⇒ t = 3 s olur.
Otobüs harekete başladığı an yolcu ile otobüs arasındaki uzaklık,
CEVAP A
∆x = xy – xo
1
. a . t2
2
1
. 2 . 32
=8.3–
2
= 24 – 9
= Vy. t –
4.
I
a1=4m/s2
K
II
|KL|
L
a2=3m/s2
x2 =750m
= 15 m olur.
M
CEVAP B
x1
Araçlar t sürede M noktasına varmış ise,
1
. a2 . t2
x2 =
2
1
750 =
. 3 . t2
2
t2 = 500 ⇒ t = 10v5 saniye olur.
8.
15. saniyede yan yana geldiklerine göre
araçların aldıkları
yollar eşittir.
xK = xL
|KL| + x2
|KL| + 750
|KL| + 750
|KL| = 250 m olur.
CEVAP E
K
30 •
L
20•
0
•
t
15 + 15 – t
D .30 = 20.15
2
30 – t = 20
t = 10 s olur.
K aracının hızlanma sırasındaki ivmesi,
30
aK =
= 3 m/s2 olur.
10
:
|KL| + 750
(15-t)
Bu durumda,
|KL| uzaklığı,
x1 =
1
. a1 . t2 =
2
1
. 4 . 500 =
2
1000 =
V(m/s)
•
15 t(s)
CEVAP B
KUVVET VE HAREKET
63
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
1.
5.
Aracın yavaşlama ivmesinin büyüklüğü,
Vs2 = Vo2 – 2a.x
102 = 302 – 2a.100
Cismin ilk hızı,
V .5
50 = o
2
V(m/s)
100 = 900 – 200.a
Vo
–800 = –200.a
a = 4 m/s2 olur.
Vo = 20 m/s olur.
a=
=
ile yavaşlamaya devam ettiğinde duruncaya kadar
TV
Tt
0
5
t(s)
aldığı yol,
ı
Vs2 = Vo2 – 2a.x
0 – 20
5–0
= –4 m/s
2.
Aracın hızı 10 m/s ye düştükten sonra, aynı ivme
50m
Cismin ivmesi,
2
ı
olur.
Aracın yavaşlama ivmesinin büyüklüğü,
Vs2 = Vo2 – 2a.x
152 = 252 – 2a.100
225 = 625 – 200.a
– 400 = –200.a
a = 2 m/s2 olur.
6.
= 4.5
V(m/s)
40
Aracın ivmesi,
CEVAP B
V(m/s)
2m
4
1
= –4
20
V
0–V
t – (t – 1)
=–
0
m/s2
t–1
0
5
t=
100m
15
25
t(s)
t (s)
olur.
40 40
=
= 10 s olur.
a
4
Alınan yol,
20
= 10 s olur.
2
x mak =
Vo . t 40 . 10
=
= 200 m olur.
2
2
Aracın aldığı toplam yol,
CEVAP D
x = 50+200+100 = 350 m olur.
CEVAP E
7.
Uçağın hızı,
Vo = 288
4.
t
Aracın durma süresi,
50m 200m
t3 =
V .1
2
V = 4 m/s olur.
= 20 m/s
olur. Aracın durma
süresi,
CEVAP B
Son saniyede 2 m yol aldığına göre V hızı,
2=
Aracın 5 saniye sonra hızı,
V1 = a 1 . t 1
ı
100 = 8. x ⇒ x = 12,5 m olur.
CEVAP A
a=
3.
ı
0 = (10)2 – 2.4.x
V(m/s)
= 288
20 •
V(m/s)
km
h
Δx=1600m
Vo=80
1000m
3600s
a=4m/s2
= 80 m/s olur.
0
100m
•
10
400m
50m
•
•
30 35
t(s)
Aracın 10 s sonraki hızı,
t+20
∆x = 1600 m
t + t + 20 E
1600 = ;
. 80
2
Aracın durma süresi,
20
tdurma =
= 5 s olur.
4
Aracın hız-zaman grafiği şekildeki gibidir.
Aracın harekete başladığı noktadan uzaklığı,
x = 100 + 400 + 50 = 550 m olur.
40 = 2t + 20
t = 10 s olur.
Durana kadar geçen toplam süre,
Σt = t + 20 = 10 + 20 = 30 s olur.
CEVAP C
KUVVET VE HAREKET
t (s)
t
Uçağın pistte sabit hızla gittiği süre,
V1 = a1.t1 = 2.10 = 20 m/s olur.
64
Durma süresi,
0
Vo 80
t durma =
=
= 20 s olur.
a
4
CEVAP D
8.
12. K ve L araçlarının hız-zaman
grafikleri şekildeki gibidir.
Hız-zaman grafiğini çizersek cismin ilk hızı,
V + 20
F . 10
250 = < o
2
b
Vo
50 = Vo + 20
t = 10 s olur.
0
10
4
a=
V(m/s)
30•
–4 =
13.
K
TV
a=
Tt
x
10•
10 – 30
t–0
t
•
t(s)
t
(30 – 10)
.5 = 10.5 = 50 m olur.
2
t(s)
VL = 8 m/s
K
L
•
•
do¤rusal
yol
42 m
Taralı alan araçlar arasındaki uzaklığı vereceğinden,
x=
•
0
10 – 30 – 20
DV
=
= –2 m/s2 olur.
=
10 – 0
10
Dt
CEVAP B
VK = 20 m/s
L
0
–4t = –20
t = 5 s olur.
L
Çarpışmanın olmaması için K aracının yavaşlama
ivmesinin büyüklüğü en az,
t(s)
CEVAP C
Araçların hız-zaman
grafikleri şekildeki gibi
olur.
100m
10 •
20t = 200
250m
9.
K
30 – 10
l .t = 100
2
20
Vo = 30 m/s olur.
V(m/s)
30 •
K aracı ile L aracı arasındaki uzaklık en az olduğu
an, K aracının hızı 8 m/s olur.
Vs = Vo – a.t
Vs = VK – at
CEVAP A
8 = 20 – 2.t
2t = 12
10.
t = 6 s olur.
VK = 30 m/s
VL = 18 m/s
K
L
•
•
K aracı ile L aracı arasındaki uzaklık
do¤rusal
yol
x
Araçların hız-zaman grafikleri şekildeki gibidir.
Araçlar arasındaki x uzaklığı,
şekildeki taralı alana eşit olduğundan,
x=
30•
18•
= (42 + 8.6) – [20.6 – 1 2.62]
2
= 90 – 84
= 6 m olur.
K
x
K aracı L aracına en az 6 m yaklaşır.
CEVAP C
L
•4
0
= 12.2
t(s)
= 24 m olur.
CEVAP D
11. Araçların hız-zaman
grafikleri şekildeki
gibi olur.
Araçların yan yana
gelme süresi,
30.t
= 120
2
t = 8 s olur.
14. K aracının yavaşlama ivmesi 2 m/s2 olduğuna göre;
30
20 – 30
–2 =
t
20
40•
t = 5 s olur.
K
10•
0
V(m/s)
TV
Tt
a=
K
x
L
–2t = –10
V(m/s)
V
1 2
at )
2
= (xo + VL.t) – (VK.t –
V(m/s)
V•
(30 – 18)
.4
2
∆x = (xo + xL) – (xK)
0
t
t (s)
Araçların arasındaki uzaklık,
120m
x=
L
•
t
=
t(s)
CEVAP C
10 . 5
2
50
2
= 25 m olmal›d›r.
CEVAP E
KUVVET VE HAREKET
65
TEST
1
1.
ÇÖZÜMLER
30•
4.
V(m/s)
HAREKET
h›z
V
K
I
0
•
•
10
L
t(s)
III
3t
zaman
Aracın hız-zaman grafiği şekildeki gibidir.
Araç II. zaman aralığında düzgün yavaşlamıştır.
10. saniyenin sonunda K ve L araçlarının arasındaki uzaklık şekildeki taralı alan kadardır.
CEVAP B
5.
40.10
= 200 m olur.
2
V(m/s)
CEVAP B
30 •
L
20 •
h›z
2.
2t
–V
–10 •
Dx =
II
t
0
Dx
ΔxK=x
V
10 •
K
K
0
0
zaman
t
ΔxL=–x
L
aL =
–V – 0 –V
=
t–0
t
DxL = 110 m olur.
xL = 0 + 110 = 110 m olur.
Buna göre, 6. saniye sonunda K aracı L den 10 m
II. yargı doğrudur.
Araçların konum değişimlerinin büyüklükleri eşittir.
III. yargı doğrudur.
CEVAP D
3.
2V•
CEVAP A
6.
h›z
•
0
2x
•
t
4x
2t
•
3t
–x
• 4t
• 5t
+x
t
•
2t
+x
•
3t
•
–x 4t
zaman
zaman
Araç, 2t anında, t = 0 anındaki konumundadır.
–2x
I. yargı doğrudur.
fiekil-II
Araç, 3t anında yön değiştirmiştir.
Yolun her aralığına x diyelim.
(0-5t) zaman aralığında aracın yer değiştirmesi,
Dx = 2x + 4x – x – 2x = +3x olur.
Buna göre, araç 5t anında N noktasından geçer.
CEVAP A
KUVVET VE HAREKET
–x
•
–V•
•
–V•
66
öndedir.
V•
h›z
•
0
t(s)
xK = 20 + 100 = 120 m olur.
a L = –a d›r.
(
6
DxK = 100 m olur.
a K = –a d›r.
(
•
4
(0-6) s aralığında,
Araçlar zıt yönde hareket etmektedir.
I. yargı yanlıştır.
0 – V –V
=
t–0
t
•
2
Doğruların altındaki alan araçların yer değiştirmesini vereceğinden,
–V
aK =
•
•
II. yargı doğrudur.
Araç, 4t anında, t = 0 anındaki konumundadır.
III. yargı yanlıştır.
CEVAP C
10. Doğrunun altındaki alan hareketlinin yer değiştir-
7.
mesini verir. Aracın ilk hızı,
Vo=10m/s
K
Vs=30m/s
L
80m
V + 3V E
100 = ;
.5
2
40 = 4V
yatay yol
V = 10 m/s olur.
Araç düzgün hızlandığına göre, zamansız hız for-
Doğrunun eğimi aracın
mülünden,
V
θ
ivmesini vereceğinden,
2
Vs2 = Vo + 2a . x
302 = 102 + 2a . 80
a=
800 = 160a
a = 5 m/s2 olur.
CEVAP E
0
TV
Tt
=
30 – 10
5
=
20
5
= 4 m/s
8.
h›z(m/s)
3V
2
5 t (s)
olur.
CEVAP C
konum
3x•
K
11.
2x•
x•
V(m/s)
15
K
L
0
•
L
–x •
• 2t
•t
• 3t
5
zaman
I
0
I
II
II
5
III
10
15
t(s)
–5
III
Hareketlinin hız-zaman grafiği şekildeki gibidir.
K ve L araçlarının konum-zaman grafikleri şekildeki gibi olur.
Hareketli I. ve II. zaman aralıklarında yön değiştirmiştir.
Şekilde görüldüğü gibi; K ve L araçları II. zaman
aralığında aynı yönde hareket etmişlerdir.
CEVAP D
CEVAP B
9.
12.
h›z(m/s)
h›z
4V
3V
K
3V
2x
V
2V
2x
0
–V
–2V
t
–2x
Δx3
zaman
Δx2
V
–x
0
L
K ve L araçlarının hız - zaman grafiği şekildeki gibi
olur.
x K 4x 4
=
=
olur.
x L 3x 3
Δx1
t
2t
3t
zaman(s)
Aracın hız-zaman grafiği şekildeki gibidir.
Grafiğe göre; I. yargı yanlıştır. II. yargı yanlıştır.
∆x3 > ∆x2 > ∆x1 III. yargı doğrudur.
CEVAP E
CEVAP C
KUVVET VE HAREKET
67
TEST
1.
2
3.
V (m/s)
30
a=5m/s2
10
80m
0
ts=6
t=4
(30 + 10)
80 =
.t
2
4.
0
t-2t aralığında –x
yönünde hızlanmıştır.
–x
zaman
3t
2t
t
CEVAP E
Hareketlinin hız-za-
V(m/s)
man grafiği şekilde-
20
ki gibi olur.
TV
Tt
10 – 30
=
4–0
–20
=
4
a=
Σ∆x = 56+40+64
12
= 160 m
8
0
56m 40m
olur.
64m
t (s)
4
6
10
CEVAP D
2
olur.
5.
Aracın durma süresi,
TV
Tt
30
& t s = 6 s olur.
5=
ts
V = Vo + a . t bağıntısına göre, araçların
ivmeleri bilinmediğinden, t anındaki
hızları bulunamaz.
h›z
K
VoK
Araçların t anındaki hızları bilinmediğinden, yer değiştirmeleri bulunamaz.
Aracın duruncaya kadar alacağı yol;
›
I. yargı doğrudur.
konum
III. yargı doğrudur.
Aracın yavaşlama ivmesi,
x =
x
2t-3t aralığında –x yönünde yavaşlamıştır.
t = 4 s olur.
a=
0-t aralığında +x
yönünde yavaşlamıştır.
II. yargı doğrudur.
t(s)
Doğrunun altındaki alan yer değiştirmeyi vereceğinden,
= –5 m/s
HAREKET
ÇÖZÜMLER
30.t s 30.6
=
= 90 m olur.
2
2
CEVAP A
Δx
L
VoL
0
zaman
t
(V o – V o )
L
. t bağıntısından, t anında, K ve
2
L araçları arasındaki uzaklık bulunabilir.
Tx =
K
CEVAP C
2.
h›z
2x
x
V
2x
x
I. yargı doğrudur.
2x
t = 0 anında L, K
nin önündedir.
L
II. yargı doğrudur.
t
2t
3t
zaman
3t anında K ve L araçları arasındaki uzaklık 10x
olur.
CEVAP C
68
K ile L araçları
aynı yönde hareket etmektedir.
–2x
0
–V
6.
K
2V
KUVVET VE HAREKET
h›z
2V•
L
V•
0
•t
•
2t
K
•
zaman
3t
t-3t zaman aralığında L, K den uzaklaşmaktadır.
III. yargı doğrudur.
CEVAP E
7.
10. Aracın hız-zaman
grafiği şekildeki
gibi olur. Aracın
yavaşlama ivmesi
3 m/s2 olduğuna
göre,
V(m/s)
t–4
16
K
12
L
0
3
4
t(s)
t
a1=2m/s2
30
20
a2=3m/s2
30
= 10 s
3
t2 =
Eşit yol aldıklarında K aracı L ye yetişir. Yetişme
süresi,
V(m/s)
0
t1=5
t2=15 t(s)
olur. Aracın t=0
anından itibaren durma süresi,
xK = xL
Σt = t1 + t2
= 5 + 10
= 15 s olur.
t + (t – 4)
<
F . 16 = 12t
2
CEVAP B
4t – 8 = 3t
t = 8 s olur.
11.
Alınan yol, xK = xL = 12 . 8 = 96 m olur.
K
CEVAP E
L
Vo
50m
A
150m
B
C
L aracının C noktasına gelme süresi,
1
. a . t2
xL =
2
8.
h›z
150 =
2V
1
. 3 . t2
2
t2 = 100
t = 10 s olur.
0
I
II
t
III
2t
Aynı sürede K aracı C noktasına geleceğinden,
zaman
3t
xK = Vo . t
–V
200 = Vo . 10
Aracın hız - zaman grafiği şekildeki gibidir. Aracın
Vo = 20 m/s olur.
hızının büyüklüğü I ve III zaman aralıklarında
CEVAP D
artmıştır.
CEVAP D
12.
h›z
h›z
K
L
2V
2V
x
V
x
0
9.
h›z
V•
0
t
•
2t zaman
0
x
t
2x
2x
2x
2x
2t
0
3t zaman
t
3t zaman
2t
ΔxL =9x olur.
h›z
M
a•
•
2x
ΔxK =6x olur.
ivme
2x
V
2V
•t
•
2t zaman
–V•
x
x
0
Aracın hız-zaman ve ivme-zaman grafikleri şekildeki gibi olur.
CEVAP B
x
V
2x
t
2x
2t
3t
zaman
ΔxM =7x olur.
Buna göre, ∆xL > ∆xM > ∆xK olur.
CEVAP A
KUVVET VE HAREKET
69
TEST
1.
3
HAREKET
ÇÖZÜMLER
4.
K aK =4m/s2
VK = 20 m/s
L aL =2m/s2
VL =15m/s
yatay yol
150m
K ve L araçlarının hızzaman grafikleri şekildeki
gibi olur. K aracı L den
120 m daha fazla yol
alacağından yan yana
gelme süresi,
h›z(m/s)
40
K
120m
V
L
10
K aracı L den 150 m daha fazla yol alacağından
120 =
yan yana gelme süresi;
(40 – 10) . t
2
0
t
30t
120 =
2
xK = 150 + xL
1
1
20t +
. 4t2 = 150 + 15t +
. 2t2
2
2
20t + 2t2 = 150 + 15t + t2
t(s)
t = 8 s olur.
CEVAP D
t2 + 5t – 150 = 0
(t – 10) (t + 15) = 0
t = 10 s olur.
CEVAP A
5.
V(m/s)
20
2.
6. saniyenin sonunda K aracının hızı
30 m/s olur.
Tx K = ;
4 + 10 E
. 30
2
V(m/s)
30
L
20
= 210 m
∆xL = 20 . 10
= 200 m
K
10
L
0
75m
5
10
t(s)
15
Hareketlinin hız-zaman grafiği şekildeki gibidir.
K
0
4
6
10
Araç (10-15) saniye aralığında,
t(s)
Tx = ;
L, K den; 200 + 40 – 210 = 30 m öndedir.
CEVAP D
10 + 20 E
. 5 = 15 .5 = 75 m
2
yer değiştirir.
CEVAP B
3.
∆xK = 9x
180 = 9x
h›z(m/s)
K
x = 20 m olur.
xK = 180 m olur.
∆xL = 10x
6.
3V
x
2x
= 200 m
0
2x
= 10 . 20
0
2x
2x
L
V
+x
L
2V
2x
t
2t
3t t(s)
2t
3t
4t
zaman
–x
C seçeneği yanlış, diğer seçenekler doğrudur.
L aracı K nin 40 m ilerisindedir.
CEVAP E
KUVVET VE HAREKET
t
2x K
xL = 20 + 200 = 220 m olur.
70
konum
Araç 3t-4t aralığında yavaşlamıştır.
CEVAP C
7.
Aracın hiç durmadan kırmızı ışık yeşile döndüğünde geçebilmesi için hızzaman grafiğinin şekildeki
gibi olması gerekir. Alınan
yol 100 m olacağından,
10. Hareketlinin hız-zaman
V(m/s)
8
Δx=100m
man grafiği şekildeki
9–t
16
gibi olur.
112 = ;
8–20a
t(s)
20
9 + (9 – t)
E . 16
2
112 m
14 = 18 – t
(8 + 8–20a)
100 =
.20
2
t = 4 s olur.
0
t
20a = 6
a=
3
2
a=
m/s olur.
10
CEVAP C
=
TV
Tt
16 – 0
4–0
= 4 m/s
h›z
2
olur.
CEVAP B
V
0
9 t (s)
Aracın hızlanma ivmesi,
10 = 16 – 20a
8.
V(m/s)
t
2t
3t
zaman
4t
–V
konum
11. Zamansız hız formülünden,
x
2
t
0
2t
3t
V2 = V o + 2a.x
4t
zaman
(40)2 = (10)2 + 2.2.(125 + ,tünel)
1600 = 100 + 4.(125 + ,tünel)
–x
1500 = 500 + 4 ,tünel ⇒ 4,tünel = 1000
Hareketlinin hız-zaman ve konum-zaman grafikleri şekildeki gibidir. Hareketli 2t ve 4t anlarında
t = 0 anındaki konumdadır.
9.
,tünel = 250 m
olur.
CEVAP C
CEVAP E
h›z
4V •
2V •
3x
2x
•
•
t
12. Aracın yol denklemi,
3x
2t
•
3t
zaman
Arac›n h›z-zaman grafi¤i flekildeki gibi olur.
ivme
Yolun zamana göre türevi
hızı verdiğinden, hız denklemi,
4•
0
•1
•2
t(s)
V = 4t olur.
a•
0
x = 2t2 olur.
a(m/s2)
•
t
•
2t
•
3t
zaman
Hızın zamana göre türevi ivmeyi verdiğinden, aracın ivmesi,
a = 4 m/s2 olur.
–a •
Aracın ivme-zaman grafiği şekildeki gibi olur.
CEVAP B
Aracın, ivme-zaman grafiği şekildeki gibi olur.
CEVAP A
KUVVET VE HAREKET
71
Adı ve Soyadı : .....................................
1.
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
a)
Bölüm
Yazılı Soruları
(Hareket)
2.
V (m/s)
ÇÖZÜMLER
a) Aracın 3 saniye sonraki hızı,
V = Vo + a . t
8
= 10 + 4 . 3
4
0
12m
16m
I
8m
II
2
= 22 m/s olur.
III
4
6
IV
–4m 8
t(s)
b) Aracın 5 saniyede aldığı yol,
–4
I. bölgede : +x yönünde, düzgün hızlanan doğrusal hareket
II. bölgede : +x yönünde, düzgün doğrusal hareket (sabit hızlı)
III. bölgede : +x yönünde, düzgün yavaşlayan
doğrusal hareket
IV. bölgede : –x yönünde, düzgün hızlanan doğrusal hareket
b) (0-8) s aralığında yer değiştirme,
(4 + 8)
2.8 2.4
–
.2 + 2.8 +
∆x =
2
2
2
x = Vo . t +
2
1
.a.t
2
= 10 . 5 +
2
1
.4.5
2
= 50 + 50
= 100 m olur.
c) Hızının 26 m/s olduğunda geçen süre,
V = Vo + a . t
26 = 10 + 4 . t
16 = 4t ⇒ t = 4 s olur.
= 12 + 16 + 8 – 4
= 32 m olur.
d) x = 100 m yol aldığında hızı,
c) (0-8) s aralığında ortalama hız,
Tx 32
V ort =
=
= 4 m/s olur.
8
Tt
V2 = Vo2 + 2ax
d) Hareketlinin ivme-zaman grafiği şekildeki gibidir.
V2 = 100 + 800
V2 = 102 + 2 . 4 . 100
a (m/s2)
V2 = 900 ⇒ V = 30 m/s olur.
2
2
0
4
6
8
t(s)
–2
–4
e) Hareketlinin konum-zaman grafiği şekildeki
gibidir.
x (m)
36
32
28
12
0
72
2
KUVVET VE HAREKET
4
6
8
t(s)
3.
a) İvme-zaman grafiğinde doğrunun altındaki
alan hızdaki değişmeyi vereceğinden cismin
hız-zaman grafiği şekildeki gibi olur.
2
2
4
6
8
V(m/s)
20
a=2m/s2
t(s)
V = Vo – a . t
t(s)
0
Cismin hız-zaman grafiği şekildeki gibidir.
a) Yavaşlamaya
başladıktan 4 saniye
sonraki hızı,
a(m/s2)
4m/s
4.
tmax=10s
= 20 – 2 . 4
–8m/s –8m/s
= 12 m/s olur.
–4
b) t = 5 saniyede alacağı yol,
V(m/s)
8
4
x = Vo . t –
0
2
= 20 . 5 –
8m
16m
12m
4
6
2
1
.2.5
2
= 100 – 25
t(s)
8
–8m
2
1
.a.t
2
= 75 m olur.
c) Hızının 8 m/s olduğunda geçen süre,
–8
V = Vo – a . t
8 = 20 – 2 . t
b) Hız-zaman grafiğinde taralı alanlar birbirini
götüreceğinden, hareketlinin 8 saniyede yer
değiştirmesi,
(4 + 8)
.2 + 2.8
Σ∆x =
2
= 12 + 16
= 28 m olur.
2t = 12 ⇒ t = 6 s olur.
d) x = 64 m yol aldığında hızı,
V2 = Vo2 – 2ax
V2 = 202 – 2 . 2 . 64
V2 = 400 – 256
V2 = 144 ⇒ V = 12 m/s olur.
c) Hareketlinin konum-zaman grafiği şekildeki
gibi olur.
e) Hareketlinin durma süresi,
x(m)
t mak =
36
28
Vo 20
=
= 10 s olur.
a
2
f) Duruncaya kadar aldığı yol,
x max =
12
0
2
4
6
8
20.10
= 100 m olur.
2
t(s)
d) Hareketlinin (0–8) saniye arasındaki ortalama
hızı,
V ort =
Tx
Tt
=
28
8
=
7
m/s olur.
2
KUVVET VE HAREKET
73
5.
a) Cismin 4 saniye
sonra hızı,
V = Vo + a . t
=8+2.4
= 16 m/s olur.
a=2m/s2
14
0
3
4
Hareketlinin hızzaman grafiği
şekildeki gibidir.
V(m/s)
16
a) Taralı
alan
hareketlinin 4.
saniyede aldığı
yolu vereceğinden, yavaşlama
ivmesi,
Δx4
8
Cismin 4. saniye içerisinde aldığı yol taralı
alan olacağından,
Tx 4 =
8.
V(m/s)
16
t(s)
(14 + 16)
30
.1 =
= 15 m olur.
2
2
16–3a
16–4a
9m
0
3
4
t (s)
t
t (s)
6(16 – 3a) + (16 – 4a)@
.1
2
18 = 32 – 7a
–14 = –7a
9=
b) Cismin 6 saniye sonra hızı,
V = Vo + a . t = 8 + 2 . 6 = 20 m/s olur.
a = –2 m/s
2
olur.
b) Hareketlinin duruncaya kadar aldığı yol,
6.
2
V2 = V o – 2a.x
Aracın yavaşlama ivmesi,
0 = (16)2 – 2.2.x
V2 = Vo2 – 2ax
256 = 4x ⇒ x = 64 m olur.
302 = 102 – 2a . 200
900 = 100 – 400a
800 = –400a
9.
a = –2 m/s2 olur.
dir. Taralı alan trenlerin
V = Vo – a . t
150 =
(40 – 10)
.t
2
V(m/s)
a=
30
ceği yol,
5 . 10
∆x =
2
a=2m/s2
10
Δx
0
10
15 t(s)
TV
Tt
=
10 – 40
10 – 0
=
–30
10
= –3 m/s
2
olur.
10. Hareketlinin hızzaman
grafiği
şekildeki gibidir.
Şekildeki grafikteki ta-
V(m/s)
ralı alan K ve L araçla-
20
rı arasındaki x uzaklı-
12
ğını verir.
KUVVET VE HAREKET
0
K treninin yavaşlama ivmesi,
Hareketlinin t = 10 sa-
74
L
t = 10 s olur.
t = 10 s olur.
= 16 m olur.
150m
10
30
150 =
t
2
10 = 30 – 2 . t
[20 – 12]
x=
.4
2
K
eşit olacağından,
Aracın hızı 10 m/s ye düşene kadar geçen süre,
7.
40
t = 0 anındaki uzaklığa
V
30
t durma = o =
= 15 s olur.
a
2
= 25 m olur.
V(m/s)
grafikleri şekildeki gibi-
Hareketlinin durma süresi,
niyeden sonra alabile-
Trenlerin hız-zaman
ah=3m/s2
∆x = 72 + 48
= 120 m
x
olur. Hareketlinin
(0-8) saniye aralığındaki ortalama
hızı,
K
L
V
0
V(m/s)
24
4
t(s)
V ort =
ay=6m/s2
12
72m
0
48m
4
120
Tx
=
= 15 m/s olur.
8
Tt
8 t(s)
5. BÖLÜM
ATIŞLAR
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
3.
Cismin suyun yüzeyine çarpma hızı,
V2 = 2g . h
V(m/s)
I. yol:
V2 = 2 . 10 . 1,8
Cisim son iki saniyede 80 m yol aldığına göre,
toplam aldığı yol,
V2 = 36
6
V = 6 m/s olur.
h2
t(s)
5m
1. saniyede
15
m
2. saniyede
25
m
3. saniyede
35
m
4. saniyede
45
m
+ 5. saniyede
Toplam yol : 125 m
0
0,4
Cisim düzgün yavaşlayıp 0,4 saniyede durduğuna
göre, grafikten havuzun derinliği,
80 m
h2 =
6 . 0, 4
2
h 2 = 1, 2 m olur.
olur. Cismin yere gelme süresi,
CEVAP A
t = 5 s olur.
Cismin yere çarpma hızı,
V = g . t = 10 . 5 = 50 m/s olur.
4.
II. yol:
grafiği
180 = 5t2
V(m/s)
Cismin hız-zaman
şekildeki
t–2
0
gibidir. Taralı alan
80 m
olduğuna
t
t(s)
t=6s
Cisimler 2 saniye ara ile bırakıldığından K yere
çarptığında L cismi 6 – 2 = 4 s yol almış olur.
Yerden yüksekliği,
80 m
– g(t– 2)
göre,
h = h1 + h2
– gt
80 = ;
K nin yere düşme süresi,
1
h=
. g . t2
2
g (t – 2) + g . t
E.2
2
180 =
1
. 10 . 42 + h2
2
180 = 80 + h2
h2 = 100 m olur.
80 = 10t – 20 + 10t
100 = 20t
CEVAP C
t = 5 s olur.
Cismin yere çarpma hızı,
V = g.t = 10.5 = 50 m/s olur.
CEVAP D
5. Serbest düşmede cismin her
K
t zaman aralığında aldığı yol
h, 3h, 5h, 7h, 9h, 11h ...
2.
Zamansız hız formülünden cisimlerin aldıkları yolların oranı,
2
V1
2
V2
=
L
h1 4
=
olur.
h2 9
şeklinde arttığından,
II
x + 3x + 5x + 7x + 9x + 11x = 144
2gh 1
2gh 2
2
h
2
= 1
2
h2
3
2t
K
36x = 144
I
t
olur. LM arası ise,
h=144m
7x
3t
•
yatay yer
V1
V2
CEVAP B
=5.4
= 20 m olur.
9x
11x
|LM| = 5 . x
•
5x
M
x=4 m
h2
h1
x
L 3x
N
yatay yer
CEVAP A
KUVVET VE HAREKET
75
6.
I. yol:
Serbest düşmede cismin aldığı yol 5 m, 15 m,
25 m ... şeklinde arttığından şekildeki yolların
hangi aralığa denk geldiğini bulmaya çalışalım.
45
55
L
1.
V
r
2r
2d
A
ϑK
80 m
8V
K
d
K
K
5
15
25
35
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
4A
ϑL
L
L
h
100 m
M
200 m
N
h = 380 m olur.
100m
M
300m
yatay yer
yatay
yer
200m
Cisimler limit hızlara ulaştıklarında cisimlere etki
eden net kuvvetler sıfır olacağından,
N
yatay yer
2
k . A . jK
V .d.g
=
8V . 2d . g k . 4A . j 2
L
II. yol:
jK 1
=
2
jL
V(m/s)
t
0
t+2
olur.
CEVAP B
t(s)
h1
100 m
–gt
200 m
2.
düfley
düfley
–g(t + 2)
r
2r
K
L
Cismin hız-zaman grafiği şekildeki gibidir. Şekildeki
taralı alandan,
A
gt + g (t + 2)
E.2
100 = ;
2
Limit hız cisimlerin en büyük kesit alanına bağlıdır.K nin en büyük kesit alanı,
100 = 10t + 10t + 20
AK = πr2 = Aı ise
80 = 20t
L nin en büyük kesit alanı,
t = 4 s olur.
AL = π.(2r)2 = 4πr2 = 4Aı olur.
h1 yüksekliği,
h1 =
A
Limit hızların oranı,
1
. g . t2
2
›
2
k . A . jK
j
m.g
& K = 2 olur.
=
m . g k . 4A › . j 2
jL
L
h1 = 5 . 42
h1 = 80 m
CEVAP D
h yüksekliği ise,
h = 80 + 300
h = 380 olur.
3.
CEVAP C
Hava direncinin olduğu bir ortamda, yeterince yüksekten serbest düşmeye bırakılan cisim limit hıza
ulaşıncaya kadar azalan ivmeli hareket, sonra yere
düşünceye kadar düzgün doğrusal hareket yapar.
CEVAP D
76
KUVVET VE HAREKET
4.
Cismin ivmesi 5 m/s2 olduğundan direnç kuvveti,
a=
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
G – Fd
Fnet
=
Rm
m
16 – Fd
1, 6
5 =
1.
Fd
I. yol:
Cisim yukarıdan aşağı düşey atış hareketi yaptı-
8 = 16 – Fd
ğından cismin yere gelme süresi,
G=16N
Fd = 8 N olur.
h = Vo . t +
Cismin hızı,
1
. g . t2
2
60 = 5t + 5t2
Fd = 0,25 ϑ2
yatay
yer
8 = 0,25 ϑ2
t2
K
+ t – 12 = 0
Vo = 5 m/s
(t – 3) (t + 4) = 0
ϑ2 = 32
t = 3 s olur.
ϑ = 4 2 m/s olur.
CEVAP C
h = 60 m
Cismin yere çarpma hızı,
V = Vo + g . t
L
= 5 + 10 . 3
5.
yatay yer
= 35 m/s olur.
hız
V
3ϑ•
2ϑ•
K
ϑ•
L
II. yol:
Cismin yere çarpma hızı,
0
V2 = V2o + 2gh
V2 = 52 + 2.10.60
zaman
V2 = 1225
K ve L cisimleri limit hıza ulaştıklarında K nin limit
hızı 2ϑ, L nin limit hızı ϑ olur. Cisimlerin ağırlıkları
direnç kuvvetlerine eşit olacağından,
2
mK g
k.A. (2j)
=
2
mL g
k.A.j
V = 35 m/s olur.
CEVAP B
2.
2
mK
4j
= 2
mL
j
mK
= 4 olur.
mL
K
I
t
1br
h1
t
3br
t
1br
t
1br
Vo
CEVAP E
L
h2
II
yatay yer
6.
K cismi serbest bırakıldığında her zaman aralığın-
h›z
da aldığı yol, h, 3h, 5h ... şeklinde artar. L cismi
aşağıdan yukarı düşey atış hareketi yapacağından
jlim•
tepe noktasından sonra serbest düşme hareketi
h
0
h
t
yapar. Bu durumda,
zaman
Dt
Cismin hız-zaman grafiği şekildeki gibi olur.
Şekildeki alanların eşit olabilmesi için cisim L-M
t
arasını
den büyük, t den küçük sürede alır.
2
CEVAP C
h1 = 1 br + 3 br = 4 br
h2 = 1 br olur.
h1 ve h2 taraf tarafa oranlanacak olursa,
h 1 4 br
=
= 4 olur.
h 2 1br
CEVAP C
KUVVET VE HAREKET
77
6.
3.
Vo
(+)
Vo
K
I
L
(+)
II
cisim
Vo
yatay
(–)
Vo
(–)
h=80m
h = 55 m
•
yatay
yer
yatay
yer
V=50m/s
V
Vo hızının büyüklüğü,
Zamansız hız formülünden cismin ilk hızı,
V2 = V2o + 2g.h
V2 = Vo2 – 2gh
502 = V2o + 2.10.80
(–60)2 = Vo2 – 2 . 10 . (–55)
2500 = V2o + 1600
3600 = Vo2 + 1100
V2o = 900
Vo2 = 2500
Vo = 30 m/s olur.
Vo = 50 m/s olur.
4.
CEVAP D
Cisimler karşılaştıklarında K nin hızı L nin hızına
eşit ise ilk atışta K nin hızı,
ı
ı
V1 = V2
V1 . t + g . t = V2 . t – g . t
1
1
. g . t 2 + V2 . t –
. g . t2
2
2
= 10 . 1 + 30 . 1
= V1 . t +
= 40 m olur.
CEVAP B
5.
t
h›z
V
balon
V•
•
0
V
t
–V •
›
•t
h =4Vt
• 2t •3t • 4t
zaman
–2V •
t
L
–3V •
cisim
h=[
V+3V
].2t=4Vt
2
3V
Cismin ve balonun hız-zaman grafikleri şekildeki
gibi olur. Grafiklerin altındaki alanlar, aldıkları yolu
verir. Bu durumda, cisim yere çarptığı anda balonun yerden yüksekliği,
Σh = h + h = 2h olur.
CEVAP A
78
20 = 10.t1
t1 = 2s olur.
10.t2 = 80
h = h1 + h2
yatay
yer
50 = 30 + 10.t1
–50 = 30 – 10.t2
olur. h yüksekliği,
h
V = Vo + g.t1
–V = Vo – g.t2
V1 = 10 m/s
K
I cisminin yere düşme süresi,
II cisminin düşme süresi,
V1 . 1 + 10 . 1= 30 . 1 – 10 . 1
t
V=50m/s
KUVVET VE HAREKET
t2 = 8s olur.
t
2 1
olur.
Buna göre, 1 = =
t2 8 4
CEVAP C
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
1.
K
I
3.
Vo
K
yatay
V yatay
h
L
II
L
2V yatay
16h
yatay
yer
x
Vy
9h
yatay yer
x1
x2
Yere düşme süresi cismin yatay atıldığı yüksekliğin karekökü ile orantılıdır. h α t2 olduğundan,
5 . 2 = Vo
I cismi 4t sürede, II cismi 3t sürede yere düşer.
Vo = 10 m/s olur.
Cisimlerin yatayda aldıkları yolların oranı,
Cisim yere çarptığında düşeydeki hızı,
x1
V . 4t
=
x 2 2V . 3t
Vy = g . t = 10 . 2 = 20 m/s olur.
x1 2
=
olur.
x2 3
Cismin yere çarpma hızı,
V2 = 100 + 400
yatay
V2 = 500
I
V = 10 5 m/s olur.
h1
V2
L
Vx =Vo =10m/s
V2 = 102 + 202
CEVAP B
V1
K
V
Şekildeki üçgenden cismin ilk hızı,
h
tan45° =
x
h=x
1
. g . t2 = Vo . t
2
5t = Vo
•
2.
Vx
45°
•
Vy =20m/s
V
CEVAP C
yatay
II
h2
M
•
O
x
yatay yer
Cisimler yatayda sabit hızlı, düşeyde serbest
düşme hareketi yaparlar.
I cisminin uçuş süresi,
x
t
t
3x
t
5x
olduğundan t1 = 3t olur.
II cisminin uçuş süresi,
t
x
t
3x
olduğundan t2 = 2t olur.
Cisimlerin yatayda aldıkları yollar eşit olduğundan,
V1.t1 = V2.t2
V1.3t = V2.2t
V1
2
=
olur.
3
V2
CEVAP D
4.
Merdivenin genişliği yüksekliğine eşit olduğundan
yatay ve düşeyde alınan yollar eşit olur. Bilyenin
basamağa düşme süresi,
Vo =2m/s
yatay
x=h
Vo . t =
20cm
1
. g . t2
2
Vo = 5t
20cm
h
2 = 5t
t=
2
s
5
x
olur. Cismin düşeceği basamak,
x = Vo . t
2
n . 0,2 = 2 .
5
n = 4 olur.
CEVAP A
KUVVET VE HAREKET
79
5.
Vo=20m/s
K
yatay
düzlem
7.
yatay
I K
V1
yatay
L
h
8h
3t
37°
.
x
M
II L
37°
V2
yatay
t
h
yatay yer
.
O
Cismin yatay ve düşeyde aldığı yollardan, şekildeki üçgenden,
M
yatay
yer
x
I cisminin uçuş süresi t1 = 3t ise,
1 2
g.t
h
tan37° =
= 2
x
Vo .t
II cisminin uçuş süresi t2 = t dir.
t1 = 3t2 olur.
2
Cisimlerin atış uzaklıkları eşit olduğundan,
5t
3
5t
=
=
& t = 3 s olur.
20
4
20t
V1.t1 = V2.t2
CEVAP B
V1.3t = V2.t
3V1 = V2 olur.
CEVAP B
6.
K
Vo = 10 m/s
8.
yatay
K
➞
Vo
yatay
80 m
h
a
B .
A
yatay
yer
LV
x
O .
53°
x=88m
x
Vy
Cismin uçuş süresi,
h=
80 =
1
g.t2
2
Cisim yere çarptığında yatay ve düşey ilk hızları,
Vo = Vx = V.cos53° = 50.0,6 = 30 m/s
1
10.t2
2
Vy = V.sin53° = 50.0,8 = 40 m/s olur.
t2 = 16
x = 88 m lik yolu cisim ve araba birlikte alacağından,
Cismin havada kalma süresi,
Vy 40
= 4 s dır.
=
tu =
g
10
aracın ivmesi,
I. yargı doğrudur.
t = 4s olur.
Vo.t +
10.4 +
➞
V=50m/s
Cisim düşeyde serbest düşme hareketi yapaca-
1 2
at = 88
2
ğından,
1
1
g t2u =
10.42 = 5.16 = 80 m olur.
2
2
II. yargı doğrudur.
1
a.42 = 88
2
h=
8a = 48
Cisim yatayda sabit hızlı hareket yaptığından,
a = 6 m/s2 olur.
CEVAP D
x = Vo.tu = 30.4 = 120 m olur.
III. yargı doğrudur.
CEVAP E
80
KUVVET VE HAREKET
9.
hız
Vo
N
hız
•.
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
2Vo
Vo
3Vo
h
h
0
t1 zaman
0
1.
3Vo
2Vo
t2 zaman
hmak =320m
53°
O
P
Vox
yatay yer
Cismin hız vektörü ile ivme vektörü arasındaki açı
90° olduğu anda cismin yerden yüksekliği maksimumdur.
Vo + 2Vo
E .t1
2
hmak eşitliğinden cismin düşey ilk hızı,
2
3 .Vo
.t2 olur.
2
h=
Vo
Voy
I cisminin t1 süredeki hızı ile, II cisminin t2 sürede
düşeydeki hızının değişim grafikleri şekildeki gibidir. Cisimler düşeyde aynı h yolunu alacaklarından,
h=;
T
hmak =
Cisimlerin düşeydeki hız-zaman grafikleri şekildeki
gibi olur.
2g
2
320 =
Düşeyde aldıkları yollar eşit olacağından,
3Vo
3 Vo
.t =
.t2
2 1
2
t1
3
=
olur.
t2
3
V oy
V2oy
V oy
2.10
= 6400
Voy = 80 m/s olur.
Düşey hızdan Vo hızının büyüklüğü,
Voy = Vo.sin53°
CEVAP A
80 = Vo.0,8
Vo = 100 m/s olur.
10.
Vo
K
CEVAP E
yatay
2.
h
yatay yer
Voy
O
L Vx
•
h=40m
37°
L
Vox
V
Cismin yatay ve düşey ilk hızları,
Vox = Vo . cos37° = 50 . 0,8 = 40 m/s
Voy = Vo . sin37° = 50 . 0,6 = 30 m/s olur.
Cisim K noktasına geldiğinde düşeyde aldığı yol
2h
g
h = 40 m olur. K noktasına gelme süresi,
1
. g . t2
h = Voy . t –
2
40 = 30t – 5t2
bağıntısı ile bulunabilir.
x = Vo.t
x
Vo
t2 – 6t + 8 = 0
(t – 4) (t – 2) = 0
bağıntısı ile bulunabilir.
t = 4 s olur.
Vy = g.t
Cismin yatayda aldığı yol,
V.sina = g.t
t=
P yatay yer
x
x
Cismin t uçuş süresi,
1
g.t2
h=
2
t=
K
Vo=50m/s
a
O
Vy=V.sina
t=
T
x = Vox . t
V. sin a
g
= 40 . 4
= 160 m olur.
bağıntısı ile bulunabilir.
CEVAP E
CEVAP C
KUVVET VE HAREKET
81
3.
5.
T
Voy
T
Vx=60m/s
Vo
Voy
Vo
α
O
O
hmak
hmak
α
K
Vox
xmak
yatay
yer
xmak =120m
Cismin en büyük hızı O ve K noktalarında, en
xmak = Vox . tu
120 = 20 . tu
Vo = 100 m/s ve
tu = 6 s
Vox = Vx = 60 m/s
tç = 3 s olur.
Voy = 80 m/s olur.
Cismin maksimum yüksekliği,
Cismin uçuş süresi,
Voy
g
hmak =
= 2.
yatay
yer
Cismin uçuş ve çıkış süreleri,
küçük hızı ise T noktasındadır. Bu durumda,
tu = 2 .
K
Vox
80
= 16 s olur.
10
1
2
. g . tiniş
2
= 5 . 32
= 45 m olur.
Cismin atış uzaklığı,
CEVAP A
xmak = Vox . tu = 60 . 16 = 960 m olur.
CEVAP E
6.
T
K
Voy
O
L
T
yatay yer
x=120m
K
Vo=50m/s
hmak
O
VK
hmak
53°
Vox
4.
37°
Cismin yatay ve düşey ilk hızları,
h=25m
Vox = Vo . cos53° = 100 . 0,6 = 60 m/s
L
yatay yer
x
Vox = Vo.cos37° = 50.0,8 = 40 m/s
Voy = Vo.sin37° = 50.0,6 = 30 m/s olur.
Cismin K noktasına varma süresi,
h = Voy.t –
1 2
g.t
2
25 = 30t – 5t2
tç =
K den
x
120
t
Voy
g
=
80
=8s
10
L ye gelme süresi;
= Vox . t
= 60 . t
=2s
T den K ye gelme süresi;
t2 – 6t + 5 = 0
tı
Eşitlik çarpanlara ayrıldığında,
Vx =Vox =60m/s
= tç – t
=8–2
=6s
(t – 1) (t – 5) = 0
VyK = g . tı
t = 5s olur.
= 10 . 6
Cismin yatayda aldığı x yolu,
VyK =60m/s
VK =60v2 m/s
= 60 m/s
x = Vox.t = 40.5 = 200 m olur.
CEVAP C
KUVVET VE HAREKET
Voy = Vo . sin53° = 100 . 0,8 = 80 m/s olur.
Cismin tepe noktasına gelme süresi,
Cismin yatay ve düşey ilk hızları,
82
Vo =100m/s
Cismin K noktasındaki hızı VK = 60 2 m/s olur.
CEVAP B
7.
•
•
V
N Vox
. Voy
K
cisim
ip
O
Cisim 5 saniyede K den L ye geldiğine göre,
düfley
M
L
•P
–Vy = Voy – g.t
Vox
–V.sin53° = Vo.sin37° – 10.5
0
–Voy
fiekil-I
–V.0,8 = Vo.0,6 – 50
yatay
4
– b Vo l .0, 8 = Vo.0,6 – 50
3
fiekil-II
–
Cismin hız-zaman grafiği şekildeki gibi olduğuna
göre, cisim N noktasında ipten kurtulmuştur.
–
16
3
V = Vo – 50
15 o
5
16
3
V – V = –50
15 o 5 o
25
V = 50
15 o
CEVAP D
Vo = 30 m/s olur.
T
8.
Voy
CEVAP B
VT
Vo
hmak
a Vox
O
P
xmak
10.
yatay yer
T
Vo
Cismin tepe noktasında yalnız yatay hızı vardır.
hmak
VT = Vox tir.
O
60°
P
Vox = Vo.cosa bağıntısıyla a açısı bulunur.
Voy = Vo.sina bağıntısıyla Voy bulunur.
tu = 2
hmak =
Voy
g
hmax ve xmax yazılıp oranlanırsa,
bağıntısıyla uçuş süresi bulunur.
2
V oy
2g
2
3
h mak
3
sin a
= 2
=
= 2 =
4
4
cos
a
1
x mak
V o .2 sin a. cos a
4.
2
g
bağıntısıyla maksimum yükseklik bulu-
olur.
xmak = Vox.tu bağıntısıyla atış uzaklığı bulunur.
CEVAP E
Vo
( + ) Voy
2
V o . sin a
2g
nur.
9.
yatay yer
xmak
CEVAP B
11.
düfley
10m/s
37°
Vox
K
yatay
balon
(–)
Vo=20 2m/s
45°
Vox=20m/s
LV
x
•
yatay
yer
53°
Vy
V
yatay
h=80m
Cismin yatay hızı her noktada aynı olduğundan,
Vox = Vx
Vo . cos37° = V . cos53°
Vo .
4
3
=V.
5
5
4
V = . Vo olur.
3
.O
•
xmax
yatay
yer
Cismin yere göre yatay doğrultudaki ilk hızı,
Vox = Vo.cos45° = 20 2 .
2
= 20 m/s olur.
2
KUVVET VE HAREKET
83
Cismin yere göre düşey doğrultudaki ilk hızı,
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
ı = V .sin45° + V
Voy
o
balon
= 20 2 .
2
+ 10
2
1.
= 20 + 10
Cisimlerin ilk hızları eşit ve a + i = 90° olduğundan
atış uzaklıkları eşittir.
x
xK = xL & K = 1 olur.
xL
CEVAP C
= 30 m/s olur.
Cismin uçuş süresi,
ı –
–h = Voy
Hava sürtünmeleri önemsiz olduğundan cisimlerin
menzil uzaklığı kütleye bağlı değildir.
1 2
g.t
2
Vo
2.
–80 = 30t – 5t2
K
t2 – 6t – 16 = 0
(t + 2) (t – 8) = 0
Vo
L
i
M
i
t = 8s olur.
Vo
h
Cismin atış uzaklığı,
yatay düzlem
xmak = Vox.tu
= 20.8
Hava direnci önemsiz olduğundan mekanik enerji
korunur. Cisimler aynı yükseklikten aynı hızlarla
atıldıklarından yere çarpma hızlarının büyüklükleri
eşittir.
= 160 m olur.
CEVAP C
Cisimlerin yere düşme süreleri tK > tL > tM olacağından eşit değildir.
12.
K
V1
I
Cisimlerin kütleleri bilinmediğinden yere çarptıkları
andaki kinetik enerjileri bilinemez.
CEVAP A
yatay
2m
3.
T
m
V2
L.
53°
II
M
yatay
yer
Cisimlerin yatayda aldıkları yollar eşit olduğundan
cisimlerin hızlarının oranı,
xmak1 = xmak2
Vo
P
L
2t
O1 t
2x
x
O2
K
O
yatay
yer
V1.t = V2.cos53°.2t
Hava direnci önemsiz olduğundan, cisimlerin yere
3
V1 = V2. .2
5
V1
6
=
olur.
5
V2
düşmeleri kütleye bağlı değildir. K cisminin yatay
hızı sabit olduğundan K nin O dan O1 e gelme
CEVAP D
süresi 2t ise O dan O2 ye gelme süresi 3t olur.
K nin O1 noktasına gelme süresi m nin O1 noktasına gelme süresine eşittir. Bu durumda m nin K
cismine çarpma hızı, V1 = g.2t olur.
K nin O2 noktasına gelme süresi 2m nin O2 noktasına gelme süresine eşittir. Bu durumda 2m nin K
ye çarpma hızı V2 = g.3t olur.
Hızların oranları,
84
KUVVET VE HAREKET
V1 2gt 2
olur.
=
=
V2 3gt 3
CEVAP B
4.
L
5cm
Vo
Voy
P
37° V
ox
K
80cm
yatay
düzlem
L cisminin P noktasına gelme süresi,
1
.g.t2
2
1
0,05 = .10.t2
2
h=
0,01 = t2 & t = 0,1 s olur.
Aynı sürede K cismi yatayda x = 80 cm yol alarak
P noktasına geldiğine göre,
x = Vox.t
x = Vo.cos37°.t
0,8 = Vo.0,8.0,1
1 = Vo.0,1 & Vo = 10 m/s olur.
CEVAP E
KUVVET VE HAREKET
85
TEST
1.
1
Serbest düşmede cismin her saniye aralığında aldığı yol, 5 m, 15 m,
25 m ... şeklinde olduğundan,
4.
K
5m
L
h
Serbest düşmede cismin her t zaman aralığında
aldığı yol h, 3h, 5h ... şeklinde olduğundan,
h1 9
=
ise,
h2 7
15m
h = 5 + 15 + 25 + 80
25m
t1 3
= =3
t2 1
35m
h = 125 m olur.
45m
M
5.
K
7h
t
Cisim L noktasındaki hızı 30 m/s, M noktasındaki
hızı 0 olduğundan,
V =0
M
hmak
2
V=30m/s
L
2
h mak =
hK
Vo =50m/s
2hK = 210
hmak
——
2
Vo
2
2
Vo
yatay yer
CEVAP C
K
= 900 . 2
yatay yer
Vo = 30 2 m/s olur.
6.
yatay
Vo
2g
Vo
90 =
2 . 10
hK = 105 m olur.
Vo = 20 m/s
7h
Cismin K noktasındaki ilk hızı,
400 = 2500 – 20hK
K
3t
h mak = 90 m olur.
202 = 502 – 2 . 10 . hK
3.
olur.
2
h mak
30
=
2
2 . 10
VK =20m/s
VK2 = Vo2 – 2g . hK
9h
5h
h mak V 2
=
2
2g
düfley
den hK yolu,
3h
CEVAP E
CEVAP C
Zamansız hız formülün-
h
80m
yatay yer
2.
ATIŞLAR
ÇÖZÜMLER
Vo
K
CEVAP B
yatay
h1=45m
h2
h = 180 m
35m
L
V
yatay
yer
x2
x=210m
Cisim düşeyde serbest düşme hareketi yapacağından,
2
1
h1 =
. g . t1
2
Cismin yere düşme süresi,
1
. g . t2
h=
2
180 = 5t 2
2
45 = 5t 1 ⇒ t1 = 3 s olur.
t = 6 s olur.
x = 210 m lik yolu cisim ve araç birlikte aldığından,
Vo . t + V . t = 210
2
1
. g . t2
2
2
Cismin yatayda aldığı yolların oranı,
6V = 90
V = 15 m/s olur.
CEVAP D
KUVVET VE HAREKET
h2 =
80 = 5t 2 ⇒ t2 = 4 s olur.
20 . 6 + V . 6 = 210
86
x1
A
B
yatay
yer
x 1 Vo . t 1 t 1 3
=
= =
olur.
x 2 Vo . t 2 t 2 4
CEVAP B
7.
9.
5
2s
15
5
Vo = 20 m/s
T
Vo
Voy
hmak
2s
(+)
15
a Vox
O
P
cisim
yatay
yer
xmak
yatay
25
(–)
2s
h = 60 m
Cismin yatay ve düşey ilk hızları,
Vox = Vo.cosα
35
Voy = Vo.sinα olur.
•
yatay yer
I. durumda:
Voy
tu = 2
I. yol:
Cisim aşağıdan yukarıya düşey atış hareketi yaptığından,
2
hmak =
1
. g . t2
–h = Vo . t –
2
g
V oy
2g
xmak = Vox.tu
–60 = 20t – 5t2
5t2 – 20t – 60 = 0
II. durumda:
2Voy
tuı = 2
g
t2 – 4t – 12 = 0
(t – 6) (t + 2) = 0
tuı = 2tu
t = 6 s olur.
Uçuş süresi iki katına çıkar.
II. yol:
ı
=
hmak
Şekil incelendiğinde,
ı
hmak
t = 2 + 2 + 2 = 6 s olur.
CEVAP A
8.
(2Voy)
2
2
2g
=4
V oy
2g
= 4hmak
Maksimum yükseklik 4 katına çıkar.
2Voy
ı
= 2Vox.2
xmak
g
ı
xmak
= 4xmak
Atış uzaklığı 4 katına çıkar.
h›z
CEVAP D
3V
2V
L
V
K
10. K cisminin yere düşme süresi,
zaman
0
Grafikten K nin limit hızı ϑ, L nin limit hızı 2ϑ olur.
Cisimlerin kütleleri oranı,
K
t = 10 s olur.
L cisminin ilk hızı,
2
mK . g
k.A.j
=
m L . g k . A . (2j) 2
2
mK
j
=
m L 4j 2
mK 1
=
mL 4
1
. g . t2
2
1
500 =
. 10 . t 2
2
h=
tu = 2 .
Vo
g
10 = 2 .
Vo
10
h=500m
Vo
L
yatay yer
Vo = 50 m/s olur.
olur.
CEVAP A
CEVAP A
KUVVET VE HAREKET
87
11. Serbest düşmede her t zaman aralıkta cismin aldığı
yol, h, 3h, 5h ... şeklinde
arttığından,
h1 = h + 3h = 4h
K
h1
h
3h
L
h2
5h
h2 = 5h
M
olacağından h1 ve h2 taraf
tarafa oranlanırsa,
h1 4
=
olur.
h2 5
12.
T
Vo
Vy
2V
3V
yatay yer
CEVAP E
Vx
hmak
O
P
Vox
xmak
yatay
yer
Cismin yatay hızı her zaman eşit olacağından,
Vx = Vox olur.
2
hmak =
V oy
2g
bağıntısıyla Voy bulunur.
2
V o = V2ox + V2oy bağıntısıyla Vo bulunur.
tu =
2Voy
g
bağıntısıyla tu bulunur.
xmak = Vox.tu bağıntısıyla xmak bulunur.
CEVAP E
88
KUVVET VE HAREKET
1.
2
Cisim düzgün yavaşlayacağından, h yüksekliği,
V2
=
Vo2
ATIŞLAR
ÇÖZÜMLER
– 2g. h
3.
T
Vo
düfley
302 = 502 – 2 . 10 . h
(+)
V=30m/s
Voy
37° V
ox
O
20h = 2500 – 900
K
20h = 1600
(–)
h = 80 m olur.
K
•
TEST
yatay
yer
yatay
240m
h=135m
h
Vo =50m/s
Aynı cisim K noktasından ser-
L
•
best bırakılırsa,
1
. g . t2
h=
2
80 = 5 . t2
x
Cisim 9 saniyede yere düştüğüne göre düşey hızı,
yatay yer
1
. g . t2
2
–135 = Voy . 9 – 5 . 92
–h = Voy . t –
t2 = 16
9Voy = 405 – 135
t = 4 s olur.
9Voy = 270
CEVAP E
Voy = 30 m/s olur.
Yatay hızı ise,
Vox = 40 m/s olur.
Cisim yatayda alacağı toplam yoldan,
240 + x = Vox . tu
240 + x = 40 . 9
x = 360 – 240
x = 120 m olur.
düfley
2.
silah
Vo
yatay
CEVAP D
K
4.
h=0,45m
120m
L
4
r(2r)3 = 8V
3
VL =
4
r.(3r)3 = 27V
3
mK = 8m ise
1
. g . t2
2
0,45 = 5t 2
h=
0,09 =
VK =
olur. Cisimler aynı maddeden yapıldıklarından
Merminin L noktasına gelme süresi,
t2
Cisimlerin hacimleri,
mL = 27m olur.
AK = 4 A ise,
AL = 9 A olur.
⇒ t = 0,3 s olur.
Merminin yatayda aldığı yol x = 120 m olduğundan,
Cisimlerin limit hızlarının oranı,
2
k.4A.j K
8 mg
=
2
27 mg
k.9A.j L
x = Vo . t
120 = Vo . 0,3
2
Vo = 400 m/s olur.
CEVAP A
j
j
2
= K2 & K =
3
jL
jL
2
olur.
3
CEVAP C
KUVVET VE HAREKET
89
5.
Cisimler aynı hızla yere
çarptıklarına göre,
t1 = 5t
t2 = 6t olur.
8.
t
t
t
2Vo t
hmak
O
I
3t
K
t1 ve t2 taraf tarafa
h
t
t 1 5t 5
=
=
olur.
t 2 6t 6
Cismin yatay ve düşey ilk hızları,
Vox = Vo . cos53° = 50 . 0,6 = 30 m/s
Voy = Vo . sin53° = 50 . 0,8 = 40 m/s olur.
3Vo
L
II
Cismin uçuş süresi,
Voy
40
tu = 2 .
= 2.
= 8 s olur.
g
10
3Vo
CEVAP D
x yolunu cisim ve araba birlikte alacağından,
x = xmak + xaraba
= Vox.tu + Va.tu
T
Vo
= 30 . 8 + 10 . 8
= 240 + 80
= 320 m olur.
hmak
α
P
Vox
x
yatay
yer
xmak
hmak =
tu = 2
2g
Voy
g
CEVAP B
9.
2
V oy
L yatay
yer
x
y
O
Va =10m/s
K
3t
3Vo
Voy
Va
53°
2Vo
oranlanırsa,
6.
T
Vo =50m/s
K
bağıntısıyla Voy bulunur.
bağıntısıyla tu bulunur.
I
5h
2Vo t
7h
3Vo t
h1
Atış uzaklığı xmak ın bulunabilmesi için α açısı yada
Vox in bilinmesi gerekir.
CEVAP B
t
h2
t
h
Vo
L
II
yatay
yer
7.
Vo
K
4Vo
yatay
Cisimlerin hızları şekildeki gibi olduğunda her t
zaman aralığını cisimler; h, 3h, 5h, 7h ... şeklinde
alacaklarından,
h 1 5h + 7h
=
= 12 olur.
h2
h
CEVAP E
düfley
duvar
h1
L
h2
O
P
•
2x
10. Cisim yatayda sabit hızlı hareket yaptığından,
•
x
yatay
yer
x
Cismin h1 ve h2 yüksekliğin-
K
h
den düşme süreleri oranı,
4x Vo . t 1
=
x
Vo . t 2
t1 4
=
olur.
t2 1
Cisim düşeyde serbest düşme
hareketi yapacağından,
h 1 h + 3h + 5h + 7h 16
=
=
olur.
h2
7h
7
90
KUVVET VE HAREKET
5h
7h
x 1 Vo . t 1
=
x 2 Vo . t 2
2 t1 t1
= & = 2 olur.
1 t2 t2
Cisim düşeyde serbest düşme hareketi yaptığından,
h1 1 + 3 4
=
=
olur.
h2
5
5
CEVAP C
3h
h1
Vo
L
h2
yatay yer
11. Küresel cismin hız-zaman
grafiği şekildeki gibi olur.
h›z
3j•
j•
0
CEVAP C
zaman
CEVAP A
TEST
3
3.
2
1.
h mak =
V oy
2g
ve
düfley
➞
➞
VK
Voy =Voy =3 br
K
ATIŞLAR
ÇÖZÜMLER
düfley
Vo=25m/s
VL
37°
L
L
K
20m/s
20m/s
15m/s
Va =20m/s
olduğundan,
➞
VM
hmak = hmak olur.
K
xaraba
yatay yer
| VK| = | VM| ve α + β = 90°
Cismin yere göre yatay doğrultudaki ilk hızı,
➞
ı = V – V .sin37°
Vox
a
o
VK
olduğundan,
= 20 – 25.0,6
➞
β
xmak =xmak olur.
M
O
II. yargı doğrudur.
yatay
yol
xcisim
45°
O
I. yargı doğrudur.
K
K
M
L
α
VM
= 20 – 15
= 5 m/s olur.
yatay
yer
Cismin yere göre düşey doğrultudaki ilk hızı,
L cismi 45° açı ile eğik atıldığından maksimum
uzaklığa düşer.
Voy = Vo.cos53°
= 25.0,8
III. yargı doğrudur.
= 20 m/s olur.
CEVAP E
Cismin uçuş süresi,
Voy
20
tu = 2 .
= 2.
= 4 s olur.
g
10
2.
Cismin ve arabanın alacakları yollar,
düfley
20m/s
ı .t = 5.4 = 20 m
xcisim = Vox
u
xaraba = Va.tu = 20.4 = 80 m olur.
(+)
Voy
Aralarındaki uzaklık,
yatay
∆x = xaraba – xcisim
12m/s
(–)
= 80 – 20
h = 25 m
= 60 m olur.
Cisim arabanın 60 m gerisine düşer.
yatay yer
CEVAP D
xmak
Cisim atıldığı anda yatay ilk hızı 12 m/s, düşey ilk
hızı Voy = 20 m/s olur. Cismin yere düşme süresi,
1
–h = Voy . t –
. g . t2
2
–25 = 20t – 5t2
4.
h›z
ϑlim
t2 – 4t – 5 = 0
h1
(t – 5) (t + 1) = 0
t = 5 s olur.
0
Cismin atış uzaklığı,
t
2t
zaman
Cismin hız-zaman grafiği şekildeki gibidir. Grafikten görüldüğü gibi,
xmak = Vox . tu
= 12 . 5
= 60 m olur.
h2
CEVAP B
h2
< h 1 < h 2 dir.
2
CEVAP E
KUVVET VE HAREKET
91
5.
I cismi için:
K
Hızı ve aldığı yol,
V=0
1
h = .g.t12
2
V
h1
Vı = V + gt
1
g t2 olur.
h1 = V.t +
2
7. Serbest düşme süresi:
I
h=45m
t1
45 = 5.t12
M
t1 = 3 s olur.
•
L
II cismi için:
V1 = g.t1 = 10.3 = 30 m/s
yatay
yer
II
V1=30m/s
h›
Yavaşlama süresi:
5V
h2
t2
yatay yer
V2 = V1 – a.t2
V2=3m/s
3 = 30 – 1.t2
Hızı ve aldığı yol,
t2 = 27 s olur.
Vı = 5V – gt
1
g t2
h2 = 5Vt –
2
Havada kalma süresi:
Σt = t1 + t2 = 3 + 27 = 30 s olur.
olur. Cisimler M noktasında eşit büyüklükte hızlarla
karşılaşacaklarından,
CEVAP C
8.
V1=10m/s
V + gt = 5V – gt
5m
10m/s
K
2gt = 4V
gt
olur.
V=
2
I
15m
10m/s
h
Bu değer cisimlerin aldıkları yollarda yazılıp oran-
35m
lanırsa,
L
gt
1 2
2
.t + gt
h1
gt
1
2
2
=
=
=
olur.
h2
gt
1 2 2gt 2 2
5 .t – gt
2
2
10m/s
25m
40m/s
V2=40m/s
II
yatay
yer
40m/s
I. yol: Cisimler eşit hızlarla yere çarpmaktadırlar.
Cisimlerin her saniye aralığında aldığı yol şekildeki
gibidir. Bu durumda h yüksekliği;
CEVAP E
h = 15 + 25 + 35 = 75 m olur.
II. yol: Cisimler aynı hızla yere çarptıklarından
aynı seviyede hızları eşittir. Ortalama hızdan,
h = Vort.t
6.
Vo =10m/s
K
yatay
düzlem
=(
yatay
= 75 m olur.
L
CEVAP D
h
.
40 + 10
) .3
2
9.
45°
•
x
M
K
Vo
yatay
45°
yatay yer
h
Cismin yatay ve düşeyde aldıkları yollar eşit olacağından,
L
h=x
α
1
g.t2 = Vo.t
2
10t
= 10
2
x
t = 2s olur.
CEVAP D
92
KUVVET VE HAREKET
yatay
yer
V
Vx = Vo = V . cosα bağıntısından, V bulunur. Yer
h
oranı
çekimi ivmesi g bilinmediğinden tu ve
x
bulunamaz.
CEVAP A
10.
Cismin yatayda aldığı yol,
Vo
Voy
hmax
x = Vox . tu
45° V
ox
= 20.2
xmak
= 40 m
I. yol: Cismin yatayda alacağı yol, xmak = 20 m
h ve x taraf tarafa oranlanırsa,
olduğuna göre,
h 50 5
olur.
=
=
x 40 4
2
V . sin 2a
xmak = o
g
CEVAP C
2
20 =
V o . sin2 . 45°
10
20 =
V o . sin90°
10
2
12.
K
Vo2 = 200
Vo = 10 2 m/s olur.
α = 45° olduğundan,
Vox = Voy = 10 2 .
2
= 10 m/s
2
80 m
Cismin çıkabileceği maksimum yükseklik,
2
h mak =
h mak =
V oy
T
2g
Vo
2
10
100
=
= 5 m olur.
2 . 10
20
hmak
O
53°
II. yol:
L
α = 45° ise xmak = 4.hmak olur.
Cismin uçuş süresi, K noktasından L ye serbest
Buna göre, 20 = 4.hmak ⇒ hmak = 5 m olur.
CEVAP A
11.
K
Vox
37°
Voy
yatay
yer
yatay
düşme süresine eşittir.
h=
1 2
.t
g u
80 = 5t u2
16 = t u2
Vo =25m/s
tu = 4 s olur.
h
tç = 2 s olur.
Cismin atılma hızı,
.
L
x
yatay yer
Cismin yatay ve düşey ilk hızları,
Vox = Vo.cos37° = 25.0,8 = 20 m/s
Voy = Vo.sin37° = 25.0,6 = 15 m/s olur.
tç =
Vo . sin53°
g
2 =
Vo . 0, 8
10
Vo = 25 m/s olur.
CEVAP B
Cismin düşeyde aldığı yol,
1
h = Voy.tu +
g t2u
2
= 15.2 + 5.22
= 30 + 5.4
= 30 + 20
= 50 m olur.
KUVVET VE HAREKET
93
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
Bölüm
Yazılı Soruları
(Atışlar)
1.
ÇÖZÜMLER
2.
T
V(m/s)
h
›
(+)
Vo = 30 m/s
53°
K
K
(–)
Vo =25m/s
Voy
30
yatay
Vox
3
0
8
t(s)
h
h=60m
O
K
L
–50
yatay yer
xmak
Vç =50m/s
fiekil- I
yatay
yer
a) Cismin yatay ve düşey ilk hızları,
fiekil- II
a) I. yol:
Vox = Vo . cos53° = 25 . 0,6 = 15 m/s
1
. g . t2
–h = Vo . t –
2
–h = 30 . 8 – 5 . 82
Voy = Vo . sin53° = 25 . 0,8 = 20 m/s olur.
Cismin yere düşme süresi,
1
. g . t2
– h = Voy . t –
2
– 60 = 20 . t – 5t2
–h = 240 – 320
h = 80 m olur.
II. yol (Grafikten):
t2 – 4t – 12 = 0
30 . 3 E ; 5 . 50 E
–h = ;
–
2
2
h = 80 m olur.
(t – 6) (t + 2) = 0
t = 6 s olur.
b) I. yol:
b) Cismin yatayda alacağı maksimum yol,
Vç = Vo – g . t
xmak = Vox . tu = 15 . 6 = 90 m olur.
= 30 – 10 . 8
= – 50 m/s olur.
3.
T
II. yol (Grafikten):
Vç = – (g . tı)
Vo =100m/s
Voy
= – 10 . 5
K
Vox
x
hmak = h +
hı
2
30
= 80 +
2 . 10
= 80 + 45
= 125 m olur.
II. yol (Grafikten):
50 . 5
= 125 m olur.
2
KUVVET VE HAREKET
yatay
yer
xmak
a) Cismin yatay ve düşey ilk hızları,
2
V
= h+ o
2g
94
37°
O
I. yol:
hmak =
hmak
h
= – 50 m/s olur.
c)
Vx
Vox = Vo . cos37° = 100 . 0,8 = 80 m/s
Voy = Vo . sin37° = 100 . 0,6 = 60 m/s olur.
t = 2 saniyede cismin yatay ve düşeyde aldığı yol,
x = Vox . t = 80 . 2 = 160 m
y = Voy . t –
olur.
1
. g . t2 = 60 . 2 – 5 . 22 = 100 m
2
b) Cismin uçuş süresi,
Voy
60
= 2.
= 12 s olur.
tu = 2 .
g
10
5.
a) Cismin çıkış ve uçuş süresi,
düfley
V
60
tç = o =
= 6 s olur.
g
10
V
tç = tiniş = 6 s
c) Cismin çıkabileceği maksimum yükseklik,
1
2 = 5 . 62 = 180 m olur.
. g . t iniş
hmak =
2
tu = tç + ti = 6 + 6 = 12 s olur.
d) Cismin tepe noktasında yalnız yatay hızı olacağın-
h
Vo=60m/s
b) Cismin 2 saniye sonraki hızı,
dan,
yatay yer
V = Vo – g . t
Vx = Vox = 80 m/s olur.
= 60 – 10 . 2
e) Cismin yatayda alacağı maksimum yol,
= 40 m/s olur.
xmak = Vox . tu = 80 . 12 = 960 m olur.
Aldığı yol,
1
. g . t2
2
= 60 . 2 – 5 . 22
h = Vo . t –
4.
düfley
= 120 – 20
30 m/s
= 100 m olur.
c) Maksimum çıkış yüksekliği,
2
2
Vo
60
3600
=
=
= 180 m olur.
2g
2 . 10
20
hmak=
Voy
(+)
yatay
40m/s
(–)
h=35m
Vx
yatay yer
Vyç
Vç
a) Cisim atıldığında yatay hızı 40 m/s, düşey ilk hızı
6.
30 m/s olur.
40m/s
Cismin yere gelme süresi,
1
– h = Voy.t – .g.t 2
2
V=0
– 35 = 30t – 5t2
t2
hmak
– 6t – 7 = 0
h
K
V1=30m/s
V2
(t – 7) (t + 1) = 0
K
t = 7 s olur.
yatay yer
b) Cisim yere çarptığında düşey hızı,
40m/s
Vyç = Voy – g.t
h mak =
K
= – 40 m/s olur.
c) Cismin yatayda alacağı maksimum yol,
= 40.7
= 280 m olur.
2
V1
30
=
= 45 m olur.
2g 2 . 10
L cisminin ilk hızı,
40m/s
Vç = 40v2 m/s olur.
x = Vox.tu
K cisminin çıkabileceği maksimum yükseklik,
2
= 30 – 10.7
Cismin yere çarpma hızı,
L
Vç = 40v2m/s
› 2
2
2
2
(V 2) = V 2 – 2g . h
40 = V 2 – 2 . 10 . 45
2
V 2 = 2500
V2 = 50 m/s olur.
KUVVET VE HAREKET
95
7.
10.
Vo
K
yatay
Vox
K
53°
Voy
h = 80 m
h
Vx
L
45°
xmak
Vy
yatay
yer
45°
•
x
Vox = Vo.cos37° = 25.0,8 = 20 m/s
Voy = Vo.sin37° = 25.0,6 = 15 m/s olur.
t = 4 s olur.
Cisim yere çarptığında düşey ve yatay hızları,
Vy = g.t = 10.4 = 40 m/s
Cisim yatayda sabit hızlı hareket, düşeyde yukarıdan aşağı düşey atış hareketi yapar. Şekildeki
üçgenden,
tan45° =
Vx = Vo = Vy = 40 m/s olur.
1=
Yatayda alacağı maksimum yol,
xmak= Vo.tu = 40.4 = 160 m olur.
= 80 + 80
cisim
Vo =20m/s
1
.g.t2
2
= 15.1 + 5.12
h2
= 20 m olur.
h2 = 400 m olur.
yatay yer
Cismin ivmesi 6 m/s2 olduğunda direnç kuvveti,
Fnet
Rm
a=
G – Fd
m
Fd
G= 20 N
20 – Fd
6=
2
12 = 20 – Fd
Fd = 8 N olur.
Cismin hızı,
Fd = 0,5 ϑ2
8 = 0,5 ϑ2
ϑ2 = 16
ϑ = 4 m/s olur.
96
KUVVET VE HAREKET
b) Eğik düzlemin yüksekliği,
h = Voy.t +
h=560m
560 = 160 + h2
a=
5t = 5
t = 1 s olur.
ği,
9.
2
1
.g. t
2
Vox . t
Voy . t +
15 + 5t
20
15 + 5t = 20
h1
= 160 m olur.
h
x
1=
Cismin 4 saniyede aldığı yol,
1
h1 = Vo.t + .g.t2
2
= 20.4 + 5.42
560 = h1 + h2
yatay
yer
a) Cismin yatay ve düşey ilk hızları,
80 = 5t 2
Cismin yerden yüksekli-
L
V
Cismin yere gelme süresi,
1
h = .g.t 2
2
8.
yatay
Vo =25m/s
yatay yer
6. BÖLÜM
ENERJİ
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
3.
V=0
m
F
•
1.
|F| = 100 N
2x
K
37°
m
yatay
Enerjinin korunumundan,
Fx
K
yatay
M düzlem
3x
L
L
8m
F . 5x = fsür . 3x
yatay
düzlem
fsür =
5
F olur.
3
CEVAP D
F kuvvetinin yatay bileşeni iş yapar. Kuvvetin cisim
üzerine yaptığı iş,
W = Fx . |KL|
= F . cos37° . |KL|
= 100 . 0,8 . 8
= 640 J olur.
2.
2m
m
K
CEVAP C
F
•
L
yatay
düzlem
3x
fiekil- Ι
•
2F
2x
fiekil- ΙΙ
4kg
•
3m
M
4.
•
K
3F
•
x
yatay
düzlem
15m/s
10m/s
•
fsür L
•
M
•
N
yatay
düzlem
LM yolunda sürtünme kuvvetinin yaptığı iş kinetik
enerjideki değişmeye eşittir.
fiekil- ΙΙΙ
Kuvvetin yaptığı iş cisme kinetik enerji olarak aktarılır.
EK = F . 3x = 3F . x
EL = 2F . 2x = 4F . x
W sür = TE k
–fsür . | LM | =
2
2
1
1
mV M – mV L
2
2
–k.mg. | LM | =
2
2
1
1
mV M – mV L
2
2
–k.10.20 =
EM = 3F . x = 3F . x
EL > EK = EM olur.
2
1 2 1
10 – .15
2
2
–200k = 50 –
Cisimlerin hızları,
–200k =
3F . x =
2
1
. m . VK
2
( VK =
6F . x
m
4F . x =
2
1
. 2m . V L
2
( VL =
4F . x
m
3F . x =
2
1
. 3m . V M
2
( VM =
2F . x
olur.
m
k=
225
2
–125
2
5
olur.
16
CEVAP D
Büyüklükleri arasındaki ilişki, VK > VL > VM olur.
CEVAP A
KUVVET VE HAREKET
97
5.
V
m
2V
2F
•
yatay
düzlem
x1
fiekil- Ι
2V
2m
•
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
1.
kuvvet
2F •
3V
3F
x2
fiekil- ΙΙ
F.x
0•
Kuvvetin yaptığı iş kinetik enerjideki değişmeye
eşit olacağından,
•x
F.x
Fx
2
•
2x
F.x
•
3x
yol
Kuvvet-yol grafiğinin altındaki alanların cebirsel
toplamı yapılan toplam işi, dolayısıyla kinetik enerji
değişimini verir.
2
2
1
. m . 8(2V) – V B
2F . x 1
= 2
2
2
3F . x 2 1
. 2m . 8(3V) – (2V) B
2
ı2
1
.m.V
4F.x
= 2
2
1
F.x
.m.V
2
2
2
2x 1
4V – V
=
2
3x 2 2 . (9V – 4V 2)
2
2x 1
3V
=
3x 2 10V 2
ı2
V
2
V
ı
V = 2V olur.
4=
x1
9
=
olur.
x 2 20
CEVAP B
CEVAP A
2.
6.
Fx
2
F•
yatay
düzlem
N = 260 N
a(m/s2)
3
37°
fsür
Fy = 60 N
6
Fx = 80 N
yatay
düzlem
0
2
F = 100 N
4
6
t(s)
–4
–2
G = 200 N
İvme-zaman grafiğinin altındaki alan hızdaki değişmeyi verdiğinden cismin hızı,
Sürtünme kuvveti,
fsür = k . N
∆V = 6 – 4 = 2 m/s
V = Vo + ∆V
=8+2
= 10 m/s olur.
= 0,2 . 260
= 52 N olur.
Sürtünme kuvvetinin yaptığı iş,
6. saniye sonundaki kinetik enerji,
1
Ek =
. m . V2
2
1
. 4 . 102
=
2
Wsür = –fsür . ∆x
= –52 . 10
= –520 J olur.
Sürtünmeden dolayı ısıya dönüşen enerji,
CEVAP D
Eısı = 520 J olur.
CEVAP E
98
KUVVET VE HAREKET
= 200 J olur.
3.
5.
net kuvvet
h›z(m/s)
2F •
2V
F•
V
K
0•
L
•x
•
M
•
3x
2x
0
yol
t
2t
zaman(s)
3t
Cismin hız-zaman grafiği şekildeki gibidir.
Buna göre,
Kuvvet-yol grafiğinin altındaki alanlar yapılan işi,
dolayısıyla kinetik enerji değişimini verir.
2
1
.m. V
E
2
=
›
2
1
E
. m . (2V)
2
K, L, M aralıklarının üçünde de alanlar pozitif olduğundan, üçünde de cismin kinetik enerjisi artmaktadır.
16 1
=
›
4
E
I. ve II. yargılar yanlıştır.
2F.x
WL =
= F.x olur.
2
F.x
WM =
olur.
2
›
olur.
E = 64 J
CEVAP D
WL = 2 WM olur.
III. yargı doğrudur.
CEVAP C
4.
6.
kuvvet(N)
net kuvvet
2F
2F •
K
L
F
F•
0•
0
x
2x
K
•x
L
•
2x
M
•
3x
yol
yol(m)
Kuvvet-yol grafiğinin altındaki alanlar yapılan işi,
Kuvvet-yol grafiklerinin altındaki alanlar yapılan işi,
dolayısıyla kinetik enerji değişimini verir.
2
1
. mK . VK
3F . x
= 2
2
2F . x
1
. mL . VL
2
dolayısıyla kinetik enerji değişimini verir.
K, L, M aralıklarının üçünde de alanlar pozitif olduğundan, üçünde de cismin kinetik enerjisi artmaktadır.
I. ve III. yargılar yanlıştır.
2
3V K
3
=
2
2
2V L
WK =
2F.x
= F.x
2
VK
= 1 olur.
VL
WL =
F.x
2
WK = 2WL olur.
CEVAP C
II. yargı doğrudur.
CEVAP B
KUVVET VE HAREKET
99
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
3.
K
2h
L
h
L
h
K
2h
1.
O2
K
4
T = – GL
3
yatay
O1
yatay
GK
X
L
2h
GL
nından,
E pI
O1 noktasına göre tork alınacak olursa,
E pII
T . 3 = GL . 4
3m K =
GK = 2GL olur.
L
=
h
2
5
m K gh + m L g h
2
5
m
2 L
3
m
2 L
mK 1
=
olur.
mL 2
K ve L cisimlerinin yere göre potansiyel enerjileri
oranı,
K
m K g2h + m L g
4m K + m L = m K +
GK . 2 = T . 3
4
GK . 2 = G L . 3
3
EP
=
h
1 2m K + m L 2
=
2
5
mK + mL
2
4
G olur.
3 L
O2 noktasına göre tork alınacak olursa,
EP
yatay
yer
fiekil- II
Cisimlerin yere göre potansiyel enerjilerinin ora-
h
yatay yer
T=
yatay
yer
fiekil- I
CEVAP B
G K . 2h 2 . 2G L
=
= 4 olur.
GL . h
GL
CEVAP C
2.
4.
Yer çekimi kuvvetine karşı yapılan iş,
düfley
düfley
duvar
K
Wyer ç. = DEP = EP2 – EP1 = mg.D.h – 0
M
L
Wyer ç. = 2.10.4 = 80 J olur.
G
I. yargı doğrudur.
yatay
F kuvvetinin yaptığı iş,
K
L
G
WF = F.Dh = 30.4 = 120 J olur.
fiekil- Ι
II. yargı doğrudur.
M
M
L
•
yatay
yer
fiekil- ΙΙ
K
5h
3h
37° 6/5h
•
yatay
yer
fiekil- ΙΙΙ
Çubuğun her bölmesinin uzunluğuna h, ağırlığına
G diyelim. Çubuğun ağırlık merkezi L noktasıdır.
Net kuvvetin yaptığı iş,
WNET = (F – G).Dh = (30 – 20).4 = 40 J olur.
III. yargı doğrudur.
CEVAP E
E 1 G . 3h 5
olur.
=
=
E2
6
2
G. h
5
CEVAP E
100
KUVVET VE HAREKET
5.
tavan
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
6πr
1.
K
L
ip
düfley
duvar
O r
T
P
2r
•
m
k
.
yatay düzlem
L
K
x
m
yatay
düzlem
Enerjinin korunumundan,
1
Eo =
k x2mak
2
∆h
Cismin yükselme miktarı,
Th =
O
x
Eo =
2r2r + 2rr 6rr
=
= 2rr olur.
3
3
1
1 2
k(2x)2 = 4
kx
2
2
1 2
1 2
kxmak = EL +
kx
2
2
Cismin potansiyel enerjisindeki artma,
1
1 2
k(2x)2 = EL =
kx
2
2
ΔEp = mgΔh = mg2πr = 2mgπr olur.
CEVAP C
EL = 3
1 2
kx olur.
2
EL ve EO taraf tarafa oranlanırsa,
1 2
E L 3. 2 kx
3
=
=
olur.
EO
1 2 4
4. kx
2
CEVAP E
6.
X s›v›s›
Y s›v›s›
h
h
2.
yatay
düzlem
düfley
duvar
m=2kg
k=200N/m
Vo =10m/s
Her iki durumda sıvıların yere göre potansiyel
enerjilerinin oranı yazılıp taraf tarafa oranlanırsa,
h
3
E 1 E X + E Y V.d X .g 2 h + V.d Y .g 2
=
=
E2
E kar
d + dY
) .gh
2V ( X
2
yatay düzlem
düfley
duvar
yatay düzlem
3
1
4 2 dX + 2 dY
=
5
dX + dY
x
Enerjinin korunumundan,
2
2 1
2
1
1
. m . Vo = . m . V + . k . x
2
2
2
5
15
d +
d = 4dX + 4dY
2 X 2 Y
2
2
2
1
1
1
. 2 . 10 = . 2 . 8 + . 200 . x
2
2
2
7
3
d =
d
2 x 2 Y
100 = 64 + 100x
dX 3
olur.
=
dY 7
36 = 100x
CEVAP C
2
2
6 = 10x
x = 0, 6 m = 60 cm olur.
CEVAP E
KUVVET VE HAREKET
101
3.
I
X
O
II
P
2k
5.
4k
M yayındaki uzama miktarı,
x
M
G + 2G = 3k.xM
3G
G
xM =
=
= x olur.
3k
k
N yayındaki uzama miktarı,
P cismi ok yönünde x kadar kaydırılırsa X yayı x
kadar açılır, Y yayı x kadar sıkışır.
Bu durumda yaylarda depolanan esneklik potansiyel enerjiler,
2G = k.xN
K
2
1
3k.x
EM
3
2
olur.
=
=
2
EN 1
4
.k. (2x)
2
Yaylarda depolanan toplam esneklik potansiyel
enerji,
m
G
EM ve EN taraf tarafa oranlanırsa,
1
1
.k .(x )2 = .4k.x2 = 2kx2 olur.
2 Y Y
2
3k
k
N
2G
xN =
= 2x olur.
k
1
1
EX = .kx.(xX)2 = .2k.x2 = kx2
2
2
EY =
tavan
GL = 2G olur.
Y
•
GK = G ise,
L
2m
2G
CEVAP B
Etop. = EX + EY = kx2 + 2kx2 = 3kx2 olur.
Bu durumda, I. yargı yanlış, II. ve III. yargılar doğrudur.
CEVAP E
4.
2k
k
O
F1
F2
x1
X
Y
x2
6.
Enerji kaybı olmadığından enerji korunacaktır. Bu durumda m
Sistem dengede olduğundan X yayını geren F1
kuvveti ile Y yayını geren F2 kuvveti eşittir.
|F1| = |F2|
kütleli cismin B seviyesine gelene kadar
kaybettiği potansiyel
enerji, yaya esneklik
k1.x1 = k2.x2
potansiyel enerji ola-
2k.x1 = k.x2 & x1 = x, x2 = 2x olur.
rak aktarılır.
Bu durumda, yaylarda depolanan esneklik potansiyel enerjiler,
EX =
1
1
.k .x2 = .2k.x2 = kx2
2 1 1 2
EY =
1
1
.k .x2 = .k(2x)2 = 2kx2 olur.
2 2 2 2
Buna göre,
m.g(h + x) =
cam macunu
m
h
tabla
A
x
B
k
,
k
fiekil-I
fiekil-II
1
.k.x2 olur.
2
Eşitliğe bakılırsa, yaydaki sıkışma miktarı x; m,
g, h ve k değerlerine bağlı, yayın boyu , ye bağlı
değildir.
CEVAP C
EX ve EY değerleri taraf tarafa oranlanırsa,
2
EX
kx
1
olur.
=
=
E Y 2kx 2 2
102
KUVVET VE HAREKET
CEVAP A
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
1.
4.
3m kütleli cismin kinetik enerjisi maksimum olduğu
anda sistem şekildeki konumdadır.
m
Enerjinin korunumundan,
Ep
Ek
=
m
mgh 2
mg (h 1 + h 2)
,
K
,
m
h2
1
=
4 h1 + h2
V
L•
h 1 + 3 = 12
h2
h 1 = 9 m olur.
M
CEVAP C
2mg, = 4
K
E=4
m
h
3m
yatay
yer
1
mV2
2
1
mV2
2
E 1
= mV2
4 2
2m
h
M
yatay
Enerjinin korunumundan,
1
1
mV2 +
3mV2
mg, + 3mg, = mg2., +
2
2
•
L
3m
,
Yeri (yatay) referans alalım.
yatay yer
2.
.
,
h1
1
3
=
4 h1 + 3
V
3m kütleli cismin kinetik enerjisi,
3E
1
mV2 =
olur.
Ek = 3
4
2
3m
h
CEVAP E
yer
VK
VL
VM
5.
Cisimlerin yere göre potansiyel enerjileri,
EP = m.g.3h = 3mgh
Vo
K
K
L
EP = 2m.g.2h = 4mgh
L
EP = 3m.g.h = 3mgh olur.
20m/s
h=25m
L
r=5m
Bu durumda, EP = EP < EP olur.
M
L
Bu durumda, EL > EK = EM olur.
CEVAP E
r=5m
•
K
Sürtünme olmadığından cisimlerin mekanik enerjileri korunur. Son durumda cisimler yere çarptıklarında da mekanik enerjileri, başlangıçtaki potansiyel enerjilerine eşit olur.
yer
Ray üzerinde sürtünme olmadığından mekanik
enerji korunur. Bu durumda, cismin K noktasındaki
ilk hızı Vo,
EK = EL
3.
Ek + Ep = EkL + Ep
K
M
L
m
h
3h
yatay
Enerjinin korunumundan,
EL
mg . h
1
=
=
olur.
E K mg . 4h 4
L
1 2
1
.V + 10.25 = .202 + 10.10
2 o
2
V
K
K
1
1
.mV2o + m.g.h = .m.V2 + m.g.2r
2
2
1 2
1
.V + g.h = .V2 + g.2r
2 o
2
2
Vo
+ 250 = 300
2
Vo2 = 100 & Vo = 10 m/s olur.
CEVAP A
CEVAP B
KUVVET VE HAREKET
103
6.
K cismi 2h yolunu alıp
.
II. yol:
.
yere çarptığında L cismi
Cismin L ve R deki hızları,
h kadar yükselir ve yerden yüksekliği 2h olur.
Sürtünme
göre
olmadığına
mekanik
enerji
EL
K
3m
korunur.
Bu durumda K ve L
2h
cisimlerin kinetik enerji-
K
VR =
2g.h R = 2.10.0, 8 , = 16 ,
VL
=
VR
h
L
12 ,
=
16 ,
3
3
=
olur.
4
2
CEVAP A
h
leri toplamı,
Eilk = Eson
2g.h L = 2.10.0, 6 , = 12 ,
olur. VL ve VR taraf tarafa oranlanırsa,
L
m
VL =
yer
EK
8.
m=2kg
3mg.2h + mg.h = EK + EL + mg.2h
K
10m/s
7mgh = EK + EL + 2mgh
5mgh = EK + EL olur.
3m
k=2000N/m
CEVAP D
•
7.
m
O
,
K
37°
53°
hL
L
•
yatay düzlem
Enerjinin korunumundan,
37°
mgh + 1 mV2 = 1 k x2mak
hR
VL
2
2
2.10.3 + 1 2.102 = 1 2000 x2mak
2
2
VR
R
60 + 100 = 1000 x2mak
I. yol:
16 = 100 x2mak
Yataya göre L ve R noktalarının yükseklikleri,
4 = 10 xmak
hL = ,.sin37° = 0,6 ,
xmak = 0,4 m
hR = ,.sin53° = 0,8 , olur.
Sürtünmeler önemsiz olduğundan enerji korunur.
Bu durumda cismin K noktasındaki potansiyel
enerjisi, L ve R noktalarındaki kinetik ve potansiyel
enerjilerin toplamına eşittir.
xmak = 40 cm olur.
CEVAP D
9.
k
L noktası için,
1
m.g., = .m.V2L + m.g.(, – hL)
2
2
g., =
2
VL
2
VL
+ g.(, – 0,6,)
2
1
2 + m.g.(, – h )
m.VR
R
2
2
2
VR
2 = 16, ........ (2)
= 8, & VR
2
(1) ve (2) denklemleri oranlanırsa,
2
VR
104
30°
K
V
g., = R + g.(, – 0,8,)
2
=
210 cm
Vo =8m/s
= 6, & VL2 = 12, ....... (1)
m.g., =
2
2m
m=2kg
R noktası için,
VL
20cm
L
V
12, 3
3
=
& L =
olur.
VR
2
16, 4
KUVVET VE HAREKET
•
yatay düzlem
Yay 20 cm sıkışır.
Enerjinin korunumundan,
2
2
1
1
. m . Vo = m . g . h + k . x
2
2
2
2
1
1
. 2 . 8 = 2 . 10 . 2, 1 + k . (0, 2)
2
2
64 = 42 + 0, 02k
22 = 0, 02k & k = 1100 N/m olur.
CEVAP E
10.
12.
T
Voy
m
Vx
P
Vo
hmak
F
53° Vox
P
O
N
h
xmak
yatay
yer
Cismin yatay ve düşey ilk hızları,
Vox = Vo.cos53° =
3
V
5 o
Voy = Vo.sin53° =
4
V olur.
5 o
K
L
2h
M
M noktasında F kuvveti kaldırıldığında cisim P noktasına kadar çıktığına göre F kuvvetinin yaptığı iş,
W = F.2x olur.
M noktasındaki bu iş, P deki potansiyel enerjiye
eşittir.
F.2x = m.g.2h
Enerjinin korunumundan,
F.x = mgh olur.
2
4
2
1
.V
E P 2 m.V oy c 5 o m
16
=
=
=
olur.
2
2
EK
1
25
V
m.V o
o
2
Cismin L noktasında ilk geçtiğinde kinetik enerjisi,
E1 = F.x = mgh olur.
CEVAP B
Cismin L noktasından ikinci kez geçtiğinde kinetik
enerjisi, P deki potansiyel enerjiye eşittir.
E2 = m.g.2h = 2mgh olur.
E1 ve E2 değerleri oranlanırsa,
E1
mgh
1
=
= olur.
E 2 2mgh 2
CEVAP B
T
11.
K
Voy
Vo
hmak
37°
O
Vox
4m
L
yatay
yer
xmak
Cismin ilk hızı,
x = Vox . t = Vo . cos37° . t
4 = Vo . 0,8 . 0,1 ⇒ Vo = 50 m/s olur.
Cismin düşeydeki ilk hızı,
Voy = Vo . sin37°
= 50 . 0,6
= 30 m/s olur.
Cisim atıldığı andaki düşeydeki kinetik enerjisi T
noktasındaki potansiyel enerjiye eşittir.
EP =
T
=
2
1
. m . V oy
2
2
1
. 0, 2 . 30
2
= 0, 1. 900
= 90 J olur.
CEVAP E
KUVVET VE HAREKET
105
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
3.
•P
h
Vo
1.
•
•
K
fs1=4N
m=2kg
Vo=6m/s
2m
•
M
V=0
fs2=6N
30°
•
yatay yer
Cisim P noktasından geri dönüşte L noktasında
durduğuna göre P den L ye gelene kadar kaybettiği potansiyel enerji, sürtünmeye karşı yapılan işe
eşittir. Buna göre,
yatay
M düzlem
L
Enerjinin korunumundan,
1
mgh +
m.V2o = fs1.|KL| + fs2.|LM|
2
2.10.2 +
2h
2h
.
K
L
Wsür = 3mgh – 2mgh = mgh olur.
Cisim K den P ye gelene kadar enerjinin korunumu
yazılırsa cismin K noktasındaki kinetik eneri,
1
.2.62 = 4.4 + 6.|LM|
2
40 + 36 = 16 + 6|LM|
E2 + 2mgh = Wsür + 3mgh
60 = 6|LM|
E2 + 2mgh = mgh + 3mgh
E2 = 2mgh olur.
|LM| = 10 m olur.
K noktasındaki potansiyel enerji de,
CEVAP C
Ep = mg.2h = 2mgh olur.
Mekanik enerji = Kinetik enerji + potansiyel enerji
olduğundan,
2.
E1 = E2 + Ep = 2mgh + 2mgh = 4mgh olur.
V=0
E1 ve E2 oranlanırsa,
P
L
K
E 1 4 mgh
=
= 2 olur.
E 2 2 mgh
h
E
M
N
Her bölmede sürtünmeye harcanan enerjiye Wsür
diyelim.
I. durumda: (K den P ye giderken)
E = 3Wsür + mgh
m
5h
2h
Cisim yere çarpıp 2h kadar
zıpladığında son enerjisi,
yer
Eson = m.g.2h = 2mgh olur.
E + mgh = 2Wsür + EL
Yere çarptığında cismin kaybolan mekanik enerjisi,
4Wsür + mgh = 2Wsür + EL
DE = |Eson – Eilk|
4Wsür + Wsür = 2Wsür + EL
= |2mgh – 5mgh|
EL = 3Wsür
= 3mgh kadardır.
E = 4Wsür olduğundan,
KUVVET VE HAREKET
K
olur.
II. durumda: (P den dönerken)
106
İlk durumda cismin mekanik enerjisi, potansiyel
enerjisine eşittir.
Eilk = m.g.5h = 5mgh
E = 4Wsür
3
E olur.
4
4.
Bu durumda,
mgh = Wsür
EL =
CEVAP D
yatay
düzlem
CEVAP C
Bu durumda cismin kaybolan enerjisinin % olarak
değeri,
3mgh
%=
.100 = 60 olur.
5mgh
CEVAP D
5.
8.
m = 2 kg
Vo =6m/s
•M
K
.
37°
yatay
yer
•
1
mV2 = mgh + Wsür
2
1
m 102 = m.10.2 + Wsür
2
1
m.100 = 20 m + Wsür
2
50 m = 20 m + Wsür
32 = 5fsür ⇒ fsür = 6,4 N olur.
CEVAP E
K
m
L
M
V=0
h
h
m
K
L
•
M
•
N
•
P
9.
•N
Vo
•
K
3h
2h
•
•
L fs
M
Cisim N noktasından geri dönüp L noktasında durduğuna göre, N den L ye gelene kadar kaybettiği
potansiyel enerji, L-M arasındaki sürtünmeye harcanan enerjiye eşittir. Bu durumda L-M arasındaki
sürtünmeye karşı yapılan iş,
Wsür = m.g.3h = 3mgh olur.
E
•
30 m ısıya dönüşürse
60 m ısıya dönüşür.
LM yolu boyunca cismin enerjisinin %60 ı ısıya dönüşmüştür.
CEVAP D
h
•R
.
50 m de
100 m de
N
7.
•
Wsür = 30 m olur.
h
h
Cisim K noktasından
atıldığında R de durP
h
ması için sürtünmeR
li yolda 3 bölme yol
alması gerekir. Cisim 3
bölmede sürtünmeye karşı 3.(2mgh) = 6mgh kadar
enerji harcar. Cisim K noktasında 6mgh lık enerjiye
sahip olmalıdır. K noktasında cisim hem kinetik hem
potansiyel enerjiye sahiptir. Bu durumda,
Ws = Ek + Ep
6mgh = Ek + m.g.5h & Ek = mgh olur.
CEVAP A
yatay
Enerjinin korunumundan sürtünmeye dönüşen
enerji,
Enerjinin korunumundan sürtünme kuvvetinin
büyüklüğü,
2
2
1
1
m . g . h + . m . V o = . m . V L + fsür . |KL|
2
2
1
1
2 . 10 . 3 + . 2 . 62 = . 2 . 82 + fsür . 5
2
2
60 + 36 = 64 + 5fsür
Cisim L noktasından
serbest bırakıldığında
N de durduğuna göre
1 bölmede sürtünmeye harcanan enerji,
m.g.2h = 2mgh dir.
.
•L
2m
L
6.
j=10m/s
K•
fsür
VL = 8 m/s
2m
m
h =3m
yatay
Her bölmede sürtünmeye harcanan enerjiye Wsür
diyelim
I. durumda:
E = 4Wsür + mgh
mgh = Wsür
E = 5Wsür olur.
II. durumda:
2E = 4Wsür + mghı
10Wsür= 4Wsür + mghı
6Wsür= mghı
6 mgh = mghı
hı = 6h olur.
CEVAP E
Cisim K den N ye kadar çıktığına göre, K noktasındaki kinetik ve potansiyel enerjilerin toplamı,
N noktasındaki potansiyel enerji ile sürtünmeye
harcanan enerjinin toplamına eşittir.
Bu durumda,
1
.m.V2o + m.g.2h = Wsür + m.g.3h
2
1
.m.V2o + 2mgh = 3mgh + 3mgh
2
1
m.V2o = 4mgh olur.
2
Eğer cisim K noktasından 2Vo hızıyla atılsaydı M-N
arasında çıkabileceği yükseklik en fazla hı olsun.
KUVVET VE HAREKET
107
12.
Bu durumda,
1
.m(2Vo)2 + m.g.2h = W + m.g.hı
2
L
Vo =6m/s
1
.m.4V2o + 2mgh = 3mgh + mghı
2
k=200N/m
1
4.( m.V2o) + 2mgh = 3mgh + mghı
2
•
K
4.4mgh + 2mgh = 3mgh + mghı
hı
enerji,
hı
2
1
. m . V o = m . g . h + W sür
2
= 15h olurdu.
CEVAP D
2
1
. 2 . 6 = 2 . 10 . 1 + W sür
2
36 = 20 + W sür
10.
W sür = 16 J olur.
m
K•
Yaydaki sıkışma miktarı,
h
L•
•S
M•
•R
N•
•P
•
O
h
m . g . h = W sür +
h
2 . 10 . 1 = 16 +
h
4 = 100x
yatay yer
mg4h = mg3h + Wsür
2
x = 0, 2 m = 20 cm olur.
CEVAP E
1
II. durumda:
mg3h = mg.hı + Wsür
2
Wsür > Wsür
1
2
olduğundan S noktasından geri dönen cisim L-M
arasına kadar çıkabilir.
CEVAP E
m
K
53°
yatay
2
1
. 200 . x
2
1
Wsür = mgh olur.
11.
2
1
.k . x
2
2 = 10x
I. durumda:
L
M
Enerjinin korunumundan,
mg . |KL| . sin53° = k.mg.cos53°.|KL| + k . mg|LM|
|KL| . 0,8 = 0,5 . 0,6 . |KL| + 0,5 . |LM|
8|KL| = 3|KL| + 5|LM|
5|KL| = 5|LM|
IKLI
= 1 olur.
ILMI
108
•
yatay düzlem
Enerjinin korunumundan sürtünmeye dönüşen
18mgh = 3mgh + mghı
18h = 3h +
1m
m=2kg
KUVVET VE HAREKET
CEVAP C
TEST
1.
1
ENERJİ
ÇÖZÜMLER
3.
m = 5kg
m
|F|=20N
.
R•
yatay
düzlem
h=6m
Dx
Vs=0
10m
.
37°
a=
F
20
=
= 4 m/s2 olur.
m
5
20m
•
fs
N
R noktasından serbest bırakılan m kütleli cisim N
noktasında durduğuna göre, L-N arasında sürtünmeye harcanan enerji, R den L ye gelene kadar
kaybedilen potansiyel enerjiye eşittir. h yüksekliği,
Cismin 6 saniyede aldığı yol,
Dx =
•
L
Cismin ivmesi,
1
1
.a.t2 = .4.62 = 2.36 = 72 m olur.
2
2
h = |RL|.sin37° = 10.0,6 = 6 m dir.
Cisim üzerine yapılan iş,
Bu durumda,
W = F.Dx = 20.72 = 1440 J olur.
m.g.h = fs.|LN|
CEVAP D
mg.h = k.mg.|LN|
h = k.|LN|
6 = k.20 & k = 0,3 olur.
II. yargı doğrudur.
2.
F=25N
4kg
Yukarıdaki denklemde m kütlesi sadeleştiğinden
kütlenin 2 m olması cismin duracağı noktayı değiştirmez.
10m/s
•
•
4m
K
L
•
3m
N
yatay
düzlem
I. yargı yanlıştır.
Kuvvet cismin hareket yönünün tersi yönünde
uygulandığından cisim üzerine yapılan iş negatiftir.
Cismin K den L ye geldiğinde hızı,
Yolun L-N arası sürtünmeli olduğundan R noktasındaki mekanik enerji, N noktasındaki mekanik
enerjiye eşit olmaz.
W KL = TE k
–F. | KL | =
–25.4 =
2
2
1
1
mV L – mV K
2
2
III. yargı yanlıştır.
CEVAP B
2
2
1
1
.4.V L – .4.10
2
2
4.
2
–100 = 2V L – 200
2
50 = V L & VL = 5 2 m/s olur.
Cismin K den N ye geldiğinde hızı,
–25.7 =
–175 =
2
2
1
1
mV N – mV K
2
2
=
2
2
1
1
.4.V N – .4.10
2
2
2
2N N
2
5
mV + 2mgh olur.
2
h
m
4m
h
yatay yer
E ilk = E son
– 200
2
25
5
= V N & VN =
m/s olur.
2
2
VL ve VN oranlanırsa,
VL 5 2
=
= 2 olur.
VN
5
2
V
Sistemin son enerjisi,
2 1
2
1
E son = mV + 4mV + mg.2h
2
2
W KN = TE k
–F. | KN | =
4m kütleli cisim yere çarptığında
m kütleli cismin yerden yüksekliği
2h olur. Sistemin ilk enerjisi,
Eilk = 4mgh + mgh = 5mgh
5mgh =
2
5
mV + 2mgh
2
3mgh =
2
5
mV olur.
2
m kütleli cismin kinetik enerjisi,
2
1
1 6
3
E = m.V = . b mgh l = mgh olur.
2
2 5
5
CEVAP E
CEVAP A
KUVVET VE HAREKET
109
5.
7.
a(m/s2)
düfley
Y
3
2
4
6
8
mY.g
t(s)
X
–3
İvme-zaman garfiğinin altındaki alan hızdaki değiş-
mX.g
yatay
h
mY
yatay
yer
fiekil- Ι
(6 + 2)
2.3
TV =
= 9 m/s
.3 –
2
2
fiekil- ΙΙ
P noktasından asılı iken dengede olduğundan,
Cismin ilk hızı sıfır olduğundan,
mX.3h = mY.h
∆V = Vs – Vi = 9 ⇒ Vs = 9 m/s olur.
mY = 3 m olur.
Cismin 8. saniye sonundaki kinetik enerjisi,
Ek =
h
mX=m
meyi verir.
X
Y
Şekil-ΙΙ de çubukların yere göre potansiyel enerjileri,
2
2
1
1
mV = .4. (9) = 162 J olur.
2
2
Ep = EX + EY
CEVAP D
= mX.g.3h + mY.g.7h
= m.g.3h + 3m.g.7h
= 24 mgh olur.
CEVAP E
6.
tavan
.
.
tavan
tavan
.
.
8.
.
4kg
R
•
5m/s
m
m
•
•
m
F1
1,5m
•
F2
m
m
3m
O
F3
1,5m
m
m
37°
•
O
K
L
2m
yatay yer
M 3m
4m
yatay yer
yatay yer
fiekil-I
fiekil-III
fiekil-II
Kuvvetlerin yaptıkları işler potansiyel enerjideki değişime eşit olduğundan,
2
sin 37° =
4
2
tığından kinetik enerjisi sıfırdır.
E K = E P + W sür
mgh +
4
2
1
.4.5 = fsür .5
2
Buna göre,
50 = 5.fsür & fsür = 10 N olur.
W3 > W2 > W1 olur.
CEVAP A
KUVVET VE HAREKET
2
1
mV = mgh + fsür . | KO |
2
2
1
mV = fsür . | KO |
2
W3 = 3mg h + mg h = 2 mgh olur.
2
2
110
3
3
& | KO | =
= 5 m olur.
| KO |
0, 6
Cisim R noktasından serbest düşme hareketi yap-
2
W2 = 4mg h + mg h + mg h = 7 mgh
4
yatay düzlem
|KO| yolunun uzunluğu,
W1 = 2mg h + mg h = 3 mgh
2
K
CEVAP C
9.
11.
V(m/s)
10
K
2h
6
m=10kg
➞
3h
L
2h
3h
2
h
h/2
yatay
yer
fiekil- I
L
h
K
h
fiekil- II
•
∆x
F
0
yatay düzlem
fiekil- I
yatay
yer
t (s)
4
fiekil- II
Cismin aldığı yol,
(6 + 10)
Tx =
.4 = 32 m olur.
2
Cisimlerin her iki durumdaki potansiyel enerjileri
yazılıp oranlanırsa,
Yapılan iş kinetik enerjideki değişmeye eşit olduğundan,
m K .g.3h + m L .g.h
E PI
=
h
3h
E PII
m K .g. + m L .g.
2
2
W = ΔEk
2
2
F.Δx = 1 m (V2 – V1)
3m K + m L
4=
m K 3m L
+
2
2
2
F.32 = 1 10(102 – 62)
2
3mK + mL = 2mK + 6mL
F.32 = 5(100 – 36)
F.32 = 320
mK = 5mL
F = 10 N olur.
mK
= 5 olur.
mL
CEVAP B
CEVAP C
m
12.
Vo
K
L
h
M
h
N
h
O
10.
h
h
P
2r
h
R
r
K noktasından 3mgh kadar kinetik enerji ile harekete başlayan m kütleli cisim R noktasında durduğuna
göre, her bir bölmede sürtünmeye harcanan enerji,
O
F
3Wsürt. = Ek + Ep
3Wsürt. = 3mgh + 6 mgh
K
L
Wsürt. = 3mgh olur.
Buna göre cisim O noktasında iken kinetik enerjisi,
Makaralar F kuvveti ile 1 defa döndürüldüğünde K cismi
2πr
kadar, L cismi
2π. 2r = 4πr
kadar yukarı çıkar. Başlangıçta cisimlerin potansiyel enerjileri eşit olduğundan, mK = mL = m olur.
Kütlelerin potansiyel enerjilerinin farkı,
E1 + Wsürt. = Ek + 4mgh
E1 + 3mgh = 3mgh + 4mgh
E1 = 4mgh olur.
Cismin O noktasındaki potansiyel enerjisi ise,
E2 = 2 mgh dır.
∆E = mK.4πr – mL.g.2πr
E1 ve E2 değerleri oranlanırsa,
= mg.(4.3.r – 2.3.r)
= 6 mgr olur.
CEVAP A
E 1 4mgh
=
= 2 olur.
E 2 2mgh
CEVAP D
KUVVET VE HAREKET
111
TEST
2
1.
2kg
3.
VK=10m/s
VL
F
•
3m
5m
k=800N/m
V o =5m/s
.
•
L
m=2kg
VN
•
K
ENERJİ
ÇÖZÜMLER
yatay düzlem
yatay
N düzlem
fiekil-I
V =3m/s
Yapılan iş kinetik enerjideki değişmeye eşittir.
Cismin L noktasındaki hızı,
.
W KL = TE k
F. | KL | =
100.3 =
yatay düzlem
2
2
1
1
mV L – mV K
2
2
2
2
1
1
.2.V L – .2.10
2
2
Enerjinin korunumundan,
1
1
m V2o =
mV2 +
2
2
1
1
2.52 = .2.32 +
2
2
2
400 = V L & VL = 20 m/s olur.
Cismin N noktasındaki hızı,
W KN = TE k
F. | KN | =
100.8 =
x
fiekil-II
1
k.x2
2
1
800.x2
2
25 = 9 + 400 x2
16 = 400x2
2
2
1
1
mV N – mV K
2
2
4 = 20 x
2
2
1
1
.2V N – .2.10
2
2
x = 0,2 m = 20 cm olur.
CEVAP E
2
900 = V N & VN = 30 m/s olur.
4.
düfley
V
VL ve VN taraf tarafa oranlanırsa,
VL 20 2
=
= olur.
VN 30 3
2m
CEVAP B
2m
2m
2m
O
•
4m
yatay
2m
2.
kuvvet
V
2F•
yatay yer
F•
2Fx
0
Fx
•x
•
2x
F.x F.x
2
•
•
3x
4x
yol
Kuvvet-yol grafiğinde doğrunun altındaki alan yapılan işi verir. Yapılan iş kinetik enerjiye eşit olduğundan,
2
1
mV
2Fx
2
=
›2
Fx
1
+ Fx
mV
2Fx + Fx +
2
2
2
V
2
=
9 V ›2
2
2
Enerjinin korunumundan,
E ilk = E son
2
2
12mg = 3mV + 8mg
2 V
=
3 V›
4mg = 3mV
2
KUVVET VE HAREKET
2
4.10 = 3V & V = 2
›
112
Sistemi serbest bıraktığımızda kütlesi büyük olan
yönde dönme hareketi oluşur. Bu durumda sistem
okla gösterilen yönde dönme hareketi yapar.
4m kütleli cismin düşey eksenden geçerken sistemin enerjisi,
2 1
2
1
E son = 2m.V + .4m.V + 2mg. (2 + 2)
2
2
= 3mV + 8mg olur.
4 V
=
9 V ›2
3
V = V olur.
2
Yere göre kütlelerin ilk durumda potansiyel enerjileri,
Eilk = 2mg.2 + 4m.g.2 = 12 mg olur.
CEVAP B
10
m/s olur.
3
CEVAP B
5.
1kg
Vo=40m/s
•M
7.
L
V=0
•
P
20m
h
h
•
K
•
L
k=0,4
›
•
K
yatay
•
O
10m
yatay
düzlem
|KL|=50m
Cisim L noktasından serbest bırakıldığında |KO|
yolunu alıp yaya çarparak enerjisini yaya verir. Yay
bu enerjiyi aynen cisme aktarır. Bunun bir kısmını
ı
|OK| yolunda sürtünmeye harcayarak h yüksekliğine çıkar. Enerjinin korunumundan,
Cisim K den M gidişte ve M den P ye gelişte sürtünmeli yolu iki defa geçtiğinden sürtünmeye harcanan
enerji,
Wsür = 2.fs.|KL|
E ilk = E son
= 2.kmg.|KL|
= 2.0,4.1.10.50
mgh = fs . | KO | + fs . | OK | + mgh'
= 400 J olur.
mgh = k.mg. | KO | + k.mg. | OK | + mgh'
1.10.20 = 0, 5.1.10.10 + 0, 5.1.10.10 + 1.10.h'
Enerjinin korunumundan, geri dönüşte cismin P
200 = 50 + 50 + 10h'
noktasındaki hızı,
2
2
1
1
mV o = W sür + mV
2
2
100 = 10h' & h' = 10 m olur.
CEVAP D
2
2
1
1
.1.40 = 400 + .1.V
2
2
2
800 = V & V = 20 2 m/s olur.
CEVAP A
8.
tavan
ip
ip
ip
4T
3T
6T
L
K
6.
düfley
duvar
düfley
duvar
GK
3
h
2
GL
2h
M
h
GM
K
•
Cisimlerin ağırlıkları iplerdeki gerilme kuvvetleri ile
doğru orantılıdır.
mg
L
mg
30°
53°
yatay düzlem
yatay
yer
•
yatay düzlem
GK = 4G ise,
GL = 3G
GM = 6G olur.
Cisimlerin potansiyel enerjilerinin oranı,
,
m . g.
EK
5
4
=
=
EL
2
8
m . g. ,
5
olur.
CEVAP C
Cisimlerin yere göre potansiyel enerjileri,
3h
= 6Gh olur.
EK = 4G.
2
EL = 3G.2h = 6Gh olur.
EM = 6G.h olur.
Buna göre, EK = EL = EM olur.
CEVAP A
KUVVET VE HAREKET
113
9.
11.
m
K
Vo
3
Voy = — Vo
2
Vo
Vo
L
5h
3h
P
h
o
60° V = V
ox —
2
O
Vo
T
K
yatay
h
3h
yer
Mekanik enerjinin korunumundan, K-L arasında
sürtünmeye harcanan enerji,
Vo
—
2
L
•
yatay yer
VL
3Vo
EK = W1 + EL
Cismin yatay ilk hızı,
m.g.5h = W1 + m.g.3h
Vox = Vo . cos60° = Vo .
5mgh = W1 + 3mgh & W1 = 2mgh olur.
1 Vo
=
olur.
2
2
Cismin düşey ilk hızı,
L-P arasında sürtünmeye harcanan enerji,
Voy = Vo . sin60° = Vo .
EL = W2 + EP
3
3
=
V olur.
2
2 o
Enerjinin korunumundan,
m.g.3h = W2 + m.g.h
2
V
2
1
1
m . d o n + m . ` 3 Vo j
E
2
2
2
=
2
E
1
m . Vo
2
2
1
1
›
m . Vo . b + 3 l
E
2
4
=
2
E
1
m . Vo
2
3mgh = W2 + mgh & W2 = 2mgh olur.
›
W1 ve W2 oranlanırsa,
W 1 2mgh
=
= 1 olur.
W 2 2mgh
CEVAP C
›
E
13
=
E
4
›
13
E =
E olur.
4
CEVAP D
10.
K•
m
h
•
12.
2h
2m
h
•
K
h
•
•
L
•
h
yatay düzlem
.
VK=2V
ip
.
yatay yer
Her bölümde sürtünmeye harcanan enerjiye Wsür
diyelim.
m
L
h
I. durumda:
VL=V
mg4h = mgh + 5Wsür
L cismi h kadar aşağı indiği anda hızı V ise, K nin
hızı 2V olur.
1
1
mgh =
mV2 +
2m (2V)2
2
2
1
mgh = 9
mV2
2
mgh
1
mV2 =
olur.
9
2
3mgh = 5Wsür
Wsür =
3mgh
olur.
5
II. durumda:
mgh + Ek = 4mgh + 5Wsür
Ek = 3mgh + 5.
3mgh
5
K cisminin mgh cinsinden kinetik enerjisi,
Ek = 6 mgh olur.
CEVAP C
114
KUVVET VE HAREKET
Ek = 8
K
8mgh
1
mV2 =
olur.
9
2
CEVAP E
TEST
3
ENERJİ
ÇÖZÜMLER
1.
3.
K•
Vo=0
O
•R
•P
m
.
•
•
K
L
h
h
2h
•
M
yatay
N
I. yol: Kürenin yarıçapı 10 m olduğuna göre h yüksekliği,
h = r.cos53° = 10.0,6 = 6 m
hı = r – h = 10 – 6 = 4 m olur.
Kürenin iç yüzü sürtünmesiz olduğundan mekanik
enerji korunur.
Cismin K noktasındaki potansiyel enerjisi R noktasındaki kinetik ve potansiyel enerjiler toplamına
eşittir.
EP = Ek + EP
I. durumda:
E = 3 Wsür + mgh
mgh = Wsür
E = 3 mgh + mgh
E = 4 mgh
K
R
R
2
ı
1
m.g.r = .m.VR + m.g.h
2
ı
1 2
g.r = .VR + g.h
2
1 2
10.10 = .VR + 10.4
2
2
VR
= 60
2
II. durumda:
ı
E = 3Wsür + 2 mgh
ı
E = 3 mgh + 2 mgh
ı
E = 5 mgh
›
5mgh 5
E
=
=
E 4mgh 4
2
VR = 120 & VR = 2c30 m/s olur.
5
E =
E olur.
4
ı
II. yol: Cismin R noktasındaki hızı,
CEVAP B
VR =
2gh =
2.10.6 =
K
O
a
h1
L
a
–
2
VL
h2
M
•
EM
3
–a
5
37°
•
Ek = mg.(h1 + h2) olur.
mg.h 2
EP
=
Ek
mg. (h 1 + h 2)
ip
m
Ep = mg.h2 olur.
Ep ve Ek taraf tarafa
oranlanırsa,
120 = 2 30 m/s olur.
CEVAP D
tavan
4.
M noktasındaki kinetik
enerjisi,
•R
L
•
Cismin L noktasındaki
yere göre potansiyel
enerjisi,
VR
10m
•
Her bölümde sürtünmeye harcanan enerjiye Wsür
diyelim.
2.
.
53°
ı
h
E
r=10m
•
2
–a
37° 5
yatay
yer
53°
yatay
yer
2
4
=
5
h1 + 4
Şekil-I de:
Cismin potansiyel enerjisi,
a 1
E = m . g . = mga olur.
2 2
Şekil-II de:
Cismin potansiyel enerjisi,
›
3
2
E = mg c a + a m
5
5
10 = h1 + 4
h1 = 6 m olur.
= mga
CEVAP A
= 2E olur.
CEVAP C
KUVVET VE HAREKET
115
5.
7.
m =2 kg
K
2r
L
h=0,8m
O
Ι.ip
•
2πr
x=0,2m
r
yatay
düzlem
4πr
ΙΙ.ip
m
yatay
yer
yatay yer
yatay
yer
fiekil- Ι
2r yarıçaplı K makarası 1 kez dönerse ip,
fiekil- ΙΙ
2π.2r = 4πr kadar çekilir.
Enerjinin korunumundan,
L makarası ipi 2πr kadar aşağı bırakır. Ι. ip,
2
1
m . g. (h + x) = . k . x
2
2 . 10 . (0, 8 + 0, 2) =
20 =
x1 = 4πr – 2πr = 2πr kadar çekilmiş olur.
Ι. ip 2πr kadar çekildiğinde ΙΙ. ip,
0, 04k
2
kilmiş olur. Bu durumda m cismi πr kadar yükselir.
Potansiyel enerji değişimi,
40 = 0, 04k
∆Ep = mgh
k = 1000 N/m olur.
= mg.πr
= 3mgr olur.
CEVAP E
6.
Cisim 4 metre yükseklikten bırakıldığında yay, 4 metre sıkıştığına göre,
mg (4 + 4) =
2
1
k (4)
2
m
k
mg = k olur.
Yaydaki sıkışmanın 6 m olması için
cisim yaydan h kadar daha yükseklikten bırakılmalıdır. Enerjinin korunumundan,
m
h
K
6m
fs
K
x
L
x
M
x
N
x
O
x
P
x
R
WF = F.4x = 4Fx olur.
Cisim R noktasında durduğuna göre sürtünmeli
yolda 4x yolunu aldığında sürtünme kuvvetinin
yaptığı iş,
Cisim R de durduğuna göre,
2
1
k (6)
2
WF = Ws
4Fx = 4.fs.x &
h + 6 = 18
KUVVET VE HAREKET
F
Ws = fs.4x olur.
1
mg (h + 6) = mg.36
2
116
F kuvveti O noktasına kadar uygulandığına göre
yapılan iş,
E ilk = E son
h = 12 m olur.
CEVAP A
8.
4m
K
4m
8mg = 8k
mg (h + 6) =
2rr
= rr kadar çe2
2
1
. k . (0, 2)
2
CEVAP C
F
= 1 olur.
fs
CEVAP B
9.
11.
N
fsür
m=2kg
m
K
K
x
F
3h
2h
x
•
L
yatay
M
Vo =4m/s
3m
x
Cismin M noktasındaki hızı ile N noktasındaki
hızı eşit olduğuna göre, bu noktalardaki kinetik
enerjileri de eşittir. Bu durumda F kuvvetinin M-N
arasında yaptığı iş, potansiyel enerjiye eşittir ve bu
değer,
V =0
•
fsür
37°
L
yatay
düzlem
M
Enerjinin korunumundan,
m.g.h +
2 . 10 . 3 +
2
1
. m . V o = W sür + W sür
2
(KL)
(LM)
2
1
. 2 . 4 = 2 . 5 + 6 . ILMI
2
60 + 16 = 10 + 6 . ILMI
W = F.x = Ep = 3mgh kadardır.
66 = 6 . ILMI
Bu durumda cismin M noktasındaki kinetik enerjisi,
ILMI = 11m olur.
Ek = 2mgh + F.2x
CEVAP E
= 2mgh + 2.(3mg)
= 8mgh olur.
CEVAP D
10. 4m kütleli cisim 2h yolunu alıp
2V
yere V hızı ile çarparsa, 2m
kütleli cisim 4h yolunu alır ve
12. Cisimlerin yayların
serbest ucuna göre
potansiyel enerjileri;
4h
hızı 2V olur. Enerjinin korunu-
Y
m
X
2h
2m
Şekil-I için
mundan,
m
h
h
Ex = 2m.g.h
xX
4m
2h
xY
k
k
fiekil-I
fiekil-II
Şekil-II için
V
yatay yer
E ilk = E son
4mg.2h + mg (2h + h) =
2 1
2
1
4m.V + m (2V) + mg. (2h + h + 4h)
2
2
2
2
11mgh = 2mV + 2mV + 7mgh
4mgh = 4mV
2
EY = m.g.2h olur.
Bu durumda, EX = EY dir.
Cisimlerin ilk durumdaki potansiyel enerjileri yayda
depolan enerjiye eşittir. Bu durumda,
Şekil-I için
2
mgh = mV olur.
2mg(h + xX) =
1 2
kx
2 X
m kütleli cismin kinetik enerjisi,
E=
=
Şekil-II için
2
1
m. (2V)
2
2mg (2h+ xY) =
2
1
m.4V
2
= 2 mV
2
= 2 mgh olur.
CEVAP E
1 2
k.x Y olur.
2
Bu iki eşitlikten de anlaşılacağı gibi, yayların sıkışma miktarları ile cisimlerin yaylara aktardıkları
enerjilerin eşitliği için kesin birşey söylenemez.
CEVAP A
KUVVET VE HAREKET
117
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
Bölüm
Yazılı Soruları
(Enerji)
3.
F(N)
1.
ÇÖZÜMLER
k=200N/m
20
2kg
•
D.N
10
40J
20J
0
a) Yayda depolanan potansiyel enerji,
80J
8
4
EP =
x(m)
12
a) W = 20 + 40 + 80 = 140 J olur.
TE K =
E=
2
2
1
m (V – V o)
2
jiye eşittir.
Emek = E = 2500 J olur.
2
d) Potansiyel enerji kinetik enerjiye eşit olduğunda
2
100 = V & V = 10 m/s olur.
2.
2kg
•
K 4m
•
L
Aral›k
•
M
•
N
hız,
•
P
E pot = E kin
•
R
2500 =
K-L
L-M
M-N
N-P
P-R
5
0
–1
1
2
Uygulanan
kuvvet (N)
a) Cismin kinetik enerjisinin artması için kuvvetin
pozitif iş yapması gerekir. |K–L|, |N–P|, |P–R|
aralıklarında kuvvet pozitif iş yapmıştır.
b) |M–N| aralığında cismin üzerine uygulanan kuvvet negatif olduğundan hızı azalmıştır.
c) Yapılan toplam iş,
W = 5.|K–L| + 0.|L–M| + (–1).|M–N|
= 5.4 + 0.4 – 1.4
= 16J olur.
W = TE k
W=
2
2
1
1
mV s – mV i
2
2
16 =
2
2
1
1
.2.V s – .2.0
2
2
2
16 = V s & Vs = 4 m/s olur.
d) |L–M| arasında kuvvet sıfır olduğundan cisim
sabit hızla hareket yapar. |M–N| arasında azalır.
|N–P| arasında artar. P deki hız M deki hıza eşittir. Bu durumda L, M ve P deki hızlar eşittir.
118
KUVVET VE HAREKET
2
1 2 1
kx' = .200. (2) = 400 J olur.
2
2
c) Sistemin mekanik enerjisi yaya depolanan ener-
2
1
140 = .2, 8. (V – 0)
2
140 = 1, 4 V
2
1 2 1
kx = .200. (5) = 2500 J olur.
2
2
b) Yay 2m sıkıştığında yaydaki enerji,
b) W = ∆Ek = 140 J olur.
c)
•
yatay düzlem
4.
2
1
.2.V mak & Vmak = 50 m/s olur.
2
a) Cismin L noktasından geçerken hızı,
2
2 1
2
1
1
. k . x mak = . k . x + . m . V L
2
2
2
2
2
2
200 . (0, 4) = 200 . (0, 1) + 1. V L
2
200 . 0, 16 = 200 . 0, 01 + V L
2
32 = 2 + V L
2
V L = 30
VL = 30 m/s olur.
b) Cismin O noktasından geçerken hızı,
2
2
1
1
k . x mak = .m . V mak
2
2
2
2
200 . (0, 4) = 1. V mak
2
V mak = 32
Vmak = 4 2 m/s olur.
5.
7.
tavan
K
,=2m
O
a) F kuvvetinin yaptığı iş,
x=20m
W=F.x
yatay
37°
2F
= 200 J olur.
h1
2F
b) m kütlesi üzerine 200J
L
G= mg
37°
4F
de 200J enerji kaza-
M
VL
4F
iş yapıldığından kütle
53°
VM
F
|F|=10N
= 10 . 20
nır.
G›
G= mg
c) 8F = P &
a) h1 = , . cos37° = 2 . 0,8 = 1,6 m
Cisim L noktasından geçerken hızı,
T
P
=8
F
m
Kuvvetten 8 kat kazanç varsa, yoldan 8 kat kayıp vardır. İp 20 çeki-
2
1
. m . VL
2
2
V L = 2g . h1
mgh1 =
lirse m kütlesi,
h' =
2
V L = 2 . 10 . 1,6
20
= 2, 5 m
8
yer değiştirir.
VL = 4 2 m/s olur.
d) T gerilme kuvveti,
8F = P = T
b) Cisim M noktasından geçerken hızı,
2
1
m . g . , = m . VM
2
8.10 = T ⇒ T = 80 N olur.
2
V M = 2g . ,
2
V M = 2 . 10 . 2
8.
2
V M = 40
2kg
VM = 2 10 m/s olur.
5m/s
6m
6.
a)
L
k=0,5
80cm
6m/s
K
yatay düzlem
Enerjinin korunumundan,
EK = EL
2
1
mV = mgh + E L
2
2
1
.2.6 = 2.10.0, 8 + E L
2
36 = 16 + E L & E L = 20 J olur.
b) Enerjinin korunumundan,
EK = EM
2
1
mV = mgh + k.mg. | LM |
2
1 2
.6 = 10.0, 8 + 0, 5.10. | LM |
2
18 = 8 + 5. | LM | & | LM | = 2 m olur.
•
M
k=100N/m
37°
K
L
8m
P
yatay
düzlem
a) Cismin ilk enerjisi,
E ilk = mgh +
2
1
mV
2
= 2.10.6 +
2
1
.2.5
2
= 145 J olur.
Cismin yaya çarparken P deki hızı,
E ilk = E P
145 =
2
1
mV P
2
145 =
2
1
.2.V P & VP =
2
145 m/s olur.
b) Yayın maksimum sıkışma miktarı,
E ilk = E pot
145 =
1 2
kx
2
145 =
2
1
.100.x & x =
2
29
m olur.
10
KUVVET VE HAREKET
119
10. a) Sistemin ivmesi,
2kg
20 = (2 + 3).a
l
20m
V=0
53o
sin 53° =
•
O
yatay
düzlem
•
K
20
20
&,=
= 25 m olur.
,
0, 8
Cismin L noktasındaki potansiyel enerjisinin bir
kısmı LO yolunda sürtünmeye harcanır, geri
kalanı ise cismin O noktasındaki kinetik enerjisidir. Enerjinin korunumundan cismin O noktasındaki hızı,
mgh =
2
1
mV + fs .,
2
2
1
mgh = mV + k.mg. cos 53°.,
2
10.20 =
1 2
V + 0, 5.10.0, 6.25
2
2
200 =
V
+ 75
2
125 =
V
2
a
2kg
20 = 5.a
a = 4 m/s2
olur. 2 kg lık cismin
yere
20N
50m
yer
çarpma hızı,
V2 = Vo2 + 2a.x
V2 = 0 + 2.4.50
V2 = 400
V = 20 m/s olur.
Cismin kinetik enerjisi,
Ek =
2
2
1
1
m V = .2. (20) = 400 J olur.
2 2
2
b) 2 kg lık cismin hızı ile 3 kg lık cismin hızlarının
büyüklükleri eşit olacağından cisimlerin maksimum hızlarının büyüklükleri 20 m/s olur.
c) 2 kg lık cismin yere gelme süresi,
250 = V & V = 5 10 m/s olur.
h=
50 =
b) Cismin O noktasındaki kinetik enerjisi K noktasına gelinceye kadar sürtünmeye gitmiştir.
E kin = W sür
2
1
mV = k.mg. | OK |
2
2
1 ^
. 5 10 h = 0, 5.10. | OK |
2
125 = 5. | OK | & | OK | = 25 m olur.
c)
fsür
mg.cos53°
53°
mg
mg.sin53°
53°
a = g . (sinα – k . cosα)
= g . (sin53° – k . cos53°)
= 10 . (0,8 – 0,5 . 0,6)
= 10 . 0,5
= 5 m/s2 olur.
KUVVET VE HAREKET
yatay
düzlem
2
2
120
3kg
•
a)
a
Fnet = mt.a
L
•
9.
1 2
at
2
2
1
.4.t
2
2
25 = t & t = 5s olur.
5s sonra 3 kg lık cisme kuvvet etki etmez. Net
kuvvet sıfır olacağından cisim sabit hızla gider.
7. BÖLÜM
İTME VE MOMENTUM
Cisme etki keden kuvvetin büyüklüğü,
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
F.3 = 30
I
V 45°
m
CEVAP A
.
45°
V
II
3.
45°
.
➞
P1 = 1,6 kg.m/s
I. engelde momentum değişiminin büyüklüğü,
D P I = Ps – P i
Pi=mV 45°
I.
➞
en
.
l
45°
2 .mV olur.
45°
Pi=mV
.
Ps=mV
.
II. engel
DPII = 2.mV olur.
PI ve PII taraf tarafa oranlanacak olursa,
DPI
2 .mV
2
olur.
=
=
2.mV
2
DPII
= 24 kg.m/s olur.
Ps=18kg.m/s
Yönü ise doğuya doğru-
–Pi=24kg.m/s
da hızı 6 m/s ve güneye
doğru olduğundan,
P
Ps=18kg.m/s
= 18 kg.m/s olur.
Yönü ise güneye doğrudur. Cismin momentum
değişimi,
∆P =
∆P =
Ps – Pi
Ps + (– Pi) olur.
=
(24)2
CEVAP E
Cisim esnek çarpışma yaptığına
göre çarptığı hızla
engelden eşit açıyla yansır. II engeline dik geldiğinden
kendi üzerinden
geri döner.
I
60°
V
.
30°
I. engelde momentum değişiminin büyüklüğü,
DPI = Ps – Pi
DPI =
m
60° 60°
3 mV olur.
II
Pi=mV
60°
Ps=mV
II. engelde momentum değişiminin büyüklüğü,
DPII = Ps – Pi
Pi=mV
.
Ps=mV
.
II. engel
DPII = 2mV olur.
PI ve PII taraf tarafa oranlanırsa,
Büyüklüğü ise,
∆P2
F = 32 2 N olur.
l
Pi=24kg.m/s
= 3.8
= 3.6
İtme, momentum değişimine eşit olduğundan düzlemin topa uyguladığı ortalama kuvvet,
F . ∆t = ∆ P
1
= 1, 6 2
F.
20
4.
Pi = m.Vi
Ps = m.Vs
yatay
düzlem
CEVAP B
Cismin ilk momentumu,
dur. Kuvvet uygulandığın-
➞
P2 = 1,6 kg.m/s
Ps=mV
II. engelde momentum değişiminin büyüklüğü,
DPII = Ps – Pi
2.
45°
45°
ΔP= 1,6v2 kg.m/s
ge
ge
DPI =
F = 10N olur.
en
Cisim esnek çarpışma yaptığına göre,
çarptığı hızla engelden eşit açıyla yansır. II engeline dik
geldiğinden üzerinden geri döner.
I.
1.
F.∆t = ∆P
+
(18)2
∆P2 = 900
∆P = 30 kg.m/s olur.
DPI
3 mV
3
=
=
olur.
2mV
2
DPII
CEVAP C
KUVVET VE HAREKET
121
5.
m = 2 kg
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
F=8N
20m/s
–x
yatay
düzlem
+x
1.
İtme momentum değişimine eşit olduğundan,
F . ∆t = m . ∆ V
F . ∆t = m . ( V2 – V1)
Serbest düşmede ismin aldığı
yol h, 3h, 5h ... olduğunda bu
yolları alma süreleri eşit olur.
tKL = tLM = t olur.
Cismin L deki hızı V ise yere
çarptığında hızı 2V olur.
–8 . 3 = 2 . (V2 – 20)
K
h
P1
V
3h
t
Cismin L ve M deki momentumları,
–12 = V2 – 20
V2 = 8 m/s; +x yönünde olur.
P1 = m.V
Cisim 3 saniye sonunda hızı ile düzgün doğrusal
hareket yapar. Bu durumda cismin hızı bundan
sonra sabit olacağından 4 saniye sonra hızı yine
8 m/s olur.
P2
2V
yatay yer
P2 = m.2V olur.
Bu eşitlikleri oranlanırsa,
P1
mV
1
olur.
=
=
P2 2mV 2
CEVAP B
2.
6.
t
L
CEVAP B
L
m
3 kg
DP
Vo
Ps=18kg.m/s
Pi=24kg.m/s
–Pilk
53°
2m
K
yatay
37°
53°
37°
4h
Pson
yatay düzlem yatay düzlem
Cismin ilk ve son momentumlarının büyüklükleri,
Pilk = 3.8 = 2.4 = 24 kg.m/s
Pson = 3.6 = 2.3 = 18 kg.m/s
Cisme uygulanan itme, düşeydeki momentum
değişimine eşittir. Bu durumda zeminin cisme
uyguladığı kuvvet,
itme = DP
F.Dt = Pilk.sin53° + Pson.sin37°
h
Vo
fiekil-I
V
2V
fiekil-II
Hava sürtünmeleri önemsiz olduğuna göre, cisimlerin yere düşme süreleri kütleye ve yatay hıza
bağlı değildir.
1
g.t2K
2
1
4h =
g.t2L
2
h=
eşitlikleri taraf tarafa oranlanırsa,
F.0,03 = 24.0,8 + 18.0,6
2
t
t
h
1
= K & K=
4h t 2
tL 2
L
F.0,03 = 19,2 + 10,8
F.0,03 = 30
tK = t & tL = 2t olur.
F = 1000 N olur.
CEVAP E
Üzerlerine uygulanan itmeler,
IK = FK.tK = 2m.g.t
IL = FL.tL = m.g.2t
olur. IK ve IL taraf tarafa oranlanırsa,
I K 2mgt
=
= 1 olur.
I L 2mgt
122
KUVVET VE HAREKET
CEVAP C
3.
m
5.
Vo
•O
K
t
4
VL
4
t
L
V
VM
Vo
t
2V
x
4
VK
Vo
x
P
x
•
K
Vo
yatay yer
L
yatay yer
M
Cisimlerin yatay momentumları değişmez.
3V
Cisimlerin kütleleri,
I. yol:
mK = mL = mM = m olsun.
Cismin yatay hızı sabit olduğundan her aralığı t
Cisimlerin uçuş süreleri,
sürede alır. Cismin düşeydeki hızı V = g.t olduğun-
tK = 3t ise,
dan düşeydeki hızları doğru orantılı olur.
tL = 3t,
Cismin O dan L noktasına geldiğinde,
tM = 2t olur.
DP1 = m.(2V – 0) = 2mV
Cisimlerin uçuş süreleri boyunca momentum değişimleri,
Cisim O dan P noktasına geldiğinde,
DPK = mg.3t = 3m.g.t,
DP2 = m.(3V – 0) = 3mV olur.
DPL = mg.3t = 3m.g.t,
DP1 ve DP2 taraf tarafa oranlanırsa,
DPM = mg.2t = 2m.gt olur.
DP1 2mV 2
olur.
=
=
DP2 3mV 3
Buna göre, DPK = DPL > DPM olur.
CEVAP A
II. yol:
Vx
6.
TP1 mg.2t 2
=
= olur.
TP2 mg.3t 3
Voy
Vo
hmax
CEVAP C
53° V
ox
yatay düzlem
Vo
Cismin ilk hızının yatay ve düşey bileşenleri
4.
Vox = Vo.cos53° = 100.0,6 = 60 m/s
Cismin 2 ve 4 saniye sonraki hızları,
V1 = Vo – gt1
V1
= 30 – 10.2
= 10 m/s
Voy = Vo.sin53° = 100.0,8 = 80 m/s olur.
düfley
(+)
V2
V2 = Vo – g t2
= 30 – 10.4
= –10 m/s olur.
Vo=30m/s
(–)
2kg
yatay yer
Momentum değişimi,
4
4
I. yargı yanlıştır.
hmax yüksekliğinde cismin yalnız yatay hızı olacağından hızı minimum olacağından momentumu da
minimum olur.
Pmin = m.Vx = 2.60 = 120 kg.m/s olur.
II. yargı doğrudur.
∆P = m.∆V
4
Cismin üzerine yerçekim kuvveti etki ettiğinden
yatay momentum korunur. Düşey momentum
korunmaz.
Cismin uçuş süresi,
2Voy 2.80
=
= 16 s
tu =
9
10
olur. Bu sürede cismin üzerine uygulanan itme,
4
= m.(V2 – V1)
= 2(–10 – 10)
= 2.(–20)
I = F.Dt = mg.tu = 2.10.16 = 320 N.s olur.
= –40 kg m/s olur.
CEVAP D
III. yargı yanlıştır.
CEVAP B
KUVVET VE HAREKET
123
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
1.
3.
V(m/s)
8
Fnet (N)
3
Vson=2
+6
0
0
4
2
5
5
t(s)
10
15
t(s)
–8
–4
Vilk=–8
Cisme (0-15) saniye aralığında verilen itme,
F.Dt = m.DV = m(Vson – Vilk)
F.Dt = 2.[2 – (–8)] = 2.10 = 20 N.s olur.
Kuvvet-zaman grafiğinde doğrunun altındaki alan
itmeyi verir.
Σ F . ∆t = 3 . 2 – 2 . 4 = –2 N.s olur.
İtme, momentum değişimine eşit olduğundan, cismin 5. saniyede sonundaki hızı,
Σ F . ∆t = ∆ P
Σ F . ∆t = m . ( V2 – V1)
CEVAP D
4.
F(N)
8
–2 = 2 . (V2 – 6)
40
–1 = V2 – 6
V2 = 5 m/s olur.
0
Cismin kinetik enerjisi,
Ek =
2
=
10
–5(t – 10)
t
t(s)
–5
2
1
. m . V2
2
Cismin ilk hızı 5 m/s ve son hızı sıfırdır. İtme,
momentum değişimine eşit olduğundan,
Σ F . ∆t = m . ( Vson – Vilk)
2
1
.2.5
2
= 25 J olur.
CEVAP C
40 – 5 . (t – 10) = 2 . (0 – 5)
40 – 5t + 50 = –10
5t = 100
t = 20 s olur.
CEVAP C
2.
5.
V(m/s)
Vilk=6
a(m/s2)
4
10
0
2
5
7
t(s)
Vson=– 4
5
= 2 . (–4 – 6)
Cismin hızındaki değişme,
∆V = 10 + 20 – 5
= 25 m/s olur.
Cismin son hızı,
CEVAP A
V2 = Vo + ∆V
= 5 + 25
= 30 m/s olur.
124
KUVVET VE HAREKET
10
–2
Cismin (0-7) saniye aralığındaki momentum değişimi,
∆ P = m . ( Vson – Vilk)
= –20 kg.m/s olur.
0
20
15
–5 20
t(s)
P2 = m . V2
•
Kuvvet-zaman grafifiğinde
doğrunun
altındaki alan itmeye
eşittir.
•
• 3t
2t
•
zaman
•t
0
•
• 3t zaman
2t
–P•
Konum-zaman grafiğinde doğrunun eğimi hareketlinin hızını verir. Kütle sabit olduğundan P = m.V
eşitliğinde görüldüğü gibi hız-zaman grafiği ile
momentum-zaman grafiğini aynı gibi düşünebiliriz.
3F•
2F•
K
F•
L
Cismin 0-3t zaman aralığında momentum-zaman
grafiği şekildeki gibi olur.
CEVAP A
•
0
t
zaman
9.
3F + F
) .t DP
2
K
=
2F.t
DPL
2
ivme
4 PK – 0
=
2 PL – 0
net kuvvet
a•
0•
PK
= 2 olur.
PL
a•
•
I
II
•
III
• zaman 0•
I
•
II
•
III
• zaman
Momentum-zaman grafiğini hız-zaman grafiği gibi düşünebiliriz. Hız-zaman grafiğinde doğrunun
eğimi ivmeyi verir. İvme-zaman grafiğini kuvvetzaman grafiği gibi düşünürsek, cisme etkiyen net
kuvvetin zamanla değişim grafiği şekildeki gibidir.
CEVAP C
momentum
Buna göre, cisme etkiyen net kuvvet,
2P•
P•
0
•t
–V•
CEVAP E
kuvvet
İtme = momentum
değişimi olduğundan,
7.
P•
0
= 60 kg.m/s olur.
(
momentum
V•
= 2 . 30
6.
hız
8.
20. saniye sonunda cismin momentumu,
I
II
III
Artıyor
Sabit
Azalıyor
CEVAP B
•t
•
2t
•
3t
zaman
Momentum-zaman grafiğinin eğimi kuvveti verir.
0-t zaman aralığında grafiğin eğimi sabittir. Cisme
etkiyen net kuvvet sabit olup, cisme hareket yönüne zıt yönde etki etmektedir.
I. yargı yanlıştır.
t-2t zaman aralığında grafiğin eğimi sabittir. Cisme
etkiyen net kuvvet sabit olup, cisme hareket
10.
hız
3V •
3P •
2V •
2P •
V•
P•
0
yönünde etki etmektedir.
II. yargı yanlıştır.
2t-3t zaman aralığında grafiğin eğimi sıfır olduğundan, cisme etki eden net kuvvet sıfırdır.
III. yargı doğrudur.
CEVAP C
momentum
•
t
•
2t
•
3t zaman
0
•
t
•
2t
•
3t zaman
Kuvvet-zaman grafiğini ivme-zaman gibi düşünebiliriz. Hız-zaman grafiği şekildeki gibidir. Kütle sabit olduğundan hız-zaman grafiğini momentum-zaman grafiği gibi düşünürsek, cismin momentumzaman grafiği şekildeki gibi olur.
CEVAP C
KUVVET VE HAREKET
125
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
1.
MODEL SORU - 5 DEKİ SORULARIN ÇÖZÜMLERİ
1.
kuvvet
VL
VK =3V
3br
4br
O
F•
Fx/2
•
•
0
x
Fx
•
Fx/2
2x
•
mL
mK
konum
3x
VK
VL
O
Kinetik enerji ile momentum arasındaki ilişki
2
Ek =
P
dir.
2m
Vagonlar t saniyede O noktasında çarpıştığından
K 3 br, L 4 br yol almıştır. Bu durumda K nin hızı
3V ise L nin hızı 4V dir. Vagonlar 2t saniye sonra
t=0 anındaki noktalarında bulunduklarına göre,
aynı hızlarla geri dönerler. Bu olayın olabilmesi
vagonların çarpışmadan önceki momentumlarının
büyüklüklerinin eşit ve zıt olmasıyla mümkündür.
|PK| = |PL|
Cismin x konumundaki momentumu,
2
P1
F.x
=
2
2m
P21 = F.x.m ........ (1)
Cismin 3x konumundaki momentumu,
2
P2
F.x
F.x
=
+ F.x +
2
2
2m
mK.VK = mL.VL
mK.3V = mL.4V
mK
4
=
olur.
3
mL
2
P2
= 2F.x
2m
P22 = 4F.x.m ........ (2)
(1) ve (2) eşitlikleri taraf tarafa oranlanırsa
2
P1
2
P2
2.
–x
K
+x
L
3V
V
F.x.m
=
4F.x.m
P1
1
=
olur.
P2
2
CEVAP D
m
m
Merkezi ve esnek çarpışmalarda cisimlerin kütleleri eşit ve hareket yönleri zıt ise, cisimler çarpıştıktan sonra çarpışmadan önceki hızlarını değiştirerek geri dönerler.
CEVAP C
2. Grafiğe bakıldığında, Ek = 1 J iken P = 1 N.s veya
K
L
–x; 3V
+x; V
CEVAP B
Ek = 4 J iken P = 2 N.s olduğu görülür. Bu verileri
formülde yerlerine yazacak olursak,
Ek =
3.
P
2m
3kg
2
1=
(1)
1
kg bulunur.
&m=
2m
2
Cismin enerjisi 9J iken momentumu,
Ek =
9=
2
P
2m
P
2.
2
1
2
& P = 3 kg.m/s olur.
Cismin üzerine uygulanan itme,
F.∆t = ΔP = Ps – Pi =3 – 0 = 3 N.s olur.
CEVAP C
126
–x
K
2
KUVVET VE HAREKET
yatay
düzlem
4m/s
+x
L
VL=0
1kg
Cisimlerin kütle merkezlerinin hızları,
mK.VK + mL.VL = (mK + mL).Vort
3.4 + 1.0 = 4.Vort
Vort = 3 m/s olur.
Çarpışmadan sonra K ve L nin hızları,
VKı = 2Vort – VK
= 2.3 – 4
= 2 m/s; +x yönünde olur.
ı
VL = 2Vort – VL
= 2.3 – 0
= 6 m/s; +x yönünde olur.
yatay
düzlem
CEVAP C
4.
VX =5V
VY =4V
K
O
5br
mX
4br
ı
VY =2V
3br
mX
2br
mY
Momentumun korunumundan,
ı ı
PX + PY = PX + PY
mX.VX – mY.VY = –mX.VXı + mY.VYı
8mX = 6mY
mX
3
=
olur.
4
mY
+x
5V
fiekil-I
ı
V K=2V
ı
K
L
O
•
V L=5V
yatay
düzlem
5m
Çarpışmadan sonra cisimler t sürede K cismi 2 m,
L cismi 5 m yol aldıklarına göre,
VKı = 2V ve VLı = 5V olur.
mK.5V – mL.3V = mK.(–2V) + mL.5V
mX.5V – mY.4V = –mX.3V + mY.2V
–x
yatay
düzlem
6m
Çarpışmada momentum korunacağından,
Pilk = Pson
mK.VK + mL.VL = mK.VKı + mL.VLı
VXı = 3V ve VYı = 2V olur.
K
10m
Çarpışmadan önce K ve L cisimleri 2t sürede K cisim
10 m, L cismi 6 m yol aldıklarına göre, VK = 5V dersek VL = 3V olur.
L
Vagonlar O noktasında çarpıştıktan t süre içerisinde X vagonu 3 br, Y vagonu ise 2 br yol almışlar.
Bu durumda,
5.
•
fiekil-II
ı
VX =3V
L
O
2m
VX = 5V & VY = 4V olur.
O
VL=3V
VK=5V
mY
Vagonlar O noktasında çarpıştıklarına göre, X
vagonu 5 br, Y vagonu 4 br yol alırlar.
K
6.
K
L
5mK – 3mL = –2mK + 5mL
7mK = 8mL
CEVAP B
mK
8
=
olur.
7
mL
CEVAP D
L
V
3m
m
yatay
düzlem
Momentumun korunumundan,
mK.VK + mL.VL = (mK + mL).Vort
3m.5V + m.V = (3m + m).Vort
16V = 4Vort
Vort = 4V olur.
K cisminin hızı,
VKı = 2Vort – VK
= 2.4V – 5V
= 8V – 5V
= 3V; +x yönünde olur.
L cisminin hızı,
VLı = 2.Vort – VL
= 2.4V – V
= 8V – V
= 7V; +x yönünde olur.
CEVAP E
KUVVET VE HAREKET
127
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
4.
VX=3V
K
1.
K
L
➞
3V
VL=0
yatay
düzlem
4
VX = 3V & VY = 5V dir.
4
Çarpıştıktan sonra ortak vagon 2 br yol aldığına
mK.3V + mL.0 = (mK + mL).V
göre Vort = 2V olur.
3mK = mK + mL
2mK = mL
mK
1
=
olur.
mL
2
K
2.
mY
X vagonu 3 br, Y vagonu 5 br yol almıştır.
mK.VK + mL.VL = (mK + mL).Vort
–x
5br
Vagonlar t saniyede O noktasında çarpıştığından
Momentumun korunumundan,
4
L
P
3br
mX
mL
mK
VY =5V
2br
O
Momentumun konumundan,
R Pi = R Ps
mX.VX + mY.VY = (mX + mY).Vort
CEVAP B
+x
L
6m/s
4kg
mX.3V – mY.5V = (mX + mY).2V
3mX – 5mY = 2mX + 2mY
VL=?
mX = 7mY
mX
= 7 olur.
mY
yatay
düzlem
1kg
CEVAP D
Momentumun korunumundan,
4
4
4
mK.VK + mL.VL = (mK + mL).Vort
5.
–x
4.6 + 1.VL = 5.4
24 + VL = 20
m1=40g V =200m/s
1
+x
Vb=0
mb=950g
V2=1000m/s m2=10g
VL = –4 m/s; –x yönünde olur.
tahta
blok
CEVAP C
yatay düzlem
Momentumun korunumundan,
3.
–x
4
+x
2V
4
4
0,04.200 – 0,01.1000 + 0,95.0 = 1.Vort
VL = 0
m
4
m1V1 + m2V2 + mb.Vb = (m1 + m2 + mb).Vort
L
K
m
yatay
düzlem
8 – 10 = Vort
Vort = –2 m/s;
Momentumun korunumundan cisimlerin ortak hız–x yönünde olur.
ları,
mK . VK + mL . VL = (mK + mL) . Vort
CEVAP C
m . 2V + m . 0 = 2m . Vort
6.
Vort = V olur.
Her iki durumda cisimlerin kinetik enerjileri,
1
1
=
. m . (2V)2 = 4 . . m . V2 = 4E
ΣEk
2
2
önce
1
1
ΣEk
=
. 2m . V2 = 2 . . m . V2 = 2E
2
2
sonra
olur. Isıya dönüşen enerji,
Eısı = ΣEk
sonra
Momentumun korunumundan,
R Pönce = R Psonra
mç . Vç = (mç + Vt) . Vort
önce
tahta
blok
0,1.90 = (0,1 + 0,8).Vort
9 = 0,9.Vort
Vort = 10 m/s olur.
– ΣEk
.
ip
90m/s
çivi
= 2E – 4E
Cisimlerin birlikte çıkabileceği yükseklik,
= – 2E olur.
2
K cisminin kinetik enerjisinin % 50 si ısıya dönüşmüştür.
128
KUVVET VE HAREKET
CEVAP C
h max =
V o (10) 2
=
= 5 m olur.
2.g
2.10
CEVAP B
7.
mK
K
VK=3V
VL=2V
O
•
3br
9.
mL
tavan
.
L
2br
yatay
fiekil-I
Vort=V
•
fiekil-II
L
K
O
h
.
Vort
yatay
3br
düfley
Cisimler sabit hızla hareket ettiklerinden çarpışmadan önce t anında K 3 br, L 2 br yol aldıklarından
VK = 3V ise VL = 2V olur.
Momentumun korunumundan,
4
4
4
mMVM + ms.Vs = (mM + ms).Vort
0,01.200 + 0,99.0 = 1.Vort
Cisimler çarpışmadan 3t sonra sürede 3 br yol
aldıklarına göre Vort = V olur.
Vort = 2 m/s olur.
Enerjinin korunumundan,
1
(mM + ms).V2ort = (mM + ms).g.h
2
1 2
.2 = 10.h
2
2 = 10.h & h = 0,2 m = 20 cm olur.
Çarpışmada momentum korunacağından,
RPönce = RPsonra
mK.VK + mL.VL = (mK + mL).Vort
mK.3V – mL.2V = (mK+ mL).V
CEVAP B
3mK – 2mL = mK + mL
10.
2mK = 3mL
mK
3
=
olur.
2
mL
1kg
K
VK.cos60°
60°
VK=20m/s
CEVAP C
4kg
VA =5m/s
60°
8.
V.cos37°
20g
37°
–x
V
37°
yatay
yatay
yol
Momentumun korunumundan,
mK . VK .cos60° + mA . VA = (mK + mA) . Vort
blok
980g
K
+x
k=0,2
1 . 20 . cos60° + 4 . 5 = 5 . Vort
1
+ 20 = 5Vort
1 . 20 .
2
30 = 5Vort
yatay
düzlem
L
4m
Kinetik enerji sürtünmeye dönüşeceğinden,
1
. (mm + mb) . V 2ort = k . (mm + mb) . g . x
2
1
. V 2ort = 0,2 . 10 . 4
2
V 2ort = 16
Vort = 6 m/s; +x yönünde olur.
CEVAP C
T
11.
Vo=100m/s
m
Vort = 4 m/s olur.
Momentumun korunumundan,
mm . V + mb . Vb = (mm + mb) . Vort
hmak
O
yatay düzlem
yatay
düzlem
xmak
Yatay momentum korunacağından,
4
0,02 . V . cos37° + 0,98 . 0 = 1 . 4
4m
37° V
ox
4
ΣPönce = ΣPsonra
0,02 . V . 0,8 = 4
m.Vo.cos37° = (m + 4m).Vort
4
V=
0, 016
m.100.0,8 = 5m.Vort
V = 250 m/s olur.
CEVAP E
80 = 5Vort
Vort = 16 m/s olur.
CEVAP C
KUVVET VE HAREKET
129
12.
m
K
MODEL SORU - 7 DEKİ SORULARIN ÇÖZÜMLERİ
L
3m
1.
80m
K
m
P
m
VK VL
(–)
numundan,
45m
L
3m
Momentumun koruı
PL
=
15 =
yatay düzlem
ı
(+)
ı
PL=15m/s
ı
mL.V L
ı
5.V L
ı
. PK=9kg.m/s
37°
PK=12kg.m/s
V L = 3 m/s olur.
K ve L cisimlerin P cisminin çarpana kadar geçen
CEVAP C
süreleri,
hK =
1 2
gt
2 K
80 =
2
1
.10.t K
2
16 =
2
tK
hL =
1 2
gt
2 L
45 =
2
1
.10.t L
2
2.
K
L
5m/s
& t K = 4s
37°
53°
5kg
10kg
L
VL›
I. yol:
2
9 = t L & t L = 3s olur.
Çarpışmadan önce cisimlerin momentumları,
Px = 5.10 = 50 kg.m/s
Py = 0
VK ve VL hızlarının büyüklükleri,
VK = g.tK = 10.4 = 40 m/s
Çarpışmadan sonra cisimlerin momentumları,
VL = g.tL = 10.3 = 30 m/s olur.
ı
Pxı = mK.VKx + mL.VLx
Cisimler çarpıştıklarında ortak hareket ettiklerine
ı
ı
= 10.VK.cos37° + 5.VL.cos53°
göre,
R Pönce = R Psonra
mK. VK + mL. VL + mP. VP = (mK + mL+mP). Vort
ı
= 10.VK.0,8 + 5.VL.0,6
ı
ı
= 8.VK+ 3.VL
ı
ı
Pyı = mK.VKy – mL.V Ly
m.40 + 3m.(–30) + m.0 = (m + 3m + m).Vort
ı
ı
= 10.VK.sin37° – 5.V L.sin53°
– 50m = 5m.Vort
ı
ı
= 10.VK.0,6 – 5.V L.0,8
Vort = –10 m/s olur.
ı
ı
= 6.VK – 4.V L
Bu durumda cisimler çarpıştıktan sonra (–) yönde
hareket ederler. Cisimler çarpıştıktan sonra h kadar
Momentumun korunumundan,
yükseğe çıkabilsinler. Enerjinin korunumundan,
ı
Py = P y
Eönce = Esonra
ı
ı
'
0 = 6.V K – 4.V L⇒ V L =
1
m .V2 = mtop.g.h
2 top ort
1
.102 = 10.h
2
ı
3 '
V olur.
2 K
Px = P x
ı
ı
50 = 8V K + 3V L
ı
50 = 10.h ⇒ h = 5 m olur.
CEVAP A
V L değerini yerine yazarsak, K cismin hızı,
›
3 ›
50 = 8.V K + 3. V K
2
50 =
›
25 ›
V & V K = 4 m/s olur.
2 K
Çarpışmadan sonra L cisminin hızı,
ı
ı
2VL= 3.VK
ı
ı
2VL= 3.4 ⇒ VL = 6 m/s olur.
130
VK›
K
KUVVET VE HAREKET
Çarpışmadan sonraki momentumlar,
II. yol:
ı
Momentumun korunumundan,
ı
ı
Px = mK . VKx + mL . VLx
ı
ı
PL = mL.VL
ı
= 5 . VK . cos53° + 10 . VL . cos53°
ı
30 = 5.VL
ı
ı
ı
PK=40kg.m/s
ı
= 5VK . 0,6 + 10VL . 0,6
PL=30kg.m/s
ı
ı
VL = 6 m/s olur.
ı
= 3VK + 6VL
53°
37°
ı
ı
Py = mK . VKy – mL . VLy
PK=50kg.m/s
ı
ı
= 5 . VK . sin53° – 10 . VL . sin53°
CEVAP D
ı
ı
= 5 . VK . 0,8 – 10 . VL . 0,8
ı
ı
= 4VK – 8VL olur.
3.
y yönündeki momentum korunacağından,
ı
Py = Py
ı
ı
ı
ı
0 = 4 . VK – 8 . VL ⇒ VK = 2VL olur.
›
VL
L
K
L
VL = 0
20 m/s
O
4 kg
2 kg
x yönündeki momentum korunacağından,
30°
60°
ı
Px = Px
Çarp›flmadan önce
ı
Çarp›flmadan sonra
Momentumun korunumundan,
Σ Py
= Σ Py
ı
5
m/s olur.
2
Momentumları ise,
K
PL = mL . VL= 10 . 1 = 10 kg.m/s
K
ı
ı
PL = mL . VL= 10 .
›
›
ı
ı
m L . V L . sin30° = m K . V K . sin60°
4 . VL .
ı
5 = 2VL ⇒ VL =
ı
ı
Py = Py
›
ı
30 = 6VK ⇒ VK = 5 m/s olur.
L cisminin çarpışmadan sonraki hızı,
ı
sonra
L
V 'K
2
VK = 2VL
ı
ı
0 = Py – Py
L
ı
30 = 3VK + 6.
10m/s
önce
ı
30 = 3VK + 6VL
K
5
= 25 kg.m/s olur.
2
PL =10kg.m/s
1
3
= 2 . 10 .
2
2
53°
›
V L = 5 3 m/s olur.
CEVAP E
PL =25kg.m/s
–PL =10kg.m/s
.
4.
K
K
5kg
4m/s
VK›
PLy =20kg.m/s
L
1m/s
10kg
•
O
PL =25kg.m/s
5kg.m/s
53°
53°
L
PLx =15kg.m/s
53°
VL›
Momentum korunacağından cisimlerin çarpışmadan önceki momentumları,
Px = mK . VK + mL . VL
= 5 . 4 + 10 . 1
= 30 kg.m/s
Py = 0 olur.
20kg.m/s
P
T PL = P 'L – PL
T PL = P 'L + (– P 'L)
∆P nin büyüklüğü,
(∆P)2 = (5)2 + (20)2
∆P = 5c17 kg.m/s olur.
CEVAP E
KUVVET VE HAREKET
131
MODEL SORU - 8 DEKİ SORULARIN ÇÖZÜMLERİ
1.
4.
2mV
5m
4
O
mV
mV
Cisimler O noktasında çarpışıp birbirlerine kenetlendikten sonra, şekilde görüldüğü gibi sistem 4
yolunu izler.
CEVAP D
Momentumun korunumundan, cisimler O noktasında çarpışıp birbirleriyle kenetlendikten sonra, şekilde görüldüğü gibi sistem 4 yolunu izler.
y
5.
CEVAP D
mV
mV
V2 =
2
➞
V1
x
O
➞
V2
2 V olur.
m2
Momentumun korunumundan,
•
O 4m
P1
m .V
= 1 1
P2
m 2 . V2
2V
m1 . V
1
=
2 m2 . 2 V
2m
Cisimler O noktasında çarpışıp birbirlerine kenetlendikten sonra, şekilde görüldüğü gibi sistem 2
yolunu izler.
CEVAP B
m1
= 1 olur.
m2
CEVAP C
6.
3.
m1
2 br
V1 = V
2 2mV
V
m
Cisimlerin çarpışmadan önce momentumları ve hızları,
P1 = 1 br
P2 =
m
V
4
2 2mV
4m
•
O
2.
•
mK
kuzey
PL
2 2V
P
4
P3=9kg.m/s
4
O•
4
|P1+P2|=15kg.m/s 53°
bat›
37° O
do¤u
4
P1=10kg.m/s
2V
4
PK
mL
P2=12kg.m/s
Momentumun korunumundan,
PK
m .V
= K K
PL
m L .VL
güney
Momentumun korunumundan,
4
4
4
m .2 2 V
1
= K
2
mL . 2 V
4
|P1| – |P2 + P3| = (m1 + m2 + m3).Vort
10 – 15 = 5.Vort
Vort = –1 m/s; batı yönünde
hareket eder.
CEVAP B
132
KUVVET VE HAREKET
2m K
1
=
2
mL
mK
1
=
olur.
mL
4
CEVAP A
Pı1y = 4.Vı1.sin37°
MODEL SORU - 9 DAKİ SORULARIN ÇÖZÜMLERİ
1.
Durmakta olan bir cisim iç
patlama
geçirdiğinden
x yönündeki momentum
Pı2 = 6Vı2 ⇒ Pı2x = 6Vı2 cos53°
m2=4kg
m3
= 6.Vı2 . 0,6
α
korunacağından,
Px =
= 2,4Vı1
6 kg kütleli parçacığın momentumu,
V2=4m/s
V1=2m/s m1=6kg
ilk momentumu sıfırdır.
= 4.0,6.Vı1
ı
Px
= 3,6 Vı2
10m/s
Pı2y = 6.Vı2.sin53°
0 = m1 .V1 + m3 .V3 .cosα
= 6Vı2 . 0,8
0 = 6.(–2) + m3 .10.cosα
= 4,8Vı2
Momentumun x bileşeninin korunumundan,
12 = m3 .10.cosα .....
Pöx = Pı1x + Pı2x
y yönündeki momentum korunacağından,
50 = 3,2 Vı1 + 3,6Vı2 ...
ı
Py = P y
Momentumun y bileşeninin korunumundan,
0 = m2 .V2 + m3 .V3 .sinα
Pöy = Pı1y + Pı2y
0 = 4.4 + m3 .(–10).sinα
0 = 2,4Vı1 – 4,8Vı2
16 = m3 .10.sinα .....
2,4Vı1 = 4,8Vı2
ve denklemlerini oranlarsak,
Vı1 = 2Vı2...
12 m 3 .10. cos a
4
=
& tan a = & a = 53° olur.
16 m 3 .10. sin a
3
Bu eşitliği nolu denklemde kullanırsak,
50 = 3,2. (2Vı2) + 3,6Vı2
50 = (6,4 + 3,6).Vı2 ⇒ Vı2 = 5 m/s olur.
Bu değeri denklem de yerine yazarsak,
12 = m2 .10.cos53°
Bulduğumuz bu sonucu nolu denklemde kullanırsak,
12 = m2 .10.0,6 ⇒ m2 = 2 kg olur.
Vı1 = 2Vı2 = 2.5 = 10 m/s olur.
Cismin kütlesi,
m = m1 + m2 + m3 = 6 + 4 + 2 = 12 kg olur.
II. yol:
CEVAP A
Momentumun korunumundan,
ı
ı
P 1 = m1.V1
2.
V1
ı
40 = 4.V1
4 kg
ı
5m/s
P2=30kg.m/s
ı
V1 = 10 m/s olur.
10 kg
ı
P1=40kg.m/s
53°
37°
P=50kg.m/s
37°
53°
O
CEVAP E
6 kg
3.
V2
5V
I. yol:
Patlamadan önceki momentum,
Pö = 10.5 = 50 kg.m/s dir.
O
•••
4
➞
V
➞
V
Patlama olduktan sonra kütlesi 4 kg olan parçacığın
momentumu
Pı1 = 4.Vı1 ⇒ Pı1x = 4Vı1.cos37°
= 4.0,8Vı1
= 3,2Vı1
Momentumun korunumundan, üçüncü parça şekilde
görüldüğü gibi 4 numaralı yolu izler.
CEVAP D
KUVVET VE HAREKET
133
4.
m=3kg
m2=2kg
V2x=60m/s
6.
m1=1kg
V1=120m/s
V1=10m/s
V=30m/s
ÖNCE
m=4kg
V2y=45m/s
x1
Vox = Vo.cos37°
= 30 m/s
P = m.Vx = 4.40 = 160 kg.m/s olur.
m2 kütlesinin hızı,
Parçalardan her birinin momentumu,
2
V 2 = V 2x + V 2y
2
V 2 = (60) + (45)
P1= 2.V1
2
= – 20 kg.m/s
2
V 2 = 5625
V2 = 75 m/s olur.
5.
CEVAP E
V1=9m/s
160 = –20 + 2.V2 ⇒ V2 = 90 m/s olur.
x2 = V2.t = 90.3 = 270 m
m1=1kg
•
O
Momentum korunacağından,
Σ P = P1 + P2
II. parçacığın atış uzaklığı,
kuzey
m = 4 kg V=5m/s
P2 = 2.V2 olur.
= 2. (–10)
= 3600 + 2025
Bize II. parçacığın cismin ilk atıldığı noktaya olan
53°
37°
do¤u
m2=2kg
V2=6m/s
güney
Yatay momentumun korunumundan,
RPxönce = RPxsonra
mV = m1.V1.cos53° + m2.V2.cos37° + m3.V3x
4.5 = 1.9.0,6 + 2.6.0,8 + 1V3x
20 = 5,4 + 9,6 + V3x
V3x = 5 m/s olur.
RPyönce = RPysonra
0 = m1.V1.sin53° – m2.V2.sin37° + m3.V3y
0 = 1.9.0,8 – 2.6.0,6 + 1V3y
0 = 7,2 – 7,2 + V3y
V3y = 0 olur.
Buna göre, 3. parça doğu yönünde 5 m/s hızla
hareket eder.
CEVAP A
KUVVET VE HAREKET
= 40 m/s
Cismin momentumu,
V2y = 45 m/s olur.
134
= 50.0,6
Cisim patladığında sadece yatay hız vardır.
90 = 2V2y
bat›
= 50.0,8
Vy = Voy – g.t = 30 – 10.3 = 0 olur.
3.30 = m2V2y
2
Voy = V.sin37°
3s sonra cisim iç patlama geçirdiğinden düşey hız,
Düşey momentumun korunumundan,
Σ Py önce = Σ Py sonra
2
yatay
yer
x2
Cismin yatay ve düşey ilk hızları,
0 = m1V1 – m2V2x
120.1 = 2. V2x
V2x = 60 m/s olur.
2
V2
Vo=50m/s
37°
Vox=40m/s
SONRA
Yatay momentumun korunumundan,
Σ PX önce = Σ PX sonra
2
V2
Voy=30m/s
α=53°
V2=75m/s
2kg 2kg
uzaklığı sorulduğuna göre,
x = x1 + x2
= 40.3 + 270
= 120 + 270
= 390 m olur.
CEVAP E
MODEL SORU - 10 DAKİ SORULARIN ÇÖZÜMLERİ
1.
I. yol:
1. Momentumun korunumundan,
RPönce = RPsonra
ı
ı
0 = mM. V M .cos60° + mt. V t
ı
1
–500 . V tx = 10.300.
2
ı
V tx = –3 m/s olur.
Roketin hızındaki değişme eşitliğinden,
TV = –
›
V – Vo = –
MODEL SORU - 11 DEKİ SORULARIN ÇÖZÜMLERİ
Tm
.V g
m
300
. (–2000)
(1500 – 300)
›
V – 200 = 500
CEVAP A
›
V = 700 m/s olur.
II. yol:
Gazın yere göre hızı,
Vgaz = Vson – Vilk
= 2000 – 200
2. Momentumun korunumundan avcının hızı,
= 1800 m/s olur.
4
4
ΣPönce = ΣPsonra
Momentumun korunumundan,
R Pönce = R Psonra
ı
ı
0 = mM.V M + (mA + mt) V ort
ı
0 = 0,02.450 + (70 + 5)V ort
m.Vı = (m – matılan).Vı – mgaz.Vgaz
1500.200 = (1500 – 300).Vı – 300.1800
ı
–9 = 75V ort
ı
300000 = 1200.Vı – 540000
V ort = 0,12 m/s olur.
840000 = 1200Vı ⇒ Vı = 700 m/s olur.
CEVAP B
CEVAP C
2. I. yol:
Roketin hızındaki değişme eşitliğinden,
TV = –
›
V – Vo =
›
V – 200 =
Tm
.V g
m
Tm
.Vg
m
400
.1000
(2000 – 400)
›
V – 200 = 250
›
V = 450 m/s olur.
II. yol:
Gazın yere göre hızı,
Vgaz = 1000 – 200 = 800 m/s olur.
Momentumun korunumundan,
4
4
RPönce = RPsonra
M.Vo = (M – matılan).Vı – matılan.Vgaz
ı
2000.200 = (2000 – 400).V – 400.800
ı
400.000 = 1600V – 320.000
720.000 = 1600 V
ı
ı
V = 450 m/s olur.
CEVAP B
KUVVET VE HAREKET
135
TEST
1
İTME VE MOMENTUM
ÇÖZÜMLER
1.
3.
2m
PX=mV
m
4
P2=20kg.m/s
ı
PY=2mV
X
kuzey
Y
4
PX=mV
bat›
ı
PY=2mV
•
37° .
O
DP=12kg.m/s
do¤u
4
P1=16kg.m/s
.
yatay düzlem
güney
X ve Y nin ilk momentumları,
İtme, momentum değişimine eşit olduğundan, cisme
etkiyen F kuvveti,
PX = m.V
4
PY = 2m.V
F.1 = 12
X ve Y nin son momentumları
PXı
PYı
4
F.Δt = ΔP
F = 12N; kuzey yönünde olur.
= m.V
CEVAP A
= 2m.V olur.
Momentum değişimlerinin büyüklükleri,
DPX =
2 mV
DPY = 4mV olur.
DPX ve DPY taraf tarafa oranlanırsa,
DPX
2 mV
2
1
=
=
=
olur.
4mV
4
DPY
2 2
2.
4.
CEVAP A
F(N)
Momentumun korunumundan,
P = P1 + P2 + P3 ise,
P3 = P – P1 – P2 olur.
P3
P
–P2
–P1
P3 vektörü,
P3 = P + (– P1) + (– P2)
10
20
İşlemi yapıldığında ΙΙ vektörü olduğu görülür.
40
4
8
12
CEVAP B
t(s)
–20
–5
Kuvvet-zaman grafiğinde doğrunun altındaki alan
itme = momentum değişimini vereceğinden,
RF.Dt = 40 N.s olur.
RF.Dt = DP
DP = 40 kg.m/s olur.
Cismin 12 saniye sonundaki hızı,
DP = m.(V2 – V1)
KUVVET VE HAREKET
4
2 2V
4
3m
V
O•
••
4
2V
V
Şekilde görüldüğü gibi, üçüncü parça 2 2 V hızıyla 3 yolunu izler.
20 = V2 – 4
136
3
4
40 = 2.(V2 – 4)
V2 = 24 m/s olur.
5.
CEVAP C
CEVAP C
6.
–x
K
8.
+x
L
6V
4m
m
(–x)
V
yatay
düzlem
4
PY = 3.(–2) = – 6 kg.m/s
4
PZ = 4.(–10) = – 40 kg.m/s olur.
4m.6V + mV = 5m.Vort
Çarpışmadan önceki toplam momentumu,
Σ Pilk = PX + PY + PZ
25V = 5Vort & Vort = 5V olur.
Çarpışmadan sonra K ve L nin hızları,
4
= 10 – 6 – 40
4
= 2Vort – VK
= – 36 kg.m/s olur.
= 2.5V – 6V
Kütleler ortak hareket ettiğinden,
Σ Pilk = Σ Pson
= 4V; +x yönünde olur.
4ı
4
–36 = (2 + 3 + 4).Vort
4
VL = 2Vort – VL
–36 = 9.Vort ⇒ Vort = – 4m/s olur.
= 2.5V – V
Cisimler çarpışmadan sonra –x yönünde 4m/s hızla
= 9V; +x yönünde olur.
hareket eder.
CEVAP E
7.
Z
4kg
PX = 2.5 = 10 kg.m/s
mK.VK + mL.VL = (mK + mL)Vort
4ı
VK
10m/s
Cisimlerin çarpışmadan önceki momentumları
Momentumun korunumundan,
4
(+x)
Y
2m/s
3kg
X
5m/s
2kg
CEVAP D
4kg
Pi
Ps
4m/s
3m/s
9.
53°
VK=0 VL=0
K
L
37°
M
2V
yatay düzlem
P
Cisimlerin kütleleri eşit ise hızlarını birbirlerine aktarırlar. Çarpışmadan sonra bilyelerin hareketi şekildeki gibi olur.
Ps
–Pi
CEVAP D
Cismin momentumları,
Pi = 4.4 = 16 kg.m/s
Ps = 4.3 = 12 kg.m/s
∆ P = Ps – Pi
= Ps + (– Pi)
∆P nin büyüklüğü,
(∆P)2 = (16)2 + (12)2
10. Momentumun korunumundan,
Σ Pilk = Σ Pson
∆P2 = 400 ⇒ ∆P = 20 kg.m/s
ı
0 = m.4 + 2m V
Kuvvetin büyüklüğü,
2m kütleli parçacık –x yönünde 2 m/s hızla hareket
F.∆t = ∆P
eder.
F.0,2 = 20
F = 100 N olur.
ı
⇒ V = –2 m/s olur.
CEVAP A
CEVAP E
KUVVET VE HAREKET
137
11.
12.
mY=4kg
yatay
düzlem
Y
•
K
m
T
K
•
10m
m
L
mg
L
Vo=30m/s
mg
h=80m
T
X m =4kg
X
a
Vx=30m/s
GX=40N
VK=40m/s
Sistemin ivmesi,
GX
40
40
2
a=
=
=
= 5 m/s olur.
mX + mY 4 + 4
8
yatay düzlem
Vy=40m/s VL=50m/s
Cisimlerin yere düşme süreleri,
h=
1 2
gt
2
80 = 5.t2
İpte oluşan T gerilme kuvveti,
16 = t2 & t = 4s olur.
T = mY.a = 4.5 = 30 N olur.
K cisminin yere çarpma hızı,
Y cisminin K den L ye gelme süresi,
| KL | =
VK = g.t = 10.4 = 40 m/s
1 2
a.t
2
L nin yere çarpma hızı,
2
1
10 = .5.t & t = 2 saniye olur.
2
Vx = Vo = 30 m/s
Vy = g.t = 10.4 = 40 m/s
X cismine etki eden net kuvvet,
V2L = V2x +V2y
Fnet = mx.g – T
= 4.10 – 20
V2L = 302 + 402
= 20 N
VL = 50 m/s olur.
Cisimler üzerlerine uygulanan itmeler,
X cismine uygulanan itme,
İtme = Fnet.t = 20.2 = 40 N.s olur.
CEVAP C
IK = FK.Dt = mg.4 = 4mg
IL = FL.Dt = mg.4 = 4mg olur.
IK ve IL taraf tarafa oranlanırsa,
I K 4mg
=
= 1 olur.
I L 4mg
Yere çarptıklarında momentumların büyüklükleri,
PK = mK.VK = m.40 = 40 m
PL = mL.VL = m.50 = 50 m
eşitlikleri taraf tarafa oranlanırsa,
PK 40 m 4
olur.
=
=
PL 50 m 5
138
KUVVET VE HAREKET
CEVAP B
TEST
2
1.
–x
K
İTME VE MOMENTUM
ÇÖZÜMLER
3.
+x
L
4V
mK
mL
25V
m
VL=0
K
4m
yatay
düzlem
37°
Momentumun korunumundan,
mK.VK + mL.VL = (mK + mL).Vort
2V
–x
yatay
yol
+x
ı
K cismi atıldıktan sonra arabanın hızı V olsun.
mK.4V + mL.0 = (mK + mL).V
K cisminin yere göre yatay hızı,
4mK = mK + mL
ı
ı
V xK = V + 25V.cos37°
3mK = mL
mK
1
=
olur.
mL
3
ı
= V + 25V.0,8
ı
= V + 20V olur.
CEVAP B
Yatay momentumun korunumundan,
4
4
4ı
4ı
ı
ı
mA.VA + mK.VK = mA.VA + mKVxK
4m.2V + m.2V = 4m.V + m.(V + 20V)
ı
ı
10mV = 4mV + mV + 20mV
ı
–10mV = 5mV
ı
ı
–10V = 5V ⇒ V = –2V olur.
Araba –x yönünde 2V hızıyla gider.
CEVAP C
2.
a(m/s2)
4.
VLy
2•
L 37°
8m/s
0
VL
•
•
4
–1•
•
8
• 12
K
4kg
t(s)
VK =5m/s
VL =0
L
2kg
K
–4m/s
DV = 8 – 4 = 4 m/s olur.
VKx
53°
VKy
VK
çarp›flmadan sonra
çarp›flmadan önce
İvme-zaman grafiğinde doğrunun altındaki alan
hızdaki değişmeyi verir.
VLx
37°
53°
I. yol:
Momentumun x bileşeninin korunumundan,
ı
ı
PKx + PLx = P Kx + P Lx
ı
ı
4.5 + 2.0 = 4.V K.cos53° + 2.V L.cos37°
Cismin son hızı,
ı
ı
P2 = m.V2
20 = 4.V K.0,6 + 2.V L.0,8
60 = 5.V2
20 = 2,4 V K + 1,6 V L.....
ı
V2 = 12 m/s olur.
ı
Momentumun y bileşeninin korunumundan,
ı
ı
PKy + PLy = P Ky + P Ly
Cismin t = 0 anındaki hızı,
DV = V2 – V1
ı
ı
0 + 0 = – 4.V K.sin53° + 2.V L.sin37°
4 = 12 – V1
ı
ı
0 = – 4.V K.0,8 + 2.V L.0,6
V1 = 8 m/s olur.
ı
CEVAP D
ı
0 = – 3,2 V K + 1,2 V L
3,2VıK = 1,2VıL⇒ VıL =
8 ı
V olur.
3 K
KUVVET VE HAREKET
139
Bu değeri denklem de yerine yazarsak,
8
20 = 2, 4V 'K + 1, 6. V 'K
3
20 =
7.
Patlamanın olduğu an cismin
›
V2=30m/s
hızı,
= 10 m/s olur.
h
Patlamanın olduğu yükseklik,
Momentumun korunumundan,
ı
ı
PK = mK.V K
h = Vo .t –
ı
PK=12kg.m/s
ı
PK=20kg.m/s
Momentumun korunumundan,
Σ Pilk = Σ Pson
ı
ı
m. V = m1. V 1 + m2. V 2
CEVAP B
5.
yatay yer
= 120 m olur.
53°
37°
ı
V K = 3 m/s olur.
50m/s
6kg
1 2
g.t
2
2
1
= 50.4 – .10 (4)
2
ı
PL=16kg.m/s
12 = 4.V K
V1=0
4kg
2kg
= 50 – 10.4
II. yol:
›
›
Vs = Vo – g.t
20V 'K
& V 'K = 3 m/s olur.
3
h
➞
➞
VL
VK
ı
6.10 = 4.0 + 2.V 2
ı
➞
ı
60 = 2V 2 ⇒ V 2 = 30 m/s olur.
VM
2 kg kütleli ismin patlamadan sonra çıkabileceği
yükseklik,
K
L
yatay yer
M
2
h' =
Cisimlerin yatay momentumları değişmez.
Cisimlerin uçuş süreleri:
V '2 (30) 2
=
= 45 m olur.
2g
2.10
2kg lık cismin yerden maksimum yüksekliği,
tK = 3t ise
ı
hmax = h + h
tL = 3t
= 120 + 45
= 165 m olur.
tM = 2t olur.
CEVAP E
Cisimlerin kütleleri, mK = mL = mM = m dir.
İtme, momentum değişimine eşittir. Cisimlere etki
eden kuvvetler F = mg ye eşit olduğundan momentum değişimleri,
ΔPK = mg3t = 3mgt
8.
L
K
K
ΔPL = mg3t = 3mgt
4m/s
O
53°
•
6kg
ΔPM = mg2t = 2mgt olur.
V
Buna göre,
L 4kg
ΔPK = ΔPL > ΔPM olur.
CEVAP A
6.
Yatay eksendeki momentum korunduğundan,
Pilkx = Psonx
mK .VK = (mK + mL).Vort.cos53°
mV
2mV
4m
•
O
2mV
6.4 = (6 + 4).Vort.0,6
4
24 = 6.Vort ⇒ Vort = 4 m/s olur.
mV
Düşey eksendeki momentum korunduğundan,
2mV
Pilky = Psony
mL .VL = (mK + mL).Vort.sin53°
Momentumun korunumundan, cisimler O noktasında çarpışıp birbirleriyle kenetlendikten sonra,
şekilde görüldüğü gibi 4 yolunu izler.
CEVAP D
140
KUVVET VE HAREKET
4.V = (6 + 4).Vort.0,8
4.V = 10.4.0,8
V = 8 m/s olur.
CEVAP C
9.
11.
net kuvvet
a(m/s2)
2•
F•
10
•t
0
•
•3t
2t
5
zaman
–F
I
II
•5
0
Buna göre, cisme etkiyen net kuvvet,
II
III
Sabit
Azalıyor
Artıyor
t(s)
İvme-zaman grafiğinde doğrunun altındaki alan
hızdaki değişmeye eşit olduğundan, ΔV = 10 m/s
olur.
Cisme etkiyen net kuvvetin zamanla değişim grafiği şekildeki gibi olur.
I
• 15
10
–5
–1•
III
•
Cismin son hızı,
V2 = V1 + ΔV = 5 + 10 = 15 m/s olur.
15. saniye sonunda cismin momentumu,
CEVAP A
P2 = m.V2 = 4.15 = 60 kg.m/s olur.
CEVAP E
10.
–x
12.
+x
Vx
L
K
5m/s
6 kg
Vo
VL = 0
yatay
düzlem
4 kg
4kg
Vo=40m/s
37° V
ox
yatay düzlem
Çarpışmadan sonra L cisminin hızı,
'
VL =
Cismin yatay ve düşey ilk hızları,
2m K
.V
mK + mL K
=
2.6
.5
6+4
=
60
10
Vox = Vo.cos37° = 40.0,8 = 32 m/s
Voy = Vo.sin37° = 40.0,6 = 24 m/s olur.
Cismin yatay hızı sabittir. Momentum değişimi
düşey hızdaki değişimle orantılıdır. Aynı zamanda
itme momentum değişimine eşittir.
= 6 m/s, +x yönünde olur.
L cisminin çarpışmadan sonra kinetik enerjisi,
›
EK =
›
EL
hmax
› 2
2
1
1
m . (V K) = . 6 . 1 = 3 J olur.
2 K
2
› 2
2
1
1
= m L . (V L) = . 4 . 6 = 2 . 36 = 72 J olur.
2
2
I = F.Dt = mg.Dt = 4.10.2 = 80 N.s olur.
I. yargı doğrudur.
Cismin uçuş süresi,
2Voy 2.24
=
= 4, 8 s olur.
tu =
g
10
CEVAP E
Uçuş süresince cisme uygulanan itmenin büyüklüğü,
I = F.tu = mg.tu = 4.10.4,8 = 192 N.s olur.
II. yargı yanlıştır.
Cismin minimum momentumu, maksimum yüksekliktedir.
Pmin = m.Vmin = 4.32 = 128 kg.m/s olur.
III. yargı doğrudur.
CEVAP D
KUVVET VE HAREKET
141
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
1.
kuzey
Bölüm
Yazılı Soruları
(İtme ve Momentum)
b) Cisim K noktasından
P2=20kg.m/s
N noktasına geldiğinde,
∆ PKN = PN – PK
= PN + (– PK) olur.
DP=16kg.m/s
V1=6m/s
batı
O•
m=2kg
ÇÖZÜMLER
.
53°
do¤u
PK
PKN
PN
∆PKN nın büyüklüğü,
P1=12kg.m/s
–PK
O
∆PKN = v2 .mV
itme = ∆PKN = v2 .mV olur.
güney
c) Cisim K noktasın-
İtme momentum değişimine eşit olduğundan,
F.Dt = DP
PK
–PK
O
dan P noktasına
60°
geldiğinde,
∆ PKP = PP – PK
= PP+(– PK) olur.
F.1 = 16
F = 16 N; kuzey yönünde olur.
PKP
PP
∆PKP nin büyüklüğü, ∆PKP = v3 .mV
İtme = ∆PKP = v3 .mV olur.
d) Cisim K noktasından R
2.
Cis me
V
uy gu la nan
şimine eşittir. Cismin
her noktada momentumlarının büyüklüğü,
K
L
itme momentum deği60°
PK
–PR
noktasına geldiğinde,
∆ PKR = PR – PK
= PR + (– PK) olur.
PKR
∆PKR nin büyüklüğü,
r
∆PKR = 2.mV
N
O
30°
İtme = ∆PKR = 2.mV olur.
3.
P
K
R
K
|PK| = |PL| = |PN| = |PP| = |PR| = m.V olur.
a) Cisim K noktasından
L noktasına geldiğinde,
∆ PKL = PL – PK
= PL + (– PK) olur.
∆PKL nin büyüklüğü,
∆PKL = m.V
İtme = ∆PKL = m.V olur.
142
KUVVET VE HAREKET
PK
PL
60°
L
5m/s
2kg
5kg
α
O
–PK
O
60°
6m/s
L
60°
PKL
VL› =15m/s
a) Momentumun,
x bileşeninin korunumundan,
ı
Px = P x
ı
5.6 + 2.5 = 5.V K.cosα + 0
ı
40 = 5.V K.cosα
8=
ı
V K.cosα.....'
VK›
5.
y bileşeninin korunumundan,
Py =
0+0=
6=
a) Cisme verilen itme,
İtme = F.∆t
ı
Py
K
= 10.20
ı
5.V K.sinα – 2.15
ı
V K.sinα .....( olur.
yatay düzlem
= 200 N.s olur.
( ve ' numaralı denklemler taraf tarafa oranla-
IFI=10N
b) Cisme uygulanan itme, momentum değişimine
nırsa,
eşittir.
›
V K . sin a
›
V K . cos a
=
tan a =
6 3
=
8 4
3
4
İtme = ∆P = 200 N.s olur.
c) Cismin kütlesi,
& a = 37° olur.
∆P = m.∆V
200 = m.40 ⇒ m = 5kg olur.
b) α = 37° değeri denklem ' de yerine yazarsak,
ı
8 = V K.cos37°
ı
d)
ı
F . ∆t = m . ( V2 – V1)
10 . 10 = 5 . (V2 – 0)
8 = V K.0,8 ⇒V K = 10 m/s olur.
V2 = 20 m/s olur.
4.
F(N)
6•
6.
4kg
4•
Pi
•
2
4
•
•
6
•
8
Ps
30m/s
40m/s
t(s)
60°
30°
yatay
düzlem
P
–4•
a) F-t grafiğinde doğrunun altındaki alan momentum değişimini verir. 4 saniyede momentum
–Pi
Ps
değişimi,
∆P = 2.6
Cismin momentumları,
Ps – Pi = 12
Pi = m.Vi = 4.40 = 160 kg.m/s
m.Vs – m.Vi = 12
Ps = m.Vs = 4.30 = 120 kg.m/s olur.
2.Vs – 2.4 = 12
2.Vs = 20 ⇒ Vs = 10 m/s olur.
b) 2-4 saniyeler arasında alan sıfır olduğundan,
itme = ∆P = 0 olur.
c) 8 saniyedeki momentum değişimi,
∆P = 2.6 – 2.4 +
2.4
2
∆P = 12 – 8 + 4
∆P = 8 kgm/s
m.Vs – m.Vi = 8
2.Vs – 2.4 = 8 ⇒ Vs = 8 m/s olur.
Momentum değişimi,
∆ P = Ps – Pi = Ps + (– Pi) olur.
∆P nin büyüklüğü,
(∆P)2 = (Ps)2 + (–Pi)2
(∆P)2 = (120)2 + (160)2
∆P = 200 N.s olur.
İtme momentum değişimine eşit olduğundan,
İtme = ∆P = 200 N.s olur.
KUVVET VE HAREKET
143
7.
PK=3m.2V=6mV
–x
K
10.
PL=2m.3V=6mV
+x
2V
L
3V
37°
2kg
Vox
.
3m
yatay
düzlem
2m
Merkezi ve esnek çarpışmalarda cisimlerin momentumları eşit ve zıt yönlü ise, cisimler çarpıştıktan sonra aynı büyüklükteki hızlarını alarak geri
dönerler.
Buna göre,
80m
.
yatay yer
Cismin yatay ve düşey ilk hızları,
Vox = 50.cos37° = 50.0,8 = 40 m/s
K
L
–x; 2V
Voy = 50.sin37° = 50.0,6 = 30 m/s olur.
+x, 3V olur.
Cismin yere düşme süresi,
1
h = Voyt – g.t2
2
–80 = 30.t –
8.
–x
V3 3kg
8kg
5m/s
(t–8).(t+2) = 0
t = – 2 çözüm olamaz.
V=0
Momentumun korunumundan 3. parçacığın hızı,
Σ Pilk = Σ Pson
8.5 = m1. V1 + m2. V2 + m3. V3
40 = 1.(–8) + 4.0 + 3.V3
48 = 3V3 ⇒ V3 = 16 m/s olur.
9.
VX
K
53°
2kg
25m/s
8kg
53°
–x
20m/s
+x
yatay
yol
Momentumun korunumundan çarpışmadan sonra
arabanın hızı,
mK.VK + mA.VA = (mK + mA).Vort
–2.25.cos37° + 8.20 = (2 + 8).Vort
–50.0,6 + 160 = 10 Vort
–30 + 160 = 10 Vort
130 = 10 Vort
Vort = 13 m/s, +x yönünde olur.
KUVVET VE HAREKET
t1 = 8s, t2 = –2s olur.
4kg
8m/s
yatay düzlem
1
.10.t2
2
–80 = 30.t – 5t2 ⇒ t2 – 6t – 16 = 0
+x
1kg
144
50m/s
Voy
Cisim 8 saniye havada kaldığına göre,
İtme = F.∆t = mg.∆t = 2.10.8 = 160 N.s olur.
8. BÖLÜM
TORK
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
4.
F1
tasına göre torkların büyüklüğü;
O
yatay
•
.
x1 = 1.1 + 2.3 = 7 br
•O
x2 = 3.2 = 6 br
F1
F3
x3 = 3.2 + 1.0 = 6 br
.
.
F3
x1 > x2 = x3 olur.
Kuvvetlerin O noktasına göre torklarının büyüklükleri eşittir.
x1 = x2 = x3
F1.1 = F2.2 = F3.2
F1 = 2F2 = 2F3 olur.
Buna göre, F1 > F2 = F3 olur.
CEVAP D
CEVAP E
5.
⏐F1⏐=⏐F2⏐=⏐F3⏐= F
F1
O
•
olsun.
.
.
O noktasına göre tork
alınırsa,
kuvvetlerin
torklarının büyüklükleri,
F1
F3
F2
olur. Buna göre,
F2
2.
Kuvvetlerin O nok-
.
x1 = F.2 = 2F br,
F3
x2 = F.1 = F br,
(–)
•
•O
x3 = F.3 = 3F br olur.
(+)
Buna göre,
F2
x3 > x1 > x2 olur.
6.
O noktasına göre tork alınırsa,
CEVAP B
4
Fmin
x1 = 1.2 = 2 br,
.
x2 = –1.2 = –2 br,
r=10cm
x3 = 1.2 = 2 br olur.
4
x1 = x2 = x3 olur.
O
8cm
G
CEVAP A
Kuvvetlerin K noktabüyüklükleri,
x1 = F1.d1
yatay
2cm
I. durumda:
RxK = 0
L
K
G.6 = F.8 ... II. durumda:
F3
F2
x2 = 2.6 = 12 N.m
x3 = F3.d3
G.6 = Fmin.20 ... ve denklemlerinden,
Fmin.20 = F.8
x3 = 2.5 = 10 N.m olur.
Fmin.20 = 30.8
Buna göre,
x1 = x2 > x3 olur.
K
6cm
yatay düzlem
F1
sına göre torklarının
x1 = 3.4 = 12 N.m
x2 = F2.d2
yatay
•
|F| = 30 N
Torkların büyüklükleri arasındaki ilişki,
3.
F2
CEVAP D
Fmin = 12N olur.
CEVAP C
KUVVET VE HAREKET
145
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
4.
.
ip
T•
1.
O
.
yatay
ip•
A
G
yatay
GX
4N
Cismin ağırlık merkezi olan O noktasına göre tork
G
G
G
alırsak, ipte oluşan T gerilme kuvveti;
3G
/M o = 0
A noktasına göre tork alırsak X cisminin ağırlığı,
G.3 + GX.2 + G.1 = G.1 + 3G.2
T.
2GX = 7G – 4G
T3 = Gx = G dir.
T = 20 N olur.
.
.
ip
ip
• T1
• T2
•
K
L
yatay
•
G
3G
T1 =
4
G
T2.4 = G.2 + G.3
5G
T2 =
olur.
4
Buna göre, T2 > T3 > T1 olur.
• T1
K
L
M
N
P
R
S
X
Y
yatay düzlem
R noktasına göre tork alınırsa,
CEVAP B
RxR = 0
T1.4 = Gx.5 + GY.2
ip
3T
tavan
.
ip
I. durumda:
3.
K
5.
yatay
olur. K noktasına göre tork alınacak olursa,
RxK = 0
ip
CEVAP D
CEVAP C
tavan
L noktasına göre
tork alınacak olursa,
RxL = 0
T1.4 = G.2 + G.1
1
5
5
+ 4. = 8.
2
2
2
T = 40 – 20
2GX = 3G
3
GX = G olur.
2
2.
8N
T1.4 = G.5 + 2G.2
T
L
O
yatay
G
4T1 = 9G
9G
olur.
T1 =
4
fiekil-I
ip
T1
K
II. durumda:
ip
R noktasına göre tork alınırsa,
T2
O
L
yatay
T2.4 = G.4 + 2G.1
G
fiekil-II
KL çubuğunun ağırlık merkezi O noktasıdır.
O noktasına göre tork alırsak,
T1.2 = T2.4
T1 = 2T2
T1
= 2 olur.
T2
146
KUVVET VE HAREKET
T2.4 = Gx.4 + GY.1
CEVAP B
4T2 = 6G
6G
olur.
T2 =
4
Buna göre,
9G
T1
3
= 4 = olur.
T2 6G 2
4
CEVAP D
6.
8.
tavan
.
L
M
O
N
ı
2T1
T1.3 =
ip
K
Sistem dengede
olduğuna göre;
P
R
S
T
T3
›
T1
ı
T2.4 = T2
yatay
›
T3
T2
T2
›
T1
ı
T3.4 = T3
Denge koşuluna göre,
T2 +
ı
T2
=
K
ı
T1
3T1
⇒10T2 = 3T1 ....
2
ı
ı
T3 + T3 = T2
I. işlemi:
T2 + 4T2 =
1.4 + 2.3 + 1.2 = 1.1 + 2.2 + 1.3 + 1.4
12 = 12 olur.
T3 + T34 = 4T2
II. işlemi:
5T3 = 4T2 ....
ve denklemleri oranlanırsa,
3T1 10T2
=
5T3
4T2
1.4 + 2.3 = 1.1 + 3.2 + 1.3
10 = 10 olur.
III. işlemi:
3T1 5 T1 25
= &
=
olur.
5T3 2 T3
6
1.4 + 1.3 + 1.2 = 2.1 + 2.2 + 1.3
9 = 9 olur.
CEVAP E
Buna göre, I, II ve III işlemleri tek başına yapılmalıdır.
tavan
9.
CEVAP E
ip
G
I T1=
2
•
G
fiekil-I
ip
G
II T2=
3
G
fiekil-II
tavan
N
K
A
L
yatay
.
•
T1 gerilme kuvveti,
yatay
6P
Y
•
Şekil-I de:
T
M
ip
2G
3
ip
G
3
L
yatay
ip
III T3= 2G
3
O
G
fiekil-III
7.
O
•
K
.
K
.
.
ip
G
2
L
yatay
O
K
tavan
.
.
L
yatay
T1 =
G
olur.
2
Şekil-II de:
X
2P
RxA = 0
X cisminin ağırlığı,
T2.3 = G.1
G
T2 =
olur.
3
X . 1 = 2P . 2
X = 4P olur.
Y cisminin ağırlığı,
Şekil-III te:
Y . 2 = 6P . 1
Y = 3P olur.
L noktasına göre tork alınırsa,
RxL = 0
T gerilme kuvveti,
T = 6P + 3P
= 9P olur.
A noktasına göre tork alınırsa,
CEVAP E
T3.3 = G.2
2G
T3 =
olur.
3
Buna göre, T3 > T1 > T2 olur.
CEVAP B
KUVVET VE HAREKET
147
10. Sistem dengede ve Y çubuğu, X çubuğunun
ağırlık merkezinden asıldığından iplerdeki gerilme kuvvetleri oranı iplerin ağırlık merkezine olan
uzaklıklarına bağlıdır. Kuvvetlerin oranı,
T
1
T1 .3 = T2 .1 & 1 =
olur.
T2 3
CEVAP A
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
1.
F2
F1
I
4G
ip
yatay
K
A
O1
GMN
3 .
M
L
GKL
O2
•
yatay
düzlem
Şekildeki çubukların ağırlık merkezleri O noktasında olur. O noktasına göre tork alınırsa,
ip
•
yatay
yatay
L
II
3G
.
2GMN
3
N
•
G
tavan
.
•O
O1 •
K
11.
.
M
.
F1.2 = F2.1
2GMN
3
N
.
F1
1
=
olur.
2
F2
yatay
GMN
CEVAP C
2.
Çubuklara etki eden kuvvetler şekildeki gibidir. A
noktasına göre tork alınırsa,
RxA = 0
2G MN
G
.3 = MN .1 + GKL.1
3
3
5G MN
= GKL
3
G KL
5
=
olur.
G MN
3
ip
T
K
L
yatay
GX =10N
Gç =40N
GY =30N
yatay
düzlem
a) Desteğe göre tork alalım.
GX . 1 + T . 3 = Gç . 1 + GY . 2
CEVAP A
10 . 1 + 3T = 40 + 30 . 2
3T = 90
12.
O
K
L
M
T = 30 N olur.
N
CEVAP B
yatay
3.
F=10G
. O
K
yatay
düzlem
•
•.
T
O noktasına göre tork alalım.
I. işlem:
G
K noktasına göre tork alınırsa,
II. işlem:
10G.2 = Gç.
1.4 + 2.2 = 2.1 + 1.2 + 1.4
8=8
20G =
5
+ G.5
2
5
.G + 5G
2 ç
30G = 5Gç & Gç = 6G olur.
III. işlem:
İpte oluşan T gerilme kuvvetinin büyüklüğü,
1.4 + 2.2 = 1.1 + 2.2 + 1.3
8=8
RFy = 0
I., II. ve III. işlemler tek başına yapılmalıdır.
CEVAP E
KUVVET VE HAREKET
yatay
yatay düzlem
1.4 + 2.2 = 3.1 + 1.2 + 1.3
8=8
148
•
Gç
ip
.
L
10G = T + 6G + G
T = 3G olur.
CEVAP B
4.
N1
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
N2
Y
X
1.
20N
I
16N
II
K noktasına göre
F
tork alacak olursak,
Σ xK = 0
yatay
düzlem
yatay
L
F . 6 = Gç . 3 + GX . 5
I. desteğe göre tork alınırsa,
6F = G . 3 + 3G . 5
N2 . 5 = 20 . 2 + 16 . 4
GX =3G
6F = 18G
N2 . 5 = 40 + 64
F = 3G olur.
104
N2 . 5 = 104 ⇒ N2 =
N
5
II. desteğe göre tork alınırsa,
Gç =G
yatay
düzlem
K
N 1 .5 = 16.1 + 20.3
CEVAP C
N 1 .5 = 16 + 60
76
N olur.
5
N1 ve N2 taraf tarafa oranlanırsa,
N 1 .5 = 76 & N 1 =
2.
76
N1
76
19
= 5 =
=
olur.
N 2 104 104 26
5
Çubuklar dengede ve
kuvvetler birbirine pa-
T
CEVAP C
GK.2 = T.4
K
F
GK
GL.2 = T.3
G
2θ
M
GL
θ
GM
θ
3
G L = T olur.
2
yatay
T
T
L
GK = 2T olur.
5.
T
ralel olduğuna göre,
GM.2 = T.4 ⇒ GM = 2T olur.
2G
Bu durumda GK = GM > GL olur.
ip
yatay
düzlem
CEVAP A
İpe göre tork alalım.
F . 1 = G . 2 + 2G . 4
F = 2G + 8G
F = 10 G olur.
CEVAP D
3.
ip
T
6.
GY =P
L
N
GY =G
GX =2G
37°
10P
10P
GX
Gç =4G
yatay
düzlem
K
K noktasına göre tork alınacak olursa,
Σ xK = 0
GX ağırlığına göre tork alınırsa,
N . 5 + P . 10 = 10 P . 4 + 10 P . 7
T . 4 + GY . 6 = Gç . 3 + GX . 5
N . 5 + P . 10 = 40 P + 70 P
T . 4 + G . 6 = 4G . 3 + 2G . 5
N . 5 + 10 P = 110 P
4T + 6G = 12G + 10G
N . 5 = 100 P
4T = 16G
T = 4G olur.
N = 20 P olur.
CEVAP D
CEVAP B
KUVVET VE HAREKET
149
4.
6.
A noktasına göre
tork alınacak
olursa,
RxA = 0
tavan
.
• T=2N
T1
Fkal
•
A
O
G
G = 12N
•
53°
• T=2N
olur.
ip
L
T.4 + T.2 = G.1
2.4 + 2.2 = G
tavan
.
ip
s›v›
K
yatay düzlem
K
G
G
yatay
1br 1br 1br 1br düzlem
fiekil-I
O
•
T2
•
L
•
G
yatay
G
yatay düzlem
fiekil-II
CEVAP C
Şekil I de :
K noktasına göre tork alınacak olursa,
RxK = 0
T1.4 = G.2 + G.3
5
T1 = G olur.
4
5.
tavan
Şekil II de :
•
•
ip
T›
T›
M
L
L
yatay
K
T
T2.3 = G.1 + G.2
N
2G
2G
yatay
düzlem
3G
T1 ve T2 gerilme kuvvetleri taraf tarafa oranlanacak olursa,
MN çubuğunda:
5G
T1
5
= 4 = olur.
T2
G
4
N noktasına göre tork alalım.
ı
T . 6 = 2G . 3 + 3G . 2
ı
T . 6 = 12G
ı
T = 2G olur.
KL çubuğunda:
Desteğe göre tork alalım.
ı
T . 2 + T . 3 = 2G . 1 + 4G . 4
2T + 2G . 3 = 18G
2T = 12G
T = 6G olur.
CEVAP B
150
KUVVET VE HAREKET
3T2 = 3G
T2 = G olur.
4G
ip
O noktasına göre tork alınacak olursa,
RxO = 0
CEVAP D
4.
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
Ty
L
T
•
1.
37°
TX
tavan
ip
Ty
T
O
•
K
yatay
Ty.4 = G.2 + Gx.3
T.sin30°.4 = G.2 + 2G.3
1
T. .4 = 8G
2
2T = 8G
T = 4G olur.
37°
CEVAP C
1,5br 1,5br
Ty
T
L
30°
60°
T
53°
•
60° Py
P =10N
P= 3G
60° Gy
60°
53°
düfley
duvar
G
yatay
K noktasına göre tork alınacak olursa,
Σ xK = 0
Ty . 6 = Gy . 3 + Py . 5
T . sin30° . 6 = G . cos60° . 3 + P . cos60° . 5
1
1
1
. 6 = G . . 3 + 3G . . 5
2
2
2
3
15
G+
G
2
2
3T = 9G
T = 3G olur.
6.
Gy
G=80N
K
•
ip
Ty
T
30°
T
ip
L
•
K
45°
düfley
duvar
T.6 = G.2 + G.3 + G.4
G
45°
K
G
G
düfley
duvar
CEVAP C
CEVAP D
30°
CEVAP B
K noktasına göre
6T = 9G
3
T = G olur.
2
53°
K noktasına göre tork alınacak olursa,
Σ xK = 0
T . 3 = Gy . 2 + Py . 4
3T = G . sin53° . 2 + P . sin53° . 4
3T = 40 . 0,8 . 2 + 10 . 0,8 . 4
3T = 64 + 32
3T = 96
T = 32 N olur.
K
tork alınacak olursa,
RxK = 0
Py
O
O
3.
CEVAP B
ip
L
3T =
.
5.
düfley
duvar
T.
X
GX=30N
GÇ=40N
K noktasına göre tork alırsak,
R xK = K
3
Ty.5 = Gç. + Gx.3
2
3
T.sin37°.5 = 40. + 30.3
2
T.0,6.5 = 60 + 90
3T = 150 ⇒ T = 50 N olur.
GX=2G
K noktasına göre tork alınırsa,
RxK = 0
2.
K
yatay
düzlem
G
düfley
duvar
•
• O 4br
53°.
16°
30°
Tx
L
5br
Tx
L
P=20N
G=40N
K noktasına göre tork alacak olursak, T gerilme
kuvvetinin büyüklüğü,
Σ xK = 0
Ty . 4 = G . 2 + P . 3
T . sin30° . 4 = 40 . 2 + 20 . 3
1
T . . 4 = 80 + 60
2
2T = 140 ⇒ T = 70 N olur.
CEVAP E
KUVVET VE HAREKET
151
7.
9.
ip
F
Fy
Fx
37°
T
TX
Ty
37°
4cm
yatay
L
K
1cm
5cm
GX=2G
düfley
duvar
3cm
120N
Gç=3G
Çubuk dengede olduğundan K noktasına göre tork
alınırsa,
RxK = 0
Bu tür soruların hepsinde destek tepkisi sorulmamış ise, desteğe göre tork alınarak sorular çözülür.
Fx . 4 + Fy . 5 = 120 . 1
Ty.4 = 3G.2 + 2G.3
(F . cos37°) . 4 + (F . sin37°) . 5 = 120
T.sin37°.4 = 12G
F.0,8.4 + F . 0,6.5 = 120
T.0,6.4 = 12G
3,2F + 3F = 120
2,4T = 12G
6,2F = 120
600
N olur.
F=
31
T = 5G olur.
CEVAP C
CEVAP B
8.
53°
T1 = 40 N
T2 = 30 N
53°
37°
10.
10N
90N
ip
L
O
GX
yatay
Ty
1br
GY
K
T1
30
F
=
=
0, 8 0, 6 1
T
•
X
GX
yatay düzlem
K noktasına göre tork alınacak olursa,
RxK = 0
T1 = 40 N
Ty.2 = Gçy.1
F = 50 N olur.
T.sin37°.2 = Gç.cos37°
O noktasına göre tork alınırsa,
3
4
T. .2 = 60.
5
5
GX . 2 = GY . 4
GX = (90 – GX) . 2
3T = 120
3GX = 180
T = 40 N olur.
GX = 60 N
KUVVET VE HAREKET
L
37°
Tx
37° Gç
y
37° Gç
T1
T2
F
=
=
sin127° sin143° sin90°
GY = 30 N olur.
•
1br
Lami teoreminden,
152
tavan
yatay
F = 50 N
F =50 N
K
yatay
37°
GX = T = 40 N olur.
CEVAP A
CEVAP D
11.
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
60°
1.
Ty
60°
L
RxK = 0
60°
O
Py
K
F.4 = G.
P= 20 N
60°
düfley
duvar
tork alınacak olursa,
T
60°
K noktasına göre
Gy
3
2
O
3
F = G olur.
8
G= 80 N
. L
F
düfley
duvar
4br
G
53° fs
K noktasına göre tork alınacak olursa,
Σ xK = 0
K
.
1,5br
yatay
düzlem
1,5br
CEVAP A
Ty . 2 = Gy . 1 + Py . 2
T . sin60° . 2 = G . sin60° + P . sin60° . 2
2T = G + 2P
2.
2T = 80 + 2 . 20
K noktasına göre
düfley
duvar
tork alınırsa,
RxK = 0
2T = 120
T = 60 N olur.
4
F1
F1.3 = G.2
CEVAP C
O
4
F2
F1.3 = 60.2
3br
G=60N
37° fS
F1 = 40N olur.
K
2br
2br
Rxx = 0 olduğundan,
12.
. L
.
yatay
düzlem
fs = F1
tavan
fs = 40 N olur.
CEVAP E
T
,
,
37°
5,
2P
3.
F
4,
•
5P
1,5,
m
O
10
1,5,
Çubuğun her bir bölmesinin uzunluğuna , diyecek olursak ağırlıkların O ya olan dik uzaklıkları
6m
0,8,
.
5m
53°
şekildeki gibi olur. O noktasına göre tork alacak
olursak,
53°
37°
O
T . 3, = 5P . 1,5, + 2P . (3, + 0,8,)
3T = 7,5P + 7,6P
151
P olur.
30
100N
200N
.
8m
Özel üçgenden çubuğun yatayla yaptığı açı 37°
olur. O noktasına göre tork alınırsa,
3T = 15,1P
T=
6m
53°
F . 10 = (200 . sin53°) . 5 + (100 . sin53°) . 6
F . 10 = 200 . (0,8) . 5 + 100 . (0,8) . 6
CEVAP D
F . 10 = 800 + 480
F = 128 N olur.
CEVAP C
KUVVET VE HAREKET
153
4.
Kuvvetlerin K noktasına göre tork
alındığında,
RxK = 0
,
F2.,.cosα = G. sinα
2
düfley
duvar
. L
F2
a
,
O
2F2 = G.tanα
F1
a
F2 = fsür
fsür
2 fsür = G.tanα
,.cosa
K
G
.
yatay
düzlem
, sina
olur.
2
CEVAP D
5.
Çubuğun uzunluğu 10 br
duvar
T
seçilirse, d = 8 br ve
x = 3 br olur.
d=8br
O noktasına göre tork
G
alınırsa,
O
53°
x=3br
T.d = G.x
T.8 = G.3 ⇒
x=3br
T 3
olur.
=
G 8
CEVAP A
düfley
duvar
. L
6.
F
O
•
37°
K
.
3br
G
2br
.
2br
4br
yatay
düzlem
K noktasına göre tork alınırsa,
RxK = 0
F.3 = G.2
2
F = G olur.
3
CEVAP C
154
KUVVET VE HAREKET
TEST
1
TORK
ÇÖZÜMLER
1.
3.
.
F2
F1
•
•O
(–)
(+)
T1
K
F3
L
yatay
X
M
yatay
T2
N
Y
O noktasına göre tork alınırsa,
yatay
düzlem
x1 = 2.2 = 4br,
T1 gerilme kuvvetinin olduğu ipe göre tork alırsak,
x2 = 2.2 – 1.0 = 4br,
GX.3 = T2.2
x3 = – 2.2 – 2.0 = –4br olur.
Torkların büyüklükleri arasındaki ilişki,
T2 =
x1 = x2 = x3 olur.
3
G olur.
2 X
Desteğe göre tork alırsak,
CEVAP C
T2.4 = GY.2
3
G .4 = GY.2
2 X
3GX = GY
GX
1
=
GY
3
olur.
CEVAP A
2.
T2
T1
T3
// //
// //
P
P
fiekil-Ι
fiekil-ΙΙ
P
fiekil-ΙΙΙ
Her bir kare bölmenin uzunluğu 1 br seçilip desteklere göre tork alınırsa,
T1 .3 = P.
T3 .2 = P.
Levhanın ağırlık merkezi P
O
–
noktasıdır. Levhanın denge-
3
P
& T1 =
2
2
T2 .2 = P.1 & T2 =
4.
de kalabilesi için levhaya uygulanan kuvvetlerin torkları-
P
2
P
F4
+
G
nın toplamı sıfır olmalıdır. G
ağırlığı levhayı (+) yönde
3
3
& T3 = P
2
4
F3
F5
F2
F1
döndürmeye çalışır.
Buna göre, iplerdeki gerilme kuvvetlerinin büyüklükleri arasında T3 > T1 = T2 ilişkisi vardır.
CEVAP A
Levhanın dengede kalabilmesi için (–) yönde bir
kuvvetin uygulanması gerekir. F4 kuvveti (–) yönde,
diğer kuvvetler (+) yönde döndürmeye çalışır. Öyleyse levhayı dengede tutacak kuvvet F4 kuvvetidir.
Σ x = G.1 – F4.3 = 0
CEVAP B
KUVVET VE HAREKET
155
5.
I. durumda:
K noktasına göre
tork alınırsa,
RxK = 0
F1.4 = G.
8.
düfley
duvar
K
O
•
•
F
O
53° Gy
4F = G . cos53° . 3
II
G
G
3G
F1 =
olur.
8
L
F . 4 = Gy . 3
O
3
2
K noktasına göre
tork alacak olursak,
Σ xK = 0
F2
.
L
I
.
L
II. durumda:
G
4F = 160 . 0,6 . 3
53°
F = 72 N olur.
F1
düfley
duvar
K
yatay düzlem
CEVAP E
K noktasına göre tork alınırsa,
RxK = 0
F2.3 = G.2
F2 =
2G
olur.
3
F1 ve F2 kuvvetleri taraf tarafa oranlanırsa,
3G
F1
9
olur.
= 8 =
F2 2G 16
3
CEVAP B
9.
6.
F2y
O 30°
a
L
G
.
G
.
G
Çubuk dengede olduğundan K noktasına göre tork
alınırsa,
RxK = 0
Ty.3 = G.2 + G.4
T = 4G olur.
CEVAP D
yatay
düzlem
Çubuğa etki eden kuvvetler şekildeki gibidir.
Çubuk dengede olduğundan,
RFy = 0
düfley
duvar
T.3 = Gç.2 + Gx.3
F2 =
ip
T=20N
L
•
20.3 = Gç.2 + 10.3
•
60 = Gç.2 + 30
GX=10N
GÇ
30 = 2Gç
F2y.2 = Gy.1
F2.sina.2 = G.cosa.1
K noktasına göre tork alınacak olursa,
K
G. cos a
olur.
2. sin a
F2 bulunabilir.
RFX = 0
fs = F2 olur.
fs bulunabilir.
CEVAP E
CEVAP C
KUVVET VE HAREKET
.
F1 bulunabilir.
RxK = 0
1
= 2G
2
Gç = 15N olur.
Gy
F1 = G olur.
T.sin30°.3 = 6G
156
a fS
K
düfley
duvar
RxK = 0
L
F1
yatay
K
7.
a
düfley
duvar
Ty
T
T.
.
F2
ip
10.
tavan
.
K
.
ip G
2
G
2
M
GX
•
ip
O
L
.
G
ip
yatay
G
2
G
2
N
yatay
G
O noktasına göre tork alınacak olursa,
R xO = 0
GX.3 +
G
G
.1 = .3
2
2
3GX = G
G
olur.
3
GX =
CEVAP B
2
2
r 2
3
11. r = x + b l & x =
r
2
2
F
r
O
r/2
K noktasına göre tork
r
alınırsa,
F. b r +
r
3
.r
l = G.
2
2
10.
3r
3
= G.
.r
2
2
15 =
K
x
r/2
G
G 3
& G = 10 3 N olur.
2
CEVAP D
12.
.
ip
K
L
yatay
8GY
.
M
X
N
.
yatay
2GY
ip
GX=24GY
6GY
yatay
düzlem
GY
ip
Y
GY
Kuvvetlerin denge şartından;
GX = 24GY
GX
= 24 olur.
GY
CEVAP E
KUVVET VE HAREKET
157
TEST
1.
2
TORK
ÇÖZÜMLER
4.
O
•
F1
.
A
yatay
2 2br
.
K
.
.
F2
F3
•
•
G
s›v›
Çubuğa etki eden kuvvetler şekildeki gibidir. A
noktasına göre tork alınırsa,
RxA = 0
x1 = x2 = x3
F1.2 = F2.3 = F3.2 2
1
3
= T.
2
2
G
= 3 olur.
T
G.
2F1 = 3F2 = 2 2 .F3 olur.
Buna göre, F1 > F3 > F2 olur.
CEVAP A
Tel ortasından ikiye bölündü-
CEVAP C
5.
ğüne göre her bir parçanın
P noktasına göre tork
alınırsa,
G
ağırlığı
olur. O noktasına
2
göre tork alınırsa,
G
2
37o T
T.r = 20.(r.sin53°)
F
l
l
T = 20.0,8
O
r
53°
T = 16N olur.
G
2
G
G
.2, + ., = F.,
2
2
G., +
ip
T
O
yatay düzlem
Kuvvetlerin O noktasına göre torklarının büyüklükleri eşittir.
2.
L
Fkal
P
37o
O
53°
G
., = F.,
2
20N
G
3
G + = F & F = G olur.
2
2
CEVAP E
CEVAP D
3.
6.
düfley
duvar
x kadar uzaklaştığında
F1
L
F2
50 N olsun. O noktası-
•
na göre tork alınırsa,
(–)
K
x
LM N P
70N
Öyleyse çocuk en fazla L noktasına kadar yürüye-
x1 = 2.6 = 12 br,
bilir.
x2 = –1.6 = – 6 br,
CEVAP B
x3 = –2.3 = – 6 br olur.
Torkların büyüklükleri arasındaki ilişki,
KUVVET VE HAREKET
37°
O
(50.0,6). 7 = 70.x ⇒ x = 3 br olur.
K noktasına göre tork alınırsa,
158
50.sin37°
(50.sin37°).7 = 70.x
F3
x1 > x2 = x3 olur.
50N
ipteki gerilme kuvveti
(+)
K
Çocuk O noktasından
CEVAP A
7.
9.
tavan
ip
.
ip
ip
T1
T2
O O1
• • •
K
G
G
2
M
O2
G
2G
•
L
yatay
.
G
. 2
N
yatay
L
K
yatay
düfley
duvar
G
GX=G
4G
K noktasına göre tork alınacak olursa,
4
RxK = 0
Çubuklara etki eden kuvvetler şekilde gösterilmiştir. O noktasına göre tork alınırsa,
T1.
Ty
Tx 37°
O
5
3
= T2.
2
2
Ty.4 = 4G.2 + G.4
T.sin37°.4 = 12G
T1
3
=
olur.
5
T2
T.0.6.4 = 12G
CEVAP B
2,4T = 12G
T = 5G olur.
CEVAP C
8.
tavan
10.
düfley
duvar
.
ip
ip
.
.
M
ip
1
O2
T1
K
G
G
2
L
yatay
G
2
L noktasına göre tork alınırsa,
RxL = 0
G
T1.6 = G.3 + .2
2
6T1 = 4G
3
L
T2
N
• O1
K
F
•
4
5
K noktasına göre tork alınırsa,
T1 =
F kuvvetinin,
x = 2v2.2v2 = 8 br olur.
2
G olur.
3
K noktasına göre tork alınırsa,
RxK = 0
G
T2.6 = G.3 + .4
2
6T2 = 5G
5
T2 =
G olur.
6
x1 = 4.2 = 8 br
x2 = 4.2 = 8 br
x3 = 4v2.v2 = 8 br
x4 = 2.4 = 8 br
x5 = 2.4 – 1.4 = 4 br
Buna göre, 5 kuvveti çubuğu şekildeki konumda
dengede tutamaz.
CEVAP E
T1 ve T2 taraf tarafa oranlanırsa,
2
T1 3 G 4
=
=
olur.
T2 5
5
G
6
CEVAP C
KUVVET VE HAREKET
159
11. Çubuk P noktasından den-
T
37°
P
geye geldiğine göre çubuğun
ağırlık merkezi P noktasıdır. L
d1
noktasına göre tork alınırsa,
L
53°
T.d1 = P.d2
K
30N
37o
d2
T.(5.sin37°) = 30. (3.cos37°)
T.(5.0,6) = 30.(3. 0,8)
T.3 = 72
T = 24 N olur.
CEVAP D
12.
tavan
ip
T
T
Ty
Tx 30°
.
L
K
GÇ
düfley
duvar
yatay
GX=G
K noktasına göre tork alınacak olursa,
RxK = 0
Gç.3 + Gx.5 = T.2+Ty.6
Gç.3 + G.5 = T.2+T.sin30°.6
1
3Gç+5G = 2T + T. .6
2
3Gç + 5G = 5T
3Gç = 5.4G – 5G
3Gç = 15G
Gç = 5G olur.
CEVAP D
160
KUVVET VE HAREKET
TEST
1.
3
tavan
4.
.
K
ip
G
G
Gç=G
G
G
G
N
P
I
R
G
S
yatay
T
Gç=G
II
Çocuk K noktasında iken çocuk ile çubuğun ağırlık
merkezi I desteğinin üzerinde, S noktasında iken
çocuk ile çubuğun ağırlık merkezi II desteğinin
üzerindedir. Şekilde görüldüğü gibi, ağırlığı G olan
çocuk, kalasın dengesi bozulmadan en fazla KS
noktaları arasında hareket edebilir.
G Y
G X
Çubuğun yatay olarak dengede kalabilmesi için
yalnız Z küresi asıldığı yerden alınmalıdır. Z küresi
alındığında O noktasına göre tork alındığında,
2G.1 + G.3 + G.4 = G.1 + 2G.2 + G.4
9G = 9G olur.
CEVAP B
Ty
M
yatay düzlem
Z
2.
L
yatay
O
G
TORK
ÇÖZÜMLER
CEVAP A
T
37°
Tx
a
a
5.
a/2 a/2
140N
O
Kare levhanın eğik düzlem ile temas ettiği O noktasına göre tork alınırsa,
a
Tx . a + Ty . a = 140.
2
Tx + Ty = 70
T . cos37° + T . sin37°
T . 0,8 + T . 0,6
1,4T
T
=
=
=
=
Çubuğa uygulanan
kuvvetler
şekilde
T
gösterildiği gibidir. O
T
noktasına göre tork
2T
T
K
alınırsa,
40N
80N
40.4 + 80.5 = T.4 + 2T.8
160 + 400 = 20T
70
70
70
50 N olur.
560 = 20T ⇒ T = 28N olur.
K cismine çubuğun uyguladığı tepki kuvveti,
N = G – T = 40 – 28 = 12 N olur.
CEVAP D
3.
I. konumunda:
4
RxK = 0
düfley
duvar
L
F1
2F1 = G
G
olur.
F1 =
2
2
L
1
G
II. konumunda:
6.
RxK = 0 olduğuna göre
F kuvvetinin büyüklüğü,
K
.
F.3 = 2G.1 + 2G.0
G
F2.4 = G.1
G
F2 =
4
Buna göre,
G
F1
= 2 = 2 olur.
F2 G
4
CEVAP B
F2
F1.4 = G.2
RxK = 0
O
3F = 2G
2G
olur.
F=
3
2G
2G
K
CEVAP D
4
F
yatay
düzlem
CEVAP C
KUVVET VE HAREKET
161
7.
10. Her bir bölmenin
tavan
•
Ty
T ip
uzunluğuna 1 br
a
dersek ve K nokta-
Tx
a
Gy
37o
yatay
K
Ty.2 = Gy.1
11.
T.sinα.2 = G.cosα.1
tavan
.
ip
G
T= KL
2
K
2T.tanα = G olur.
CEVAP C
•O1
Kuvvetlerin K nokF1
yatay
eşittir.
GKL
M 53°
F3
F2
tasına göre torkla-
. L
.
GKL
2
L A O2
•
3br
.
37°
K
4br
olur. Buna göre, F1 > F3 > F2 olur.
N
•
GKL
2
5br
x1 = x2 = x3
yatay
GMN
yatay düzlem
G KL
büyüklüğünde
2
kuvvet uygular. A noktasına göre tork alınırsa,
RxA = 0
yatay
düzlem
KL çubuğu MN çubuğuna
CEVAP A
G KL
1
.1 = GMN.
2
2
GKL = GMN
9.
F
G KL
= 1 olur.
G MN
T
T
L
•
37°
O
CEVAP E
53°
•
12.
ip
G
T
Gç =40N
yatay
düzlem
53°
•
37°
10
K
K noktasına göre tork alalım.
10
24
P
37o
P
10
37o
O
F
20
=
0, 8 0, 6
KUVVET VE HAREKET
8
16°
Küre
için:
________
F
T
=
sin127° sin143°
F = 15 N olur.
P
10
T . 2 = Gç . 1
2T = 40
T = 20 N olur.
162
yatay
düzlem
(T.0,6) .4 + (T.0,8).3 +(24G.0,6).2 = (24G.0,8).3
2,4T + 2,4T = 57,6G – 28,8G
4,8T = 28,8G
T = 6 G olur.
CEVAP E
K noktasına göre tork alınırsa,
RxK = 0
3F1 = 5F2 = 4F3
K
Tx.4 + Ty.3 + Px.2 = Py.3
düfley
duvar
F1.3 = F2.5 = F3.4
P=24G
Py
G
rının büyüklükleri
Px
37°
•
a
8.
Tx
sak,
O
T
53°
sına göre tork alır-
L
Gx
Ty
CEVAP B
6
P
Çubukların uzunlukları 10 br seçilip, O noktasına
göre tork alınırsa,
T.24 = P.4 + P.11 + P.19 + P.24
24T = 58 P
29
T=
P olur.
12
CEVAP C
Adı ve Soyadı : .....................................
1.
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
F1 kuvvetinin O noktasına
göre torkunun büyüklüğü,
x = F1y.d1 – F1x.d1ı
Bölüm
Yazılı Soruları
(Tork)
4
F1y
–
4
F
1
4
+
O
3.
ÇÖZÜMLER
a) P
noktasına
göre
T
53°
O
tork alınırsa,
r
F1X
F2
T.d1 = P.d2
= 4 br olur.
a) F2 kuvvetinin torkunun bü-
P
d2
4
= 2.4 – 2.2
d1
37°
4
40N
T.(2r.sin53°) = P.(r.sin37°)
F3
T.2.0,8 = P.0,6
yüklüğü
x2 = F2.d2 = 2.2 = 4 br = x olur.
1,6 T = 40.0,6
T = 15 N olur.
b) F3 kuvvetinin torkunun bü yüklüğü,
x3 = – F3.d3
b) Desteğin küreye uyguladığı tepki kuvveti,
N = T.cos53° + 40.cos37°
= –2.5
= –10 br
5
= – x olur.
2
= 15.0,6 + 40.0,8
= 9 + 32
= 41 N olur.
2. a)
T
Ty
53°
Tx
Fx
O
yatay
8N
Fy
20N
4.
F
a) Duvarın merdivene uyguladığı tepki kuvveti F
O noktasına göre tork alınacak olursa,
Ty . 4 = 8 . 3 + 20 . 6
olsun. O noktasına göre
tork alınırsa;
8m
N
(T . sin53°) . 4 = 24 + 120
3,2T = 144
T = 45 N olur.
(G M + G Ç) .3 = F.8
Fx = Tx = T . cos53°
= 45 . (0,6)
= 27 N olur.
olsun.
Denge koşuluna göre;
N = GM + GÇ
= 100 + 200
= 300 N olur.
36 = Fy + 28 ⇒ Fy = 8 N olur.
3m
b) Yerin merdivene uyguladığı tepki kuvvet N
Ty = Fy + 8 + 20
45 . 0,8 = Fy + 28
s
3m
300.3
225
=F&F=
N olur.
8
2
c) Duvarın düşey tepki kuvveti (Fy),
45 . sin53° = Fy + 28
O
(100 + 200) .3 = F.8
b) Duvarın yatay tepki kuvveti (Fx), T kuvvetinin
yatay bileşenine (Tx) eşittir.
100N
200N
53° f
c) Denge koşuluna göre;
fs = F =
225
N olur.
2
KUVVET VE HAREKET
163
5.
T2
8.
T
Ty
L
K
T
T1
10N
L
X cisminin asıldığı noktaya göre tork alınırsa,
T1 . 3 = 5 . 4 + 2 . 8
T1 . 3 = 36 ⇒ T1 = 12 N olur.
K
K noktasına göre tork alınacak olursa,
Σ xK = 0
T . 0,6 . 5 =
3T =
3T =
T=
T
K
9.
L
M
yatay
•
53°
Ty
T=5G
53°
GMN = 3T
K
KL
çubuğunda:
____________
K ucuna göre tork alalım.
düfley
2T . 1 + GKL . 2 = T . 3
T
olur.
2
GMN = 3T olur.
GKL ve GMN taraf tarafa oranlanırsa,
T
G KL
1
= 2 =
G MN 3T 6
3G
Gç
olur.
10. Dikdörtgen levhada 24 br
Ty
kare olduğundan levha-
7.
T
nın ağırlığı,
53°
L
37°
53°
K
37°
G = 24 . 10 = 240 N olur.
T=10N
53°
53°
Gy
G
L noktasına göre tork alınırsa,
Σ xL = 0
Tx
O
53° Gy
K noktasına göre tork alınırsa,
Gx
G
53°
K
Tx . 4 + Ty . 4 + Gx . 2 = Gy . 3
(T . 0,8) . 4 + (T . 0,6) . 4 + (G . 0,8) . 2 = (G . 0,6) . 3
3,2T + 2,4T = 1,8G – 1,6G
T.4 = Gy.2
5,6T = 0,2G
T.4 = G.sin53°.2
5,6T = 0,2.240
60
T=
N olur.
7
10.4 = G.0,8.2
40 = 1,6G ⇒ G = 25 N olur.
164
Tx
L
K noktasına göre tork alalım.
Ty . 6 = Gç . 3 + 3G . 4
T . sin53° . 6 = Gç . 3 + 12G
5G . 0,8 . 6 = 3Gç + 12G
24G = 3Gç + 12G
3Gç = 12G
Gç = 4G olur.
2GKL = T
GKL =
ip
yatay
GKL = T
–
2
N
yatay
2T
3
+P.3
2
3
+ 20 . 3
24.
2
36 + 60
96
32 N olur.
Ty . 5 = Gç .
34
⇒ T=
N olur.
3
II
T
3/2br 3/2br
3br
T . 3 = 10 . 1 + 12 . 2
I
53°
yatay düzlem
T2 gerilme kuvvetinin olduğu ipe göre tork alınırsa,
6.
4br
Gç =24N
X
16°
T . 3 = 34
P=20N
Tx
ip
5N
2N
37°
KUVVET VE HAREKET
9. BÖLÜM
KESİŞEN KUVVETLERİN DENGESİ
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
3.
.
.
20 3N
1.
60° 20 3N
F2.cosi
F2
F1
F1.cosa
i
.•
F2.sini
m=2v3kg
a
O
•
20 3N
TK
F1.sina
TL
G=20v3N
Cismin altındaki destek çekildiğinde cismin bağlı
olduğu ipteki gerilme kuvveti,
F3
Cisim dengede olduğuna göre, F1 ve F2 kuvvetleri
T = G = mg = 20v3 N olur.
bileşenlerine ayrılırsa,
L halkasının bağlı olduğu ipteki gerilme kuvveti
TL = 20v3 N olur.
F1.sina = F2.sini
F1.cosa + F2.cosi = F3
K halkasının bağlı olduğu ipteki gerilme kuvveti,
TK = 20v3.v3 = 60 N olur.
eşitlikleri sağlanır.
Bu durumda verilen eşitliklerden yalnız II. eşitlik
doğrudur.
Halkalar 50 N a dayanabildiklerine göre K halkası
kopar. Bundan sonra L halkasındaki gerilme kuvveti
ı
cismin ağırlığına eşit olacağından (TL = 20v3 N) ve
L halkası bu kuvvete dayanabileceğinden kopmaz.
CEVAP B
CEVAP A
2.
4.
T1
30°
T=P
150°
120°
T
•
T1
60°
150°
30°
T2
K
O
GK
P
Sistem dengede olduğuna göre, Lâmi teoremini yazarsak,
GK
T
=
sin120° sin150°
Sistem dengede olduğuna göre, Lâmi teoremini yazarsak,
T1
T2
P
=
=
sin90° sin150° sin120°
T
40
=
1
3
2
2
T1
T2
=
1
3
2
2
T = 40 3 N olur.
CEVAP C
T1
1
3
=
=
T2
3
3
olur.
CEVAP A
KUVVET VE HAREKET
165
5.
yatay
80°
•
T1
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
1.
30°
80°
•
T
•
•
37°
T1
T2
60°
40°
53°
T3
1
37° 53°
düfley
T
37°
2
O
X
G +G
K
T =G
3
Sistem dengede olduğuna göre, Lami teoremini
yazaksak,
6N
O
L
L
G
T3
T1
T2
=
=
sin 150° sin 170° sin 40°
L
GK + GL = 4 + 6
= 10 N
T3
T1
T2
=
=
sin 30° sin 10° sin 40°
T 3 = GL = 6 N
sin40° > sin30° > sin10° olduğundan,
cos53° =
T2
3
3.10
=
& T2 =
= 6N
5 GK + GL
5
sin53° =
T1
4
4.10
=
& T1 =
= 8N
5 GK + GL
5
T3 > T1 > T2 olur.
CEVAP B
T1 > T2 = T3 olur.
2.
6.
CEVAP D
I. ip kesilmeden önce
L ve M noktalarındaki
gerilmeler,
i
i
I. ip
•
K
II. ip
•L
i
TL < GX
T2
T2y
TM = GX dir.
T1
O
T2x
20N
•M
GX
I. ip kesildiğinde X
X
cisminin ağırlığı II. ipe
X
GX
geçer.
Bu durumda M noktasındaki gerilme TM değişmez-
G=20N
ken, L noktasındaki gerilme TL artar.
Sistem dengede olduğuna göre O noktasındaki
yatay ve düşey bileşenlerin eşitliğine bakalım.
X cisminin ağırlığı 20 N olduğuna göre T2 gerilme
kuvvetinin düşey bileşeni T2y = 20 N olur.
α
T2x = 2.20 = 40 N olur.
θ
T2 kuvveti ise,
T2 =
2
2
Tx + Ty
β
K
=
2
2
20 + 40 = 20v5 N olur.
O noktasındaki yatay bileşenlerin eşitliğinden,
T1 = T2x = 40 N olur.
Bu durumda; T1 = 40 N, T2 = 20v5 N dur.
CEVAP D
KUVVET VE HAREKET
CEVAP C
3.
T2y = 1 br, T2x = 2 br olduğundan,
166
T2
53°
K
4N
GX
GK + GL
L
yer
İp kesilince K cismi ok yönünde hareket eder. α
artar, θ ve β açıları azalır.
I. ve III. yargılar doğrudur.
II. yargı yanlıştır.
CEVAP E
4.
5.
I. yol:
T2x
T2
K
•
T1
O T3x
30°
60° 30°
T2y T3y T3
60°
30°
L
Sistem dengede olduğuna göre O noktasındaki
kuvvetlerin dengesine bakalım.
O noktasındaki yatay kuvvetlerin dengesinden,
T2.cos30° = T3.cos60°
3
1
= T3.
& T3 = v3.T2 olur.
2
2
•
•
I. ip
T1
a
T1.cosa
T2
T1.sina
•
•
T3
X
GX
T2 = T1.sina olduğundan T1 ve sina azalacağından T2 de azalır.
Bu durumda,
T1 = T2y + T3y
= T2.sin30° + T3.sin60°
3
1
+ T3.
2
2
1
= T2. +
2
L
T2 kuvveti II. durumda,
O noktasındaki düşey kuvvetlerin dengesinden,
= T2.
K
II. durumda a açısı küçüleceğinden T1.cosa = T3
olduğundan a küçülürse cosa artar, T1 kuvveti de
azalır.
T2x = T3x
T2.
Sistem dengede olduğundan,T3 gerilme kuvveti X cisminin ağırlığına eşittir.
I. ipin K noktasından L noktasına
gelmesi X cisminin
ağırlığını değiştirmeyeceğinden T3
gerilme
kuvveti
değişmez.
T1
T2
T3
Azalır
Azalır
Değişmez
CEVAP D
3
3 .T2.
2
= 2T2 & T1 = 2T2 olur.
T3 = v3.T2 ve T1 = 2T2 eşitliklerine göre,
T1 > T3 > T2 olur.
II. yol:
T1
120°
•.
6.
150°
O
T2
T3
T1
T3
Bu soruyu O noktasına Lami teoremini uygulayarak da çözebiliriz.
T3
T1
T2
=
=
= sabit
sin 90° sin 150° sin 120°
FK
β
s›v›
θ
T2
K
T3
T1
T2
=
=
= sabit
sin 90° sin 30° sin 60°
T3
α
T1
GM
GL
GL
sin90° > sin60° > sin30° & T1 > T3 > T2 olur.
CEVAP B
θ > β > α olduğuna göre, T2 > T3 > T1 olur.
I. yargı doğrudur.
GL = T2 , GM = T3 , GK > T1 dir.
GL > GM > GK olabilir.
II. yargı doğru olabilir.
GL > GK > GM de olabilir.
III. yargı doğru olabilir.
CEVAP E
KUVVET VE HAREKET
167
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
1.
T1 II
Küre I düzlemine
T1 = 24 N kuvvet uygu-
I
T2
larsa yüzey de aynı
büyüklükte
4.
tepkide
T. sin 60° = N
30°
O
30°
60°
T.
bulunur. Küreye etki
O
Tx
G
yatay düzlem
3
= 12v3 N olur.
2
CEVAP B
1
= G & G = 10 3 N olur.
2
60°
ğuna göre,
T
60°
ı
N
Tv3 + N = G
T=5
›
O
yatay
60°
T=5 3N
30°
ip
30°
Sistem dengede oldu-
CEVAP B
5.
F
G
3N
yatay
düzlem
60°
ı
5v3 . v3 + N = 30
60°
Lami teoreminden,
O
ı
N = 15 N
G
T
F
=
=
sin90°
sin120° sin150°
olur.
G=30N
G
F
=
1
1
2
CEVAP A
F =
G
2
olur.
CEVAP D
I
F2
6.
II
37°
F1
O
53°
37°
G
53°
yatay
düzlem
Küreye etki eden kuvvetler şekildeki gibidir.
Lami teoreminden,
F1
F2
G
=
=
sin 53° sin 90° sin 37°
II
N1
I
N2
53°
O
53°
37°
G
N1=30N
37°
yatay düzlem
N1
N2
G
=
=
sin 90° sin 143° sin 127°
30 =
N2
G
=
& N 2 = 18 N
0, 6 0, 8
G = 24 N olur.
I düzlemi ok yönünde çevrilirse açı azalacağından
kürenin I düzlemine uyguladığı kuvvet azalır.
F1
F
60
= 2=
0, 8
1
0, 6
eşitliğinden F1 = 80 N, F2 = 100 N olur.
CEVAP C
KUVVET VE HAREKET
Küre I düzlemine
30 N luk kuvvet uygularsa, yüzey de aynı
büyüklükte tepkide
bulunur. Küreye etki
eden kuvvetler şekildeki gibidir. Lami teoreminden,
N2
30
G
=
=
1
sin 37° sin 53°
F1
F2
G
=
=
sin 127° sin 90° sin 143°
168
N
N
3
= 30
2
20 3 .
60°
T2 = T1.cos30° = 24.
3.
60°
T. cos 60° = G
de gösterilmiştir. Küre
2.
T 60°
Ty
T = 20 3 N olur.
G
eden kuvvetler şekildengede olduğundan,
Küreye etki eden kuvvetler şekilde gösterildiği gibidir. Sistem dengede olduğuna göre,
I. ve II. yargılar doğru, III. yargı yanlıştır.
CEVAP C
7.
Yatay kuvvetlerin bileşkesi sıfırdır. Bu durumda F
kuvveti,
N
N2
yatay
•
37°
T
N1
R Fx = 0
F2 . cos 60° + T . cos 30° = F
O
N
IFI = 120N
5G 1 G
3
2G
=F ( F=
. + .
olur.
2 3 2 2 2
3
37°
O 37°
CEVAP C
37°
yatay
G=50N
Gx 37°
T
G=50N
Gy = 40N
yatay düzlem
37°
9.
I
K
T
düfley
Yatay ve düşey kuvvetlerin dengesinden kürelerin
birbirlerine uyguladıkları tepki kuvveti,
F
II
O
•
53°
•
37°
T + GX = F . cos 37°
•
L
T2
T + 30 = 120 . 0,8
P
37° O 53°
53°
T = 66 N
T1
•
Yüzeyin tepki kuvveti,
•
37°
T = G . sin 37° + N . sin 37°
F
66 = 50 . 0,6 + N . 0,6
P
36 = 0,6 N
N = 60 N olur.
CEVAP D
53°
•
yatay
Sistem dengede olduğuna göre Lâmi teoremini
yazarsak,
8.
F1
T
K
60°
F2
30°
L
60° O
30°
T
60°
30°
P
F
=
sin90° sin127°
O
60°
G
P
F
=
1
4
5
F
F =
30°
G
K küresinde:
yatay düzlem
L küresi için denge şartı yazılırsa:
T2 . sin37° = F . cos37° + P
K küresinde: Lami teoremi uygulanırsa,
T2 .
T
G
=
sin150° sin90°
T=
41
P
15
I yüzeyinin tepki kuvveti,
T2 =
1
G olur.
2
L küresinde: Düşey kuvvetlerin dengesinden,
T1 = T2 . cos37° + F . cos53°
=
41
4 4
3
P. + P.
15
5 5
5
=
164
12
P+
P
75
25
R Fy = 0
F2 . sin 60° = G + T . cos 60°
3
G 1
= G+ .
2
2 2
3
5
. F2 = G
2
4
F2 =
3 4
4
= P. +P
5 5
5
3
16
25
T =
P+
P
5 2 25
25
T
G
=
1
1
2
F2 .
4
P olur.
5
5
2 3
G olur.
=b
164 + 36 l
P
75
=
200
P
75
=
8
P olur.
3
CEVAP E
KUVVET VE HAREKET
169
10.
12.
düfley
duvar
K
N
ip
O1
T
30°
K
T
F
53°
L
O
O
37°
F
30°
5 cm
yatay
düzlem
N
F
G
T
=
=
sin90° sin127° sin143°
100
F
T
=
=
1
0, 8 0, 6
T = 80 N
F = 60 N olur.
L küresinde:
Denge şartından,
RF y = 0
T + N = F . cos 53° + G
80 + N = 60 . 0, 6 + 100
80 + N = 136
CEVAP D
N = 56 N olur.
11.
NL
K
L
θ
θ
T
GLx
37°
GLy
20N
37°
GKy
37° 10N
Sistem dengede olduğuna göre, K ve L cisimlerinin
ağırlıklarının yatay bileşenlerin toplamı T gerilme
kuvvetine eşittir.
GK . sin37° + GL . sin37° = T
10 . 0,6 + 20 . 0,6 = T
6 + 12 = T
T = 18 N olur.
CEVAP E
170
T
GK
sin30°
T
=
cos30°
120
T = 40 3 N olur.
Lami teoreminden,
GKx
tan30° =
1
T
=
120
3
K küresinde:
NK
60°
K küresi dengede olduğundan,
G
8 cm
•
37°
G
5 cm
•
GK
10cm
53°
T
KUVVET VE HAREKET
CEVAP E
1.
1
Sistem dengede olduğuna
göre Lâmi teoreminden;
•
yatay
T1
GK
T2
=
=
sin90° sin127°
sin143°
5.
T1
• •
T2 = 60 N
K
olur.
Sistemler
şekildeki gibi dengede olduğuna
göre,
T1 = G olur.
30°
T1
30°
30°
K
30°
L
G
L
M
GM
GL
GM=T
GK=T
T
olur.
2
120°
120°
120°
CEVAP D
G
6.
İpler arasındaki açı
120°
olduğundan
gerilme kuvvetleri her
zaman eşit olur.
Halkalar 10 N a dayanabildiğinden uygula
nan F kuvveti 10 N ve
daha küçük olduğun-
|F|=T
TY=T
120°
120°
•
120°
O
TX=T
dan sistem dengede kalır. Halkalar kopmaz. F
kuvveti 10 N dan büyük olduğundan halkalar aynı
anda kopar.
CEVAP E
I. ve II. yargılar doğrudur. III. yargı yanlıştır.
CEVAP C
F1
7.
III
•O
–F1
karşısında büyük kuvvet bulunur.
T1 $ 135° _b
b
T2 $ 120° ` T3 > T2 > T1 olur.
b
T3 $ 105° b
a
•
IV
K
127° 53°
T
T
L
CEVAP C
Sistem dengede olduğuna göre, Lâmi teoremini yazarsak,
Kesişen üç kuvvet şekildeki
gibi dengede ise küçük açı
143°
37°
yatay
III ve IV kuvvetlerinin
bileşkesi –F1 e eşittir.
4.
T
2GL
Buna göre, iplerdeki gerilme kuvvetleri arasında
Bu durumda seçeceğimiz iki kuvvetin bileşke
sinin –F1 olması gerekir.
yatay
GL
GK = GM > GL olur.
G
3
ve T3 =
G olur.
2
2
Cisim dengede olduğuna göre, kuvvetlerin
bileşkesi sıfır olmak
zorundadır.
30°
K
T = 2GL ⇒ GL =
T
T2
G
= 3 =
1
1
3
2
2
T1 > T3 > T2 ilişkisi vardır.
30°
T3
60°
T3
T2
G
=
=
sin 150° sin 120 sin 90°
T2 =
T
GK
60°
T2
120° T1
T
T
GK = 80N
CEVAP B
3.
K ve M cisimlerinin ağırlıkları eşit olur.
Sabit makaraların ağırlığı
dengeyi değiştirmez.
T2
53°
T
80
= 2
0, 8
0, 6
2.
KESİŞEN KUVVETLERİN DENGESİ
ÇÖZÜMLER
•
TEST
GK
T
=
sin127° sin143°
45°
G
T
= K
0, 8 0, 6
T2
T1
105°
60°
45°
30°
T=
T3
K
CEVAP A
olur.
4
G
3 K
GL
T
=
sin143° sin127°
4
G
3 K = GL
3
4
5
5
G L 16
olur.
=
GK
9
CEVAP E
KUVVET VE HAREKET
171
8.
I. ip L noktasına bağlan-
K
ğında I. ve II. ipler arasın-
Ι. ip
L
ΙΙ. ip
T1
daki açı küçüldüğünden
α
11. Sistem dengede olduğuna göre,
T1 ve T2 gerilme kuvvetleK
2T
a
150°
T4
K
T2 = 2T olur.
CEVAP D
9.
150°
T3 gerilme kuvvetine T
dersek, T1 = 2T ve
ri azalır.
i
2T
T1 = T2 = 2T3 ise
T2
θ
a
GK
T1 = T2 olduğundan a = i
dır.
T3=GL=T
L
I. eşitlik doğrudur.
Çengellere cisimler asılınca
T1 ve T3 gerilme kuvvetleri
artar. T2 değişmez. T1 ile T3
kuvvetlerinin bileşkesinin şiddeti değişmediğine göre α artar.
GL
a = i olduğundan,
T1
a + a + i = a + a + a = 180° & a = 60° olur.
T2
α
Lami teoremini kullanırsak,
yatay
T1
T2
T4
=
=
sin 150° sin 150° sin 60°
T3
T4
2T
=
sin 30° sin 60°
T
2T
= 4
1
3
2
2
I. ve II. yargılar doğrudur.
& T4 = 2 3 T olur.
T4 gerilme kuvveti, T3 ve GK nın toplamına eşittir.
III. yargı yanlıştır.
CEVAP C
T4 = T3 + GK
2v3T = T + GK ve GL = T olduğundan GK ≠ GL dir
10.
II. eşitlik yanlıştır.
T1 + T2 + T4 = 0 ve T4 ≠ T3 olduğundan
tavan
X + 3Y
127°
53°
yatay
T
III. eşitlik yanlıştır.
CEVAP A
T 143° 37°
yatay
K
X
X
Y
Y
12.
Y
Sistem dengede olduğuna göre, Lâmi teoremini yazarsak,
T1
T1
T
K
=
sin143° sin127°
T
K
=
0, 6 0, 8
T =
GK
3
K
4
X=
172
9
Y
2
=
T
0, 8
T = 6Y
KUVVET VE HAREKET
=
T2
•
FK
s›v›
T3
GL
X
Musluk açılınca cisme etkileyen kaldırma kuvveti
azalır. T3 gerilme kuvveti artar. T1 = GK , T2 = GL
olduğundan ve cisimlerin ağırlıkları değişmediğinden, T1 ve T2 gerilme kuvvetleri değişmez. α açısı
azalır.
X
T
X + 3Y
=
=
sin143° sin127° sin90°
X
0, 6
T2
α
X + 3Y
1
K = 8Y olur.
II. yargı doğrudur. I. ve III. yargılar yanlıştır.
CEVAP D
CEVAP B
TEST
1.
2
Küre dengede olduğuna
II
T1
göre,
I
G = T1.sin45°
30v2 = T1.
KESİŞEN KUVVETLERİN DENGESİ
ÇÖZÜMLER
T2
45°
O
45°
2
2
4.
45°
G
T
30 = 1 & T1 = 60 N
2
olur.
Küreye etki eden kuvvetler şekildeki gibidir.
N1 ve N2 kuvvetlerinin
büyüklükleri eşit ve
aradaki açı 120° olduğundan,
I
N2
N1
120°
O
60° 60°
G
|N1| = |N2| = |G| = 50 N
olur.
45°
a
a
CEVAP E
CEVAP A
5.
37°
O2
50N
50N
53o
N1
53°
53°
O1
3 cm
Sistem dengede olduğuna göre O2 noktası için
37°
G=20N
53°
37°
K
N2
N1
o
T 37
L
53°
37°
O2
53°
N
T
N
N2
Lâmi teoremini yazalım.
N
50
=
sin 143° sin 90°
37°
4 cm
G=20N
Küreye etki eden kuvvetler şekilde gösterilmiştir.
N2.sin53° = 20 N
N2.0,8 = 20
N2 = 25 N olur.
CEVAP B
N
= 50 & N = 30 N olur.
0, 6
CEVAP B
6.
➞
|F|=20v2N
NK
NK
Fx
NL
O
NL
45°
45°
45°
3.
yatay
düzlem
a
yatay düzlem
2.
II
Fy
N=120N
N
L
K
F=20v2N
G
F kuvveti bileşenlere ayrıldığında,
O 150°
150°
30°
T
O
θ
θ
30°
G
T
2
= 20 N,
2
Fy = 20 2 .
2
= 20 N olur.
2
30°
G
Küre dengede olduğuna göre O noktası için Lâmi
teoremini yazabiliriz.
N
G
T
=
=
sin 60° sin 150° sin 150°
120 G
=
& G = 40 3 N olur.
1
3
2
2
Fx = 20 2 .
Yüzeylerin tepki kuvvetleri,
NL = Fx = 20 N
NK
=4
NL
NK
= 4 ⇒ NK = 80 N olur.
20
CEVAP C
Kürenin ağırlığı,
NK = G + 20
80 = G + 20 ⇒ G = 60 N olur.
CEVAP D
KUVVET VE HAREKET
173
7.
İlk durumda, denge şartından
10. Küreye etki eden kuvvetler şekildeki gibidir.
Küre dengede olduğundan,
L
F1.sin30° = G olur.
F1
K
Düzlem θ açısı kadar
30°
30°
60°
N
döndürüldüğünde
F2.sin60° = G olur.
30°
30°
F1.sin30° = F2.sin60°
O
i
G
olur. II düzlemi ok
yönünde çevrilirse i
açısı artar.
i
yatay düzlem
cosi değeri küçülür.
3
F1 sin 60°
=
= 2 =
F2 sin 30°
1
2
T2.cosi = G eşitliğinde G sabit olduğundan T2
kuvveti artar. T1 = T2.sini eşitliğinde T2 ve sini
değerleri arttığından T1 kuvveti de artar.
CEVAP E
3 olur.
CEVAP C
11.
8.
T1
T1 = T2.sini
30°
I
Lami teoreminden kürenin I ve II düzlemlerine
uyguladığı kuvvetler,
F1
F2
G
=
=
sin143° sin127° sin90°
NK
K
L
NK
➞
60°
II
➞
60°
G
30N
30N
F
F
24
= 1 = 2
0, 6 0, 8
1
O2
30°
T
O1
F1
O
G
NL
TT
O1
30°
F2
37°
I
i
II
T2.cosi = G
G
Bu durumda,
T2
30°
60°
Önce ipteki T gerilme kuvvetini bulalım.
K küresi için Lâmi teoremini yazacak olursak,
F1 = 32 N
F2 = 40 N olur.
NK
30
T
=
=
sin 90° sin 150° sin 120°
53°
yatay düzlem
30
T
=
1
3
2
2
CEVAP D
T = 10 3 N
P
F
=
0, 6 1
düfley
duvar
37°
T
N1
L
143°
O
37° •
60°
30°
T=10v3N
30°
60°
G
G = 10 N olur.
CEVAP A
53° O 37°
53°
53°
12.
N2 P
N
N.sin37°
K
N
L
37°
F
37°
N.cos37°
P
30N
F
37o
F M
F
37o
30N
30N
T . sin 53° = P + F . cos 53°
5
3
4
T . = P + P.
3
5
5
4
T = 2P
5
5
T = P olur.
2
F
37o
olur.
L küresinde:
KUVVET VE HAREKET
NL
G 10 3
=
1
3
2
2
F
5
F = P
3
174
G
10 3
=
sin 150° sin 120°
K
ip
•
P
F
=
sin143° sin90°
L küresi için Lâmi teoremini yazacak olursak,
düfley
duvar
•
Sistem dengede ol duğuna
göre Lâmi teoremini yazarsak, K küresinde:
•
9.
CEVAP D
Denge şartından,
N.sin37° = 30
N.0,6 = 30
N = 50 N olur.
F kuvvetinin büyüklüğü ise,
F = N.cos37° = 50.0,8 = 40 N olur.
CEVAP C
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
Bölüm
Yazılı Soruları
(Kesişen Kuvvetlerin Dengesi)
1.
yatay
ÇÖZÜMLER
3.
düfley
•
37°
37°
Ty
T2
T1
53°
K
GLx
T 30°
60°
30°
37°
•
düfley
GL
GK = 40 N
düfley
yatay
Tx
GLy
GK
•
Lami teoreminden T1 ve T2 gerilme kuvvetleri,
GK
T1
T2
=
=
sin90° sin127° sin143°
L
GL
T
T
40
= 1 = 2
1
0, 8 0, 6
Sistem dengede olduğuna göre,
TX = G Lx
T.cos60° = G L .cos30°
T1 = 32 N
T2 = 24 N
olur.
1
3
= GL .
2
2
T = 3 GL
T.
GLy + GK = Ty
2.
yatay
G L .sin30° + G K = T.sin60°
•
53°
T2y
•
•
ip T = 12 N
1
GL .
T2
53°
T2x
yatay
1
3
+ GK = ` 3 GLj.
2
2
GK = GL
GK
= 1 olur.
GL
4.
T3
•
•
37°
P=10N
yatay
düzlem
Denge şartından T2 gerilme kuvveti,
Σ Fx = 0
K
T1
37°
T1x
T2
G
37°
T1
L
37°
M
T1x
T2x = T1
T2 . cos53° = 12
T2 . 0,6 = 12
T2 = 20 N olur.
Denge şartından T3 gerilme kuvveti,
Σ Fy = 0
T2y = T3 + P
T2 . sin53° = T3 + 10
T1y
O1
N
30N
a) Sistem şekildeki gibi dengede olduğuna göre,
T1.sin37° = GL
T1.0,6 = 30
T1= 50 N olur.
b) T2 = T1.cos37° = 50.0,8 = 40 N olur.
c) M noktasına uygulanan kuvveti N olsun.
20 . 0,8 = T3 + 10
T1.cos37° = N
16 = T3 + 10
T1.0,8 = N
T3 = 6 N olur.
50.0,8 = N ⇒ N = 40 N olur.
KUVVET VE HAREKET
175
5.
45°
30°
45°
T
120°
T
T
b) Denge şartından yüzeyin küreye uyguladığı
tepki kuvvetinin büyüklüğü,
Σ Fx = 0
30°
T
.
Tx + N = F
T . cos53° + N = F
X
Y
30 . 0,6 + N = 40
GX
GY
fiekil-I
fiekil-II
N = 22 N olur.
Şekil-I de aralarındaki açı 90° olan eşit kuvvetlerin
bileşkesi R1 = Tv2 dir.
8.
a
a
T1
.
i
i
T1
T2
60°
T2
Şekil-II de aralarındaki açı 120° olan eşit kuvvetlerin bileşkesi R2 = T dir.
Şekil-I deki kuvvetlerin dengesinden,
GX = R1 = Tv2
P
fiekil-I
Şekil-II deki kuvvetlerin dengesinden,
Şekil-I deki ip gerilmeleri eşit ve T1 dir. Eşit kuvvetlerin arasındaki açı 90° olduğuna göre P = v2T1 olur.
GY = R2 = T olur.
GX ve GY oranlanırsa,
Şekil-II deki ip gerilmeleri eşit ve T2 dir. Eşit kuvvetlerin arasındaki açı 60° olduğundan P = v3T2 olur.
GX T 2
=
= 2 olur.
GY
T
6.
Bu durumda T1 ve T2 gerilme kuvvetlerinin oranı,
T
3
2 .T1 = 3 .T2 & 1 =
olur.
2
T2
N
N
10cm
P
fiekil-II
53° 53°
10cm
53° 6cm
8cm
8cm
9.
8cm
N
Ny
N
37°
G
F
N kuvvetlerinin düşey bileşenlerinin toplamı kürenin
ağırlığına eşittir. N kuvvetinin büyüklüğü,
N
53° 53°
2N.0,6 = G
1,2N = 120
53°
düfley
Ty
O
G
tavan
ip
T
53°
F = 40N
a) N.cos37°= 80
N.0,8 = 80 ⇒ N = 100 N olur.
Tx
N
100.0,6 = F ⇒ F = 60 N olur.
10. Sistem dengede
olduğuna göre,
a) T1 gerilme kuvveti,
G= 24 N
a) Denge şartından ipteki T gerilme kuvvetinin
büyüklüğü,
Σ Fy = 0
Ty = G
T . sin53° = 24
T . 0,8 = 24
T = 30 N olur.
KUVVET VE HAREKET
37°
T1
T2
N=20N
N + T1 = Gy
N + T1 = G.cos37°
20 + T1 = 100 . 0,8
176
G
b) N.sin37° = F
N = 100 N olur.
7.
37°
37°
Sistem dengede olduğuna göre,
N
N.cos53° + N.cos53° = G
G=80N
F
O
Nx
Nx
16 cm
Ny
37°
T1 = 80 – 20
T1 = 60 N olur.
b) T2 gerilme kuvveti,
T2 = Gx
T2 = G.sin37°
= 100 . 0,6
= 60 N olur.
O
37°
Gy
Gx
G=100N
37°
10. BÖLÜM
AĞIRLIK MERKEZİ
4.
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
y
Şekilde görüldüğü
gibi, cisimlerin ortak kütle merkezinin koordinatları
A(2,3) olur.
mK
4m
m
5•
y
2m
•A
3m
4•
m
8m
16m A
3•
2•
4m
1•
0•
•
•
1
•
2
•
3
•
4
x
Şekilde görüldüğü gibi, cisimlerin
ortak kütle merkezinin koordinatları
A(4,2) olur.
y
m 1 x 1 + m 2 x 2 + ...
m 1 + m 2 + ...
3=
6m.3 + m K .4
m + 2m + 6m + m K
5
6•
5•
2•
m K = 9m olur.
3m
CEVAP D
15m
4•
3•
18m + 4m K = 27m + 3m K
5m
2m
5.
10m
y(m)
45m
A
6
30m
1•
5
•
1
0
•
2
•
4
•
3
•
5
•
6
x
4
L
CEVAP D
3
2
y
3.
1
4m
6•
–2
5•
•
•
–1
0
•
K
•
•
•
•
M
•
•
•
1
2
•
•
3
4
•
•
3•
–2
•
5
–1 •
4•
6
x(m)
N
•
3m
2•
1•
2m
0
6m
x KM =
CEVAP A
2.
x
0•
24m
•
1
•
2
m
3
•
4
m 1 x 1 + m 2 x 2 + ...
m 1 + m 2 + ...
4m.6 + 3m.1 + m.3
=
4m + 3m + 2m + m
30m
=
10m
=3
m y + m 2 y 2 + ...
y KM = 1 1
m 1 + m 2 + ...
4m.6 + 3m.2
=
4m + 3m + 2m + m
30m
=
10m
=3
A (3, 3) olur.
•
5
•
6
x KM =
1.5 + 1.3 + 1.5 – 1.1 12
=
= 3 br
1+ 1+ 1+ 1
4
y KM =
1.5 + 1.1 + 1.3 – 1.1 8
= = 2 br
1+ 1+ 1+ 1
4
x
A (3, 2) olur.
x KM =
6.
mK = m ise
CEVAP C
mK=m
K
mL = 2m,
mM = 3m olur.
Buna göre, I., II. ve
III. yargılar doğrudur.
A
4m
• 6m
M
L
mL=2m
mM=3m
CEVAP C
CEVAP E
KUVVET VE HAREKET
177
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
1.
düfley
yatay
•
K
•O
•
düfley
Fd=12br
x
L
•
4.
•
M
K
A
L
M
yatay
•
3br
2br
2G
1br
2br
4br
2G
4G
A noktasına göre tork alınırsa,
3
Fd.x = 3. + 2.3 + 2.4 + 1.5
2
12x = 4,5 + 6 + 8 + 5
Telin düşey düzlemde şekildeki konumda dengede
kalabilmesi için L noktasından iple asılmalıdır.
CEVAP C
2.
12x = 23,5
Fd=12br
düfley
x = 1,95 br olur.
x
K
L
2br
M
Buna göre, telin düşey düzlemde şekildeki konumda dengede kalabilmesi için bir iple KL arasından
asılmalıdır.
CEVAP B
yatay
2br
5.
düfley
2br
L
4br
O
yatay
K
M
2br
O
O noktasına göre tork alınırsa,
12.x = 2.1 + 4.2 + 2.3 + 2.4 + 2.5
12x = 2 + 8 + 6 + 8 + 10
2G
12x = 34
4G
x = 2,83 br olur.
Şekilde görüldüğü gibi, telin ağırlık merkezi O noktasıdır. Telin düşey düzlemde şekildeki konumda
dengede kalabilmesi için bir iple LM arasından
asılmalıdır.
CEVAP D
Buna göre, telin düşey düzlemde şekildeki konumda dengede kalabilmesi için bir iple KL arasından
asılmalıdır.
CEVAP B
.
.
.
• ip
• ip
• ip
.
•
.
.
3.
fiekil-II
fiekil-III
•
fiekil-I
•
Şekil-I deki tel serbest bırakıldığında, konumu
değişir, sağ tarafa döner.
Şekil-II deki tel serbest bırakıldığında konumunu
değiştirmez.
Şekil-III teki tel serbest bırakıldığında konumunu
değiştirmez.
CEVAP E
178
KUVVET VE HAREKET
2G
6.
ip
fiekil- I
ip
fiekil- II
ip
fiekil- III
Şekil-I deki tel asıldığı konumu koruyamaz, sol
tarafa döner.
Şekil-II deki tel asıldığı konumu korur.
Şekil-III teki tel asıldığı konumu koruyamaz, sol
tarafa döner.
CEVAP B
7.
9.
.
.
• ip
Y
O1
X
K
•
yatay
GX
.
3G
• ip
•
O2
Z
GZ
L
M
•
yatay
2G
3G
T = 3G + 2G + 3G + GÇ
Y
10G = 8G + GÇ
yatay
GÇ = 2G olur.
GY
fiekil-II
•
Gç=2G
GY
fiekil-I
ip
• T=10G
L noktasına göre moment alırsak,
3G.2 + 2G.1 + GÇ.x = 3G.3
O1 noktasına göre tork alırsak;
8G + 2G.x = 9G
GX.1 = GY.3
2x = 1
1
x=
olur.
2
GX = 3GY olur.
O2 noktasına göre tork alırsak;
GZ.3 = GY.1
Çubuğun ağırlık merkezi KL arasındadır.
3GZ = GY olur.
CEVAP B
Buna göre. GX > GY > GZ olur.
CEVAP A
10.
tavan
.
•T
8.
.
• ip
K
O
x
•
T•
2m
2m
•
•
L
T•
yatay
4br
x/2
3m
A .
•M
5br
L
.
M
•
•
• 2T
yatay
Gç=2G
G
T gerilme kuvveti;
O noktasına göre tork alırsak,
x.
•
x
53°
xbr
K
T + 2T = 2G + G
x
= 4.2 + 5.2
2
T = G olur.
2
A noktasına göre tork alırsak;
x
= 18
2
GÇ.x + G.6 = 2T.5
2
x = 36
2G.x + G.6 = 2G.5
x = 6 m olur.
2x = 4
x = 2 olur.
Çubuğun boyu,
Çubuğun ağırlık merkezi L noktasıdır.
, = 6 + 4 + 5 = 15 m olur.
CEVAP C
CEVAP C
KUVVET VE HAREKET
179
11.
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
I
Fd
III
K
r
1.
II
x
O1
O2
L M
r
r
r
2a
a
O
O3
r
G
O›
G2=1br
G3=2br
G1=3br
I. yol:
Her bir kenardan bir bölme çıkarılırsa ağırlık merkezi değişmez. Bir kenardan 2 birim diğer kenardan bir birim çıkarılırsa ağırlık merkezi 1/2 birim
değişir. Her bir bölme a olduğuna göre ağırlık merkezindeki değişme miktarı;
Çubukların ağırlıkları uzunluklarıyla doğru orantılıdır.
G1 = 2r3r = 6rr
G2 = 2rr
G3 = 2r2r = 4rr
G1 = 3 br
Tx =
G2 = 1 br
G3 = 2 br
a
olur.
2
II. yol:
Dengeleyici kuvvet,
Tx =
Fd = 3 + 1 + 2 = 6 br olur.
2a a a
– =
olur.
2
2 2
CEVAP C
O1 noktasına göre tork alırsak,
Fd.x = G2.4r + G3.5r
6x = 1.4r + 2.5r
2.
K
L
a
O
M
N
6x = 14r
x = 2,33r
10G
Sistemin ağırlık merkezi LM arasındadır.
CEVAP D
12.
Fd=8br
II
III
I
O2
O1 r
x
2r
2r
2d
2r
O3
2r
Her bir parçanın ağırlığı G ve parçalar çıkarılmadan önce ağırlık merkezi O noktasındadır. KL parçası çıkarılırsa ağırlık merkezi ok yönünde a/2 kadar değişir. MN parçası üzerine eklenince, ağırlık
merkezi;
K
L
a/2
G3=4br
G1=2br
d
G2=2br
4a–Tx
G
ı
Ağırlık merkezi O noktasına kayar. Bu durumda;
G2 = Ç2.d = 2π.2r.d = 2 br
9G.∆x = G.(4a – ∆x)
G3 = Ç3.2d = 2π.2r.2d = 4 br alınabilir.
10∆x = 4a ⇒ ∆x =
Dengeleyici kuvvet, Fd = 2 + 2 + 4 = 8 br olur.
O2 noktasına göre tork alınırsa,
2
a olur.
5
İlk duruma göre toplam yer değiştirme,
a
2
a
2
= a+
2
5
9
=
a olur.
10
∆x1 = ∆x +
Fd.x = 4.4r – 2.3r
8.x = 16r – 6r
KUVVET VE HAREKET
N
10G
G1 = Ç1.(2d) = 2πr.2d = 2 br
180
Tx
M
9G
2d
Tellerin ağırlıkları,
8x = 10r
5
x=
r olur.
4
O›
O
CEVAP D
CEVAP D
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
3.
I
II
O
Fd
1.
O1
•
4G
O
4G
2G
yatay
düzlem
G
x
K
L
•
•
•
M
•
O2
2G
A
A
6G
7G
G2=1br
fiekil-I
fiekil-II
III
G1=2br
O
4G
Levhaların ağırlıkları,
G1 = rr2 = 3.22 = 12 br
a.h 4.3
G2 =
=
= 6 br
2
2
G1 = 2 br
2G
G
yatay
düzlem
A
7G
fiekil-III
G2 = 1 br olur.
Sistemlerin ağırlık merkezlerinin düşey uzantıları taban yüzeylerinden geçerse sistemler dengede
kalır.
Dengeleyici kuvvet,
Fd = G1 + G2
=2+1
Her bir küpün ağırlığına G diyelim.
= 3 br olur.
Şekilde görüldüğü gibi I ve III sistemleri bırakıldığı
konumda dengede kalır.
O1 noktasına göre tork alırsak,
Fd.x = G1.4
II sistemi sağ tarafa devrilir.
3.x = 1.4
4
x=
br olur.
3
Sistemin ağırlık merkezi KL arasındadır.
CEVAP C
CEVAP B
4.
X
K
O
2.
.
.
• ip
.
• ip
I
II
• ip
III
G
1 katl›
Fd
x
Y
Z
L
2G
2 katl›
M
W
N
3G
3 katl›
4G
4 katl›
Dengeleyici kuvvet;
Fd = G + 2G + 3G + 4G = 10G olur.
2P
2P
2P
2P
2P
fiekil-I
O noktasına göre tork alırsak,
2P
2P
2P
fiekil-II
2P
2P
fiekil-III
Fd.x = 2G.2 + 3G.4 + 4G.6
10G.x = 4G + 12G + 24G
10x = 40
Şekil-I deki I levhası konumu koruyamaz, sol tarafa döner. Şekil-II deki II levhası asıldığı konumu
koruyamaz, sol tarafa döner. Şekil-III teki III levhası asıldığı konumu korur.
Buna göre, levhanın ağırlık merkezi M noktasındadır.
CEVAP C
CEVAP D
x = 4 br olur.
KUVVET VE HAREKET
181
5.
tavan
.
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
ip
1.
X
Y
O
mX
O1
mY
Z
x
r
O2
3r – x
G2
düfley
mZ
G1
G1 +G2
X in kütlesi, Y ve Z nin kütlelerinden büyüktür.
I. yargı kesinlikle doğrudur.
Küreler türdeş olduğundan hacimleri ağırlıkları olarak alınabilir.
II. yargı yanlıştır.
Y ve Z nin kütlelerini karşılaştıramayız.
III. yargı için kesin birşey söylenemez.
CEVAP A
G1 =
3
4
r . (2r) = 8G
3
G2 =
3
4
r . (r ) = G
3
olur.
Bu durumda sistemin ağırlık merkezinin O1 den
uzaklığı;
G1 . x = G2 . (2r + r – x)
8G . x = G . (3r – x)
8x = 3r – x
9x = 3r
r
x=
3
6.
olur.
CEVAP B
I
yatay
düzlem
2.
K
fiekil-I
d
L
4d
II
yatay
düzlem
O1
O2
2r
r
fiekil-II
III
yatay
düzlem
GK =2G
fiekil-III
I sisteminin ağırlık merkezinin izdüşümü sistemin
taban yüzeyinden geçtiğinden bırakıldığı konumda
dengede kalır.
II sisteminin ağırlık merkezinin izdüşümü sistemin
taban yüzeyinden geçtiğinden bırakıldığı konumda
dengede kalır.
III sisteminin ağırlık merkezinin izdüşümü sistemin
taban yüzeyinden geçtiğinden bırakıldığı konumda
dengede kalır.
CEVAP E
182
KUVVET VE HAREKET
GL =G
GK =
3
4
4 3
r. (2r) .d = 8. ( rr .d) = 2G
3
3
GL =
4 3
4 3
rr .4d = 4 ( rr .d) = G olur.
3
3
Sistemin ağırlık merkezi O1
den ∆x kadar uzakta ise,
3r
O1
3r–
2G.∆x = G. (3r – ∆x)
2∆x = 3r – ∆x ⇒ ∆x = r
olur.
O2
G
2G
3G
CEVAP B
3.
Koninin ağırlık merkezinin taban merkezinden
h = 4r
uzaklığı,
ı
h/2
x =
r
O1
2r
O2
K
Silindirin ağırlığı,
G2 = πr2.h2 = πr2.4r = 4πr3 = 4G olur.
G1
G2
silindir
küre
Kürenin ağırlığı,
4
4
G3 = πr3 = G olur.
3
3
K noktasına göre tork alınırsa,
h
G1 .
= G2 . r
2
2
r . r . h . d silindir .
d silindir .
d silindir .
3r
olur.
4
Fd
x
3
h 4
= . r . r . d küre . r
2 3
2
2
h
4
= . d küre . r
2
3
G1 =G
3r
2
16r
4
= . d küre . r
2
3
G1 , G2 ve G3 ağırlıklarını dengeleyen kuvvet,
Fd = G1 + G2 + G3
= G + 4G +
olur.
=
CEVAP A
O1 h K h
L h M h
O2
19
G olur.
4
Gd . x = G1 . 0 + G2 . 3r + G3 . 6r
A
19
11
4
23
G . x = 0 + 4G .
r + G.
r
4
4
3
4
56
19
.x=
r
3
4
224
r olur.
x=
57
Tx
G2 =6G
G1 =8G
14G
G1 = 4A.4h.2d = 4G
O1 den yaklaşık 3,93r kadar uzaktan sistemi asarsak dengede kalır.
CEVAP E
G2 = 2A.4h.3d = 3G
Taban alanı 4A olan silindirin ağırlığı 4G ise, taban
alanı 2A olan silindirin ağırlığı 3G olur. Cismin ağırlık merkezinin yeri;
G1.∆x = G2.(4h – ∆x)
6.
P
d
3d
4G.∆x = 3G.(4h – ∆x)
12
h olur.
7
Ağırlık merkezi KL arasında olur.
CEVAP C
r
4∆x = 12h – 3∆x ⇒ ∆x =
koni
4G
3
Bu kuvvetlerin uygulama noktası ağırlık merkezidir.
O1 olan uzaklığı x ise O1 e göre tork alırsak,
2d
3d
5.
G3 = 4
–G
3
G2 =4G
2
d silindir
1
=
d küre
6
4A
O3
11
—r
4
6d silindir = d küre
4.
O2
O1
silindir
r
2r
K
r L
O1
G1
h1 = 3 r
2r
2r
r
r
O3
O2
G2
h2 = 4 r
G3
h3 =2r
Koni, silindir ve küre aynı maddeden yapıldıklarından ağırlıkları olarak hacimlerini alabiliriz.
Koninin ağırlığı,
G1 =
O2
r
küre
GS=G
x›
r
O1
1 2
1
.πr .h1 = πr2.(3r) = πr3 = G olur.
3
3
GK=G
Cisimlerin kütleleri;
2
3
G S = (rr ) .4r.d = 4rr .d = G
GK =
3
4 3
rr .3d = 4rr .d = G olur.
3
Kürenin ve silindirin ağırlıkları eşittir. Ağırlık merkezi ise tam K ile L nin orta noktasındadır. Silindir
P noktasından asıldığında ipin uzantısı KL nin orta
noktasından geçer.
I. ve III. yargılar doğrudur. II. yargı yanlıştır.
CEVAP D
KUVVET VE HAREKET
183
4.
1.
45° 45°
45° O 45°
K
45°
45° r/2
45° 45°
r
Dairesel levha serbest bırakıldığında 1
yönünde 110° dönerek şekildeki konumu alır.
düfley
•
1
2
20°
20°
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
.
45°
45°
•O
.
2br
2br
yatay
düzlem
CEVAP C
5.
4br
Fd =5br
Şekilde görüldüğü gibi, yeni sistemin ağırlık merkezi
r
kadar uzaklıktadır.
O dan
2
CEVAP C
G2 =1br
6cm
O1
O
r=12cm
x
O2
4cm
6cm
G1 =6br
2.
18cm
Levhaların ağırlıkları,
Fd = 3 br
2
G2 = 1 br
G2 =
O1
12cm
x
6 cm
3 cm
Fd = G1 – G2 = 6 – 1 = 5 br olur.
O1 noktasına göre tork alırsak,
Fd . x = G2 . 4
5.x=1.4
4
x=
cm olur.
5
CEVAP E
+y
–x
O
+x
–y
Levhadan taralı kareler kesilip çıkarılırsa, kütle
merkezi +x yönünde yer değiştirir.
CEVAP A
184
KUVVET VE HAREKET
2
a . h 12 . 12
=
= 72 cm
2
2
Dengeleyici kuvvet,
6.
3.
2
G1 = 6 br
G2 = 1 br
G1 = 4 br
O1 noktasına göre tork alırsak,
Fd . x = G2 . 6
3.x=1.6
x = 2 cm olur.
2
G 1 = r . r 1 = 3 . 12 = 432 cm
CEVAP C
Levhanın ağırlık merkezi
.
O noktasında ya da ip
• ip
doğrultusunda
olduğu
sürece denge konumu
değişmez.
1
6
1 ve 4 parçaları kesilip
çıkarıldığında, levhanın
2
5
O
ağırlık merkezi değişme4
3
diğinden levhanın denge
konumu değişmez.
6 parçası kesilip çıkarılıp, 4 ün tam üzerine yapıştırıldığında levhanın
denge konumu değişmez.
3 levhası kesilip çıkarılıp 2 nin tam üzerine yapıştırıldığında levhanın denge konumu bozulur, levha
sol tarafa döner.
CEVAP C
TEST
1.
1
Şekilde görüldüğü
gibi, 12 m kütleli
noktasal
cisim
1 noktasına konulmuştur.
2m
5.
3m
3m
2
•
Şekilde görüldüğü
gibi, telin ağırlık
merkezi O noktasıdır. Telin düşey
düzlemde şekildeki konumda dengede kalabilmesi
için iple KL arasından asılmalıdır.
•
3
m
•
A
1
12m
4
y
Her levhanın
kütlesine
m
diyelim.
•
4
3
Şekilde görüldüğü gibi, levhaların ortak
kütle merkezi
A(1,1) noktası olur.
6m
•
2.
AĞIRLIK MERKEZİ
ÇÖZÜMLER
•
5
M
–2
•
•
N
•
2
• 4m
•
• 6m
1
0
–1
•
–1 •
R
K
•
–2
•
1
2
L
•
•
3
• 2m
•
x
•
CEVAP A
düfley
4
P
CEVAP C
K L M
yatay
6.
I
II
O
4G
3G
•
K
2G
3G
yatay
düzlem
L
2G
G fiekil-II
fiekil-I
4G
•
III
8G
CEVAP B
3.
.
.
• ip
• ip
•
•
4G M
2G
yatay
düzlem
•
fiekil-III
Şekil-I de:
fiekil-I
K noktasına göre tork alırsak,
fiekil-II
3G.
.
• ip
1
< 2G.1
2
3
< 2 olur.
2
•
I sistemi sağ tarafa devrilir.
Şekil-II de:
fiekil-III
Şekil-I deki tel asıldığı konumu koruyamaz, sol tarafa döner. Şekil-II deki tel asıldığı konumu korur.
Şekil-III teki tel asıldığı konumu korur.
L noktasına göre tork alırsak,
G.
1
3
+ 3G. > 2G.1
2
2
3>2
CEVAP D
4.
Şekilde görüldüğü
gibi, noktasal cisimlerin ortak kütle merkezi 3 bölgesindedir.
3m
m
2m
Şekil-III te:
M noktasına göre tork alırsak,
1
8m
3
5
4m
4m
2
4G.
1
= 2G.1
2
2=2
4
m
CEVAP C
Buna göre II ve III sistemleri bırakıldığı konumda
dengede kalır.
CEVAP D
KUVVET VE HAREKET
185
7.
Fd
10.
O1
•
x
K
L
•
•
M
•
•O
2
O
•
2
G1=4br
G2=3br
G1 = 4 br
G2 = 3 br
Şekilde görüldüğü gibi, levhadan taralı parça ile
birlikte 2 numaralı parça kesilip çıkartıldığında kütle merkezi değişmez.
Fd = G1 + G2
Fd = 4 + 3 = 7 br olur.
CEVAP B
O1 noktasına göre tork alırsak,
Fd.x = G2.4
7.x = 3.4
12
x=
= 1, 71br
7
Sistemin ağırlık merkezi KL arasındadır.
CEVAP B
8.
Levhanın ağırlık
merkezi O noktasıdır. Levha L noktasından bir iple asılırsa, ipin uzantısı P
noktasından geçer.
K
L
M
2G
N
O
2G
4G
2G
11. Levhadan taralı karelerle
birlikte N harfiyle belirtilen kareler kesilerek çıkarılırsa kütle merkezi
yine O noktası olur.
O
P
CEVAP B
K
L
M
N
P
CEVAP D
12.
tavan
ip
9.
Şekilde görüldüğü gibi,
K
ip
GY > GX tir.
M
T
I. yargı doğrudur.
K
N
T = GX + GY dir.
II. yargı doğrudur.
Sistemin ağırlık merkezi O noktası olduğundan, sistem L noktasından asılırsa, ipin
uzantısı yine O noktasından geçer.
III. yargı doğrudur.
L
.
düfley
r
GX
O
Levhadan taralı karelerle birlikte:
.
r
X
GY
Y
GX+GY
CEVAP E
186
KUVVET VE HAREKET
L
K ve L kareleri kesilip çıkarıldığında levhanın dengesi bozulmaz.
M ve N kareleri kesilip çıkarıldığında levhanın dengesi bozulmaz.
K ve N kareleri kesilip çıkarıldığında levhanın dengesi bozulmaz.
CEVAP E
TEST
1.
2
AĞIRLIK MERKEZİ
ÇÖZÜMLER
Levhadan taralı karelerle
birlikte K ve P harfleriyle
belirtilen kareler kesilerek çıkarılırsa kütle merkezi yine O noktası olur.
4.
K
Her bir bölmenin kenarı 3 br seçilirse,
L
O
22P
P
M
O
N
K
x
L M
2br
K
L
3br
3br
R
3br 1,5br
O
M
8P
6P
CEVAP B
2.
ip
.
. I
•
K
L
P
M
•
• II
•
•
•
•
•
N
•
•
II
5.
P
•
M
•
N
•
.
ip
d2
K
L
6P
fiekil-II
2G .
Cisim Şekil-I ve Şekil-II deki gibi dengede kaldı-
2G
2G
2G
2G
1
3
5
7
+ 2G . + 2G . + 2G . = T2 . 4
2
2
2
2
16G = T2 . 4
ğına göre, cismin kütle merkezi d1 ile d2 doğrula-
T2 = 4G olur.
rının kesiştiği L noktasıdır. Şekil-I de ipin uzantısı
T1 + 4G = 8G ⇒
L, M, N; Şekil-II de ipin uzantısı L, P noktalarından geçmektedir. Ortak nokta olan L noktası
8P
P
K
O noktasına göre
tork alalım.
d1
8P
O noktasına göre moment alınırsa,
22P.x = 6P.(12,5) + 8P.(7,5)
22x = 75 + 60
x ≅ 6,13
Bu durumda ağırlık merkezi LM arasındadır.
CEVAP D
L ve N nin üzerine
birer levha daha
T1
T2
koyalım. Her bir
1br
O
parça ağırlığı
G
L
M
N
olsun.
T1 + T2 = 8G
•I
fiekil-I
8P
T1 = 4G olur.
6.
CEVAP C
Fd=4br
ağırlık merkezidir.
CEVAP B
x
O1
3.
K
L
düfley
duvar
Tip
N
M
N
G
.
yatay düzlem
Çubuğun şekildeki gibi kalabilmesi için kütle merkezi
M - N arasında olmalıdır. I. yargı yanlış, II. yargı
doğrudur.
Tip > G olabilir. III. yargı doğru olabilir.
CEVAP D
.r
O2
K. L M N
r r r r r .
G2=1br
G1=3br
Levhaların ağırlıkları,
G = r(4r)2 = 16rr2
G = 4 br,
G2 = r(2r)2 = 4rr2
G2 = 1 br,
G1 = 3 br olur.
O1 noktasına göre tork alınırsa,
Fd.x = G2.6r
4.x = 1.6r
3
x = r olur.
2
Buna göre, oluşan yeni sistemin ağırlık merkezi KL
arasındadır.
CEVAP B
KUVVET VE HAREKET
187
II. işlemi: 2 kesiliyor, 3 üzerine yapıştırılıyor.
Fd=3P
7.
4P.3 + 4P.1 > 3P.1 + 3P.3
x
r
r
r
3r
O
›
3r
16P > 12P
K
Gçember=P
Gtel=2P
III. işlemi: 1 kesilip, 2 üzerine yapıştırılıyor.
Tellerin ağırlıkları uzunlukları ve çevreleri ile doğru
orantılıdır.
2rr
G çember =
= 3r = P
2
4P.3 + 2P.1 = 3P.3 + 5P.1
14P = 14P
I ve III. işlemleri tek başına yapılmalıdır.
CEVAP E
G tel = 6r = 2P olur.
10. O noktasına göre
Dengeleyici kuvvet,
ip
tork alalım.
Fd = 3P olur.
mX.2 + mY.1 = mT.2
K noktasına göre tork alınırsa,
Y
2mX + mY = 2mT
3P.x = P.7r + 2P.3r
13r
olur.
x=
3
X
olur.
Z
T
1br
mY
Buna göre,
CEVAP E
O
mT > mX olur.
mX
mZ
mX ≠ mT dir.
mT
CEVAP C
8.
K
L
M
N
a
P
R
S
T
U
Δx
G
8G
Her bir parçanın ağırlığı G olsun. Çubuğun ağırlığı
8G olur. K-L parçası kesilip L-M üzerine yapıştırılırsa, ağırlık merkezi Tx =
Tx =
2
a
kadar yer değiştirir.
,o
2
a
a
=
olur.
8a 8
I. işlemi: 4 kesiliyor, 3 üzerine yapıştırılıyor.
soldan sağa = sağdan sola
çevirenler
çevirenler
3P.3 + 4P.1 = 3P.3 + 4P.1
13P = 13P
188
KUVVET VE HAREKET
III
O
X
•
II
I
L
I. yargı kesinlikle
doğrudur. X-Y nin
kütle merkezi KL
arasında olabilir.
Y
IV
•
X ve Y cisimlerinin kütleleri eşit olabilir ya da olmayabilir.
III. yargı için kesin birşey söylenemez.
Ağırlık merkezi P-R arası olur. II. yargı yanlıştır.
P-R nin tam ortasına destek konulunca çubuk dengede kalmaz. III. yargı yanlıştır.
CEVAP A
Her bir bölmenin ağırlığı P
olsun. K ve L parçaları kesilip çıkartılıyor. Her bir işlem
için O noktasına göre tork
alalım.
K•
II. yargı için kesin birşey söylenemez.
a
Çubuğun ağırlık merkezi
yer değiştirir.
8
I. yargı doğrudur.
9.
11. X ve Y cisimlerinin
şekildeki gibi dengede kalabilmesi
için; X in kütle merkezi I. bölgede olmalıdır.
L
3
K
12. L noktasına göre
tork alalım.
mX.g.1 = mY.g.1
mX = mY olur.
Y
I. yargı doğrudur.
O
4
CEVAP A
2
Çubukların kütle
merkezi KP nin
orta noktasıdır.
•
1br
X
K
•
.
•
P
GY
•
M
•
N
L
GX
II. yargı yanlıştır.
1
2br
Çubuklar N noktasından asılınca ip uzantısı LM
arasında geçer.
III. yargı doğrudur.
CEVAP E
TEST
1.
3
.
•
ÇÖZÜMLER
.
O1
4.
.
•
O2
AĞIRLIK MERKEZİ
9cm
18cm
Fd =4br
O3
•
x
O1
12cm
K
L
M
.
ip
X
X
4 . x = 21
21
= 5,25 cm olur.
x=
4
Y
mX
mY
fiekil - I
Sistemin ağırlık merkezi KL arasındadır.
CEVAP C
mX
ip
X
Z
mX
T
mZ
fiekil - II
5.
K çıkarılıp T nin üzerine
mT
eklendiğinde ağırlık mer-
fiekil - III
kezi aşağı kayar. Fakat
•
ip
L
her iki tarafın ipe göre
Şekil-I de,
torku eşit olduğundan den-
mX = mY dir.
ge bozulmaz.
Şekil-II de,
M
K
N
T
P
R çıkarılıp M nin üzerine
S
R
eklendiğinde ağırlık mer-
mX = mZ dir.
kezi yukarı kayar. Fakat
Şekil-III te,
her iki tarafın ipe göre momentleri eşit olduğundan
mX ile mT arasında kesin birşey söylenemez.
denge bozulmaz.
Bu durumda, mX = mY = mZ olur.
L ve N nin üzerlerine özdeş parçalardan birer tane
I. yargı kesinlikle doğrudur. II. ve III. yargılar için
kesin birşey söylenemez.
CEVAP A
3.
1br
Fd . x = 1 . 6 + 1 . 15
.
ip
6cm
O1 noktasına göre tork alırsak,
CEVAP E
.
O2
L M
3cm
1br
2br
Çubuklar oklarla gösterilen yönlerde dönerler.
Hiçbiri dengede değildir.
2.
K
6cm
Kütle merkezinin yerinin
değişmemesi için simetriden K parçası çıkarılırsa 5
nolu parça, L parçası çıkarılırsa 1 nolu parça çıkarılmalıdır.
•
2
1
3
CEVAP C
Levha şekildeki konumda
dengede kaldığında düşey
eksene olan uzaklıkları,
5
I. yargı kesinlikle doğrudur.
6
CEVAP D
ip
K
dK
dK = dM olduğundan,
GK = GM dir. GK ile GL ve GL
ile GM arasında kesin birşey
söylenemez.
4
L
olduğundan levha saat ibresi yönünde döner.
6.
ip
K
eklendiğinde sağ tarafın ipe göre torku daha büyük
O
L
GK
dM M
GL
GM
II. ve III. yargılar için kesin
birşey söylenemez.
CEVAP A
KUVVET VE HAREKET
189
7.
10.
K
K
.
ip
P
L
mK=2m
O
mL=m
düfley
K ve L nin ağırlık merkezi P noktasıdır. Cisim O
noktasından asıldığında uzantısı bu noktadan ge-
Levha bir iple tavana asıldığında şekildeki gibi
çer.
dengede kalır.
CEVAP B
8.
K
M
OX
N
O
m
OY
3m
4m
X levhasının ağırlık merkezi OX, Y levhasının ağırlık merkezi OY dir. Levhalar yapıştırıldığında sistemin ağırlık merkezi O noktasında olur. Cisim K
den asıldığında uzantısı buradan geçecek şekilde
dengede kalır.
CEVAP B
9.
K
O
4G
L 2G
2G
Levha düzleme dik eksen etrafında serbestçe
dönebildiğine göre, K çıkarılıp L nin üzerine yapıştırılırsa, O noktasına göre toplam momenti sıfır
olacağından levha şekildeki gibi dengede kalır.
CEVAP D
190
KUVVET VE HAREKET
CEVAP E
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
1.
Bölüm
Yazılı Soruları
(Ağırlık Merkezi)
3.
y(m)
•
6
•
3
–2
•
M
•
•
–1
• ip
P
2P
P
2P
•
1
2m
2
•
•
3
4
•
•
•
5
x(m)
6
•N
•
fiekil-I
m
K, L, M, N levhalarının ortak kütle merkezinin koordinatları A(3, 2) olur.
düfley
P
2P
P
3P
düfley
2P
–1 •
–2
.
• ip
m
•A
•
1
•
• ip
•L
•
2
0
tavan
.
2m
•
4
m
•
tavan
.
m
K
•
5
tavan
ÇÖZÜMLER
2P
2P
fiekil-II
2P
düfley
fiekil-III
Levhalar serbest bırakıldıklarında, I ve III levhalarının konumları değişmez, II levhası ok yönünde
döner.
4.
ip
ip
T1
T2
G2=1br
2r
r
r
O2
.
.
• ip
• ip
.
2.
.
•
•
O1
r
r
K
O3
yatay
G3=1br
G1=4br
Levhaların alanları,
G1 = r(2r)2 = 4rr2 = 4 br
fiekil-I
.
fiekil-II
• ip
.
•
G2 = rr2 = 1 br
O3 noktasına göre tork alırsak,
T1.3r = G1.3r – G2.4r
fiekil-III
Şekil-I deki tel konumunu koruyamaz, sağ tarafa
döner.
Şekil-II deki tel konumunu koruyamaz.
Şekil-III teki tel konumunu koruyamaz, sağ tarafa
döner.
T1.3 = 4.3 – 1.4
8
T1 =
br olur.
3
O1 noktasına göre tork alırsak,
T2.3r = G3.3r + G2.r
T2.3 = 1.3 + 1.1
4
br
3
T1 ve T2 taraf tarafa oranlanırsa,
8
T1
= 3 = 2 olur.
4
T2
3
T2 =
KUVVET VE HAREKET
191
5.
8.
y(cm)
2m
12
9
6m
•
M
3m
O
9m
4m
12
Şekilde görüldüğü gibi; 2m, 3m, 4m kütleli noktasal cisimlerin ortak kütle merkezi M noktasıdır.
9
6
4
3
›
4
O
1cm
3
7cm
6
9
x(cm)
Ağırlık merkezi başlangıçta O noktasında iken, ikinı
ci durumda O noktasında olur. Ağırlık merkezi düşeyde 1 cm aşağı, yatayda 3 + 4 = 7 cm sola kayar.
Toplam yer değiştirme,
O
x2 = 7 2 + 12
x
x2 = 50
O
1cm
›
7cm
x = 5v2 cm olur.
6.
L
Fd=4P
K
r
O1
9.
x
2r
O2
2r
6r
3r
3r
P
P
P
3r
3r
O r
2P
r
r
r
r
r
3r
K ve L tellerinin ağırlıkları,
GK = ÇK = 2πr = 2.3.r = 6r
3P
GL = ÇL = 2π.2r = 4πr = 12r = 2P olur.
O
O2 noktasına göre tork alınırsa,
r r
4P . x = P . 5r + P . 9r
P
Fd=3P
P
x
r r
r r
3P
4x = 14r
P
Levhaların ağırlıkları alanları ile doğru orantılıdır.
x = 3,5r olur.
O1 noktasından uzaklık, 9r – 3,5r = 5,5r olur.
Gd = πr2 = 3.(3r)2 = 27r2
a.h 6r.3r
Gü =
= 9r2
=
2
2
Bu durumda Gd = 3P ve Gü = P alınabilir.
3P.x + P.r = P.5r
3x = 4r ⇒ x =
4r
olur.
3
10. Parçaların ağırlıkları şekilde gösterildiği gibidir.
7.
50cm
2G
Fd=5P
50cm
K
P
O
50cm
x
50cm
50cm
2P
K noktasına göre tork alınırsa,
5P.x = 2P.50 + 2P.125
5x = 350
x = 70 cm = 0,7 m olur.
KUVVET VE HAREKET
G
o
O 60
60o
x
60o
r–x
G
120°
2G
25cm
2P
Tellerin ağırlığı uzunlukları ile doğru orantılıdır.
192
120°
4G
2G
R=6G
4G
2G
Bileşke noktasına göre tork alınırsa,
4G.x = 2G.(r – x)
2x = r – x
3x = r
r
x=
olur.
3
11. BÖLÜM
BASİT MAKİNELER
5.
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
Verim %100 olduğundan sürtünme yoktur. İlk
durumda 30 N ile ikinci durumda 50 N ile denge
sağlanıyor. İlk durumda verim % 100 ise ikinci
durumda verim,
F
30
verim = 1 =
= 0, 6
F2 50
% verim = 100.0,6 = %60 olur.
CEVAP D
olur. Kuvvet kazancı yoldan kayıp olduğu anlamına gelir. Bu durumda cismi 30 m yükseltmek için
ipin 90 m çekilmesi gerekir.
CEVAP E
6.
|F|=20N
Desteğe göre tork alırsak,
•
2.
Basit makine sisteminde kuvvet kazancı 3 ise, sistemi dengede tutan kuvvet,
yük
kuvvet kazancı =
kuvvet
60
3=
& F = 20 N
F
K
P.4 = F. (4 + 8)
4P = 12F &
3.
Kuvvet kazanc› =
P 12
=
= 3 olur.
F
4
GK
Desteğe göre tork alınırsa,
GK.4 + 30.2 = 20.5
4.GK = 100 – 60
4.GK = 40
GK = 10 N olur.
yük
P 80
= =
= 2 olur.
kuvvet F 40
yük
F
•K
O
•
F
O•
L
7.
yük
F
K
L
G
G
G
fiekil-II
yük
•
CEVAP B
O
•
fiekil-I
O
yük
G
yatay
düzlem
CEVAP B
CEVAP D
4.
30N
L
O noktasına göre tork alırsak,
F
3.F = 1.G + 5.G
•K
3F = 6G
G
F = 2G olur.
fiekil-III
Basit makinelerde yükün kuvvete oranı, basit
makinenin kuvvet kazancını verir.
yük
G
kuvvet kazancı = kuvvet =
F
Bu oran 1 den büyükse kuvvetten kazanç, 1 den
küçükse kuvvetten kayıp vardır. Eğer bu oran 1 e
eşitse kuvvetten kazanç yoktur.
Şekil-I de |KO| ile |LO| uzunlukları bilinmediğinden
kesin birşey söylenemez.
G
Şekil-II de |LO| > |KO| olduğundan
< 1 dir. Yani
F
kuvvetten kayıp vardır.
G
Şekil-III te |KO| > |LO| olduğundan
> 1 dir. Yani
F
kuvvetten kazanç vardır.
CEVAP C
CEVAP C
8.
T
X
O
G
GY=G
GX=2G
Çubuk dengede olduğuna göre, desteğin olduğu O
noktasına göre tork alacak olursak,
3.2G + 4.G + 6.G = 8.T
16.G = 8.T
T = 2G olur.
CEVAP C
KUVVET VE HAREKET
193
4.
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
1.
X cisminin bağlı olduğu ipteki gerilmeye F dersek, Y
cisminin bağlı olduğu ipteki
gerilme kuvveti 10F olur.
20N
Gç
yatay düzlem
Desteğe göre moment alınırsa,
Denge şartından,
F F F
GX
F
=
G Y 10F
Gç.4 + 20.3 = 20.7
F
Gç.4 + 60 = 140
X
4Gç = 80
3F F
F
GX
1
=
G Y 10
GL=20N
Gç = 20 N olur.
5F
olur.
CEVAP D
5F
10F
5.
Y
4
F
F
CEVAP A
F
F F
2F
2.
F F
2F 2F
F F
F F
F
2F 2F
2F
yatay
4F
GK GK
4
4
GK
4
GK
4
4F
4F
GL
İpler üzerindeki gerilmeler şekilde gösterildiği gibi-
8F
dir. Çubuğun asıldığı noktaya göre tork alınırsa,
yatay
Gs
GK
G
G
G
.5 + K .4 + K .3 + K .2 = G L .4
4
4
4
4
Silindirin ağırlığı bağlı olduğu iplerdeki gerilme kuv-
GK
(5 + 4 + 3 + 2) = G L .4
4
vetlerinin toplamına eşittir.
Gs = 4F + 8F = 12F = 12.2 = 24 N olur.
G K .14
= G L .4
4
CEVAP E
GK 8
=
olur.
GL 7
6.
X makarası dengede olduğundan,
ı
ı
ı
3T = 30
CEVAP D
3.
10N
10N
Y makarası dengede olduğundan,
ıı
20 20 20 20 20
GK = 40N olur.
L cismi dengede olduğundan,
ı
T = 10 N olur.
K cismi dengede olduğundan,
GK + 40 = 80
ı
T + T + T = 4 + 26
20
40
40
40
80
K
40
GL = 40 + 40
GK
= 80N olur.
ı
T
Z
ı
T =T +T +4
F
››
T 4N
= 10 + 10 + 4
= 24 N olur.
Y
Üstteki K cismi dengede olduğundan,
ı
F = T + GK
K
GK
›
›
›
T 4N T T
= 10 + 26
X
= 36 N olur.
4N
Z makarası dengede olduğundan,
F
GK=26N
ıı
T=F+F+4+T
L
= 36 + 36 + 4 + 24
CEVAP E
194
KUVVET VE HAREKET
= 100 N olur.
CEVAP E
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
3.
1.
5m
T
T
K
s
T
T
h
T
h
T
X
37°
5m
2T
GK.sinθ
L
P
37°
•
θ
yatay düzlem
Y cismi 5 m aşağı çekildiğinde X cismi eğik düzlem
üzerinde 5 m yol alır.
Sistem dengede olduğuna göre,
Buna göre, X cisminin düşey konumu h = 3m değişir.
K cisminin ağırlığı,
GK.sinθ = T
h
GK . = T
s
GK .
Y
•
CEVAP A
1
=T
2
G K = 2T olur.
L cisminin ağırlığı,
GL = 2T olur.
P cisminin ağırlığı,
GP = 3T olur.
Buna göre, cisimlerin ağırlıkları arasında,
GP > GK = GL ilişkisi vardır.
CEVAP C
4.
2.
GK
T
α
T
GK
T
O
L
α
K
M
T
h
T.cosα
s
K
1m
L
α
θ
yatay
düzlem
yatay
düzlem
O noktasına göre tork alınırsa,
T gerilme kuvveti,
T = GM.sinα = GM.
O
•
•
GL
GL.sinθ
GM.sinα
3m
GK.4 = T.cosα.2
1
olur.
3
Üçgenin ağırlık merkezi olan O noktasına göre tork
GK = T.cosα.
1
2
h h 1
GK = (GL. ). .
s s 2
alınırsa,
GK.1 = T.2
GK h2 1
=
.
GL s2 2
3
1
GK = GM. .2 ⇒ GM = GK olur.
2
3
1
GL = GK + GM.
3
= GK +
=
1 2 1
=b l .
2
2
3
1
G .
2 K 3
=
3
G olur.
2 K
Bu durumda, GM = GL > GK olur.
1
olur.
8
CEVAP A
CEVAP D
KUVVET VE HAREKET
195
5.
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
F
T
K
F
F
1.
T
X
30.sin30°
K
30.sin30°
30o
F.R = P.r
10N
L
10N
Sistem dengede olduğundan,
40.2r = P.r ⇒ P = 80 N olur.
•
Toplam kütle,
yatay düzlem
P = mg
X makarası dengede olduğundan T gerilme kuvveti,
80 = m.10 ⇒ m = 8 kg olur.
2T = GK.sin30° + Gmakara.sin30°
CEVAP A
1
1
+ 10.
2
2
2T = 15 + 5
2T = 30.
T = 10 N olur.
F kuvvetinin büyüklüğü,
F = T + 30.sin30°
1
2
= 25 N olur.
= 10 + 30.
Bu durumda L cisminin ağırlığı,
2.
2F = GL + 10
F
2.25 = GL + 10 ⇒ GL = 40N olur.
R=60cm
r=10cm
CEVAP E
P
6.
R kolu, F kuvvetiyle 10 kez döndürüldüğünde P
yükünün düşey uzaklığı,
T
F
F
F
h = n.2rr
= 10.2.3.10
GM
K
= 600 cm
GM
30°
= 6 m değişir.
GK
CEVAP D
yatay düzlem
F kuvvetinin büyüklüğü,
3F = GK.sin30°+GM.sin30°
1
1
+ 20 .
2
2
3F = 20+10
3F = 40 .
F = 10 N olur.
T gerilme kuvveti,
T = 2F + GM.sin30°
= 2.10 + 20.
1
2
= 20 + 10
= 30 N olur.
CEVAP E
196
KUVVET VE HAREKET
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
1.
1.
b
F kuvveti ile P direnme
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
L
1
kuvveti arasındaki ilişkiden,
F
a
b
.F=P
a
3r
2
2 . 3 . 10 . F = P
P = 60F olur.
M
r
2r
2π . b . F = P . a
2.3.
K
P
tahta
blok
P yükünü 4πr yukarı çıkarmak için M silindirinin
dönme sayısı,
P
fM . 2π . r = 4π . r
fM = 2 devir olur.
CEVAP E
L ve M kasnakları eş merkezli olduğundan,
fM= fL = 2 devir olur.
K silindirinin dönme sayısı,
fL . rL = fK . rK
2 . 3r = fK . 2r
fK = 3 devir olur.
K silindirine 1 yönünde 3 devir yaptırılmalıdır.
2.
CEVAP C
F kuvvetinin büyüklüğü,
b
2π . b . F = P . a
F=
F
P.a
2r . b
2.
2r
a
olur. F kuvvetinin büyüklüğü N dönme sayısına
bağlı değildir.
L
K
r
M
3r
h
N
tahta
blok
P
4r
1
CEVAP B
2
N silindiri 1 yönünde döner.
M silindirinin dönme sayısı,
fK . rK = fM . rM
2 . 2r = fM . r
fM = 4 olur.
M ve L kasnakları eş merkezli olduğundan,
fM = fL = 4 olur.
N kasnağının dönme sayısı,
fL . rL = fN . rN
4 . 3r = fN . 4r
fN = 3 devir olur.
N silindiri 1 yönünde 3 devir yapar.
CEVAP C
KUVVET VE HAREKET
197
3.
6.
L
K
N
1
M
2r
ile aynı yönde 150° dönmüş olması gerekir.
Bu sırada M dişlisi fM =
2r
r
M dişlisinin Şekil II deki görünümü alabilmesi için K
3r
2
150
5
devir yapmıştır.
=
360 12
K dişlisinin dönme sayısı ise,
fK.nK = fM.nM
L dişlisinin dönme sayısı,
fK.20 =
fK . rK = fL . rL
6 . 2r = fL . 3r
Bu durumda K dişlisi 5 .360 = 225° dönmüştür.
8
fL = 4 devir olur.
CEVAP D
L ve M eş merkezli olduğundan,
fL= fM = 4 devir olur.
N kasnağının dönme sayısı,
fM . rM = fN . rN
4 . r = fN . 2r
fN = 2 devir olur.
N silindiri 2 yönünde 2 devir yapar.
CEVAP D
4.
–
K
K
+
2r
L
r
fiekil-I
fiekil-II
K dişlisi Şekil-II deki konuma gelmesi için (+)
1 5 9
yönde
, , , …… devir yapması gerekir. Bu4 4 4
1 5 9
nun için de L dişlisi (–) yönde, , , , …… devir
2 2 2
yapması gerekir. Ya da K dişlisinin (–) yönde
3 7 11
, , , …… devir yapması gerekir. Bunun için
4 4 4
3 7 11
de L dişlisi (+) yönde , , , …… devir yapması
2 2 2
gerekir.
I. yargı yanlıştır.
II. ve III. yargılar doğrudur.
CEVAP E
5.
L, K ye göre zıt
yönde döner.
fK . rK = fL . rL
3
. r = fL . 2r
2
3
fL = devir.
4
Dişlillerin görüntüsü şekildeki gibi olur.
CEVAP A
198
KUVVET VE HAREKET
5
5
.30 ⇒ fK =
olur.
12
8
MODEL SORU - 7 DEKİ SORULARIN ÇÖZÜMLERİ
1.
MODEL SORU - 8 DEKİ SORULARIN ÇÖZÜMLERİ
1.
K
.
(–)
r
fX.rX = fY.rY
2r
M
L
3r
Y dişlisinin dönme sayısı,
x1
3.4r = fY.3r
x2
M
fY = 4 devir olur.
(+)
•
x1 > x2 olduğundan M ma-
•
karası 1 yönünde döner.
F
1
O3
2
x1 – x2
2
M.D.S =
M.Ç
X
İp F kuvvetiyle aşağı yönde çekildiğinde, M makarası (+) yönde, L makarası (–) yönde döner.
3.2r2r – 4.2rr
2
=
2r2r
K makarası üzerindeki ip hareket etmediğinden K
makarası dönmez.
=
2rr
4rr
=
1
devir olur.
2
Bu durumda yalnız M makarası (+) yönde döner.
2r
P
P yükünün x 1 + x 2
yükselmesi =
2
CEVAP A
=
12rr + 8rr
2
= 10rr olur.
2.
.
I. ve III. yargılar doğrudur.
.
II. yargı yanlıştır.
X
Y
r
CEVAP D
r
ip
F
K
Z
,
2.
x1 > x2 olduğundan M makarası 2 yönünde döner.
2r
x1 – x2
2
M.D.S =
M.Ç
L
İp F kuvveti ile , kadar çekildiğinde X makarasındaki dönme sayısı,
nX =
,
2rr
olur.
2
(2r.2r)
=
4rr
=
4rr
x1
M
1
r
•
2
P
= 1 devir
Z makarası ,/2 kadar döner, ,/2 kadar yükselir.
Dönme sayısı;
,
nZ =
2r3r – 2rr
2
=
2rr
x2
,
8rr
P yükünün x 1 + x 2
yükselmesi =
2
=
6rr + 2rr
2
= 4rr olur.
olur. Y makarası sabit makara ve ipin uçu bağlı olduğundan dönmez.
III. yargı doğrudur.
nY = 0 olur. Bu durumda; nX > nZ > nY olur.
I. ve II. yargılar yanlıştır.
CEVAP B
CEVAP C
KUVVET VE HAREKET
199
3.
Z
X
r
MODEL SORU - 9 DAKİ SORULARIN ÇÖZÜMLERİ
Y
T
1.
r
3r/2
A
2r
r
ip
B
r
+y I.uç
L
–y
II.uç
C
(–)
P
2r
(+)
Silindir bir kez döndürüldüğünde P cisminin yer değiştirmesi,
P
Ok yönünde X silindiri 4 tur atarsa Z dişlisi de 4 tur
Y dişlisi 2 tur atar. Bu durumda I. uç merkeze bağlandığından hareket etmez. Y ve T (–) yönde döneceğinden ipin II. ucu –y yönünde 2.(2rr) = 4rr kadar hareket eder. İpin I. ucu hareket etmediğinden
L makarası (+) yönde 2rr kadar döner. –y yönünde
2rr kadar aşağı düşer.
İp A noktasına bağlı ise xA = 4rr
İp B noktasına bağlı ise xB = 2rr
İp C noktasına bağlı ise xC = 2rr – 2rr = 0
olur.
I. ve II. yargılar doğrudur.
III. yargı yanlıştır.
I. yargı doğrudur.
CEVAP C
2rr
1
L nin dönme miktarı
=
olur.
2r. (2r) 2
II. yargı doğrudur.
L nin yer değiştirmesi P nin yer değiştirmesine eşit
olduğundan P de 2rr kadar –y yönünde yer değiştirir.
2.
II.ip
I.ip
K
rK
III. yargı yanlıştır.
rL
r
L
2r
CEVAP C
4.
Y
L dişlisinin dönme sayısı,
fK.rK = fL.rL
x1
x2
3.2r = fL.3r
1
fL = 2 devir olur.
fL = fM = 2 devir olur.
P yükünün x 1 + x 2
yükselmesi =
2
=
2.2rr + 2.2r.3r
2
=
4rr + 12rr
2
=
16rr
2
kadar hareket eder.
N
2
kadar hareket eder.
Bu durumda dönme miktarı 2 ve 3 olduğuna göre
yarıçapları;
x1 = 2rrK.2 = 6rr
x2= 2rrL.3 = 8rr
Eşitlikleri taraf tarafa oranlarsak;
rK 9
=
olur.
rL 8
kadar 1 yönünde yer değiştirir.
CEVAP A
KUVVET VE HAREKET
L makarasından geçen II. ip ise,
x2 = 2r(2r) + 2r(2r) = 8rr
P
= 8rr
200
2r yarıçaplı makara ok yönünde bir kez çevrildiğinde I. ip,
x1 = 2r(2r) + 2rr = 6rr
O3
r
L ve M eş merkezli olduğundan,
X
CEVAP E
3.
K
r2
r1
L
Tx
P
h
K silindirine ok yönünde 2 tur attırılırsa, silindirin
yer değiştirmeleri ∆x;
∆x = 2.(2rr2)
= 2.(2.3.3)
= 36 cm olur.
K ve L silindirlerinin yer değiştirmeleri eşittir.
I. ve II. yargılar doğrudur.
Makaralar döndürüldüğünde ip r1 yarıçaplı makaraya sarılır. Bu durumda P cisminin konumundaki
değişme h;
h = ∆x – (2rr).N
= 36 – 2.3.2.2
=12 cm olur.
III. yargı doğrudur.
CEVAP E
4.
r2
N
r1
Tx
h
P
Makaralar ok yönünde N defa döndürüldüğünde P
cisminin konumunda meydana gelen değişiklik;
h = N.(2rr2 – 2rr1) olur.
Bu durumda N ve r2 artarsa h artar, r1 artarsa azalır.
CEVAP D
KUVVET VE HAREKET
201
4.
L
r
2r
O
3r
r
P
> 1 olduğunda kuvvetten kazanç vardır.
F
P 5
kuvvetten kazanç
Şekil-I de: 2.P = 5.F1 &
=
F1 2
vardır.
P
Şekil-II de: 3.P = 3.F2 &
= 1 kuvvetten ya da
F2
yoldan kazanç yoktur.
P 2
Şekil-III te: 3.P = 2F3 &
= yoldan kazanç vardır.
F3 3
CEVAP A
Dişlilerin dönme sayısı yarıçapları ile ters orantılıdır. K dişlisi 6n döndüğünde L dişlisi 2n döner. L ile
M eş merkezli olduğundan M, 2n dönerse N, n kez
döner. O ve P ise 2n kez döner. Bu durumda en
yavaş N dişlisi döner.
CEVAP D
yatay
•
2.
r
P
N
fiekil - III
fiekil - II
fiekil - I
yatay
düzlem
M
yatay P
düzlem
P
P
K
yatay
düzlem
F3
F2
F1
1.
BASİT MAKİNELER
ÇÖZÜMLER
1
TEST
5.
F
F
F
F
F
0,8F
F
2F
K
X
53°
yatay
2F
Y
r
2r
1,8F
r
T
Z
3r
K
N
L
3r
—
2
M
GK
X dişlisi ok yönünde 2 defa döndüğünde 2r yarı-
Sistem dengede olduğuna göre,
GK = 2F + 2F + 1,8F
290 = 5,8F ⇒ F = 50 N olur.
çaplı dişli zıt yönde 1 defa dönecektir. Bu durumda
r yarıçaplı Z dişlisi de X ile aynı yönde 2 tur atar. Y
CEVAP E
ve Z eş merkezli olduğundan Y de Z ile aynı yönde
K
3.
2 tur döner. Bu durumda T kasnağı Y ile zıt yönde
fY.rY = fK.rK
4r
2.3r = fK .
L
M
3r
⇒ fK = 4 tur döner.
2
Bu durumda T kasnağı tam tur attığından Y kas-
r
nağı ile N noktasından temas eder.
3r
1
2r
2
N
M kasnağının dönme sayısı,
fK . rK = fM . rM
2 . 4r = fM . r
fM = 8 olur.
L ve M kasnakları eş merkezli olduğundan,
fM = fL = 8 olur.
N kasnağının dönme sayısı,
fL . rL = fN . rN
8. 3r = fN . 2r
fN = 12 olur.
N kasnağı 2 yönünde 12 devir yapar.
CEVAP B
202
KUVVET VE HAREKET
CEVAP D
6.
K kasnağı,
10 saniyede
1 tam dönme yaparsa
15 saniyede
x dönme yapar.
__________________________________
x.10 = 15.1
x = 1,5 tur döner.
Bu durumda L kasnağı aynı yönde,
fK.rK = fL.rL
1,5.2r = fL.3r ⇒ fL = 1 tur döner.
L ve M eş merkezli olduğu için L cismi de aynı
yönde döner. Bu durumda X cismi (–) yönde,
x = 2πr = 2.3r = 6r kadar hareket eder.
CEVAP E
7.
Vida tahta blok içinde ilerlerken tahtanın uyguladığı direnç kuvveti,
10.
F
r=15cm
l=1m
F.2rb = P.a
eşitliği ile bulunur.
I vidası için,
2F.2rb = P1.a .... (1)
II vidası için,
R = 1 m ve r = 15 cm dir.
3F.2r.2b = P2.2a .... (2) olur.
F.R = P.r
(1) ve (2) eşitlikleri taraf tarafa oranlanırsa,
P .a
2F.2rb
= 1
3F.2r.2b
P2 .2a
30.100 = P.15 ⇒ P = 200 N olur.
Kovanın ağırlığı 100 N olduğuna göre,
Gsu = 100 N = 10 kg olur.
P1
2
=
olur.
3
P2
CEVAP B
P 1
1
= 1.
&
3
P2 2
8.
Vsu = 10.000 cm3 = 10 dm3 = 10 , olur.
CEVAP A
11. I. K makarası denT
gede olduğundan,
30N
30N
30N
T = 15 + 15 + 5
Y
K
L
M
N
F=10N
10N 10N
5N
15N
I. yargı doğrudur.
GY=30N
G
15N
= 35N olur.
P
Z
K
II. L makarası dengede olduğundan,
X
5N
5N
M
5N
5N
5N
L
X
5N
GY+5 = 15+5+5
5N
5N
Z
5N
Y
GY = 20N olur. II. yargı doğrudur.
Şekilde görüldüğü gibi, Z levhasının ağırlık merkezi
M noktasıdır.
III. Kuvvet kazancında makaraların ağırlığı dikkate
CEVAP C
alınmaz. M makarasında kuvvet kazancı 2 dir.
Kuvvetten kazanç 2 ise, yoldan kayıp 2 dir. X
9.
•
yatay
53°
4
28 N
hz =
F2
F2
F2 .sin53°
IF1I= 28 N
20
= 10 m yükselir. III. yargı yanlıştır.
2
CEVAP C
F2
•
28 N
cismi 20 m çekilirse, Z cismi,
•
53°
yatay
12.
K
L
P =56N
P=56N
r
fiekil- II
fiekil - I
2r
•
Şekil-I deki hareketli makaranın denge şartından,
P = 28 + 28 = 56 N olur.
Şekil-II deki makara sisteminde düşey kuvvetlerin
dengesinden,
F2 + F2 + F2 . sin53° = P
M
yatay düzlem
r
P
2F2 + F2 . 0,8 = 56
Çekilen ipin uzunluğu = 2 . (2π . 2r – 2 π r) = 4 π r
2,8F2 = 56
P yükünün yükselmesi =
F2 = 20 N olur.
CEVAP D
4rr
= 2rr olur.
2
CEVAP C
KUVVET VE HAREKET
203
TEST
2
BASİT MAKİNELER
ÇÖZÜMLER
1.
3.
2F
F
F
P1
s
F
h
10N
P1 .sinθ
θ
T3
2F
P2
10N
20N
yatay
düzlem
20N
T1 = 20N
T2 = 10N
Sistem dengede olduğuna göre,
10N
40N
P1 . sin i = 2F
h
P1 . = 2F
s
1
P1 . = 2F & P1 = 6F olur.
3
K
L
M
x
yatay
N
R
S
P=70N
Sistem dengede olduğuna göre, çubuğun ağırlığı;
P = 20 + 40 + 10 = 70 N dur.
P2 yükü ise,
I. yargı doğrudur.
F + F + F = P2 ⇒ P2 = 3F olur.
K noktasına göre tork alırsak çubuğun ağırlık merkezi,
P1 ve P2 taraf tarafa oranlanırsa,
70 . x = 40 . 3 + 10 . 5
P1 6F
=
= 2 olur.
P2 3F
70x = 120 + 50
70x = 170
CEVAP D
x = 2,42
MN arasındadır.
II. yargı doğrudur.
T3 = 10 + 20 + 10 + 10 = 50 N dur.
III. yargı doğrudur.
CEVAP E
4.
ip
2.
G cismine etki eden kuvvet,
r Z
2r
G = F + 3F + F
G = 5F &
G
= 5 olur.
F
F
F
A
F F
uygulandığı ipi,
F
3F
gerekir.
L düzeyi
20cm
G
K düzeyi
CEVAP D
204
KUVVET VE HAREKET
X
3r
F
G
= 5 ise yükü 20 cm yükF
seltebilmek için kuvvetin
h = 5.20 = 100 cm çekmek
Y
K
L
M
N
P
R
S
X silindiri ok yönünde 1 tam devir yaptığında
2π.(3r) = 6πr kadar ilerler. Bu durumda Y silindiri
de 1 devir yapar ve ipi etrafına 2π.(2r)=4πr kadar
saracaktır. Bu durumda A cismi, 6πr + 4πr = 10πr
kadar yükselir. Her bir aralık 2πr olduğuna göre A
cismi L noktasına kadar yükselir.
CEVAP B
5.
K ΙΙ
3r L
M
A B C O2 D E
r
2r
7.
K
L
2cm
T
Ι
hip
N
P
r
O1
M
2r
,ö=2.(2rrK)
hx
30N
N ve P silindirlerinin dengede kalabilmesi için O1
X
K makarası 5 kez döndürüldüğünde konumundaki
değişme ötelenme miktarına eşittir. Bu miktar,
noktasına göre tork alırsak,
T.r = 30.2r
xö = 5.(2rrK) = 5.(2.3.2) = 60 cm olur.
T = 60 N olmalıdır.
I. yargı doğrudur.
II. silindirlerin dengede kalması için de O2 ye göre
K makarası 5 kez dönerse ipteki çekilme miktarı
hem ötelenmeden hem de dönmeden oluşur.
İpteki çekilme miktarı,
tork almalıyız. 40 N O2 noktasından x kadar uzaklıktan asıldığında denge sağlanmışsa,
T.2r = 40.x
xip = xö + xd = 60 + 60 = 120 cm olur.
60.2r = 40.x ⇒ x = 3r olur.
X cismindeki yükselme, ipteki çekilmenin yarısı
kadar olduğuna göre,
x ip
120
hX =
=
= 60 cm olur.
2
2
O2 noktasından 3r kadar uzak olan nokta A dır. Bu
durumda 40 N luk ağırlık A noktasından asılmalıdır.
CEVAP A
II. yargı yanlıştır.
L ve M nin yarıçapları bilinmediğinden dönme
sayıları için kesin birşey söylenemez.
CEVAP A
8.
II. ip
K
x2
L
I. ip
r
3r
x1
hY
Z
3P
I. yargı doğrudur.
Y makarasının ağırlığı 2P ise, L cisminin
ağırlığı 2P dir.
II. yargı doğrudur.
L cisminin ağırlığı 3P
ise, Y makarasının
ağırlığı P dir.
hX
•
Şekilde görüldüğü
gibi, X makarasının
ağırlığı P ise, K cisminin ağırlığı 3P dir.
•
6.
•
Y
X
3P
3P
Y
M
T
4P
2P
3P
L
2P
T = 2P
2P
I. ip toplam x1 = 12rr – 4rr = 8rr kadar çekilir.
X cisminin konumundaki değişme,
x
8rr
hX = 1 =
= 4rr olur.
2
2
Y cisminin konumundaki değişme, II. ipteki salınma ve K makarasının konumundaki değişme 12rr
kadardır.
hY = 12rr + 12rr = 24rr olur.
h
4rr
1
Bu iki değer oranlanırsa, X =
=
olur.
24rr
6
hY
X
P
III. yargı yanlıştır.
K silindiri ok yönünde 2 tam devir yaptığında I. ip
K silindirinden dolayı 2.(2r.3r) = 12rr kadar çekilir.
L silindirinden dolayı da 2.(2rr) = 4rr kadar salınır.
K
3P
CEVAP C
CEVAP B
KUVVET VE HAREKET
205
9.
x1 > x2 olduğundan M makarası 1 yönünde döner.
x1
x2
Y dişlisinin dönme sayısı,
fX . rX = fY . rY
M
1
2 . 3r = fY . 2r
2
fY = 3 devir yapar.
P
x1 – x2
M.D.S =
=
2
M.Ç
2 . 2r . 2r – 3 . 2r . r
2
2r . r
=
2r r
4r r
=
1
olur.
2
M makarası 1 yönünde
1
devir yapar.
2
CEVAP A
10. K silindiri 2 tur yaparsa L de 2 tur yapar. Bu durumda;
K
L
I. ip: +y yönünde
2.(2r.3r) = 12rr kadar çekilir.
II. ip: +y yönünde
2.(2rr) = 4rr kadar
çekilir.
r
O
3r
I.ip
II.ip (–)
M
+y
r
M makarasını I. ip
(+) yönde II. ip (–)
Th
yönde döndürür. M
makarası (+) yönünde döner. I. yargı doğrudur.
(+)
–y
P
Makaranın dönme miktarı;
6rr – 2rr = 4rr olur.
MDS =
4rr
4rr
=
= 2 olur.
çevre 2rr
III. yargı doğrudur.
I. ip M makarasını ve P yükünü +y yönünde 6rr kadar yükseltir.
II. ip ise +y yönünde 2rr kadar yükseltir. İlk konuma göre yer değiştirme;
∆h = 6rr + 2rr = 8rr olur.
II. yargı doğrudur.
CEVAP E
206
KUVVET VE HAREKET
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
Bölüm
Yazılı Soruları
(Basit Makineler)
1.
F
F
F
F
F
F
2F
2F
F
K cismi dengede olduğundan,
G K . sin 30° = T
F
F
GK .
F
2F
2F
ÇÖZÜMLER
G K = 2T
80cm
4F
1
=T
2
L cismi dengede olduğundan,
4F
GL = 2T + 2T + 2T
GL = 6T olur.
GK ve GL kuvvetleri oranlanırsa,
K
G K 2T 1
=
= olur.
G L 6T 3
G
G = 8F ise kuvvet kazancı
selme miktarı,
G
= 8 olur. Cismin yükF
b)
F.x = G.y
I. yol:
X makarası ok yönünde 1 kez döndüğünde Y
F
1
y = .x = .80 = 10 cm olur.
G
8
ve Z makaraları da aynı yönde 1 kez döner.
Bu durumda Z makarası etrafına 2πr kadar ip
sarar. X makarası da 2π.3r = 6πr kadar ilerler.
2.
P
Şekil-I de: 2F = P ⇒
> 1 olduğundan kuvvetten
F
kazanç vardır.
Şekil-II de: F = P ⇒ kuvvetten ve yoldan kazanç
yoktur.
Şekil-III te: F.2 = P.3 ⇒
P
< 1 olduğundan yoldan
F
kazanç vardır.
a) Bu durumda yalnız I de kuvvetten kazanç vardır.
b) Yalnız III de yoldan kazanç vardır.
Bu durumda Z makarasına bağlı ip 2πr + 6πr = 8πr
kadar ip 1 yönünde çeker. Bu durumda L cismi
8rr
kadar yukarı çıkar. X makarası ok yönün3
de döndüğünde Y makarasına bağlı ip 2 yönün
de 4πr kadar ilerler. Bu durumda K cismi
6πr – 4πr = 2πr kadar ilerler. Öyleyse K cismi
2rr
= rr kadar aşağı iner.
2
Öyleyse kütleler arasındaki düşey uzaklık,
8rr
11rr
+ rr =
= 11r olur.
3
3
II. yol:
3.
2T
X
Y
Z
r
2T
2T
2T
2r
2
L cismi yükselir. L cisminin yükselme miktarı,
1
hL =
olur.
T T
K cismi alçalır. K cisminin alçalma miktarı,
3r
K
h=
L
30o
2r . 3r – 2r . 2r 2rr
=
= rr
2
2
olur.
GK.sin30°
a) İpler üzerindeki kuvvetler şekilde gösterildiği
gibidir.
2r . 3r + 2rr 8rr
=
3
3
Cisimler arasındaki düşey uzaklık,
8rr
11rr
Th = h K + h L =
+ rr =
= 11r olur.
3
3
KUVVET VE HAREKET
207
4.
7.
T
(+)
20N
20N
K
yatay
L
20N
30N
(–)
20N
(–)
F
(+)
yatay
düzlem
K ve L silindirleri eş merkezli olduğundan K 2 defa
dönerse L de 2 defa döner.
M makarasının I. ucu,
2.(2rr) = 4rr kadar yukarı
çekilir.
II. ucu ise,
2.(2r.3r) = 12rr kadar
aşağı iner.
K
2tur
L
r O
3r
I. uç
4rr
12rr
M
2r
Bu durumda M makarası
üzerindeki ipler makarayı
(+) yönde,
Desteğe göre tork alınırsa,
30.5 + 20.1 = F.3 + 20.5
170 = 3F + 100
II. uç
(+)
X
4rr + 12rr
= 8rr kadar döndürür.
2
M makarasının dönme sayısı,
70
N olur.
70 = 3F ⇒ F =
3
İpteki T gerilme kuvveti,
n=
T = 20 + 20 = 40N olur.
8.
F ve T kuvvetleri oranlanırsa,
8rr
= 2 olur.
2r. (2r)
X makarası dengede
T=50N
olduğundan,
70
F
7
olur.
= 3 =
T 40 12
X
F
T = 2F + 10
F
50 = 2F + 10 ⇒ F = 20N
F
10N
olur. P yükünün büyüklüğü,
P = 30 + 5 + 5 = 40N
5.
5N
5N
olur.
10N
10N
30N
K dişlisi 2 devir yaptığında M dişlisi de aynı yönde
P
N K .fK = N M .fM
9.
M dişlisi 1 tam ve 1/3 devir yapar.
Bu durumda M dişlisinin görünümü
şekildeki gibi olur.
4
devir yapar.
3
20.2 = 30.fM & fM =
M
K cisminin 3 cm yükselebilmesi için eğik
düzlemde
F
3
sin 37°
3
=
0, 6
= 5 cm
d=
ilerlemesi gerekir.
3F
K kasnağı 120°
döndürüldüğünde,
K
d
M
N K .fK = N M .fM
1
.30 = N M .10 & N M = 1 olur.
3
L ve M eş merkezli olduğundan L kasnağı da 1 tur
döner. L kasnağı 1 turda 2πr = 40 cm ip salar. Bu
208
KUVVET VE HAREKET
X
X
durumda,
durumda X cismi de 40 cm yer değiştirir.
Y
3cm
Sistemde kuvvetten kazanç
120 1
tur
NK =
=
360 3
dönme sayısı bu
3F
3F
GK
= 9 olur.
F
Bu durumda yükün 5 cm ilerleyebilmesi için F
kuvvetinin 9.5 = 45 cm çekilmesi gerekir.
L
K
atmıştır. M nin
3F
3F
37o
6.
F F
F
10. K silindiri öteleme hareketinden dolayı 2h kadar
yol almıştır.
Y cisminin alçalması = 2h + 2h = 4h kadar olur.
L silindirinin dönmeden dolayı sardığı ip,
2π . 2r
2h olursa,
2π . r
h olur.
X cisminin yükselmesi = 2h + h = 3h olur.
X ve Y cisimleri arasındaki düşey uzaklık;
∆h = 4h + 3h = 7h olur.
1. BÖLÜM
ELEKTRİKSEL KUVVET VE ELEKTRİKSEL ALAN
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
4.
F kuvveti bileşenlerine ayrıldığında yatay ve düşey bileşenler birbirine eşit olur. Bu durumda,
F
F2
F1 = F2
k.
q 1 .q
2
d1
= k.
q1 = –4q
q 2 .q
2
d2
•
F1
d
= 2 & 1 = 2 olur.
2
d1 d2 d2
4q
F
=
2F
45°
O
45°
d1
+q
k.
k.
F
2 .1
2
a
q4 . 1
F
^ 2 ah2
1
2
=
q4
2
2
q 4 = + 4 2 nC olur.
q
d2
q2 =+q
q4 yükünün işareti (+)
olmalıdır. q1 yükünün
q2 yüküne uyguladığı
elektriksel kuvvet F
olsun.
CEVAP D
5.
q1 =+q
A
CEVAP B
2.
F1 = 1 br
F2
F2 = 2 br olur.
F1
=
F2
k.
k.
2F
q1 . q
4
2
2
2
q2 . q
B
+q
q1
F
–q
F
3F
q2 =+3q
q
1
= 1
2
4q 2
q1
=2
q2
O
F
R=v3F
2F
F
2F
C
q3 =+2q
F1
–q yüküne etki eden elektriksel kuvvetlerin bileşkesi,
q2
R = v3F olur.
olur.
CEVAP C
CEVAP D
6.
3.
q1
L
K
A
q2
.
F1
F
M q3
F4
N q4
B
O
.
q4
F
F F
.
q2
R=2F
q3
C
Şekilde görüldüğü gibi:
F2
Şekilde görüldüğü gibi, q1 ve q4 yükleri aynı işaretli, q1 ve q2 yükleri zıt işaretli olmalıdır.
I. ve II. yargılar doğrudur.
q1 ve q2 yükleri zıt işaretlidir.
I. yargı doğrudur.
q2 ve q3 yükleri aynı işaretlidir.
II. yargı doğrudur.
|q1| > |q4| tür.
III. yargı yanlıştır.
q1
q3 ve q4 yükleri zıt işaretlidir.
CEVAP C
III. yargı doğrudur.
CEVAP E
ELEKTRİK VE MANYETİZMA
209
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
1.
3.
ip
T1
. FMK
•
–q
d
K T T
2
2
•
FML
FLK FKL +q
F1 1
M
L
•
.
–2q
a
tavan
.
ip
b
T1•
yalıtkan
ayak
d
.
m1
.
•
a
yatay
düzlem
• T2
m2
.
q1
q2
G1
G2
q ] q2 olabilir.
T2 gerilme kuvveti,
I. yargı için kesin birşey söylenemez.
T2 + FKL = FML
T2 + k
d
=k
2
T2 = k
Kuvvetlerin büyüklükleri eşit,
| F1| = | F2| = F ve
q.2q
d
2
q
2
d
2
F
F
, tan β =
G1
G2
tan α =
olur.
olduğundan,
b > a ise, m1 > m2 dir.
K küresi için:
II. yargı kesinlikle doğrudur.
T1 gerilme kuvveti,
1 ve 2 iletken kürelerine etki eden itme kuvvetlerinin büyüklükleri eşittir. G1 > G2 olduğundan,
T1 + FMK = T2 + FLK
T1 + k
q.2q
(2d)
2
=k
q
2
d
2
T1 = 2k
+k
q
2
d
2
q.q
d
T1 > T2 dir.
2
III. yargı kesinlikle doğrudur.
2
–
1 q
k
2 d2
CEVAP E
4.
2
T1 =
3 q
olur.
k
2 d2
T=7G
7G = GK + Fe
K
7G = 3G + Fe
2
3 q
k
T1 2 d 2 3
olur.
=
=
2
T2
2
q
k 2
d
I. durumda:
K küresi dengede olduğundan,
T1 ve T2 taraf tarafa oranlanırsa,
F=4G
II. durumda:
CEVAP A
Küreler birbirine dokundurulduğunda yükleri,
›
+ q – 4q
F. r
r + 2r
›
K ve L kürelerinin ağırlıklarına G
diyelim.
Küreleri birbirine bağlayan ipin
uzunluğu biraz azaltılırsa, kürelerin
birbirine uyguladığı elektriksel kuvvetin büyüklüğü artar.
T2 = G + F olur. F arttığından T2 artar.
K
F
+q
•
T2
G
T2
L
•
+q
F
G
CEVAP B
210
ELEKTRİK VE MANYETİZMA
T›
F › =2G
K
›
q L = –2q
ip
T1
T1 = 2G olur.
T1 değişmez.
q K = –q
tavan
T1 + F = G + T2
T1 + F = G + G + F
3G
Fe = 4G olur.
qK = <
2.
b
q1 = q2
L küresi için:
q.q
2 F2
•
olur.
Küreler aynı yükle yüklendiğinden
3G
birbirini iter. İpteki gerilme kuvveti,
4G
F
›
k.
=
k.
4q
2
2
d
2
2q
d
2
›
F = 2G
›
T = 3G – 2G
›
T =G
olur.
CEVAP C
5.
tavan
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
T
1.
45° 45°
TK
E2=E.sin37°
TL
d
K
m2
FK
➞
E
L
mK.g
37°
E1=E.cos37°
•
FL
d
K
+q1
2d
mL.g
Yüklerin birbirlerine uyguladıkları kuvvetlerin
büyüklükleri eşittir.
+q2
E alan bileşenlerine ayrılıp oranlanırsa,
q .q
| FK| = | FL| = k. K 2 L
d
olur. Açılar eşit olduğundan cisimlerin ağırlıklarıda
eşittir.
E1
=
E2
GK = GL = mK.g = mL.g
k
k
q1
2
d1
q2
2
d2
q1
T gerilme kuvveti cisimlerin ağırlıkları toplamına
eşittir.
E. cos 37°
=
E. sin 37°
T = mK.g + mL.g = 2mKg = 2mLg
2
= d
q2
q2
(2d)
TK = TL ve aradaki açı 90° olduğundan,
q1
2
d1
2
4d
2
4q 1
0, 8
=
q2
0, 6
T = v2TK = v2 TL olur.
I. yargı yanlıştır. II. ve III. yargılar doğrudur.
4q 1
4
=
q2
3
CEVAP D
q1
1
= + olur.
q2
3
CEVAP D
2.
6.
tavan
.
.
a
1
m1
F1
E1 =
b
ip
ip
.
.
q1
E elektrik alan bileşenlere ayrıldığında,
m2
E1
K
2 br
d1
E2 = 2 2 br olur.
2
F2
q2
a = b ise, m1 = m2 dir.
q1 = q2
q1 ] q2 olabilir.
d2
q1 ve q2 yükleri+q1
nin K noktasındaki
elektrik alanı yazılıp oranlandığında,
E1
=
E2
I. yargı kesinlikle doğrudur.
•
k
k
E
E2
–q2
q1
2
d1
q2
2
d2
q1
II. yargı için kesin birşey söylenemez.
| F1| = | F2| dir.
III. yargı kesinlikle doğrudur.
CEVAP D
(2 2 )
2
=
–q 2
2 2
2
(2 2 )
2
&
q1
1
=–
olur.
q2
2
CEVAP B
ELEKTRİK VE MANYETİZMA
211
3.
6.
E
➞
➞
➞
E3
E2
EK
E1
E1
➞
K .
•
K
m
q1
=
d1
q2
Şekilde görüldüğü gibi, q1 ve q2 yüklerinin K noktasında oluşturdukları elektrik alanlar E1 ve E2 olduğunda bileşkesi şekildeki gibi E olur. Bu durumda,
| E| = v5 br, | E1| = v5 br, | E2| = v2 br olacağından,
E = E1 > E2 olur.
v
30
2c
➞
E2
30 v2cm
30cm
30cm
q1 =+8μC
➞
IE 1 +E 2 I=4v2.10 5 N /C
30cm
•
q3 =+3μC
q2 =–8μC
–6
q
8.10
I E1I = I E2I = k. 12 = 9.109
–1 2
(3. 2 .10 )
d1
CEVAP E
= 9.109.
–6
8.10
–2
9.2.10
= 4.105 N/C
4.
4
E
E3 = k.
4
q1 = +q
d
E
B.
2
d3
= 9.109 .
4
v3E
A
4
v2d
q3
= 9.109.
3.10
–6
–1 2
(3.10 )
3.10
–6
9.10
–2
4
E
v2E
= 3.105 N/C
d
D
K noktasındaki elektrik alanın büyüklüğü,
C
q3 = + 2q
EK2 = (4v2.105)2 + (3.105)2
q2 = – q
EB2 = (v2E)2 + E2
EK2 = 32.1010 + 9.1010
EB2 = 2E2 + E2
EK2 = 41.1010
EB2 = 3E2
EK = c41.105 N/C olur.
EB = v3E olur.
CEVAP C
5.
–2q
A
2d
+q
M
E
E
•
2E
B
+2q
O
2d
K
–q
E
d
d
2E
L
+q
O
E
2E
+2q
•
60° 60°
E
C
E
–2q yükünün O noktasında oluşturduğu elektriksel
alan E olduğuna göre, yüklerin O noktasında oluşturduğu bileşke elektrik alan,
EO = 2 E – 4 E = –2 E olur.
212
ELEKTRİK VE MANYETİZMA
CEVAP A
CEVAP C
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
1.
q1=+q
E2
K
O
•
q1=+q
q2
E1
d
3.
L
•
q2=–q
2d
K
•L
q1 ve q2 yüklerinin O noktasında oluşturdukları
elektriksel alanların bileşkesi sıfır olduğuna göre;
q3=+q
| E1| = | E2|
k
q
d
2
=k
q3 yükünün K noktasına olan uzaklığı değişmediğinden,
q2
(2d)
2
I. ve II. durumlarda VK değişmez.
q2 = +4q olur.
VK = k
q
q
q
– k + k = kq olur.
1
1
1
q1 ve q2 yüklerinin O noktasında oluşturdukları
Elektriksel potansiyel enerji ise,
toplam potansiyel,
I. durumda:
q
q
VO = k 1 + k 2
d1
d2
=k
2
EP = –k
q
4q
+k
d
2d
= +3k
2
2
q
q
q
+k
–k
2
2
2
= kq2(–0,7 + 0,5 – 0,7)
q
olur.
d
= –0,9 kq2 olur.
CEVAP E
II. durumda:
2
ı
EP = –k
2
2
q
q
q
+k
+k
2
2
2
= –0,5 kq2 olur.
Sistemin elektriksel potansiyel enerjisi azalır.
CEVAP D
2.
q1=+15q
A
4d
5d
D
q3=–8q
4d
q2=–12q
B
3d
•C
Yüklerin C noktasında oluşturdukları toplam elektriksel potansiyel,
VC = k
4.
Sistemin elektriksel potansiyel enerjisi,
Ep = k.
q
q1
q
+k 2 +k 3
d1
d2
d3
q .q
q .q
q 1 .q 2
+k 1 3 +k 2 3
d1
d2
d3
= 9.109.(–
15q
12q
8q
=k
–k
–k
5d
3d
4d
q
=k
(3 – 4 – 2)
d
q
= –3k
olur.
d
6.10
–10
3.10
–1
+
12.10
3.10
–10
–1
–
18.10
3.10
–10
–1
)
= 9.109.10–9(–2 + 4 – 6)
= 9.(– 4)
= –36 J olur.
CEVAP B
CEVAP A
ELEKTRİK VE MANYETİZMA
213
5.
E alanı bileşenlere ayrıldığında,
E1 = 2 br
E2 = 1 br olur.
➞
➞
E2
+q1
E
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
1.
➞
K
E1
A
•
q1 ve q2 yüklerinin K noktasında oluşturdukları
elektrik
k
q1
k
q2
d
d
alanları
oranından,
E1
=
E2
q2 = +q
d
B
q1=–2q
2
d1
2
2
= d
q
1
2
4d
q
olur.
2
q1 ve q2 yüklerinin K noktasında oluşturdukları
potansiyelleri toplamı ise,
q
q
VK = k 1 + k 2
d1
d2
q
q
= k 2 +k
d
2d
q
=k
olur.
d
6.
q
q
q
V = k 1 + k 2 + k 3 dir.
d
d
d
| E2| = | E3| > | E1|
C
q2=+3q
VA = –k
2q
3q
q
+k
=k
d
d
d
VK = –k
q
2q
3q
= 2k
olur.
+k
d
d
d
2
2
A ve K noktaları arasındaki VAK potansiyel farkı,
q
q
q
olur.
VAK = VK – VA = 2k – k = +k
d
d
d
CEVAP D
2.
Yapılan iş iki farklı yolla bulunabilir.
1. yol:
W = TE P = E P2 – E P1
2
2
q
4q
– 0 = –2k
d
2d
2
2
2
2
2
q
4q
4q
4q
2q
+k
= –2k
W 2 = –k
) = –k
– (–k
d
d
d
d
2d
2
q
W 1 –2k d
=
= 1 olur.
2
W2
q
–2k
d
W 1 = –k
CEVAP C
I. durumda:
+q2 = +q3 > q1 dur.
.
•
K
d
A ve K noktalarındaki potansiyeller,
2
d2
q1
q1 = +
d
2. yol: Yapılan iş iki nokta arasındaki potansiyel
farkla yükün çarpımıdır. Bu durumda V∞ = 0
olduğundan;
|E2+E3|
E3
E2
120°
120°
•
120°
E1
II. durumda:
| E2 + E3| > E1 olduğundan E artar.
q
q2
+ k 3 olduğundan,
d
d
V > Vı olur.
Vı = k
V azalır.
CEVAP B
W 1 = (VM – V3) . (–q)
–kq.4q
=
2d
2
2kq
=–
d
=2W
W 2 = (VL – VM) . ( – q)
k.4q. (–q) k.4q. (–q)
–
=
2d
d
2
q
= –2k
d
= 2 W olur.
Oranları ise;
W 1 2W
=
= 1 olur.
W 2 2W
CEVAP A
214
ELEKTRİK VE MANYETİZMA
3.
A
5.
q1=+q
q1=+10q
A
d
d
4d
B
q2=–3q
C
q3=+2q
d
.
B
q2=–2q
q2 ve q3 yüklerinin A noktasında oluşturduğu
potansiyel,
VA = –k
q
= k (–3 + 2)
d
q
= –k
olur.
d
W = DEP = EP2 – EP1
2
= –k
2
= +k
q
d
olur.
q
)]
d
CEVAP B
6.
2
q
= +k
d
2
q
(–4 + 5)
d
=k
= +q(V3 – VA)
q
d
20q
20q
+k
5d
4d
2
q1 yükünü A noktasından sonsuza taşınması sırasında yapılan iş,
W = q1.VA3
= +q.k
•C
q2 yükünün B köşesinden C köşesine taşınması
sırasında yapılan iş,
3q
2q
+k
d
d
= +q[0 – (–k
3d
olur.
q1 =+6.10–8 C
B
40cm
A
CEVAP B
30cm
D
4.
A
∞
VB = k f
1m
1m
q1 q2
+
p
d1 d2
= 9.109 f
B
C
q1 = +2.10–4 C
1m
–4
6.10
–
1
–8
4.10
–1
+
4.10
–8
5.10
–1
p
= 9.23.101
= 2070 V
–4
VC = 9.109 f
o
6.10
–8
5.10
–1
+
4.10
–8
4.10
–1
p
= 9.109.10–8.(12 + 10)
= 9.109.10–4(2 – 6)
=
6.10
= 9.109.10–8.(15 + 8)
q3 =–6.10–4 C
A noktasındaki potansiyel,
q
q
VA = k 1 + k 2
d1
d2
2.10
= 9.109 e
1
C
q2 =+4.10–8 C
q=1.10–5 C
= 9.22.101
9.105(– 4)
= 1980 V
= –36.105 V
Yapılan iş,
Yapılan iş,
W = q.VBC = q(VC – VB)
W = q.V∞A
= 2.10–8(1980 – 2070)
= q(VA – V∞)
= 2.10–8.(– 90)
= 1.10–5.(– 36.105 – 0)
= –180.10–8
= –36 J olur.
= –18.10–7 J olur.
CEVAP C
CEVAP D
ELEKTRİK VE MANYETİZMA
215
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
tavan
3.
ip
1.
3q
–
–
–
L
K
–
–
r
O
r
–
B
qL =–4.10–8 C
C
Kürelerin ortak potansiyelleri,
2r
–
qK =+1.10–8 C
r
A
rL =2cm
rK =1cm
–
–
–
ip
–
Vort = k
–
–
–
–
–
q + qL
Σq
= k> K
H
Σr
rK + rL
= 9.109 >
A ve C noktalarındaki potansiyeller,
–3q
3 q
=– k
VA = k
2 r
2r
–3q
q
VC = k
= –k
olur.
3r
r
1.10
–8
– 4.10
–8
1.10
–2
+ 2.10
–2
= 9.10 . >
9
–3.10
3.10
–8
–2
H
H
= –9.103 V olur.
AC potansiyel farkı,
CEVAP C
VAC = VC – VA
q
3 q
– (– k )
2 r
r
1 q
=+ k
olur.
2 r
= –k
CEVAP B
4.
L
qL =+3q
+
+
+
+
+
qK =+q
+
K + + +
+
+
r
r
r
O r
+
A
r
=r
+
+
+
K
+
+
+
+
rL =3r
+
+
+
2.
+
+
qL=+2q
+
qK=–q
+
–
+
–
–
+
–
+
–
r
2r
+
+
–
+
–
+
L
+
+
–
+
+
•
–
+
r
A
–
+
EA = k
+
A noktasındaki elektriksel potansiyel,
q
q
VA = k K + k L
rK
rL
EB = k
= 0 olur.
CEVAP E
ELEKTRİK VE MANYETİZMA
+
qK
2
d1
=k
q
(2r)
(q K + q L)
2
d2
2
=
=k
1 q
k
4 r2
q + 3q
(4r)
2
=k
4q
16r
2
=
1 q
k
4 r2
olur. EA ve EB taraf tarafa oranlanırsa,
q
2q
= –k
+k
r
2r
216
+
A ve B noktalarındaki elektrik alanların büyüklükleri yazılıp oranlanırsa,
+
+
+
+
+
+
– K
–
r
O
–
+
+
B
1 q
k
4 r2
EA
=
= 1 olur.
EB
1 q
k 2
4 r
CEVAP D
5.
qL=–3q L
– – –
–
II. yol:
K ve L kürelerinin sığaları,
–
–
–
qK=+q
–
+ + +K
+
+
–
–
O r
r
r
r
• • A• • B
•
+
r
+
–
+
+ + +
–
–
3r
–
–
–
–
– – –
CK = C & CL = 3C olur.
–
VA = k
(2r)
=
B noktasında:
EB = k
VB = k
(q – 3q)
(4r)
2
= –k
2q
1 q
= – k 2
8 r
16r
(q – 3q)
2q
1 q
= –k
= – k dir.
2 r
4r
4r
Buna göre, O noktasında hem elektriksel alan hem
de elektriksel potansiyel sıfırdır.
CEVAP A
qL
3r
–2V
+6V
–2V + 18V
4
= +4V olur.
=
1 q
dır.
k
4 r2
q
3q
1 q
= – k dır.
–k
2r
3r
2 r
r
qK
C. (–2V) + 3C.6V
C + 3C
=
A noktasında:
2
ip
L
K
C K .VK + C L .VL
CK + CL
Vort =
EO = 0 dır.
q
3q
VO = k – k
= 0 dır.
r
3r
q
ip
K küresi L küresine dokundurulup bir süre beklendikten sonra çekildiğinde,
ortak potansiyel,
+x
O noktasında:
EA = k
tavan
7.
VK = k
V=k
CEVAP D
qK
rK
q
olur.
r
M
L
K
r
2r
3r
q =+q
L
küresi yalıtkan K
qL =–7q
qM =+14q
ipinden tutulup önce
K ye, sonra da M ye birer kez dokundurulduğunda
kürelerin yeni yükleri,
L küresi K ye dokunduğunda,
qK = >
qK + qL
H.r
rK + rL K
ı
qK = <
+ q – 7q
–6q
F.r =
= –2q
r + 2r
3
ı
ı
q L = –4q olur.
6.
I. yol:
K ve L kürelerinin yükleri,
k.q K
– 2V =
r
k.q L
6V =
3r
eşitlikleri taraf tarafa oranlanırsa,
1 3q K q K
1
– =
&
=–
olur.
3
qL
qL
9
qK = – q & qL = 9q olur.
K ve L birbirine dokundurulduğunda K nin yeni
yükü,
(– q + 9q)
8q
›
qK =
.r =
.r = 2q
(r + 3r)
4r
olur. K nin yükü –q iken 2q olmuş. Potansiyel yükle
doğru orantılı olduğundan potansiyel 4V olur.
L küresi M ye dokunduğunda,
›
ıı
L
=>
qL + qM
H.r
rL + rM L
ıı
L
=;
–4q + 14q
E.2r
2r + 3r
q
ıı
L
=
ıı
L
ıı
qM
= +4q
q
q
q
+ 10q
.2
5
= +6q olur.
Kürelerin potansiyelleri,
ı
V K = –2V olur.
+ 4q
q
ı
VL = k
= 2k
2r
r
ı
V L = +2V olur.
ı
ı
V L = V M = +2V olur.
CEVAP C
ELEKTRİK VE MANYETİZMA
217
8.
–
–
10.
qL=–2q L
– –
qK=+6q
+ + + K
+
+
–
–
–
+
–
+
–
–
+
–
–
+
+x
• • C
•
+
+
qK =4.10–5 C
+
K + + +
+
+
+
O 1m 1m 1m
+
AA
rK = 1m
+
+
+
–
–
+
–
–
+
+
A noktasındaki elektriksel alan sıfırdır.
+
+
+
rL = 3m
+
+
+
I. yargı doğrudur.
+
+
B noktasındaki elektriksel alan +x yönündedir.
VA = k d
II. yargı doğrudur.
6q
6q
2 q
EB = k
=k 2 = k 2
2
3 r
(3r)
9r
EC = k
+
+
–
+
+
+
–
r
r
+ B
2r
+
4r +
–
L
–
• A
• •
+
+
–
r +r
O r
qL =6.10–5 C
–
(+ 6q – 2q)
(5r)
2
4q
=k
25r
2
=
qK qL
+ n
d K rL
9 4.10
= 9.10 d
2
q
4
k
25 r 2
+
+
–5
+
6.10
3
–5
n
= 9.109.10–5(2 + 2)
= 36.104 V olur.
EB > EC dir.
W = q.V∞A = q(VA – V∞)
III. yargı doğrudur.
CEVAP E
= 1.10–4(36.10–4 – 0)
= 36 J olur.
CEVAP C
9.
L
+
+
K +
+
+
qL = 4μC
+
+
qK = 3μC
+
+
+
+
+
+
rK = 2 m
+
+
+
+
O
+
+
+
+
+
+
+
rL = 3 m
+
+
VA = k c
6m
+
+
+
A
+
+
+
qK + qL
m
d
9 3.10
= 9.10 d
–6
+ 4.10
6
–6
n
3
7
= 9. .10
6
=
21 3
10 V olur.
2
W = q.V∞A = q(VA – V∞)
= 2.10–3. c
3
21
.10 – 0 m
2
= 21 J olur.
CEVAP E
218
ELEKTRİK VE MANYETİZMA
TEST
1.
1
ÇÖZÜMLER
F1=F
3.
q1 =–q
ta sın da
K
et ki yen
L
2F
F
F
dan, 3 yönünde
60°
q2 = +q
R
yönünde olduğun-
60°
O
+q yüküne O nokbileşke kuvvet 3
F
60°
+q
ELEKTRİKSEL KUVVET
O
+q
harekete başlar.
F2=F
F
2d
d
M
q3 =+2q
30°
CEVAP C
–q2
+q yüküne etki eden kuvvetlerin büyüklükleri eşit
ve şekildeki gibi olduğunda bileşkesi F şekildeki
4.
q1 =+2q
gibi olur.
| F1| = | F2|
k
q 1 .q
d
2
=k
q2 =+3q
30°
2F F
3F
(–q 2) .q
(2d)
v3F
q
–q 2
1
q1 =
⇒ 1 =–
olur.
q2
4
4
2F
F
2
2F
q3 =+q
CEVAP A
+q yüküne uygulanan bileşke elektriksel kuvvetin
büyüklüğü Fv3 olur.
y
2.
F
O +q 30°
•
.
+q1
CEVAP C
F
F2
5.
53° 37° F1
37° 53°
3d
ki
.
O
+q
O noktasında-
x
yüke
etki
2F
eden kuvvetle-
2d
rin bileşkesi,
+q2
Fo=Fv3
O
olur.
C
q2 =+3q
q3 = +2q
vetler,
F1 =
F2 =
k.q 1 .q
(3d)
2
k.q 2 .q
2
=
=
CEVAP B
k.q 1 .q
9d
6.
2
2
mesi için kuvvetlerin yatay bileşenleri birbirine eşit
olmalıdır.
F1.0,6 = F2.0,8
9d
2
.0, 6 =
4d
2
q1
= 3 olur.
q2
F
›
=
k.
q
2
.0, 8
q1 =+3q
A
2
d
2
3q
30°
^ 3 dh2
›
F = F olur.
+q yüküne etki
eden bileşke kuvvet,
F1.sin37° = F2.sin53°
k.q 2 .q
k.
F
k.q 2 .q
(2d)
4d
olur. F1 ve F2 nin bileşkesinin şekildeki gibi olabil-
k.q 1 .q
3F
+2q
F
B
q1 ve q2 yüklerinin +q yüküne uyguladıkları kuv-
2F
F F
2F
Fo = Fv3
+q1
q1 =+q
A
R = v2F olur.
2d
v3d
B
q2 =+q
•
F
C
d
q3 = –q
F
CEVAP C
CEVAP B
ELEKTRİK VE MANYETİZMA
219
7.
F1
=
F2
k.
k.
q1 . q
4d
q2 . q
d
2
T2 gerilme kuvveti,
4
•
q1
F1 =1br
30 = mg +
olur.
q3 = +3q olur.
q1 = + 2q
20 = 2.
O
F
F
2F
3F
q2 = – q
+
+
–
–
M
2
⇒
2
fi kil
2
kq
d
2
= 10 N olur.
2
tavan
T›1
m L
Tı2 gerilme kuvveti,
Tı2 = 2 mg + Fı
= 2 mg + k.
qM
2q.q
(2d)
2m
2
K
L
O
qK
V
= 25 N
qK = qL dir.
II. yargı kesinlikle
doğrudur.
A
ı
ı
T1 ve T2 kuvvetleri taraf tarafa oranlanırsa,
+q
›
T1
+q yüklü cisim O noktasında durduğuna göre
M küresi (+) yüklüdür.
=
›
T2
30 6
=
olur.
25 5
CEVAP C
III. yargı kesinlikle doğrudur.
CEVAP E
12.
tavan
α β
q2
10.
F1 = F
3d
K
mK
➞
60°
F
60°
F1
60°
+q
k.
d
2
q1
= k.
F2
mL .g
I. yargı için kesin birşey söylenemez.
β > α ise, mK > mL dir.
2
q
1
=
& 1=
2
2
q
9
2
d
9d
q2
II. yargı kesinlikle doğrudur.
| F1| = | F2| dir.
olur.
III. yargı kesinlikle doğrudur.
CEVAP A
220
➞
qL
qK ≠ qL olabilir.
q 2 .q
(3d)
L
mL
qK = qL
q1
| F1| = | F2|
q 1 .q
qK
mK .g
d
F2 = F
q
F›K=F›
1
.10
2
= 2.10 +
qL
4
K
2mg
2
olabilir.
2q
2d
T›2
1 kq
.
2 d2
= 2 mg +
I. yargı için kesin birşey söylenemez.
F›L=F›
mg
q3
CEVAP E
qK =
qL =
qK =
qL =
d
d
2
Tı1 gerilme kuvveti,
Tı1 = mg + 2 mg
= 3 mg
= 3.10
= 30 N olur.
q4 =–q
+q
kq
kq
T2 d
m L
2q
mg
FL=F
2
d
30 = 10 + 2.
3F
9.
k.q.2q
FK=F
q
K
2m
2mg
T2 = mg + F
30° d
CEVAP D
8.
T1
30 = 3 mg ⇒ mg = 10 N
+q
O
2d
tavan
T1 = 2 mg + mg
30°
q
1
= 1
2
4q 2
q1
=+2
q2
11. T1 gerilme kuvveti,
4
F
4
F2 = 2 br
2
ELEKTRİK VE MANYETİZMA
CEVAP D
TEST
1.
2
ELEKTRİKSEL ALAN
ÇÖZÜMLER
4
4
E
E
3.
q1=+2q
q2=–3q
+qK
d1
E0= 3E r
3E E
30°
+qL
d2
E
•.
O
30°
elektrik alan zay›f
r
2E
2E
elektrik alan fliddetli
q3=–2q
2E
q4=+q
q
Kürelerin elektrik alanın kuvvet çizgilerinin yönü
dışa doğru olduğundan yükler pozitiftir.
E = k.
K nin kuvvet çizgilerinin sayısı fazla olduğundan
qK > qL dir. Yarıçapları için kesin birşey söylenemez.
Şekildeki yüklerin O noktasında oluşturdukları
elektrik alanlar ayrı ayrı gösterildiğinde bileşke
elektrik alan,
I. ve II. yargılar kesinlikle doğru,
kesinlik yoktur.
III. yargıda
CEVAP C
2.
r
olsun.
2
EO =
3E
EO =
3 k
•
+q1
•
4.
E. cos 53°
=
E. sin 53°
CEVAP B
q1 = +q
A
q1
d
O
3E
K
B
2
q2 = –3q
d1
q2
8E
8E
2d
q1 ve q2 yüklerinin K noktasındaki elektrik alanları
yazılıp oranlandığında,
k
olur.
E
–q2
k
2
53°
d2=d
E2=Esin53°
k
r
K E1=Ecos53°
d1=2d
E1
=
E2
q
O
3E
3E
E
C
q4 = +2q
q3 = –3q
60° 60°
E
3E
3E
q1 yükünün O noktasında oluşturduğu elektriksel
alan E,
2
d2
q1
2
(2d)
–q
k 22
d
q1
q
0, 6
=
& 1 = –3 olur.
–4q 2
q2
0, 8
CEVAP D
E=
k.q
(2d)
2
=
kq
4d
2
olur. Yüklerin O noktasında oluşturdukları elektriksel alanların bileşkesi,
EO = 4 E – 8 E = – 4 E olur.
CEVAP A
ELEKTRİK VE MANYETİZMA
221
5.
E1 = 2 br
E2 = 2v2 br
E1
=
E2
k
k
+q2
q1
+q1
E
➞
E1
q1 =–2q
4
K
–q3
4
E1+E3
2
d2
2
(2 2 )
➞
➞
E
E2
2
q2
=
2 2
4
E2
q2
q1
2
K
2
d1
4
8.
q2 =+8q
E = 2 br
2
2
E + E 3 = 1br olur.
1
2q 1
1
=
q2
2
q1
1
2
=+
=
4
q2
2 2
1
E
olur.
– q3
k
E + E3
2
=
2
k
2
– 2q
– dk
+ 8q
2
2
2
n
2
1 – q 3 + 2q
=
2
8q
CEVAP B
–q 3 + 2q = + 4q
q 3 = – 2q olur.
q1 ve q2 yüklerinin A noktasında oluşturdukları
elektrik
alanlar
eşit olur.
4
60°
k
(2d)
2
–q 1
4d
2
=k
=
9.
4
E
2d
d
Şekildeki yükle-
q3 =+2q
rin O noktasın-
d
q2
da oluşturdukları
2
B
q2
d
A
60°
| E1 | = | E2 | = E
–q 1
CEVAP A
E
4
E
30°
•
q1
elektrik
C
alanlar
➞
E
E
O
30°
30°
Bileşke elektrik
alan,
2E
➞
➞
3E
EO = 2E + 3E – E
CEVAP E
q2 = –q
E
➞
şekildeki gibidir.
q2
2
q1
= –4 olur.
q2
➞
q1 =–q
•
6.
EO = 4E olur.
q4 =–3q
CEVAP D
7.
q1 = + q
q2 = – 2q
a
4
A
4
B
2E
A
–4q
3E
4
4
4
E
4
M
4E
E
–q
4
+4q
CEVAP E
EO = 4 E olur.
4
2E
–q
E
2E
E
O
B
ELEKTRİK VE MANYETİZMA
L
E
E
E
C
q3 = – 3q
EO = 5E
= 5.200
= 1000 N/C olur.
222
4
4
EO = 5 E
3E
q4 = + q
4
EO=4E
O
D
10.
4
E
O
K
+q
C
+4q
CEVAP A
11.
q1
K
•
E2
q2
E1
E
E elektrik alan bileşenlere ayrıldığında,
E1 = 2 br
E2 = 2 br olur.
q1 ve q2 yüklerinin K noktasında oluşturduğu elektrik alanlar yazılıp oranlanırsa,
E1
=
E2
k
q1
(2 2 )
q
k 22
2
q
2
= 1
2
2q 2
2
&
q1
= + 2 olur.
q2
12.
CEVAP B
E2=1br
E
2d
.
30°
•A
E1=2br
d
.
30°
B
C
+q2
–q1
Şekildeki üçgenden,
E1 = 2 br
& E2 = 1 br olur.
q1 ve q2 yüklerinin A noktasındaki elektrik alanları
yazılıp oranlandığında,
E1
=
E2
k
–q 1
2
(2d)
q
k 22
d
–q 1
q
2
=
& 1 = –8 olur.
4q 2
q2
1
CEVAP E
ELEKTRİK VE MANYETİZMA
223
TEST
1.
3
ELEKTRİKSEL POTANSİYEL
ÇÖZÜMLER
q1 = +3q
K
q1 ve q2 yüklerinin K noktasında oluşturdukları
potansiyel ayrı ayrı yazılacak olursa,
q3
q1
V1
d1
=
V2
q
k 2
d2
k
–2q
V1 k 4
=
V2
q
k
2
q2 =–12q
q1, q2 ve q3 yüklerinin K noktasında oluşturduğu
potansiyel sıfır olduğundan q3 yükü,
V1
= – 1 olur.
V2
VK = 0
CEVAP C
q
q
q
k 1 +k 2 +k 3 =0
d1
d2
d3
k
q
3q
12q
+k 3 =0
–k
4
2
3
kq – 3kq + k
q3
=0
2
3.
q
k 3 = 2 kq
2
q 3 = + 4q olur.
A
–q1 yükü sonsuza
götürülürse O noktasındaki,
4
E
4
E1
E → azalır.
CEVAP C
–q1
4
4
E3
V → artar.
E2
O
B
C
+q2
2.
E bileşenlerine
ayrıldığında,
E1 = 1 br
E2 = 2 br olur.
q1 ve q2 yüklerinin K noktasında oluşturdukları elektrik
alanlar,
E1
=
E2
k
CEVAP A
4
E
4.
q1
4
2
2
K
E1
d
d
q2
B
q2=–6q
d
q3
C
Sistemin elektriksel potansiyel enerjisi sıfır olduğuna göre,
q .q
q .q
q .q
k 1 2 +k 1 3 +k 2 3 = 0
d
d
d
2
–k
q1
=–2
q2
2q.q 3
6q.q 3
12q
=0
+k
–k
d
d
d
–4q.q3 = 12q2
q3 = –3q olur.
q 1 = – 2q
q2 = + q
q1=+2q
A
2
4
2
q
1 – q1
=
2 4q 2
224
4
E2
(–q 1)
k
+q3
olur.
ELEKTRİK VE MANYETİZMA
CEVAP A
5.
I. durumda:
7.
A
Sistemin elektriksel potansi-
q1 =–q
q3
–2q
➞
E3
E1
yel enerjisi,
d
2
2
2q
6q
3q
+k
–k
E = –k
d
d
d
➞
2
olur.
C
+q
➞
+3q
E2
q3 =–2q
II. durumda:
Elektrik alanlar şekildeki gibi olacağından,
q 3 = –q olur.
B ve C köşelerindeki küreler birbirlerine dokundurulduğunda,
qBı = qCı =
V=k
q + 3q
= 2q
2
VO = k
olur. Sistemin elektriksel potansiyel enerjisi,
2
2
4q
4q
4q
–k
+k
d
d
d
–q
d
(–q)
(–2q)
(–q)
+k
+k
d
d
d
VO = – 4V
2
olur.
CEVAP E
2
Eı = – 4
E
O
B
2
q
E = –5k
d
Eı = –k
➞
q
olur.
d
8.
q1 = 6.10–8C
q2 = 3.10–8C
4m
B
A
Eı ve E taraf tarafa oranlanırsa,
2
ı
E
=
E
q
d
2
q
–5k
d
–4k
3m
•
D
ı
ı
E
4
4
=
& E = E olur.
E 5
5
6.
CEVAP D
➞
➞
E›
E1
➞
➞
E›2
➞
E
A
VC = k
E›1
q1
q
+k 2
d1
d2
9 6.10
VC = 9.10 d
5
–8
9 6.10
VD = 9.10 d
3
–8
+
3.10
3
–8
n = 9.22 = 198V olur.
+
3.10
5
–8
n = 9.26 = 234V olur.
VCD = VD – VC = 234 – 198 = 36 V
A
➞
•
C
E2
d
CEVAP B
d
d
d
9.
–q
B
B
C
d
q1 = +5q
q2 = – q
q›1 =+2q
d
›
E
120°
A
120°
O
+q
4
120°
E
4
E
Şekilde görüldüğü gibi O noktasındaki bileşke
elektrik alanın büyüklüğü sıfırdır.
5q
q
q
– k = 4k
d
d
d
O noktasındaki elektrik potansiyeli,
2q
2q
q
+k
= 4k
d
d
d
V=k
V → Değişmez.
E → Azalır.
+q
4
q›2 =+2q
Potansiyel ise,
V =k
C
C
E1 = 5E ⇒ E2 = E olur.
ı
ı
E 1 = 2E ve E 2 = 2E olur.
ı
Bu durumda E > E olduğundan E azalır.
V=k
B
›
V =k
CEVAP C
q
dir.
r
q
q
q
q
– k + k = k = V olur.
r
r
r
r
CEVAP E
ELEKTRİK VE MANYETİZMA
225
10. K küresinin potansiyeli,
VK = k.
–V = k
V=k
qK
r
ip
–q
r
II. yol:
tavan
Kürelerin sığaları yarıçaplarıyla orantılıdır.
r
C=
d›r.
k
ip
L
K
q
olur.
r
r
CK = 2C & CL = 3C olur.
3r
C=
qK = – q
qL = +9q
K ve L küreleri birbirine dokundurulduğunda K
küresinin son potansiyeli –2V olduğuna göre,
Kürelerin ortak potansiyelleri,
Vort = k
q + qL
Σq
= k> K
H
Σr
rK + rL
Vort = k <
–q + 9q
+ 8q
q
F= k
= 2k
r + 3r
4r
r
Vort = +2V olur.
q + qL
q
& Vort = K
eşitliğinden bulunur.
V
CK + CL
Vort =
C K .VK + C L .VL
CK + CL
–2V =
2C.7V + 3C.VL
2C + 3C
–10V = 14V + 3VL
CEVAP D
3VL = –24V
VL = –8V olur.
tavan
11.
ip
ip
12.
+5q
+
L
K
2r
3r
I. yol:
–
›
qK
›
& q K = – 4q olur.
2r
L nin son yükü yarıçapı 3r olduğundan – 6q olur.
K küresi L ye dokundurulduğunda L nin ilk yükü,
qK + qL =
ı
qK
+
ı
qL
14q + qL = –4q + (– 6q)
qL = 24q olur.
L küresinin potansiyeli,
V L = k.
(–24q)
= – 8V olur.
3r
ELEKTRİK VE MANYETİZMA
+
–
r
–
K küresinin elektriksel potansiyeli 7V olduğuna
göre V değeri,
+
– K
–
+
O 0,2m – 0,2m 0,2m A
–
2r
+
– 2V = k.
–
–
+
qK = 14q olsun. Bu durumda K küresi L küresine
dokundurulduğunda elektriksel potansiyeli –2V
olduğundan yükü,
L
+
–
+
+
qK
q
& V = k. K olur.
2r
14r
+
–q
+
+
7V = k.
+
+
+7V
226
CEVAP B
–
–
+
–
+
–
+
+
+
+
+
+
Yüklerin A noktasındaki elektrik alan ve elektriksel potansiyeli yazılıp taraf tarafa oranlarsak,
E
=
V
^ – q + 5q h
0, 6 . 0, 6
^–q + 5q h
k
0, 6
k
50
1
=
V
0, 6
V = 30V olur.
CEVAP D
TEST
1.
4
ÇÖZÜMLER
q1=–6q
K
L•
q2=+4q
N
•M
d
d
ELEKTRİKSEL
L
POTANSİYEL ENERJİ VE İŞ
3.
q1=+2q
A
d
d
d
q1 ve q2 yüklerinin L ve M noktalarındaki potansiyelleri,
6q
4q
VL = –k
+k
d
2d
q
= – 4k
olur.
d
6q
4q
VM = –k
+k
2d
d
q
=k
olur.
d
B
q2=+q
C
q3=–q
d
Sistemin elektriksel potansiyel enerjisi,
q .q
q .q
q .q
EP = k 1 2 + k 1 3 + k 2 3
d
d
d
=
+q yükünü L noktasından M noktasına taşınması
sırasında yapılan iş,
k
(2q2 – 2q2 – q2)
d
2
= –k
W = +q VLM
q
d
olur.
CEVAP A
= +q(VM – VL)
= +q [k
q
q
– (– 4k )]
d
d
= +q.5k
q
d
2
= +5k
q
d
olur.
CEVAP E
4.
A
q1 =4.10–5 C
30°
2.
q1 =+2q
K›
q2 = – 3q
K
L›
d1 =40cm
d
d
d
B
q1 ve q2 yükleri Kı ve Lı noktalarına getirildiğinde
yapılan iş,
q2
W = TE P = E P2 – E P1
=k
= k=
2
=k
2
6q
6q nH
– d–
d
3d
2
2
–10
–10
4.10
4.10 pH
– f–
–1
–1
5.10
4.10
= 9.109.10–9.(–0,8 + 1)
= 9.(0.2)
2
q
d
C
=–1.10–5 C
q1 q2
q q
–k 1 2
d2
d1
= 9.109 >–
6q
2q G
–
d
d
= + 4k
30cm
•
W = ∆EP = EP2 – EP1
q 1 .q 2
q q
–k 1 2
d2
d1
= k >–
d2 =50cm
L
olur.
= 1,8 J olur.
CEVAP D
CEVAP E
ELEKTRİK VE MANYETİZMA
227
5.
∆Ek = W = F.∆x
q1 = 4.10–4C
W = q.E.∆x
K
3.10–7 = 2.10–8.6.∆x
5
m olur.
2
N
q› = 1.10–4C
1m
10 = 4.∆x = ∆x =
q2 = –3.10–4C
M
L
1m
1m
Yük M noktasında ise,
CEVAP D
9 4.10
E P2 = 9.10 d
2
–8
–
3.10
1
–8
–
12.10
3
–8
n
= 90. (–5)
= – 450 J olur.
Yapılan iş,
6.
W = TE P = E P2 – E P1
= (–450) – (–135)
L
K
q2=+q
= –450 + 135
= – 315 J olur.
O
q1=–4q
CEVAP A
r
2r
q2 yükünün K noktasından L noktasına taşınması
sırasında yapılan iş,
W = DEP = EP2 – EP1
2
8.
2
4q
4q
– (–k
)
= –k
2r
r
+q
A
•
3
2
=k
q
(–2 + 4)
r
d
d
2
= +2k
q
r
olur.
CEVAP B
7.
q1 = 4.10–4C
K
L
q2 = –3.10–4C
M
N
q› = 1.10–4C
1m
1m
1m
İki yük arasındaki elektriksel potansiyel enerji
q .q
E = k. 1 2 eşitliğinden bulunur.
d
9 4.10
E p = 9.10 d
1
1
= 90 . b –
3l
2
= – 135 J olur.
228
ELEKTRİK VE MANYETİZMA
d
C
q2=+3q
A noktasındaki potansiyel
5q
3q
+k
VA = –k
d
d
q
= k (–5 + 3)
d
q
= –2k
olur.
d
+q yükünün sonsuzdan üçgenin A köşesine taşınması sırasında yapılan iş,
W = +q.V3A
= +q(VA – V3)
Yük L noktasında ise,
–8
B
q1=–5q
–
3.10
2
–8
–
12.10
3
–8
n
= +q (–2k
q
– 0)
d
2
= –2k
q
d
olur.
CEVAP B
9.
q1=–15q
A
11.
4d
A
•B
5d
3d
2m
2m
5d
•C
D
q2=+10q
q1 = –8.10–4C
15q
10q
7 q
VB = –k
+k
=– k
olur.
4 d
4d
5d
15q
10q
1 q
VC = –k
+k
=– k
olur.
5d
4d
2 d
VA = k
q2 = +6.10–4C
q1
q
+k 2
d1
d2
= 9.109 d
–8.10
2
= 9.105.(–1)
+q yükünü B noktasından C noktasına taşınması
sırasında yapılan iş,
–4
6.10
2
+
–4
n
= –9.105 V olur.
W = +q.VBC
1.10–4
C luk yükü üçgenin A köşesinden ∞ a taşımak için yapılan iş,
= +q(VC – VB)
= +q[–
C
B
W = qıVA∞
q
7 q
1
k
– (– k ) ]
4 d
d
2
=qı(V∞ – VA)
=1.10–4 [0 – (–9.105)]
2
q
1 7
=k
(– + )
d
2 4
=10–4.9.105
=90 J olur.
2
5 q
=+ k
4 d
CEVAP C
olur.
CEVAP B
12.
+
+
–
+
–
d
Ek = 90 J
Kinetik enerji yükler arasındaki potansiyel enerjiye
eşit olduğunda,
9.109
4.10
–4
q1 q2
= 90
d
.1.10
d
–4
L
+
r
–
+
+
–
+
–
+
•
–
r
+
•
+
–
r
•A
+
+
+
+
A noktasındaki potansiyel,
q + qL
VA = k ( K
)
d
–2q + 5q
=k(
)
3r
+ 3q
=k
3r
q
=k
olur.
r
Sonsuzdaki +q yükünü A noktasına getirmek için
yapılan iş,
EP = EK
k
•
2r
+
r
O
–
+
+
– K
–
–
+
+
q2 =+1.10–4 C
–
–
+
q1 =+4.10–4 C
+
qK=–2q
+
10.
qL=+5q
W = qV3A
= q(VA – V3)
q
= +q(k – 0)
r
= 9.101
d = 4 m olur.
2
CEVAP D
= +k
q
r
olur.
CEVAP C
ELEKTRİK VE MANYETİZMA
229
Adı ve Soyadı : .....................................
1.
Sınıfı
: .....................................
Numara
: .....................................
Bölüm
Yazılı Soruları
Aldığı Not
: .....................................
(Elektriksel Kuvvet ve
Elektriksel Alan)
F1 = F . cos53° = F . 0,6
k.
F1
=
F2
(–q 1) . q
q1
2
k.
L
FL =10N
F2
➞
F1
FML =6N
O
•
qK =4.10–6 C
3cm
q2
qM =3.10–6 C
FKL = k .
qL =12.10–8 C
+
+
+
FML = k .
+
2
+
–
+
qM . qL
2
d2
2
2
2
F L = (8) + (6)
–2 2
(3.10 )
3.10
–6
. 2.10
–7
–2 2
(3.10 )
+3μC
+
+
–8
+
–1 μC
–
K –
–
+
= 8N
= 6N
–8
2.10
12.10
+
–1
–1 p
2.10
3.10
9
–7
+
–
+
–
0,4m
+
= 2700 V olur.
–8
0,2m
0,2m
A
–
–
+
+
+
+
A noktasındaki elektrik alan,
B noktasındaki potansiyel,
q + qL
m
VB = k c K
d
–2.10 + 12.10
–1
4.10
9
–7 10
= 9.10 .10 . b l
4
= 2250 V olur.
+
–
0,2m
+
= 9.10 .3
+
O 0,2m
–
. (–1 + 4)
+
–
–
9
EA = k
–8
p
VAB = VB – VA = 2250 – 2700 = –450 V olur.
(q K + q L)
d
E A = 9.10
9
2
= 9.10
9
(–1.10
–6
–6
+ 3.10 )
–1 2
(6.10 )
–6
2.10
2
5
4
–2 = 4 .10 = 5.10 N/C olur.
36.10
A noktasındaki potansiyel,
VA = k
İki nokta arasındaki potansiyel fark,
ELEKTRİK VE MANYETİZMA
–7
2
+
2
230
. 2.10
FL = 10 N olur.
L
A noktasındaki potansiyel,
q
q
VA = k K + k L
dK
rL
9
–6
2
+
+
= 9.10 f
9
= 9.10 .
4.
+
= 9.10 .10
2
d1
4.10
+
+
= 9.10 f –
9
= 9.10 .
–
–
rL = 30 cm
+
qK . qL
M
F L = F KL + F ML
qK =–2.10–8 C
+
K – – –
–
O 10cm 10cm 10cm 10cm
–
B
rK = 10 cm A
–
+
+
qL =2.10 C
K
x
FKL =8N
–7
d
+
+
L
3cm
+q
2
0, 6F –q 1
=
0, 8F 4q 2
q
3
=– 1
4
4q 2
q1
= –3 olur.
q2
2.
y
➞
53°
2d
4d
q2 . q
d
3.
➞
F
F2 = F. sin53° = F . 0,8
ÇÖZÜMLER
VA =
–6
–6
(q K + q L)
9 (–1.10 + 3.10 )
= 9.10
–1
d
6.10
9
9.10 .2.10
–1
6.10
–6
4
= 3.10 V olur.
5.
7.
+q1
q1 =+q
A
4
E2
0,3m
4
K
E
O
➞
➞
2E
➞
➞
E1
E bileşenlere ayrıldığında,
2
E2 = v2 br olur.
9
–2 = 10 . c
8
q1
2
q = 2.10
2
q2
(2 2 )
E=k
2
2q 1
1
=
q2
2
q3 =–2q
q–2q–2q
3.10
–1
n
–3q
m
3
–8
C olur.
q
d
2
= 9.10
q1
1
2
=
=+
q2 2 2
4
➞
EO =3E
–18.10 = 9.10 d
E1 = 1 br
k
➞
q1 q2 q3
+
+
n
d1 d2 d3
VO = k d
k
C
q2 =–2q
+q2
E1
=
E2
E
2E
B
4
2E
9
–8
2.10
–1 2
(3.10 )
3
= 2.10 N/C olur.
olur.
EO = 3 E
= 3.2.10
3
3
= 6.10 N/C olur.
Elektrik alan ↓ yöndedir.
6.
M noktasındaki potansiyel sıfır ise q2 yükü,
VM = 0
k
q1
q
+k 2 = 0
d1
d2
k
q
8q
+k 2 = 0
d
2d
8.
y
q
4q
k 2 =–k
d
d
q1 =5.10–4 C
q 2 = – 4 q olur.
K
E1
L
q1 = +8q
E2
d
d
5m
N
EL =E1 + E 2
M
q2 =–4q
3m
d
EL = E1 + E2
=k
8q
d
+k
2
= (8 + 1) k
= 9k
q
d
2
EP = k
4q
(2d)
q
d
2
olur.
2
3m
x
q3 =–3.10–4 C
q2 =4.10–4 C
L noktasındaki elektrik alan,
5m
4m
q .q
q .q
q 1 .q 2
+k 1 3 +k 2 3
d1
d2
d3
–4
9 5.10 .4.10
= 9.10 e
5
9
–4
–
–4
5.10 .3.10
5
–4
–
–4
–4
4.10 .3.10 o
6
–8
= 9.10 .10 (4 – 3 – 2)
1
= 9.10 (–1)
= – 90 J olur.
ELEKTRİK VE MANYETİZMA
231
9.
q1 = –3.10–4 C
q2 =+4.10–4 C
L
K
∞
q=1.10–5 C
M
1m
2m
VL = k
q1
q
+k 2
d1
d2
9
3.10
= 9.10 d –
1
9
–4
4.10
2
+
–4
n
–4
= 9.10 .10 (–3 + 2)
5
= 9.10 (–1)
5
= –9.10 V olur.
q yükünü ∞ dan L noktasına getirmekle yapılan iş,
W = q.V∞L
= q(VL – V∞)
= 1.10–5.(–9.105)
= –9 J olur.
10.
q1 = 6.10–4C
q2 = 4.10–4C
4m
A
B
5m
3m
5m
D
C
C noktasındaki potansiyel,
q
q
VC = k d 1 + 2 n
d1 d2
–4
= 9.10 . d
6.10
5
= 9.10 . b
18 + 20
l
15
9
5
+
4.10
3
–4
n
5
= 22, 8.10 V olur.
D noktasındaki potansiyel,
VD = 9.10 . d
9
6.10
3
–4
+
4.10
5
–4
n
5
= 9.10 . (2 + 0, 8)
5
= 25, 2.10 V olur.
Yükün C den D ye getirilmesiyle yapılan iş,
W = q.VCD
= q.(VD – VC)
= 2.10–6.(25,2 – 22,8).105
= 48.10–2 J olur.
232
ELEKTRİK VE MANYETİZMA
2. BÖLÜM
PARALEL LEVHALAR
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
Cisim dengede kaldığından,
q
4.10–6
3
d=
4.10
10
K
Fe=q. V
d
V
= mg
d
–3
1
2.10
= 2.10 .10
d
3.
m=2g
L
2d
M
3d
m
2m
+2q
+q
q=–4μC
+ –
–3
N
G=mg
–2
+ –
V
2V
fiekil-I
fiekil-II
Parçacıkların hızlarının oranı,
= 4.10–1 m
2q.V
j1 a 1 .t
m
.2d = 1
=
=
q.2V
1
j2 a 2 .t
3
2m.3d
= 40 cm olur.
CEVAP C
j1
= 3 olur.
j2
CEVAP E
2.
K
2d
+
+
E
+
+ m Fe
+
+ +2q
+
+
V1=10V
L
–
–
–
– jL
–
–
–
–
+ –
fiekil - Ι
M
d
+
+
E
+
+ m Fe
+
+ +q
+
+
V2
N
–
–
–
– jN
–
–
–
–
4.
q yükü dengede olduğundan,
tan45° =
1=
+ –
fiekil - ΙΙ
2
1
1 q.V m 2
a . t = .c
.t
2
2 m.d
q
eşitliğinden verilen değerler yerine yazılırsa potansiyeller oranı,
3
–1
K
+
+
+
+
+
+
+
+
+
+
= 2.10–3.101
45°
L
–
–
–
–
–
45°
–
düfley
–
–
G=mg
E
–
–
20cm
Fe=q V
d
+ –
4000V
q = 1.10–6 C olur.
CEVAP A
1 2q . V1 2
V
2d 2 . m . 2d . t
=
& 1 = 2 olur.
d
V2
q
.
V
1
2 2
.
.t
2 m.d
V1 = 10V olduğundan V2 = 5V olur.
4.10
2.10
V
d
mg
q
V
= mg
d
q.
Levhalar arasında yükler ivmeli hareket eder.
x=
Fe
G
CEVAP B
ELEKTRİK VE MANYETİZMA
233
5.
Parçacığın L levhasına
daha hızlı çarpması için,
K
+
ϑ=
E
+
2qV
m
+m
bağıntısına göre,
I ve III işlemleri tek başına
8.
L
–
d
K
–
+ q
–
+
–
+
–
+2q
+ –
+–
L
levhasına
6.
CEVAP D
K
L
2d
2m
M
t1
3d
fiekil-ΙΙ
V1
= 4 olur.
V2
CEVAP E
+4q
+q
9.
+ –
+ –
2V
V
fiekil-I
fiekil-II
Şekil-I de:
Yükler ivmeli hareket yaparlar. Levhalara ulaşma
V
2d
2mg = mg + q
V
2d
V
2d
T1=2mg
+q
m
Fe1=q V
2d
mg
olur.
Şekil-II de:
1 q.2V 2
2d 2 2m.2d .t 1
=
3d
1 4q.V 2
.t
2 m.3d 2
3q
2
V
= mg + T2
d
6mg = mg + T2
2 3t 1
=
3 8t 2
2
=
T = mg + q
1
mg = q
süreleri,
2
t1
2
t2
V2
fiekil-Ι
V
2
= 1
1 2V2
N
t2
m
+ –
V1
1 qV1 2
2d 2 . m.2d .t
=
d
1 2qV2 2
.
.t
2 2m.d
çarpma hızı levhalar arasındaki d uzaklığına bağlı
değildir.
N
d
2m
m
+q
j
•V•
Parçacığın
M
–
Fe
yapılmalıdır.
L
2d
Fe2=q 3V
d
m
+q
mg
T2 = 5 mg olur.
T2
16
9
t1 4
=
t2 3
CEVAP D
10. Şekil-I de:
olur.
CEVAP D
mg kuvveti ile yük aşağı yönde j limit hızıyla gitmektedir.
mg $ j olur.
7.
q.V
a=
bağıntısına göre,
md
d azalınca a artar.
t=d
2m
bağıntısına
qV
göre, d azalınca t azalır.
ϑ=
2qV
bağıntısına
m
Şekil-II de:
d
K
+
E
–
Fe
–
+ +q
+
+
V
q = mg olur.
d
–
+
+m
Yük dengede olduğundan,
L
–
E
j
Şekil-III te:
mg
–
q2V
– mg = 4mg – mg = 3mg olur.
d
2
3mg $ 3j
F
net
+ –
•V•
V
d
+q j=0
Yüke etki eden net kuvvet,
CEVAP B
ELEKTRİK VE MANYETİZMA
m
–
göre; ϑ, d ye bağlı değildir, değişmez.
234
Fe=q
=
Parçacığın limit hızı yukarı doğru, 3j olur.
CEVAP C
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
1.
4.
Levhalar arasında
yüke etki eden kuvvet sabittir.
Yükün C ve D noktalarındaki hızları yazılıp oranlanırsa,
K d
2
1
V
mjC
2 = 2
2
1
3V
q.
mjD
2
4
d
d L
d
1
F .d = .m.j2
A
e
2
q.
2
=
3
2
3
1
.m.j2D
2
Fe.4d =
A
2
jC
2
jD
jC
=
jD
I. yol:
m
+q B
C
E
D
K
+
d
d
d
d
L
–
d
–
+
–
+m
+ +q
A
B
C
+
+
D
–
–
E
+
E
–
–
V
eşitlikleri taraf tarafa oranlanırsa
jA 1
=
olur.
jD 2
jA = j ise,
olur.
jD = 2j olur.
+ –
V
A ve D noktalarından geçerken momentumları
yazılıp oranlanırsa,
CEVAP C
PD m.2j
=
= 2 olur.
PA
m.j
2.
Enerjinin korunumundan,
V
1
.d
mj
4d
= 2
2
1
V
q.
.x
m (2j)
2
4d
2
q.
d
1
=
x
4
x = 4d olur.
K d
d
d
d L
+
–
+
–
+m
+ +q
j
A
II. yol:
Kinetik enerji ile momentum arasındaki ilişkiden,
–
• B •C
–
+
–
+
–
D
2
2j
+ –
F.4d =
PD
2m
eşitlikleri taraf tarafa oranlanırsa,
2
P
1 PA
=
& D =2
4 P2
PA
D
CEVAP E
3.
PA
2m
2
• V•
Buna göre, parçacık D
noktasından 2j hızıyla
geçer.
F.d =
CEVAP D
E
➞
ϑo = 0
+q
K
➞
2ϑ
ϑ
L
M
E
Yapılan iş kinetik enerji değişimine eşittir. Bu eşitlik
kullanılırsa hızları oranı,
5.
q.VKL = ∆Ek1
1
mϑ2
2
= ∆Ek2
q.V1 =
q.VLM
q.V2 =
Yükü A noktasından B noktasına, B den de C noktasına
taşımak için yapılan iş,
AC
2
1
mj
q.V1
2
=
2
1
q.V2
m3j
2
+
= q(VC – VA)
= 5.10–6 (100 – 300)
= 5.10–6 (–2.102)
–3
= –1.10
V1
1
=
olur.
V2
3
+
+
W = q.V
1
1
1
m(2ϑ)2 – mϑ2 = m 3ϑ2
2
2
2
K
+
J olur.
+
L
–
B
•
•
C
m
A q=+5nC
–
–
–
–
–
+
+ –
• •
V=400V
CEVAP C
CEVAP B
ELEKTRİK VE MANYETİZMA
235
6.
K levhasındaki potansi-
K
L
yel 5V ise L levhasındaki
+
–
potansiyel 0 dır. K den L
+
ye giderken 5V lık potan-
+
–
siyel her aralıkta V aza-
+
–
larak L de sıfır olur.
+
–
+
Bu durumda
+
–
+ϑ
o
+
VA = 5V – V = 4V,
V = 5V – 4V = V
B
+
B
+q
m A
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
–
1.
–
A
+ –
K
+
d=4cm
+
E
+
L
B
Fe
5V
+ –
V=100V
olur.
q yüküne şekilde gösterilen yönde elektriksel kuvvet etki eder. Yükün A noktasından B noktasına
gelme süresi,
+q yüklü parçacığın A dan B ye taşınması sırasında yapılan iş,
W = +q.VAB
d=
= +q.(V – V )
B
A
= +q.(V – 4V)
4.10
–2
=
= –3qV olur.
1 2 1 qV 2
at =
.t
2
2 md
–6
2
t = 16.10
CEVAP A
2
1 2.10 .1.10 2
.
.t
2 1.10 –4 .4.10 –2
t = 4.10
–4
–2
s olur.
CEVAP C
2.
2m
bağıntısına
qV
t = d.
K
+
göre, t süresini azaltmak
+
için parçacığın kütlesi (m)
+m
azaltılmalıdır.
L
–
d
E
–
Fe
. –
+ +q
–
+
–
+
–
A
+ –
V
CEVAP A
3.
,
+
+
V –
A
+
m
+
+
+
+
+
jo
+ K
d
i
+q
–
O
P
Fe
–
.
–
–
–
–
–
– L
R
S
ekran
I. durumda:
Parçacığın düşeyde aldığı yol,
y=
2
1 q.V ,
.
. 2 olur.
2 md j
o
236
ELEKTRİK VE MANYETİZMA
yatay
y
5.
II. durumda:
,
– – – – – – – – –
Parçacığın levhalar arasına giriş hızı 2 katına,
Fe
levhalar arasındaki uzaklık yarıya indirildiğinde,
qV
,
.
d (2j ) 2
m.
o
2
1
y =
2
=
q
E
2
ı
=
y
olur.
2
–
+
V
Parçacık ivmeli hareket yaptığından sapma miktarı,
2
1 2 1 qE ,
a.t = .
. 2
2
2 m j
o
s=
o
2
1 1 qV ,
. .
2 2 md j 2
o
E
+ + + + + + + + +
2
1 2qV ,
. 2
2 md 4j
=
s
jo
bağıntısından bulunur.
Bu durumda sapma miktarı, cismin yüküne, kütlesine, ilk hızına ve levhaların boyuna bağlıdır.
Buna göre, parçacık II. durumda P noktasına çarpar.
CEVAP E
CEVAP C
K
E=400N/C
+
+
+
5m/s
+
F
+
+ mg
+
4.
d=12m
L
–
–
–
–
– h j
x
–
–
6.
– – – – – – – – – – – – – – –
K
ϑo=5.106m/s
ϑoy
37° ϑ
ox
+ + + + + + + + + + + + + + +
O
L
jy
E=4,5.103N/C
yatay
Fe=qE
Cisme etki eden elektriksel kuvvetin büyüklüğü,
F = q.E = 1.10–2.400 = 4 N olur.
Elektronun ivmesi,
a=
Cismin yatay ivmesi,
F = m.a
qE 1, 6.10 –19 .4, 5.10 3
14
2
=
= 8.10 m/s olur.
–31
m
9.10
Elektronun hızının yatay ve düşey hızları,
x
2
4 = 4.ax ⇒ ax = 1 m/s olur.
Cismin yatayda aldığı yol 12 m olduğuna göre,
2
1
d = j o t + a x .t
2
12 = 5.t +
ϑox = ϑo.cos37° = 5.106.0,8 = 4.106 m/s
ϑ
oy
= ϑo.sin37° = 5.106.0,6 = 3.106 m/s olur.
Uçuş süresi,
2
1
.1.t
2
t = 2.
u
2
t + 10t – 24 = 0
(t – 2) . (t + 12) = 0 & t = 2s olur.
joy
a
= 2.
3.10
8.10
6
14
=
–8
3
.10 s olur.
4
Cismin menzil uzaklığı,
Cismin düşeyde aldığı yol,
xmak = ϑox.tu
2
1 2 1
h = g.t = .10. (2) = 20 m olur.
2
2
3
= 4.106. .10–8
4
CEVAP D
= 3.10–2 m
= 3 cm olur.
CEVAP E
ELEKTRİK VE MANYETİZMA
237
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
3.
1. Enerjinin korunumundan +q yüklü parçacığın A ve B
deki hızları,
2
4V
1
.d = mj 1
q.
2d
2
q.2V =
q.4V – q.
K
–
d
q.2V =
2
1
mj 2
2
2
1
mj 2 ...Y
2
+
–
+
–
–m
+
A
+
–
+
d L
d
e
d
d
d
B
V1=6V
V2=12V
KL arasında elektriksel kuvvetin yaptığı iş,
E = F .x = q
k
e
Ek1 = e.
V
.x
d
–
– +
+–
4V
3V
K
–
–
–
–
– m
A –
– –q
–
–
–
L
+
+
+
+
d
+
+
+
+
2d
B
CEVAP A
M
–
–
–
–
–
–
–
–
– +
+ –
4V
3V
C noktasından geçerken hızı,
Yüklü parçacık B noktasından,
2
1
mj
q.4V
2
=
q. (4V – 3V)
›2
1
mj
2
2
j
4
= ›2
1
j
EKo + EK1 – EK2 = EKB
8eV + 4eV – 9eV = EKB
2
j
= ›
1
j
EKB = 3eV
kinetik enerjiyle geçer.
CEVAP B
ELEKTRİK VE MANYETİZMA
–
C
Parçacığın B noktasından geçerken hızı ϑ olsun.
6V
.2d = 4eV olur.
3d
LM arasında elektriksel kuvvetin yaptığı iş,
12
.3d = 9eV olur.
EKB = e.
4d
238
ı
M
4.
+ –
j
–D
CEVAP C
ϑo
– +
C
B
2 j
j
=
& jı =
olur.
1 jı
2
d
A
–
j
+
–
2
j
j
2
= 12 & 1 = 1 olur.
2
j2
j2
d
M
–
2
1
mj
q.4V
2
=
ı2
1
q. (4V – 3V)
mj
2
2
4
j
= ı2
1
j
2
1
m j1
q.2V
= 2
q.2V
2
1
m j2
2
K
d
Enerjinin korunumundan parçacığın D noktasından geçerken hızı,
' ve ( eşitlikleri oranlanırsa,
2.
d
–
2
3V
1
.2d = mj 2
3d
2
q. (4V – 2V) =
d
–
– –q
2
1
mj 1 ...X
2
L
+
d
ϑı =
j
olur.
2
Parçacığın levhalar arasındaki hız-zaman grafiği,
7.
K
–
h›z
–
F
ϑ
ϑ/2
d
t
t=
4d
M
–
E1
+
+
E2
–
A
+
t
C
–
–
+
zaman
›
B
–
E
–
D
+
–
şekildeki gibi olur. Hız-zaman grafiğinde doğrunun
altındaki alan hareketlinin aldığı yolu dolayısıyla
levhalar arasındaki uzaklıkları vereceğinden,
d
=
2d
L
+
–
2d
0•
–
–
–
3d
– +
+ –
2V
3V
Enerjinin korunumundan,
q.2V = q.
j.t
2
›
j
+
j
/
2
c
m (t – t)
2
3V
.x
4d
8d = 3x & x =
8
d olur.
3
Buna göre, elektronlar C-D arasından geri dönerler.
CEVAP D
3 ı
(t – t)
4
4t = 3tı – 3t
ı
t =
tı – t =
5.
7
t
3
7
4
t – t = t olur.
3
3
K
m
3d
L
CEVAP C
2d
8.
d1
K
–
M
–
– m
– –q
+q
Eko=2qV
–
– +
6V
3V
M
–
–
–
j=0
B
A
+ x
+
+
–
+ –
d2
L
+
+
+
C
D E–
–
–
– +
+ –
V1
V2
I. durumda:
Yüklü parçacık M levhasına enerjinin korunu-
Yük B noktasına kadar ulaşabildiğine göre,
mundan,
x=
Eson = Eilk + EKL + ELM
= 2qV + 6qV – 3qV
V1
.d olur.
V2 2
II. durumda:
= 5qV
Yükün D noktasına ulaşabilmesi için,
kinetik enerjiyle çarpar.
CEVAP E
6.
ı
3x =
E kA = q.2V = 2qV
E k = q.3V – q
.d2 olur.
V1 gerilimi 3 katına çıkarılırsa parçacık D noktasına ulaşır.
3
qV
2
E kA 2qV 4
=
=
olur.
E kB 3
3
qV
2
ı
V2
Yükün aldığı yol d uzaklığına bağlı değildir.
1
2V
.3
4
3
= qV b 3 – l
2
=
V1
V2 gerilimi üçte birine indirilirse parçacık D noktasına ulaşır.
II ve III işlemleri tek başına yapılmalıdır.
CEVAP D
CEVAP D
ELEKTRİK VE MANYETİZMA
239
9.
Hız-zaman grafiğinde doğrunun altındaki alan yükün
aldığı yolu verir. Şekildeki
grafikten x = 2d olur.
h›z
Enerji korunumundan,
V
q.V = q. 2 .x
1
3d
V
V = 2 .2d
1
3d
V1
2
=
olur.
3
V2
10.
K
d1
–
–
–
E1
+ m
0
+ +q
–
–
–
+
+
2d
t
2t zaman
CEVAP B
(+)
L
+
+
d
,
+
+
+
+
d2 j
o
E2
+
+
+ M
d2/2
i
–
–
–
–
–
y
–
–
N
yatay
d2/2
j
(–) Vs
+ –
Vh
2qVh
bağıntısına göre, hızlandırıcı gerilim
m
j =
o
4 katına çıkarıldığında, parçacığın M ve N levhaları arasına giriş hızı 2j olur.
o
I. durumda:
t=
,
jo
y=
2
1 qVs ,
. 2
2 md 2 j
o
II. durumda:
tı =
,
t
=
olur.
2
2j o
ı
y =
2
y
1 qVs ,
=
olur.
2 md 2 4j 2 4
o
I. durumda:
j =
y
qVs
.t
md 2
jy
j
II. durumda:
jı =
y
jyı
=
qVs t
.
md 2 2
jy
2
jo
.
i
jo
.
i
jy/2
ı
j
I. yargı doğrudur.
II. ve III. yargılar yanlıştır.
240
ELEKTRİK VE MANYETİZMA
CEVAP A
TEST
1
PARALEL LEVHALAR
ÇÖZÜMLER
1.
3.
kuvvet
hız
F
37°
ivme
a
j
4
E
m
q
0
Fe=q.E
0
t zaman
I
0
t zaman
II
III
Grafiklerin üçü de bu parçacığa ait olabilir.
37°
düfley
t zaman
G=m.g
CEVAP E
Şekildeki yük dengede olduğundan,
tan 37° =
Fe q.E
=
G m.g
–6
3
6.10 .E
=
4 2.10 –3 .10
–4
3
= 3.10 .E
4
E=
10.000
1
=
= 2500 N/C olur.
–4
4
4.10
4.
Yükü A noktasından C noktasına getirmekle yapılan iş,
K
W = F.x = q.
CEVAP D
= 4.
L
V
.x
d
B
20
.3
4
C
= 60 J olur.
A
2.
K
d
t1
+ +q
+
m
q=–4C
–
+
+ 2m
L
+ –
–
V=20V
–
t2
m –
CEVAP E
–2q –
–
+
+
+ –
V
Şekildeki yükler karşı levhalara çarptıklarında eşit
5.
yollar alırlar.
Yapılan iş kinetik enerji
K d
d
d L
d
değişimine eşittir.
d1 = d2 = d
2
V
1
.d
mj
4d
2
=
2
V
1
q.
.x
m ( 3 j)
4d
2
q
2
2
1
1
a t = a t
2 1 1 2 2 2
q.E 2 2q.E 2
.t =
t
m 2
2m 1
2
t1
=
m
+q
ϑ
A
•
B
•
C
•
D
d 1
=
x 3
2
4t 2
x = 3d olur.
t 1 = 2t 2
t1
= 2 olur.
t2
+ –
• •
V
Parçacık C noktasından v3 ϑ hızıyla geçer.
CEVAP B
CEVAP C
ELEKTRİK VE MANYETİZMA
241
6.
Enerjinin korunumundan,
K
2
2
1
1
mj ! q.V = mj 2
2
2
olur. j2 hızının artması
rılmalıdır.
–
E
+
–
m j1
+
–
+
–
+
–
I. durumda:
+ –
işlemi için kesin birşey
V
+q
II. durumda:
CEVAP A
V1
›
V2
.d 2
9.
+
+
+
+
V –A
+q
jo
+
A
V –
+
+
+ K
jo
i
+q
–
–
–
–
–
y
–
–
h=
yatay
d/2
Parçacığın levhalar arasından geçme süresi ve
sapma miktarı,
y=
2
1 qV ,
. 2 olur.
2 md j
o
,
+
+
+
+
+ K
yatay
–
–
B
–
–
–
– L
1
a.t2
2
2
m.d
q.V
t=d
x = j .d
o
,
t
t =
=
olur.
2
2j o
ı
m
olur.
qV
m
olur.
qV
Buna göre, x yolunu artırmak için I ve IV nicelikleri
artırılmalıdır.
CEVAP D
10. Şekil-I de:
mg → ϑ limit hız kazandırır.
Şekil-II de:
t $ yarıya iner.
F e =qE = q
Yük dengede olduğundan ϑ = 0
2
1 q.4V ,
.
.
2 md 4j 2
dır.
o
m
V
d
q
Şekil-III te:
2
1 qV ,
.
. 2 olur.
2 md j
=y
+
–
x = jo.t
Parçacığın levhalar arasından geçme süresi ve
sapma miktarı,
=
V2
Yükün yatayda alacağı yol,
II. durumda:
ı
y =
– +
V1
d
1 q.V 2
=
.t
2 m.d
2
–
–
L
yatay
t2 =
,
jo
E
+q yükünün sapma miktarından,
I. durumda:
t=
+ –
x
d/2
m
–
+
D
d/2
,
+
C
d/2
m
+
B
d1 aralığına bağlı değildir. V1 gerilimi dört katına
çıkarılmalı, V2 gerilimi dörtte birine indirilmelidir.
Parçacığın E noktasına kadar ulaşabilmesi için I
ve II işlemleri tek başına yapılmalıdır.
CEVAP B
değildir.
+
A
olur.
j2 hızı levhalar arasındaki d uzaklığına bağlı
+
M
›
4x =
söylenemez.
7.
d2
m
j2
Parçacığın yükünün işareti bilinmediğinden II
L
d1
K
V
x = 1 .d 2
V2
–
+
için j1 hızı kesinlikle artı-
8.
L
d
+
q
o
y $ değişmez.
CEVAP A
V
2V
– mg = q
– mg
d
d
2
mg
q
V
=mg
d
Fnet = 2mg – mg = mg kuvveti ϑ hızı kazandırır.
Yukarı yönde, ϑ olur.
CEVAP C
242
ELEKTRİK VE MANYETİZMA
TEST
2
1.
3.
37° ip
K
–
m
–
–
düfley
–
E
–
+
Fe
+
2md
qV
t2 =
t=d
–
+ –
V
2
2m
qV
4.
A noktasındaki gerilim
VA = V dir. Her aralıktaki
V
olacağıngerilim ∆V =
4
dan B noktasındaki gerilim,
V = V – 3.
B
d
L
V V
=
4 4
K
L
B
A
m
q=–2μC
olur.
–
+
E
+
+
–
+
CEVAP C
3 mgd
olur.
4 V
K
–
E
+
bağıntısına göre, d artınca t artar.
V
d
CEVAP A
2.
–
1 qV 2
d= .
.t
2 md
Fe
G
q= –
–
Yapılan iş ifadesinden,
m ϑo
W = q.VAB = q.(VB – VA)
ϑ
+q
6.10–4 = – 2.10 – 6 c
–
+
E
–
3.102 =
–
+
+ –
V
–
+
3
V
4
V
– Vm
4
V = 400 V olur.
+ –
CEVAP C
• •
V
Yapılan iş kinetik enerji değişimine eşittir. Parçacığın karşı levhaya çarpma hızı,
W = TE k = E k2 – E k1
qV =
2
2
1
1
mj – mj o
2
2
2
jo +
5.
X ve Y parçacıklarının aldıkları yollar eşit ve d dir.
K
Yüklerin kütleleri oranı,
+
1
1
a .t2 =
a .t2
2 X X 2 Y Y
2
2
1
1
mj = mj o + qV
2
2
j=
–
değişmez.
–q yüküne etki eden kuvvetler şekildeki gibidir.
Yük dengede olduğundan,
mg
–
E
+ +q
ye bağlı değildir. ϑ hızı
V
(–q) .
L
d
+
+
2qV
bağıntısı d
m
ϑ=
– +
3
=
4
K
+ m
37° +
+
mg +
d
qV
bağıntısına göre,
md
a=
d artınca a azalır.
L
+
–q
–
tan37° =
PARALEL LEVHALAR
ÇÖZÜMLER
1 q.V
1 2q.V 2
(2t)2 = .
.
.t
2 m X .2d
2 m Y .2d
2qV
olur.
m
4
2
=
mX
mY
Levhalar arasındaki uzaklığa bağlı değildir.
CEVAP B
mX
= 2 olur.
mY
d
d
X
+
+
+
L
–
+
t
mX 2t
+q
–
–
–
mY
Y
–2q
–
–
+
+ –
V
CEVAP D
ELEKTRİK VE MANYETİZMA
243
6.
K
2d
L
m
8.
M
4d
Yüke etki eden net kuvvet sıfır ise sabit hızla hareketini sürdürür.
ϑ=0
–q
A
B
C
D
E
m
V
= mg
d
q
+ –
V2
.3d
q.V1
d
4
=
q.2V1
3V
q. 2 .x
4d
jo
yatay
+q
bağıntısına göre, levhalar aramg
sındaki uzaklık yarıya indirildiğinde, I işlemi tek başına yapılmalıdır.
V2
V1
– +
Fe=q V
d
Fe = G
CEVAP A
q.
9.
1 d
=
2 x
x = 2d
Parçacığın levhaları terk
etme süresi,
t=
olur.
jo
.
i
jy=Dj
,
jo
j
olur. Yükün yatay hızı sabittir. Yalnızca düşey hız
zamanla artar. Parçacığın hızının değişim miktarı,
II. durumda parçacık C noktasına ulaşabilir.
CEVAP B
Dj = jy = a.t
Dj =
qV ,
.
olur.
md j o
Buna göre, parçacığın j hızının değişimi, I, II, III
ve IV niceliklerine bağlıdır.
CEVAP E
7.
K
M
L
N
10.
A
•
W2
B
m
•
+2q W1
C
•
•
D
+q
3V
fiekil-Ι
– +
a2 =
A noktasındaki potansiyel VA = –3V, B noktasındaki potansiyel VB = –V olur. A ve B noktaları arasındaki potansiyel fark VAB = –V – (–3V) = 2V olur. C
noktasındaki potansiyel VC = –4V, D noktasındaki
potansiyel ise VD = –V olur. C ve D arasındaki
potansiyel fark VCD = –V – (–4V) = 3V olur. Yapılan
işlerin oranı,
–
–
–
+ –
– +
V1
V2
M
+
+
+
+
+
+
+
q.V2
m.d 2
E K2 = q (V1 – V2)
d 2 = j o .t 2 –
1 2
at
2 2
II. durumda:
›
a2 =
q.V2
›
md 2
d2 > d2ı olduğundan a2ı > a2 olur.
I. yargı doğrudur.
W 1 2q.2V
4
=
=
olur.
W2
q.3V
3
EK2ı = q(V1 – V2)
II. yargı doğrudur.
1 ı ı 2
ı
ı
d2 = ϑo.t 2 – a 2t 2
2
ı
t 2 < t2 olur.
II. yol:
ELEKTRİK VE MANYETİZMA
d2
I. durumda:
4V
fiekil-ΙΙ
I. yol:
3V
W 1 2q. 3d 2d
4
olur.
=
=
W2
3
4V
q.
.3d
4d
L
–
–
–
d1
+
+
+m
+
+q
+
+
+
2m
– +
244
K
III. yargı doğrudur.
CEVAP D
CEVAP E
TEST
1.
3
(1) ve (2) eşitlikleri taraf tarafa oranlanırsa,
Cisme etki eden elektriksel
kuvvet,
F = q.E
e
= 6.10–2.300
= 18 N olur.
Cisim dengede olduğundan
Lami teoremi uygulanırsa,
T
F
=
sin 127° sin 143°
37°
T
2
1
q.V1 2 m 4j
=
2
q.V2 1
m 5j
2
V1 4
=
olur.
V2 5
Fe
53°
37°
G
4.
T
F
=
sin 53° sin 37°
d
d
L
–
d
+
d
d
–
+
–
+
+
A
+
–
B
+
C
–
E1
E2
–
+ –
– +
V
40
= 3.
= 6N
d
20
Cismin ivmesi,
M
+
Fnet = m.a
+
G + Fe = m.a
+
30 + 6 = 3a
+
yatay
+ + + + + + +
+
20m V =12m/s
o
– – –
G
2
40V
–
3kg
– – –
Fe
36 = 3.a ⇒ 12 m/s olur.
Cismin uçuş süresi,
+
+
tu =
4V
6V
Cisme etki eden kuvvetler,
Fe = q.
CEVAP C
K
CEVAP E
G = m.g = 3.10 = 30 N
T
18
=
& T = 24 N olur.
0, 8 0, 6
2.
PARALEL LEVHALAR
ÇÖZÜMLER
2Vo 2.12
=
= 2 s olur.
a
12
CEVAP A
KL levhaları arasındaki elektrik alanı her yerde aynıdır.
E =E =E =
1
A
B
6V
V
= 2 dir.
3d
d
LM levhaları arasındaki elektrik alanı her yer de aynıdır.
4V
V
=2
dir.
E2 = EC =
2d
d
Buna göre; EA = EB = EC olur.
5.
q.
E
2j
L
–m
V
.d = Ek
d
Ek = q.V dir.
Buna göre; I ve IV niceliklerine bağlı değildir.
3j
M
L
+
E
–
F.d = Ek
CEVAP B
d
K
–
W = DEk = Ek2 – Ek1
3.
jo = 0
+q
K
Enerjinin korunumundan L levhasına çarptığında
kinetik enerjisi,
+
Fe
+ Ek
– –q
+
–
+
–
+
– +
•V•
CEVAP C
E
KL aralığında enerjinin korunumundan,
q.V
= DEk1
1
q.V1 =
m (2j)2 – 0
2
1
q.V =
m 4j2 ... (1)
1
2
LM aralığında enerjinin korunumundan,
q.V
KL
LM
6.
q=5.1020C
2m
4m/s
4m/s
O
2kg
2kg
= DEk2
1
1
m(3j)2 –
m(2j)2
2
2
1
1
q.V2 =
m 9j2 –
m 4j2
2
2
1
q.V2 =
m 5j2 ... (2)
2
q.V2 =
Kürenin içinde elektrik alan olmadığından cisme bir
kuvvet etki etmez. Bu durumda cismin hızı değişmez.
Ek =
2
2
1
1
mj = .2. (4) = 16 J
2
2
CEVAP D
ELEKTRİK VE MANYETİZMA
245
7.
+ + +
+ + +
+
–
V
K
m
+q
2d
N + + +
+q
d
+ + +
M – – –
– – –
Eğik düzlemin yüksekliği 16 m olduğundan,
+
16 = | KL | .0, 8 & | KL | = 20 m olur.
– 2V
| KL | =
›
ϑ
– – –
– – –
20 =
L
ϑ
2
1
.10.t & t = 2 s olur.
2
Cismin L noktasına vardığında hızı,
fiekil- II
fiekil- I
1 2
a.t
2
ϑ = a.t = 10.2 = 20 m/s olur.
L
Yerçekimi ihmal edildiğinden elektriksel kuvvetlerin
İtme = momentum değişimi olduğundan,
yaptığı iş kinetik enerjideki değişmeye eşittir.
F.∆t = ∆P
W = ∆E
k
F.∆t = P – P
s
i
2
1
Şekil-I de, q.V = mj
2
Şekil-II de, q.2V =
F.∆t = Ps – 0
F.∆t = m.ϑ
›2
1
mj eşitlikleri oranlanırsa,
2
L
F.∆t = 2.20
2
F.∆t = 40 N.s olur.
›
1 j
=
& j = 2 j olur.
2 j›2
CEVAP D
CEVAP A
9.
+
8.
+
+
+
+
+
G
L
–
–
–
F
–
F
F
= G + F = 20 + 5 = 25 N olur.
net
°
K
53
›
2
L
53°
53°
Fnet=25N 16m
ı
Cismin ivmesi,
–
–
–
G
Cismin yatay ve düşey hızları,
Cisme etki eden kuvvetler,
G = m.g = 4.10 = 40 N
F = q.E = 2.10–2.400 = 8 N olur.
Cismin ivmesi,
F
net
= m.a
Cismin uçuş süresi,
2.j y 2.12
=
= 2 s olur.
tu =
a
12
xmen = ϑx.tu = 16.2 = 32 m/s olur.
2
20 = 2.a ⇒ a = 10 m/s olur.
ELEKTRİK VE MANYETİZMA
–
hmax
Cismin menzil uzaklığı,
= m.a
F = m.a
246
37° ϑX
– – –
40 + 8 = 4.a ⇒ a = 12 m/s2 olur.
F = F .sin53° = 25.0,8 = 20 N olur.
net
net
ı
+
G + F = m.a
Cismi eğik düzlemde hareket ettiren kuvvet,
F
+
ϑ = ϑ.sin37° = 20.0,6 = 12 m/s olur.
y
Cisme düşey düzlemde etki eden net kuvvet,
F=
+
ϑ = ϑ.cos37° = 20.0,8 = 16 m/s
x
V
200
= 0, 5.
= 5N
d
20
ϑL
ϑy
–
G = m.g = 2.10 = 20 N
in
5.s
+
E
Cisme etki eden kuvvetlerin büyüklükleri,
F = q.
+
ϑ=20m/s
+
200V
–
–
53°
–
+
+
K
20m
+
CEVAP D
10.
12.
qX = –q
mX = m olsun.
fiekil-Ι de
Fe1=q
m
V
2d
m
–q
T
mg
a
2V
Fe2=q
d
a=
G = Fe1
q
8m
–q
G=mg
mg = q
T
fiekil-ΙΙ de
V
2d
=
V
= 2 mg olur.
d
›
T
X
Y
2kg
4kg
Fnet
m
FX
2m
›
GX
FY
a
GY
2V
d
mg + q
m
Cisimlere etki eden kuvvetler şekilde gösterilmiştir.
mg + 4mg
=
m
Bu kuvvetlerin büyüklükleri,
= 5g olur.
G X = m X .g = 4.10 = 40 N
G Y = m Y .g = 2.10 = 20 N
Aşağı yöndedir.
CEVAP E
FX = q.
V
220
= 2.
= 44 N
d
10
FY = q.
V
220
= 4.
= 88 N
d
10
GY + FY > GX + FX olduğundan sistem ok yönünde ivmeli hareket yapar. Dinamiğin temel prensibi
sisteme uygulanırsa,
Fnet = mt.a
(G + F ) – (G + F ) = (m + m ).a
Y
Y
X
X
X
Y
(20 + 88) – (40 + 44) = (4 + 2).a
108 – 84 = 6.a
24 = 6.a ⇒ a = 4 m/s2 olur.
Y cismine dinamiğin temel prensibi uygulanırsa,
11. Cisme etki eden kuvmiştir. Cismin hareket
–
–
doğrultusunu değiştirmemesi için, elektriksel
–
– Fe
E
–
–
Fnet = m.a
–
–
vetler şekilde gösteril-
V
+
60°
ϑo
ı
GY + FY – T = mY.a
ı
20 + 88 – T = 2.4
ı
4m
kuvvetin düşey bileşeninin cismin ağırlığına
60°
+
+
+
G + +
+
+
+ 60°
yatay
eşit olması gerekir.
ı
108 – 8 = T ⇒ T = 100 N olur.
İpteki T gerilme kuvveti,
ı
T = 2T = 2.100 = 200 N olur.
CEVAP B
Fe . cos 60° = G
q.
4.10
–2
.
V 1
. = m.g
d 2
V 1
. = 2.10
4 2
V = 4000 volt olur.
CEVAP E
ELEKTRİK VE MANYETİZMA
247
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
1.
fiekil-Ι de
(Paralel Levhalar)
fiekil-ΙΙ de
Fe= q V
d
m
Bölüm
Yazılı Soruları
+q
3.
a)
›
Fe= q. 2V = 4q. V
d
d
2
+q
m
G = mg
ÇÖZÜMLER
400V
+ –
m
K
•
d/2 q
L
d/2
,
G = mg
•
a) Hareket yönü yukarı yöndedir.
b)
ϑy
›
Fe = G
Fnet = F e – G
= 4q
V
q = mg olur.
d
ϑx
P
ϑ
Yük düşeyde serbest düşme hareketi yapacağın-
V
– mg
d
dan levhaların boyu,
= 4mg – mg
, = 1 gt2
= 3mg
2
F
3mg
a = net =
= 3g olur.
m
m
=
1
10.(0,2)2
2
= 5.0,04
= 0,2 m = 20 cm olur.
b) Levhalar arası uzaklık,
2.
(+)
d
1 qV 2
= .
.t
2
2 md
+ + + + + + + + +
K
m Vo=2.105m/s
•
q
E=400V/m
y
1 2
at
2
. (0, 2)
2
–19
.64.10
–4
Yüke yukarı yönde elektriksel
kuvvet, aşağı yönde ağırlığından dolayı kuvvet etki eder.
Fe=q.E
= mg – q.E
2
–7 2
1 1, 6.10 .4.10
=
. (8.10 )
–27
2
3, 2.10
–14
m
= 6, 4 mm olur.
248
2.10
–4
2
m=2.10–2kg
Fnet
a) Fnet = G – Fe
1 q.E 2
.t
2 m
= 64.10
.4.10
d = 40 cm olur.
–2
10
–6
d = 4.10–1 m
–7
,
16.10
=
= 8.10 s olur.
5
jo
2.10
= 10
2.10
d = 4.4.10–2
4.
=
d2 =
2
(–)
b) y =
qV 2
.t
m
– – – – – – – – –
L
a) t =
d2 =
ELEKTRİK VE MANYETİZMA
–2
–5
3
= 2.10 .10 – 4.10 .2.10
G=mg
= 20.10–2 – 8.10–2
= 12.10–2 N
Cismin ivmesi,
a=
Fnet 12.10 –2
2
=
= 6 m/s olur.
–2
m
2.10
b)
d=
8.
1 2
at
2
a=
1
= .6.(0,2)2
2
= 3.0,04
=
= 0,12 m
d)
E=
V=
=
=
=
ϑ=
qV
md
–6
K
10 cm
–
–
–
– m = 4.10–6kg
–
– q = –2.10–6C
–
–
–
2
2.10 .4.10
–6
–1
4.10 .1.10
3
2
= 2.10 m/s
= 12 cm olur.
c)
a) Parçacığın ivmesi,
olur.
b) Levhaya çarpma hızı,
V
d
E.d
2.103.12.10–2
24.101
240 V olur.
a.t = 6.0,2 = 1,2 m/s olur.
=
V = 400V
2.2.10
=
–6
4.10
4.10
+
+
+
+
– +
2qV
m
j=
L
+
+
+
+ ϑ
.4.10
2
–6
2
= 20 m/s olur.
5.
FeX=q
4V
3d
V
2d
FeY=4q
X
c) Yükün L levhasına ulaşma süresi,
ϑ = a.t
3
20 = 2.10 .t
Y
–2
t = 1.10
GX=mX.g
GY=mY.g
mX . g= q 4V
3d
9.
mY .g = 4q V
2d
V
F qd
tan 37° =
=
G mg
–5
5.10 .V
–1
3
= 5.10
4 4.10 –3 .10 1
K
+
37°
–
+
–
37°
–
+
düfley
+
mg –
+
–
d=50cm
2
1 2qV 2 1 qV
.
.t = .
. 4t
2 mX d
2 mY d
d/2
mX t
X
+2q
+
+
+
mX 1
=
olur.
mY 2
d/2
L
–
+
–
–
+
A+
q=+4.10–4C
+
+ –
500V
–
–
Cismin A noktasından B noktasına taşınması sırasında elektriksel kuvvetlerin yaptığı iş,
W = q.V
= –16.10–2 J olur.
+
2m X = m Y
–
+
= 4.10–4(– 400)
–
+
–
+
= 4.10–4.(100 – 500)
+
2
4
=
mX mY
–
AB
V
K
B
+
= q(VB – VA)
+ –
–4
X ve Y parçacıklarının ald
dıkları yollar eşit ve
dir.
2
V
F=q
d
L
–
+
B noktasındaki potansiyel,
V = 500 – 4.∆V
B
= 500 – 4.100
= 500 – 400
= 100 V olur.
L
–
+
10 .V
3=
–2
10
V = 300 V olur.
7.
K
+
Her aralıktaki potansiyel,
500
TV =
= 100 V
5
olur.
mX 2
=
olur.
mY 3
Yük levhalar arasında
şekildeki gibi dengede
olduğundan şekildeki
üçgenden,
A noktasının potansiyeli,
VA = VK = 500V olur.
4V
q
m X .g
3d
=
m Y .g
V
4q
2d
6.
s olur.
2t
–
–
–
mY
Y
–q
–
–
–
+
+ –
V
10. q yükü L levhasını geçtikten x
kadar uzaklıkta
dursun. Enerjinin
korunumundan,
V
q.V1 = q. 2 .x
d2
x=
V1
.d
V2 2
x=
100
.10
250
K
+
d1=4cm
L
–
+
–
+ m
–
+ +q
–
+
–
+
–
+ –
100V
d2=10cm
M
+
+
ϑ=0
+
+
x
+
– +
+
250V
x = 4 cm olur.
ELEKTRİK VE MANYETİZMA
249
250
ELEKTRİK VE MANYETİZMA
3. BÖLÜM
KONDANSATÖRLER
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
4.
enerji(J)
4.10–4
1.
Bir kondansatörün sığası yapısına bağlıdır. Yüküne ve uçları arasındaki elektriksel potansiyel farkına bağlı değildir.
C=
1.10–4
0
q 2q 3q 4q
=
=
=
= sabit
V 2V 3V 4V
10
gerilim(V)
Kondansatörün sığası,
1
E = .C.V2
2
CEVAP C
4.10–4 =
C=
2.
5
1
.C.102
2
8.10
10
–4
2
= 8.10–6 F olur.
Kondansatöre 100 V luk gerilim uygulandığında
yükü,
r yarıçaplı iletken bir kürenin sığası,
q = C.V
r
C=
k
= 8.10–6.102
8
=
6.10
9
9.10
=
1
F olur.
15
= 8.10–4 C olur.
r
CEVAP D
5.
I. Yol:
Kondansatörün üzerindeki gerilim,
q
5
160
V= =
= 4.10 volt olur.
C 400.10 –6
CEVAP A
Kondansatörün enerjisi,
E=
2
–6
5 2
7
1
1
.C.V = .400.10 . (4.10 ) = 3, 2.10 J
2
2
olur.
3.
CY
CX
A
A
f
d
X
A
CZ
A
2f
2d
Y
A
d
Z
Kondansatörlerin sığaları,
A
CX = f = C
d
CY = 2f
II. Yol:
A
2
2f
E=
6.
2
1 q
1 (160)
7
.
= .
= 3, 2.10 J olur.
2 C 2 4.10 4
CEVAP E
Kondansatörün sığası,
C=
q 1.10 –4
–6
=
= 4.10 F olur.
V
25
İlk durumda kondansatörün enerjisi,
A
A
=f =C
2d
d
2
E1 =
A
= 2C olur.
d
Buna göre, CZ > CX = CY olur.
CZ = 2f
1 q
.
2 Co
–4 2
=
1 (1.10 )
.
2 4.10 –6
=
–2
1
.10 J olur.
8
CEVAP B
ELEKTRİK VE MANYETİZMA
251
A
eşitliğinde görüld
düğü gibi sığa d ile ters orantılı olduğundan,
d, 4 katına çıkarılırsa, C = f o .
C=
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
1.
C o 4.10 –6
–6
=
= 1.10 F
4
4
a)
L
6F
olur. Son durumda kondansatörün enerjisi,
seri
4F
2
1 q
E2 = .
2 Co
K
–4 2
1 (1.10 )
= .
2 1.10 –6
C KL = 6 +
–2
1
= .10 J olur.
2
Bir sistem üzerine yapılan iş, sistemin enerji değişimine eşittir. Bu durumda,
6F
K
CEVAP C
Kondansatörün yaprakları arasındaki potansiyel
fark her zaman üretecin potansiyeline eşittir. V
sabittir. Yapraklar arasına dielektrik bir madde
konursa sığası,
C = l . εo .
4.2
4F
=
4 +2
3
=
6.4 12 F
=
6+4
5
M
seri
4F
C efl =
C1.C 2
C1 + C2
2F
M
iş yapılmış olur.
7.
=
L
–2 1
–2
1
= .10 – .10
2
8
–2
3
.10 J
8
C 1.C 2
C1 +C 2
4 22 F
=
olur.
3
3
b)
W = TE = E 2 –E 1
=
2F
C efl =
A
artar.
d
C KM = 2 +
c) C ML = 4 +
12 22 F
=
olur.
5
5
3 11F
=
2
2
L
seri
olur.
6F
Kondansatörün yükü ise,
K
Q = C.V
4F
2F
V sabit, C arttığından Q da artar.
CEVAP D
8.
Kondansatör V potansiyeli ile dolunca
yükü;
q = C.V olur.
C
•
•
K
L
q
Kondansatörün sığası;
C = εo .
A
dir.
d
d azaltılınca C değeri artar.
II. yargı doğrudur.
Artık kondansatörün uçları üretece bağlı olmadığından yapılan değişiklikler kondansatörün yükünü değiştirmez. q sabittir.
I. yargı yanlıştır.
q = C.V eşitliğinde q sabit olduğundan C artarsa
eşitliğin korunabilmesi için V nin azalması gerekir.
III. yargı doğrudur.
252
ELEKTRİK VE MANYETİZMA
CEVAP E
C efl =
C1.C 2
6.2
3F
=
=
C1 + C2 6 + 2 2
M
2.
a)
6F
M
K
c)
K
K
paralel
6F
6F
K
4F
L
4F
2F
3F
L
Cefl=12F
4F
6F C =12F
efl
12 .8
24F
=
12 + 8
5
8F
L
M
4F
1F
K
L
Cefl=8F
C efl =
seri
12F
4F
M
1F
M
4F
6F paralel
seri
4F
Cefl=2F
3F
6F
L
L
2F
K
K
1F
4F
L
3F
C ML =
2F
24
44F
olur.
+4 =
5
5
seri
4F
4F
Cefl=2F
3.
4F Cefl=3F
seri 12F
1F
K
L
3F
2F
2F
CKL = 3 + 1 + 3 + 2 + 2 = 11 F olur.
a) K-M noktaları arasında sığa bulunurken akımın K den
girip M den çıktığını
düşünmeliyiz. Eğer
devre çok karışık
ise noktalama yapılarak devre açılmalıdır.
paralel
paralel
2F
4F
1F
1F
3F
K
M
5F
C2
C1
C1 = 2 + 4 + 1 + 5 = 12F
b)
C2 = 1 + 3 = 4F
6F
M
K
K
K
C KM =
6F
K
4F
2F
3F
L
L
paralel
değer sığa ise,
M
3F
= 12F olur.
4F
1F
1F
3F
K
4F
L
2F
5F
4F
4F
L
Cefl=2F
seri
6F
c) L-M arasındaki eşde-
6F
seri
L k›sa devre
2F
CKL = 2 + 4 + 1 + 5
1F
K
M
b) K-L arasındaki eş-
4F
6F
K
4F
4F
L
6F
12F
K
= 3F olur.
K
1F
12.4
12 + 4
8F
M
4F
C efl =
8 44F
olur.
C KM = 6 + 6 + =
3
3
8.4
8F
=
8+4 3
k›sa devre
ğer sığa, 1F ve 3F lik
kondansatörler paralel
L paralel
2F
bağlı olduğundan,
4F
CLM = 1 + 3
1F
= 4F olur.
1F
M
3F
5F
L
ELEKTRİK VE MANYETİZMA
253
4.
a) Noktalama yöntemiyle devrenin açık şekli çizilir ve eşdeğer sığa bulunur.
M
3F
4F
K
a)
K
K
L L
4F
3F
M
L
L
1F
L
5F
5F
12F
6F
C24=6F
1F
K
K
4F
K
2F
L
K
2F
paralel
3F M
4F
2F
5.
3F
7F
M
6F
M
M
7F
4F paralel
K
12F
K
3F ve 6F lık kondan-
3F
seri
6F
M
2F
satörler seri bağlı
4F
olduğundan eşdeğer
1F
K
paralel
Cefl=6F 6F
L
L
M
6F
Cefl=12F
5F
sığa,
3F
7F
C 36 =
seri
3.6
= 2F olur.
3+6
12F
K-L arasındaki eşde-
4F
12F
Cefl=3F
2F paralel
ğer sığa,
K
CKM = 3 + 4 + 3 = 10 F olur.
L
1F
Ceş = 2 + 1 + 5 + 7
5F
= 15F olur.
7F
b)
K
K
K
2F
K
4F
L
L
K
paralel
5F
L
7F
4F
K
7F
L
6F
3F
›
C efl
78 135
=
F
19
19
olur.
3F
6F
K
M
L
Cefl=12F
4F
78
19 F
12F
seri
12F
L
Cefl=4F
paralel
seri
4F
7F
12F
C efl =
4F
C KL =
ELEKTRİK VE MANYETİZMA
6F
K
K
254
M
Cefl=6F
CLM=6F
M
6F paralel
3F
13.6
78
=
=
F
13 + 6 19
C efl = 3 +
3F
M
4F paralel
12F
2F
K
CKL=13F
K
M
M
2F
1F
5F
L
paralel
1F
K
12F
6F
L
3F
4F
2F
4F
M
3F
Cefl=4F
M
seri
b)
6F
K
84
160 F
olur.
+4=
19
19
7.12
84F
=
7 +12 19
L
c)
K
K
K
4F
2F
K
4F
L
3F
M
6F
L
K
12F
6F
L
M
M
3F
4F
seri
C3=8F
CX=4F
8F
2F
M
M
C1=4F
paralel
12F
4F
8
C5=—=4F
2
C4=4F
CX=4F
C5=4F
K
2F
Cefl=6F
6F
L
Wheatstone
köprüsü
2F
M
6F
M
3F
seri
6F
4F
C1=4F
CX C5
=
olduğundan, 2F lik kondansatör kısa
C1 CY
12F
Cefl=4F
6F
L
CY=4F
devredir. Üzerinde yük birikmez. Bu durumda,
M
6F
seri 4F
7F
C efl =
4.7
28F
=
4 + 7 11
C6 =
4.4
= 2F
4+4
K
4F C6
4F
seri
4.4
= 2F
C7 =
4+4
6F
L
C7
M
4F
seri
M
4F
6F
CKM =C6 + C7 = 2 + 2 = 4F olur.
160F
28
+6+6=
olur.
11
11
CLM =
b) K-L noktaları arasındaki eşdeğer sığa ise,
6F paralel
3F
4F
6F
K
seri
C1
6.
a) K - M noktaları arasındaki eşdeğer sığa,
L
6F
8F
3F
4F
K
6F
8F
seri
2F
8F
2F
8F
C1 =
seri
4F
6.3
= 2F
6+3
8F
C2
C1 ile 6F lık kondansatör paralel bağlı olduğun-
8F
M
C1
da, C2 = 2 + 6 = 8F
4F
4F
8.8
6.3
= 4F ve C 2 =
= 2F olur.
C1 =
8+8
6+3
K
8F
6F
C3=8F
8F
2F
4F
L
8F
C2=2F
4F
K
paralel
C3
8F
seri
1
1 1 1
= + + & C 3 = 2F olur.
C3 8 8 4
8F
2F
M
C1=4F
4F
C3 ile 2F lık kondansatör paralel bağlı olduğundan, C4 = 2 + 2 = 4F dır.
ELEKTRİK VE MANYETİZMA
255
4F lık ve 8 F lık kondansatörler seri olduğundan,
1
1 1 1
= + +
C5 4 4 8
K
KK
K
6F
C5
K
4F
6F
6F
K
K
L
12F
4F
8
F olur.
5
C5 =
9.
6F
6F
K
8F
3F
12F
3F
8F
Cefl=3F
L
L
seri
L
L
L
C5 ile 8F lik kondansatör paralel bağlı olduğundan,
K
8 48
C KL = 8 + =
F olur.
5
5
KK
6F
K
2F
4F
K
3F
Cefl=6F
2F
C 6
C efl = = = 3F
n 2
3F
LK
2F
6F
6F
L
L
2F
L
L
L
L
CKL = 12 + 6 + 3 + 4 + 2 + 3 = 30 F olur.
2F
CEVAP C
3F
K
L
Şekilde görüldüğü gibi tüm kondansatörler K-L
arasına bağlanmış olup, birbirlerine paraleldir. Bu
durumda,
seri
3F
paralel
2F
paralel
3F
K
K
L
12F
Cefl=6F
K
L
Cefl=2F
Cefl=4F
C KL = 8 + C 5
7.
L
L
CKL = 3 + 2 = 5 F
olur.
2F
paralel
CEVAP E
1μF
8.
Y
Y
10.
2μF
6μF
1F
X
2μF
X
X
X
X
1μF
Y
3μF
X
X
3F
M 2F
X
8F
M
M
1μF paralel
8F
2μF
3F paralel
Cefl=3μF
X
X
Cefl=6F
3μF
seri
X
Cefl=2μF
2μF
seri
6F
Cefl=4F
Y
X
C XY =
256
ELEKTRİK VE MANYETİZMA
CEVAP D
M
N
6F
N
6F
Y
M
8F
Cefl=12F
8F
M
C1=12F
Y
12F
C2=6F
Y
1μF
CXY = 2 + 3 + 2 + 1 = 8 μF olur.
paralel
4F
1F
1μF
3μF
2F
Y
2μF
Y
N
X
3μF
6μF
8F
6F
4F
X
6μF
X
M
C 1 .C 2
12.6
=
= 4F olur.
C 1 + C 2 12 + 6
CEVAP A
11.
1μF
K
K
K
2μF
1.
2μF
K
k›sa
devre
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
M
K
6μF
L
C
C
C/2
L
M
C
6μF
M
12μF
1μF
L
L
4μF
+
paralel
2μF
K
C
2C
seri
6μF
M
12μF
Cefl=4μF
L
–
• •
V
2V
fiekil-I
4μF
fiekil-II
Şekil-I deki devrede:
Cefl=6μF
1μF
+
–
• •
2μF
Ceş = 2C
qtop = q1 = Ceş.2V = 2C.2V = 4CV olur.
seri
K
L
6μF
6μF
Şekil-II deki devrede:
Cefl=3μF
Ceş =
C KL = 1+ 3 = 4μF olur.
C
2
C
.V olur.
2
qtop = q2 = Ceş.V =
CEVAP B
q1 ve q2 taraf tarafa oranlanırsa,
q 1 4CV
=
= 8 olur.
q2
CV
2
K
2.
•
•
C
12.
paralel paralel
K
C
C
C
Cefl=2C
L
k›sa devre
L
L
C
L
L
L
L
L
C
Cefl=3C L
L
L
L
L
Ceş =
L
qtop = q1 =
+
2C
C
L
L
C
C
L
C
K
CEVAP E
•
•
–
• •
V
K ve L anahtarları açık iken:
3C
C
3
C
.V olur.
3
K açık L kapalı iken:
1
1
1
1
= +
+
C KL C 2C 3C
Ceş = C
1
6+3+2
=
C KL
6C
qtop = q2 = C.V olur.
1
11
6C 6.22
=
& C KL =
=
= 12F olur.
C KL 6C
11
11
CEVAP E
K ve L kapalı iken:
Ceş = 3C
qtop = q3 = 3CV olur.
Buna göre, q3 > q2 > q1 olur.
CEVAP B
ELEKTRİK VE MANYETİZMA
257
3.
6.
qı=q
3C
X
q
q
2C
2C
6C
3C
X
C
Y
4C
6C
q
3q
q
2C
2q
Y
+
4C
q
2C
Y
–
• V•
+
Kondansatörlerde depolanan yükler şekilde gösterildiği gibidir. Y kondansatöründe depolanan yük,
–
• V•
2C
4C
q
qY = q + 2q = 3q olur.
CEVAP C
4C
2C
q
2C
4.
3C
6C
3C
V
6C
Y
X
+
2V
+
Y
V
+ –
–
• •
4C
fiekil-II
Y
qX = 3C.2V = 6CV
+
CEVAP C
5.
C
2C
Y
V
3V
–
3C
C
V
3V
fiekil-I
+
–
• •
4V
fiekil-II
Kondansatörlerin üzerlerindeki gerilimler şekildeki
gibidir. X ve Y kondansatörlerinin yükleri,
qX = C.2V = 2CV
qY = 2C.V = 2CV
olur. qX ve qY taraf tarafa oranlanırsa,
q X 2CV
=
= 1 olur.
q Y 2CV
258
ELEKTRİK VE MANYETİZMA
–
qY = 2q olur.
q X 6CV
=
= 1 olur.
q Y 6CV
• •
2q
Y kondansatörünün yükü,
olur. qX ve qY taraf tarafa oranlanırsa,
+
2q
• V•
qY = 6C.V = 6CV
X
2V
2C
2C
Kondansatörlerin üzerlerindeki yükler,
2C
2q
V
fiekil-I
C
4C
2q
• •
3V
–
• V•
CEVAP A
CEVAP D
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
1.
3.
C
V
V1
C
C
4C
24V
12V
2C
4V
+
2V
V2
+
2C
12C
–
• •
4C
V
4V
V=40V
–
2C, 4C ve 12C kondansatörleri seri bağlıdır.
• •
Kondansatörlerin yükleri eşit olmalıdır. Bunun için,
Şekildeki üç kondansatör birbirine seri bağlı olduğundan,
V = 40V luk gerilim ters orantılı olarak dağıtıldığında, devredeki voltmetre 12 volt u gösterir.
V1 = 4V + 2V = 6V
CEVAP C
V2 = 2V + V = 3V
olur. V1 ve V2 taraf tarafa oranlanırsa,
V1 6V
=
= 2 olur.
V2 3V
CEVAP D
4.
K anahtarı açık iken:
C
C
K
Y
C
X
2.
6C
C
12C
Z
4C
V
X
•
•
V
Y
+ –
• •
2V
+
–
• •
V1
fiekil-I
+
–
• •
K anahtarı kapalı iken:
V2
fiekil-II
2C
C
Şekil-I deki devrede:
C
qX = C.V1 olur.
K
• •
Y
C
X
Şekil-II deki devrede:
Ceş = 4C olur.
+ –
• •
2V
qtop = qY = Ceş.V2 = 4C.V2 olur.
X kondansatörünün yükü Y kondansatörünün
yüküne eşit olduğundan,
qX = qY
K anahtarı kapatıldığında Z kondansatörünün
uçları arasındaki potansiyel fark,
VZ =
C.V1 = 4C.V2
V1
= 4 olur.
V2
Z
2
3V
4
3V
2
V olur.
3
CEVAP B
CEVAP E
ELEKTRİK VE MANYETİZMA
259
5.
V
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
3C
2C
6C
1.
2C
K
•
10V
L
•
5V
2C
30V
4C
+
C
C
2C
X
Y
Z
V
–
+
• •
2V
–
+ –
•3V•
fiekil-II
• V•
fiekil-I
K ve L noktaları arasındaki VKL potansiyel fark,
V
Kondansatörlerin üzerlerindeki gerilimler,
VKL = 10V + 5V + 30V = 45V olur.
VX = V, VY = 2V, VZ = V olur.
CEVAP A
Kondansatörlerde depolanan enerjiler,
1
EX = .C.V2 = E
2
EY =
1
1
.C.(2V)2 = 4 CV2 = 4E
2
2
EZ =
1
1
.2C.V2 = 2 CV2 = 2E olur.
2
2
Buna göre, EY > EZ > EX olur.
6.
4nF
K
L
•
L
•
•
•
2.
1nF
6nF
CEVAP C
M
V
2nF
CX
3nF
K•
X
•M
•
L
CY
+
VX
–
• •
VY
Y
45V
4nF
V
1nF
K
•
•L
6nF
2nF
3nF
+
–
• •
V
•
M
Kondansatörlerin yükleri,
qX = CX.V
2nF
qY = CY.V dir.
+
–
CX > CY olduğundan, qX > qY dir.
• •
45V
I. yargı doğrudur.
Kondansatörlerin üzerlerindeki gerilimler,
V
K
•
6nF
•
15V
L
3nF
•
M
30V
+
VX = VY = V dir.
II. yargı doğrudur.
Kondansatörlerde depolanan enerjiler,
EX =
1
.C .V2
2 X
EY =
1
.C .V2 dir.
2 Y
–
• •
45V
Voltmetre 30 volt u gösterir.
CEVAP E
CX > CY olduğundan, EX > EY dir.
III. yargı doğrudur.
CEVAP E
260
ELEKTRİK VE MANYETİZMA
3.
5.
C
X
C
q
Z
2C
Y
3q
3C
2q
+
–
+
• •
+
–
2V
V
fiekil-I
X kondansatörün yükü q ise, qY = 2q ve qZ = 3q
–
• •
• •
V
fiekil-II
Şekil-I deki devrede:
olur. Z kondansatörün enerjisi,
1 (3q)
E Z 2 6C
=
2
EX
1.q
2 C
6C 2C
3C
4C
6C
Ceş = C + 3C = 4C
2
Kondansatörlerde depolanan toplam enerji
1
E1 = .4C.V2 = 2CV2 olur.
2
EZ 3
3
& EZ =
E olur.
=
2
E
2
Şekil-II deki devrede:
CEVAP D
Ceş =
3C.6C
= 2C
3C + 6C
Kondansatörlerde depolanan toplam enerji,
E2 =
1
.2C.(2V)2 = 4CV2 olur.
2
E1 ve E2 taraf tarafa oranlanırsa,
4.
C
2C
X
Y
+
E 1 2CV 2 1
=
=
olur.
E 2 4CV 2 2
CEVAP B
–
• •
V
X ve Y kondansatörleri seri bağlı olduğundan,
6.
qtop = qX = qY dir.
I. yargı doğrudur.
6C
q
X
qX = qY
12C
2C
Y 2q
4C
q
C.VX = 2C.VY
VX = 2VY dir.
+
–
• V•
II. yargı doğrudur.
X kondansatörün yükü q ise Y kondansatörün
yükü 2q olur. Kondansatörlerin enerjileri oranlanırsa Y kondansatöründe depolanan enerji,
2
EX
EY
4C
q
1 q
.
= 2 C2 = 2 & EX = 2EY dir.
1 q
.
2 2C
III. yargı doğrudur.
CEVAP E
1 . (2q)
EY
= 2 2C
2
EX
1. q
2 6C
2
EY
= 12 & EY = 12E olur.
E
CEVAP A
ELEKTRİK VE MANYETİZMA
261
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
1.
+
+
C
X
3C
+ –
+ –
Y
–
–
+
+
+
K
C
3.
8V
fiekil- I
X
X
•
X
+
L
•
L
–
• •
10V
4C
12C
Y
Z
fiekil-I
3C
fiekil-II
Şekil-I deki devrede:
qX = 2C.10V = 20CV olur.
Şekil-I deki devrede:
3
C . 3C
=
C
4
C + 3C
3
= qX = qY =
C.8V = 6CV olur.
4
Ceş =
qtop
2C
K
–
–
3C
+ –
+ –
Y
fiekil- II
–
2C
Şekil-II deki devrede:
K-L uçları arasındaki potansiyel fark,
qX
20CV
20V
VKL = Vort =
=
=
= 4V olur.
ı
2C + 3C
5
CX + C
Şekil-II deki devrede:
CEVAP C
K-L noktaları arasındaki potansiyel fark,
qX + qY
12V
6CV + 6CV
=
=
= 3V
4
CX + CY
C + 3C
VKL = Vort =
olur.
CEVAP D
4.
+
+
C
X
–
–
+
–
3C
+ –
+ –
Y
+
K
–
5V
V
fiekil- I
fiekil- II
+
+
C
X
–
–
L
3C
– +
– +
Y
fiekil- III
Şekil-I deki devrede:
2.
C1 = 4μF
+ –
+ –
qX = C.5V = 5CV olur.
C1 = 4μF
+ –
+ –
C2 = 6μF
+ –
+ –
+
K
Şekil-II deki devrede:
qY = 3C.V olur.
L
C2 = 6μF
– +
– +
–
V = 50V
fiekil- I
Şekil-III teki devrede:
fiekil- II
K-L uçları arasındaki potansiyel fark,
Şekil
- I deki devrede:
_________________
VKL = Vort =
q1 = C1 . V = 4 . 50 = 200 μC
olur.
qX – qY
5CV – 3CV
2CV
1
=
=
=
V
CX + CY
C + 3C
4C
2
q2 = C2 . V = 6 . 50 = 300 μC olur.
CEVAP A
Şekil
- II deki devrede:
__________________
q – q1
VKL = Vort = 2
C1 + C2
=
300 – 200
4+6
=
100
10
5.
C 12 =
q12 = C12.V = 2.100 = 200 C,
CEVAP A
ELEKTRİK VE MANYETİZMA
3.6
= 2F olur. C1 ve C2 kondansatörlerinin
3+6
yükleri,
= 10 V olur.
262
Şekil-I de C1 ve C2 kondansatörleri birbirlerine seri
bağlı olup yükleri eşittir.
q1 = q2 = q12 = 200 C olur.
Şekil-II de kondansatörler birbirine paralel bağlandığından toplam yükü sığalarıyla doğru orantılı olarak paylaşırlar. C1 ve C2
boş olan kondansatöre şekildeki
gibi bağlandığında,
q1
+ –
+ –
C1=3F
MODEL SORU - 7 DEKİ SORULARIN ÇÖZÜMLERİ
+ –q2
+ –
C2=6F
+ –q3
+ –
C3=1F
1.
A/2
A
Κ1=2
d
bofl
A/2
Κ2=3
d
q1 = 200 C ve q2 = 200 C
olduğundan Şekil-II deki toplam yük 400 C olur.
fiekil-ΙΙ
fiekil-Ι
q12 = qı1 + qı2 + qı3
400 = C1.Vı + C2.Vı + C3.Vı
⇓
Şekil-I deki kondansatörün sığası,
400 = 3.Vı + 6.Vı + 1.Vı
400 = 10Vı ⇒ Vı = 40 volt olur.
C = fo .
C1 kondansatörünün yükü,
A/2
A
olur.
d
Şekil-II deki kondansatör birbirine paralel
iki kondansatörün birleşmesiyle oluşmuştur.
qı1 = C1.Vı = 3.40 = 120 C olur.
C1 kondansatörünün yükündeki azalma,
q1 – qı1 = 200 – 120 = 80 C olur.
CEVAP B
A/2
Κ1=2
Κ2=3 d
d
C1
C2
A
C
C
C 1 = l 1 .f o . 2 = l 1 . = 2. = C
d
2
2
A
C
C 3
C 2 = l 2 .f o . 2 = l 2 . = 3. = C olur.
d
2
2 2
6.
+
+
3V
+
+
C
X
–
–
+
C
Y
V
–
–
+
+
2C V
+ –
+ –
Z
–
K
4V
fiekil- I
+
+
C
X
C
Y
Kondansatörler birbirine paralel olduğundan,
–
–
C efl = C 1 + C 2 = C +
3
5
C = C olur.
2
2
CEVAP D
L
–
–
2C
+ –
+ –
Z
fiekil- II
Şekil-I deki devrede:
2.
+
–
20V
κ
κ
qX = C.3V = 3CV
qY = C.V
2m
qZ = 2C.V olur.
qX + qY + qZ
CX + CY + CZ
C 1 = C 2 = l.f o .
3CV + CV + 2CV
=
C + C + 2C
=
+
+
K-L uçları arasındaki potansiyel fark,
2m
+
+
Şekildeki kondansatörlerin
birer ucu üretecin (+), diğer +
ucu (–) kutba bağlandığın- – 20V
dan birbirlerine paralel iki
kondansatör oluşur. Kondansatörler özdeş olduklarından,
Şekil-II deki devrede:
VKL = Vort =
2m
C
– – 1
C
– – 2
A
1
4
=
.f . = 2F olur.
d fo o 2
C1 ve C2 paralel olduğundan,
6V
4
Ceş = C1 + C2 = 2 + 2 = 4F olur.
Toplam yük,
3
V olur.
=
2
qtop = Ceş.V = 4.20 = 80C olur.
CEVAP B
CEVAP D
ELEKTRİK VE MANYETİZMA
263
TEST
1.
1
KONDANSATÖRLERİN BAĞLANMASI
ÇÖZÜMLER
4C ve 12C seri bağlıdır.
+
3.
–
K anahtarı açık iken:
1
1
1
=
+
C 1 4C 12C
C1=3C
3C
6C
X
X
K
•
•
12C
12C
C 1 = 3C
2C
4C
X
C
12C
8C
C1, C ve 2C birbirine paralel bağlıdır.
Y
Y
12C 4C
6C
C2 = C1 + C + 2C
Y
X
= 3C + C + 2C
12C
= 6C
8C
C2 ile 3C seri bağlıdır.
12C
1
1
1
=
+
C efl C 2 3C
=
1
1
+
6C 3C
=
3
6C
12C
Y
X
X-Y arasındaki eşdeğer sığa,
12C
= 6C olur.
C1 =
2
C efl = 2C olur.
K anahtarı kapalı iken:
CEVAP A
X
6C
X
K
Y
• •
12C
X
12C
8C
6C
2.
K
4C
6C
L
K
X
K
3C
L
L
4C
12C
X
L
12C
Y
Y
Y
12C
8C
4C
24C
6C
6C
X=8C
L
K
Y
X
3C
6C
8C
24C
X-Y arasındaki eşdeğer sığa,
Şekilde görüldüğü gibi X kondansatörünün sığası
8C olduğunda K-L uçları arasındaki eşdeğer sığa,
C1 ve C2 taraf tarafa oranlanırsa,
Ceş = 3C + 4C = 7C olur.
CEVAP C
264
ELEKTRİK VE MANYETİZMA
C2 = 6C + 6C = 12C olur.
C1
6C
1
=
=
olur.
C 2 12C 2
CEVAP C
4.
C ve 2C sığalı kondansatörler kısa
devre olur.
L
K anahtarı kapalı iken:
kısa
devre
•
12C
kısa
2C devre
C
12C ile 6C birbirine
paralel bağlıdır.
K
•
L•
L
CKL = 12C + 6C
2C
= 18C olur.
6C
•
X
L
•
Cefl=C2=4C
2C
X
Y
•K
•
•
kısa
devre
X
C
Y
Y
X
X
L
C
Y
CEVAP E
Y
C1 ve C2 taraf tarafa oranlanırsa,
C 1 3C 3
=
=
olur.
C 2 4C 4
5.
C1, C2 ve C3 grup
C3
Z
içindeki
kondan-
C2
satörler
birbirine
C
C
7.
T
•
•
•Z
C
lanınca; C1
1
1
1
=
+
C 1 3q
2q
V
3V
C
C
C3 = C + C = 2C
•
X•
Y
C1
•
+
X
6q
C1 =
olur.
11V
•
–
T
C2 =
1
1
1
1
=
+
+
C efl 2C 3C 2C
Buna göre;
8.
3
C olur.
4
K
••
Cefl=C1=3C
C
2C
Y
C
Y
•
•
2V
3V
Y
Y
C1
4C
4C
24C
2C
+
–
C
1
1
1
=
+
C 2 24 8
C
Y
2C
X
•
V
C1 = 4C + 4C
Eşdeğer sığası C2
olsun.
1
1
1
=
+
C 2 24 C 1
K anahtarı açık iken:
X
0•
4C ile 4C birbirine
paralel bağlıdır.
24C ile C1 birbirine
seri bağlıdır.
X
potansiyel
fark
C 1 6q/11V
18
=
=
olur.
C 2 11q/3V 121
= 8C olur.
2C
q•
CEVAP A
CEVAP B
X
L
2q •
3q 2q 11q
+
=
olur.
V
3V
3V
1
1
1
1
=
+
+
C efl C 1 C 2 C 3
1
8
=
C efl 6C
6.
K
CK ile CL paralel bağlanınca; C2
C1, C2 ve C3 birbirine seri bağlıdır.
C efl =
yük miktar›
3q •
CK ile CL seri bağ-
C
Y•
C2 = C + C + C = 3C
3q
2q
, CL=
V
3V
olur.
C
paraleldir.
C1 = C + C = 2C
CK =
CEVAP C
1
4
=
C 2 24
C 2 = 6C olur.
C2, 2C ve C birbirine paralel bağlıdır.
Ceş = C2 + 2C + C
= 6C + 2C + C
= 9C olur.
CEVAP D
ELEKTRİK VE MANYETİZMA
265
9.
2C, 2C ve 2C sığalı kondansatörler
birbirine paraleldir.
11.
2C
C
K
K
6C
L
2C
•
6C
3C
12C
•
Wheatstone
köprüsü
C
2C
C
Cefl=6C
C1
L
3C
6C
6C
C2
K-L arasındaki eşdeğer sığa,
C1 = 2C + 2C + 2C = 6C olur.
C, C ve C birbirine paralel bağlıdır.
Ceş = 3C + 3C = 6C olur.
C2 = C + C + C
CEVAP D
= 3C olur.
C1 ile C2 birbirine seri bağlıdır.
1
1
1
=
+
C KL C 1 C 2
1
1
1
=
+
C KL 6C 3C
C KL = 2C olur.
CEVAP B
10. Doğrunun eğimi kondansatörün sığasını vereceyük
ğinden,
2q
V
q
=
2V
C
= X olur.
4
CX =
CXY
CXY
2q•
12.
4C
4C
2C
K
X
•
X
q•
0•
XY
•
V
•
2V
4C
gerilim
4C
2C
L
K
CX
X ve Y kondansatörlerin sığaları arasındaki ilişki,
6C
3C
C X .C Y
CX + CY
2C
CX
C X .C Y
=
4
CX + CY
K-L uçları arasındaki eşdeğer sığa 6C olduğuna
göre, X kondansatörün sığası,
4CY = CX + CY
Cı = CX + 2C
CX = 3CY olur.
6C = CX + 2C
II. yargı doğrudur.
X ve Y den elde edilecek en büyük sığa, kondansatörlerin paralel bağlanması ile olur.
Ceş = CX + CY
= 3CY + CY
= 4CY olur.
III. yargı doğrudur.
CEVAP E
ELEKTRİK VE MANYETİZMA
3C
2C
I. yargı doğrudur.
266
•
2C
Kondansatörler seri bağlanmıştır.
CXY =
L
CX = 4C olur.
CEVAP B
TEST
1.
2
KONDANSATÖRLER
ÇÖZÜMLER
Seri bağlı kondansatörlerin yükleri
eşittir.
q
V=
olur.
C
V1 =
q
V
=
2C 2
V2 =
q
V
=
olur.
3C 3
C
2C
q
V
3C
q
4.
V1
Elektroskopların yüklerinin işareti bilinmediğinden hangi elektroskoptan hangisine yük geçtiği
q
bilinemez. Yük geçişi bittiğinde elektroskopların
V2
potansiyelleri eşit olur.
Elektroskoplar özdeş olmadıklarından üzerlerindeq
eşitliğinde yük dengesi
V
kurulduğunda elektroskopların potansiyelleri (V)
ki yükler eşit olmaz. C =
+
–
eşit olur. Bu durumda,
CEVAP A
qX = q ⇒ qY = 3q olur.
I. yargıda kesinlik yoktur.
2.
Özdeş ve birbirine
paralel kondansatörlerin yükleri birbirine eşittir.
II. yargı yanlıştır.
q
III. yargı kesinlikle doğrudur.
K
CEVAP C
qL = q olsun.
L
qL=q
Paralel bağlı kondansatörlerin toplam yükü 2q olur. K
+ –
kondansatörü bunlara seri olduğu için K nin yükü de 2q olur. qK = 2q
q K 2q
=
= 2 olur.
qL
q
CEVAP D
5.
•K
•
K anahtarı açık iken:
C q
=
2 V
2C
Cefl=C/2
2q
V=
olur.
C
C
C
+
3.
C
C
–
V
C
Cefl=2C
K anahtarı kapalı iken:
Cefl=C/2
C
1
1
1
= +
C efl C 2C
+
–
+
1
3
=
C efl 2C
–
V1
V2
E1
E2
C efl =
2C
olur.
3
C
2C
C
1
CV2 olduğuna göre, iki devrenin
2
toplam enerjileri eşittir.
+ –
V=2q/C
Enerji, E =
Devrenin toplam yükü ise;
E1 = E2
2
1 C 2 1
V = 2C.V 2
2 2 1 2
2
V1
2
V2
C efl =
q top
V
q top = C efl .V
=4
V1
= 2 olur.
V2
C
CEVAP C
=
2C 2q
.
3 C
=
4
q olur.
3
CEVAP D
ELEKTRİK VE MANYETİZMA
267
6.
Seri bağlı kondansatörlerin yükleri
eşittir.
C
2C
VX
VY
3C
QX = QY
VX.C = VY.2C
VX = 2V
+
VZ = VX + VY
= 3V
2
2
1
1
E X = C X V X = C (2V) = 4E
2
2
EY =
2
2
1
1
C V = 2C (V) = 2E
2 Y Y 2
EZ =
2
2
1
1
C V = 3C (3V) = 27E
2 Z Z 2
Cefl=C/2 C
C
T
X
C
3
C olur.
2
3C
2C ile
sığalı
2
= 2V + V
V
Y
sığası
–
V
2C
C sığalı kondansatörlerin eşdeğer
VZ
VY = V
10. X kondansatörünün potansiyeli V
ise, T nin potansiyeli de V olur.
2C
3/2C
Y
2V
kon dan sa tör le rin
yükleri eşittir.
q _b 4 2V
2C =
VY b 3 = V
Y
`
q b V = 3 V olur.
3
b
C=
Y
2
2
2V a
CEVAP C
Buna göre; EZ > EX > EY olur.
CEVAP E
7.
8.
q
olduğuna göre q artınca V de artar.
V
1
E = CV2 den V artınca E de artar.
2
CEVAP B
C=
K nin potansiyeli
E=
1
CV2 olduğuna göre,
2
CEVAP E
X
CEVAP A
•• K
X
C
C
C
C
C
3V
3V
4V
C
2C
2V
+ –
6V
son durum
K anahtarı kapatıldığında X kondansatörünün
yükü ve potansiyeli artar.
A
, d azaltılınca C artar.
d
CEVAP A
ΙΙ. yargı doğrudur.
q
C = , q sabit ve C artıyor. Buna göre V azalır.
V
ΙΙΙ. yargı yanlıştır.
CEVAP B
ELEKTRİK VE MANYETİZMA
•K
•
+ –
6V
ilk durum
Ι. yargı yanlıştır.
268
C1 > C2 > C3 olabilir.
12. Üretecin gerilimini 6V olarak seçelim.
Kondansatörün yükü sabittir, değişmez.
C = εo
C2 ile C3 arasındaki ilişkiyi bilmeliyiz.
V
, L nin potansiyeli V dir.
2
V 2
1
EK 2 Cb 2 l
1
=
=
olur.
2
EL
1
4
CV
2
9.
11. VKL = VLM olduğuna göre, C1 = C2 + C3 olur.
TEST
1.
3
KONDANSATÖRLER
ÇÖZÜMLER
2C ile C sığalı kondansatörler birbirine paralel
olduğu için sığaları ile yükleri doğru orantılıdır.
K kondansatörünün yükü,
q3 = q ise q2 = 2q olur.
K kondansatörünün kaybettiği yük,
qK = C.V = C.60 = 60 C olur.
∆qK = qilk – qK
q1 = q2 + q3
= 140 – 60
= 2q + q
= 80 C olur.
= 3q olur.
CEVAP D
Buna göre; q1 > q2 > q3 olur.
CEVAP C
2C
2.
6C ile 3C sığalı
kondansatörlerin eşdeğer sığası 2C
olur. Potansiyeli
30 V, yükü de 2q
olsun.
2q
4.
Anakol üzerindeki X kondansatörünün yükü diğerlerinden büyük olur.
CEVAP A
5.
V = VX + VY dir. V
sabit, CX azaltılınca Ceş azalır.
30volt
••
Y
2C
+
Y kapatılınca; 2C
ile 2C birbirine paralel olur ve yükleri
paylaşırlar.
•
•
–
X
2C
q
Bu durumda ortak
potansiyel
30
= 15 V olur.
2
C efl =
q
q top
V
X C
X
qX
Y C
Y
qY
VX
VY
den;
qtop azalır. qX ve qY
2C
azalır.
CEVAP B
CY =
+
–
V
qY
; CY sabit,
VY
qY azalınca, VY de azalır.
3.
M
A
V = VX + VY ; V sabit, VY azalınca, VX artar.
CEVAP A
C
V
C
L
C
C
N Cefl=
3
V
C
A
K
C
B
P
Anahtar kapatıldığında A ve B noktaları arasındaki kondansatörler paralel bağlanmış olur.
Kondansatörlerin yükleri,
qK = C.V
qL = C.V
qM = qN = qP =
C
V olur.
3
Yükün korunumundan,
qilk = qK + qL + qM
C
140 C = C.V + C.V + V
3
7
140C = CV ⇒ V = 60 volt olur.
3
6.
Şekil-Ι deki iki kon1μF
+ –
dansatörün yükü
+ –
6μC
eşit olur ve 6μC
dur. Şekil-ΙΙ de ise
6μC
+ –
iki kondansatörün
+ –
2μF
aynı kutupları birbirine bağlandığı için yük kaybı olmaz. Bu iki kondansatörün potansiyeli eşit olur.
Toplam yükü,
6μF + 6μF = 12μF
sığaları ile doğru orantılı paylaşırlar.
2μF lik kondansatörün yükü 8μC olur.
CEVAP D
ELEKTRİK VE MANYETİZMA
269
7.
C = f
Toplam enerji: Eı
A
bağıntısına
d
X
göre, f azaldığından
kondansatörün sığası
azalır.
+
+
+
+
–
–
–
–
›
2
1
.2C. (2V)
2
›
2
1
.2C.4V
2
E =
E =
I. yargı doğrudur.
Kondansatör üretece
bağlı iken, levhaları
arasındaki potansiyel
farkı değişmez.
C1=C olur.
2
1
E = C efl .V efl
2
›
2C
2C
V
V
C
+–
V
+ –
2V
Buna göre, Eı = 4E olur.
CEVAP B
II. yargı doğrudur.
1
C V2 bağıntısına göre, kondansatörün sığa2
sı azaldığından enerjisi azalır.
E=
10.
3C
+ –
+ –
X
6C
+ –
+ –
Y
III. yargı doğrudur.
+
CEVAP E
K
3C
+ –
+ –
X
L
6C
+ –
+ –
Y
fiekil- II
–
V
fiekil- I
Şekil-I
deki devrede:
_________________
C efl =
8.
Y ve Z kondansatörleri birbirine seri
bağlı ve yükleri
eşittir. Potansiyelleri ise sığaları ile
ters orantılıdır.
X
qtop = qX = qY = Ceş . V = 2CV olur.
CX=4μF
Y
Z
E1 =
2
2
1
. 2C . V = CV olur.
2
CY=2μF
CZ=3μF
VX =
2
V,
3
VY
VZ
VY =
1
V olur.
3
2VY = 3VZ olur.
+ –
50 volt
VY + VZ = 50 volt olduğuna göre; VZ = 20 volt olur.
q
CZ = Z
VZ
3.10
–6
3C . 6C
= 2C olur.
3C + 6C
Şekil-II
deki devrede:
_________________
VKL = Vort =
q
= Z
20
q Z = 6.10
–5
C olur.
CEVAP D
E=
4
V olur.
9
4
4
V = CV olur.
9
3
›
4
8
V = CV olur.
9
3
Y nin yükü artar.
2C
II. yargı doğrudur.
C
E2 =
2C
V
=
C
Ceş = C1 + C
= 2C olur.
ELEKTRİK VE MANYETİZMA
1
4 2
. 9C . c V m
2
9
2
8
CV olur.
9
Kondansatörlerin toplam enerjisi azalır.
=C+C
270
=
›
C
2
1
2CV olur.
2
Devrenin eşdeğer
sığası;
2CV + 2CV
3C + 6C
I. yargı doğrudur.
q Y = 6C .
2C nin potansiyeli
V olsun.
=
X in uçları arasındaki potansiyel farkı azalır.
q X = 3C .
9.
qX + qY
CX + CY
III. yargı yanlıştır.
+
–
CEVAP C
11. K anahtarı açık iken:
K
Kondansatörlerin yükleri
1
V
CV
qX = C. =
2
2
V
1
qY = C. =
CV
2
2
qZ = C.V olur.
•
•
C
C
X
Y
C
Z
K anahtarı kapalı iken:
+
X kondansatörünün yükü,
–
• •
V
ı
q X = 0 (X nötr olur.)
I. yargı doğrudur.
ı
Y kondansatörünün yükü, q Y = C.V olur.
Y nin yükü artar.
II. yargı doğrudur.
ı
Z kondansatörünün yükü, q Z = C.V olur.
Z nin yükü değişmez.
III. yargı doğrudur.
12.
CEVAP E
6μF
12μF
X
Y
4μF
Z
2
K 1
+–
V=200V
K
anahtarı 1 konumunda iken:
_________________________
qZ = CZ . V
= 4 . 200
= 800 μC olur.
K
anahtarı 2 konumunda iken:
_________________________
CXY = 4 μF olur.
Vort =
800
= 100 V olur.
4+4
›
q Y = C XY . Vort = 4 . 100 = 400 nC olur.
› 2
EY =
1 (q Y)
2 CY
–4 2
=
1 (4.10 )
.
2 12.10 –6
=
16.10
–6
24.10
=
–2
2
.10 J olur.
3
–8
CEVAP A
ELEKTRİK VE MANYETİZMA
271
TEST
1.
4
ÇÖZÜMLER
qK= 2qL olduğuna
göre;
qL = q, qK = 2q
olsun.
C1=12C
3.
6C q
KONDANSATÖRLER
K ile L nin yükleri toplamı M nin yüküne eşittir.
Buna göre, Ι ve ΙΙΙ ün bilinmesi yeterlidir.
CEVAP B
6C
K
6C ile C1 birbirine seri bağlıdır.
Eşdeğer sığaları
C2 olsun.
qK=2q
6C q
4.
L
1
1
1
=
+
C 2 6C C 1
qL=q
+
4C
2q
C 2 = 4C olur.
3C
+
q
+
–
V2
6C
2C =
q
V
CX =
3q
V
3q
X
+
–
V
2C 1
= & C X = 6C olur.
CX 3
12C
2C
–
2C
L
eşitlikleri oranlanırsa,
C
q
X
CEVAP B
2.
6C
q
2C ile X in potansiyeli eşittir.
q
Paralel bağlı kondansatörlerin sığası ile
yükü doğru orantılıdır.
Buna göre CL = 2C
olur.
Cefl=2C
Devrenin eşdeğer
yükü 4q ise X kondansatörünün yükü
3q olur.
–
V
1
1
1
=
+
C 2 6C 12C
3C nin yükü q ise
6C nin yükü de q
olur.
CEVAP E
4C
C
+
–
• •
V1
fiekil-I
+
5.
–
• •
2nF
fiekil-II
X
V2
2nF
X
K
Şekil-I deki devrede:
fiekil- I
Şekil-II deki devrede:
Z
fiekil- II
Şekil-I deki devrede:
Ceş = 4C
qX = CX.V
qtop2 = 4CV2
= 2.24
Şekil-I deki devrenin toplam yükü, Şekil-II deki
devrenin toplam yüküne eşit olduğuna göre,
qtop1 = qtop2
= 48nF
Şekil-II deki devrede:
K-L uçları arasındaki potansiyel fark,
2C.V1 = 4C.V2
V1 = 2V2
ELEKTRİK VE MANYETİZMA
4nF
–
V=24V
qtop1 = 2CV1
272
L
Y
+
Ceş = C + C = 2C
V1
= 2 olur.
V2
6nF
VKL = Vort =
CEVAP D
qX
48
=
= 4V olur.
2+6+4
CX + CY + CZ
CEVAP A
6.
K ile L nin yükleri
eşittir. Ι. yargı doğrudur.
K
9.
L
K ile L nin sığaları bilinmediği için potansiyel farkları kesinlikle eşit diyemeyiz. ΙΙΙ. yargı yanlıştır.
ΙΙΙ. yargı için kesin birşey söylenemez.
CEVAP C
qX = CX . Vort
60 = 3 . Vort
Vort = 20 V olur.
q + qY
Vort = X
CX + CY
20 =
0 + C Y . 30
3 + CY
3C Y = 6 + 2C Y
C Y = 6 nF olur.
L
V/2
M kondansatörüM
nün
po tan si ye li
üretecin potansiyeline eşittir. K ile L
nin toplam potan+ –
V
siyeli de üretecin
potansiyeline eşittir. Buna göre K nin potansiyeli
M ninkinden küçük olur. ΙΙ. yargı doğrudur.
7.
K
2/3V
V
+
–
4/3V
V
+ –
2V
fiekil-Ι
fiekil-ΙΙ
K kondansatörünün potansiyeli
V
olur.
2
L kondansatörünün potansiyeli
2
V olur.
3
q = CV olduğuna göre;
V
C
qK
2 = 3 olur.
=
qL
2V 4
C
3
CEVAP A
10. Şekil-I deki devrede:
_________________
CX = 3μF
X
C efl =
CY
2
Y
K 1
+–
C1 . C2
C1 + C2
=
2.8
2+8
=
16
nF
10
C1 =2μF
+
+
+
+
+
–
–
–
V=50V
qtop = q1 = q2 = Ceş . V =
V=30V
C2 =8μF
–
–
16
. 50 = 80 μF olur.
10
CEVAP C
Şekil-II deki devrede:
__________________
VKL = Vort =
=
=
8.
Kondansatörün yükü sabittir.
C = εo
q1 + q2
C1 + C2
80 + 80
2+8
160
10
= 16 V
C1 =2μF
+ –
+ –
K
L
C2 =8μF
+ –
+ –
olur.
CEVAP B
A
; d azalınca C artar.
d
q
den; q sabit, C artarsa V azalır.
V
q
q
A
qd
q
V C fo d
E=
=
=
=
=
f o A.d f o A
d
d
d
C=
Buna göre; E değeri değişmez.
CEVAP E
ELEKTRİK VE MANYETİZMA
273
11. Anahtar açıkken
eşdeğer sığa;
C + C1 = C +
C
C 3C
=
2
2
C
1
1
1
=
+
C efl 3C C
2
C efl =
•X
•
3C
olur.
5
+
K
ile 2C birbirine
–
O
•
devrenin
eşdeğer sığası C
C
C1=C/2
Anahtar kapatılınca,
C
•
L
K•
•
L
•
•
O
L•
seri olur. Eşdeğer
sığaları C1 olsun.
•
K
1
1
1
= +
C 1 C 2C
•L
+
L•
–
C
K
O
•
2
C 1 = C olur.
3
2C
•
L
•
L
C
C
Devrenin eşdeğer
sığası ise;
2
5
C efl = C + C = C olur.
3
3
Devrenin eşdeğer sığası artar, potansiyeli sabit
olduğuna göre, devrenin yükü de artar.
CEVAP A
12.
VKM
•M
C
Cefl=2C
C
•L
•
K
VKL
C
+
–
Kondansatörlerin sığası C olsun.
VLM = V ise VKL = 2V olur.
VKL
VKL
2V
2
=
=
=
olur.
VKM VKL + VLM 2V + V 3
CEVAP D
274
ELEKTRİK VE MANYETİZMA
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
1.
2q 4μF
Bölüm
Yazılı Soruları
(Kondansatörler)
ÇÖZÜMLER
4μF 2q
C2=5F
6μF 12μF
K
L
P
K
q=4C
fiekil-Ι
C34=3F
C2 ile C34 kondansatörleri paralel bağlı oldu-
2μF q2=8C
ğundan eşdeğer sığa,
6μF 12μF
K
L
C1=8F
1μF
L
C234 = C2 + C34
=5+3
1μF
q1=4C
= 8 F tır.
fiekil-ΙΙ
q = C.V ifadesine göre yük ile sığa doğru oran-
N tane özdeş kondansatör seri bağlı ise eşdeC
ifadesiyle bulunur.
ğer sığa kısaca, C efl =
N
C234, C1 e seri olduğundan sistemin eşdeğer
tılı olduğundan 2μF lık kondansatörün yükü 8C
sığası,
a) Şekil-II de 1μF ile 2μF lik kondansatörler birbirine paralel bağlı olduğundan gerilimleri eşittir.
olur. 2μF lık kondansatör Şekil-I deki 4μF lık
kondansatörlerin eşdeğeri ve seri bağlamada
C efl =
yükler eşit olduğundan q = q2 = 8C olur.
olur.
b)
6μF
12μF
3μF
C 8
= = 4F
N 2
K
L
C1=8F
C234=8F
b) C3 ün yükü, C4 ün yüküne eşit (q3 = q4), C3 ile
q12=12C
C4 ün bağlı olduğu kol C2 nin bağlı olduğu kola
paraleldir. Dolayısı ile gerilimleri eşittir.
Şekilde kondansatörler seri bağlandığından 6μF
lık kondansatörün yükü de 12C olur.
q3 = C34.VPL
60 = 3.VPL ⇒
c) Seri bağlamada toplam yük herhangi bir kon-
VPL = 20 volt
q2 = C2.VPL
= 5.20
dansatörün yüküne eşit olduğundan,
qtoplam = 12C olur.
= 100 C olur.
c) C1 kondansatörü C2 ile C34 ün eşdeğerine seridir. Dolasıyla devrenin yükü C1 in yüküne, bu
2.
yükte q2 ile q3 ün toplamına eşittir. Bu durumda;
a)
qT = q1
C2=5F
K
= q2 + q3
P
L
C1=8F
C34 C3=4F
C4=12F
C3 ve C4 kondansatörleri seri bağlı olduğundan
eşdeğer sığa,
C 34 =
4.12
= 3F olur.
4 + 12
= 100 + 60
= 160 C dur.
K-L noktaları arasındaki potansiyel fark ise,
q = C.V
160 = 4.VKL ⇒ VKL = 40 volt olur.
ELEKTRİK VE MANYETİZMA
275
3.
C1 ile C2 seri bağlı olduğundan, yükleri aynıdır.
N
A
q1 = q2
C
V
V
C
L
V
K
A
a)
C3 kondansatörü C1 ve C2 ye paralel bağlı
B
C
B
olduğundan gerilimi,
Anahtar kapatıldığında K, L ile M ve N nin eşdeğeri
birbirlerine paralel olmuş olur. K kondansatörünün
üzerindeki yük diğer kondansatörlerin sığalarıyla
doğru orantılı olarak paylaşılır.
N ile M kondansatörleri seri bağlandığından üzerlerindeki yükler eşittir.
qN = qM =
C
.V
2
V3 = V1 + V2
=10 + 20
= 30 V bulunur.
Enerjisi ise,
2
1
E 3 = .C 3 .V 3
2
2
1
.C . (30) & C 3 = 2F bulunur.
2 3
900 =
K ve L nin üzerindeki yükler ise,
q3 = C3.V3
= 2.30
= 60 C olur.
Devrenin eşdeğer sığası;
qL = C.V ve qK = C.V olur.
Yükler korunacağından,
qilk = qK + qL + qN
50 C = C.V + C.V +
50 C =
q1 = C2.V2
40 = C2.20 ⇒ C2 = 2F olur.
M
C
C
.V
2
seri C =4F
1
5
C.V & V = 20 volt olur.
2
C2=2F C12
C4=2F
K
L
C3=2F
Yeni durumda kondansatörlerin yükleri,
ı
q K = C.V = C.20 = 20 C
C 12 =
q K = C.V = C.20 = 20 C
q L = C.V = C.20 = 20 C
C12 ile C3 paralel bağlı olduğundan,
b)
C
qN = qM = .V = 10 C olur.
2
c)
K kondansatörü 50 C – 20 C = 30 C yük kaybeder.
4.
a)
C 123 =
V1=10V
q1
V2=20V
q2
C1
C2
K
V3
4.2
8 4
= = F
4+2 6 3
q3
4
10
+2 =
F t›r.
3
3
K
L
C123= 10 F
3
C4=2F
10
.2
5
= F bulunur.
C KL = 3
4
10
+2
3
q4
L
C4=2F
C3
Bir kondansatör üzerindeki enerjinin gerilime
b) C4 kondansatörü C3 ve C1 ile C2 ye seri bağlı
olduğundan,
q4 = q1 + q3 = q2 + q3 = 40 + 60 = 100 C
olur.
bağlı ifadesi,
E=
C 1 için, E 1 =
200 =
2
1
CV ile bulunur.
2
2
1
C .V
2 1 1
2
1
.C . (10) & C 1 = 4F
2 1
q 1 = C 1 .V1
= 4.10
= 40 C olur.
276
ELEKTRİK VE MANYETİZMA
c) K-L arasındaki potansiyel,
qKL = q4
qKL = CKL.VKL
100 =
olur.
5
. VKL ⇒ VKL = 80 V
4
5.
7.
Şekil-I deki devrede:
a)
CKL=6C
K
C .C
C efl = 1 2
C1 + C2
=
20 . 30
20 + 30
=
600
50
C1 = 20μF
+ –
+ –
K
C2 = 30μF
+ –
+ –
L
2C
K
C
CLM=3C
K
+
= 12 nF
qtop = q1 = q2 = Ceş . V = 12 . 50 = 600 μC olur.
M
L
–
K
VK=60volt
2C N
C
L
3C
V=50V
M
2C
6C
V
L
3C
2V
M
VL
3V
2C
N
VN=0
VM
Şekildeki kondansatörler seri olduğundan yükleri
eşittir. q = C.V ifadesine göre 6C nin üzerindeki
Şekil-II deki devrede:
VKL = Vort =
gerilim V ise, 3C nin üzerindeki gerilim 2V, 2C nin
q1 + q2
C1 + C2
=
600 + 600
20 + 30
=
1200
50
üzerindeki gerilim 3V olur. VK = 60 volt, VN = 0 oldu-
C1 = 20μF
+ –
+ –
K
ğundan,
∆VKN = VK – VL
L
C2 = 30μF
+ –
+ –
V + 2V + 3V = 60 – 0
6V = 60 ⇒ V = 10 volt olur.
= 24 V olur.
L noktasındaki potansiyel,
∆VKL = V = 10
VK – VL = 10
60 – VL = 10 ⇒ VL = 50 volt olur.
6.
Şekil-I de C1 ve C2 kondansatörleri seri olduğundan
b) M noktasındaki potansiyel,
C1 ve C2 nin üzerindeki yükler birbirlerine eşittir.
C 12 =
∆VLM = 2V
4.12
= 3F olur.
4 + 12
VL – VM = 2.10
50 – VM = 20 ⇒ VM = 30 volt olur.
q12 = C12.V = 3.100 = 300C
olur. Bu durumda,
q1 = q2 = q12 = 300 C olur.
C3 kondansatörün yükü,
q3 = C3.V = 6.100 = 600C
olur.
C1 ve C3 ters bağlandığından
yük geçişi potansiyel eşitleninceye kadar devam eder.
qı1 + qı3 + qı4 = q3 – q1
4.Vı + 6.Vı + 5.Vı = 600 – 300
15Vı = 300
Vı = 20 volt olur.
C1 kondansatörünün yeni yükü,
qı1 = C1.Vı = 4.20 = 80C olur.
Yükündeki değişme,
∆q1 = q1 – qı1
= 300 – 80
q1
C =4F
+ –1
+ –
q3 C =6F
– +3
– +
C4=5F
q1
C =4F
– +1
– +
q3
C =6F
– +3
– +
q4
C =5F
– +4
– +
8.
2μF ile 4μF sığalı kondansatörler
paralel bağlıdır.
2μF
C1
L
•
C1 = 2 + 4
= 6μF olur.
12μF
12μF ile C1 birbirine seri bağK
lıdır. Bu ikisinin
•
eşdeğer sığası
C2 olsun.
1
1
1
=
+
C 2 12 C 1
4μF
8μF
1
1
1
=
+
C 2 12 6
C 2 = 4nF olur.
C2 ile 8μF lik kondansatörler ise birbirine paralel
bağlıdır.
CKL = C2 + 8 = 4 + 8 = 12 μF olur.
= 220 C olur.
ELEKTRİK VE MANYETİZMA
277
9.
M 2F N
2F
k›sa
devre
N 5F
M
P
4F
N 1F
M
4F
P
N
M
2F
P
6F
M 2F N
L
5F
4F
M
4F
L
L
KL
Cefl=8F 2F
5F
P
K
4F M
4F
N
M
4F
Cefl=3F
1F
L
5F
2F
K
6F
8F
N
8F
L
1
1 1 1
= + +
C KL 4 8 8
1
4
=
C KL 8
C KL = 2F olur.
10. a) Kondansatör teflon ile dokundurulduğunda sığası,
Cı = l.C = 2.2 = 4μF olur.
b) Kondansatörün yeni durumda yükü,
q = Cı.V
= 4.400
= 1600μC
= 1600.10–6C
= 1,6.10–3C olur.
c) Kondansatörün enerjisi,
E=
=
1 › 2
C .V
2
–6
2
1
.4.10 . (400)
2
= 0, 32 J olur.
278
ELEKTRİK VE MANYETİZMA
4. BÖLÜM
MANYETİZMA
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
3.
BK=2B • K
B1K=3B •
B2K=B x
d
X
1.
BK
B1
B2
BL=5B x L
K
10cm
i1 = 8A
B1L=3B x
2d
i2 =4i
Y
20cm
BM=13B • M
4
i2 =12A
i1 akımının K noktasında oluşturduğu manyetik alan;
2i
–7 2 . 8
–6
B 1 = K . 1 = 10 . –1 = 16.10 T ;
d1
10
2i 2
–7 2 . 12
–6
= 10 .
= 8.10 T ;
–1
d2
3.10
B1M= 3B x d
4
B2M=4B •
2i
olsun. K, L ve M noktalarındaki manyetik
d
alanların büyüklükleri,
B=K
9
BK = 2B,
i2 akımının K noktasında oluşturduğu manyetik alan;
B2 = K .
d
B2L=2B x
X
Y
i1 =3i
BL = 5B,
13B
= 3,25B olur.
BM =
4
Buna göre,
9
K noktasındaki toplam manyetik alan;
BK = B1 + B2
BL > BM > BK olur.
= 16.10–6 + 8.10–6
CEVAP A
= 24.10–6
= 2,4.10–5 T ; ☼ olur.
CEVAP E
4.
2.
i1 = 2i
X
2i
2d
|B1|=B x
|BK|=4B K
|B2|=3B x
x
Y
45°
Y
i1 ve i2 akımlarının K noktasında oluşturdukları
manyetik alanlar,
2.2i
2i
= K.
=B,
B1 = K.
2d
d
2.3i
6i
B2 = K.
= K.
= 3B , olur.
d
d
K noktasındaki manyetik alanların bileşkesi,
BK = B + 3B = 4B , olur.
CEVAP D
BY=B
i
d
i2 = 3i
45° 2d
d
O
BX d
X
i akımının O noktasında oluşturduğu manyetik alan,
2i
; . olur.
BY = B = k.
d
2i akımının O noktasında oluşturduğu manyetik
alan,
2. (2i)
4i
BX = k.
= k.
= –2B ; , olur.
d
d
O noktasındaki bileşke manyetik alan
Bbileşke = BX + BY = B – 2B = –B olur.
CEVAP A
ELEKTRİK VE MANYETİZMA
279
5.
X
8.
Y
i1 = 4i
X
i1=i
i2 = i
i2=3i
Y
d
B1=B; x B =6B; x
2
2d
K
B3=2B; • B =5B; x
K
d
i3 = 3i
Z
d
d
B x
2B • K
3B •
BK=–4B •
i akımının K noktasında oluşturduğu manyetik
alanın şiddeti B ise, bu noktada oluşan bileşke
manyetik alan,
BK = B – 2B – 3B
BK = –4B olur.
CEVAP D
6.
i1 akımının K noktasında oluşturduğu manyetik alan
şiddeti B ise, bu noktadaki bileşke manyetik alan,
BK = B + 6B – 2B = +5B olur.
CEVAP D
9.
X
i1=i
B x d
K
B •
d
d
B x
B x
L
d
Y
d
d
B •
B •
N
B •
d
d B x
i3=i
Z
d
i akımının O noktasında oluşturduğu
manyetik alanın şiddetine B diyelim. O
noktasında oluşan
bileşke manyetik alan
şiddeti BO olduğuna
göre i3 = 3i ve ,
yönündedir.
3B
Bo
2B
X
Z
O
i1 =i
2B
B
Y
i2=i
i2 =2i
CEVAP C
10.
M
BK
B1K
Şekilde görüldüğü gibi; K ve M noktalarında bileşke manyetik alan şiddeti sıfırdır.
CEVAP B
7.
i2 =8A
K
X
0,1m
L
Y
0,1m
BL
0,1m
B2L
x
B2K
i1 = 4A
X
B1 = K .
K
B2 = K .
40cm
K
i2 =12A
Y
Akımlar zıt yönde ise tellerin dışında ve küçük
akıma yakın bir noktada manyetik alan sıfır olabilir.
K noktasındaki manyetik alan sıfır ise,
K
K
= 24.10
–6
+ 16.10
= 40.10
–6
T
–6
–5
–7
L
T olur.
–6
2 . 12
.
= 8.10 T
–1
3.10
B 2 = 16.10
2 . i1
2 . i2
K.
= K.
0, 4 + x
x
–6
L
T
L noktas›ndaki bileflke manyetik alan,
BL = B2 – B1
4
12
=
0, 4 + x
x
L
L
= 16.10
1
3
=
0, 4 + x
x
= 8.10
–6
–6
– 8.10
–6
T olur.
BK ve BL taraf tarafa oranlanırsa,
0, 4 + x = 3x
0, 4 = 2x
ELEKTRİK VE MANYETİZMA
2i 2
–7 2 . 8
–6
= 10 . –1 = 16.10 T
d2
10
K noktas›ndaki bileflke manyetik alan,
BK = B1 + B2
B 1 = 10
I B 1K I = I B 2K I
x = 0, 2 m = 20 cm olur.
2i 1
–7 2 . 12
–6
= 10 .
= 24.10 T
–1
d1
10
= 4.10
BK = 0
280
B1L
B2K
i1 =12A
K
B1K
i3 =3i
CEVAP C
B K 4.10 –5
=
= 5 olur.
B L 8.10 –6
CEVAP E
11. B manyetik alan
BY
O
bileşenlere ayrıldı- X
3d
4 5°
i1
45°
ğında i1 ve i2 akımlarının O noktasınBX
B
da oluşturdukları
2d
manyetik alanların
büyüklükleri eşittir.
i2
Y
Manyetik alan vektörel bir büyüklüktür. Manyetik alanın şekildeki gibi
olabilmesi için i1 akımının sayfa düzleminden içeri
(,), i2 akımının sayfa düzleminden dışa (.) doğru
olması gerekir.
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
1.
Y
X
i2 =8A
i1 =4A
I. yargı yanlıştır. III. yargı doğrudur.
|BX| = |BY|
2.i
2.i
K. 1 = K. 2
3d
2d
B1
BO
B2
O r=20cm
B1 = K .
2r . i 1
–7 2 . 3 . 4
–6
= 10 .
= 12.10 T ; 9
–1
r
2.10
B2 = K .
2i 2
–7
–6
2.8
= 10 .
= 8.10 T ; 9
–1
d
2.10
O noktas›ndaki bileflke manyetik alan,
2i1 = 3i2
BO = B1 + B2
II. yargı doğrudur.
= 12.10
CEVAP D
= 2.10
–6
–5
+ 8.10
–6
T; 9
olur.
CEVAP D
12.
B=3.10–6 T
•
Btel
r=20cm
i= 4A
L
BL
2.
B
Y
X
•
i2 =6A
B1 B2 BO
Telden geçen akımın L noktasında oluşturduğu
r=20cm
O d=12cm
manyetik alanın büyüklüğü,
B tel = K .
= 10
2i
d
–7
= 4.10
.
2.4
2.10
–6
i1 =4A
–1
T olur.
L noktasındaki toplam manyetik alan,
2
2
2r . i 1
–7 2 . 3 . 4
–6
= 10 .
= 12.10 T ; 7
–1
r
2.10
B2 = K .
2i 2
–7
–6
2.6
= 10 .
= 10.10 T ; 9
–2
d
12.10
2
B L = B + B tel
2
B L = (3.10–6)2 + (4.10–6)2
2
O noktasındaki bileşke manyetik alan,
B L = 9.10–12 + 16.10–12
2
BL
B1 = K .
BO = B1 – B2
= 25.10–12 olur.
= 12.10
BL = 5.10–6 T olur.
CEVAP C
= 2.10
–6
–6
– 10.10
–6
T ; 7 olur.
CEVAP B
ELEKTRİK VE MANYETİZMA
281
3.
i1 ve i2 akımlarının O
noktasında oluşturdu-
X
i2 =i
ğu manyetik alanlar,
2i
B2 = K
r
= B; . olur.
2r.2i 1
B1 = K
.
r
4
3i
=K
r
3
=
B; , olur.
2
6.
Y
r
i1 = 2i
O noktasındaki manyetik alanlar,
= 10
r
B1 x
O r
–7
B2 = K .
= 10
CEVAP A
B1
2.3.4
–1
2.10
–6
T
•
B2
O
2r . i 2
r
–7
= 9.10
O noktasındaki bileşke manyetik alan,
3
1
BO = –
B + B = – B olur.
2
2
.
= 12.10
B2=B •
BO
2r . i 1
B1 = K .
r
.
2.3.3
–1
2.10
–6
T
O noktasındaki bileşke manyetik alan,
B O2 = (12.10–6)2 + (9.10–6)2
4.
i1 akımının O noktasında
oluşturduğu manyetik alan,
2i
B1 = K.
=B ;.
X
Y
i1 = i
i2 =i
Z
r
B3=3B x
B1=B • O
B2=B •
olur.
i3 = i
CEVAP C
5.
X
i1 = 4A
Y
i2 = 8A
r = 20 cm
B1
Z
B2
B3
O
BO
i3 = 2A
B1 = K .
B2 = K .
B3 = K .
2i 1
–7
–6
2.4
= 10 .
= 4.10 T ; 9
–1
d1
2.10
2i 2
–7
–6
2.8
= 10 .
= 8.10 T ; 9
–1
d2
2.10
2r . i 3
–7 2 . 3 . 2
–6
= 10 .
= 6.10 T ; 7
–1
r
2.10
O noktasındaki bileşke manyetik alan;
BO = B1 + B2 – B3
282
= 4.10
–6
+ 8.10
= 6.10
–6
T; 9
ELEKTRİK VE MANYETİZMA
–6
– 6.10
olur.
BO = 1,5.10–5 T olur.
CEVAP E
olduğuna göre bu noktada
bileşke manyetik alan,
BO = B + B – 3B = –B
BO = 15.10–6
–6
CEVAP D
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
1.
1.
N=500
F2
B1
eksen
1
•
i
i
B2
,=15cm
F1
fiekil-I
i
fiekil-II
+y
2
–x
+x
Akımın büyüklüğü,
Bsolenoid = K
24.10–3
=
10–7
B3
–y
4r.N.i
,
fiekil-III
Manyetik alanlar içerisindeki teller kuvvetler
yönünde eğilir. Kuvvet sağ el kuralı ile bulunur.
Şekil-I de tele etki eden kuvvet –y yönünde, manyetik alan sayfa düzleminden içe (,) doğrudur.
Şekil-II de tele etki eden kuvvet +y yönünde, manyetik alan safya düzleminden dışa (.) doğrudur.
Şekil-III te tel eğilmediğinden tel üzerine kuvvet
etki etmemiştir. Bu durumda manyetik alan +x ve
–x yönündedir.
CEVAP B
2
4.3.5.10 i
15.10
i = 6A olur.
B3
i
–2
Akımın yönü sağ el kuralına göre 2 yönünde olur.
CEVAP D
2.
B
i 2a
F2
i
F1
2.
X
S
B
–x
S
Y
S
N
F3
i
a
•
a F4
• a i
2a
F5
Manyetik alan içerisinde tele etkiyen kuvvet,
N
N
•
•
B
S
Z
N
+x
K
f
+ –
r=0
K anahtarı kapatılarak solenoidden elektrik akımı
geçirildiğinde, Y ve Z mıknatıs iğneleri konumlarını
değiştirmezler. X mıknatıs iğnesi hareket ettiğinden konumu değişir.
CEVAP A
F = B.i.,.sina eşitliğiyle bulunur. a: Manyetik alan
ile tel arasındaki açıdır. Telin üzerinden geçen
akım manyetik alana paralel ise a = 0° olacağından
tele etki eden kuvvet sıfırdır. Bu durumda F2 ve F4
kuvvetleri sıfırdır. Diğer kuvvetlerin büyüklükleri,
F1 = B.i.2a
F3 = B.i.2a
F5 = B.i.a olur.
Tele etki eden bileşke manyetik kuvvet,
Fbileşke = F1 + F3 + F5
= 2Bia + 2Bia + Bia
= 5Bia olur.
Yönü ise, sağ el kuralına göre sayfa düzleminden
dışa (.) doğrudur.
CEVAP D
ELEKTRİK VE MANYETİZMA
283
3.
5.
I. yol:
B
B
Manyetik alan içerisinde tellere etki
eden kuvveti bulabilmek için KL parçasının manyetik
alan yönünde 3 br,
manyetik alana dik
2 br parça gibi
düşünebiliriz.
1br
•M
B
.
3br
•
K
α1
i
α2
F2
a
60°
a
A
i
.
2br
i
i
a
L
•
60°
i
F1
i
F3
C
Tel eşkenar üçgen şeklinde bükülüp manyetik alan
içerisine konulduğunda açılar 60° dir.
Telin AB kısmına etki eden kuvvet,
3br
Manyetik
alana
paralel parçaya kuvvet etki etmez. Dik parçaya
etki eden kuvvet,
3
B.i.a
2
F1 = B.i.a.sin60° =
FKL = B.i.2 = 2B.i
,
Telin BC kısmına etki eden kuvvet,
olur. LM parçasının manyetik alana dik 3 br, paralel 1 br parçası vardır. Dik parçasına etki eden
kuvvet,
3
.B.i.a
2
F2 = B.i.a.sin120° =
.
Telin AC kısmı manyetik alana paralel olduğundan
tele etki eden kuvvet, F3 = 0 olur.
FLM = B.i.3 = 3B.i
olur. Kuvvetler taraf tarafa oranlanırsa,
FKL 2B.i 2
olur.
=
=
FLM 3B.i 3
Üçgen tele uygulanan toplam kuvvet,
Fbileşke = F1 + F2 + F3
=
II. yol:
3
3
.B.i.a –
.B.i.a + 0
2
2
= 0 olur.
Tele etki eden kuvvetin büyüklüğü, F = B.i.,.sinα
eşitliğinden de bulabilir.
2
= 2.B.i
FKL = B.|KL|.i.sinα1 = B.c13.i
13
3
FLM = B.|LM|.i.sinα2 = B.c10.i
= 3.B.i
10
Not: Düzgün manyetik alan içindeki kapalı bir
ilmek üzerinden i akımı geçtiğinde, ilmeğe etkiyen
toplam kuvvet her zaman sıfırdır.
CEVAP A
olur. FKL ve FLM taraf tarafa oranlanırsa,
FKL 2B.i 2
=
=
olur.
FLM 3B.i 3
CEVAP A
4.
X
6.
y
i=5A
F
i
L
i
F
53°
,= 50 cm
p
o
z
Telin KL kısmına etkiyen manyetik kuvvet,
B
Telin n ve p parçaları manyetik alana paralel
olduğundan bu parçalara manyetik kuvvet etki
F = i., B.sina
etmez. xy düzlemindeki o parçası manyetik alana
= 5.0,5.2.sin53°
diktir. Bu parçaya etki eden kuvvet sağ el kuralın-
= 5.0,8
ELEKTRİK VE MANYETİZMA
n
x
K
284
tel
B
F
= 4 N olur.
i
dan +y yönündedir.
CEVAP B
CEVAP C
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
3.
X
Y
i1 =i
X
1.
K
F
ZY
Y
FY
F
0,1m
L
2
iterler. Kuvvetin büyüklüğü,
2 . i1 . i2
.,
d
–7 2 . 12 . 5
= 10 .
.1
–1
1.10
.
FZ
d
Y teline etkiyen bileşke manyetik kuvvet,
FY = FXY + FZY
2,
FY = K
(4i2 + 8i2)
d
–5
N,
FYZ
.
2
i
F = 6K , olur.
d
F = K.
–4
.
2
2,
2i
F=K
(4i2 –
)
d
2
Tellerden zıt yönde akımlar geçtiğinden birbirlerini
= 1, 2.10
FXZ
.
X teline etkiyen bileşke manyetik kuvvet,
FX = F = FYX – FZX
i2 = 5A
= 12.10
i3 =2i
.
FX=F
d
1m
1
i2 =4i
. . FYX FXY .
.
F
FZX
i1 =12A
Z
2 yönünde olur.
2
CEVAP D
i
,
d
= – 4F olur.
= 24K
Z teline etkiyen bileşke manyetik kuvvet
FZ = FXZ + FYZ
2
2, 2i
FZ = K
(
+ 8i2)
d
2
2.
X
Y
i1 = i
FYX=F
i2 = 2 i
.
.
i3 =6i
CEVAP C
FXY=F
.
FZY=3F
.
d
2
i
FZ = 18K
,
d
FZ = 3F olur.
Z
FY=4F
4.
Ι1=6A
1.tel
2d
4cm
Y telinin X teline uyguladığı manyetik kuvvet,
F
F12
2
2i.2i
i
., = 4K ., olur.
FYX = F = K
d
d
60°
2.tel
Ι2=8A
3.tel
Ι3=6A
F32
Y teline etki eden bileşke kuvvet,
Tellerden aynı yönde akım geçtiklerinden birbirini
2
i
2.2i.6i
,
FY = FXY + FZY = 4K ., + K
d
2d
= –F – 3F
çekerler;
1. telden geçen akımın 2. tele uyguladığı kuvvet,
F12 =
= – 4F
olur.
=
CEVAP D
2K . I 1 . I 2 . ,
d
–7
2 . 1.10 . 6 . 8
.5
–2
4.10
= 12.10
–4
N olur.
ELEKTRİK VE MANYETİZMA
285
3. telden geçen akımın 2. tele uyguladığı kuvvet,
F32 =
=
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
2K . I 2 . I 3 . ,
d
2 . 1.10
–7
4.10
= 12.10
–4
1.
.8.6
–2
N
y
.5
B
L
•
olur.
F
F32 ile F12 arasındaki açı 60° ve kuvvetler birbirine
i ,
eşit olduğundan,
yo
F = F32.v3 = 12v3.10–4 N olur.
•K
CEVAP E
.
5.
|FZY| > |FXY|
X
olduğundan Y teli X
teline doğru yaklaşır.
ı
ı
|FXY
| = |FYZ
| olunca
Y teli dengede kalır.
Y
i1 =i
F = B.i.,
i3 =3i
. .
FZY
Tel üzerine uygulanan manyetik kuvvet,
Z
i2 =i
›
FZY
olur. y eksenine göre tele etki eden tork,
x = F.xo
FXY
= B.i.,.xo
›
FXY
Y telinin X telinden
uzaklığı,
K
Y
x
(2d–x)
d
d
olur. yo uzaklığına bağlı değildir.
CEVAP C
2i 2 .i 3
2i 1 .i 2
., = K
.,
(2d – x)
x
i.i
i.3i
=
x
2d – x
2.
1
3
=
x
2d – x
y
F1
4x = 2d & x =
d
olur.
2
F2
b
O•
ı
a
.
dengede kalır.
i1 akımı artırılırsa,
FXY > FZY olduğundan
Y teli Z teline doğru
kayar.
I. yargı doğrudur.
X
Y
i1
i3
i2
x
Kuvvetlerin büyüklükleri;
F1 = B.i.a
FZY
..
FXY
F2 = B.i.b
F3 = B.i.a
d1
d2
II. yargı doğrudur.
i1 akımının yönü değiştirilirse,
FY = FXY + FZY olur. Y teli X teline yaklaşır.
III. yargı doğrudur.
CEVAP E
ELEKTRİK VE MANYETİZMA
F3
Sağ el kuralını uyguladığımızda tel çerçeveye etki
eden kuvvetlerin yönleri şekildeki gibidir.
Z
i3 akımı artırılırsa,
FZY > FXY olur. Y teli X teline yaklaşır.
286
B
F4
CEVAP B
FXY = – FZY ise, Y teli
i
O•
3x = 2d – x
6.
x
xo
F4 = B.i.b
olur. F2 ve F4 kuvvetleri dönme ekseninden geçtiğinden momentleri sıfırdır. F1 ve F3 kuvvetleri zıt
yönde olduğundan y eksenine göre momentleri,
a
a
M = F1. – F3.
2
2
a
a
= (B.i.a). – (B.i.a).
2
2
= 0 olur.
CEVAP A
3.
z
5.
B
FKL
K
y
|B|=4T
L
i=2A
A
D
d
FLM
M
y
FBC
i
.
.
2m
a
i
B
FAD
2a
N
d
i
2m
C
2m
.
x
3a
I. yol:
x
d doğrusu halkanın merkezinden geçtiğinden halkayı iki eşit parçaya böler. Telin AB ve DC kesimlerinden geçen akımlar manyetik alana paralel
olduğundan bu kesimlere etki eden kuvvetler
sıfırdır.
Tel çerçevenin KN ve LM kenarlarından geçen
akımlar manyetik alana paralel olduğundan bu
kenarlara etki eden kuvvetler sıfırdır. KL ve MN
kenarlarına etki eden kuvvetler,
FKL = B.i.|KL|
FAB = FCD = 0
= B.i.3a
AD ve BC kesimlerine etki eden kuvvetler,
|FAD| = B.i.|AD| = 4.2.2 = 16 N ; ,
|FBC| = B.i.|BC| = 4.2.2 = 16N, . olur.
= 3B.i.a ; sayfa düzleminden içe (,)
FMN = B.i.|MN|
= B.i.3a
d doğrusuna göre toplam tork,
x = |FAD|.2 + |FBC|.2
= 3B.i.a ; sayfa düzleminden dışa (.) doğrudur. Kuvvetlerin d doğrusuna göre torkun büyüklüğü,
= 16.2 + 16.2
= 64 N.m olur.
x = FKL.2a + FMN.a
II. yol:
= 3B.i.a.2a + 3Bi.a.a
Torkun büyüklüğü,
= 9Bia2 olur.
x = B.i.A.sinθ
CEVAP D
= 4.2(2.4).sin90°
= 64 N.m olur.
CEVAP E
4.
B=10T
6.
i=5A
z
B=20T
2m
A
FAB
i
B
i
FAD
53°
FDC
Tel çerçevenin alanı,
A=
a2
= 0,2.0,2 =
4.10–2
FBC
4m
D
a=0,2m
y
C
x
m2
yüzeyin normali ile manyetik alan arasındaki açı
a= 90° olduğunda manyetik tork,
x = B.i.A.sina
= 10.5.4.10–2.sin90°
= 2 N.m
olur.
CEVAP B
I. yol:
FAB ve FDC kuvvetlerinin torklarının büyüklükleri
eşit ve zıt yönlü olduğundan bu kuvvetlerin z
eksenine göre toplam torkları sıfırdır. FAD kuvveti
dönme eksenine uygulandığından torku sıfırdır.
Bu durumda halkaya etki eden tork FBC kuvvetinin
oluşturduğu torktur.
ELEKTRİK VE MANYETİZMA
287
FBC kuvvetinin y eksenine
göre torku,
x = FBC.d
= FBC.(2.sin53°)
= B.i.|BC|.(2.0,8)
= 20.0,1.4.1,6
B
MODEL SORU - 7 DEKİ SORULARIN ÇÖZÜMLERİ
FBC
D
53°
d
2m
1.
Ek
53°
X
= Ek
Y
2
2
1
1
. mX . VX = . mY . VY
2
2
C
2
2
4m . V X = m . V Y
2VX = VY
VX = V (
= 12,8 N.m olur.
II. yol:
Torkun büyüklüğü,
VY = 2V olur.
X ve Y parçacıklarının manyetik alan içerisindeki
ve çembersel yörüngelerindeki yarıçapları oranı,
x = B.i.A.sinθ
= 20.0,1.(2.4).sin53°
m X . VX
4m . V
rX
qX . B
q.B
=
=
= 4 olur.
rY
m Y . VY
m . 2V
2q . B
qY . B
= 2.8.0,8
= 12,8 N.m olur.
Parçacıkların kinetik enerjileri eşit ise hızları,
CEVAP D
2.
CEVAP E
Parçacığın yükünün kütlesine oranı,
mV
eşitliğinden,
r=
q.B
q
V
=
m r .B
=
2.10
8.10
–2
6
. 5.10
–2
8
= 5.10 C/kg olur.
3.
CEVAP B
Parçacık manyetik alanda dairesel hareket yaptığından,
Fmer = Fman
2
m
j
= q.j.B
r
2
r
j
r
.m.
= q.j.B.
2
r
2
qjBr
1
.m.j2 =
2
2
qjBr
Ek =
olur.
2
4.
CEVAP B
Yüklerin büyüklükleri eşit olduğundan,
qX = qY = q olur.
Parçacıkların yörünge yarıçapları rX = r, rY = 2r
olduğundan momentumları,
m X .j X
rX
q X .B
=
rY
m Y .j Y
q Y .B
PX
q.B
r
=
2r
PY
q.B
PX
1
=
olur.
PY
2
288
ELEKTRİK VE MANYETİZMA
Kinetik enerjileri oranından,
bağıntılarına göre, jX ve jY bilinmediğinden, merkezcil
kuvvetlerin büyüklükleri için kesin birşey söylenemez.
2
PX
E kX
2m X
=
2
E kY
PY
2m Y
2
1
mX
Elektronun yörünge yarıçapı,
r=
=
m. V
q.B
9.10
–31
1, 6.10
. 6, 4.10
–19
. 3.10
TX =
2r.m X
2r.m Y
, TY =
qB
qB
CEVAP C
9.
5.
2r.r
2r.r
, TY =
ya da
jX
jY
bağıntılarına göre, jX ve jY, mX ve mY bilinmediğinden dolanım periyotlarının büyüklükleri için
kesin birşey söylenemez.
CEVAP A
1
= 2
4
2
mY
mY
mX
1
=
&
= 1 olur.
4m X
mY
4
TX =
6
Tele etkiyen manyetik kuvvet, sağ el
kuralına göre, sayfa
düzlemine dik içe
doğrudur.
N
F
X
–4
F
B
i
–2
= 12.10 m
= 12 cm olur.
6.
CEVAP D
S
Parçacık dairesel hareket yaptığından,
CEVAP C
Fmer = Fman
2
m
j
= q.j.B
r
mj = q.r.B
q
j
=
olur.
rB
m
OX
10.
B
rX
CEVAP C
qX
jX
rY
X
7.
Parçacık dairesel hareket yaptığından periyodu,
Fmer = Fman
m.~2.r = q.j.B
m.~2.r = q.~r.B
m.~ = q.B
qB
~=
m
qB
2r
=
T
m
T=
8.
2rm
olur.
qB
OY
jY
Y
I.
CEVAP A
PX = PY = P
P
q X .B
rX
=
rY
P
q Y .B
qX = qY = q
q
3
= Y
qX
4
rX = rY
qX > qY olur.
m X .j X
m .j
= Y Y
q.B
q.B
PX = PY olur.
Çizgisel momentumlarının büyüklükleri kesinlikle eşittir.
Fmer = Fman
FmerX = q.jX.B
FmerY = q.jY.B
qY
I. yargı kesinlikle doğrudur.
II. X parçacığı (+) yüklü ise Y parçacığı (–) yüklüdür.
X parçacığı (–) yüklü ise Y parçacığı (+) yüklüdür.
II. yargı kesinlikle doğrudur.
III. B manyetik alanının yönü , ya da . olabilir.
III. yargı için kesin birşey söylenemez.
CEVAP D
ELEKTRİK VE MANYETİZMA
289
11.
y
y
V
B
F
B
+q
K
F
–q
x
x
L
V
z
z
fiekil-I
fiekil-II
y
V
F
+q
x
M
B
z
fiekil-III
Manyetik alan içerisindeki yüke etki eden kuvvetin
yönü sağ el kuralı ile bulunur. Baş parmak hız
yönünde, dört parmak manyetik alan yönünde
tutulduğunda avuç içi manyetik kuvvetin yönünü
verir.
Bu durumda,
Şekil-I de kuvvet –z yönünde,
Şekil-II de kuvvet +x yönünde,
Şekil-III te kuvvet +x yönündedir.
CEVAP D
12.
mZ
jZ
OZ
OX
rX
qZ
rZ
B
mX j
X
qX
rY
OY
jY
mY
qY
Sağ el kuralına göre parçacıkların yüklerinin işareti,
qX
qY
qZ
–
+
+
olur.
CEVAP B
290
ELEKTRİK VE MANYETİZMA
TEST
1
MANYETİZMA
ÇÖZÜMLER
1.
4.
i
X
d
2i
Y
2i
B = K.
d
d
K
B
ol du ğu na gö re,
akımların K noktasında oluşturduğu manyetik alan
şiddeti, BK = – 3 B
olur.
BK = 3B
4B
i akımının K noktasında oluşturduğu manyetik alan
şiddeti,
K noktasındaki bileşke manyetik alan,
BK = – 3 B olur.
CEVAP B
X
3i
3B
K
d
B
B
d
Y
i
d
Z
2i
CEVAP D
2.
BK1
BK2
K
BK
d
i1
X
d
BL
BL1
5.
L
BL2
d
i2
K.
Y
K ve L noktalarındaki manyetik alan şiddetleri eşit
olduğundan akımların oranı,
B1
K
BK = BL
+ B2 = B2 – B1
K
L
2r . i 1
2r . i 2
= K.
r
3r
i
i1 = 2
3
i1 =
L
Y
3r
X
i1
B1
O
r
B2
12i
3
i1 = 4i olur.
2i
2i
2i
2i
K. 1 +K. 2 = K. 2 –K. 1
d
3d
d
d
3i 1 + i 2 i 2 – i 1
=
3
1
3i 1 + i 2 = 3i 2 – 3i 1
6i 1 = 2i 2
i1
1
olur.
=
i2
3
i2 =12i
CEVAP C
CEVAP A
6.
3.
m
| B1| = | B2|
i1 ve i2 akımlarının O noktasındaki
manyetik alanları şekildeki gibidir.
B1
BO
B
j
+q
B2
O
r
O
K
L
M
N
m.j
eşitliğinde hız iki katına
q.B
çıkarsa yörünge yarıçapı iki katına çıkar.
Yörünge yarıçapı r =
Şekilde görüldüğü gibi, parçacık M noktasından
alandan çıkardı.
CEVAP D
2r.i 1
2.3.8
= 10–7.
= 16.10–6 T olur.
B1 = K
–1
r
3.10
2r.i 2
2.3.6
= 10–7.
= 12.10–6 T olur.
B2 = K
–1
r
3.10
O noktasındaki bileşke manyetik alan,
BO = 20.10–6T = 2.10–5 T olur.
CEVAP B
ELEKTRİK VE MANYETİZMA
291
7.
Şekilde görüldüğü
gibi bölgedeki manyetik alan +z yönündedir.
10. Bobini 4 parmak akı-
y
,=6m
mın yönünü göstere-
Fmag
B
cek şekilde sağ elimizin içine aldığımızV
–q
i=2A
X
da baş parmak olu-
x
– +
şan manyetik alanın
B
yönünü verir. Şekilde gösterildiği gibi manyetik
alan sağa doğrudur. Büyüklüğü ise,
Fel
z
CEVAP E
B = K.
–7 4.3.2.100
–5
2
4r.i.N
= 10 .
= 4.10 Wb/m
6
,
olur.
8.
i akımının O noktasında oluşturduğu manyetik
alan şid de ti ne
B diyelim. O noktasında oluşan
bileşke manyetik
alan vektörü BO
olduğuna göre,
X
11.
5B
CEVAP D
i1 =3i
BO
4B
Y
FZY
?
O
i1
2d
B
Y
X
Y
i1 =2i
2.2i.i 3
2 . 3i . 2i
= K.
d
2d
FYZ =3F
FYX = 2F
FXZ =3F
FY = 5F
FZY = 3F
B
B
FZ =6F
––––
––––
–x
–x
+x
ELEKTRİK VE MANYETİZMA
45°
a
F2
a
F1
olsun.
––––
.
i
+x
X, Y ve Z tellerine etki eden kuvvetler şekilde gösterilmiştir. X teline etki eden kuvvet –x, Y teline
etki eden kuvvet –x, Z teline etki eden kuvvet +x
yönündedir.
FX
FY
FZ
292
12.
d
–x
2i . i
.,
d
CEVAP C
i3 =3i
d
F = K.
3
i
2
1 yönünde olur.
Z
i2 = i
d
Y teli dengede olduğundan üzerine uygulanan net
kuvvet sıfırdır.
| FXY| = | FZY|
i2 = 2i
i3 =
FYX = 2F
FXY
2
i3 =i
2B
K.
FZX = 3F
i3
Z
X
CEVAP E
FX = F
i2 =2i
1
i1 = 5i ve . yönündedir.
9.
Z
CEVAP A
a
fiekil- I
a
i
fiekil- II
Şekil-II de manyetik alan telediktir.
Tellere etki eden kuvvetleri yazıp oranlarsak,
F1
i.a.B
=
=
F2 i. 2 a.B. sin 90°
1
2
=
olur.
2
2 .1
CEVAP B
TEST
2
ÇÖZÜMLER
1.
4.
B
B
BK
K
MANYETİZMA
d
X
Y
i1 =3i
i1 = i
i2 =i
3B
X
B
L
BL = 2B
d
3B
M
B
B
B
d
d
i2 = 3i
i3 =i
d
B
–
3
2i
B = K.
olsun. Bu durumda,
d
2i
olsun.
d
BK = B, BL = B olur.
B K = 2B
BK B
= = 1 olur.
BL B
B L = 2B
10
BM =
B
3
5.
olur.
BM > BK = BL
L
d
Z
BM = 10
—B
3
i akımının O nok-
X telinden geçen
CEVAP A
X
Y
Z
akımın Y teline
CEVAP E
2.
d
B
3B d
Y
B = K.
B
K
d
uyguladığı kuvvet
F ise, Z teline
i1 =i
FZ = 2F
FYZ = 3F
FXZ =F
d
olur.
tasında oluştur-
i3 =6i
FXY =F
uygulanan kuvvet,
FZ = 2 F
4
i2 =2i
2d
2B
duğu manyetik
alanın şiddetine
B
X
B diyelim.
O
i1 = i
BO
B
CEVAP B
Z
i3 =i
2B
O nok ta sın da ki
6.
B
+qX
bileşke manyetik alan vektörü
Y
i2 = 2i
2m
V
OX
şekilde görüldü-
r
2V
ğü gibi 4 yönünde olur.
2r
CEVAP D
m
OY
–qY
qX yükü (+), qY yükü (–) yüklüdür.
3.
tavan
tavan
S
N
X
N
Y
S
N
1
S
4
i
+ –
Şekilde görüldüğü gibi X çubuk mıknatısı 1 yönünde, Y çubuk mıknatısı 4 yönünde hareket eder.
CEVAP B
m X . VX
rX
qX . B
=
rY
m Y . VY
qY . B
2m . V
qX . B
r
=
m . 2V
2r
(–q Y) . B
qY
–
1
=
2
qX
qX
= –2 olur.
qY
CEVAP B
ELEKTRİK VE MANYETİZMA
293
7.
9.
Z
Y
X
i3
i1 =i
X
i1 = i
2r
. . FYX=2F
FZX=F
yön
2
Z
i2 =2i
FZY=4F.
1
r
B2 x O
B1 • B3 •
Y
. FXZ=F
.
FXY=2F
.
FX=F
i2 = 3i
FYZ=4F
FZ=5F
FY=6F
d
d
+x
–x
O noktasındaki bileşke manyetik alan sıfır olabilmesi için i3 akımının büyüklüğü ve yönü
|B1| + |B3| = |B2|
K
F=K
i3 =2i
2i.i
, olsun.
d
X, Y ve Z tellerine etki eden manyetik kuvvetler,
2i
2r.i 1
2r.i 2
+K 3 =K
2r
r
2r
2r.i1 + i3 = r.i2
FX = F ; +x
FY = 6F ; –x
2.3.i + i3 = 3.3i
FZ = 5F ; +x olur.
i3 = 3i; 1 yönünde olur.
CEVAP C
CEVAP A
8.
I. durumda:
i1 = 2i
X
B x K
B1 x
d
10.
y
B2 x
2d
i2 = 3i
Y
K
2.2i
2.3i
i
B = B1 + B2 = K
+K
= 7K
; , olur.
d
2d
d
L
I
FKL
FLM
II. durumda:
i1 = 2i
X
ı
B • K
B1 •
z
d
Y
i2 = 3i
Bı = B1 + B2
M
Bu durumda KL parçasında kuvvet – y yönünde,
2.2i
2.3i
i
Bı = K
–K
=K
;.
d
2d
d
Buna göre, B nin yönü değişir, büyüklüğü azalır.
CEVAP D
ELEKTRİK VE MANYETİZMA
x
Tele etki eden kuvvetin yönü sağ el kuralı ile
bulunur. Teli sağ elimizin içine aldığımızda dört
parmak manyetik alan, baş parmak akım yönünü
gösterecek şekilde açıldığında elimizin içinden
çıkan dik vektör kuvveti gösterir.
B2 x
2d
294
N
B
LM parçasında kuvvet –x yönünde olur.
MN parçasında akım manyetik alana paralel olduğundan kuvvet oluşmaz.
CEVAP C
TEST
3
ÇÖZÜMLER
1.
X
Telin PR parçasına etki eden kuvvet,
Y
i1 = 4i
FPR = B.i.|PR|
i2 = i
= 30.10.1
i3 = 6i
Z
= 300 N
2B
d
olup yönü sayfa düzleminden dışa (.) doğrudur.
Tel çerçeve y ekseni etrafında dönebildiğine göre
FKL kuvvetinin torku sıfırdır. Halkanın torku FPR
kuvvetinden kaynaklanır.
B
d
d
6B
K
i akımının K noktasında oluşturduğu manyetik
alan şiddeti,
2i
B = K.
d
x = FPR.|KR|
= 300.2
= 600 N.m olur.
olduğuna göre K noktasındaki bileşke manyetik alan,
BK = B + 6 B – 2 B
= +5 B olur.
CEVAP E
2.
MANYETİZMA
i akımının O noktasında oluşturduğu manyetik
alanın şiddetine
B diyelim.
O noktasındaki
bileşke manyetik alan vektörü
şekilde görüldüğü gibi 3 yönünde olur.
II. yol:
Torkun büyüklüğü,
T = B.i.A.sinθ
= 30.10.(2.1).sin90°
= 600 N.m olur.
i1 = i
X
CEVAP D
BO
B
Y
B
O
i2 = i
Z
3
2B
B
4.
Şekilde görüldüğü
gibi, bölgede elektrik
alan –z yönündedir.
y
B
Fel
i3 = i
E
+q
CEVAP C
3.
z
B=30T
i=10A
2m
CEVAP D
P
i
FKL
K
x
Fman
y
L
V
•R
1m
FPR
.
x
I. yol:
Telin LP ve KR kesimlerinden geçen akımlar
manyetik alana paralel olduğundan bu kesimlere
kuvvet etki etmez. FLP = FKR = 0
Telin KL parçasına etki eden kuvvet,
FKL = B.i.|KL|
= 30.10.1
= 300 N
5.
r=
T=
m. V
bağıntısına göre, B azaltılırsa r artar.
q.B
2r . m
bağıntısına göre, B azaltılırsa T artar.
q.B
Parçacığın V çizgisel hızı, manyetik alan şiddetine
bağlı değildir.
CEVAP C
olup yönü sayfa düzleminden içe (,) doğrudur.
ELEKTRİK VE MANYETİZMA
295
6.
Tellerin üzerine uygulanan kuvvetler tellerin
manyetik alana dik
olan büyüklükleri ile
orantılıdır.
9.
N•
y
B
M
L
M
•
KL telinin manyetik
alana dik bileşeni,
i
,KL = 3 br,
•
3br
B
L
a
B
B
x
K
• 1br
,LM = 0,
K
,MN = 3 br olur.
z
FKL = B.i.3 = 3Bi
KL ve LM tellerine etki eden kuvvetler yazılıp taraf
tarafa oranlanırsa,
FLM = 0
FMN = B.i.3 = 3Bi olur.
FKL
i.a.B
=
=
FLM i 2 a.B cos 45°
Bu durumda kuvvetlerin büyüklükleri,
FKL = FMN > FLM olur.
F
10.
.
O
•
2.
i
tavan
.
CEVAP B
tavan
.
F3
B1
Fman=i,B
B2
i
i
Çubuğun ağırlığı çubuğa uygulanan manyetik kuvvetin yarısına eşit ve çubuk dengede olduğundan,
F1
2F = G + Fman
tavan
.
B3
F=
F2
F1
F2
K
fiekil-I
i, B
+ i, B
2
2
3i, B
kx =
4
3i, B
k=
olur.
4x
= 1 olur.
2
2
yatay
i,B
G=mg=
2
8.
1
CEVAP A
F
.
a
i
Tellere etki eden kuvvetlerin büyüklükleri,
7.
a
F4
L
fiekil-II
F1
i
F2
CEVAP B
K telinde, manyetik alanın akım ile paralel olduğu
kesimlerinde kuvvet etki etmez. Manyetik alana dik
olan kenarlarına şekildeki yönlerde bir kuvvet etki
eder. Bu kuvvetler K tel çerçevesini okla gösterilen
yönde dönme hareketi yaptırır.
Z
Y
3r
X
2r
O
r
i2
i1
M
fiekil-III
L teline etki eden kuvvetler,
|F1| = |F2| ve |F3| = |F4|
olduğundan ve bu kuvvetler zıt yönlerde dönme
hareketi yaptırdığından L tel çerçevesi dönmez.
i3
Halkaların merkezinde manyetik alanın sıfır olabilmesi için her üç yargı da ayrı ayrı uygulandığında
hepside doğru olur.
Yargıların üçü de doğru olabilir.
296
ELEKTRİK VE MANYETİZMA
CEVAP E
M telinde, manyetik alanın akım ile paralel olduğu
kesimlerinde kuvvet etki etmez. Manyetik alana dik
olan kenarlarına şekildeki yönlerde bir kuvvet etki
eder. F1 ve F2 kuvvetleri dönme ekseninden geçtiğinden torkları sıfırdır. M tel çerçevesi dönmez.
CEVAP A
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
Bölüm
Yazılı Soruları
(Manyetizma)
1.
ÇÖZÜMLER
3.
i1 = 4A
X
i1 =16A
X
10cm
B1
K
B2 +B3 =3B
10cm
B2
BO =5B
B3 =2B
BK
B2 =B
20cm
Y
Y
i2 =4A
i2 =12A
B1 = K .
B2 = K .
2i 1
–7 2 . 4
–6
= 10 . –1 = 8.10 T ;
d1
10
B O = 5K .
BK = B2 – B1
= 12.10–6 – 8.10–6
= 4.10–6 T ; . olur.
2i 2
d2
= 5.10
–7
= 4.10
–5
.
2.4
1.10
–1
T olur.
4.
B2
F
B1
A
i1 =20A
B
i2 =10A
K
10cm
i3 =8A
Şekilde görüldüğü gibi BO = 5B olur.
9
K noktasındaki bileşke manyetik alan,
2.
10cm
i2 akımının O noktasında oluşturduğu manyetik
alan şiddetine B diyelim.
7
2i 2
–7 2 . 12
–6
= 10 .
= 12.10 T ;
–1
d2
2.10
Z
B1 =4B
•
O
10cm
i1
X
F1
20cm
2
F2
40cm
1
8cm
D
Y
12cm
C
i2 =12A
K noktasındaki bileşke manyetik alan sıfır olduğuna göre,
| B1| = | B2|
K.
2 . i1
10
–1
= K.
2.i 2
3.10
–1
–x
F = K.
F
+x
2 . i1 . i2
.,
d
F1 = 10
–7
.
–1
–4
2 . 20 . 10
. 4.10 = 2.10 N olur.
–2
8.10
–7
.
–1
–5
–4
2 . 20 . 10
.4.10 = 8.10 N = 0, 8.10 N
–2
20.10
i1 =
i2
3
F2 = 10
i1 =
12
3
olur. Çerçeveye uygulanan bileşke kuvvet,
i1 = 4A; 2 yönünde olur.
R = F1 – F2 = 2.10–4 – 0,8.10–4 = 1,2.10–4 N olur.
–x yönünde olur.
ELEKTRİK VE MANYETİZMA
297
5.
7.
X
X
Y
i1=2i
i1 = 8A
i2=3i
i2 = 4A
Y
53°
r = 20 cm
BO
O
B1
,
Z
,
F1
F2
B
B3
B2
i3 = 2A
B1 = K .
2i 1
–7
–6
2.8
= 10 .
= 8.10 T ; 7
–1
d1
2.10
B2 = K .
2i 2
–7
–6
2.4
= 10 .
= 4.10 T ; 9
–1
d
2.10
B3 = K .
2r . i 3
–7 2 . 3 . 2
–6
= 10 .
= 6.10 T ; 9
–1
r
2.10
Tellerin , uzunluğundaki kısımlarına etkiyen manyetik kuvvetler yazılıp oranlandığında,
F1
i 1 .B.,
2i
5
=
=
= olur.
F2 i 2 .B., . sin 53°
4 6
3i.
5
O noktasındaki bileşke manyetik alan,
BO = B2 + B3 – B1
= 4.10–6 + 6.10–6 – 8.10–6
= 2.10–6 T ;
☼ olur.
6.
8.
, =30cm
S
BK
N
Y
B1
i2 = 6A
i1 = 8A
K
X
0,1m
1
i =5A
0,1m
B solenoid = K .
2i 1
–7
–6
2.8
= 10 .
= 16.10 T ()
–1
d1
1.10
= 10
B2 = K .
2i 2
–7
–6
2.6
= 10 .
= 12.10 T ( )
–1
d2
1.10
= 1.10
K noktasındaki bileşke manyetik alan,
B K = (16.10–6)2 + (12.10–6)2
= 20.10–6
= 2.10–5 T olur.
298
4r . N . i
,
B1 = K .
2
ELEKTRİK VE MANYETİZMA
2
B2
–7
.
2
4 . 3 . 5.10 . 5
–1
3.10
–2
T;
sağ el kuralına göre 1 yönünde olur.
9.
Yüklerin momentumları oranı,
rX
rY
PX 1
=
PY 2
2
X
Y
=
PX
2m X
2
PY
2m Y
2
(1)
mX
1
=
2
8
(2)
mY
mY
1
=
8
4m X
mX
=2
mY
olur.
B=50T
60cm
A
B
FAB
i=5A
100cm
D
y
60°
FDC
x
C
B
Tel çerçevenin BC ve AD kenarlarından geçen
olur. Kinetik enerjileri oranından,
Ek
z
m X . VX
qX . B
=
m Y . VY
qY . B
PX
q.B
r
=
PY
2r
q.B
Ek
10.
akımlar manyetik alana paralel olduğundan bu
tellere etki eden kuvvetler sıfırdır.
FAD = FBC = 0
AB ve BC kenarlarına etki eden kuvvetler ters
yönde olup büyüklükleri
FAB = B.i.|AB|
= 50.5.0,6
= 150 N olur.
FDC = B.i.|DC|
= 50.5.0,6
= 150 N olur.
Bu kuvvetlerin z eksenine göre torku,
x = FAB.|AB|.sin60° – FDC.|DC|.sin60°
= 150.0,6.
3
3
– 150.0,6.
2
2
= 0 olur.
ELEKTRİK VE MANYETİZMA
299
300
ELEKTRİK VE MANYETİZMA
5. BÖLÜM
ELEKTROMANYETİK İNDÜKSİYON
Manyetik akı değişimi,
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
DU = U2 – U1 = 0 – 2 = –2 Wb/m2 olur.
K-L uçlarında oluşan indüksiyon emk sı,
1.
50cm
B
f=–
.
(–2)
DU
=–
= 4V olur.
0, 5
Dt
CEVAP C
40cm
.
3.
Çerçevenin alanı,
manyetik ak›
2Φ
A = a.b = 40.50 = 2000 cm2 = 0,2 m2 olur.
Manyetik akı, U = B.A.cosa eşitliğinden bulunur.
a, yüzeyin normali ile manyetik alan arasındaki
açıdır.
Φ
0
Çerçeve manyetik alana dik iken a = 0 olduğundan,
U1 = B.A.cos0 = 400.0,2.1 = 80 Wb olur.
t
2t
zaman
3t
Halkada oluşan indüksiyon emk larını yazıp taraf
tarafa oranlarsak,
Çerçeve manyetik alana paralel getirildiğinde
a = 90° olduğundan,
2U – U
U
ε 1 – c 2t m – 2t
1
=
=
=–
olur.
ε 2 – c 0 – 2U m
2U
4
U2 = B.A.cos90° = 400.0,2.0 = 0 olur.
Manyetik akı değişimi,
t
t
CEVAP A
DU = U2 – U1 = 0 – 80 = –80 Wb olur.
CEVAP D
4.
2.
3B
9B
B
K
O
•
•L
3r
40cm
O
r
ı
L
50 cm
K
Tel halkaların alanları,
Tel çerçevenin alanı,
A = a.b = 50.40 = 2000 cm2 = 0,2 m2 olur.
İlk durumda tel çerçeveden geçen akı,
U1 = B.A.cos0° = 10.0,2.1 = 2 Wb olur.
Tel çerçevenin periyodu T = 2 saniye olduğundan
0,5 saniye sonra levha 90° döner. Bu durumda
levha manyetik alana paralel olur. Yüzeyin normali
ile manyetik alan çizgileri arasındaki açı 90° olacağından tel çerçeveden geçen akı,
U2 = B.A.cos90° = 10.0,2.0 = 0 olur.
AK = π . (3r)2 = 9π . r2 = 9A
AL = π . r2 = A olur.
α = 0° olduğundan halkalardan geçen manyetik
akılar,
ΦK = 3B . 9A . cos0° = 27B A
ΦL = 9B . A . cos0° = 9B A olur.
Akıların oranı,
UK 27B A
=
= 3 olur.
9B A
UL
CEVAP B
ELEKTRİK VE MANYETİZMA
301
5.
Tel çerçevede oluşan maksimum indüksiyon emk sı,
f = N.B.A.~
= N.B.A.2rf
1
= 10.2.0,06.2.3.
2
= 3,6 V olur.
CEVAP D
K
I
L
K
II
~
L
B
N
37°
53°
53°
37°
M
N
7.
K
Çerçevenin alanı,
I
A = a.b = 0,5.0,4 = 0,2
m2
L
olur.
~
B
I konumunda:
K
Halkadan geçen akı,
M
II
U1 = B.A = 5.0,2 = 1 Wb olur.
N
II konumunda:
Dikdörtgen levhanın alanı,
Halkadan geçen akı,
A = a.b = 0,5.0,4 = 0,2 m2 olur.
U2 = B.A cos37°
= 5.0,2.
I konumunda:
4
5
Tel çerçeveden geçen akı,
U1 = B.A = 5.0,2 = 1 Wb olur.
= 0,8 Wb olur.
II konumunda:
Tel çerçevede oluşan ortalama indüksiyon emk sı
f=–
L
Tel çerçeveden geçen akı,
DU
Dt
U2 = 0 olur.
=–
(U 2 – U 1)
Dt
=–
(0, 8 – 1)
0, 1
Tel çerçevede oluşan ortalama indüksiyon emk sı
f=–
DU
Dt
0, 2
=
0, 1
=–
(U 2 – U 1)
Dt
= 2V olur.
=–
(0 – 1)
0, 2
CEVAP A
=
10
2
= 5V olur.
CEVAP B
6.
O›
| B|= 2 T
8.
emk
K
2f
L
O
Tel çerçevenin alanı,
A = a.b = 30.20 = 600 cm2 = 0,06 m2 olur.
Tel çerçeve,
60 saniyede
30 devir yaparsa,
1 saniyede
f devir yapar.
f.60 = 30.1
1 –1
f=
s olur.
2
302
ELEKTRİK VE MANYETİZMA
0
2t
4t
5t
zaman
–f
Halkada oluşan indüksiyon emk sının zamanla
değişim grafiğinin eğimi şekildeki gibi olur.
CEVAP D
Tel çerçevenin alanı,
~
A = a.b
K
= 0,2.0,1
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
10cm
L
1.
= 2.10–2 m2 olur.
B
K
Tel çerçevenin frekansı,
L
20cm
40 devir
f=
= 5 s–1
8s
,
olur.
N
60°
,
j
•
2j
M
Çerçevede oluşan maksimum indüksiyon emk sı,
K ve L çubuklarının uçları arasında oluşan indük-
fmak = N B A ~
siyon emk ları yazılıp oranlanırsa,
= N B A 2rf
fK
–B., .j
=
=
fL –B., .2j. sin 60°
5
= 1. .2.10–2.2.3.5
3
= 1V olur.
3
2.
2
1
3
=
3
3
=
olur.
CEVAP A
10.
1
CEVAP B
B
NX=N
NY=N
A
A
eksen
X
Y
2.
B
K
•
K
L
fiekil-I
j
j
L
B
fiekil-II
fiekil-I
NX=N
B
•
9.
A
A
M
X
Y
K
•
NY=N
j
B
L
fiekil-III
B
fiekil-II
Her iki durumda bobinlerden geçen manyetik akılar,
U1 = NBA + NBA = 2NBA
fK = –B.,K.j . sin 90° = –B,Kj olur.
\
U2 = NBA + 0 = NBA olur.
1
K-L uçları arasında oluşan indüksiyon emk sının
mutlak değeri,
DU
Dt
(U 2 – U 1)
=–
Dt
(NBA – 2NBA)
=–
t
NBA
=
olur.
t
K, L ve M çubuklarının uçları arasında oluşan
indüksiyon emk sı,
fL = –B.,L.j sin90° = –B,Lj olur.
fM = –B.,M.j. sin 0° = 0 olur.
[
f=–
0
Buna göre, K ve L çubuklarının uçları arasında
indüksiyon emksı oluşur.
CEVAP D
CEVAP C
ELEKTRİK VE MANYETİZMA
303
3.
CEVAP A
B
2j
•
2,
K
3
2j
53°
3,
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
1. K-L uçları arasında oluşan indüksiyon emk sı,
j
f = –B . , . 2j
•
L
= –4 . 4.10
M
,
K ϑ=5m/s
–1
.
5
2
,=40cm
= –4 V olur.
K, L ve M çubuklarının uçları arasında oluşan
L
indüksiyon emk sı,
fK = –B.,.2j = –2B,j
fL = –B.2,.
B
3
j = –3B,j
2
CEVAP B
fM = –B.3,.j.sin53° = –B.3,.j.
4
12
=–
B,j
5
5
Buna göre, fL > fM > fK olur.
2.
L-M noktaları arasında,
K
CEVAP B
B.~.,
f1 = –
= 2V olur.
2
B
3,
K-L noktaları arasında,
B.~. (3,)
2
2
9 B~ ,
=–
2
L
2
~
f2 = –
4.
–
2,
B
K
~
2
,
M
= 18V olur.
K-M noktaları arasında,
•
j
f = f2 – f1 = 18 – 2 = 16V olur.
L+
CEVAP D
,
M+
3. K-L noktaları arasında,
Sağ el kuralına göre,
K deki
yükün işareti
L deki
yükün işareti
M deki
yükün işareti
–
+
+
f1 = –
olur.
CEVAP C
=–
B ~ (3,)
2
K
B
3,
L
9
B ~ ,2 olur.
2
2,
~
L-M noktaları arasında,
f2 = –
~
2
B ~ (2,)
2
M
2
= – 2B ~ ,2 olur.
K-M noktaları arasında,
9
5
B ~ ,2 – 2B ~ ,2 =
B ~ ,2
f = f 1 – f2 =
2
2
olur. K-M
emk sı 10
5
f=
2
5
10 =
2
noktaları arasında oluşan indüksiyon
V olduğundan,
B.~.,2
B ~ ,2 ⇒ B ~ ,2 = 4V olur.
K-L noktaları arasında oluşan indüksiyon emk
sının mutlak değeri,
f1 =
304
ELEKTRİK VE MANYETİZMA
9
.4 = 18V olur.
2
CEVAP C
4.
K-L noktaları arasında;
K
B
ω
K
r1=30cm
ϑ1 = ω . r1
L
2j
L
r2=20cm
= 20 . 0,3
L
ω
= 6 m/s olur.
M
B
K-L arasında oluşan
indüksiyon emk sı,
–1
fiekil- I
fiekil- II
Tel çubuklarda oluşan indüksiyon emk larının
büyüklükleri yazılıp oranlanırsa,
j
f 1 = –B . , 1 . 21
= –4 . 3.10
B
Y
,
•
,
j
•
K noktasının çizgisel
hızı,
6.
K
.
f1 –B., .2j
=
= 4 olur.
f2
j
–B., .
2
6
2
= –3, 6 V olur.
CEVAP E
L-M noktaları arasında;
M noktasının çizgisel hızı,
ϑ2 = ω . r2
= 20 . 0,2
= 4 m/s olur.
L-M arasında oluşan indüksiyon emk sı,
j
f 2 = –B., 2 . 2
2
= 4.2.10
–1
.
4
2
= –1, 6 V olur.
K-M noktaları arasında oluşan indüksiyon emk sı,
f = f1 – f2 = –3,6 – (–1,6) = –2 V olur.
CEVAP C
5.
Çubuğun M noktasının çizgisel hızı ϑ ise, K
noktasının çizgisel hızı 3ϑ olur.
L-M
noktaları arasında;
___________________
f 1 = –B . , . 2j
3ϑ
K
=V
K-L
noktaları arasında;
___________________
f 2 = –B . 3, . 32j
L
M
ϑ
B
= 9V
K-M
noktaları arasında;
___________________
ε = ε2 – ε1 = 9V – V = 8V olur.
CEVAP D
ELEKTRİK VE MANYETİZMA
305
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
1.
X
4.
eşitliğinden bulunur. Akı sürekli
U(t)
arttığına göre A ve B sürekli artıyor olabilir. Açı sürekli artarsa,
akı sürekli olarak artmaz. Belirli
bir süre artar sonra azalır veya belirli bir süre azalır
sonra artar. Fakat tel çerçevenin tamamı manyetik alan içerisinde şekildeki (+) veya (–) yönlerde
dönme hareketi yaparsa akı değişmez. III. öncülde kesinlik yoktur.
CEVAP C
i
4
Z
B
3
1
O
B
2
d
(+)
(–)
U = B.A.cosa
Y
i
Tel çerçeve üzerinde geçen akı,
d
Z tel halkasında belirtilen yönde indüksiyon akımı
oluşması için B manyetik alanın artması gerekir.
Halka ' veya ) yönünde hareket ederse içinden
geçen akı artar. Sistem bunu azaltmak için ok
yönünde indüksiyon akımı oluşturur.
5.
B
,=20cm
CEVAP D
ϑ
•
2.
N
K
ϑ=4m/s
R=4X
L
1
•
, = 50 cm
Çerçevede oluşan indüksiyon emk sı 8 volt oldu2
ğuna göre tel çerçevenin hızı,
M
B
f = –B.,.j
Çerçevede oluşan indüksiyon emk sı,
8 = –4.2.10–1.j
f = –B . , . j
= –2 . 5.10
j = 10 m/s olur.
–1
.4
CEVAP D
= –4 V olur.
Çerçeveden geçen indüksiyon akımı,
ε 4
i = = = 1A olur.
R 4
6.
B
Lenz kanununa göre, 1 yönünde olur.
CEVAP A
K
i
•
,=0,5m
i
N
K
1
•
i
2
F
L
•
,= 40 cm
j=4m/s
•
R =2X
3.
KL çubuğunda oluşan emk,
B
L
1
2
M
Çerçeveye etki eden manyetik kuvvetten,
Fman = i . , . B
16.10–2 = i . 4.10–1 . 2
2.10–1 = i
i = 0,2 A
Lenz kanununa göre akım, 2 yönünde olur.
CEVAP D
306
ELEKTRİK VE MANYETİZMA
f = –B , j
= –2.0,5.4
= –4V olur.
Halkadan geçen akım,
i=
f = 4 = 2A olur.
R
2
Lenz kanununa göre, akımın yönü 2 yönünde olur.
CEVAP D
7.
B›
10.
B
B
X
y
ϑ
•
B›
fiekil-I
Y
N
fiekil-II
•
,=20cm
ϑ
B
ϑ
•
B
2
K
1
N
x
O
Z
ϑ=5m/s
L
M
z
›
B
S
fiekil-III
İndüksiyon akımının oluşturduğu manyetik alan
İndüksiyon emk sı,
(Bı) sayfa düzleminden dışa doğrudur. Lenz kanu
nuna göre, I ve III devrelerinde düzgün B man-
f =–B.,.ϑ
= – 4.10–1 . 2.10–1 . 5
yetik alanın yönü sayfa düzlemine dik ve içeri
= – 4.10–1 V olur.
doğrudur.
CEVAP D
Çevreden geçen indüksiyon akımı,
8.
B
M
K
i=
R
f = 4.10 –1 = 2.10 –1 = 0, 2 A olur.
R
2
Lenz kanununa göre, 1 yönünde olur.
i
•
ϑ
ı
i
CEVAP C
N
P
L
Lenz kanununa göre:
Tel çerçevenin MN kenarında N den M ye doğru
indüksiyon akımı geçer.
I. yargı doğrudur.
Tel çerçevenin PR kenarında P den R ye doğru
indüksiyon akımı geçer.
11.
S
II. yargı yanlıştır.
KL çubuğunda K den L ye doğru indüksiyon akımı
geçer.
III. yargı doğrudur.
B
O
2
1
N
ok
CEVAP C
R
A
X
9. Oluşan manyetik
X
alan akıyı azaltacak
yönde olduğundan
i
akı artmaktadır. Bu
durumda halka –x
yönünde hareket
ediyor veya telden –x
geçen akım artıyordur. Lenz kanununa
göre II ve III işlemleri tek başına yapılmalıdır.
Lenz kanununa göre:
Çubuk mıknatıs sabit j hızıyla solenoide yaklaştırılırsa X devresinde ok yönünde indüksiyon akımı
oluşur.
Y
Btel
r
r
O
B›
+x
Solenoid 2 yönünde hareket ettirilirse, X devresinde ok yönüne zıt yönde indüksiyon akımı oluşur.
Çubuk mıknatıs O noktası çevresinde sabit hızla
90° döndürülürse X devresinde ok yönüne zıt
yönde indüksiyon akımı oluşur.
CEVAP E
CEVAP A
ELEKTRİK VE MANYETİZMA
307
12.
d
–x
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
+x
eksen
1. Solenoidde oluşan öz indüksiyon emk sı,
1
R
Di
f = –L . D
t
K
2
+ –
A
reosta
X
= –L .
Y
(i 2 – i 1)
Dt
= –0, 2 .
Lenz kanununa göre:
L=0,2H
(0 – 4)
0, 1
1
i
= 8 V olur.
Reostanın sürgüsü ok yönünde çekilirken, Y devresinde 1 yönünde indüksiyon akımı oluşur.
K
i
2
1 yönünde olur.
A
+ –
I. yargı doğrudur.
CEVAP C
Y devresindeki solenoid +x yönünde hareket ettirilirken, Y devresinde 2 yönünde indüksiyon akımı
oluşur.
2.
II. yargı doğrudur.
K anahtarı kapatılırken, Y devresinde 1 yönünde
indüksiyon akımı oluşur.
i
1
III. yargı doğrudur.
CEVAP E
i + –
2
reosta
13. Tel çerçeve içinden
geçen akı değiştiğinde
telde bir indüksiyon
emk sı oluşur.
Tele etki eden kuvvet bu akı değişimi ile
doğru orantılıdır.
Makarada oluşan öz indüksiyon emk sının büyüklüğü,
Di
f = –L
Dt
4
= –0,25.
0, 2
kuvvet
zaman
0
t
3t
2t
–F
= –5V olur.
Devreden geçen akım arttığından, akım makarasında oluşan öz indüksiyon emk sı 1 yönünde olur.
Soruda verilen akı-zaman grafiği dikkate alındığında tel üzerindeki kuvvetin-zamanla değişim grafiği
şekildeki gibi olur.
CEVAP D
CEVAP C
3.
+y
14. Halka manyetik alana girerken halka üzerinde akı
oluşmaya başlar. Bu durumda akının, oluşan emk
nın ve manyetik kuvvetin halkanın konum bağlı
grafikleri şekildeki gibi olur.
–x
ak›
emk
kuvvet
konum
0
2x
konum
0
2x
konum
0
2x
CEVAP C
ELEKTRİK VE MANYETİZMA
+ –
Devredeki K anahtarı kapatılırken devre akımı
artacağından, devrede oluşan öz indüksiyon akımı
–y yönündedir.
K anahtarı açılırken devre akımı azalacağından,
devrede oluşan öz indüksiyon akımı +y yönündedir.
–f
308
+x
K
reosta
F
Φ
R
–y
I. yargı doğrudur.
Reostanın sürgüsü +x yönünde çekilirken devre
akımı artacağından, devrede oluşan öz indüksiyon
akımı –y yönündedir.
6.
2
B
1
4
II. yargı doğrudur.
R
i
i›
Reostanın sürgüsü –x yönünde çekilirken devre
akımı azalacağından, devrede oluşan öz indüksiyon akımı +y yönündedir.
Y
B›
+ –
reosta
III. yargı yanlıştır.
X
CEVAP D
4.
3
i(A)
X devresinde reosta ok yönünde çekildiğinde
direnç azalacağından devreden geçen i akımı
artar. Öz indüksiyon akımı bunu azaltacak şekilde
2 yönünde olur.
Y devresinde, X devresindeki akım arttığından
manyetik alan artar. Sistem bunu azaltacak şekilde 3 yönünde indüksiyon akımı oluşturur.
6
0
1
0,8
Öz indüksiyon akımı X devresinde 2 yönünde,
indüksiyon akımı Y devresinde 3 yönünde olur.
t(s)
CEVAP C
Akım makarasında oluşan öz indüksiyon emk sı
eşitliğinden,
Di
f = –L.
Dt
(0 – 6)
3
= –L
(1 – 0, 8)
2
3
6
=L
2
0, 2
L=
0, 3
= 0,05 H olur.
6
CEVAP E
ak›m(A)
5.
5
•K
•
zaman(s)
+ –
0,2
fiekil-I
fiekil-II
Şekil-I deki devrede K anahtarı kapatıldığında
oluşan akım Şekil-II deki gibi olduğuna göre
Di = 5A, Dt = 0,2 s ve oluşan emk f = 50 volttur.
Bu durumda öz indüksiyon katsayısı
Di
Dt
5
50 = L.
0, 2
f = –L.
50 = L.25 & L = 2 H olur.
CEVAP D
ELEKTRİK VE MANYETİZMA
309
TEST
1.
1
ELEKTROMANYETİK İNDÜKSİYON
ÇÖZÜMLER
3.
B
K
•
,
2,
•
2,
2ϑ
30°
10cm
O
ϑ
ϑ
L
eksen
20cm
K
B
M
L
O›
Tel çerçevenin alanı,
Çubukların uçların arasında oluşan indüksiyon emk
ları,
A = a . b = 0,2 . 0,1 = 2.10–2 m2 olur.
Her iki durumda tel çerçeveden geçen manyetik
akı,
εK = – B . , . 2ϑ = – 2B . , . ϑ
εL = – B . 2, . ϑ = – 2B . , . ϑ
εM = – B . 2, . ϑ . sin30° = – B . 2, . ϑ . 1 = – B . , . ϑ
Φ1 = B . A = 5 . 2.10–2 = 1.10–1 Wb
Φ2 = 0 olur.
2
olur. Büyüklükleri arasındaki ilişki ise,
K-L uçları arasında oluşan indüksiyon emk sı,
f = – DU
εK = εL > εM olur.
Dt
CEVAP B
(U2 – U1)
Dt
=–
(0 – 0, 1)
1
4
=–
= 0, 4 V olur.
2.
B
i1
ϑ
ϑ
•
B›
i1
CEVAP D
B
4.
•
–
i1
K
j
•
fiekil- I
B›
i2
+
L
M
+
+
–
•
+
–
N
fiekil-II
fiekil-I
fiekil- II
Sağ el kuralına göre,
i3
ϑ
•
B›
i3
j
i2
i2
B
B
B
–
i3
K deki
yükün
işareti
L deki
yükün
işareti
M deki
yükün
işareti
N deki
yükün
işareti
–
+
+
–
fiekil- III
olur.
CEVAP D
Lenz kanununa göre, indüksiyon akımının yönü
Şekil-II ve Şekil-III de doğru olarak gösterilmiştir.
CEVAP E
5.
Solenoidde oluşan öz indüksiyon emk sı,
Di
f = –L . D
t
= –0, 25 .
4
0, 5
1
i
= –2 V,
i + –
1 yönünde olur.
2
reosta
CEVAP C
310
ELEKTRİK VE MANYETİZMA
6.
İkinci durumda tel çerçeveden geçen manyetik akı,
ϑ
S
Φ2 = B . A . cos90°
N
1
= 20.1.10–2.0
3
= 0 olur.
2
R
A
4
X
R
A
Akı değişimi,
Y
∆Φ = Φ2 – Φ1
Lenz kanununa göre, indüksiyon akımının yönü X
devresinde 1 yönünde, Y devresinde 3 yönündedir.
= 0 – 0,2
= –0,2 Wb olur.
CEVAP A
CEVAP A
9.
2T
7.
T
50cm
O1
O2
X
Y
40 cm
B
1
B
2
fiekil- Ι
A = a . b = 0,5 . 0,4 = 2.10–1 m2 olur.
İki durumda da çerçeveden geçen akılar,
Φ1 = B1 . A = 2 . 2.10–1 = 4.10–1 Wb
Φ2 = B2 . A = 6 . 2.10–1 = 12.10–1 Wb olur.
Çerçeveden geçen indüksiyon emk sı,
–1
–1
– 4.10 )
2.10
2r
.,
T
jY =
2r
. 2,
2T
jY =
2r
.,
T
Çubuklarda oluşan indüksiyon emk ların oranı,
j
ε X –B . , . 2 1
=
ε Y –B . 2, . j = 2 olur.
2
CEVAP B
(U 2 – U 1)
Dt
(12.10
jX =
j X = j & j Y = j olur.
f = – DDUt
=–
fiekil- ΙΙ
X çubuğunun ucunun çizgisel hızı,
Çerçevenin alanı,
=–
B
–1
8
2
= –4 V olur.
=–
10.
B
K
N
Akımın büyüklüğü,
f 4 = 0, 4 A olur.
i= =
R 10
ϑ
•
Lenz kanununa göre, 1 yönünde olur.
CEVAP E
8.
Çerçevenin alanı,
A = a.a
= 0,1.0,1
= 1.10–2 m2 olur.
İlk durumda tel çerçevedengeçen manyetik akı,
Φ1 = B . A . cos0°
= 20.1.10–2.1
= 0,2 Wb olur.
B=20Wb/m2
L
1
2
M
İletken tel çerçeve sabit ϑ hızıyla şekildeki gibi
çekildiğinde:
] Tel çerçevenin K-L kenarında K ve L uçları
arasında indüksiyon emk sı oluşur.
I. yargı doğrudur.
] Lenz kanununa göre, çerçeveden geçen indüksiyon akımı 1 yönündedir.
II. yargı yanlıştır.
B
] Çerçeve duruyorken, çerçevede indüksiyon
akımı oluşmaz.
III. yargı doğrudur.
CEVAP C
ELEKTRİK VE MANYETİZMA
311
TEST
2
1.
4.
B
2,
•
,
ELEKTROMANYETİK İNDÜKSİYON
ÇÖZÜMLER
K
____
–
olur.
53°
ϑ
2ϑ
Sağ el kuralına göre;
O
____
+
ϑ
– K
L
____
–
ω
,
+
+
O
K
,
L
–
ω
Çubukların uçları arasında oluşan indüksiyon emk
ları yazılıp oranlanırsa,
εK
–B . , . 2j
ε L = –B . 2, . j . sin 53°
B
CEVAP A
5.
1
4
5
5
=
olur.
4
=
2.
L
ϑ
B
X
Y
•
CEVAP D
Bir devrede indüksiN
yon akımının oluşması
için akı değişmelidir.
O
M
Halka OK, LM yollarında hareket ederken
akı değişmez akım i
K
oluşmaz. Halka KL ve
MN yolu boyunca
hareket ederken halL
kadan geçen magnetik akı değişir. Bu değişim de indüksiyon akımını
oluşturur.
CEVAP E
O
X çubuk O noktası etrafında döndüğünden oluşan
indüksiyon emk sı,
f X = –B.j ort .2,
j
= –B. ( ) .2,
2
= –B.j., olur.
Y çubuğu manyetik alan içinde ötelendiğinden,
indüksiyon emk sı,
fY = –B . ϑ . , olur.
εX ve εY taraf tarafa oranlanırsa,
f X –B . j . ,
f Y = –B . j . , = 1 olur.
3.
K
CEVAP C
B
6.
ϑ=5m/s
•
1
2
L
Akı-zaman
grafiğine
baktığımızda (0-t) zaman aralığında akı azalmaktadır.
I. yargı doğrudur.
zaman
0
t
2t
Çerçevede oluşan indüksiyon emk sı,
f = –B . , . ϑ
= –2.10–1 . 4.10–1 . 5
= 4.10–1 V olur.
Akı, U = B.A.cosa olduğundan B veya A azalmaktadır. (t-2t) aralığında
akı sıfır olduğundan halka manyetik alan dışında
veya manyetik alana paraleldir.
Devrede oluşan indüksiyon akımı,
II. yargı doğrudur.
i=
–1
f = 4.10 = 0, 8 A
–1
R
(t-2t) zaman aralığında akı sıfır olduğundan halkaya etkiyen kuvvet sıfırdır.
5.10
Lenz kanununa göre, 2 yönünde olur.
312
ak›
U
ELEKTRİK VE MANYETİZMA
CEVAP B
III. yargı yanlıştır.
CEVAP C
10. L-M noktaları arasında
zılıp oranlanırsa,
oluşan indüksiyon emk sı;
K
B
2
B., 1 ~
f1 – 2
=
2
f2
B., 2 .~
–
2
f1 = B.,. j = 10 volt
,
L
,1
2
,
2
M
ϑ
K-M noktaları arasında;
L
f = 40 – 10 = 30 V olur.
CEVAP D
2
2
2
1
CEVAP E
B
11. L-M noktaları arasında oluşan indüksiyon
elektromotor kuvveti,
B
C
C
fiekil- Ι
fiekil- ΙΙ
If 1 I =
N
A = a.b = 0,4.0,5 = 0,2
ω
M
B
2
K-L noktaları arasında oluşan indüksiyon elektromotor kuvveti,
ε 2 = –B . (j 2) ort . IKLI
olur.
Çerçeveden her iki durumda geçen akılar,
= –B . b
Φ1 = B.A = 4.0,2 = 0,8 Wb
~ . 3, l
. 3,
2
B.~.,
2
= 9 V olur.
Φ2 = B.A.cosα
= 9.
= 4.0,2.cos60°
1
= 0,8.
2
= 0,4 Wb olur.
2
I. yargı doğrudur.
VKM = VKL – VLM = 9 – 1 = 8 volt olur.
Çerçevede oluşan ortalama indüksiyon emk sı,
II. yargı doğrudur. III. yargı yanlıştır.
CEVAP D
12.
ϑ
2ϑ
2,
•
f = – DDUt
(U – U 1)
=– 2
Dt
(0, 4 – 0, 8)
=–
0, 2
0, 4
=
0, 2
= 2 V olur.
,
= 1 V olur.
Çerçevenin alanı,
m2
B.~.,
2
M
L
2
B.~.,
=–
2
30°
60°
D
D
3,
~.,l
= –B . b
.,
2
A
30°
ω
f 1 = –B . (j 1) ort . ILMI
B
60°
K
•
A
B
9.
B
f2 = B.2,. 2j = 40 volt
O
= 4 olur.
8.
,
K-L noktaları arasında;
,2
=
2ϑ
2
2
=
K
➞
.
İndüksiyon emk ları ya-
.
7.
O
CEVAP C
Y tel çerçevesinde
X
kuzey
şekilde belirtilen yöni1
Y
de i indüksiyon akımının oluşması için,
i
Lenz kanununa göre bat›
O
do¤u
çerçevenin X teline
yaklaştırılması gerekir.
güney
Buna göre, çerçeve
sayfa düzleminde batıya doğru hareket ettirilmelidir.
CEVAP B
Y
X
,
P
|B1|=B
|B2|=2B
fiekil- I
fiekil- II
X çubuğunun iki ucu arasında oluşan indüksiyon emk,
ε X = –B 1 . j ort . , = B . j2 . , olur.
Y çubuğunun iki ucu arasında oluşan indüksiyon emk,
ε Y = B 2 . j ort . 2, = 2B . b 22j l . 2, = 4B . j . ,
olur. emk ların oranı,
j
εX B . 2 . , 1
=
ε Y 4B . j . , = 8 olur.
CEVAP A
ELEKTRİK VE MANYETİZMA
313
TEST
3
ELEKTROMANYETİK İNDÜKSİYON
ÇÖZÜMLER
1.
4.
2ϑ
2ϑ
O1
O›
•
O2
X
N
S
•
Y
B
K
B
L
B
fiekil- Ι
O
fiekil- ΙΙ
ϑ X = 2ω., = 2ϑ
Tel çerçevenin alanı,
A=a.b
= 0,15 . 0,2
= 0,03
= 3.10–2 m2 olur.
ϑ Y = ω.2, = 2ϑ
X ve Y çubuklarının uçları arasında, indüksiyon
emk ları yazılıp oranlanırsa,
2j
f X –B . , . 2
1
f Y = –B . 2, . 2j = 2 olur.
2
CEVAP B
2.
K-L uçları arasında oluşan maksimum indüksiyon
emk sı,
f=
Solenoidde oluşan öz indüksiyon emk sı 3,2 V
olduğuna göre,
i(A)
f = –L . Di
8
Dt
–1
40 devir
=4s
olduğundan,
10 s
εmak = N . B . A . ω
=N.B.A.2πf
= 1 . 4 . 3.10–2 . 2 . 3 . 4
8
–3, 2 = –L .
0, 5
L =
= 288.10–2
= 2,88 V olur.
1, 6
8
0
L = 0, 2 H olur.
CEVAP E
t(s)
0,5
CEVAP B
3.
Çubuğun M ucunun çizgisel hızı ϑ ise, K ucunun
çizgisel hızı 3ϑ olur.
K-L
noktaları arasında;
__________________
= –9 . B . , .
B
37°
N
B
53°
2
fiekil- I
L
V
M
Φ1 = B . A . cos37°
B
İkinci durumda akı,
Φ2 = B . A . cos53°
= 4.104 . 5.10–4 . 0,6
= 12 Wb olur.
Oluşan indüksiyon emk,
B.r.,
B.r., n
– d–
T
T
= –8 .
B.r.,
T
ELEKTRİK VE MANYETİZMA
f = – DU
2
= –9 .
2
= 4.104 . 5.10–4 . 0,8
= 16 Wb olur.
K-M noktaları arasında;
__________________
f = f2 – f1
2
fiekil- II
İlk durumda akı,
T
L-M noktaları arasında;
__________________
f 2 = –B . , . 2j
2r,
= –B . , . T
2
2
B.r.,
=–
T
314
N
T
2r,
T
2
B.r.,
= –9 .
T
3ϑ
K
f 1 = –B . 3, . 32j
5.
Dt
(12 – 16)
=–
2
olur.
CEVAP C
= 2 V olur.
CEVAP A
6.
9.
ϑ
S
y
emk
N
B
halka
f
konum
x
R
t1
A
X
t2
t3
–f
] ϑ hızı artırılırsa, X devresinden geçen indüksiyon akımının şiddeti artar.
fiekil-I
] Solenoidin sarım sayısı azaltılırsa X devresin-
fiekil-II
0-t1 aralığında, emk –f olduğundan akı artmıştır.
den geçen indüksiyon akımının şiddeti azalır.
Bu durumda halka +x yönünde hareket etmiştir.
] R direnci azaltılırsa, X devresinden geçen
I. yargı kesinlikle doğrudur.
indüksiyon akımının şiddeti artar.
t1-t2 aralığında, emk +f olduğundan akı azalmıştır.
I ve III işlemleri tek başına yapılmalıdır.
CEVAP E
Bu durumda halka –x yönünde hareket etmiştir.
II. yargı kesinlikle doğrudur.
t2-t3 aralığında, emk f = 0 olduğundan U = 0 veya
d
7.
U = sabittir.
III. yargı için kesin birşey söylenemez.
eksen
CEVAP D
1
K
+ –
2
reosta
A
Y
X
10.
Lenz kanununa göre:
öz indüksiyon
emk
K anahtarı kapatılırken Y devresinde 1 yönünde
indüksiyon akımı oluşur.
I. yargı doğrudur.
K anahtarı açılırken Y devresinde 2 yönünde
indüksiyon akımı oluşur.
0
t1
t2
t3
zaman
II. yargı doğrudur.
K anahtarı kapalı iken reostanın sürgüsü ok
yönünde çekilirse, Y devresinde 2 yönünde indüksiyon akımı oluşur.
III. yargı yanlıştır.
Akım makarasında oluşan öz indüksiyon emk
sının zamanla değişim grafiği şekildeki gibi olur.
CEVAP A
CEVAP C
8.
akım
i
0
t
2t
3t
zaman
–i
Halkada oluşan indüksiyon akımının zamanla
değişim grafiği şekildeki gibi olur.
CEVAP E
ELEKTRİK VE MANYETİZMA
315
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
Bölüm
Yazılı Soruları
(Elektromanyetik İndüksiyon)
ÇÖZÜMLER
3.
1.
B
K
K
i
N
i
i
ϑ=2m/s
i
ϑ=4m/s
•
•
,= 50 cm
R = 10 X
,=20cm
i
i
1
2
L
f = –B . , . ϑ
= –2 . 5.10–1 . 2
= –2 V olur.
b) Akımın şiddeti,
f = 2 = 0, 2 A
R
2
M
Lenz kanununa göre, 2 yönünde olur.
10
c) KL kenarına etki eden kuvvet,
Lenz kanununa göre, 2 yönünde olur.
Fman. = i . , . B
= 5.10–1 . 2.10–1 . 5
= 5.10–1 N olur.
Sağ el kuralına göre, çerçevenin hareket yönüne ters yönde olur.
2.
i
K
i
N
4.
ϑ=5m/s
L
1
a) Reostanın sürgüsü M noktasındayken devre-
•
, = 50 cm
den geçen akım,
i
2
M
B
a) Çerçevede oluşan indüksiyon emk sı,
f = –B . , . ϑ
= – 4 . 5.10–1 . 5
= –10 V olur.
b) Çerçeveden geçen indüksiyon akımı,
f 10 = 2 A
i= =
R
5
Lenz kanununa göre, 1 yönünde olur.
c) Çerçeveyi sabit hızla çeken kuvvetin büyüklüğü,
Fç = i . , . B
= 2 . 5.10–1 . 4
= 4 N olur.
316
1
a) Çerçevede oluşan indüksiyon emk sı,
f = –B . , . ϑ
= –5 . 2.10–1 . 4
= –4 V olur.
b) İndüksiyon akımı,
f 4
i = = = 0, 5 A olur.
R 8
a) Devrede oluşan indüksiyon emk sı,
i=
i
B
L
ELEKTRİK VE MANYETİZMA
i1 =
f = 40 = 4 A olur.
10
R1
Reostanın sürgüsü L noktasındayken devreden
geçen akım ise,
i2 =
f = 40 = 8 A olur.
5
R2
Solenoidde oluşan öz indüksiyon emk sı;
f = – L . Ti
Tt
= –L .
(i 2 – i 1)
Tt
= –0, 2 .
(8 – 4)
0, 2
= –4 V olur.
b) Reostanın sürgüsü M noktasından L noktasına
çekildiğinde devreden geçen akım arttığından devrede oluşan öz indüksiyon akımı Lenz kanununa
göre, 2 yönündedir.
5.
8.
N
i(A)
8
53°
B
0
0,6
Levhadan geçen akı,
Φ = B . A . cosα
t(s)
1
Makarada oluşan öz indüksiyon emk sının büyüklüğü,
= 500 . 20.10–2 . 50.10–2 . cos53°
(i – i )
ε = –L Di = –L 2 1
= 50 . 0,6
Dt
= 30 Wb olur.
(t 2 – t 1)
eşitliğinden bulunur. Değerler yerine yazılırsa,
ε = –0,2
(0 – 8)
(–8)
2.8
= –0,2
=
= 4V
(1 – 0, 6)
0, 4
4
olur.
9.
6.
K
, = 50 cm
37°
L-M noktaları arasında;
ε1 = –B . , . 2j
= 10 V olur.
ϑ=5m/s
L
B
Çubuğun K-L uçları arasında oluşan indüksiyon
emk sı,
ε = – B . , . ϑ . sinα
= –2 .
5.10–1
Çubuk L noktası etrafında ω açısal hızıyla döndürüldüğünde M noktasının çizgisel hızı ϑ ise, L
noktasının çizgisel hızı 2ϑ olur.
3
.5.
5
= –3 V olur.
2ϑ
K
ω
2,
L
K-L noktaları arasında;
ε2 = –B . 2, . 2j
2
= 40 V olur.
,
ω
ϑ
M
B
K-M noktaları arasında;
ε3 = ε2 – ε1
= 40 – 10
= 30 V olur.
7.
2ω
ω
,
O1
X
2,
Y
O2
10. Çerçevenin alanı,
A = a . b = 0,2 . 0,1 = 2.10–2 m2 olur.
B
fiekil- I
B
fiekil- II
Çubukların uçlarının çizgisel hızları,
ϑX = ω . , = ϑ
ϑY = 2ω . 2, = 4ω . , = 4ϑ olur.
Çubuğun uçları arasında oluşan indüksiyon emk
ları yazılıp oranlanırsa,
j
–B . , .
fX
1
2
=
=
olur.
f Y –B . 2, . 4j 8
2
Çerçevenin frekansı,
f=
–1
40 devir
= 10 s olur.
4s
Çerçevede oluşan maksimum emk sı,
εmak = N . B . A . ω
=N.B.A.2πf
= 1 . 5 . 2.10–2 . 2 . 3.101
= 6 V olur.
ELEKTRİK VE MANYETİZMA
317
318
ELEKTRİK VE MANYETİZMA
6. BÖLÜM
ALTERNATİF AKIM
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
4.
fm = im.R
300 3 = im.300 & im =
V(t) = 30.sin2πt ise gerilimin maksimum değeri,
Vm
2
=
30
= 15 2 V olur.
2
3 A olur.
Alternatif akımın denklemi,
Vm = 30 volt etkin değeri de,
Ve =
Devredeki alternatif akımın maksimum değeri,
i(t) = im.sin2rft
CEVAP D
=
3 .sin2r.100.t
=
3 .sin200rt olur.
CEVAP C
2.
Akımın zamanla değişim denkleminden,
i(t) = imax.sin~t
5.
i(t) = 20 2 .sin100rt
i(t) = 10v2 sin50π.t = imax.sinωt
şeklinde tanımlanan akım denklemine bakıldığında,
Maksimum akım, imax = 20 2 A olur.
ω = 50π
2π.f = 50π
İletkenin iki ucu arasındaki maksimum gerilim,
f = 25 s–1 olur.
Vmax = imax.R = 20 2 .10 = 200 2 V olur.
CEVAP D
I. yargı yanlıştır.
İletkenin iki ucu arasındaki etkin gerilim,
Ve =
Vmax
2
=
6.
200 2
= 200 V olur.
2
i(t) = imax.sin~t
II. yargı yanlıştır.
i(t) = 5 2 .sinrt
Devredeki frekans,
Frekans,
~ = 100r
f = 50 s–1 olur.
Periyot ise,
I. yargı doğrudur.
1
1
=
s olur.
f 50
III. yargı doğrudur.
~=r
2rf = r
1 –1
f=
s
2
1
Periyot, T =
= 2 s olur.
f
2rf = 100r
T=
Alternatif akımın zamanla değişim denkleminden,
Akımın etkin değeri,
CEVAP C
ie =
i max
2
=
5 2
= 5 A olur.
2
II. yargı doğrudur.
3.
Alterntif akımın maksimum değeri,
im =
0 değerini geçtikten t = 0,5 saniye sonra akımın
Vm
200 2
=
= 2 2 A olur.
R
100
değeri,
Akımın anlık değeri,
i(t) = 5 2 .sinr.
i(t) = im.sin2rft
=
=
=
=
= 5 2 .sin
1
2 2 .sin2r.100.
800
r
2 2 .sin
4
2
2v2.
2
2A olur.
1
2
r
2
= 5 2 .1
=5 2 A olur.
Akım maksimumdur.
III. yargı doğrudur.
CEVAP B
CEVAP E
ELEKTRİK VE MANYETİZMA
319
7.
Akımın etkin değeri,
ie =
im
2
=
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
30 2
= 30 A olur.
2
1.
I. yargı kesinlikle doğrudur.
4Ω
6Ω
2Ω
2Ω
Devredeki akım denklemine göre,
4Ω
~ = 100r
3Ω
2rf = 100r
f = 50 s–1 olur.
II. yargı kesinlikle doğrudur.
Devrenin eşdeğer direnci,
Direnç bilinmeden gerilimin maksimum değeri için
kesin bir şey söylenemez.
Refl =
III. yargı için kesin birşey söylenemez.
Gerilimin etkin değeri,
CEVAP C
Ve =
8.
ie =
i = i m sin 2r f t
1
300
2
=
12 2
= 12V olur.
2
Ve 12
= 3A olur.
=
Refl 4
Bu akım 6Ω ve 3Ω luk dirençlerde ters orantılı
geçeceğinden 6Ω’luk dirençten 1A, 3 Ω luk dirençten 2A akım geçer.
r
2 3 = i m sin
3
2 3 = im .
Vm
Anakoldan geçen akımın etkin değeri,
Akım denkleminden akımın maksimum değeri,
2 3 = i m sin 2r 50 .
4 6.3
= 4Ω olur.
+
2 6+3
3
2
CEVAP B
i m = 4A olur.
Gerilimin maksimum değeri,
Vm = im.R
= 4.50
= 200 V olur.
2.
Gerilim denklemi,
Alternatif gerilimin zamanla değişimi,
V(t) = Vm.sin2rft
V(t) = Vmsin2π.f.t
= 200v2.sin2r.50.t
= 200sin2π.50.t
= 200v2.sin100rt
= 200sin100πt olur.
CEVAP E
şeklindedir.
t = 0 anında sin0° = 0, V(t) = 0 ve i(t) = 0 olur.
1
Gerilimin t =
s sonraki anlık değeri,
400
1
V(t) = 200 2 .sin100r.
400
r
= 200 2 .sin
4
= 200 2 .
2
2
= 200 V olur.
R = 100 X olduğundan akımın anlık değeri,
i=
V
200
=
= 2 A olur.
R
100
CEVAP C
320
ELEKTRİK VE MANYETİZMA
3.
Bobinin alternatif
akıma karşı göstermiş olduğu direnç,
yani indüktansı,
7.
L=0,4H
Kondansatörün alternatif akıma karşı göstermiş
olduğu direnç, yani kapasitans,
XC =
XL = ω.L
1
~.C
eşitliği ile bulunur.
= 50.0,4
Gerilim denklemine bakıldığında ω = 800 rad/s
olduğu görülür. Bu durumda,
= 20 Ω olur.
XC =
CEVAP D
6
1
10
1000
=
=
= 250 X olur.
–6
4000
4
800.5.10
CEVAP E
4.
Kaynağın maksimum emk sı 100 V olduğundan
akımın maksimum değeri,
im =
fm
100
=
= 4 A olur.
25
Z
Alternatif akım ile beslenen kondansatörde akım
gerilimden 90° öndedir.
C
I. yargı doğrudur.
Devrede ve dolayısıyla
kondansatör üzerinde
akımın yönü ve şiddeti sürekli değişir.
~ = 2rf = 2r.25 = 50r olur.
Devrenin akım denklemi,
i(t) = im.sin~t
II. yargı doğrudur.
i(t) = 4.sin50rt olur.
CEVAP B
5.
8.
Dirençlerden biri üzerindeki gerilimin etkin değeri
50 2 V olduğuna göre, devredeki kaynak geriliminin maksimum değeri,
Sığa artarsa doğru akımda yük artar.
Alternatif akımda kondansatör yük depolamaz.
Sığa artarsa kapasitans (XC) azalır.
III. yargı yanlıştır.
CEVAP C
Vm = Ve 2 + Ve 2
= 50 2 . 2 + 50 2 . 2
= 200 V olur.
Devredeki alternatif gerilimin frekansı 50 s–1 olduğuna göre kaynağın gerilim denklemi,
V(t) = Vm.sin2rft
= 200.sin2r.50.t
= 200.sin100rt olur.
CEVAP D
6.
Devredeki bobinin indüktansı,
L=1H
XL = ~.L = 60.1 = 60 X
olur. Gerilimin etkin değeri,
Ve =
Vm
2
=
30 2
= 30 V
2
olur. Akımın etkin değeri,
V
V
30 1
ie = e = e =
= A olur.
Z
X L 60 2
V(t)=30 2.sin60t
CEVAP B
ELEKTRİK VE MANYETİZMA
321
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
1. Devrenin empedansını
bulmak için öncelikle
bobinin indüktansını
bulmamız gerekir.
R=20Ω
4.
Devredeki eşdeğer
direnç,
Reş = 24 + 24
= 48 Ω
L=0,4H
Bobinin indüktansı,
A
XL = ω.L
XL = ω.L
= 50.0,4
= 2.π.20.
= 20 Ω olur.
Z
XL=20Ω
ϕ
Z2 = R2 + XL2
•
.
ϕ
R = 48 Ω
Z2 = R2 + XL2
Z2 = 482 + 202
Ampermetre akımın etkin değerini gösterir.
Z = 52 Ω olur.
CEVAP E
Vm
100
=
= 50 2 volt
2
2
5.
Ve 50 2 5
=
= A olur.
Z
20 2 2
Bobinin indüktansı,
XL = ~.L = 100.0,4 = 40 X
CEVAP A
2
Z=
RL devresi için,
2
VZ
=
2
VL
+
2
2
R=40Ω
2
Devreden geçen akımın maksimum değeri,
V
80 2
im = m =
= 2 A olur.
Z
40 2
1002 = 602 + V L
VZ=100V
VL = 80 V olur.
Makaranın indüktansı,
ϕ
VL = ie.XL
VL=80V
Faz açısı,
.
cos { =
VR=60V
80 = 4.XL
R
40
2
r
=
=
& {=
olur.
Z 40 2
2
4
Devreden geçen akımın denklemi,
XL = 20Ω olur.
i(t) = im.sin(~t – {)
r
= 2.sin(100t – ) olur.
4
CEVAP B
6.
80Ω
160Ω
Voltmetrenin gösterdiği
değer 90V, etkin değerdir.
CEVAP A
L
R=30X
Akımın etkin değeri,
XL=80Ω
k›sa
devre
80Ω
ϕ
2
R + XL
= 40 + 40
= 40 2 X olur.
2
VR
3.
XL=40Ω
Z=40v2Ω
olur.
Devrenin empedansı,
2.
XL = 20 Ω
Devrenin empedansı,
R=20Ω
Z = 20v2 Ω olur.
Ie =
1
2r
= 20 Ω olur.
.
Z2 = 202 + (20)2
Ve =
Z = 52Ω
= 2π.f.L
V=100.sin50t
80Ω
V
im
3 2
=
=3A
2
2
ie =
olur.
•
•
Ve
Bobinin indüktansı,
Bobinin öz indüksiyon katsayısı,
XL =
XL = ω.L
Bobinin öz indüksiyon katsayısı,
80 = 2π.f.L
80 = 2.3.20.L ⇒ L =
XL = ω.L
2
H olur.
3
CEVAP A
322
ELEKTRİK VE MANYETİZMA
Ve 90
=
= 30 X olur.
ie
3
30 = 100.L ⇒ L = 0,3 H olur.
CEVAP B
7.
9.
R=20X
R
ϕ
A
XC=15X
•
K •• n
o
•
Anahtar konumunda iken ampermetre 10 amperi gösterdiğine göre, kaynağın etkin potansiyel
değeri,
Anahtar konumuna getirildiğinde devrenin
empedansı,
2
2
R + XC
2
20 + 15
=
A
XC=15X
625
=
= 25 X olur.
•
•
V(t) = 100.sin100rt
olduğundan Vm = 100 V olur.
Akım denkleminden,
R=20X
2
Gerilim denkleminden,
V = Vm.sin~t
Ve = ie.R = 10.20 = 200 V olur.
Z=
XC
Z
•
K•
o
i = im.sin(~t + {)
i(t) = 10.sin(100rt +
r
)
4
r
= 45° olur.
4
olduğundan im = 10 A ve { =
Bu durumda ampermetreden okunan değer,
V
200
= 8 A olur.
ie = e =
25
Z
CEVAP B
Devrenin empedansı,
im =
Vm
V
100
& Z= m =
= 10X olur.
10
Z
im
I. yargı doğrudur.
8.
Kondansatörün kapasitansı,
1
XC =
C.~
=
–2
R=4Ω
C=1.10 F
R = Z.cos{ = 10.cos45° =
V=40.sin25t
Devrenin empedansı,
=
Kondansatörün kapasitansı,
XC = Z.sin{ = 10.sin45° = 10.
= 4 X olur.
Z=
10 2
= 5 2 X olur.
2
II. yargı doğrudur.
1
–2
1.10 .25
100
=
25
R direnci,
2
2
2
= 5 2 Ω olur.
2
Yani XC = R dir.
III. yargı doğrudur.
R + XL
2
4 +4
CEVAP E
2
= 4 2 X olur.
Gerilimin etkin değeri,
Ve =
Vm
2
=
40
= 20 2 volt olur.
2
Devreden geçen akımın etkin değeri,
V
Ie = e
Z
=
20 2
4 2
= 5A olur.
Kondansatörün iki ucu arasındaki etkin potansiyel,
VC = Ιe.XC
= 5.4
= 20 volt olur.
CEVAP C
10. Devrenin empedansı,
Z=
=
R
2
2
2
+ XC
4 +4
2
R=4Ω
ϕ
XC=4Ω
Z
= 4 2 X olur.
Devreden geçen akımın maksimum değeri,
im =
Vm 40 2
=
= 10 A olur.
Z
4 2
CEVAP D
ELEKTRİK VE MANYETİZMA
323
11. Akım denkleminden,
R
i = im.sin(~t + {)
i(t) = 4.sin(200rt +
faz açısının { =
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
ϕ
r
)
3
XC
Z
1.
VLM
r
= 60°
3
V KN
VLM–VMN
VKL
VKL
olduğu görülür. Akımın maksimum değeri ise
im = 4 A dir.
VMN
Gerilim denkleminden,
K-L arasındaki gerilim,
V = Vm.sin~t
VKL = ie.R = 5.3 = 15 V olur.
V(t) = 400.sin200rt
L-M arasındaki gerilim,
gerilimin maksimum değerinin Vm = 400 V olduğu
görülür.
VLM = ie.XL = 5.5 = 25 V olur.
M-N arasıdaki gerilim,
Bu durumda devrenin empedansı,
im =
Vm
Z
4=
400
Z
VMN = ie.XC = 5.1 = 5 V tur.
K-N rasındaki etkin gerilim,
&
R direnci ise,
R
cos{ =
&
Z
R = Z.cos{
2
=
15 + (25 – 5)
=
625
2
2
= 25 V olur.
= 100.cos60
= 100.
2
V KL + (VLM – VMN)
VKN =
Z = 100 X olur.
Buna göre; I, II ve III. yargılar doğrudur.
1
2
CEVAP E
= 50 X olur.
CEVAP C
2.
XC=7X
XL=3X
R=4X
A
•
12.
V, i
•
K anahtarı konumundayken devrenin empedansı,
Vm •
V
im •
Z1 =
2
2
2
R + XL =
2
4 + 3 = 5 X olur.
i
R=4X
0•
XL=3X
t
–im •
XC=7X
A
–Vm •
Grafiğe bakıldığında akım ile
gerilim arasında herhangi bir
faz farkı olmadığı görülür. Bu
ise sadece direnç üzerinde
mümkündür.
Ve
K •• n
o
•
•
R
Ve
K
•
o
K anahtarı konumundayken devrenin empedansı,
Z2 =
•
•
CEVAP D
=
2
R + (X C – X L)
2
4 + (7 – 3)
2
2
= 4 2 X olur.
Gerilimin etkin değeri değişmeyeceğinden,
i1.Z1 = i2.Z2
i1.5 = i2.4 2 &
324
ELEKTRİK VE MANYETİZMA
i1
4 2
=
olur.
5
i2
CEVAP C
5.
3.
VL
K anahtarı açık, L anahtarı kapalı iken:
Devrenin empedansı,
R
Z21 = R2 + R2
Z1 =
2 R olur.
Etkin akım şiddeti,
i e1 =
Z1
Ve
Ve
=
olur.
Z1
2R
e=
13
V
VC–VL
Kondansatörün iki ucu arasındaki etkin gerilim,
V2e = VR2 + (VC – VL)2
132 = 52 + (VC – VL)2
Devrenin empedansı,
122 = (VC – VL)2 & VC – VL = 12 V olur.
Z22 = R2 + (2R)2
5 R olur.
Z2
Ve
Ve
=
Z2
5R
VC – VL = 12 V
XL=2R
Etkin akım şiddeti,
i e2 =
V
VC
XC–XL=R
K anahtarı kapalı, L anahtarı açık iken:
Z2 =
VR=5V
VR=5V
ϕ1
VC – 4 = 12 & VC = 16 V olur.
CEVAP D
ϕ2
R
olur.
Z2 > Z1 olduğundan empedans artar.
ie1 > ie2 olduğundan etkin akım şiddeti azalır.
6.
XL=8Ω
CEVAP B
Z
R=8Ω
XL– XC=6Ω
ϕ
R=8Ω
XC=2Ω
XL > XC olduğundan devrede gerilim akımdan
öndedir.
4.
R
L
C
I. yargı doğrudur.
ie
Devrenin empedansı,
•
Z=
•
V(t)=Vm.sinωt
Bobinin indüktansı,
XL = 2rfL dir.
Devrenin empedansı,
2
8 + (8 – 2)
=
100
2
Gerilimin etkin değeri,
V
20 2
= 20 V olur.
Ve = m =
2
2
1
XC =
dir.
2rfC
R + (X L – X C )
2
=
2
= 10 X olur.
Kondansatörün kapasitansı,
Z=
2
R + (X L – X C )
2
dir.
Alternatif akım kaynağının frekansı f değişirse XL
ve XC kesinlikle değişir.
Devrenin empedansı ve akımın etkin değeri için
kesin birşey söylenemez.
Kaynak geriliminin maksimum değeri değişmediğinden, gerilimin etkin değeri kesinlikle değişmez.
CEVAP B
Akımın etkin değeri,
V
20
= 2 A olur.
ie = e =
10
Z
II. yargı doğrudur.
Devrenin güç çarpanı,
cos{ =
R
8
=
= 0,8 olur.
Z
10
III. yargı doğrudur.
CEVAP E
ELEKTRİK VE MANYETİZMA
325
7.
9.
XL=10Ω
Z
R=4Ω
C=5.10–4F L=0,03H
A
XL– XC=3Ω
R=3X
ϕ
R=4Ω
•
•
V(t)=30 2.sin200t
XC=7Ω
Bobinin indüktansı,
XL = ω.L = 200.0,03 = 6X olur.
XL > XC olduğundan { pozitif, dolayısıyla gerilim
akımdan öndedir.
Kondansatörün kapasitansı,
1
1
XC =
=
= 10 X olur.
–4
~.C
200.5.10
I. yargı doğrudur.
Devrenin empedansı,
Devrenin empedansı,
Z=
2
R + (X L – X C )
2
=
4 + (10 – 7)
=
4 +3
2
Z=
2
=
2
2
R + (X L – X C )
2
3 + (6 – 10)
2
2
= 5 X olur.
2
Gerilimin etkin değeri,
= 5 X olur.
Ve =
II. yargı doğrudur.
Güç çarpanı,
Vm
2
=
30 2
= 30 V olur.
2
Akımın etkin değeri ise,
R 4
cos { = = = 0, 8 olur.
Z 5
ie =
III. yargı yanlıştır.
Ve
30
=
= 6 A olur.
5
Z
CEVAP D
CEVAP C
10.
K
6X
8.
XL
3X
XL
•
Z=20v2Ω
•
K anahtarı açılırsa 6 X luk direnç devreden çıkar.
Anahtar kapalıyken 6 X luk direnç ile 3 X luk direncin eşdeğer direnci,
3.6
Reş =
= 2 X dur.
3+6
K anahtarı açılınca Reş = 3 X olur yani artar.
XL–XC=20Ω
ϕ=45°
Ve
XC
.
R=20Ω
XC
Devrenin empedansı,
Devrenin empedansı,
Z=
Z=
Vm 100 2
=
= 20 2 X olur.
im
5
Akımın etkin değeri,
V
ie = e eşitliğinden Z arttığından ie azalır.
Z
R = Z. cos 45°
Bobinin uçları arasındaki etkin potansiyel,
2
= 20 2 .
2
VL = ie.XL
eşitliğinden ie azaldığından VL azalır.
= 20 Ω olur.
CEVAP D
ELEKTRİK VE MANYETİZMA
2
olduğundan Reş arttığından Z artar.
Devredeki R direnci,
326
2
R efl + (X L – X C)
CEVAP A
11.
VL
MODEL SORU - 5 TEKİ SORULARIN ÇÖZÜMLERİ
V2
V2
ϕ
VL–VC
1.
ϕ
VR= V1=30 2V
Bu durumda devredeki alternatif gerilimin frekans değeri,
r
Akım denkleminden faz açısının { =
olduğu
4
görülür.
Bu durumda V2 gerilimi,
L=
1
H
4π 2
•
•
–4
C=10 F
V(t)=Vm.sin~t
XL = XC
V
cos{ = 1
V2
2rfL =
V
r
= 1
4
V2
f2 =
cos
R
Z = R ve XL= XC dir.
VR=V1
VC
Devre rezonansta
olduğuna göre,
2
30 2
=
& V2 = 60 V olur.
2
V2
1
2rfC
1
4r LC
1
2
f =
2
–4
1
4r . 2 .10
4r
CEVAP C
2
f2 = 104 & f = 100 s–1 olur.
CEVAP D
12. Gerilim denklemine bakıldığında ω = 20π rad/s
olduğu görülür. Kondansatörün kapasitansı alternatif akımın frekansına bağlıdır. Değeri ise,
XC =
1
~.C
=
1
20 r.
1
200 r
2.
= 10X olur.
XL=5Ω
Z2 = 52 + (5 – 10)2
Z = 5v2 Ω olur.
.
.
R=5Ω
R=5Ω
ϕ
fiekil-II
Z
•
•
ie1 =
Ve
V
100
& Z1 = e =
= 20 X olur.
5
Z
i e1
XC–XL=10–5=5Ω
Şekil-II deki devrede XL = XC olduğundan,
V
100
Z2 = R = e =
= 10 X olur.
ie
10
Şekil-I deki devreden,
Vm
20 2
=
= 20 volt olur.
2
2
Z12= R2 + XC2
Devreden geçen akımın etkin değeri ise,
ie =
fiekil-I
Şekil-II de ampermetre 10 A i gösterdiğine göre,
Gerilimin etki değeri,
Ve =
Ve=100V
•
XC=10Ω
.
ifadesinde istenen değerler yerine yazılırsa,
A
Şekil-I de ampermetre 5 A i gösterdiğine göre
devrenin empedansı,
Devrenin empedansı,
Z2 = R2 + (XL–XC)2
L
Ve=100V
•
1
= 5 X olur.
4r
C
R
A
Bobinin indüktansı ise,
X L = ~.L = 20 r.
C
R
Ve
20
=
= 2 2 A olur.
Z
5 2
202 = 102 + XC2 & XC = 10 3 Ω olur.
CEVAP C
CEVAP B
ELEKTRİK VE MANYETİZMA
327
3.
•K
•
•L
•
•M
•
5.
R
reosta
R
XL
XC
XC
XL
R
•
•
•
Reostanın sürgüsü ok yönünde çekilirse R direnci
azalır.
Şekildeki devrede akım ve gerilim aynı fazda olduğundan devre rezonanstadır. Yani XL = XC dir.
Devrenin empedansı,
Zo = 2R dir.
Z=
K anahtarı kapatılırsa R direnci kısa devre olur.
Devrenin empedansı,
R = R olur.
Akımın etkin değri,
I. yargı yanlıştır.
ie =
L anahtarı kapatılırsa devrenin empedansı,
2
Rezonans frekansı,
f=
II. yargı doğrudur.
L ve M anahtarları birlikte kapatılırsa empedans
değişmez. Dolayısıyla akımın etkin şiddeti değişmez.
III. yargı doğrudur.
XL
C=5F
L
K anahtarı kapalı L açık iken devrenin empedansı,
R
Z
4 4
=
5 Z
Z = 5 X olur.
Bobinin indüktansı,
CEVAP C
Bobinin indüklansı:
XL = 2πf.L
= 2.π.100.10–2
= 2.3
= 6 Ω olur.
Kondansatörün kapasitansı:
L
XC =
2rf.C
1
=
–2
10
2r100
2
4r
= 2π
= 2.3
= 6 Ω olur.
2
Z2 = R2 + X L
XL = XC olduğuna göre devre rezonans halindedir.
2
52 = 42 + X L
XL = 3 Ω olur.
Ι. yargı doğrudur.
K açılıp L kapatıldığında devre rezonansa geldiğine göre,
XC = XL
1
1
1 –1
=3&f=
=
s
2r.f.C
2.3.3.5 90
1
1
=
= 90 s olur.
f
1
90
CEVAP D
328
III. yargı yanlıştır.
6.
K
Periyot ise T =
1
olduğundan f değişmez.
2r L.C
CEVAP D
R=4Ω
cos { =
Ve
olduğundan ie artar.
Z
II. yargı doğrudur.
2
(R + R) + X C olur.
Devrenin empedansı artar.
4.
2
I. yargı doğrudur.
Empedans azaldığından akımın etkin değeri artar.
Z1 =
2
R + (X L – X C )
olduğundan Z değeri azalır.
2
Z=
•
ELEKTRİK VE MANYETİZMA
VKL > VKM olur. ΙΙ. yargı doğrudur.
Akım ile gerilim aynı fazdadır. ΙΙΙ. yargı yanlıştır.
CEVAP C
MODEL SORU - 6 DAKİ SORULARIN ÇÖZÜMLERİ
1.
4.
Ve =
Ve 100
=
= 2A olur.
Z
50
ie =
Gerilimin etkin değeri,
12Ω
Vm
2
V(t)=24.sin10πt
24
=
2
X ve Y noktaları arasındaki ortalama güç;
6Ω
= 12 2 V olur.
Port = Ve.ie.cosϕ
= 100.2.0,6
6 Ω luk dirençten geçen akımın etkin değeri,
= 120 W olur.
ie =
CEVAP A
Ve 12 2
=
= 2 2 A olur.
R
6
6 Ω luk direncin gücü,
2.
Ve =
Vm
2
XL =100 Ω
2
P = i e.R
XC
= (2v2)2.6
200 2
=
2
= 8.6
= 200 V
cos { =
ie =
Z=100 Ω
4
5
= 48 watt olur.
XL – XC =60Ω
ϕ=37°
CEVAP B
•
R= 80 Ω
Ve 200
=
=2A
Z
100
XC = 40Ω
Devrenin ortalama gücü,
Port = Ve . ie . cosϕ
= 200 . 2 .
4
5
= 320 W olur.
CEVAP D
3.
•
XL > XC olduğundan gerilim akımdan öndedir.
XL = 60Ω
XC
I. yargı doğrudur.
•
Ve =
=
Vm
100 2
2
•
•
R= 30 Ω
XC = 20Ω
100
50
Port = Ve . ie . cosϕ
= 100 . 2 .
Ve
•
Isı enerjisi direnç üzerinde açığa çıkar. Bu enerjinin değeri,
W = ie2.R.t
eşitliğinden bulunur. Bu durumda devredeki akımın etkin değeri,
= 2 A olur.
II. yargı doğrudur.
•
C
L
XL – XC =40Ω
ϕ=53°
= 100 V
V
ie = e
Z
=
R=30X
Z = 50 Ω
2
5.
3
5
cosϕ =
3
5
W = ie2.R.t
144.103 = ie2.30.(20.60)
4 = ie2 & ie = 2 A olur.
= 120 W olur.
CEVAP D
III. yargı doğrudur.
CEVAP E
ELEKTRİK VE MANYETİZMA
329
6.
Alternatif akım devrelerinde güç direnç üzerinden
çekilir. Devredeki ortalama güç,
Port = Ve.ie.cos{
eşitliğiyle bulunur.
Şekil-I de devrenin güç çarpanı,
1
R
=
olur.
5
5R
cos{1 =
Devrenin ortalama gücü,
P1 = Ve.ie.cos{1
Ve
= Ve.
5R
.
R
ϕ1
1
5
XC=2R
Z= 5R
2
=
Ve
5R
=
P
olur.
5
Şekil-II de devrenin güç çarpanı,
2R
2
=
olur.
5R
5
cos{2 =
Devrenin ortalama gücü,
P2 = Ve.ie.cos{2
Z= 5R
V
= Ve . e . cos ϕ 2
Z
XL=R
ϕ2
Ve
2R
2
= Ve.
.
5R 5
2
=
2V e
5R
=
2P
olur.
5
Şekil-III te devrenin güç çarpanı,
cos{3 =
1
R
=
olur.
2
2R
Devrenin ortalama gücü,
P3 = Ve.ie.cos{3
Ve
1
.
= Ve.
2R 2
V
= e
2R
=
Z= 2R
XL–XC=R
ϕ3
R
P
olur.
2
Devrelerdeki ortalama güçler arasında, P3 > P2 > P1
ilişkisi vardır.
CEVAP D
330
ELEKTRİK VE MANYETİZMA
TEST
1.
1
ÇÖZÜMLER
V(t) = 20.sin2πt ise gerilimin maksimum değeri,
4.
Vm = 20 volt etkin değeri de,
Vm
Ve =
2
=
20
= 10 2 V olur.
2
R DEVRESİ - L DEVRESİ - C DEVRESİ
Akımın etkin değeri,
im
20 2
= 20 A olur.
2
I. yargı yanlıştır.
ie =
CEVAP B
2
=
Devredeki akım denklemine göre frekans,
~ = 50r
2rf = 50r
f = 25 s–1 dir.
2.
II. yargı kesinlikle doğrudur.
Devredeki alternatif akımın maksimum değeri,
Direnç bilinmeden gerilimin maksimum değeri için
kesin bir şey söylenemez.
fm = im.R
80 3 = im.20 & im = 4 3 A olur.
III. yargı için kesin birşey söylenemez.
Akımın zamanla değişim denklemi
CEVAP B
i(t) = im.sin2rft
= 4 3 .sin2r.100.t
= 4 3 .sin200rt olur.
CEVAP E
5.
i(t) = 20v2 sin40π.t = imax.sinωt
şeklinde tanımlanan akım denklemine bakıldığında,
3.
ω = 40π
Alternatif akımın zamanla değişim denkleminden,
2π.f = 40π
i(t) = imax.sin~t
f = 20 s–1 olur.
i(t) = 2 2 .sinrt
CEVAP E
Frekans,
~=r
2rf = r
1 –1
f=
s
2
1
Periyot, T =
= 2 s olur.
f
6.
Akım denkleminden akımın maksimum değeri,
i = i m sin 2r f t
I. yargı doğrudur.
5 = i m sin 2r 20 .
Maksimum akım, imax = 2 2 A olduğundan etkin
akım,
i
2 2
i e = max =
= 2 A olur.
2
2
5 = i m sin
II. yargı doğrudur.
1
80
r
2
5 = im . 1
i m = 5A olur.
Gerilimin maksimum değeri,
0 değerini geçtiği andan t = 1 saniye sonra akım,
i(t) = 5 2 .sinr.1
Vm = im.R
= 5.10
= 5 2 .sinr
= 50 V olur.
= 5 2 .0
V(t) = Vmsin2π.f.t
= 0 A olur.
= 50 sin2π.20.t
III. yargı yanlıştır.
= 50 sin40πt olur.
CEVAP C
CEVAP A
ELEKTRİK VE MANYETİZMA
331
7.
10.
Akımın zamanla değişim denkleminden,
6X
3X
6X
2X
i(t) = imax.sin~t
6X
i(t) = 10 2 .sin100rt
3X
Maksimum akım, imax = 10 2 A olur.
Maksimum gerilim,
Vmax = imax.R = 10 2 .5 = 50 2 V olur.
I. yargı yanlıştır.
Reş =
Etkin akım,
im
Gerilimin etkin değeri,
Devredeki frekans,
Anakoldan geçen akımın etkin değeri,
=
Ve =
~ = 100r
ie =
2rf = 100r
f = 50 s–1 olur.
T=
1
1
=
s olur.
f 50
III. yargı doğrudur.
CEVAP E
Alternatif akım ile beslenen
kondansatörde,
kondansatör yük depolamaz.
Devredeki alternatif gerilimin frekansı 100 s–1
olduğuna göre, kaynak gerilimi,
V(t) = Vm.sin2rft
= 160.sin2r.100.t
CEVAP C
CEVAP D
Devredeki bobinin indüktansı,
L=0,6H
XL = ~.L = 50.0,6 = 30 X
olur. Gerilimin etkin değeri,
V(t)=30 2.sin50t
olur. Akımın etkin değeri,
V
V
30
ie = e = e =
= 1 A olur.
Z
X L 30
ELEKTRİK VE MANYETİZMA
12. Alternatif gerilimin zamanla değişimi,
V(t) = Vm.sin2rft
= 50v2.sin2r.100.t
= 50v2.sin200rt şeklindedir.
III. yargı doğrudur.
332
30
= 6 A olur.
5
= 160.sin200rt olur.
Alternatif akımda kondansatör yük depolamaz.
1
Sığa artarsa kapasitans X C =
olduğundan
ωC
azalır.
30 2
= 30 V
2
=
= 160 V olur.
Sığa artarsa doğru akımda yük artar.
=
Reş
11. Dirençlerden birinin iki ucu arasındaki gerilimin
etkin değeri 40v2 V olduğuna göre, devredeki
kaynak geriliminin maksimum değeri,
II. yargı doğrudur.
2
Ve
30 2
= 30V olur.
2
= 40 2 . 2 + 40 2 . 2
Devrede ve dolayısıyla
kondansatör üzerinde akımın yönü ve şiddeti
sürekli değişir.
Vm
2
=
Vm = Ve 2 + Ve 2
C
I. yargı yanlıştır.
Ve =
Vm
Bu akım 6Ω ve 3Ω luk dirençlerde ters orantılı
geçeceğinden 6Ω’luk dirençten 2A, 3 Ω luk dirençten 4A akım geçer.
CEVAP B
Periyot ise,
9.
6
6.3
= 5X olur.
+
2 6+3
10 2
= 10 A olur.
2
2
II. yargı doğrudur.
ie =
8.
Devrenin eşdeğer direnci,
t = 0 anında sin0° = 0, V(t) = 0 ve i(t) = 0 olur.
1
Gerilimin t =
s sonraki anlık değeri,
800
1
V(t) = 50 2 .sin200r.
800
r
= 50 2 .sin
4
2
2
= 50 V olur.
R = 10 X olduğundan akımın anlık değeri,
= 50 2 .
i=
CEVAP A
V
50
=
= 5 A olur.
R
10
CEVAP C
13. Devredeki kondansatörün kapasitansı,
1
~.C
1
=
10.0, 5
= 0, 2 X olur.
XC =
Gerilimin etkin değeri,
Ve =
Vm
2
=
20 2
= 20 V olur.
2
Kondansatör üzerinden geçen akımın etkin değeri
ise,
ie =
Ve
20
=
= 100 A olur.
X C 0, 2
14.
CEVAP D
i(A)
imax= 5 2 •
0•
4
•
T=8
•
t(s)
–5 2 •
Şekil-II deki grafiğe bakıldığında alternatif akımın
frekansı,
f=
1 1 –1
olur.
= s
T 8
Bobinin indüktansı,
1
XL = ~.L = 2rf.L = 2.3 .8 = 6 X olur.
8
Maksimum gerilim,
Vm = im.XL = 5v2.6 = 30v2 V olur.
Gerilimin etkin değeri,
V
30 2
Ve = m =
= 30 V olur.
2
2
CEVAP D
ELEKTRİK VE MANYETİZMA
333
TEST
1.
2
ÇÖZÜMLER
Devredeki etkin gerilim 2V olduğundan L-M
arasındaki etkin gerilim,
(2V)2
=
V2
+ (VLM
)2
5.
Z2
VLM
ϕ
VLM = v3V olur.
Devrenin empedansı,
Z2 = R2 + (XC – XL)2
Ve=2V
4V2 = V2 + V2LM
RLC DEVRESİ
Z2
V
=
82
+ (14 –
=
82
+ 62
R=8Ω
8)2
XL=8Ω
XC=14Ω
Z = 10 Ω olur.
CEVAP D
Etkin akım,
Ve = ie.Z
40 2
= ie.10
2
ie = 4 amper olur.
2.
XL uçları arasındaki etkin potansiyel Ve olduğuna
göre, Z = XL olur.
CEVAP C
Z2 = R2 + (XL – XC)2
XL2 = 152 + (IXL – 5I)2
XL2 = 225 + (XL2 – 10XL + 25)
10XL = 250
XL = 25 Ω olur.
CEVAP E
6.
Şekildeki grafiğe göre akım gerilimden geridedir.
Buna göre XL > XC olmalıdır.
Ι. şekil olabilir.
ΙΙ. şekil olamaz.
3.
Şekil-Ι de
Şekil-ΙΙ de
V = i.R
Ve = ie.Z
60 = 10.R
60 = 6.Z
R = 6 Ω olur.
ΙΙΙ. şekil olamaz.
CEVAP A
Z = 10 Ω
Omik direnç 6 Ω dur.
Z2 = R2 + XL2
64 = XL2
7.
Z
102 = 62 + XL2
ϕ
XL
Şekil-II deki devrede:
XL = XC
Z=R
R=6Ω
XL = 8 Ω olur.
CEVAP A
V
100
R= e =
= 20 X
ie
5
olur.
Şekil-I deki devrede:
4.
cosϕ = 0,6
6
= 0,6
Z
Z = 10 Ω olur.
Z=
R=6Ω
ϕ
Z
XC–XL=8Ω
ELEKTRİK VE MANYETİZMA
R =20 Ω
ϕ
•
XC = 15 Ω
Z=25 Ω
XC – 6 = 8
334
XC = 15 Ω
XL = 15 Ω olur.
XC – XL = 8 Ω olur.
XC = 14 Ω olur.
Ve 100
=
= 25 X olur.
ie
4
CEVAP E
CEVAP B
8.
Z2 = 42 + (4v3)2
11. Devrenin empedansı,
R=4Ω
θ
Z = 8 Ω olur.
Z
ϕ = 60°
r
ϕ=
olur.
3
XC=4v3Ω
Z2 = 32 + (6 – 2)2
Z = 5 Ω olur.
XL=6Ω
R=3Ω
Etkin akım,
XC=2Ω
Ve = ie.Z
Vm = i mak.Z
15 = ie.5
40v2 = i mak.8 ⇒ imak = 5v2 A olur.
ie = 3 amper olur.
R2 direncinin iki ucu arasındaki etkin gerilim,
i(t) = imaksin(ωt + ϕ)
r
i(t) = 5v2 sin(100πt + ) olur.
3
VR = ie.R = 3.3 = 9 V olur.
CEVAP B
R2 üzerinden geçen etkin akım ise: ie
VR = ie.R2
9 = ie.4
9.
K anahtarı kapatıldığında lambanın parlaklığı
değişmediğine göre devrenin empedansı değişmemiştir.
XL = XC – XL
ie =
CEVAP D
12. Şekil-I de
XC = 2XL olur.
XL=R
Devrenin empedansı,
Ι. yargı kesinlikle doğrudur.
2
Z1 =
ΙΙΙ. yargı yanlıştır.
(2R) + R
2R
2
= R 5 olur.
R ve XC yi karşılaştıramayız.
ΙΙ. yargı için kesin birşey söylenemez.
CEVAP A
•
Akımın etkin değeri,
V
Ve
ie1 = e =
= ie olur.
Z1
R 5
Devrenin ortalama gücü,
Ve
•
P1 = i2e.2R olur.
10. Devrenin empedansı,
Ve = ie.Z
Şekil-II de
100 = 5.Z
Devrenin empedansı,
Z = 20 Ω olur.
R
Akımın etkin değeri,
Ve
V
= ie olur.
i2e = e =
Z2
R 5
400 – 144 = (IXL – XCI)2
256 = (IXL – XCI)2
IXL – XCI = 16 Ω olur.
XC=2R
2
= R 5 olur.
202 = 122 + (IXL – XCI)2
•
Ve
•
Devrenin ortalama gücü,
IXL – 20I = 16 Ω
P2 = i2e.R olur.
XL = 36 Ω veya
Şekil-III te
XL = 4 Ω olabilir.
Devrenin empedansı,
Bobinin öz indüksiyon katsayısı,
Z3=
XL = 2πf.L
XL = 2.3.200.L
2
R + (3R – R)
= R 5 olur.
XL = 36 Ω ise,
36 = 2.3.200.L ⇒ L =
2
R + (2R)
Z2 =
Z2 = R2 + (IXL – XCI)2
3
Henry olur.
100
XL = 4 Ω ise
4 = 2.3.200.L
L=
9
A olur.
4
1
Henry olur.
300
CEVAP D
2
R
XL=3R
XC=R
Ve
• •
Akımın etkin değeri,
Ve
V
= ie olur.
ie3 = e =
Z3
R 5
Devrenin ortalama gücü,
P3 = ie2.R olur.
Buna göre P1, P2 ve P3 arasındaki ilişki,
P1 > P2 = P3 olur.
CEVAP C
ELEKTRİK VE MANYETİZMA
335
TEST
1.
3
ÇÖZÜMLER
5.
i = imaxsin(2πf.t) amper dir.
i max
2
Güç, P = ie2.R eşitliğinden bulunur.
Güçler yazılıp oranlanırsa,
Buna göre,
ie =
RLC DEVRESİ
=
2
PI i e .R 1 4
=
= = 1 olur.
PII i 2 .R
4
2
e
50
= 25 2 amper olur.
2
CEVAP B
2πf = 100π
6.
f = 50 s–1 olur.
CEVAP E
Grafiğe göre akım gerilimden öndedir. Buna göre
XC > XL olmalıdır. Bu devre A seçeneğindeki devre
olabilir.
CEVAP A
2.
Devrenin empedansı, Z = 5Ω olur.
7.
Devreye uygulanan etkin gerilim,
2rf.L =
Ve = ie.Z
= 2v2.5
Rezonans halinde: XL = XC olur. Devrenin frekansı,
R=5Ω
= 10v2 volt olur.
XL=5Ω
f=
XC=5Ω
=
CEVAP C
=
1
2rf.C
1
2r LC
2.3
1
–2
–4
1
.10 .10
36
1
–3
10
6.
6
3
= 10 hertz olur.
3.
Rezonans halinde XL = XC olduğundan Z = R dir.
L artınca XL de arttığından Z de artar.
CEVAP D
•X
•
8.
Ι. yargı yanlıştır.
Z artınca ie azalır ve R nin uçları arasındaki etkin
gerilim de azalır.
•Y
•
R
C
L
ΙΙ. yargı yanlıştır.
L artınca XL > XC olur.
•
ΙΙΙ. yargı doğrudur.
CEVAP C
•
Devrenin rezonans halinde olup olmadığı konusunda kesin birşey söylenemez.
I. ve III. yargılar için kesin birşey söylenemez.
4.
Şekildeki RLC devresinin empedansı,
Şekil-II deki akım-zaman grafiğine göre,
1 –1
s olur.
T = 6 s ve f =
6
Z=
1
= 10 X olur.
1
2.3. .0, 1
6
Devreden geçen etkin akım şiddeti,
i
4 2
= 4A olur.
ie = max =
2
2
Devreye uygulanan etkin gerilim,
XC =
1
=
2rf.C
Ve = ie.XC
336
ELEKTRİK VE MANYETİZMA
2
eşitliği ile ifade edilir.
X anahtarı kapatılırsa R direnci kısa devre olur. Bu
durumda Z azalır.
V
ie = e olduğundan ie artar.
Z
II. yargı kesinlikle doğrudur.
Y anahtarı kapatırsa XC devreden çıkar.
= 4.10
= 40 volt olur.
2
R + (X L – X C )
CEVAP B
I. ve III. yargılar için kesin birşey söylenemez.
CEVAP B
9.
K anahtarı açıkken, XL = XC olduğundan, devre
rezonans haldedir.
Ι. yargı doğrudur.
12. Akım gerilimden
ϕ=
Anahtar kapatılınca XL > XC olur. Z artar, ie azalır.
Direncin uçları arasındaki etkin gerilim azalır.
T
saniye geridedir.
6
r
olur.
3
Etkin akım,
Ve = ie.Z
ΙΙ. yargı doğrudur.
ie azalınca, P de azalır.
100 = ie.20
ΙΙΙ. yargı yanlıştır.
CEVAP B
ie = 5 A olur.
Maksimum akım,
10. Devrenin empedansı,
imax = ie.v2 = 5v2 A olur.
Z2 = R2 + XL2
Gerilim akımdan önde olduğundan faz açısı
Z2 = 42 + 32
negatiftir.
Z = 5 Ω olur.
Akım denklemi,
Akımın etkin değeri,
i(t) = imaxsin(ωt – ϕ)
Ve = ie.Z
10 = ie.5 ⇒ ie = 2 amper olur.
r
)
3
r
= 5v2sin(100πt – ) olur.
3
= 5v2sin(2πft –
5 saniyede açığa çıkan enerji,
W = ie2.R.t
W = 22.4.5
W = 80 J olur.
CEVAP A
CEVAP D
11.
XL=4Ω
R=6Ω
ϕ=53°
.
XC–XL=8Ω
Z=10Ω
XC=12Ω
XC > XL olduğundan, devreden geçen akım gerilimden öndedir.
Ι. yargı doğrudur.
Ve =
ie =
Vm
2
=
40 2
= 40V
2
Ve 40
=
= 4A olur.
Z
10
ΙΙ. yargı doğrudur.
Port = Ve.ie.cosϕ
= Ve.ie.cos53°
= 40.4.0,6
= 96 W olur.
ΙΙΙ. yargı doğrudur.
CEVAP E
ELEKTRİK VE MANYETİZMA
337
Adı ve Soyadı : .....................................
1.
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
Bölüm
Yazılı Soruları
(Alternatif Akım)
a) XL = 2πfL
c)
200 1
.
r 20
= 20 Ω olur.
Port = Ve.ie.cosϕ
= 100.4.cos37°
= 2π.
Z=25Ω
= 400.0,8
XL=20Ω
Devrenin empedansı,
ϕ=53°
Z2 = (15)2 + (20)2
= 320 W olur.
.
R=15Ω
Z = 25 Ω olur.
b) ie =
Ve 100
=
= 4A olur.
Z
25
4.
a)
c) Devrenin güç çarpanı;
Bobinin indüktansı,
XL = ω . L = 80π .
cosϕ = cos53° = 0,6 olur.
2.
ÇÖZÜMLER
1
= 40 Ω olur.
2r
Devrenin empedansı ise,
Z2 = R2 + XL2
a) Devre rezonans halinde ise, XL= XC dir.
Z2
Z = R = 10 Ω olur.
+
(40)2
XL=40Ω
ϕ=53°Ω .
R=30Ω
Z = 50 Ω olur.
b) Bir RLC devresi rezonansta ise, XL= XC dir.
Bu durumda,
b)
X L = 25 X
=
(30)2
Z
Ve =
Vm
2
=
100
= 50 2 V olur.
2
2 r.f.L = 25
2 r.f.
–1
1
= 25 & f = 50 s olur.
4r
ie =
Ve 50 2
=
= 2 A olur.
Z
50
Direnç üzerinde harcanan güç,
c) Devreden geçen akımın maksimum değeri,
2
P = i e.R = (v2)2.30 = 60 W olur.
Im = Ie.v2 = 2v2A olur.
Devreye uygulanan gerilimin maksimum değeri,
Vm = Im.Z = 2v2.10 = 20v2 volt olur.
c)
Direncin iki ucu arasındaki etkin gerilim,
VR = ie.R
3.
a) Devrenin empedansı,
= v2.30
Z2 = (20)2 + (30 – 15)2
= 30v2 V olur.
Z2 = (20)2 + (15)2
Z = 25 Ω olur.
b) Ve =
Vm
2
100 2
=
2
= 100 V olur.
V
ie = e
Z
100
=
25
= 4A olur.
338
ELEKTRİK VE MANYETİZMA
XL=30Ω
XC
d) Bobinin iki ucu arasındaki etkin gerilim ise,
VL = ie.XL
= v2.40
Z=25Ω
ϕ=37°
XL–XC=15Ω
.
R=20Ω
XC=15Ω
= 40v2 V olur.
5.
K anahtarı 1 konumunda iken:
Ve =
Z1 =
Vm
2
=
8.
80 2
= 80 V
2
Etkin gerilim,
Ve =
Ve 80
=
= 20 X olur.
i e1
4
XL=20Ω
Vm
XC
2
100 2
2
=
Z=20Ω
XL–XC=16Ω
= 100 V olur.
XL=22Ω
XC
Z1=20Ω
Devrenin empedansı,
Z=
XL–XC=16Ω
=
ϕ
.
.
R=12Ω
Ve
ie
XC=4Ω
100
5
= 20 X olur.
R=12Ω
XC=6Ω
Bobinin indüktansı,
XL – XC = 16
K anahtarı 2 konumunda iken:
i e2 =
ϕ
XL – 4 = 16
Ve
80
80
=
=
= 5A olur.
X L – X C 22 – 6 16
XL = 20 Ω olur.
K anahtarı 2 konumuna getirildiğinde ampermetre
5 amperi gösterir.
9.
6.
K anahtarı 1 konumunda iken:
VC
olur.
Ve = 5.8 = 40 V olur.
Bobinin üzerindeki
Z=10Ω
XL=6Ω
K anahtarı 2 konumunda iken:
Ve 40
=
= 4A olur.
Z
10
.
ϕ
VZ=20V
VL–VC=16Ω
etkin gerilim,
VL– VC = 16
R=8Ω
K anahtarı 2 konumuna getirildiğinde ampermetre
4 amperi gösterir.
7.
VL
Ve = VZ = 20 V
Ve = ie1.R
i e2 =
Etkin gerilim,
VL – 6 = 16
.
ϕ
VR=12V
VL = 22 V
VC=6V
olur.
Akımın maksimum değeri,
i = im.sin.2πf.t
2v2 = im.sin.2π.50.
1
400
r
2v2 = im.sin
4
2
2v2 = im.
2
im = 4A olur.
Gerilimin maksimum değeri,
Vm = im.R = 4.25 = 100 V olur.
Gerilim denklemi,
V = Vm.sin.2πft
= 100.sin.2π50t
10. Etkin gerilim ve akım,
Ve =
ie =
Vm
2
im
2
=
=
80 2
= 80V
2
5 2
= 5A olur.
2
Ortalama güç,
Port = Ve.ie.cosϕ
= 80.5.cos60°
= 400.
1
2
= 200 W olur.
= 100.sin.100πt olur.
ELEKTRİK VE MANYETİZMA
339
340
ELEKTRİK VE MANYETİZMA
7. BÖLÜM
TRANSFORMATÖRLER
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
1.
primer
iP
girifl
VP
sekonder
IP
girifl
VP
4.
NP
IS
NP
is akımını artırmak için,
ç›k›fl
VS
NS
R2
sekonder
R1
primer
ç›k›fl
VS
NS
iS
N P VP i S
=
=
bağıntısına
N S VS i P
göre, I, II ve III işlemleri tek başına yapılmalıdır.
Transformatör ideal olduğundan,
CEVAP E
N S VS I P
=
=
dir.
N P VP I S
NP > NS olduğundan, transformatör gerilim alçaltıcı
olarak kullanılır.
5.
VP > VS ve IP < IS dir.
IP
IS
NS=5N
NP=4N
VP
VS
Buna göre I ve II yargıları doğru, III. yargı yanlıştır.
CEVAP D
2.
IP
VP
NP=4N
IS
NS=3N
Transformatör ideal olduğundan, sekonder devrede oluşan akım değeri,
VS
N P VP I S
=
=
N S VS I P
4N I S
=
& IS = 8A olur.
5N 10
Transformatör ideal olduğundan sekonder gerilimi,
CEVAP C
N P VP
=
N S VS
4N 120
& VS = 90 volt olur.
=
3N
VS
3.
Transformatörde değiştirme oranı
Buna göre;
CEVAP B
N2
= 4 tür.
N1
V1 i 2 N 1 1
= =
=
V2 i 1 N 2 4
200 1
=
V2
4
V2 = 800 V olur.
6.
Şekildeki transformatörler ideal olduğuna göre
direncin iki ucu arasındaki gerilim,
V1 N 1
=
V2 N 2
100 200
=
V2
400
V2 = 200 V olur.
I. yargı doğrudur.
Direnç üzerinden geçen akım,
I. yargı doğrudur.
i2 1
i
=
& 1 = 4 tür.
i1 4
i2
II. yargı doğrudur.
V2 > V1 olduğundan transformatör gerilim yükselticidir.
III. yargı doğrudur.
CEVAP E
I2 =
V2 200
=
= 5A olur.
R
40
II. yargı doğrudur.
Direncin gücü,
2
P = I2 . R = (5)2 . 40 = 1000 watt olur.
III. yargı yanlıştır.
CEVAP C
ELEKTRİK VE MANYETİZMA
341
Y transformatörü için,
MODEL SORU - 2 DEKİ SORULARIN ÇÖZÜMLERİ
1.
K
L
M
VM N M
=
VP N P
20 N M
=
50 N P
NM 2
=
olur.
NP 5
P
•~ girifl
•
•
ç›k›fl ~
•
N
3N
2N
X
Y
VP geriliminin etkin değeri,
4.
NP NL
.
.V
NM NK K
VP =
CEVAP C
5N
X
K
girifl
V1=200V
5N 3N
=
.
.200
2N N
Y
L
M
P
NK NL
ç›k›fl
V2
NM NP
= 15.100
= 1500 V olur.
2.
X
L
M
NK NL
VL = VM = 400 V
VM N M
=
VP N P
200 1
=
VL
2
Y
K
girifl
V1
VK N K
=
VL N L
CEVAP D
P
400
=8
V2
VL = 400 V
ç›k›fl
V2
NM NP
V2 = 50 V olur.
CEVAP D
Çıkış gerilimi,
N N
V2 = P . L .V1
NM NK
bağıntısına göre,
V2 çıkış gerilimini artırmak için,
• V1 gerilimi artırılmalıdır.
• NK azaltılmalıdır.
5.
• NP artırılmalıdır.
K
L
M
P
Ι, ΙΙ ve ΙΙΙ işlemleri tek başına yapılmalıdır.
CEVAP E
3.
K
girifl
V1 =200V
L
NK NL
M
girifl
V1
X transformatörü için,
VK N K
=
VL N L
200 10
=
VL
1
VL = 20V olur.
VL = VM = 20 V
342
ELEKTRİK VE MANYETİZMA
NM NP
X
Y
ç›k›fl
V2
P
NM NP
ç›k›fl
V2 =50V
NL > NM ve V1 > V2 olduğuna göre,
V2 =
X
NK NL
Y
NP NL
.
.V bağıntısından,
NM NK 1
NK > NP dir.
I. yargı kesinlikle doğrudur.
NL ve NP yi karşılaştıramayız.
II. yargı için kesin birşey söylenemez.
NM ve NP yi karşılaştıramayız.
III. yargı için kesin birşey söylenemez.
CEVAP A
6.
K
L
M
N
P
9.
R
A
V1
•
~
•~
•
K
2N
VL
X
3N
VM
Y
N
2N
VN
VP
Z
4N
VR
C
M
V2
NK NL
•
N
VK
L
B
P
•
VL = VM ve VN = VP dir.
V3
NM NP
D
F
X
I. yol: X, Y, Z transformatörleri ideal ve birbirlerine
paralel olarak bağlandığından,
E
Y
X trasformatörü gerilim yükseltici olduğuna
göre, V2 > V1 dir.
I. yargı kesinlikle doğrudur.
Y transformatörü için,
VM 3N
& VM = 3VN olur.
=
VN
N
•
II. yol: Bobinler üzerindeki gerilim sarım sayıları
ile orantılıdır.
•
Sarım sayıları bilinmediğinden V1 ile V3 ü karşılaştıramayız.
II. yargı için kesin birşey söylenemez.
VK = 3V ⇒ VL = 6V, VM = 6V, VN = 2V
Y trasformatörü gerilim düşürücü olduğuna
göre, V2 > V3 tür.
III. yargı kesinlikle doğrudur.
VN = VP = 2V ve VR = 4V olur.
CEVAP D
Bu durumda,
VL = VM > VN = VP olur.
7.
K
girifl
V1
L
CEVAP B
M
NK NL
P
ç›k›fl
V2
NM NP
10.
K
X
Y
N N
V2 = L . P . V1 bağıntısına göre, NL ve NM
NK NM
girifl
V1
değiştirilmeden V2 yi azaltmak için; I, II ve III işlemleri tek başına yapılmalıdır.
CEVAP E
K
girifl
V1=160V
L
NK NL
X
V2 =
M
P
NM NP
ç›k›fl
V2=40V
M
P
NK NL
NM NP
X
Y
ç›k›fl
V2
V1 alternatif giriş gerilimi değiştirilmeden, V2 çıkış
gerilimini azaltmak için,
V2 =
8.
L
NL NP
.
.V
NM NK 1
bağıntısına göre; I ve II işlemleri tek başına
yapılmalıdır.
CEVAP C
Y
NL NP
.
. V bağıntısına göre, V1 = 160 V luk
NK NM 1
giriş gerilimi değiştirilmeden V2 gerilimini 40 volttan
10 volta düşürmek için, NK iki katına çıkarılmalı,
NP yarıya indirilmelidir. Bu durumda I ve IV işlemleri birlikte yapılmalıdır.
CEVAP B
ELEKTRİK VE MANYETİZMA
343
MODEL SORU - 3 TEKİ SORULARIN ÇÖZÜMLERİ
3.
K
2N
1.
N
VP=300V
VP=200V
K
5N
M
N
L
N
R
3N
M
5N
L
S
2N
R
K ile L noktaları arasındaki gerilim,
200 5N
& VKL = 80 V olur.
=
VKL 2N
Bobinlerden alınan gerilimler sarım sayıları ile
orantılıdır.
M ile N noktaları arasındaki gerilim,
K ile L noktaları arasındaki gerilim,
VP
5N
=
N
VKL
200 5N
& VMN = 40 V olur.
=
VMN
N
K ile N noktaları arasında bobinler aynı yönlü sarıl-
300
= 5 & VKL = 60 V olur.
VKL
dığından,
V1 = VKL + VMN
M ile R noktaları arasındaki gerilim,
VP
5N
=
2N
VMR
= 80 + 40
= 120 V olur.
R ile S noktaları arasındaki gerilim,
300
5
=
& VMR = 120 V olur.
VMR
2
200 5N
=
& VRS = 120 V olur.
VRS 3N
M ile S noktaları arasında bobinler ters yönlü sarıldığından,
Bobinlerin sarım yönleri düz olduğundan, K ile R
noktaları arasındaki gerilim,
V2 = VRS – VMN
VKR = VKL + VMR = 60 + 120 = 180 V olur.
= 120 – 40
CEVAP D
= 80 V olur.
V1 ve V2 taraf tarafa oranlanırsa,
V1 120 3
=
= olur.
V2
80
2
2.
K
CEVAP D
3N
600V
6N
L
2N
R
S
4.
K ile N noktaları arasındaki gerilim,
600 6N
& VKL = 300 V olur.
=
VKL 3N
V1
R ile S noktaları arasındaki gerilim
600 6N
& VRS = 200 V olur.
=
VRS 2N
Bobinlerin sarım yönleri düz olduğundan,
K ile S noktaları arasındaki gerilim,
VKS = VKL + VRS
= 300 + 200
= 500 V olur.
I. ve II. yargılar doğrudur. III. yargı yanlıştır.
CEVAP C
344
ELEKTRİK VE MANYETİZMA
5N
V2
2N
V3
4N
Bobinlerden alınan alternatif gerilim değerleri
sarım sayıları ile orantılıdır. Bu durumda,
V1 4N
=
& V2 =
V2 5N
V1 4N
=
& V3 =
V3 2N
5
V olur.
4 1
V1
olur.
2
Buna göre, V2 > V1 > V3 ilişkisi vardır.
CEVAP A
5.
500V
10N
N
MODEL SORU - 4 TEKİ SORULARIN ÇÖZÜMLERİ
K
3N
L
M
1.
primer
P
R
2N
sekonder
IP=1A
S
IS=2A
VP=500V
VS=200V
K ile L noktaları arasındaki gerilim,
500 10N
& V1 = 150 V olur.
=
V1
3N
Transformatörün verimi,
M ile P noktaları arasındaki gerilim
Verim =
VS .I S
VP .I P
=
200.2
500.1
500 10N
& VMP = 50 V olur.
=
VMP
N
K ile P noktaları arasında bobinler ters bağlandığından,
V2 = VKL – VMP = 150 – 50 = 100 V olur.
2.
R ile S noktaları arasındaki gerilim,
500 10N
& V3 = 100 V olur.
=
V3
2N
Bu durumda, V1 > V2 = V3 olur.
= 0,8
% verim = 100.0,8 = 80 olur.
primer
CEVAP A
sekonder
IP=0,5A
IS
VS=20V
VP =200V
CEVAP B
6.
K
3N
160V
8N
2N
4N
Transformatörün verimi %80 olduğuna göre
L
Verim =
M
N
P
20.I S
80
=
100
200.0, 5
R
Bir bobinden elde edilen çıkış gerilimi sarım sayılarıyla orantılıdır.
VS .I S
VP .I P
4
1
= .IS & IS = 4A olur.
5
5
3.
primer
K ile L noktaları arasındaki gerilim,
sekonder
IP=2A
160 8N
& VKL = 60 V olur.
=
VKL 3N
VP
CEVAP D
IS=4A
NP
NS
VS
M ile N noktaları arasındaki gerilim,
160 8N
& VMN = 40 V olur.
=
VMN 2N
Transformatörün verimi eşitliğinden,
P ile R noktaları arasındaki gerilim,
Verim =
160 8N
& VPR = 80 V olur.
=
VPR 4N
V .4
80
= S
100
VP .2
V1, V2 ve V3 gerilimlerini tanımlarsak,
V1 = VKL = 60 V olur.
KL ve MN bobinleri ters bağlandığından,
V2 = VKL – VMN = 60 – 40 = 20 V olur.
MN ve PR bobinleri aynı yönlü bağlandığından,
V3 = VMN + VPR = 40 + 80 = 120 V olur.
Buna göre, V3 > V1 > V2 olur.
VS .I S
VP .I P
CEVAP E
V
V
4
2
= S .2 & S =
5
5
VP
VP
olur. Tüm transformatörlerde,
VS
N
= S olduğundan,
VP
NP
NS
2
=
olur.
5
NP
CEVAP B
ELEKTRİK VE MANYETİZMA
345
4.
primer
6.
sekonder
primer
sekonder
IP=2A
VP
4N
IP
2N
IS
VS
Transformatörlerde primer ve sekonderdeki gerilim değerleri sarım sayılarıyla orantılıdır.
VP N P 4N
=
=
= 2 ve IP = IS olduğundan,
VS N S 2N
Transformatörün verimi,
Verim =
1
= 50 olur.
2
5N
3N
VS
Primer devrenin sarım sayısı 5N, sekonder devrenin sarım sayısı 3N olduğuna göre, gerilimlerin
oranı,
VP N P 5N 5
=
=
= olur.
VS N S 3N 3
Transformatörün verimi,
VS .I S
V.I
1
=
=
olur.
VP .I P 2V.I 2
% verim = 100.
VP
IS=3A
Verim =
CEVAP E
VS .I S 3 3
9
olur.
= . =
VP .I P 5 2 10
%verim = 100.
9
= 90 olur.
10
Buna göre primer devreye 100 J enerji verildiğinde
sekonder devreden 90 J enerji alınır. Primer devreye 200 J verildiğinde sekonder devreden 180 J
enerji alınır.
CEVAP C
5.
Bir transformatörde her zaman primer ve sekonder
devreler için,
VP N P
=
VS N S
eşitliği vardır. Bu durumda,
VP N P
=
= 3 tür.
VS N S
Transformatörün verimi,
Verim =
VS .I S
VP .I P
VS
oranı bilinVP
diğine göre, IS ve IP nicelikleri de bilinirse verim
eşitliğinde verimi bulabilmek için
bulunabilir.
CEVAP D
346
ELEKTRİK VE MANYETİZMA
TEST
1
1.
TRANSFORMATÖRLER
ÇÖZÜMLER
1000
4.
800
5N
V1=200V
V2
100V
R=16Ω
10N
V
K
2N
girifl
V1 N 1
=
V2 N 2
ç›k›fl
5N sarımlı bobini gerilimi V1 olsun.
100 10N
=
& V1 = 50 volt olur.
V1
5N
200 1000
=
& V2 = 160 volt olur.
V2
800
2N sarımlı bobinin gerilimi V2 olsun.
V2 = i2.R
100 10N
=
& V2 = 20 volt
V2
2N
160 = i2.16
i2 = 10 A olur.
Çıkıştaki bobinlerin sarım yönleri ters olduğundan
voltmetrenin gösterdiği değer,
CEVAP E
V1 – V2 = 50 – 20 = 30 V olur.
2.
CEVAP A
A
Girifl
VP
V
NP
NS
R=10Ω
5.
VP N P
=
VS N S
N1=200
100volt
VP
N
= P
i S .R S N S
N2=50
+
–
V
primer
100 N P
=
2.10 N S
sekonder
Transformatörler doğru akım kaynağı ile çalışmaz.
Voltmetre sıfır değerini gösterir.
NP
= 5 olur.
NS
CEVAP A
CEVAP B
6.
3.
N1
NP
NS
N2
V1
i1
VP
VS
V2
primer
sekonder
VP N P
bağıntısına göre,
=
VS N S
V2 gerilimini artırmak için,
V1 N 1
bağıntısına göre,
=
V2 N 2
NP artırılırsa, VS azalır. Ι. yargı yanlıştır.
V1 gerilimi ya da N2 sarım sayısı artırılmalıdır.
I ve III işlemleri tek başına yapılmalıdır.
CEVAP E
NS artırılırsa, VS artar. ΙΙ. yargı yanlıştır.
NP
artırılırsa, VS azalır. ΙΙΙ. yargı doğrudur.
NS
CEVAP C
ELEKTRİK VE MANYETİZMA
347
7.
N1
N2
N3
9.
N4
V1
V4
V2
V1
V2
3N
V3
6N
V3
K
4N
L
N1 > N2 olduğuna göre, V1 > V2 olur.
V1 6N
V
3
=
& 1 = olur. I. eşitlik doğrudur.
V2 4N
V2 2
Ι. yargı kesinlikle doğrudur.
N4 > N3 olduğuna göre, V4 > V3 ve V3 = V2 dir.
V1 6N
V
=
& 1 = 2 olur. II. eşitlik doğrudur.
V3 3N
V3
ΙΙ. yargı yanlıştır.
V2 4N
V
4
=
& 2 = olur. III. eşitlik yanlıştır.
V3 3N
V3 3
V1 ile V4 gerilimleri karşılaştırılamaz.
ΙΙΙ. yargı için kesin birşey söylenemez.
CEVAP C
V4 > V2 olur.
IV. yargı kesinlikle doğrudur.
CEVAP E
10.
8.
4N
N
2N
N
K
V1
4V
V1
fiekil-I
N
N
3N
V
V2
V2
N
+
–
L
fiekil-II
N
2N
3N
3V
V3
N
M
V3
fiekil-III
Transformatörler doğru akım ile çalışmaz. L lambası kesinlikle ışık vermez.
4V 4N
=
& V1 = V olur.
V1
N
CEVAP B
V
N
=
& V2 = 3 V olur.
V2 3N
3V
N
=
& V3 = 9 V olur.
V3 3N
Buna göre, V3 > V2 > V1 olur.
CEVAP D
348
ELEKTRİK VE MANYETİZMA
TEST
2
1.
TRANSFORMATÖRLER
ÇÖZÜMLER
K
L
M
4.
P
V1
N
V1 =12volt
V2
girifl
V2
girifl
ç›k›fl
10
20
40
X
4N
ç›k›fl
10
Y
V1 N 1 12
N
=
&
=
V2 N 2
V2 4N
V1 N K .N M
=
V2 N L .N P
V2 = 48 volt olur.
10.40
=
20.10
Transformatörler ideal olsaydı giriş ve çıkış güçleri
= 2 olur.
eşit olurdu. Transformatörler ideal olmadığından
P1 > P2 dir. Bu durumda,
CEVAP D
V1.i1 > V2.i2
2.
N1
12.i1 > 48.i2
i1
> 4 olur.
i2
i
Buna göre, 1 oranı 3 olamaz.
i2
N2
V1
V2
girifl
5.
ç›k›fl
A
N1 > N2 ise, alçaltan transformatördür.
girifl
Ι. yargı doğrudur.
2Ve
K
L
C
M
P
E
ç›k›fl
NK NL
İdeal transformatörün verimi %100 dür.
CEVAP A
NM NP
Ve
B
2Ve
D
ΙΙ. yargı yanlıştır.
F
X
Y
Y bobini için;
V1 > V2 olur.
VM N M
=
VP N P
ΙΙΙ. yargı doğrudur.
CEVAP D
Ve
N
= M
2Ve N P
2N M = N P olur.
3.
N M = N P olamaz.
K
VP
V2
L
6.
K
V1
L
NK
NL
CEVAP E
M
P
NM
NP
V2
V1
İdeal transformatörler giriş gücü, çıkış güçlerinin
toplamına eşittir. P = P1 + P2 olur.
ΙΙ. yargı kesinlikle doğrudur.
VP, V1, V2 değerlerini karşılaştıramayız.
Ι. ve ΙΙΙ. yargılar için kesin birşey söylenemez.
CEVAP B
X
Y
Çıkış gerilimi bağıntısına göre, V2 =
NP NL
.
.V
NM NK 1
olduğundan V1 gerilimi değiştirilmeden NK yarıya
indirilip, NP iki katına çıkartılınca, V2 gerilimi 4
katına çıkar.
CEVAP C
ELEKTRİK VE MANYETİZMA
349
7.
K
•
~ VK
•
L
NK
M
NL
N
NM
2N
•
~ VP
•
NP
3N
X
9.
P
L
K
N
V1
M
P
4N 3N
NL
V2
6N
Y
X
X ve Y transformatörleri paralel bağlı olduklarından VL = VM = 60 volt tur.
Y
X ve Y transformatörleri ideal olduğundan verimleri
% 100 olur. Buna göre,
P1 = P2 olur.
X transformatörü için;
VK N K
N
N
=
& VK = VL . K = 60.
= 30V olur.
VL N L
NL
2N
I. eşitlik kesinlikle doğrudur.
Y transformatörü için;
II. ve III. eşitlikler için kesin birşey söylenemez.
NL bilinmediğinden V1 ve V2 yi karşılaştıramayız.
CEVAP A
VM N M
N
6N
=
& VP = VM . P = 60
= 120V olur.
VP N P
NM
3N
Buna göre,
VK = 30 V,
VL = 60 V,
VM = 120 V olur.
CEVAP C
10.
8.
K
•
~ V1
•
L
NK
NL
X
M
NM
NP
•
•
V2 ~
•
~
•
L
NK
NL
X
Y
VP =
V2
= 2 olduğuna göre,
V1
M
P
•
~
•
NM
Y
NP NL
.
.V bağıntısına göre,
NM NK K
N L N P V2
.
=
N K N M V1
VK = 600 V gerilimi değiştirilmeden VP gerilimini
100 volttan 25 volta düşürmek için NP yarıya düşürülmeli, NK iki katına çıkarılmalıdır.
3N 2N
.
= 2 olur.
N 3N
II ve III işlemleri birlikte yapılmalıdır.
CEVAP B
Buna göre,
NK = N,
NL = 3N,
NM = 3N,
NP = 2N olur.
CEVAP E
350
K
P
ELEKTRİK VE MANYETİZMA
TEST
3
ÇÖZÜMLER
120 12N
=
& VMP = 40V olur.
VMP
4N
1.
A
girifl
VP
Np
V
Ns
Ns
=
II. yargı doğrudur.
K-L uçları ve M-P uçları arasındaki sarımların
yönleri ters olduğundan,
VKP = VMP – VKL
= 40 – 10
= 30 V olur.
III. yargı doğrudur.
CEVAP E
R=25Ω
Sekonder devreden geçen akım şiddeti,
Palınan = Pverilen
i s2 . R = Vp . ip
i s2 . 25 = 200 . 2
i s2 = 16
is = 4A olur.
Sekonder devredeki potansiyel,
Vs = Is.R = 4.25
= 100 V olur.
Primer devredeki bobinin sarım sayısının sekonder
devredeki bobinin sarım sayısına oranı,
N p Vp
=
N s Vs
Np
4.
L
1600
800
L
V2
M
Tüm transformatörler gerilim sarım sayıları ile
orantılıdır.
Vp N p
=
V1 N K
Vp
V2
P
V1=220V
I
=
Np
NL
dir.
Buna göre,
V1 N K 1600
=
=
= 2 olur.
V2 N L
800
V2=55V
V1 N K .N M
=
V2 N L .N P
220 N K
.12 & 4 =
=
NL
55
NK
=
NL
V1
primer
200
= 2 olur.
100
K
K
Vp=220V
II. yol: Transformatör ideal olduğundan akım oranı
sarım sayıları oranı ile ters orantılıdır.
Np Is 4
=
= = 2 olur.
Ns Ip 2
CEVAP C
2.
TRANSFORMATÖRLER
II
5.
K
NK
.12
NL
L
1
olur.
3
CEVAP C
3.
N
K
ç›k›fl
L
12N
4N
M
ç›k›fl
P
120 12N
=
& VKL = 10V olur.
VKL
N
I. yargı doğrudur.
M
P
•
~ V1=100V
•
•
•
V2=25V ~
NK=N
NL
X
girifl
120V
CEVAP B
NK = NP = N
NM
NP=N
Y
V2 1
=
V1 4
olduğundan L ve M nin sarım sayılarının oranı,
V2 N L N P
=
.
V1 N K N M
1 NL N
=
.
4
N NM
NL 1
=
olur.
NM 4
CEVAP A
ELEKTRİK VE MANYETİZMA
351
6.
X
L
girifl
V1
M
NK NL
V2 =
9.
Y
K
primer
P
sekonder
IP
girifl
VP
ç›k›fl
V2
NM NP
NP NL
.
.V bağıntısına göre,
NM NK 1
IS
NP
NS
ç›k›fl
VS
Primer devrenin sarım sayısının, sekonder devrenin sarım sayısına oranı,
V1 alternatif giriş gerilimi değiştirilmeden,
VP N P
=
VS N S
V2 çıkış gerilimini artırmak için,
150 N P
=
120 N S
• NK ya da NM azaltılmalıdır.
• NL ya da NP artırılmalıdır.
NP 5
=
olur.
NS 4
CEVAP D
I. yargı yanlıştır.
7.
primer
Transformatörün verimi %60 olduğundan primer
akımı ile sekonder akımı arasındaki ilişki,
sekonder
IS
IP
Vg
NP
Verim =
Vç
NS
I .120
60
= S
100
I P .150
4I
I
3
4
= S & P =
olur.
5
3
IS
5I P
Bir transformatörün verimi;
Verim =
I S .VS
I P .VP
Palınan
P
V .I
= S = S S ile bulunur.
Pverilen
PP
VP .I P
II. yargı doğrudur.
Transformatörde verim %60 olduğundan enerji
kayıbı %40 tır.
Verimi bulabilmek için primer devrenin akım ve
gerilim değerleri ile sekonder devrenin akım ve
gerilim değerlerini bilmek gerekir.
Giriş ve çıkış gerilimlerinin etkin değerleri bilindiğinden akım değerlerinin bilinmesi yeterlidir.
CEVAP B
III. yargı doğrudur.
10.
primer
CEVAP E
sekonder
primer
sekonder
Vç
N
8.
K
L
M
N
2N
Vç=0
fiekil-I
P
NK NL
NM NP
N
Vç=Vg≠0
fiekil-II
primer
girifl•
~
V1 •
Vç
sekonder
• ç›k›fl
~
V2
•
Vç
X
V2 =
Y
NP NL
.
.V bağıntısına göre,
NM NK 1
V1 = 400 V gerilimi değiştirilmeden V2 gerilimini
100 volttan 50 volta düşürmek için M bobininin
sarım sayısı NM 2 katına çıkartılmalıdır.
I işlemi tek başına yapılmalıdır.
CEVAP A
352
ELEKTRİK VE MANYETİZMA
N
2N
Vç=2Vg≠0
fiekil-III
Şekil-I deki devre doğru akım ile Şekil-II ve III teki
devreler ise alternatif akımlarla beslenmektedir.
Transformatörler alternatif akım ile çalıştığından
Şekil-I deki devrenin çıkış gerilimi sıfırdır.
CEVAP A
Adı ve Soyadı : .....................................
Sınıfı
: .....................................
Numara
: .....................................
Aldığı Not
: .....................................
1.
K
L
Bölüm
Yazılı Soruları
(Transformatörler)
M
ÇÖZÜMLER
3.
P
A1
V1
NK NL
NM NP
V2
girifl
girifl
A2
V1
V2
ç›k›fl
ç›k›fl
X
Y
NP=1200
L bobini üzerindeki gerilim,
VK N K
=
VL N L
NS=300
a) Transformatör ideal olduğu için,
NP iS
=
NS iP
200
= 10
VL
1200 8
=
300
iP
VL = 20 V olur.
VL = VM = 20 V olur.
i P = 2 A olur.
Çıkış gerilimi,
b) Sekonder gerilimi,
VM N M
=
VP N P
VP N P
=
VS N S
20 1
=
V2 2
200 1200
=
VS
300
V2 = 40 V olur.
VS = 50 V olur.
4.
A
girifl
2.
K
V1
L
NK NL
M
NM NP
V2
ç›k›fl
V2 N L N P
=
.
V1 N K N M
1200 5 N P
= .
80
2 NM
NP
= 6 olur.
NM
NP
NS
R=16Ω
P
girifl
X
V
Y
Palınan = Pverilen
iS2.R = VP.iP
is2.16 = 100.1
iS.4 = 10 ⇒ iS =
5
A olur.
2
NP iS
=
NS iP
5
NP 2
=
NS 1
NP 5
=
olur.
NS 2
ELEKTRİK VE MANYETİZMA
353
5.
K
L
M
8.
P
A1
V1
4N
N
3N 2N
girifl
V2
girifl
V1=200V
X
i .R
VS .i S
.100 = S
.100
VP .i P
VP .i P
2
4 4 .10
=
5 200.i P
1
4
=
& i P = 1A olur.
5 20.i P
9.
NS
N
1
= 10 & P =
olur.
NP
N S 10
% Verim =
VS .i S
.100
VP .i P
=
36.5
.100
100.2
NP iS
=
NS iP
= 90
2
1
=
10 i P
Verim = %90 olur.
i P = 20 A olur.
10.
M
VP N P
=
VS N S
K
20
1
=
VS 10
V1
N2
P
R
N3
V1 N 1
=
V2 N 2
7.
2V N 1
=
V
N2
A
NP
NS
R=10Ω
N2 =
N1
olur.
2
N3 sarım sayısı,
›
NS 1 NP
= &
= 5 olur.
NP 5 NS
VP N P
=
VS N S
VP
N
= P
i S .R N S
100
=5
i S .10
i S = 2 A olur.
ELEKTRİK VE MANYETİZMA
V3
S
N2 sarım sayısı,
girifl
V1=100V
V2
N1
L
VS = 200 V olur.
354
R=10Ω
2
% Verim =
V2 1
olur.
=
V1 6
b)
NS
Y
V2
N 2N
=
.
V1 4N 3N
a)
NP
ç›k›fl
V2 N L N P
=
.
V1 N K N M
6.
A2
V1 N1
=
V3 N 3
6V N 1
=
V
N3
N1
6
N2 ve N3 taraf tarafa oranlanırsa,
N3 =
N1
N2
= 2 = 3 olur.
N3
N1
6