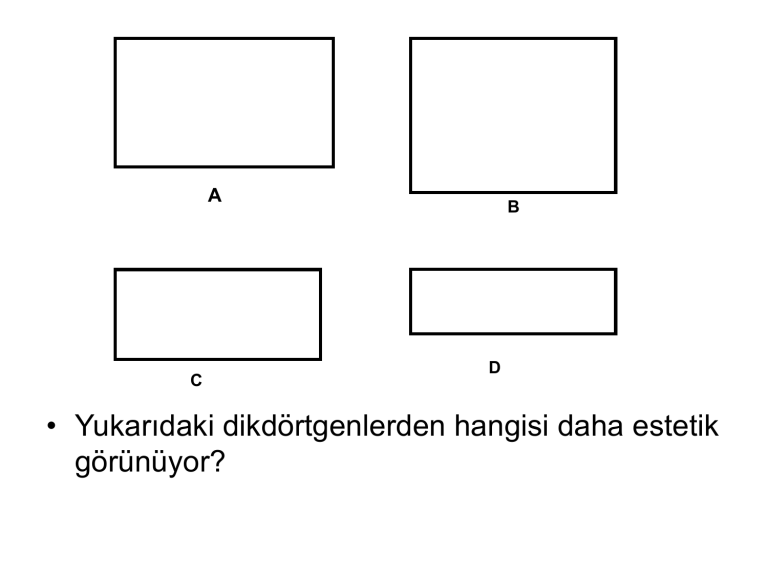
A
C
B
D
• Yukarıdaki dikdörtgenlerden hangisi daha estetik
görünüyor?
ALTIN ORANIN ELDE EDİLMESİ
• Bir kareyi tam ortasından iki eşit diktörgen
oluşturacak şekilde ikiye bölelim.
• Dikdörtgenlerin ortak kenarının, karenin tabanını kestiği
noktaya pergelimizi koyalım. Pergelimizi öyle açalım ki,
çizeceğimiz daire, karenin karşı köşesine değsin, yani
yarı çapı, bir dikdörtgenin köşegeni olsun.
• Sonra, karenin tabanını, çizdiğimiz daireyle kesişene
kadar uzatalım.
• Yeni çıkan şekli bir dikdörtgene tamamladığımızda, karenin yanında
yeni bir dikdörtgen elde etmiş olacağız.
• İşte bu yeni dikdörtgenin taban uzunluğunun (B) karenin taban
uzunluğuna (A) oranı Altın Oran'dır. Karenin taban uzunluğunun (A)
büyük dikdörtgenin taban uzunluğuna (C) oranı da Altın Oran'dır. A / B
= 1.6180339 = Altın Oran C / A = 1.6180339 = Altın Oran
• Elde ettiğimiz bu dikdörtgen ise, bir Altın Dikdörtgen'dir. Çünkü kısa
kenarının, uzun kenarına oranı 1.618 dir, yani Altın Oran'dır.
İnsanda Altın Oran
• Parmaklarımız üç boğumludur. Parmağın tam boyunun İlk iki
boğuma oranı altın oranı verir (baş parmak dışındaki parmaklar için).
Ayrıca orta parmağın serçe parmağına oranında da altın oran
olduğunu fark edebilirsiniz. 2 eliniz var, iki elinizdeki parmaklar 3
bölümden oluşur. Her elinizde 5 parmak vardır ve bunlardan sadece
8'i altın orana göre boğumlanmıştır. 2, 3, 5 ve 8 fibonocci sayılarına
uyar.
İnsan Yüzünde Altın Oran
• Her uzun çizginin kısa çizgiye oranı altın orana denktir.
• Yüzün boyu / Yüzün genişliği,
Dudak- kaşların birleşim yeri arası / Burun boyu,
Yüzün boyu / Çene ucu-kaşların birleşim yeri arası,
Ağız boyu / Burun genişliği,
Burun genişliği / Burun delikleri arası,
Göz bebekleri arası / Kaşlar arası.
Bunların hepsinde altın oran mecuttur.
Sanat Ve Mimaride Altın Oran
•
Sanatta ve mimaride ise Altın Oranı veren birçok eser bulabilmekteyiz. Eski Yunan Mimarisinden
Leonardo Da Vinci, Raphael, Rubens, Boticelli gibi ünlü ressamlar da resimlerinde Altın Oran’ı
kullananların başında gelmektedir.
Leonardo Da Vinci’ ye ait olan “The Annonciation” adlı yukarıdaki tablonun da gelişi güzel değil,
belli bir oran dahilinde yapıldığı görülmektedir. Leonardo ve çağdaşlarının o dönem sadece resim
ve mimari ile uğraşmadığı, çok yönlü, yani matematik, fizik gibi dallarla da yakından ilgili olduğu
düşünüldüğünde bunu tablolarına yansıtmaları mantıklı durmaktadır.
Tabloyu belli noktalarından dikey ve yatay olmak üzere iki çizgiyle kesersek kenarlarda oluşacak
oran 1/1.618 dir. Günümüzde ve geçmişte resim yapma tekniğinde altın üçgen, dikdörtgen ve
çokgenler sıkça kullanılmıştır (2).
Bunun dışında Fibonacci sayı dizisinin ve altın oranın; şiir, müzik notaları, ekonomi gibi değişik ve
birçok kullanım alanı bulunmaktadır. Aşağıdaki örnek bunlardan biri olan mimari alanındandır. Altın
Oran’a özellikle eski Yunan mimarisinde sıkça rastlamaktayız.
• Mısır Piramitleri: İşte size Altın Oran'ın en eski örneklerinden biri...
Şimdi ne alaka Altın Oran ve Milattan Önce yapılan Mısır Piramitleri?
Alaka şu; Her bir piramitin tabanının yüksekliğine oranı evet yine
altın oranı veriyor.
• b) Mona Lisa tablosunun boyunun enine oranı bize altın oranı verir.
• Mimar Sinan'ın da bir çok eserinde altın oran
görülmektedir. Mesela Süleymaniye ve Selimiye
Camileri'nin minarelerinde bu oran görülmektedir.
Kar Kristallerinde Altın Oran
• Kar Kristallerinde Altın Oran: Altın oran kristal yapılarda da kendini
gösterir. Bunların çoğu gözümüzle göremeyeceğimiz kadar küçük
yapıların içindedir. Ancak kar kristali üzerindeki altın oranı
gözlerinizle göre bilirsiniz. Kar kristalini oluşturan kısalı uzunlu
dallanmalarda, çeşitli uzantıların oranı hep altın oranı verir.
• Artık bu dikdörtgenden her bir kare çıkardığımızda
elimizde kalan, bir Altın Dikdörtgen olacaktır.
Fotoğrafta Altın Oran
• Fotoğraftaki kullanımına gelince; her ne kadar küsüratlı
bir sayı gibi görünse de Altın Oranı fotoğrafta
kullanmamız mümkündür. Bunun için yapmamız gereken
kadrajımızı 9 eşit dikdörtgene bölerek ilgi noktasını
ortada yer alan kesişim noktalarından birine yakın
yerleştirmek. Tam bir Altın Oran olmasa bile bu işimizi
görecek prensip 1/3 kuralı olarak bilinir.
ALTIN SPİRAL
• İçinden defalarca kareler çıkardığımız bu Altın
Dikdörtgen'in karelerinin kenar uzunluklarını yarıçap alan
bir çember parçasını her karenin içine çizersek, bir Altın
Spiral elde ederiz. Altın Spiral, birçok canlı ve cansız
varlığın biçimini ve yapı taşını oluşturur.Buna örnek
olarak Ayçiçeği bitkisini gösterebiliriz. Ayçiçeğinin
çekirdekleri altın oranı takip eden bir spiral
Ayçiçeğinde Ve Papatyada
Tohumların Dizilişi
Deniz Canlılarında Altın Oran
• Bilim adamları deniz altındaki yumuşakçaları araştırdıklarında "İç
yüzey pürüzsüz, dış yüzeyde yivliydi. Yumuşakça kabuğun içindeydi
ve kabukların iç yüzeyi pürüzsüz olmalıydı. Kabuğun dış köşeleri
kabukların sertliğini artırıyor ve böylelikle, gücünü yükseltiyordu.
Kabuk formları yaratılışlarında kullanılan mükemmellik ve faydalarıyla
hayrete düşürür. Kabuklardaki spiral fikir mükemmel geometrik
formda ve şaşırtıcı güzellikteki 'bilenmiş' tasarımda ifade edilmiştir."
• Filler ile soyu tükenen mamutların dişleri, aslanların
tırnakları ve papağanların gagalarında logaritmik sarmal
kökenli yay parçalarına göre biçimlenmiş örneklere
rastlanır.
• Ayçiçeği ve papatya gibi bitkilerde çekirdeklerin ya da
tohumların diziliş şekli altın dikdörtgenden elde ettiğimiz
sarmal gibidir.
Altın Oranın Fibonacci Dizisi İle İlişkisi
•
Fibonacci Sayıları: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987,
1597, 2584, ...
Fibonacci sayılarının ilginç bir özelliği vardır. Dizideki bir sayıyı kendinden önceki
sayıya böldüğünüzde birbirine çok yakın sayılar elde edersiniz. Hatta serideki 13.
sırada yer alan sayıdan sonra bu sayı) sabitlenir. İşte bu sayı "altın oran" olarak
adlandırılır.
ALTIN ORAN = 1,618
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618
987 / 610 = 1,618
1597 / 987 = 1,618
2584 / 1597 = 1,618
Yapraklarda Fibonacci Dizisi
•
•
Bir yapraktan başlayıp, gövde etrafında dönerek aynı hizadaki diğer yaprağa
rastlayıncaya kadar yapılan tur sayısı ile, bu turlar sırasında karşılaşılan yaprak sayıları
bize Fibonacci sayısını verir. Eğer saymaya ters yönden başlarsak bu kez aynı yaprak
sayısı için farklı tur sayısı elde ederiz. Her iki yöndeki tur sayısı ile bu turlar sırasında
karşılaşılan yaprak sayısı bize üç ardışık Fibonacci sayısını verir.
Yandaki resimde üstte görülen bitkide, ilk yaprağın hemen üstündeki yaprağa ulaşmak
için saat yönünde üç tur dönmek ve yol üzerinde 5 yaprak geçmek gerekir. Saatin aksi
yönünde dönüldüğünde ise sadece iki tura ihtiyacımız olacaktır. Dikkat ederseniz elde
edilen sayılar 2, 3 ve 5 ardışık Fibonacci sayılarıdır. Alttaki bitkide ise, 8 yaprak geçerek
saat yönünde 5 tur, aksi yönde ise 3 tur gövde çevresinde dönülür. Bu kez 3, 5 ve 8
ardışık Fibonacci sayılarını elde ederiz. Bu sonuçları üstteki bitki için: saat yönündeki tur
için yaprak başına 3/5; ikinci bitki içinse yaprak başına 5/8 dönüş olarak ifade edebiliriz
DNA da Altın Oran
• DNA'da altınoran:Canlıların tüm fiziksel özelliklerinin depolandığı
molekül de altın orana dayandırılmış bir formda yaratılmıştır. yaşam
için program olan DNA molekülü altın orana dayanmıştır. DNA düşey
doğrultuda iç içe açılmış iki sarmaldan oluşur. Bu sarmallarda her
birinin bütün yuvarlağı içindeki uzunluk 34 angström genişliği 21
angström'dür. (1 angström; santimetrenin yüz milyonda biridir) 21 ve
34 art arda gelen iki Fibonacci sayısıdır.












