EET 148 Ölçme Laboratuvar*

T.C. DÜZCE ÜNİVERSİTESİ
TEKNOLOJİ FAKÜLTESİ
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ
2014-2015 BAHAR DÖNEMİ
EET 148
ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİNDE ÖLÇME
LABORATUVARI DENEY FÖYÜ
Öğrencinin Numarası :
Öğrencinin Adı Soyadı :
Deneyin Adı
:
Deneyin Yapıldığı Tarih:
Raporun Teslim Tarihi:
DEĞERLENDİRME ÖLÇÜTLERİ
Puanlama
Değerlendirme
Format
ve Tertip
Doğruluk
Raporda
İstenilenler
Sonuçlar
Deney
Performansı
%20
%25
%25
%20
%10
Toplam
EET 148 Ölçme Laboratuvarı
DENEY NO: 3 OHM KANUNUN İNCELENMESİ
AMAÇ:
DA devrelerinde akım, gerilim ve direnç veya empedans arasındaki ilişkiyi
bilir, Ohm Kanununu DA devrelerine uygular ve gerekli hesaplamaları yapar.
3.1. DENEYİN TEORİSİ
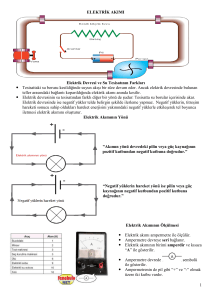
Bir iletkenin akıma karşı gösterdiği zorluğa ve bu amaçla; Krom-Nikel, Tungsten, Volfram vb
iletkenlerden yapılmış devre elemanlarına direnç denilmektedir. Bir direnç elemanı bir DA
kaynağına bağlandığında dirençten, uygulanan gerilim ve direncin kendisiyle orantılı bir akım
geçer. Dirençten geçen akım direnç elemanını ısıtarak ısı enerjisi açığa çıkarır. Böylece
kaynaktan dirence aktarılan güç dirençte tamamen ısıl enerjiye dönüştürülerek harcanır. Başka
bir ifade ile dirençte enerji depolanmaz. Bunun sonucu olarak, direnç elemanına uygulanan
gerilim kesildiğinde geçen akım hemen sıfır olur ve direnç uçlarında herhangi bir emk
indüklenmez. Bir direnç elemanının akım, gerilim ve direnci arasındaki ilişki Ohm Kanunu ile
açıklanmaktadır.
3.2. OHM Kanunu
Direnç elemanlı bir DA devresinde (Şekil 3.1), dirençten geçen akım (I); direncin uçlarına
uygulanan gerilimle (Şekil 3.1 de kaynak gerilimi ile) (E) doğru, direncin kendisiyle (R) ters
orantılıdır. Ohm Kanunu: elektrik devresinde akım, gerilim ve direnç veya empedans
arasındaki bağıntıyı açıklar. AA devresinde direncin yerini empedans almaktadır. Ohm
Kanununa göre bir DA devresinde akım gerilimle doğru dirençle ters orantılı olarak değişir.
Bir başka ifade ile devreye uygulanan gerilimin (V), devre akımına (I) oranı sabit olup devre
direncini (R) verir. Ohm kanununun bu tanımı, iletkenler (metaller) için ve sıcaklığın etkisi
dikkate alınmadığı zaman geçerlidir. Devre direncine aynı zamanda devre sabiti de
denilmektedir. Şekil 3.2 de, bir DA devresinde direnç sabit iken akımın gerilimle, gerilim
sabitken de akımın dirençle değişim eğrileri verilmektedir.
2014-2015 Öğretim Yılı | Bahar
Dönemi
2
EET 148 Ölçme Laboratuvarı
I
+
R
V
-
Şekil 3.1: Temel doğru akım devresi.
I(A)
I(A)
R=Sabit
V=Sabit
V(V)
a)
R(ohm)
b)
Şekil 3.2. Bir DA devresinde a) Akım-gerilim (I-V) b) Akım-direnç (I-R) eğrileri.
Şekil 3.1 de verilen DA devresinde, Ohm Kanununa göre devre akımı gerilimi ve direnci
arasındaki bağıntılar aşağıdaki gibidir.
Akım:
I
V
R
A 
(3.1)

(3.2)
Direnç:
R 
V
I
Gerilim:
V  I.R
V
(3.3)
Eşitlik 3.1 den, devre akımının uygulanan gerilimle doğru, devrenin direnci ile ters; eşitlik 3.2
den, devre geriliminin devre akımına oranı devrenin direncine eşit ve eşitlik 3.3 den, devreye
uygulanan gerilimin devre direnci ve akımı ile doğru orantılı olduğu görülmektedir. Ohm
2014-2015 Öğretim Yılı | Bahar
Dönemi
3
EET 148 Ölçme Laboratuvarı
kanunu ile ifade edilen bir devredeki; akım, gerilim ve direnç arasındaki ilişkiler grafiksel
olarak da açıklanabilmektedir.
Şekil 3.2-a da, akımın devreye uygulanan gerilimle doğru orantılı olarak arttığı görülmektedir.
Akımın gerilime bağlı değişimi, eğimi sabit bir doğruyu vermektedir. Doğrunun eğimi de
devre direncini vermektedir. Şekil 3.2-b de, gerilim sabit iken akımın dirençle ters orantılı ve
hiperbolik olarak değiştiği görülmektedir. Ayrıca, akım-direnç değişim eğrisinin eksenleri
kesmediği görülmektedir. Bunun anlamı, direnç çok küçüldüğünde akımın çok fazla arttığı ve
kısa devreye gittiğini, direnç çok fazla artırıldığında ise akımın azaldığı fakat sıfır olmadığı
görülmektedir. Bir başka ifade ile bir devrede direncin değeri sıfır ile sonsuz arasında
değiştirilememektedir.
3.3. DENEYİN YAPILIŞI
R1=2kΩ
R2=2kΩ R3=2.2kΩ R4=2.2kΩ
V
+ V
-
A
Şekil 3.3: Dirençli DA devresinde Akım-gerilim (I-V) Karakteristik Eğrisinin elde edilmesi.
R1=2kΩ
R2=2kΩ
R3=2.2kΩ R4=2.2kΩ
2
1
3
4
V
+ V
-
A
Şekil 3.4: Akım-direnç (I-R) karakteristik eğrisinin elde edilmesi.
2014-2015 Öğretim Yılı | Bahar
Dönemi
4
EET 148 Ölçme Laboratuvarı
1. Şekil 3.3 deki devreyi kurunuz. Güç kaynağının gerilimini sıfıra getiriniz.
2. Kaynağın gerilimini, 5V aralıklar la 20 volta kadar artırarak her kademedeki akım ve
gerilim değerlerini Tablo 3.1’e kaydediniz.
3. Şekil 3.4 deki devreyi kurunuz ve gerilim kaynağının gerilimini 20 volta ayarlayınız
4. Anahtar “1” konumunda iken, akım ve gerilim değerlerini alarak Tablo 3.1’e
kaydediniz.
5. Sırasıyla anahtarı; 2, 3 ve 4. konumlara getirerek akım ve gerilim değerlerini Tablo 3.1
ye kaydediniz.
6. Kaynak çıkış gerilimini sıfıra getirerek deneye son veriniz.
3.4. DENEYLERDEN ALINAN DEĞERLER
Tablo 3.1. Deneyden alınan değerler
I–V Karakteristiği
Reş. Reş_ölç. = V/I
V
I
[V]
[A]
[]
[]
5
10
15
20
Reş.
[]
I–R Karakteristiği
Reş_ölç.= V/I
V
[V]
[]
I
[A]
20
3.5. SORULAR
1. Gerilim yatay, akım dikey eksende olmak üzere, akım-gerilim karakteristik eğrisini
ölçekli olarak (Exel, proteus, Matlab v.b.) programlarından birini kullanarak çiziniz.
2. Akım - gerilim grafiğini açıklayınız.
3. Ohm Kanunundan bulunan direnç değeri ile devredeki direncin etiket değerlerini
karşılaştırarak açıklayınız.
4. Ohm Kanununun Yarı-iletkenlere nasıl uygulandığını açıklayınız.
5. Direnç yatay, akım dikey eksende olmak üzere, akım-direnç karakteristik eğrisini
ölçekli olarak (Exel, proteus, Matlab v.b.) programlarından birini kullanarak çiziniz.
6. Akım- direnç eğrisini açıklayınız.
7. Deneyden çıkardığınız sonuçları yazınız
2014-2015 Öğretim Yılı | Bahar
Dönemi
5