Biot-Savart Yasası – Giriş
Bölüm 30
Manyetik Alan Kaynakları
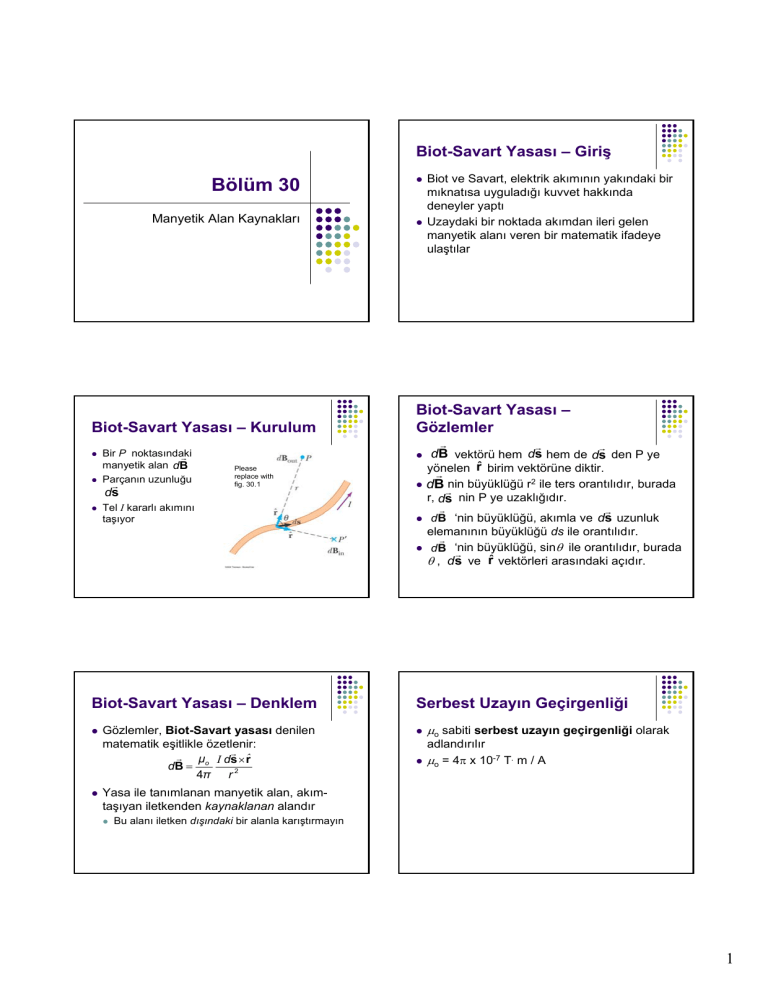
Biot-Savart Yasası – Kurulum
z
z
z
Bir P noktasındaki
r
manyetik alan dB
Parçanın uzunluğu
r
ds
z
z
Biot-Savart Yasası –
Gözlemler
r
r
r
dB vektörü hem ds hem de ds den P ye
r̂ birim vektörüne diktir.
yönelen
r
z dB nin büyüklüğü r2 ile ters orantılıdır, burada
r
r, ds nin P ye uzaklığıdır.
r
r
z dB ‘nin büyüklüğü, akımla ve ds uzunluk
z
Please
replace with
fig. 30.1
Tel I kararlı akımını
taşıyor
z
Biot-Savart Yasası – Denklem
z
z
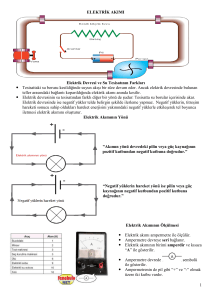
Biot ve Savart, elektrik akımının yakındaki bir
mıknatısa uyguladığı kuvvet hakkında
deneyler yaptı
Uzaydaki bir noktada akımdan ileri gelen
manyetik alanı veren bir matematik ifadeye
ulaştılar
Gözlemler, Biot-Savart yasası denilen
matematik eşitlikle özetlenir:
r µ I dsr × ˆr
dB = o
4π r 2
elemanının büyüklüğü ds ile orantılıdır.
r
dB ‘nin
r büyüklüğü, sinθ ile orantılıdır, burada
θ , ds ve r̂ vektörleri arasındaki açıdır.
Serbest Uzayın Geçirgenliği
z
z
µo sabiti serbest uzayın geçirgenliği olarak
adlandırılır
µo = 4π x 10-7 T. m / A
Yasa ile tanımlanan manyetik alan, akımtaşıyan iletkenden kaynaklanan alandır
z
Bu alanı iletken dışındaki bir alanla karıştırmayın
1
Biot-Savart Yasası – Son
Notlar
Toplam Manyetik Alan
z
z
r
dB , ds uzunluk parçasındaki akımın
oluşturduğu alandır
r
Toplam alanı bulmak için, bütün I ds akım
elemanlarının katkılarını toplarız
r µ I dsr × ˆr
B= o ∫ 2
4π
r
z
z
z
z
Mesafe
z
z
z
Örneğin, bu bir TV deki elektron demetine
uygulanabilir
İntegral akım dağılımının tamamı üzerinden alınır
r
r
B ve E ‘nin kıyaslanması, 2
r
r
B ve E ‘nin kıyaslanması
z
Yasa uzayda akan yüklerden oluşan bir akım
için de geçerlidir
r
ds , yüklerin aktığı küçük bir uzay parçasında
uzunluğu temsil eder
z
Manyetik alanın büyüklüğü, kaynaktan mesafenin
karesiyle ters olarak değişir
Bir nokta yükten ileri gelen elektrik alanı da,
yükten mesafenin karesiyle ters olarak değişir
Doğrultu
z
z
Bir nokta yükün ürettiği elektrik alan, doğrultuda
radyaldır (yükten çıkan doğru bıyunca)
Bir
r akım elemanının ürettiği manyetik alan, hem
ds uzunluk elemanına hem de r̂ birim vektöre
diktir
r
r
B ve E ‘nin kıyaslanması, 3
Örnek 1
Kaynak
z
z
z
Bir elektrik alanı, izole bir elektrik yüküyle kurulur
Manyetik alan üreten akım elemanı, uzatılmış bir
akım dağılımının parçası olmalıdır
z
Bu nedenle tüm akım dağılımı üzerinden integral
almalısınız
Uzun, Düz bir İletken için
z
z
r
B
İnce, düz tel sabit bir
akım taşıyor
r
ds ׈r = ( dx sin θ ) kˆ
Tüm akım elemanları
üzerinden integral
alınırsa
B=
θ2
µ0 I
sin θ dθ
4πa θ∫
1
=
µ0 I
(cos θ1 − cos θ 2 )
4πa
2
Uzun, Düz bir İletken için
Özel Durum
z
z
r
B,
Eğer iletken sonsuz
uzun düz bir tel ise,
θ1 = 0 ve θ2 = π
Alan
olur
µ I
B= o
2πa
r
Kavisli bir Tel Parçası için B
Tel parçasının O
noktasında oluşturduğu
alanı bulalım
dB =
z
I ve R sabittir
z
z
z
Dairesel bir Tel İlmeği için
z
z
θ = 2π
µo I
µ I
µ I
θ = o 2π = o
4πa
4πa
2a
Bu ilmeğin merkezindeki alandır
µ0 I
µI
s= 0 θ
2
4πa
4πa
θ , radyan cinsindendir
(s=aθ)
İlmeklerin kıyaslanması
z
µ I ds cos θ
Bx = ∫ dB cos θ = 0 ∫ 2
4π x + a 2
z
z
Önceki sonucu tam bir daire için bakarsak
z
İlmeğin yarıçapı a dır
ve I kararlı akımı taşır
B=Bxi ve
z
r
B
B=
r
Dairesel bir akım İlmeği için B
z
Manyetik alan çizgileri, telle
aynı eksenli dairelerdir
Alan çizgileri tele dik
düzlemlerde bulunurlar
Alanın büyüklüğü, a
yarıçaplı herhangi bir
dairede her noktada aynıdır
Alanın doğrultusunu
belirlemek için sağ-el kuralı
gösteriliyor
Örnek 3
µ0 I ds
4π a 2
z
B=
z
z
Örnek 2
z
r
Uzun, Düz bir İletken için B ,
Doğrultu
z
Akım ilmeğinin merkezindeki akımı dikkate
alalım
Bu özel noktada, x = 0
Böylece,
Bx =
P noktasındaki alan
Bx =
z
µo I a 2
(
2 a +x
2
2
)
3
2
µo I a 2
(
2 a +x
2
2
)
3
=
2
µo I
2a
Bu eğri telden elde edilen sonuçla tamamen
aynıdır
3
Bir ilmek için manyetik alan
çizgileri
İki paralel iletken arasındaki
manyetik kuvvet
z
z
z
z
z
Şekil (a) bir akım ilmeğini saran manyetik alan
çizgilerini gösteriyor
Şekil (b) demir tozlarıyla alan çizgilerini gösteriyor
Şekil (c) alan çizgilerini bir çubuk mıknatısınki ile
kıyaslıyor
Kararlı akım taşıyan iki
paralel tel
2. teldeki
r akımdan ileri
gelen B2 manyetik alanı
1. tele bir kuvvet
uygular; F1 = I1ℓ B2
PLAY
ACTIVE FIGURE
İki paralel iletken arasındaki
manyetik kuvvet, devam
z
r
B2 yi denklemde yerine yazarsak
µ I I
F1 = o 1 2 l
2πa
z
z
z
z
z
Aynı yönde akım taşıyan paralel iletkenler
birbirlerini çekerler
Zıt yönde akım taşıyan paralel iletkenler
birbirlerini iterler
Amper tanımı
z
İki paralel iletken arasındaki
manyetik kuvvet, son
İki paralel tel arasındaki kuvvet amper tanımı
için kullanılabilir
Özdeş akım taşıyan ve 1 m aralıklı iki uzun,
paralel tel arasındaki birim uzunluktaki
kuvvetin büyüklüğü 2 x 10-7 N/m olduğunda,
her bir teldeki akım 1 A olarak tanımlanır
Sonuç, genellikle iki tel arasındaki manyetik
kuvvet olarak ifade edilir, FB
Bu, birim uzunluktaki kuvvet olarak ta verilir:
FB µo I1 I 2
=
l
2πa
Coulomb tanımı
z
z
SI de yük birimi, coulomb’dur, amper
cinsinden tanımlanır
Bir iletken 1 A lik kararlı bir akım taşırken,
iletkenden 1 s ‘de akan yük miktarı 1 C ‘dur
4
Andre-Marie Ampère
z
z
z
1775 – 1836
Fransız fizikçi
Elektromanyetizmanın
keşfi
z
z
Bir telin manyetik alanı
z
z
Elektrik akımı ve
manyetik alan arasındaki
ilişki
z
Matematik de çalıştı
Bir pusula manyetik
alanı tespit etmek için
kullanılabilir
Telde akım yoksa,
akımdan ileri gelen alan
yoktur
Tüm pusula iğneleri
Yerkürenin kuzey
kutbunu gösterir
z
Bir telin manyetik alanı, 2
z
z
z
z
Yerkürenin manyetik
alanı nedeniyle
Bir telin manyetik alanı, 3
Burada tel yüksek bir
akım taşıyor
Pusula iğneleri daireye
teğet yönde sapıyor
Bu, telin ürettiği
manyetik alanın yönünü
gösterir
Akımı değiştirmek için
aktif şekli kullanın
z
Tel etrafındaki dairesel
manyetik alan, demir
tozlarıyla gösteriliyor
PLAY
ACTIVE FIGURE
Ampere Yasası
r r
z B ⋅ d s çarpımı, uzun düz tel için pusula
z
iğneleriyle tanımlı dairesel yörüngedeki küçük
r
uzunluk elemanları ds ile değerlendirilebilir
Ampere yasasına göre;
bir kapalı
r herhangi
r
yörünge civarındaki B ⋅ d s ‘nin çizgi integrali
µoI ‘ya eşit olur; burada I kapalı yörüngenin
sardığı herhangi bir yüzeyden geçen toplam
kararlı akımdır:
µ0 I
Ampere yasası, devam
z
Ampere yasası, tüm sürekli akım
düzenlemelerinde manyetik alanların
üretilmesini tanımlar
z
z
Akım düzenlemesi yüksek simetri derecesine
sahipse çok kolaylık sağlar
Sağ elinin baş parmağını amper ilmeğinde
akım yönünde koyun ve ilmek civarında
integral alacağın yönde parmaklarınızı bükün
∫ B ⋅ ds =B ∫ ds = 2πr (2πr ) = µ I
0
5
Örnek 4
Uzun Düz bir Telden kaynaklanan
Alan –Amper Yasasından
z
z
Kararlı bir I akımı
taşıyan bir telin
merkezinden r
mesafesindeki
manyetik alanı
hesaplayalım
Akım telin kesitinde
düzgün olarak dağılır
Uzun Düz bir Telden kaynaklanan
Alan – Sonuçların Özeti
z
z
z
Alan, tel içinde r ile
orantılıdır
Alan tel dışında 1/r ile
değişiyor
Her iki denklem r = R
‘de eşittir
Uzun Düz bir Telden kaynaklanan
Alan –Amper Yasasından Sonuçlar
z
z
Telin dışında, r > R
r r
∫ B ⋅ ds = B( 2πr ) = µo I
z
z
Bir selenoid (akım
kangalı), heliks biçimli
uzun bir tel sarımıdır
Makul düzgünlükte bir
manyetik alan, tel
sarımlarıyla çevrili
uzayda elde edilebilir
z
µo I
2πr
Telin içinde (r<R), amper dairesi içindeki I’
akımına ihtiyacımız var
r r
r2
B
s
(
2
)
I
'
I
'
I
⋅
d
=
B
πr
=
µ
→
=
o
∫
R2
µ I
B = o 2 r
2πR
Örnek 5
Bir Toroid’in Manyetik Alanı
z
z
Toroidin merkezinden r
uzaklığında bir
noktadaki alanı bulalım
Toroid N tel sarımı var
r
r
∫ B ⋅ ds = B( 2πr ) = µ N I
B=
Bir Selenoidin Manyetik Alanı
→ B=
o
µo N I
2πr
Bir Selenoidin Manyetik Alanı,
Tanım
z
İç kısımdaki alan çizgileri
z
z
z
z
Birbirlerine yaklaşık paraleldir
Düzgün dağılmıştır
Birbirlerine yakındır
Bu, alanın kuvvetli ve hemen hemen düzgün
olduğunu gösterir
Selenoidin iç kısmı
6
Sıkı Sarılı bir Selenoid’in
Manyetik Alanı
z
z
Alan dağılımı bir çubuk
mıknatısınkine benzer
Selenoidin uzunluğu
arttıkça
z
z
z
Amper yasası, selenoidin iç manyetik alanını
bulmak için kullanılabilir
İç alana paralel ℓ kenarlı ve alana dik w
kenarlı bir dikdörtgen düşünelim
z
z
z
Bu, şekildeki 2. ilmektir
z
z
r
r
r r
B ⋅ ds = B
path 1
z
∫
ds = Bl
path 1
Dikdörtgen yol boyunca toplam akım, bir
sarımdan geçen akımın sarım sayısıyla
çarpımına eşittir
r r
B
∫ ⋅ ds = Bl = µo NI
Manyetik Akı
z
Manyetik alan için Amper yasası çözülürse
N
B = µo I = µo n I
l
z
z
z
z
Bu sadece çok uzun bir selenoidin merkezi
civarındaki noktalarda geçerlidir
n = N / ℓ , birim uzunluktaki sarım sayısıdır
Amper yasasını uygularsak
∫ B ⋅ ds = ∫
Bu, şekildeki 1. kenardır
Bir Selenoid’in Manyetik Alanı,
Son
sarımlar yakın olmalıdır
uzunluk sarımların
yarıçapından çok daha
uzun olmalıdır
Amper Yasasının bir Selenoid’e
Uygulanması, devam
Selenoidin içindeki uzun ℓ kenarı alana katkı
yapar
z
İdeal bir selenoid ‘e
yaklaşmak için:
z
iç alan daha düzgün hale
gelir
dış alan zayıflar
Amper Yasasının bir
Selenoid’e Uygulanması
z
İdeal Selenoid – Özellikleri
Manyetik alanla ilişik
manyetik akı, elektrik
akıya benzer tarzda
tanımlanır
Keyfi şekilli bir yüzey
üzerinde bir dA alan
elemanı düşünelim
7
Bir Düzlemden Geçen
Manyetik Akı, 1
Manyetik Akı, devam
z
z
z
z
z
r
Bu
r elemandaki manyetik alan B dir
dA , yüzeye dik bir vektördür
r
dA , büyüklüğü dA alanına eşittir
Manyetik akı
r r
Φ B = ∫ B ⋅ dA
Manyetik akı birimi T.m2 = Wb
z
z
z
z
Wb; weber
Özel bir durum;
r A alanlı
bir düzlem, dA ile θ
açısı yaparsa olur
Manyetik akı:
ΦB = BA cos θ
Bu durumda, alan
düzleme paraleldir ve
Φ = 0 dır.
PLAY
ACTIVE FIGURE
Bir Düzlemden Geçen
Manyetik Akı, 2
z
z
z
z
Manyetizmada Gauss Yasası
Manyetik akı: ΦB = BA cos θ
Bu durumda, alan düzleme
dik ve Φ = BA dır
Bu akının maksimum
değeridir
Farklı açıları görmek için
aktif şekli kullanın
z
Manyetik alanlar herhangi bir noktada
başlamaz veya bitmez
z
z
Bir yüzeye giren çizgilerin sayısı, yüzeyden
ayrılan çizgilerin sayısına eşittir
Manyetizmadaki Gauss yasası’ na göre,
herhangi bir kapalı yüzeyden geçen manyetik
akı daima sıfırdır:
r
r
∫ B ⋅ dA = 0
PLAY
ACTIVE FIGURE
Problem 1, p.968
Problem 16, p.970
Neils Bohr’un 1913 de önerdiği hidrojen atomu modelinde bir
elektron, protonun etrafında 5.3x10-11 m yarıçaplı bir dairesel
yörüngede 2.2x106 m/s süratle dolanır. Elektronun hareketinin,
protonun bulunduğu konumda oluşturduğu manyetik alanın şiddetini
bulunuz.
Aralarında 10 cm uzaklık bulunan iki uzun paralel iletkenden aynı yönde
akım geçmektedir. Birinci iletkenden geçen akım I1=5A, ikinciden I2=8A dir.
(a) I1 in I2 nin bulunduğu yerde oluşturduğu manyetik alanın büyüklüğü nedir?
(b) I1 in I2 ‘ye birim uzunluk başına etkiyen kuvvet nedir? (c) I2 nin I1 ‘in
bulunduğu yerde oluşturduğu manyetik alanın büyüklüğü nedir? (d) I2 nin I1 ‘e
birim uzunluğu başına uyguladığı kuvvet nedir?
ÇÖZÜM
Dairesel bir tel ilmeği için manyetik alan şiddeti:
(R: yarıçap)
Sabit akım:
q qv
qv
I= =
=
t
x 2πR
B=
µ0 I
2R
ÇÖZÜM
İlki y=0, ikincisi y=10cm deki tellerin ikisi de x-yönünde
akım taşısınlar.
(a) B =
(b)
B=
4π x 10 −7 x 1.6 x 10 −19 x 2.2 x 106
= 12.5 T
4π (5.3 x 10 −11 ) 2
sayfadan dışa
FB = I 2 LxB = 8(1i x 1 x 10 −5 k ) = 8 x 10 −5 N(− j) birinci tele doğru
(c) B =
(d)
µ0 I
4π 10 −7 (5)
k=
k = 1 x 10 −5 T
2πr
2π (0.1)
4π 10 −7 (8)
µ0 I
(-k) =
(-k) = 1.6 x 10 −5 T sayfadan içe
2πr
2π (0.1)
FB = I1LxB = 5[1i x 1.6 x 10 −5 (-k )] = 8 x 10 −5 N( j) ikinci tele doğru
8
Problem 23, p.971
Problem 33, p.972
Bir füzyon reaktörünün manyetik alan kangalları, iç yarıçapı 0.7 m ve
dış yarıçapı 1.3 m olan bir toroid biçimindedir. Toroidin kalın tellerden
oluşan 900 sarımı varsa ve bunların her birinden 14 kA geçiyorsa,
toroidin (a) iç yarıçapı boyunca (b) dış yarıçapı boyunca manyetik
alanın büyüklüğünü bulunuz.
Kenar uzunluğu l=2.5 cm olan bir küp,
şekildeki gibi, B=(5i+4j+3k) Tesla ifadesi
ile verilen düzgün bir manyetik alan içine
yerleştirilmiştir. (a) Küpün boyalı yüzünden
geçen akıyı hesaplayınız. (b) Küpün altı
yüzünden geçen toplam akı nedir?
ÇÖZÜM
(a)
(b)
Biçteki =
Bdistaki
µ 0 NI 4π (10 −7 )(900)14000
=
= 3. 6 T
2πr
2π (0.7)
µ NI 4π (10 −7 )(900)14000
= 0
=
= 1.94 T
2πr
2π (1.3)
ÇÖZÜM
(a) Φ B = B ⋅ dA =B ⋅ A = (5i + 4 j + 3k )(2.5 x 10 −2 ) 2 i
∫
Φ B = 3.13 Tm 2 = 3.13 x 10 −3 Wb
(b) (Φ ) = B ⋅ dA = 0
B top
∫
(manyetizmada Gauss yasası gereği; herhangi kapalı bir yüzey için)
9