temel prensipler

HİDROLİK
TEMEL PRENSİPLER
Öğr. Gör. Adem ÇALIŞKAN
TEMEL PRENSİPLER
Hidrolik veya Pnömatik sistemlerle ilgili çalışmalar
yapabilmek için akışkanlar ve hava ile ilgili fiziksel
prensiplerin bilinmesinde yarar vardır.
HİDROLİK PRENSİPLER
Akışkan gücünden yararlanarak iş elde edilen hidrolik
sistemlerde kullanılan sıvılar; hidrolik yağlar ve
emülsiyonlarıdır. Sıvıların sahip oldukları fiziksel prensipler
Arşimet, Pascal, Bernoulli ve Toriçelli gibi bilim
adamlarının çalışmalarıyla günümüze kadar getirilmiştir.
Hidrolik sistemlerde kullanılan akışkanların sahip oldukları
prensipler hidrostatik ve hidrodinamik olarak iki grupta
incelenebilir.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
2
TEMEL PRENSİPLER
HİDROSTATİK PRENSİPLER
Hidrolik sistemlerde kullanılan akışkanların durgun haldeyken
sahip oldukları fiziksel prensiplerdir.
Hidrostatik basınç
Bir sıvı sütununun, tabanına yapmış olduğu basınç [ p
(Newton/m2 ya da Pascal)];sütun yüksekliğine [ h ( metre) ],sıvı
yoğunluğuna [ (kg/m3 ) ] ve yerçekimi ivmesine [ g ( m/sn2 ) ]
bağlıdır. p=h .  . g dir.
Hidrostatik basınç özellikleri
Farklı şekillerde ancak yükseklikleri aynı olan kaplara
yoğunlukları aynı olan bir sıvı konduğunda kapların şekline
bakılmaksızın
tabanlarında
oluşan
basınç
birbirine
eşittir.P1=P2=P3=P4
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
3
TEMEL PRENSİPLER
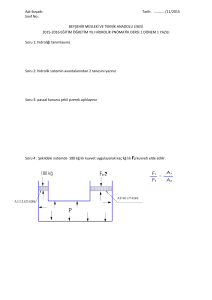
ÖRNEK PROBLEM 1
Yoğunluğu 0,74 gr/cm3 olan bir sıvının sütun yüksekliği 0,81 metredir.
 Bu sıvı daire kesitli bir kapta iken kabın tabanına yaptığı basınç ne
kadardır?
 Bu sıvı kare kesitli bir kapta iken kabın tabanına yaptığı basınç ne
kadardır?
ÇÖZÜM
sütun yüksekliği [ h ( metre) ]=0,81m
sıvı yoğunluğu [ (kg/m3 ) ]= 0,74 gr/cm3=740 kg/m3
yerçekimi ivmesi [ g ( m/sn2 ) ]=9,81 m/sn2
basınç [ p (Newton/m2 ya da Pascal)]=?
p=h .  . g olduğundan p=0,81*740*9,81=5880,1 N/m2 ya da Pascal
Daire kesitli kap ile Kare kesitli kapta yükseklik ve yoğunluk eşit
olduğundan basınçta eşittir.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
4
TEMEL PRENSİPLER
Pascal kanunu
Yerçekimi dikkate alınmadığında kapalı bir kap içinde bulunan
bir akışkana A alanı ile bir F kuvveti uygulandığında meydana
gelen basınç kuvvetin uygulandığı alana ve uygulanan kuvvete
bağlı olarak değişir.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
5
TEMEL PRENSİPLER
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
6
TEMEL PRENSİPLER
ÖRNEK PROBLEM 2
Piston çapı 22 cm ve kuvvetin uygulandığı kütle 185 kg olduğuna göre
meydana gelen basınç ne kadardır?
ÇÖZÜM
Piston çapı=d=22 cm=0,22 m
 * D 2 3,14 * 0,22 2
Kuvvetin uygulandığı alan= A  4
4
A=0,037994 m2
Uygulanan kuvvet=G=F=m*g=185 kg * 9,81 m/sn2
F=1814,85 N
Meydana gelen basınç=
F
1814,85
p 
A 0,037994
p=47766,8 N/m2 ya da Pascal
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
7
TEMEL PRENSİPLER
İtme Kuvveti-Basınç ve alan arasındaki ilişki
Hidrolik kuvvet iletimi ( Kuvvetin sıvı yardımıyla taşınması )
Bununla beraber meydana
gelen basınç kabın her
noktasına
aynen
(sıvı
tarafından) iletilir.
Şekilde iki pistonun birincisine
uygulanan kuvvet sonucu oluşan
basınç her noktada aynı ( Pascal
prensibine göre ) olacağından
ikinci
pistonda
meydana
gelebilecek olan kuvvet pistonun
alanıyla doğru orantılı olacaktır.
HİDROLİK VE PNÖMATİK SİSTEMLER
p  F1  F 2
A1 A2
ise ve pistonların kat
ettikleri mesafeyi de L
(metre) ile ifade edilirse
L1  A2
L2 A1
olacaktır.
Öğr. Gör. Adem ÇALIŞKAN
8
TEMEL PRENSİPLER
İtme Kuvveti-Basınç ve alan arasındaki ilişki
Hidrolik kuvvet iletimi ( Kuvvetin sıvı yardımıyla taşınması )
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
9
TEMEL PRENSİPLER
ÖRNEK PROBLEM 3
Bir hidrolik krikoda I. Piston (El pompası pistonu) çapı 5 cm, II. piston çapı
(kaldırma pistonu çapı) 42 cm ve I. Pistona kuvvetin uygulandığı kütle 37 kg
olduğuna göre
a) Meydana gelen basınç ne kadardır?
b) II. Pistonda elde edilen kuvvet ne kadardır.
c) I. Piston 23 cm yol aldığında II. pistonun aldığı yol ne kadardır?
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
10
TEMEL PRENSİPLER
 ÇÖZÜM
a)
I. Piston çapı=d1=5 cm=0,05 m
I. Kuvvetin uygulandığı alan 𝐴1 =
𝜋∗𝑑12
4
=
m2
=
m2
𝐴1 =
3,14∗0,052
4
= 0,0019625 m2
II. Piston çapı=d1=42 cm=0,42 m
II. Kuvvetin uygulandığı alan=𝐴2 =
𝜋∗𝑑22
4
𝐴2 =
3,14∗0,422
4
= 0,138474 m2
I. Pistona uygulanan kuvvet=F1=37 kg*9,81 m/sn2=362,97 N
Meydana gelen basınç
𝑃1 =
𝐹1
𝐴1
=
362,97
0,0019625
= 184952,9 N/m2 ya da Pascal
Birleşik kap olmasından ve pascal prensibinden yararlandığımızda 𝒑𝟏 =
olduğundan p1=p2 buradan da
𝑭𝟏
𝑨𝟏
=
𝑭𝟐
𝑨𝟐
= 𝒑𝟐
p2=184952,9 N/m2 ya da Pascal olacaktır.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
11
TEMEL PRENSİPLER
 ÇÖZÜM
b)
F2=p2*A2=184952,9*0,138474=25611,17
 ÇÖZÜM
N
c)
I. Pistonun aldığı yol=L1=23 cm (Sonuçta orantı olduğundan birim
değiştirmeye gerek yoktur. Birinci değer hangi birimde verilirse ikinci
değer de aynı birimde çıkacaktır.)
Alan hacim ilişkisiyle pascal prensibinin formülü uygulandığında
𝑳𝟏
𝑳𝟐
=
𝑨𝟐
denklemi çıkacak ve buradan
𝑨𝟏
𝐿2 =
23∗0,0019625
=0,326 cm
0,138474
HİDROLİK VE PNÖMATİK SİSTEMLER
𝐿2 =
𝐿1 ∗𝐴1
olacaktır.
𝐴2
Öğr. Gör. Adem ÇALIŞKAN
12
TEMEL PRENSİPLER
Basınç iletimi ( Arttırma-azaltma )
Çapları farklı iki pistonun ( Bir mil
ile birleştirilmiş ) birinci alana P1
basıncı
uygulandığında
ikinci
piston alanı sıvıya alanların
birbirine oranı kadar basınç artışına
sebebiyet verir.
yani F1=F2 olduğundan
P1 x A1 = P2 x A2 olacağından
𝑝1 . 𝐴1
𝑝2 =
𝐴2
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
13
TEMEL PRENSİPLER
Basınç iletimi (Arttırma ve azaltma)
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
14
TEMEL PRENSİPLER
 Örnek Problem 4
Şekilde görülen düzenekte birinci pistonun çapı
42 cm ikinci pistonun çapı 5 cm ve
uygulanmakta olan birinci basınç 184952,9
pascal olduğuna göre
F1=? F2=? P2=?
 ÇÖZÜM
I. Piston çapı=d1=42 cm=0,42 m
I. Basıncın uygulandığı alan=𝐴1 =
I. Pistonda meydana gelen kuvvet
𝜋∗𝑑12
=m2
4
𝐴1 =
3,14∗0,422
=0,138474
4
F1=p1 *A1 = 184952,9 * 0,138474 = 25611,17 N
II. Pistonda meydana gelen kuvvet (Mekanik bağlantı )
II. Kuvvetin uygulandığı alan𝐴2 =
m2
𝜋∗𝑑22
4
m2
𝐴2 =
F2=F1= 25611,17 N
3,14∗0,052
=0,0019625
4
m2
II. Pistonda Meydana gelen basınç
𝑃2 =
𝐹2 25611,17
=
=13050276,624
𝐴2 0,0019625
HİDROLİK VE PNÖMATİK SİSTEMLER
N/m2 ya da Pascal
Öğr. Gör. Adem ÇALIŞKAN
15
TEMEL PRENSİPLER
HİDRODİNAMİK PRENSİPLER
Hareket halindeki sıvıların esaslarını içerir. Sıvılar hareket ettikleri
sürece hareketlerini yönlendiren kapların fiziksel yapılarına bağımlı
olarak değişik özellikler sergilemektedirler.
Bu özellikler;
Akış esasları ( Süreklilik denklemi )
Birim bir kesitten birim zamanda geçen akışkan miktarına DEBİ denir.
DEBİ  HACIM  Kesit  Hiz
ZAMAN
Formülüzasyonu ise
V
Q   A v
t
HİDROLİK VE PNÖMATİK SİSTEMLER
olacaktır.
Öğr. Gör. Adem ÇALIŞKAN
16
TEMEL PRENSİPLER
HİDRODİNAMİK PRENSİPLER
Akış esasları ( Süreklilik denklemi )
Değişik çaplara sahip bir borunun her kesitindeki akış miktarı ( DEBİ )
aynı olduğu durumda çapların farklılığına bağlı olarak akışkanın
sadece hızı değişmektedir.
Debi her kesitte aynı
olacağından
dolayı
formülden çıkaracak
olursak
A1  v1  A2  v2  A3  v3
Q1  A1  v1  Q2  A2  v2  Q3  A3  v3
Olduğu görülecektir.
Yukarıdaki denkleme süreklilik denklemi de denmektedir.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
17
TEMEL PRENSİPLER
 Örnek Problem 5
Kesiti aşağıdaki şekilde verilen bir borudan geçmekte
olan akışkanın sabit debisi 7,8 lit/dak dır. Birinci
kesitteki boru çapı d1=28 cm, ikinci kesit alanı
A2=0,00785 m2 ve üçüncü kesitteki borunun yarıçapı r3=
110 mm olduğuna göre her çap için akışkan hızını
bulunuz?
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
18
TEMEL PRENSİPLER
 ÇÖZÜM
VERİLENLER
SABİT DEBİ : Q1=Q2=Q3= 7,8 lt /dk
BİRİNCİ KESİTİN ÇAPI : 28 cm = 0,28 m
7,8 lt / dk
𝑑𝑚3
= 𝑑𝑘
=
7,8 𝑚3
1000 𝑑𝑘
𝜋 ∗ 𝑑12
𝐴1 =
=m2
4
İKİNCİ KESİTİN ALANI= 0,00785 m2
3. KESİTİN YARI ÇAPI= 110 mm
𝑣1 =
𝑣2 =
= 𝟎, 𝟎𝟎𝟎𝟏𝟑
𝜋∗𝑑12
4
=
3,14∗0,222
4
= 0,038 m2
𝑄2 0,00013
=
= 𝟎, 𝟎𝟏𝟔𝟓𝟔 𝒎/𝒔
𝐴2 0,00785
𝑄3 0,00013
𝑣3 =
=
= 𝟎, 𝟎𝟎𝟑𝟒𝟐 𝒎/𝒔
𝐴3
0,038
HİDROLİK VE PNÖMATİK SİSTEMLER
𝒎𝟑
𝒔
3,14 ∗ 0,282
𝐴1 =
= 0,061544 m2
4
A2= 0,00785 m2
D3= 22 cm = 0,22 m A3 =
𝑄1
0,00013
=
= 𝟎, 𝟎𝟎𝟐𝟏 𝒎/𝒔
𝐴1 0,061544
=
7,8
𝑚3
1000∗60 𝑠
Öğr. Gör. Adem ÇALIŞKAN
19
TEMEL PRENSİPLER
AKIŞ TÜRLERİ
Sıvılar genellikle sıkıştırılamaz kabul edilirler ve dolayısıyla  = sabit olur. ’nun
değişebilmesi ancak çok yüksek seviyeli basınçlarda mümkündür. Bir su
pompasının girişi ile çıkışı arasında önemli bir basınç artışı olmasına rağmen
yoğunluk sabit kalır. Yoğunluğun değişmediği ve her an her noktada sabit kaldığı
akışlara, Sıkıştırılamaz Akış adı verilmektedir. Hızların yüksek değerlere çıkmadığı
ve basınç artışının az olduğu gaz akışları da bu kategoride düşünülebilir.
Yoğunluktaki değişimin ihmal edilemeyecek kadar yüksek olması durumunda ise,
Sıkıştırılabilir Akış söz konusudur. Akış büyüklükleri zaman ve konumun
fonksiyonudur. Ancak akış büyüklükleri zamanla değişmiyorsa bu tür akışlara
Daimi (=Kararlı=Sürekli Rejim) Akış adları verilmektedir. Akış büyüklükleri
konuma ilaveten zamanın da fonksiyonu ise bu halde, Daimi Olmayan (=Kararsız,
Geçici Rejim) Akış söz konusudur. Bir su pompası ilk çalıştırıldığında, akış
kararsızdır ve bir süre sonra kararlı akım şartları sağlanır. Konuma bağımlılık
açısından akışlar genellikle 3 boyutludur. Borulardaki akışlarda, sadece boru ekseni
boyunca akış büyüklüklerinin değiştiği ve boru eksenine normal doğrultuda bir
değişiklik olmadığı kabul edilir. Bu akışlara bir boyutlu akış denilmektedir.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
20
TEMEL PRENSİPLER
AKIŞ TÜRLERİ
Gerçekte radyal yönde hızda değişim söz konusudur ve eksende maksimum olan
hız cidara doğru azalır ve cidarda sıfır olur. Bu durumda tek boyutlu akışta boru
içerisinde bir ortalama akış hızı kabulü yapılır.
AKIŞ PROFİLLERİ
Ortalama hızın her noktada aynı olduğu (konuma bağlı olmadığı) akışlara ise
Üniform Akış, bir kesitten diğerine değişiklik gösterdiği akışlara da Üniform
Olmayan Akış adı verilir. Kesiti değişmeyen boru ve kanallarda akış Üniform
kabul edilebilir.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
21
TEMEL PRENSİPLER
KATMANLI (LAMİNER) AKIŞ:
Boru içerisinde akmakta olan akışkanın borunun merkezinde hızının en yüksek
olduğu boru cidarlarına gidildikçe daha yavaşladığı bununla beraber akışkan
parçacıklarının birbirine göre paralel hareket ettikleri ve hidrolik sistemlerde tercih
edilen bir akış şeklidir. Re<2300 = Laminer akış
TEDİRGİN (TÜRBÜLANSLI) AKIŞ:
Akış hızına göre boru çapının çok küçük olmasından veya viskozitenin çok yüksek
olmasından kaynaklanan, akışkan parçacıklarının birbirine çarparak hareket ettiği ve
hidrolik sistemlerde hiç tercih edilmeyen bir akış şeklidir. Re>2300 = Türbülanslı akış
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
22
TEMEL PRENSİPLER
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
23
TEMEL PRENSİPLER
REYNOLDS SAYISI
Reynolds sayısı akışkanların akım tipini belirlemeye yarayan çok
önemli bir boyutsuz sayıdır. Akışkanlar mekaniğinde birlikte
kullanıldığı diğer katsayıların en önemlilerinden biridir ve dinamik
benzerliği tanımlamak için kullanılır. İki geometrik olarak benzer akış
davranışı, akış değerleri farklı olan iki farklı sıvı içinde olsalar bile,
eğer aynı ilgili katsayıya sahip iseler, bunlara dinamik benzer denir.
Laminer ya da türbülans karakterinde akışı ayırmak için kullanılan
sayıdır. Bu ayrım için tek bir sayı yoktur, durumdan duruma değişir.
düz bir levhada türbülans başlangıcı için bu sayı 500 000 iken, boru
içerisinde 2300 olmaktadır.
Örneğin bir sineğin kanadının nasıl çalıştığını anlayabilmek için sinek
kanadının büyütülmüş modelleri su içerisinde çalıştırılıp daha yavaş bir
hızda aynı olay gerçekleştirilip gözlenebilmektedir. Burada önemli olan
suyun ve havanın çalışma koşullarında aynı Re sayısına sahip
olmalarıdır. Ele alınan sistemde Re sayısı 2300 den küçük ise Laminer
akış, büyük ise türbülanslı akış olarak göze alınır. Isı Transferi'nde de
Re teoremi farklı orantılarla kullanılmaktadır.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
24
TEMEL PRENSİPLER
Reynold sayısı adını 1842 ile 1912 yılları arasında yaşamış
olan ve bu sayıyı tanımlayan Osborne Reynolds'tan almıştır.
Tipik olarak aşağıdaki gibi tanımlanır.
Fiziksel anlamda; akış ortamındaki (μ/d) ile verilen atalet
kuvvetlerinin (vs*ρ) ile verilen viskoz kuvvetlere oranını
ifade eder ve Re ile gösterilir. Sonuç olarak bu değer bu iki
tip kuvvetin belli bir akış şartı altında birbirine olan göreceli
önemini verir. Bundan ötürü, Reynolds sayısı, düzgün akış
ve türbülanslı akış gibi değişik akış rejimlerini nitelemek
için kullanılır.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
25
TEMEL PRENSİPLER
REYNOLDS SAYISI
Reynolds sayısı; akış hızının (vs) karakteristik uzunluk (L) ile çarpılıp akışkanın
kinematik viskozitesine (v) bölünmesiyle de ifade edilebilen boyutsuz bir sayıdır.
Re=vs*Lv
En önemli husus ise uzunluk olarak karakteristik uzunluğun tespitidir ki bu da
akışın olduğu geometrinin alanının 4 ile çarpımının, çevreye bölümüyle bulunabilir.
Küre için
Silindir
Silindir
L=D
L=D (akış silindir ekseni boyunca)
L=Ls (Akış silindir eksenine dik olarak dıştan)
Dairesel olmayan kanallar için
L=4AÇ=4*Kesit Alanı*Akışın ıslattığı çevre
olarak hesaplanır ve buna özel olarak “hidrolik çap” adı verilir.
Bu duruma göre Reynolds sayısının bulunması için; Re=ρ*vs*dμ
Re=vs*Lv=Atalet kuvvetleri*Viskoz kuvvetleri formülleri kullanılmaktadır.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
26
TEMEL PRENSİPLER
REYNOLDS SAYISI
Yukarıdaki formüllerde kullanılan semboller ve anlamları
vs=Akışkanın hızı ( m/s )
L=Karakteristik uzunluk ( m )=4*Alan/Çevre
d=Boru iç çapı ( m )
μ=Akışkanın dinamik viskozitesi ( pascal Saniye ) pas
ν=Akışkanın kinematik viskozitesi ( m2/s ) ν = μ / ρ
ρ=Akışkanın yoğunluğu kg/m3
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
27
TEMEL PRENSİPLER
 ÖRNEK PROBLEM 6
4 oC’ deki su 0,305 cm çapında yatay silindirik borudan 0,914 m/s hızla
akmaktadır. Bu akışın türünü belirleyiniz.(μ=0,001545 kg/m . s )
 ÇÖZÜM
ρ=1000 kg/m3
μ=0,001545 kg/m . s
𝟏𝟎𝟎𝟎 𝐤𝐠/𝐦𝟑 𝟎, 𝟗𝟏𝟒𝐦/𝐬 (𝟎, 𝟎𝟎𝟑𝟎𝟓 𝐦)
𝛒𝐕𝐬 𝐃
𝐑𝐞 =
=
= 𝟏𝟖𝟎𝟒
𝐤𝐠
𝛍
𝟎, 𝟎𝟎𝟏𝟓𝟒𝟓
𝐦 .𝐬
1804<2300 olduğundan akış laminerdir.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
28
TEMEL PRENSİPLER
BERNOULLİ ( ENERJİ ) TEOREMİ:
Hareket halindeki sıvıların temel denklemleri Newton yasalarından elde edilir.
Hareketli sıvıların basıncını elde etmek üzere, şekildeki gibi yüksekliği değişen bir
boru içine viskozluğu olmayan, kararlı ve sıkıştırılamaz bir akışkanın hareketini
inceleyelim.
Sürtünme kuvveti ihmal edilecek olursa akışkanın sahip olduğu Potansiyel,
Kinetik ve Basınç enerjilerinin toplamı bir akım çizgisi boyunca sabittir. Bir
akışkan 3 çeşit enerji taşır.
1) POTANSİYEL ENERJİ
Bir referans düzlemine göre sıvıların sahip olduğu
POTANSİYEL ENERJİ = Ep=-mg(Z2 -Z1)
Ep= Potansiyel enerji (Kgm2/ s2 ) ( Nm )
m=Kütle (Kg)
g=Yerçekimi ivmesi ( m/s2 )
Z=Yükseklik ( m )
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
29
TEMEL PRENSİPLER
BERNOULLİ ( ENERJİ ) TEOREMİ:
2) BASINÇ ENERJİSİ
Bu iki referans yüksekliğindeki ∆V ( İki nokta arasındaki sıvı hacmi ) hacmindeki
akışkanın meydana getirdiği BASINÇ ENERJİSİ = EB=(P1-P2) ∆V şeklindedir.
EB=Basınç enerjisi ( Nm )
∆V=m/ρ=m3
P=Basınç ( N/m2 )
3) KİNETİK ENERJİ
Akışkanın bu iki nokta arasındaki hızından dolayı sahip olduğu KİNETİK
ENERJİ yükseklik cinsinden 𝑬𝒌 = 𝒎(𝒗𝟐𝟐 − 𝒗𝟐𝟏 )/𝟐
Ek=Kinetik Enerji ( Nm )
m=Kütle (Kg)
v=Hız (m/s)
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
30
TEMEL PRENSİPLER
BERNOULLİ ( ENERJİ ) TEOREMİ:
Akışkanların taşıdığı bu üç enerjisinin formülleri düzenlendiğinde
𝑃1 − 𝑃2 ∆𝑉 − 𝑚𝑔 𝑍2 − 𝑍1
1
= 𝑚(𝑉22 − 𝑉12 )
2
Olur.
Bu denklemin her iki terimini ∆V=m/ρ ye böler ve yeniden düzenlersek
1 2
1 2
𝑃1 + 𝜌𝑉1 + 𝜌𝑔𝑍1 = 𝑃2 + 𝜌𝑉2 + 𝜌𝑔𝑍2
2
2
Olur.
Bu denklemin her iki tarafını ρg ile bölerek yeniden düzenlersek,
𝑃1 𝑉12
𝑃2
1 2
+
+ 𝑍1 =
+
𝑉2 + 𝑍2
𝜌𝑔 2𝑔
𝜌𝑔 2𝑔
HİDROLİK VE PNÖMATİK SİSTEMLER
Sonucuna varılacaktır.
Öğr. Gör. Adem ÇALIŞKAN
31
TEMEL PRENSİPLER
Akım Çizgisi: Bir akış ortamında akışkanın belli bir andaki
akış doğrultusunu temsil eden hayali bir çizgidir.
Akım çizgisi boyunca A1*v1=A2*v2 = Q = Sabit
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
32
TEMEL PRENSİPLER
Bernoulli teoremini basınç enerjisi yönünden değerlendirecek
olursak
Bernoulli teoremine göre akışkanın hareket ettiği kesit alan
azaldıkça hız artar, arttıkça hız düşer.
Toplam enerji sabit olduğundan kesit azalınca Potansiyel ve Basınç
enerjisinde azalma meydana gelecektir. Potansiyel enerjide
ölçülebilen bir değişiklik olmadığından hız ve basınç dikkate
alınmaktadır. Buna göre kesit değişiminden dolayı hız azaldığında
basınç artar, hız arttığında da basınç düşer.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
33
TEMEL PRENSİPLER
Sürtünme ve basınç kayıpları
Buraya kadar sürtünme yok sayılarak kabuller
yapılmıştı. Ancak hiçbir enerji kayıpsız nakil
yapılamayacağına göre hidrolik enerjide de
kayıplar söz konusudur. Sürtünme boru
yüzeylerinde ve akışkanın kendi içinde meydana
gelirken ısı da ortaya çıkar. Hidrolik enerjinin bu
yol ile ısıya dönüşmesi sonucunda da devrelerde
basınç kayıpları oluşacaktır. Bu durum sistemin
verimini de düşürmüş olacaktır.
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
34
=
TEMEL PRENSİPLER
 Örnek Problem 7
Bir hidrolik sistemde 6 cm çapında bir boruda ortalama olarak
6 m/s lik bir hızla hareket etmekte olan akışkanın 12 mm
çapında bir kesitten geçmek zorunda kaldığında sahip olacağı
hızı bulunuz?
 ÇÖZÜM
𝐴1 =
𝜋∗𝐷12
4
D2=12 mm= 0,012 m 𝐴2 =
𝜋∗𝐷22
4
D1=6 cm= 0,06 m
=
3,14∗0,062
4
=
3,14∗0,0122
4
= 0,002826 𝑚2
= 0,00011304 𝑚2
𝑨𝟏 ∗ 𝒗𝟏
𝟎, 𝟎𝟎𝟐𝟖𝟐𝟔 ∗ 𝟔
𝒎
𝒗𝟐 =
=
= 𝟏𝟓𝟎
𝑨𝟐
𝟎, 𝟎𝟎𝟎𝟏𝟑𝟎𝟒
𝒔
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
35
TEMEL PRENSİPLER
Anlaşılmayanları sormanın tam zamanı?
HİDROLİK VE PNÖMATİK SİSTEMLER
Öğr. Gör. Adem ÇALIŞKAN
36