ALTIN ORAN VE LEONARDO da VİNCİ

MEHMET FİDAN







ALTIN ORANA GİRİŞ
TARİHTE ALTIN ORAN
İNSANLARDA ALTIN ORAN
HAYVANLARDA ALTIN ORAN
BİTKİLERDE ALTIN ORAN
ALTIN ORAN VE SANAT
ALTIN SÖZLÜK
MEHMET FİDAN
ALTIN ORAN NEDİR ?
Dünyanın, insanların,
bitkilerin, ağaçların... ,
kısacası Kainat'ın
yaratılışında yaratıcının
kullandığı orandır.Aynı
zamanda insanlar da
teknolojide ve hayatta bu
oranı kullanmaktadırlar.
Kısaca biz altın orana
"göz nizamının oranı"
diyebiliriz. Çoğu zaman
doğayı gözlediğimizde bu
oranın varlığını görebiliriz.
MEHMET FİDAN
ALTIN ORAN
MEHMET FİDAN
►
ALTIN ORANIN TARİHÇESİ
►
Altın orana ilişkin matematik bilgisi ilk kez İ.Ö. 3. Yüzyılda Öklid’in Stoikheia
("Öğeler") adlı yapıtında "aşıt ve ortalama oran" adıyla kayda geçirilmiştir.
Eldeki veriler,bu bilginin geçmişinin aslında Eski Mısır’da İ.Ö. 3000 yılına kadar
dayandığını göstermektedir. Grek dünyasına da Pythagoras ve Pythagoras’cular
tarafından tanıtıldığı ileri sürülür.
Altın oran, (Fi) sayısı olarak bilinir. Bu sayı, Eski Yunan düşünürleri tarafından
bulunmuştur, ancak Fi sayısını kimin tanımladığı kesin olarak belli değildir. Eski
Yunan düşünürlerinin bazılarının, Fi sayısının yerine (to) sayısını kullandıkları
da bilinmektedir.
İ.Ö. 500’lü yıllarda yaşamış olan tüm zamanların en büyük matematikçilerinden
biri olan Pisagor (Pythagoras), altın oranla ilgili aşağıdaki düşüncelerini dile
getirmiştir:
Bir insanın tüm vücudu ile göbeğine kadar olan yüksekliğinin oranı, bir
pentagramın uzun ve kısa kenarlarının oranı, bir dikdörtgenin uzun ve kısa
kenarlarının oranı, hepsi aynıdır. Bunun sebebi nedir? Çünkü tüm parçanın
büyük parçaya oranı, büyük parçanın küçük parçaya oranına eşittir.
Altın oran, günlük yaşantımızda, matematiğin estetik güzelliğe etki ettiği her
alanda karşımıza çıkan bir kavramdır. Altın oranın çok çeşitli tanımları verilebilir
ama altın oran, neticede matematiksel bir kavramdır ve değeri de 1,618033....
olarak devam eden ondalık bir sayıdır. Altın oranın matematiksel anlamına
geçmeden önce altın oranın karşımıza çıktığı bazı alanlara değinelim.
Altın oran, örneğin bir dikdörtgenin göze en estetik gözükmesi için uzun kenarı
ile kısa kenarı arasındaki orandır. Buna benzer olarak, bir doğru parçasının
ikiye ayrıldığında göze en hoş gelen ikiye ayrılma oranıdır. Altın oran, sadece
MEHMET FİDAN
dikdörtgen ve doğru için değil, neredeyse
tüm geometrik cisimler ve yapılar için
kullanılabilir.
►
►
►
►
►
Fibonacci Dizisi ve Altın Oran
FİBONACCİ KİMDİR?
Orta çağın en büyük
matematikçilerinden biri olarak kabul
edilen Fibonacci İtalya'nın ünlü Pisa
şehrinde doğmuştur. Çocukluğu
babasının çalıştığı Cezayir'de geçmiştir.
İlk matematik eğitimini Müslüman bilim
adamlarından almış ve İslam aleminin
kitaplarını incelemiş ve çalışmıştır.
Avrupa'da Roma rakamları kullanılırken
ve sıfır kavramı ortalarda yokken
Leonarda Arap rakamlarını ve sıfırı
öğrenmiştir.
MEHMET FİDAN
Tabiatta çok fazla karşılaşılan Fibonacci
sayı dizisi bu mantıkla elde edilmektedir.
Dizi şöyledir: 1, 1, 2, 3, 5, 8, 13, 21, 34,
55… Dizinin ilerleyen sayılarında alınan bir
terimin bir önceki terime oranı altın orana
yakınlaşmaktadır. Bu dizi deniz kabuğu
spirallerinin oranlarını ve ayçiçeğindeki
çekirdeklerin dizilişini belirler.
MEHMET FİDAN
ALTIN ORAN = 1,618
55 / 34 =1,617
89 / 55 = 1,618
144 / 89 = 1,618
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618
MEHMET FİDAN
ALTIN ORAN VE İNSAN
MEHMET FİDAN
Altın oran ve insanı incelemeden evvel
resimlerdeki renklerle insanda altın oranın
nasıl oluştuğunu anlayabilmek için, renklerin
anlamını görelim.
Öncelikle bir altın cetvel oluşturalım, ve
buna göre resimlerdeki altın oranı
inceleyelim.
MEHMET FİDAN
Altın cetvel oluşturmak için;
Şekildeki gibi öncelikle bir doğru parçasını ( beyaz )
altın oran oluşturacak şekilde iki parçaya [AB]'e
( mavi ) ve [AC]' ye ( sarı ) bölüyoruz. Ve aynı
mantıkla hareket ederek [AB] doğrusunu da iki
altın parçaya bölüyoruz ve bunu devam ettirerek
2. şekildeki doğruları elde ediyoruz.
MEHMET FİDAN
Kısaca ;
Mavi çizgi: Beyaz çizginin altın bölümü
Sarı çizgi: Mavi çizginin altın bölümü
Yeşil çizgi: Sarı çizginin altın bölümü
Pembe çizgi: Sarı çizginin altın bölümüdür.
MEHMET FİDAN
İnsan parmaklarında görülen altın oran;
Şekilde işaret parmağınızın her bölümü bir öncekinden
1,618...( yani altın oranın değeri ) kadar büyüktür ve
üstteki cetvele dikkat ederseniz her bölüm 2, 3, 5, 8 e
yani ardışık fibonacci sayılarına karşılık gelmektedir.
Şekilde pembe, yeşil, sarı ve mavi çizgiler altın oranı
gösterir.
MEHMET FİDAN
İnsan kolunda görülen altın oran;
Şekilde görüldüğü üzere elimizin, dirseğimizle bileğimiz
arasında kalan bölgeye oranı 1,618 dir. ( beyaz çizginin
mavi çizgiye oranı )
MEHMET FİDAN
İnsan yüzünde görülen altın oran;
Şekildeki resimde de gördüğünüz gibi kafa bir altın
dikdörtgenin içinde. Kulaklar arasındaki mesafe, gözle
üst dudak arasındaki, burnun altı ile çene arasındaki
mesafe (resimde mavi çizgi ile gösterilmiş) hep altın oran
içermektedir. Resmi incelerseniz daha başka altın oranlar
da görebilirsiniz. Bunlarda sarı ve yeşil çizgilerle
MEHMET FİDAN
gösterilmiştir.
DNA'da Altın Oran
Canlıların tüm fiziksel özelliklerinin depolandığı molekül de altın
orana dayandırılmış bir formda yaratılmıştır. yaşam için program
olan DNA molekülü altın orana dayanmıştır. DNA düşey
doğrultuda iç içe açılmış iki sarmaldan oluşur. Bu sarmallarda her
birinin bütün yuvarlağı içindeki uzunluk 34 angström genişliği 21
angström'dür. (1 angström;MEHMET
santimetrenin
yüz milyonda biridir)
FİDAN
21 ve 34 art arda gelen iki Fibonacci sayısıdır.
ALTIN ORAN VE HAYVAN
MEHMET FİDAN
Penguendeki altın oran;
Şekilde penguenin farklı gösterilen bölgeleri
arasında altın oran görülmektedir
MEHMET FİDAN
Kelebekteki altın oran;
Şekildeki kelebeğin hem eninde hem boyunda
gösterilen delikler arasında altın oran
görülmektedir.
MEHMET FİDAN
YUNUSTAKİ ALTIN ORAN;
Şekilde yunusta boyunda burnu ve
kuyruğu arasındaki bölgede, kuyruk
bölgesinde enine ve de süzgeç kısmında
altın oran görülür.
MEHMET FİDAN
Deniz kabuğundaki altın oran;
Şekildeki deniz kabuğunda farklı renklerle
gösterilmiş bölgelerdeki altın oranı fark edebildiniz
mi?
MEHMET FİDAN
MEHMET FİDAN
Şaşırtıcıdır ki karıncalardada bu orana
rastlanır resimde görünen organaller
arasındaki oranlar altın orandır. pembenin
yeşile sarının yeşile ... oranları altın orandır.
MEHMET FİDAN
MEHMET FİDAN
ALTIN ORAN VE BİTKİLER
MEHMET FİDAN
Eğer bir bitkiyi dikkatle incelerseniz fark edersiniz ki,
yapraklar ,hiç bir yaprak alttaki yaprağı kapamayacak şekilde
dizilmiştir. Bu da demektir ki, her bir yaprak güneş ışığın eşit
bir şekilde paylaşıyor ve yağmur damlaları bitkinin her bir
yaprağına değebiliyor.
Bir bitkinin sapındaki yaprakların, bir ağacın dallarının
üzerinde hemen her zaman Fibonacci sayıları bulursunuz.
Eğer yapraklardan biri başlangıç noktası olarak alınırsa ve
bundan başlayarak, aşağıya ya da yukarıya doğru, başlangıç
noktasının tam üstünde veya altında bir yaprak buluncaya
kadar yapraklar sayılırsa bulunan yaprak sayısı farklı bitkiler
için değişik olacaktır ama her zaman bir Fibonacci sayısıdır.
MEHMET FİDAN
Mesela, üstteki resimde en baştaki dalı incelersek, başlangıç
noktası olarak 1 numaralı yaprağı alırsak, kendisiyle aynı
yönde bir başka yaprakla karşılaşabilmemiz için 3 defa saat
yönünde bir dönüş yapmamız gerekir ve bu esnada 5 tane
yaprak sayarız. Eğer bu dönüşü saat yönünün tersinde
yaparsak 2 tane dönüş gerekecektir. Ve 2, 3, 5 ardışık
Fibonacci sayılarıdır.
Üstteki resimde yer alan dalı incelediğimizde ise 8 yaprak
üstünden geçtiğimiz 5 tane saat yönünde dönüş yaparız.
Saat yönünün ters istikametinde ise bu dönüş sayısı 3
olacaktır.
3, 5, 8 ise ardışık Fibonacci sayılarıdır. Ardışık Fibonacci
sayılarının birbirine oranı altın orana yaklaştığından
bahsetmiştik. Demek oluyor ki bitkinin yapraklarının çıkışında
bile altın oran görülür. Bunu üsteki bitki için şöyle
deyazabilirsiniz. 3/5 (saat yönündeki dönüş başına yaprak
sayısı)
MEHMET FİDAN
AYÇİÇEĞİ VE ALTIN ORAN
ALTIN ORANI ayrıca çiçeklerin
tohumlarında da görülebilir. Eğer
bir papatyanın ve ya bir
ayçiçeğinin çiçek kısmını
büyütseniz muhtemelen yandaki
resme benzer bir görüntü elde
edersiniz.
Eğer şekildeki modelde, saat
yönünde olan ve saat yönünde
olmayan sarmalları sayarsanız, 21
ve 34 sayılarını elde edersiniz ki
bu sayıların oranı altın oran olan
sayısına eşittir.
MEHMET FİDAN
Altın Oranı sadece ayçiçeklerinde veya
papatyalarda değil, bir kıvırcığın yapraklarında
bir ananas veya kozalakların kat kat
kabuklarında, soğanın katmanları arasında da
rastlayabilirsiniz.
İşte aşağıda kozalaklar ALTIN ORANI çok
açık bir şekilde gösterirler. Kırmızı ve yeşil
spiralleri sayın ve oranlayın
altın oran
kırmızı=13
yeşil =8
MEHMET FİDAN
ALTIN ORAN VE SANAT
Türk mimarisi ve sanatı da altın orana ev sahipliği
yapmıştır. Mimar Sinan'ın da bir çok eserinde bu altın oran
görülmektedir. Mesela Süleymaniye ve Selimiye Camileri'nin
minarelerinde bu oran görülmektedir Türk mimarisi ve
sanatı da altın orana ev sahipliği yapmıştır: Konya'da
Selçukluların inşa ettiği İnce Minareli medresenin taç kapısı,
İstanbul'daki Davut Paşa Camisi, Sivas'ta
Mengüçoğulları'dan günümüze miras kalan Divriği Külliyesi
genel planlarından kimi ayrıntılarına
dek f ile iç içe bir
MEHMET FİDAN
görünüm sunar.
Eski Yunanda da altın dikdörtgen bir çok sanat dalında
kullanılmıştır. Bunlardan bir tanesi de Atina'daki Partenon
'dur. Partenon İ.Ö. 430 ve ya 440 yıllarında Athena adlı
tanrıça için yapılmıştır. Tapınağın orijinal planları elimizde
olmasa da , tapınağın uzunluğu genişliğinin kök 5 katı olan
bir dikdörtgen üzerine inşa edildiği gözükmektedir. Ayrıca
aşağıdaki resimlerde görebileceğiniz gibi tapınakta daha
başka altın dikdörtgenlerde göze çarpmaktadır. (altın
FİDAN
dikdörtgen kenarları oranıMEHMET
altın
oran olan dikdörtgenlerdir.)
Altın oran sadece
Yunanlılar tarafından
kullanılmamıştır.
Mısır'daki Keops
piramidinde, Paris'in
ünlü Notre Dame
Katedralinde altın
oranın izlerini görmek
mümkündür.
MEHMET FİDAN
Eski Mısırlılar inşa ettikleri piramitlerde de altın oranı
olduğu saptanmıştır. Piramitlerin tabanı ile yüksekliği
arasındaki oranın 0.618 ( yani altın oranın değeri )olduğu
görülmüştür. Ayrıca piramitlerin dizilimi yani bulundaki
bölgeye yerleşimi de bize altın spirali verir. Bu da şekilde
aşağıdaki şekilde açıkça gösterilmiştir.
Sonuç olarak piramitler hem kendi içerisinde hem de
birbirleri arasında altın oran içermektedir
MEHMET FİDAN
ALTIN ORAN VE LEONARDO da VİNCİ
Mona Lisa'nın başının
etrafına bir dikdörtgen
çizdiğinizde ortaya çıkan
dört kenar bir altın
dikdörtgendir. Bu
dikdörtgeni, göz hizasında
çizeceğiniz bir çizgiyle ikiye
ayırdığınızda yine bir altın
oran elde edersiniz.
Resmin boyutları da altın
oran oluşturmaktadır.
MEHMET FİDAN
Bu tamamlanmamış
resimde, aziz altın
dikdörtgenin içine
sığmaktadır. Bunun bir
tesadüf olmadığı,
Leonardo da Vinci'nin
matematiğe olan ilgisini
resme taşıdığına
inanılmaktadır.
MEHMET FİDAN
Burada Leonardo
da Vinci'nin insan
vücudunda altın oranı
gösteren tablosudur
MEHMET FİDAN
ALTIN SÖZLÜK
BURADA ;
► Altın Dikdörtgen
► Altın Üçgen
► Altın Spiral
ÖRNEKLERİ GÖSTERİLECEKTİR
MEHMET FİDAN
ALTIN DİKDÖRTGEN
Altın oranı içeren ve de uzun kenarı komşu kısa
kenarla kare elde edecek şekilde parçalandığında,
dikdörtgenin kalan kısmında altın oran içeren
kendisine benzer dikdörtgenler elde edilen
dörtgendir. Şekilde altın dikdörtgenin oluşumu
verilmiştir. Şekilde görüldüğü gibi oluşan
dikdörtgenlerde uzun kenarla kısa kenar arasında
altın oran vardır.
MEHMET FİDAN
ALTIN ÜÇGEN
Tepe açısı 36° olan
ikizkenar üçgene Altın
Üçgen denir. Çünkü,
uzun kenarın taban
kenara oranı altın oranı
verir.
A
D
AB = q = 1 + 5
BC
2
B
C
MEHMET FİDAN
► Altın
spiral: Altın
dikdörtgenin içinde şekildeki
gibi çizilen spirale altın spiral
denir.
MEHMET FİDAN
ALTIN ORAN KULLANILAN DİĞER
YERLER
Kar Kristallerinde Altın Oran
Uzayda Altın Oran
Evrende, yapısında altın oran barındıran birçok spiral galaksi
bulunur.
MEHMET FİDAN
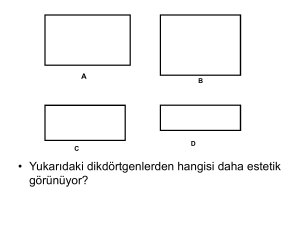
Bir grup insana birçok üçgen ve dikdörtgen
içerisinden bir üçgen ve bir dikdörtgen
seçmeleri istendiğinde büyük çoğunluğunun
altın üçgeni ve altın dikdörtgeni seçtikleri
görülmüştür.
► Ayrıca otomotiv devi TOYOTA otomobil
tasarımında altın oranı kullanmıştır.
►
MEHMET FİDAN