Sağ el kuralı: Vektörün Dik bileşenleri: Birim vektör: Şiddeti 1 birim

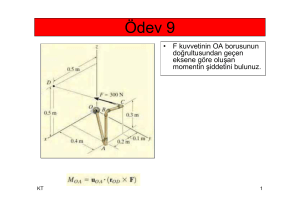
Kaynak: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall
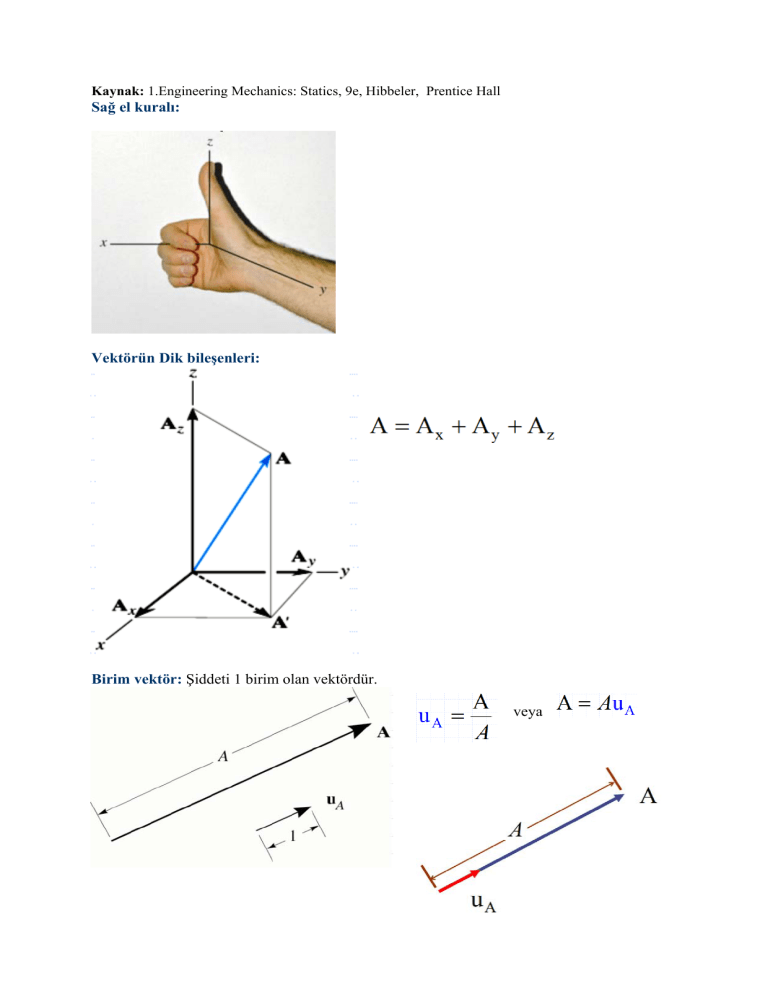
Sağ el kuralı:
Vektörün Dik bileşenleri:
Birim vektör: Şiddeti 1 birim olan vektördür.
veya
Kartezyen birim vektörler:
i: x-yönündeki birim vektör
j: y-yönündeki birim vektör
k: z-yönündeki birim vektör
Kartezyen vektör gösterimi:
Şiddet:
Burada α, β ve γ A vektörünün doğrultu açılarıdır. Bunlar A
vektörünün referans eksenlerle yaptığı açıdır. Bu açıların
kosinüsleri doğrultman kosinüs adını alır.
Kartezyen vektörlerin toplanması ve çıkarılması:
Kartezyen bileşenler yardımı ile bileşke bulma:
Örnek Problem 3:
Yandaki bağlantı F1 ve F2 kuvvetlerinin
etkisi
altındadır.
Bu
kuvvetlerin
bileşkesinin yön ve şiddetini bulunuz
ÇÖZÜM
Örnek Problem 4:
Kancaya uygulanan iki kuvvetin bileşkesi
+y yönünde 800 N ise F2 vektörünün
doğrultman kosinüslerinin bulunuz.
ÇÖZÜM:
Konum vektörü:
Rölatif konum vektörü:
Bir doğru boyunca kuvvet:
Örnek Problem 4:
Şekildeki çocuk ipi 70 N luk bir kuvvetle çekiyor. A noktasına
etkiyen kuvveti kartezyen koordinatlarda ifade ediniz.
Vektörün doğrultusunu bulunuz.
ÇÖZÜM:
Örnek Problem 4:
Şekilde görülen tavan B ve C noktalarına bağlanmış ipler
yardımı ile duvarda bulunan A noktasındaki kancaya
bağlanmıştır. FAB=100 N ve FAC=120 N olduğuna göre A
nokrasına etkiyen bileşke kuvveti bulunuz.
ÇÖZÜM:
Skaler Çarpım:
-Özellikleri:
1.
2.
3.
-Kartezyen vektörlerde:
Skaler çarpımın sonucu vektörel olamaz.!!!!
-Skaler çarpımın kullanılış yerleri:
1. İki vektör arasındaki açı değerinin bulunması
Eğer A.B=0 ise bu iki vektör birbirine diktir.
2. Bir vektörün bir doğruya paralel ve dik yöndeki bileşenlerinin bulunması. (Bu durumda
paralel bileşen izdüşüm adını alır.)
A vektörünün bir doğru boyunca izdüşüm vektörü:
Örnek Problem 5:
B noktasına etkiyen F kuvvetinin AB
doğrusuna paralel ve dik bileşenlerini bulunuz.
ÇÖZÜM:
Örnek Problem 6:
a) F kuvveti ile AB
doğrusu arasındaki açı
değerini
b) F kuvvetinin AB ye
paralel ve dik yöndeki
bileşenlerin şiddetlerini
bulunuz.
ÇÖZÜM: