üçgenler - WordPress.com

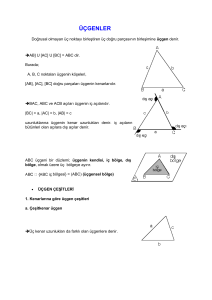
Hayatımızdaki Üçgenler
ÜÇGENLER
ÜÇGENLER
 Üçgen Nedir?
 Üçgen Çeşitleri
 Üçgen Çizilebilmesi İçin
 Bir Üçgenin Yardımcı Elemanları
 Üçgenin Kenarları Arasındaki Bağıntılar
 Üçgenin Kenar Uzunluklar ve Açıları
Arasındaki Bağıntılar
 Üçgenin Açıları Arasındaki Bağıntılar
 Kaynakça
Üçgen Nedir?
Bir doğru üzerinde
olmayan (doğrusal
olmayan) A,B,C gibi
üç noktanın
birleşiminden oluşan
çokgene üçgen denir.
Üçgen Çeşitleri
1.Kenarlarına Göre Üçgenler
a)Eşkenar Üçgen
b)İkizkenar Üçgen
c)Çeşit Kenar Üçgen
2.Açılarına Göre Üçgenler
a)Dar Açılı Üçgen
b)Geniş Açılı Üçgen
c)Dik Açılı Üçgen
1.Kenarlarına Göre Üçgenler
Eşkenar üçgen İkizkenar üçgen Çeşitkenar üçgen
a)Eşkenar Üçgen:
Üçgenin kenarlarının hepsi eşit
olan üçgene “Eşkenar Üçgen” denir.
Bir eşkenar üçgenin iç açıları 60º `dir.
b)İkizkenar Üçgen:
Üçgenin kenarlarının iki tanesi eşit olan
üçgene “İkiz Kenar Üçgen” denir. Bir
ikizkenar üçgenin, taban açıların ölçüleri
birbirine eşittir.
c)Çeşit Kenar Üçgen:
Üçgenin kenarlarının
hepsi farklıysa bu üçgene
“Çeşit Kenar Üçgen”
denir.
2.Açılarına Göre Üçgenler
Y
X
Z
X
X<90 º Y<90 º Z<90 º
Dar açılı üçgen
X>90 º
Geniş açılı üçgen
.
X=90 º
Dik üçgen
a)Dar Açılı Üçgen:
Üçgenin açılarından her birinin ölçüsü
90º`den küçük olan üçgene “Dar Açılı
Üçgen” denir.
b)Geniş Açılı Üçgen:
Bir açısı 90º`den büyük olan üçgene “Geniş
Açılı Üçgen” denir.
c)Dik Açılı Üçgen:
Açılarından birisi dik açı (90 º) olan üçgene
“Dik Açılı Üçgen” denir.
Üçgen Çizilebilmesi İçin:
Üç kenar uzunluğu,iki kenar uzunluğu
ile bu kenarlar arasındaki açının ölçüsü
veya bir kenarının uzunluğu ile iki açının
ölçüsü verilen bir üçgen cetvel, açıölçer
ve pergel kullanılarak çizilir.
SONRAKİ
İki kenarı ve bir açısı bilinen üçgen çizilmesi
B
xº
A
C
SONRAKİ
Bir kenarı ve iki açısı bilinen üçgen çizimi
A
B
C
Bir Üçgenin Yardımcı Elemanları
1) Üçgenin Yüksekliği
2.Üçgenin Kenar Ortayları
3.Üçgenin Açı Ortayı
1) Üçgenin Yüksekliği: Üçgenin bir
köşesinden karşı tarafa indirilen, köşe
ile kenar arasında kalan dik doğru
parçasına “Üçgenin Yüksekliği” denir.
İndiği yerde 90 derecelik açı oluşur.”h”
ile gösterilir.Yükseklikler dik üçgenlerde
dik açının köşesinde, geniş açılı
üçgenlerde ise üçgenin dışında
kesişirler.
SONRAKİ
Üçgenlerin yükseklikleri
h
h
2.Üçgenin Kenar Ortayları: Üçgenin
bir köşe ile bu köşenin karşısındaki
kenarın orta noktasını birleştiren doğru
parçasına “Üçgenin Kenar Ortayı”
denir.Üçgenin iç bölgesinde kalır. “v” ile
gösterilir.
A
v
B
V
C
3.Üçgenin Açı Ortayı: Üçgenin
açılarını iki eş açıya bölen doğru parçasına
“Üçgenin Açı Ortayı” denir. ” n ” ile
gösterilir.
A
n
B
N
C
Üçgenin Kenarları Arasındaki
Bağıntılar
Bir üçgende iki kenarın
uzunlukları toplamı üçüncü kenar
uzunluğundan büyük; iki kenar
uzunluğunun farkı, üçüncü kenarı
uzunluğunda küçüktür.Bu bağıntıya
üçgen eşitsizliği denir.
SONRAKİ
Üçgen eşitsizliği A
lb-cl<a<b+c
la-cl<b<a+c
la-bl<c<a+b
b
c
B
a
C
Üçgenin Kenar Uzunluklar ve
Açıları Arasındaki Bağıntılar
Bir üçgende büyük açı karşısında
uzun kenar, küçük açı karşısında kısa
kenar vardır. Dik üçgendeki en uzun
kenar 90 derecenin karşısındaki
hipotenüstür.Hipotenüs uzunluğu dik
kenar uzunluklarından büyüktür.
SONRAKİ
Üçgenin Kenar Uzunluklar ve
Açıları Arasındaki Bağıntılar
A
A
c
B
b
a
m(A)<m(B)<m(C)
a>b>c
b
c
C
B
a
b>a ve b>c
C
Üçgenin Açıları Arasındaki
Bağıntılar
Bir üçgendeki iç açıların ölçüleri
toplamı 180 derecedir.
Bir üçgenin dış açılarının ölçüleri
toplamı 360 derecedir.
SONRAKİ
Bir üçgende, bir köşedeki iç açı ile
dış açının toplamı 180º`dir.
Bir üçgende bir dış açının ölçüsü,
kendisine komşu olmayan iki iç açının
ölçüleri toplamına eşittir.
Bir üçgenin dış açılarının ölçüleri toplamı 360
derecedir.
A
y+z
x
m(A)+m(B)+m(C)=180º
x+y+z=180º
2(x+y+z)=360º
m(A’)+m(B’)+m(C’)=360º
B
y
z
x+z
C
x+y
Bir üçgendeki iç açıların ölçüleri toplamı 180
derecedir.
A
Y
X
Z
m(A)+m(B)+m(C)=180º
Y
X
C
B
X+Y+Z=180º
Bir üçgende, bir köşedeki iç açı ile dış açının
toplamı 180º`dir.
x+x’=180º
y+y’=180º
z+z’=180º
A
x’
x
y’
B
y
z
C
z’
Bir üçgende bir dış açının ölçüsü,
kendisine komşu olmayan iki
iç açının ölçüleri toplamına eşittir.
A
Z’=X+Y
X’=Y+Z
Y’=X+Z
X
Z’
Y
m(A’)=m(B)+m(C)
m(B’)=m(A)+m(C)
m(C’)=m(A)+m(B)
X
B
Z’
Z
C
KAYNAKÇA
YAZILAR İÇİN:
www.matematikcifatih.com
Fatihler.net
Matematik.TC
tr.wikipedia.org/wiki/Üçgen
RESİMLER İÇİN:
Google Görseller
BENİ DİNLEDİĞİNİZ
İÇİN TEŞEKKÜRLER
SAYGILARIMLA…