FİZİK

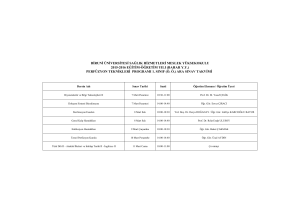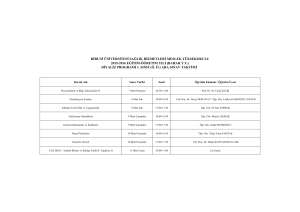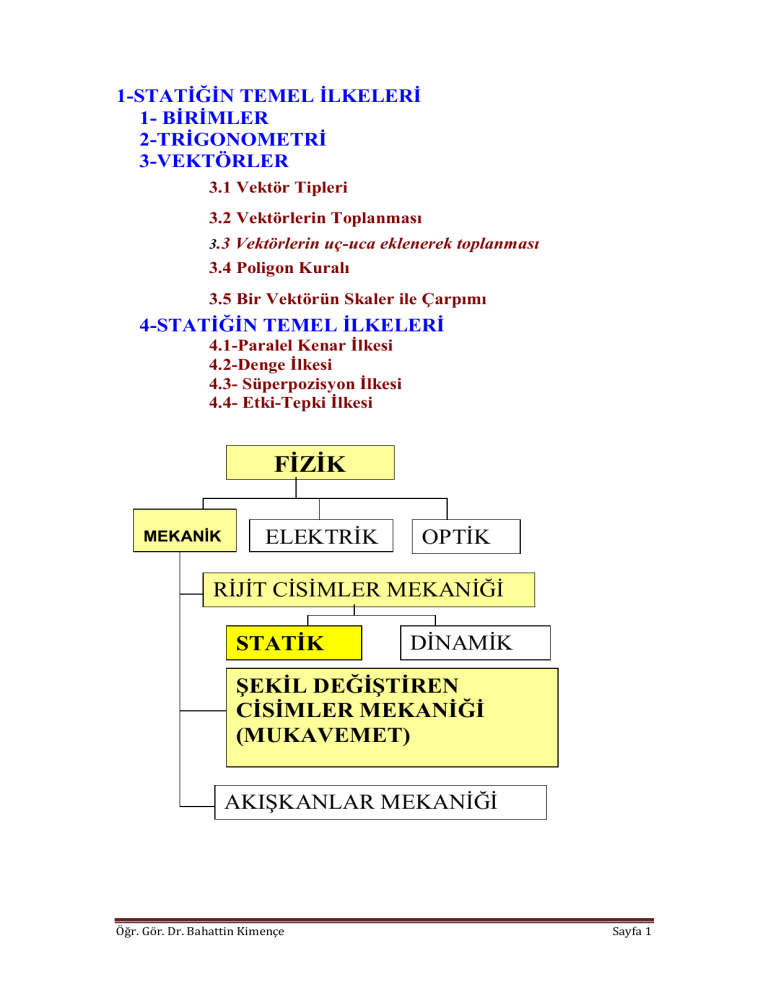
1-STATİĞİN TEMEL İLKELERİ
1- BİRİMLER
2-TRİGONOMETRİ
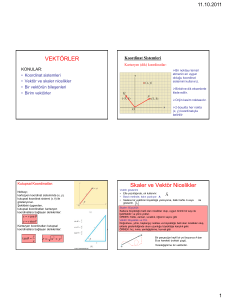
3-VEKTÖRLER
3.1 Vektör Tipleri
3.2 Vektörlerin Toplanması
3.3 Vektörlerin uç-uca eklenerek toplanması
3.4 Poligon Kuralı
3.5 Bir Vektörün Skaler ile Çarpımı
4-STATİĞİN TEMEL İLKELERİ
4.1-Paralel Kenar İlkesi
4.2-Denge İlkesi
4.3- Süperpozisyon İlkesi
4.4- Etki-Tepki İlkesi
FİZİK
MEKANİK
ELEKTRİK
OPTİK
RİJİT CİSİMLER MEKANİĞİ
STATİK
DİNAMİK
ŞEKİL DEĞİŞTİREN
CİSİMLER MEKANİĞİ
(MUKAVEMET)
AKIŞKANLAR MEKANİĞİ
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 1
-Rişit Cisim (Statik); kuvvet etkisinde şekil değiştirmeyen
-Esnek (şekil değiştiren) Cisim (Mukavemet)
P
P
P
P
L
L
Rişit Cisim
L
Esnek Cisim
1- BİRİMLER
Uzunluk
Kuvvet
Kütle
Ağırlık ,W=mg
SI
1m
N, kg.m/s2
1kg
N, g=9.81m/s2
39.37 inç
35.27 ons
Birimler
Yoğunluk (kütle/birim hacim)
t/m3
Ağırlık W=mg
kilonewton (kN)
Birim Ağırlık
Gerilme
kN/m3
kilopascals (kPa)
B
ntities
Öğr. Gör. Dr. Bahattin Kimençe
asi
US
3.281 foot
pound (lb)
2.205 slug(lb.s2/ft)
pound, g=32.2ft/s2
c
Sayfa 2
Birimler:
Kütle
Uzunluk
Kuvvet
Zaman
SI
Kilogram
Metre
Newton
saniye
M
L
F
T
kg
m
N
s
U.S.
slug
feet
pound
saniye
ft
lb
sec
Birimler arasındaki dönüşümde F=ma bağıntısı temel alınmıştır.
1 N = (1 kg) (1 m/s2)
1 lb= (1 slug) (1 ft/sec2 )
Örneğin kütlenin U.S. sisteminde hesabı: Kütle, m, parçacığın ağırlığı W=10 lb ve
yertçekim ivmesi g=32.2 ft/sec2 ise, kütle:
W
10
m

slugs
g 32.2
Birim dönüşümleri:
l lb
1 slug
1 ft
1 ft
1 mile
1 kip
1 ton
=
=
=
=
=
=
=
4.4482 N
14.5938 kg
0.3048 m
12 in
5,280 ft
1,000 lb
2,000 lb
1MPa=1N/mm2=10kg/cm2
1kN/m2=10kg/m2
1 kPa = 1 kN/m2
2-TRİGONOMETRİ
Dik Üçgende
1. Hipotenüs C2 = A2 + B2
2. Sin Ø = B/C
3. Cos Ø = A/C
4. Tan Ø = B/A
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 3
Herhangi bir üçgende
1. Kosinüs Teoremi:
C2 = A2 + B2 - 2AB cos c
2. Sinüs Teoremi:
(A/sin a) = (B/sin b) = (C/sin c)
A,B,C kenar uzunluklar, a, b, c kenarın karşısındaki açılar.
Bazı Trigonometri bağıntıların özellikleri
3-VEKTÖRLER

Scaler: herhangi bir cismin miktarı, veya ölçüsü, (zaman, yoğunluk,
sıcaklık,kütle)

Vektor: Şiddeti, yönü ve uygulama noktası olan fiziksel büyüklük, (hız, ivme
moment, kuvvet)
3.1 Vektör Tipleri
(1). Bir noktaya bağlı veya sınırlandırılmış VEKTÖR
(2). Serbest VEKTÖR (Hareket edebilen vector)
(3). Kayan VEKTÖR (Kuvvet doğrultusunda haraket edebilen vector)
(4). Eşit VEKTÖRLER (Şiddet ve yönleri aynı olan vektörler)
(5). Negatif VEKTÖRLER (Şiddetleri aynı yönleri ters olan vektörler).
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 4
3.2 Vektörlerin Toplanması
Vektörlerin toplanmasıiçin dört temel metot vardır.
a..) Paralel kenar metodu
b..) Üçgen metodu
c..) Poligon metodu
d..) Analitik metot
Vektörlerin Çıkarılması
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 5
Vektörlerin toplama işleminde değişim özelliği vardır.
Vektörlerin toplamında şiddetleri toplanamaz.
Bileşke vektör
3.3 Vektörlerin uç-uca eklenerek toplanması
Paralel kenar kuralıyla bir VEKTÖR, diğer VEKTÖRÜN ucuna kaydırılarak,
BİLEŞKE VEKTÖR elde edilebilir.
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 6
Bu metoda da değişim özelliği vardır.
3.4 Poligon Kuralı
Aynı düzlemde ikiden fazla vector uç-uca eklenerek bileşkeleri elde edilebilir.
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 7
3.5 Bir Vektörün Skaler ile Çarpımı
P vektörünün n skaleri ile çarpımı, o vektörün şiddetini n katı kadar
büyütür.
Not: Eğer n negative ise P vektörünün yönü değişir
3.5 Vektör Bileşenleri
İki vektörün bileşeni bu iki vektörün toplanmasıyla elde edilir.
P ve Q vektörleri biliniyor. F bileşke vektörü hesaplanıyor.
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 8
Özel durumlar: (F vektörü biliniyor)
P ve Q vektörlerinin şiddetleri parallel kenar kuralından hesaplanabilir..
Kartezyen koordinatlarda (x,y) vektörler
Analitik Metot
Bir vektörü(birbirine dik doğrultularda) kartezyen koordinat
sisteminde iki bileşene ayırmak mümkündür. Vektörün eksenlerden
birisi ile yaptığıaçıθise .Vektör sin(θ) ve cos(θ) ile çarpılarak dik
koordinatlardaki izdüşümübulunabilir.
• x ve y eksen sisteminde her vektörün şiddeti ve yönü belirlenir
• x ve y eksenlerinde birim vektörler olan, ” i ve j ile gösterilir.
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 9
FRX = -F1X – F2X
FRY = -F1Y + F2Y
Bileşke vektörün şiddeti ve açısı
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 10
FR  FRx2  FRy2
ÖRNEK
Şekildeki kuvvet sisteminde bileşke kuvvetin şiddetini ve yönünü hesaplayınız
Çözüm
F1 = { 15 sin 40° i + 15 cos 40° j } kN
= { 9.642 i + 11.49 j } kN
F2 = { -(12/13)26 i + (5/13)26 j } kN
= { -24 i + 10 j } kN
F3 = { 36 cos 30° i – 36 sin 30° j } kN
= { 31.18 i – 18 j } kN
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 11
i ve j bileşenleri toplanır
FR = { (9.642 – 24 + 31.18) i + (11.49 + 10 – 18) j } kN
= { 16.82 i + 3.49 j } kN
FR = ((16.82)2 + (3.49)2)1/2 = 17.2 kN
= tan-1(3.49/16.82) = 11.7°
4- STATİĞİN TEMEL İLKELERİ
4.1-Paralel Kenar İlkesi
Bir kuvvet, diğer kuvvetin ucuna paralel olarak kaydırılarak bileşke kuvvet
elde edilebilir.
4.2-Denge İlkesi
Zıt yönlü ve eşit şiddetli iki kuvvetin etkisindeki bir cisim dengededir.
P
P
4.3- Süperpozisyon İlkesi
Her hangi bir kuvvet sistemine, eşit ve zıt yönlü iki kuvvetin etkimesiyle, söz
konusu kuvvet sisteminin özelliği değişmez.
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 12
F
=
-F
P
P
4.4- Etki-Tepki İlkesi
Bir cismin temas ettiği yüzeylerde, temas yüzeyine teğet düzlemine dik
doğrultuda tepki kuvveti oluşur.
A
W
B
RA
RB
Şekildeki silindir şeklindeki cismin ağırlığı W olduğuna
göre, temas yüzeylerindeki tepki kuvvetlerini bulunuz.
W= 25 (a+e)kN
tan1=3/4, tan 2= 4/3
2
1
'Çözüm
w = 25 * (a + e)
R1 = 15 * w / 25
R2 = 20 * w / 25
Şekildeki W ağırlığındaki bloğun B değme
yüzeyindeki yatay tepkisi Ax ve Bx nedir.
sin 45  cos 45  2 / 2
A
B
W=(a+e) kN
Ağırlığı W olan şekildeki küre için, A
ve
B
noktalarındaki
değme
yüzeylerinde, x yönündeki kuvvetlerin
A
toplamı Ax + Bx =
45
A) 0
B) W
C) 2W D) W/2
45o
Öğr. Gör. Dr. Bahattin Kimençe
Sayfa 13
B
45
Rdc Pozisyon vektörü
Hangisidir
Şekildeki W ağırlığındaki bloğun A
değme yüzeyindeki yatay tepkisi Ax
nedir.
A
B
sin 45  cos 45  2 / 2
A) W
B) 0 C)
45o
Öğr. Gör. Dr. Bahattin Kimençe
2W D)
2
W
2
Sayfa 14