BOLUM-3sc

BÖLÜM III
Örnek 1.
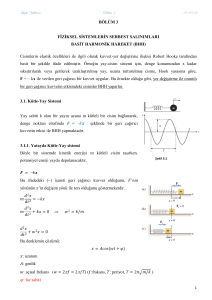
𝑚 kütleli bir cisim, yay sabiti 𝑘 olan homojen yaylara şekillerdeki gibi asılmıştır. Her iki asılma
biçimi için periyot değerlerini bulunuz.
Çözüm:
a) 𝐹 = −(𝑘1 𝑥 + 𝑘2 𝑥) = −2𝑘𝑥 , (𝑘1 = 𝑘2 = 𝑘)
𝑑2𝑥
𝑚 2 + 2𝑘𝑥 = 0
𝑑𝑡

𝐹
𝐹
1
2
b) 𝑥1 = 𝑘 ve 𝑥2 = 𝑘
𝐹
𝜔2 =
𝐹
2𝑘
,
𝑚
𝑇=
𝑘 +𝑘
𝑥 = 𝑥1 + 𝑥2 = − [𝑘 + 𝑘 ] = − [ 𝑘1 𝑘 2 𝐹] = −
1
2
𝑑2𝑥 𝑘
𝑚 2+ 𝑥=0
𝑑𝑡
2

1 2
𝜔2 =
𝑘
,
2𝑚
2𝜋
𝑚
= 2𝜋√
𝜔
2𝑘
2𝐹
𝑘
𝑇=
,
(𝑘1 = 𝑘2 = 𝑘), 𝐹 = −
𝑥𝑘
2
2𝜋
2𝑚
= 2𝜋√
𝜔
𝑘
Örnek 2.
Bir platform düşey yönde saniyede 10⁄𝜋 titreşim ve 5 cm genlikle BHH
yapmaktadır. Küçük bir blok platform üzerine konuyor.
a) Blok hangi noktada platformu terk eder?
b) Blok, platformun ulaştığı en üst noktadan ne kadar yukarıya
yükselecektir? (French-p3.2)
Çözüm:
a) Sistem BHH yaptığı için
𝑦(𝑡) = 𝐴𝑠𝑖𝑛𝜔𝑡
yazabiliriz. Bu durumda sistemin ivmesi
olacaktır. Platformun ivmesi yer çekim ivmesine eşit olduğunda blok ile platformun teması
kesilir. Bu andaki konuma 𝑦0 diyelim.
1
b) Blokun platformdan ayrıldığı anda 𝑦0=2,5 cm olacaktır. Bu anda
0,025 𝑚 = 0,05𝑠𝑖𝑛20𝑡
yazabiliriz. Buradan
bulunur. Blokun platformdan ayrıldığı andaki hızına 𝑣0 diyelim, 𝑣 = 𝐴𝜔𝑐𝑜𝑠𝜔𝑡
Bağıntısı kullanılarak
elde edilir. Blok platformdan ayrıldığı anda 𝑣0 hızı ile yukarı doğru atılmış cisim gibi davranır. Konumun
zamana bağlı değişiminin
bağıntısı ile verildiğini biliyorsunuz. Blok en yüksek noktaya çıktığında hızı sıfır olacaktır,
Bu durumda
sonucu elde edilir ve buradan blokun çıkabileceği en yüksek noktanın koordinatı için
değeri bulunur. Platformun çıkabileceği yükseklik en fazla 𝐴 = 0,05 𝑚 = 5 𝑐𝑚 genliği
kadar olur. Bu durumda blok en yüksek noktaya ulaştığında platform ile arasındaki mesafe
ise 6,25 − 5,00 = 1,25 cm olur.
Örnek 3.
Uzunluğu L olan homojen bir çubuk belli bir amaç için
uzunluğunun
2/3’ünden şekildeki gibi asılmış halde iken titreşim hareketi
yapmaktadır.
L/3

d
K
Çubuğun küçük titreşimlerinin periyodunu bulunuz. (Frenchp3.3)
𝐹 = 𝑚𝑔𝑠𝑖𝑛𝜃
𝐹 = 𝑚𝑔𝑐𝑜𝑠𝜃
𝑚𝑔
2
Çözüm:
Problemin çözümüne uygun bir şekil yukarıda verilmiştir.
Şekilde KM’nin asılma noktasına uzaklığı d ile gösterilmiştir. Bu şekilden
yazabiliriz. Çubuğun ağırlığı KM’ine etkir. Bu kuvvetin çubağa dik bileşeni olan 𝐹 = 𝑚𝑔𝑠𝑖𝑛𝜃
kuvveti çubuğu döndürmeye çalışacaktır. Bu kuvvetin
uyguladığı tork (𝜏) için
olacaktır. Burada eksi işareti torkun geri çağırıcı olduğu anlamındadır. Dönen cisimleri incelerken
tork ile eylemsizlik momenti (I) arasındaki ilişkinin
𝜏 = 𝐼𝛼
bağıntısı ile verildiğini biliyorsunuz. Burada 𝛼 açısal ivmedir. Bu durumda tork için
ifadesi yazılabilir.
veya
yazılabilir. Küçük titreşimlerde 𝑠𝑖𝑛𝜃 ≅ 𝜃 alınabilir ve bu durumda yukarıdaki eşitlik
şeklinde yazılabilir. Burada
alınarak
yazılabilir. Bu denklem daha önce incelediğimiz BHH’in denklemi ile aynıdır.
Buradan periyod için
3
yazabiliriz. Bu çubuğun dönme eksenine göre eylemsizlik momentini paralel eksen teoremini
kullanarak
yazılabilir. Bu değer yukarıda verilen periyot ifadesinde kullanılırsa
sonucu elde edilir. Periyodun kütlesinden bağımsız olduğuna dikkat ediniz.
Örnek 4.
Yarıçapı R ve kütlesi M olan homojen bir disk, uzunluğu L ve kütlesi m olan homojen bir çubuğun
ucuna bağlıdır. Çubuğun diğer ucu, sürtünmesiz bir mile asılıdır. Bu sistemin küçük titreşimler
yapması durumunda periyodunu bulunuz.
Çözüm:
Problemin çözümüne uygun bir şekil yanda verilmiştir.
𝑚𝑔𝑠𝑖𝑛𝜃 ve 𝑀𝑔𝑠𝑖𝑛𝜃 kuvvetleri sistemi P noktası etrafında döndürmeye
çalışacaktır. Geri çağırıcı tork için
ifadesini yazabiliriz. Tork ile eylemsizlik momenti (I) arasındaki
ilişkinin
𝜏 = 𝐼𝛼
bağıntısı ile verildiğini biliyorsunuz. Burada 𝛼 açısal ivmedir. Bu
durumda tork için
ifadesi yazılabilir. Buradan
yazılır. Küçük titreşimlerde 𝑠𝑖𝑛𝜃 ≅ 𝜃 alınabilir ve bu durumda yukarıdaki
eşitlik
4
veya
Burada I eylemsizlik momenti için
ifadesini yazabiliriz. Bu durumda hareket denklemi
olacaktır. Burada
alınabilir ve periyot için
ifadesi yazılabilir.
Örnek 5.
Kütlesi m ve boyu L olan homojen ince bir çubuk, bir ucundan serbestçe dönecek şekilde, duvara
menteşelenmiştir. Çubuğun diğer ucu kütlesi ihmal edilebilen ve kuvvet sabiti k olan bir yaya şekildeki gibi
bağlıdır. Çubuk yatay durumdayken,
yayın boyu serbest haldekine göre 𝑦0
kadar uzamıştır. Daha sonra çubuğun yaya
bağlı ucu y kadar aşağı çekilip bırakılıyor.
Çubuğun basit harmonik hareket (BHH)
yapacağını, hareket denklemini yazarak
gösteriniz
ve
hareketin
titreşim
periyodunu bulunuz. Problemi çözerken y
ve ’nin küçük olduklarını kabul ediniz.
1
Çubuk için 𝐼𝑘𝑚 = 12 𝑚𝐿2 .
5
Çözüm:
Sistem denge durumundayken yayın boyunun 𝑦0 kadar
uzadığını kabul edelim.Bu durumda sistem dengede olduğuna
göre çubuk üzerine etki eden net tork sıfır olur.
𝐿
𝑚𝑔 = 𝑘𝑦0 𝐿
2
Yayı şekildeki gibi 𝑦 kadar aşağı çekip bırakırsak, yaya etki
edecek geri çağırıcı tork için
𝐿
𝜏 = 𝑚𝑔 − 𝑘(𝑦 + 𝑦0 )𝐿 = −𝑘𝑦𝐿
2
𝑦
Küçük salınımlar için
𝑠𝑖𝑛𝜃 ≅ 𝑡𝑎𝑛𝜃 ≅ 𝜃 ≅ 𝐿
 𝑦=
𝐿𝜃
𝜏 = −𝑘𝑦𝐿 ≅ −𝑘𝐿2 𝜃
𝑑2 𝜃

𝐼 𝑑𝑡 2 + 𝑘𝐿2 𝜃 = 0 
𝑑2 𝜃
𝑑𝑡 2
+
𝑘𝐿2
𝐼
𝜃=0
Çubuğun bir ucundan sabitlenerek döndürülmesi durumunda eylemsizlik momenti:
𝐿2
𝐿
𝐿
1
𝐼 = 𝐼𝑘𝑚 + 𝑀(2)2 = 𝑀 12 + 𝑀(2)2 = 3 𝑀𝐿2
Çubuğun açısal momentumu:
𝑘𝐿2
𝑤2 = 1
3
𝑀𝐿2
𝑘
= 3𝑚
𝑚
Periyot: 𝑇 = 2𝜋√3𝑘
Örnek 6.
Kütlesi 𝑀, yarıçapı 𝑅 olan bir tekerlek, şekildeki gibi bir ucu duvara bağlanmış
ve yay sabiti 𝑘 olan bir yayın diğer ucuna bağlı olarak yatay doğrultuda
kaymadan yuvarlanarak basit harmonik kareket yapmaktadır. (Yayın kütlesi
ihmal edilecek, tekerlek için 𝐼𝑘𝑚 = 𝑀𝑅 2 ).
Bu sistemin küçük genlikli titreşimler yapması durumunda periyodunu bulunuz. 𝑡 = 0 anında
tekerlek yayın denge noktasından (𝑥 = 0) itibaren sağa doğru bir tur hareket edecek şekilde
çekilerek serbest bırakılıyor. Tekerleğin kütle merkezinin 𝑥(𝑡) yer değiştirme ifadesini 𝑘, 𝑀 ve 𝑅
cinsinden elde ediniz.
Çözüm: I.Yol
Tekerlek kaymadan yuvarlandığı için tekerleğin kütle merkezi yatayda 𝑥 kadar hareket ettiğinde,
tekerleğin dönme açısı 𝜃 =
𝑥
𝑅
kadar olacaktır. Açısal hız 𝜔 =
𝑑𝜃
𝑑𝑡
=
1 𝑑𝑥
𝑅 𝑑𝑡
olacağından, tekerleğin
kütle merkezinin hızı 𝑣 = 𝜔𝑅’ dir.
a) Tekerlek ve yay sisteminin toplam mekanik enerjisi
1
1
1
1
1
1 𝑥̇ 2 1
1
1
𝑥̇ 2
𝐸 = 𝑘𝑥 2 + 𝑀𝑣 2 + 𝐼𝜔2 = 𝑘𝑥 2 + 𝑀𝑥̇ 2 + 𝐼 2 = 𝑘𝑥 2 + 𝑀𝑥̇ 2 + 𝑀𝑅 2 2
2
2
2
2
2
2 𝑅
2
2
2
𝑅
1 2
= 𝑘𝑥 + 𝑀𝑥̇ 2
2
𝑑𝐸
Sistemin mekanik enerjisi korunur, dolayısıyla 𝑑𝑡 = 0 ‘dır.
𝑑𝐸
= 𝑘𝑥 + 2𝑀𝑥̈ = 0
𝑑𝑡
6
𝑘
Sistemin hareket denklemi: 𝑥̈ + 2𝑀 𝑥 = 0,
𝑘
hareketin açısal frekansı 𝜔2 = 2𝑀
2𝑀
periyot ise 𝑇 = 2𝜋√
dır.
𝑘
b) Bu denklemin çözümü 𝑥(𝑡) = 𝑥0 𝑐𝑜𝑠(𝜔𝑡 + ∅) şeklinde olacaktır.
Başlangıç koşulu: 𝑡 = 0’da 𝑥 = 𝑥0 = 2𝜋𝑅 ve 𝑣 = 0 olarak verilmektedir. Başlangıç koşullarını
çözüm ifadesinde kullanarak faz sabitini bulabiliriz.
𝑥(0) = 𝑥0 𝑐𝑜𝑠(∅) = 𝑥0  ∅ = 0 olarak bulunur.
𝑥(𝑡) = 𝑥0 𝑐𝑜𝑠(𝜔 𝑡) = 2𝜋𝑅𝑐𝑜𝑠(√𝑘/2𝑀 𝑡)
II: Yol.
Tekerlek üzerine etki eden kuvvetler: −𝑘𝑥 ve statik sürtünme 𝑓𝑠 kuvveti.
Tekerleğin dönmesini sağlayan kuvvet statik sürtünme 𝑓𝑠 kuvveti
𝑑2𝜃
𝜏=
−𝐼𝛼
⏟
= −𝐼 2 = 𝑓𝑠 𝑅
𝑑𝑡
𝑠𝑎𝑎𝑡 𝑦ö𝑛ü𝑛𝑑𝑒𝑘𝑖 𝑑ö𝑛𝑚𝑒
Yatay yönde kayma olmadan ötelenme var. Tekerleğin kütle merkezinin lineer ivmesi 𝑎𝑘𝑚
olacaktır.
∑ 𝐹𝑥 = 𝑀𝑎𝑘𝑚 = −𝑘𝑥 + 𝑓𝑠  𝑓𝑠 = 𝑀𝑎𝑘𝑚 + 𝑘𝑥 = 𝑀𝑥̈ + 𝑘𝑥
𝑥̈
Lineer yer değiştirme ile açısal yer değiştirme arasındaki ilişki: 𝑥 = 𝑅𝜃 ve 𝜃̈ =
𝑅
𝑑2 𝜃

−𝐼 𝑑𝑡 2 = 𝑓𝑠 𝑅
𝑘
−𝐼𝜃̈ = 𝑓𝑠 𝑅
𝑘
𝜔2 = 2𝑀
𝑥̈ + 2𝑀 𝑥 = 0 ;
𝑥̈
 −𝐼 𝑅 = 𝑅(𝑀𝑥̈ + 𝑘𝑥) 
𝑥̈
𝑀𝑅 2 𝑅
+ 𝑅𝑀𝑥̈ + 𝑅𝑘𝑥 = 0
2𝑀
periyot ise 𝑇 = 2𝜋√ 𝑘
Örnek 7.
4 g kütleli bir cisim, bir yaya asılmış halde titreşim hareketi yapmaktadır. Cismin 𝑡 = 0 anındaki
yer değiştirmesi 43.785 𝑐𝑚, ivmesi ise −1.7514 𝑐𝑚/𝑠 2 dir. Yay sabitinin değeri nedir?
Çözüm: 𝒙(𝒕) = 𝑨𝒄𝒐𝒔(𝝎𝒕 + 𝜶) ,
𝒗(𝒕) =
𝒅𝒙
𝒅𝒕
= −𝑨𝝎𝐬𝐢𝐧(𝝎𝒕 + 𝜶) , 𝒂(𝒕) =
𝒅𝟐 𝒙
𝒅𝒕𝟐
= −𝑨𝝎𝟐 𝐜𝐨𝐬(𝝎𝒕 + 𝜶)
𝒕 = 𝟎’da 𝒙(𝒕 = 𝟎) = 𝑨𝒄𝒐𝒔𝜶 = 𝟒𝟑. 𝟕𝟖𝟓 𝒄𝒎 ve 𝒂(𝒕 = 𝟎) = −𝝎𝟐 ⏟
𝑨 𝐜𝐨𝐬 𝜶 = −𝟏. 𝟕𝟓𝟏𝟒 𝒄𝒎/𝒔𝟐
𝟒𝟑.𝟕𝟖𝟓
𝜔=
1.7514
𝑟𝑎𝑑
= 0.2
,
43.785
𝑠
𝜔2 =
𝑘
,
𝑚
𝑘 = 𝑚𝜔2 = 4(0.2)2 = 0.16 𝑑𝑦𝑛/𝑐𝑚
Örnek 8.
𝑥 = 𝐴𝑒−𝛼𝑡𝑐𝑜𝑠𝜔𝑡
ifadesinin,
𝒅𝟐 𝒙
𝒅𝒕𝟐
𝒅𝒙
+ 𝛾 𝒅𝒕 + 𝜔02 𝑥 = 0 denkleminin bir çözümü olabilmesi için
sağlanması gereken koşulları belirleyiniz ve buradan 𝛼 ve 𝜔’yı bulunuz.
Çözüm:
Verilen fonksiyonun çözüm olabilmesi için fonksiyonun
𝒅𝒙
𝒅𝒕
𝒅𝟐 𝒙
𝑣𝑒 𝒅𝒕𝟐 türevlerini alarak verilen
diferansiyel denklemde yerine yazdığımızda denklemi sağlaması gerekir.
Birinci türev için
7
yazılabilir. İkinci türev için
ise
veya
veya
yazılabilir. Bunlar verilen diferansiyel denklemde yerine yazılırsa
𝐴𝑒−𝛼𝑡[(𝛼2 − 𝜔2)𝑐𝑜𝑠𝜔𝑡 + 2𝛼𝜔𝑠𝑖𝑛𝜔𝑡 − 𝛼𝛾𝑐𝑜𝑠𝜔𝑡 − 𝜔𝛾𝑠𝑖𝑛𝜔𝑡 + 𝜔02𝑐𝑜𝑠𝜔𝑡 ] = 0
veya
𝐴𝑒−𝛼𝑡[(𝛼2 − 𝜔2 − 𝛼𝛾 + 𝜔02)𝑐𝑜𝑠𝜔𝑡 + (2𝛼𝜔 − 𝜔𝛾)𝑠𝑖𝑛𝜔𝑡 ] = 0 elde edilir. Bunun her
zaman sağlanabilmesi için büyük parantez içindeki 𝑠𝑖𝑛𝜔𝑡 ve 𝑐𝑜𝑠𝜔𝑡’in katsayılarının sıfır olması
gerekir yani,
2𝛼𝜔 − 𝜔𝛾 = 0
olmalıdır. Bu iki eşitlikten
sonuçlarını elde ederiz. Bu sonuçları daha önce anlatılanlardan da biliyorsunuz.
Örnek 9.
Kütlesi m olan bir cisim şekilde görüldüğü gibi kuvvet sabiti k olan ve
gerilmemiş haldeki uzunlukları 𝑎0 olan iki özdeş yaylara bağlanmıştır.
Sistem sürtünmesiz bir masa üzerindedir. Her iki yay 𝑎0’dan daha
büyük l uzunluğuna kadar uzayabilmektedir. m kütlesinin denge
konumunda yatay yer değiştirmesi x ile ve düşey yer değiştirmesi y ile
gösterilmiştir.
8
a) 𝑥 doğrultusundaki küçük yer değiştirmelere karşılık gelen hareketin diferansiyel denklemini
yazınız.
b) 𝑦 doğrultusundaki küçük yer değiştirmelere karşılık gelen hareketin diferansiyel denklemini
yazınız (𝑦 ≪ 𝑎 kabul ediniz).
c) 𝑎 ve 𝑎0 vasıtasıyla 𝑥 ve 𝑦 boyunca titreşim periyotlarının oranını hesap ediniz.
d) 𝑡 = 0 da m kütlesi 𝑥 = 𝑦 = 𝐴0 noktasından sıfır hızla harekete geçerse, herhangi bir t anında
cismin 𝑥 ve 𝑦 koordinatları nedir? (French-p3.19)
Çözüm:
a) Denge halinde yayların ikisi de a kadar gerilmiş durumda olsun (Yayların serbest boyu 𝑎0 ).
m kütlesini sağa doğru x kadar çektiğimizi düşünelim. Bu durumda m kütlesine etkiyen
bileşke kuvvet
𝐹 = −2𝑘𝑥 olacağı açıktır. 2. Newton yasasından
veya
veya
alarak
yazabiliriz. b)
m kütlesini şekildeki gibi y doğrultusunda hafifçe çektiğimizi düşünelim. Yayların eşit miktarda
uzayacağı açıktır. Yayların yeni boyunun L olduğunu kabul edersek, yaylardaki uzama miktarı
∆𝐿 = 𝐿 − 𝑎0
olacaktır. Bu durumda yayların kütleye uygulayacağı geri çağırıcı kuvvet
𝑇 = −𝑘(𝐿 − 𝑎0)
olacaktır. T gerilimlerinin yatay bileşenleri (𝑇𝑐𝑜𝑠𝜃) eşit ve zıt yönlüdür. Bu nedenle kütleye yatay
doğrultuda net bir kuvvet etkimez. T gerilimlerinin düşey bileşenleri (𝑇𝑠𝑖𝑛𝜃) eşit ve aşağı doğrudur.
Bu nedenle m kütlesine düşey doğrultuda etkiyen bileşke kuvvet
𝐹𝑦 = −2𝑇𝑠𝑖𝑛𝜃
olacaktır. Bu durumda
9
yazabiliriz. Şekilden
yazılabilir. Bunu yukarıdaki ifadede kullanırsak
veya
yazılabilir. Şekilden
𝐿2 = 𝑎2 + 𝑦2
olduğu açıktır. Bu değeri yukarıda yerine yazarsak
elde ederiz. Burada y’nin katsayısı sabit olmadığı için bu denklem BHH denklemi değildir. Ancak
𝑦 ≪ 𝑎 yaklaşımında olaya baktığımız için
yazılabilir. Bu durumda y’nin katsayısı
seriye açılarak
için
alınabilir (𝑦 ≪ 𝑎 olduğu için). Bu yaklaşımda y doğrultusunda hareket denklemi için
ifadesini yazabiliriz. Burada y’nin katsayısı pozitif olduğu için
alınabilir. Bu durumda
yazabiliriz. Bu denklemin BHH’in hareket denklemi olduğuna dikkat ediniz.
c) x-doğrultusundaki hareket denkleminden
ve y-doğrultusundaki hareket denkleminden
elde etmiştik. Buradan periyotlar için
10
ifadelerini yazabiliriz. Buradan periyotlar oranı için
sonucunu elde ederiz.
d) Kütlenin x ve y doğrultusundaki hareketi BHH olduğu için
ve
yazabiliriz.
Örnek 10.
Kütlesi m olan küçük bir top uzunluğu 𝑙1 ve 𝑙2 olan iki tel ile şekildeki gibi duvara bağlanmıştır.
Denge durumunda her iki teldeki gerilim 𝑇0’dır. m kütlesi düşey doğrultuda hafifçe çekilip serbest
bırakılıyor. Küçük titreşimlerin periyodunu bulunuz.
Çözüm:
𝑇1 ve 𝑇2gerilimlerinin yatay bileşenleri birbirine zıt yöndedir ve kütlenin yatay doğrultuda
titreşimine bir katkı sağlamaz. 𝑇1 ve 𝑇2 gerilimlerinin düşey bileşenleri aşağı doğrudur. Bu
bileşenlerin toplamı m kütlesine geri çağırıcı kuvvet uygular. Bu kuvvet
𝐹 = −𝑇1𝑠𝑖𝑛𝜃1 − 𝑇2𝑠𝑖𝑛𝜃2
şeklinde yazılabilir. Küçük salınımlar için
alınabilir. Ayrıca küçük titreşimler için 𝑇1 = 𝑇2 = 𝑇0 alınabilir. Bu durumda F kuvveti için
yazabiliriz. Bu durumda m kütlesinin hareket denklemi için
veya
veya
11
Burada
alarak
yazabiliriz. Buradan Periyot için
ifadesi elde edilir.
Örnek 11.
0.2 kg kütleli bir cisim yay sabiti 80 N/m olan bir yaya asılıdır. Bu cisim – 𝑏𝑣 ile verilen bir sürtünme (sönüm)
kuvvetine maruz kalırsa (burada cismin hızıdır),
a) Sistemin serbest salınımlarının diferansiyel denklemini yazınız.
b) Eğer sönümlü harmonik hareketin frekansı, sönüm olmadığı zamanki frekansın √3/2 ’si ise b
sabitinin değeri nedir?
c) Sistemin 𝑄 kalite faktörü nedir, 10 salınım sonunda titreşimin genliği hangi faktör (kaç kat) ile
azalır? (French-p3.14)
Çözüm:
a) 𝐹 = −𝑏𝑣 − 𝑘𝑥 sisteme etkiyen net kuvvet
𝑑2 𝑥
𝑑𝑥
𝑚 𝑑𝑡 2 + 𝑏 𝑑𝑡 + 𝑘𝑥 = 0 sistemin hareket denklemi
𝑑2 𝑥
𝑏 𝑑𝑥
𝑘
+ 𝑚 𝑑𝑡 + 𝑚 𝑥 = 0
𝑑𝑡 2
𝑘
buradan
80
𝑑2 𝑥
𝑑𝑡 2
𝑑𝑥
+ 𝛾 𝑑𝑡 + 𝜔02 𝑥 = 0
𝑏
𝜔02 = 𝑚 = 0.2 = 400 (𝑟𝑎𝑑/𝑠)2 , 𝛾 = 𝑚
b) 𝜔 = √𝜔02 − 2 ⁄4 =
√3
2
𝜔0
3
ise 𝜔02 − 2 ⁄4 = 4 𝜔02
,
𝛾 2 = 𝜔02 , 𝛾 = 𝜔0 = 20 𝑠 −1
𝑏 = 𝛾𝑚 = 20 ∗ 0.2 = 4 𝑘𝑔/𝑠
c) 𝑄 =
𝜔0
𝛾
=1 ,𝜔 =
γt
√3
2
𝜔0 =
√3
2
∗ 20 = √300 , 𝑡 = 10𝑇 = 10
2𝜋
𝜔
=
20𝜋
√300
≅ 3.63 𝑠
20∗3.63
𝐴(𝑡) = 𝐴0 e− 2 = 𝐴0 e− 2 𝐴0 (1.72 × 10−16 ) , 𝐴(𝑡) ≪ 𝐴0 hareket tamamen sönmüş kabul
edilebilir. Başka bir deyişle sistem çok kısa sürede sönüme gider.
12
Örnek 12.
Bir çok titreşen sistemde depolanan enerji zamanla 𝐸 = 𝐸0𝑒−𝛾𝑡 şeklinde üstel azalır. Böyle bir
𝜔
titreşim hareketi için Q ifadesi 𝑄 = 𝛾0 ile verilir. Burada 𝜔0 titreşimlerin doğal frekansıdır.
a) Bir piyanonun orta C’sine vurulduğu zaman titreşim enerjisi 1s’de ilk değerinin yarısına
düşer. Orta C’nin frekansı 256 Hz’dir. Sistemin Q değeri nedir?
b) Daha yüksek oktavlı bir notasında (f=512Hz) enerji azalması aynı sürede oluyorsa Q değeri
nedir?
c) 0,1 kg kütlesindeki bir cisim yay sabiti k=0,9 N/m olan bir yaya asılıdır.
Bu sistem sönüm sabiti b (𝐹𝑠ö𝑛ü𝑚 = −𝑏𝑣)olan bir akışkan içinde hareket ederek 4 s’de
enerjisi ilk değerinin 1/e’sine düşüyor. Q ve b değerlerini bulunuz. (French-p3.15)
Çözüm:
a) 𝐸 = 𝐸0𝑒−𝛾𝑡
ifadesi
yazabiliriz. Buradan
ve
verilenler
kullanılarak
0,5𝐸0
=
𝐸0𝑒−𝛾.1
𝑒𝛾 = 2 ⇒ 𝛾 = 𝐿𝑛2 elde edilir.
b)
c)
𝑏 = 𝑚𝛾 = 0,1𝑥0,25 =
0,025 kg/s
√
Örnek 13.
Şekildeki LRC devresindeki C sığası başlangıçta 𝑞0 yükü ile yüklüdür.
Devredeki S anahtarı kapandıktan sonra Krichhoff’un ilmek kuralını kullanarak devre denklemini (𝑞 yükü
cinsinden) yazınız. Bu denklemi mekanik sistemdeki sönümlü harmonik osilatörün devre denklemi ile
karşılaştırarak 𝑞, 𝐿, 𝐶 ve 𝑅’nin mekanik karşılıklarını belirleyiniz.
b) Mekanik benzerlikten yararlanarak 𝑞 yükünün zamana bağlı değişimini veren ifadeyi yazınız.
c) Şekildeki devre elemanlarının değeri 𝐿 = 10 𝑚𝐻 , 𝐶 = 1.0 𝜇𝐹 ve 𝑅 = 2.0 Ω ’dur. Salınımların açısal
frekansının yaklaşık değeri nedir? Sistemin 𝑄 kalite faktörünün değeri nedir? Bu devrede yük
salınımlarının genliği ne kadar süre sonra dörttebirine düşer. Bu sürede kaç periyotluk salınım olur?
a)
13
Çözüm:
LRC devresindeki 𝐶 sıgası başlangıçta 𝑞0 yükü ile yüklüdür.
S anahtarı kapatılırsa, Krichhoff’un ilmek (çevirim) kuralını kullanarak devre denklemini
a)
𝑑𝐼
𝑞
𝐿 𝑑𝑡 + 𝑅𝐼 + 𝐶 = 0
şeklinde yazabiliriz. 𝐼 =
𝑑2 𝑞
𝑑𝑞
𝑑𝑞
𝑑𝑡
𝑑2 𝑞
𝑞
𝐿 𝑑𝑡 2 + 𝑅 𝑑𝑡 + 𝐶 = 0 
𝑑𝐼
𝑑𝑡
𝑣𝑒
𝑑𝑡 2
=
𝑑2 𝑞
𝑑𝑡 2
𝑅 𝑑𝑞
eşitlikleri yerine konulursa,
𝑞
+ 𝐿 𝑑𝑡 + 𝐿𝐶 = 0 
𝑑2 𝑞
𝑑𝑡 2
𝑑𝑞
+ 𝛾 𝑑𝑡 + 𝜔02 𝑞 = 0
denklemi elde edilir. Bu denklem sönümlü harmonik hareket denklemi olan,
𝑑2 𝑥
𝑑2 𝑥
𝑑𝑥
𝑏 𝑑𝑥
𝑘
𝑚 𝑑𝑡 2 + 𝑏 𝑑𝑡 + 𝑘𝑥 = 0  𝑑𝑡 2 + 𝑚 𝑑𝑡 + 𝑚 𝑥 = 0 
𝑑2 𝑥
𝑑𝑡 2
𝑑𝑥
+ 𝛾 𝑑𝑡 + 𝜔02 𝑥 = 0
Mekanik
Elektrik
sistem
sistemi
𝑥
𝑞
𝑚
𝐿
𝑘
1/𝐶
𝑏
𝑅
 = 𝑏/𝑚
 = 𝑅/𝐿
denklemi ile aynıdır.
Bu iki denklem karşılaştırıldığında, mekanik sistemdeki büyüklükler ile LRC elektrik devresindeki büyüklükler arasında
benzerlikler yandaki tabloda verilmiştir.
Bu benzetişimden yararlanarak, sönümlü harmonik hareket için verilmiş olan çözüm ifadesini devre
denkleminin çözümü için kullanabiliriz.
b)
𝑅𝑡
𝑞(𝑡) = 𝑞0 e−2𝐿 cos(ω𝑡) = 𝐴(𝑡)cos(𝜔𝑡)
Burada 𝑞0 , başlangıçta kondansatör üzerinde depolanan yük, 𝐴(𝑡) ise devrede salınan yükün genliğidir. Yine
𝑅2
1
1/2
benzerlikten yararlanarak, sistemin açısal frekansı için 𝜔 = [𝐿𝐶 − 4𝐿2 ]
ifadesini yazabiliriz.
Devre elemanlarının değeri 𝐿 = 10 𝑚𝐻, 𝐶 = 1.0 𝜇𝐹 ve 𝑅 = 2.0 Ω’dur.
Salınımların açısal frekansı :
c)
1
𝜔=
1
[𝐿𝐶
𝑅2 2
− 4𝐿2 ]
1
1
[10−2 ∗10−6
=
4
− 4∗10−4 ]2
1
= [108 − 104 ]2 ≅ 104
𝑟𝑎𝑑
𝑠
Devrede 𝑅/2𝐿 ≪ 1/𝐿𝐶 olduğu görülmektedir. Bu nedenle sönüm çok yavaş olmakta ve frekansda LC devresinin doğal
titreşim frekansına yaklaşık eşit çıkmaktadır (𝜔0 ≅ √1/𝐿𝐶).
Devrenin 𝑄 değeri: 𝑄 =
𝜔0
𝛾
=
√1/𝐿𝐶
𝑅/𝐿
=
√𝐿/𝐶
𝑅
10−2
1
= 2 √10−6 = 50
Devrede salınan yükün genliğinin başlangıç değerinin ¼’üne düşmesi için geçen zamana 𝑡1 diyelim. Bu durumda
𝑅𝑡
𝑅𝑡1
𝐴(𝑡) = 𝑞0 e−2𝐿  𝐴(𝑡1 ) = 𝑞0 e− 2𝐿 =
𝑅𝑡1
e 2𝐿 = 4 
𝑅𝑡1
2𝐿
= ln(4)
Bu süredeki salınım sayısı: 𝑛 =
𝑡1
𝑇

𝑡
𝑡1 =
1
= 2𝜋/𝜔
=
𝑞0
4
olacaktır.
2𝐿 ln(4)
𝑅
=
2∗10−2 ∗1.386
2
13.86×10−3 ∗104
6.28
= 13.86 𝑚𝑠
≅ 22
14
Örnek 14.
Sönümlü salınım yapan bir LRC devresinde bir devirlik sürede enerji kayıp oranı
olması durumunda yaklaşık olarak
2𝜋𝑅
𝜔𝐿
∆𝑈
𝑈
’ın R’nin küçük
ile verilebileceğini gösteriniz.
Çözüm:
Şekildeki LRC devresinde S anahtarı kapandıktan sonra kondansatör
üzerindeki yük harmonik hareket yapar. Bu LRC devresinde yük için
ifadesini türetmiştik. R’nin küçük olduğu durumda bu ifadeyi
şeklinde yazabiliriz. Başlangıçta anahtar açık iken kondansatör yüklüdür ve devreden akım geçmez.
Bu durumda kondansatördeki enerji
ifadesi ile verilir. Anahtar kapandıktan sonra kondasatördeki yük yukarıda verilen bağıntıyla tanımlı
osilasyon yapar. Bir periyotluk süre sonunda yük için
ifadesini yazabiliriz (
kondansördeki enerjiyi U ile gösterirsek,
olduğuna dikkat ediniz). Bu anda
yazabiliriz. Buradan
15
yazabiliriz. Buradan
elde ederiz. 𝑒x ifadesini seriye açılımının
ifadesi ile verildiğini biliyoruz. Burada x’in küçük değerlerinde 𝑒x ≅ 1 + 𝑥 alabiliriz. Bu bilgiden
yararlanarak
yazabiliriz. R’nin küçük değerlerinde açısal frekans 𝜔 =
periyot için 𝑇 =
2𝜋
𝜔
1
√𝐿𝐶
ifadesi ile verilebilir. Bu durumda
yazabiliriz ve değeri yukarda elde ettiğimiz sonuçta kullanırsak,
sonucunu elde ederiz.
Örnek 15.
Kütlesi 0,5 kg olan bir blok, kuvvet sabiti k=12,5 N/m olan bir yayın ucuna bağlı olarak kritik altı sönümlü
hareket yapıyor. Hareketin frekansı, sönümsüz hareketin frekansından % 0,2 daha az olduğu gözlemleniyor.
a) Hareketin sönüm sabiti b’nin değerini bulunuz.
b) Hareketin genliğinin zamana bağlı değişimini bulunuz.
c) Mekanik enerjinin başlangıç değerinin %1’ine düşmesi için geçen süreyi bulunuz.
d) Sistemin kritik sönüm durumunda hareket edebilmesi için sönüm sabiti (𝑏𝑘) ne olmalıdır?
Çözüm:
a) Sönümlü harmonik hareketin açısal frekansının
ile verildiğini biliyorsunuz. Buradan sönüm sabiti 𝑏 için
yazılabilir. Verilenler kullanılarak sönüm sabiti b için
16
elde edilir.
b)
elde edilir.
c) Sönümlü hareketin toplam enerjisinin genliğin karesi ile orantılı olduğunu biliyoruz (Ders notlarına
bakınız)
𝐸𝑡𝑜𝑡
𝐸0
= 0,01 olması için geçen süre soruluyor.
d) Kritik sönüm halinde
olduğunu hatırlayınız. Buradan
elde edilir.
17