DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
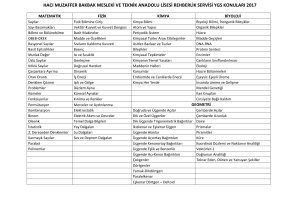
GEOMETRİ
10
GEOMETRİK KAVRAMLAR
Nokta,doğru,düzlem tanımı
dk
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Nokta,doğru,düzlem,ışın ve uzayı kavrayabilme
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
Nokta,doğru ve düzlem geometride tanımsız terimlerdir. Şekil
Sözel dilsel
olarak aşağıdaki gibi belirtilirler.
Doğacı
. A A noktası
<-----B-------C------> d
d (BC) doğrusu
Sosyal – Kişiler arası
Uzay: Tüm noktaların kümesine uzay denir.
Mantıksal – Matematiksel Doğru parçası: Doğru üzerinde alınan iki nokta arsındaki kısma
denir.
İçsel bireysel
Yarı doğru (Işın): Bir noktası sabit diğeri sonsuz olan doğrunun
Görsel – Uzaysal
bir parçasına denir.
Müziksel – Ritmik
KONVEKS(DIŞBÜKEY) VE KONKAV(İÇBÜKEY) ŞEKİLLER
Bedensel - Kinestetik
Bir K şeklinin, noktalar kümesinin her P,Q nokta ikilisi için
[PQ] K ise K kümesine konveks (dış bükey) nokta kümesi
denir. Konveks olmayan şekillere de konkav(içbükey) şekil
denir.
- Konveks iki şeklin arakesitleri de konvekstir.
- Birleşimleri konveks olmayabilir.
- İç bölgesi konveks olan çokgenlere, genellikle konveks
çokgen denir.
DÜZLEM AYIRMA: Bir düzlemdeki d doğrusu, kendisi dışında
Düzlemi iki ayrık bölgeye ayırır. n tane farklı doğru ise düzlemi
Enaz n+1, en çok
n.(n 1)
1 ayrık bölgeye ayırır.
2
AÇI: Başlangıç noktaları aynı,doğrusal olmayan iki ışının
birleşimine Açı denir. Şekildeki açı BAC, CAB yada A
Biçiminde yazılır. Bir açının ölçüsü, derece olarak 0 ile 180
arasında bir gerçel sayıdır
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
9/D
GEOMETRİK KAVRAMLAR
Açı çeşitleri
40+40 dk
21/12/2010
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Açı ile ilgili temel kavramları kavrayabilme
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
AÇI ÇEŞİTLERİ:
Sözel dilsel
DAR AÇI: ölçüsü 90 den küçük olan açılara denir.
Doğacı
DİK AÇI: Ölçüsü 90 olan açılara dik açı denir.
Sosyal – Kişiler arası
GENİŞ AÇI: Ölçüsü 90 ile 180 arasındaki açıdır.
Mantıksal – Matematiksel DOĞRU AÇI: Ölçüsü 180 olan açılardır.
TAM AÇI: Ölçüsü 360 olan açılardır.
İçsel bireysel
Görsel – Uzaysal
EŞ AÇILAR: Ölçüleri eşit olan açılara denir. A B ile göster.
Müziksel – Ritmik
KOMŞU AÇILAR: Köşeleri ve birer kenarları ortak, iç bölgeleri
ayrık olan iki açıya, komşu açı denir.
Bedensel - Kinestetik
AÇIORTAY: Bir açıyı iki eşit parçaya bölen ışına açıortay
denir. Açıortay üzerinde alınan herhangi bir noktadan, açının
kollarına indirilen dikme uzunlukları eşittir.
TÜMLER AÇILAR:
Ölçüleri toplamı 90 olan iki açıya tümler açılar denir. α+ß=90
olduğundan α ile ß birbirinin tümleyenidir.
Komşu tümler iki açının, açıortaylarının oluşturduğu açı 45 tir.
BÜTÜNLER AÇILAR:
Ölçüleri toplamı 180 olan iki açıya bütünler açılar denir. Açılar
komşu ise, komşu bütünler iki açı yada doğrusal çift adını alır.
α+ß=180 olduğundan α ile ß birbirinin bütünleyenidir.
Komşu bütünler iki açının açıortayları birbirlerine daima diktir.
TERS AÇILAR:
Doğruların kesişmesiyle oluşan açılara ters açılar denir.
Ters açıların ölçüleri eşittir.
KENARLARI DİK OLAN AÇILAR:
Kenarları dik olan açılar eşittir.
Kenarları dik açılardan biri dar, diğeri geniş ise açılar
bütünlerdir.
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
Atl9/B
GEOMETRİK KAVRAMLAR
Paralel İki Doğrunu Bir Kesenle Yaptığı Açılar
40+40 dk
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
22/12/2010
Paralel iki doğrunun kesenle yaptığı açıların
ilişkisini söyleme ve yazma
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
PARALEL İKİ DOĞRUNUN BİR KESENLE YAPTIĞI
Sözel dilsel
AÇILAR
Doğacı
- Yöndeş açılar eşittir.
Sosyal – Kişiler arası
- İç ters açılar eşittir.
Mantıksal – Matematiksel
- Dış ters açılar eşittir.
- Karşı durumlu açılar bütünlerdir.
İçsel bireysel
- Yanal durumlu açılar bütünlerdir.
Görsel – Uzaysal
- Karşı durumlu açıların açıortayları diktir.
Müziksel – Ritmik
Bedensel - Kinestetik
KENARLARI PARALEL AÇILAR
-
Kenarları aynı yönde paralel olan iki açı eşittir.
Kenarları zıt yönde paralel olan iki açı eşittir.
Birer kenarları aynı yönde, diğer kenarları zıt yönde
paralel olan iki açı birbirinin bütünleyenidir.
ÜÇGEN: Düzlemde doğrusal olmayan üç noktanın ikişer ikişer
birleştirilmesiyle elde edilen şekle Üçgen denir.
ABC [ AB] [ BC ] [CA]
A, B, C iç açılar
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
9/D
ÜÇGENLER
Üçgenlerin kenarları ve açılar arasındaki ilişki
40+40 dk
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
5/04/2011
Bir üçgende,kenarlar ile açılar arasındaki ilişkiyi söyleme
ve gösterme
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve
Ders Kitabı
kaynakça
Öğretmen
Öğrenci
ÜÇGEN: Düzlemde doğrusal olmayan üç noktanın ikişer ikişer
Sözel dilsel
birleştirilmesiyle elde edilen şekle Üçgen denir.
Doğacı
Sosyal – Kişiler arası
ABC [ AB] [ BC ] [CA] A, B, C iç açılar
Mantıksal –
ÜÇGENDE KENAR AÇI BAĞINTILARI
Matematiksel
1-Bir üçgende eş açılar karşısındaki kenar uzunlukları eşittir.
İçsel bireysel
m( B) m(C ) b c dir .
Görsel – Uzaysal
2- Bir üçgende büyük açı karşısında büyük kenar, küçük açı karşısında
Müziksel – Ritmik
küçük kenar bulunur.
Bedensel - Kinestetik
m( A) m( B) m(C ) a b c dir .
3- Bir üçgende herhangi bir kenarın uzunluğu, diğer iki kenarın
uzunlukları toplamından küçük, uzunlukları farkının mutlak değerinden
büyüktür.
b c a b c,
a c b a c ,
a b c a b
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
4- Bir üçgende geniş açı karşısındaki kenar en büyüktür.
5-
m( A) 90o ise : b c a b2 c 2 dir.
6- m( A) 90 ise : b c a b c
7- Üçgenin dış açılarının ölçüleri
o
2
2
dir .
m( Aı ) , m( Bı ) , m(C ı ) olmak üzere;
m( B ı ) m(C ı ) m( Aı ) m( B ı ) m(C ı )
m( Aı ) m(C ı ) m( B ı ) m( Aı ) m(C ı )
m( Aı ) m( B ı ) m(C ı ) m( Aı ) m( B ı )
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
Üçgenlerin kenarları ve açılar arasındaki ilişki
dk
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Bir üçgende,kenarlar ile açılar arasındaki ilişkiyi
söyleme ve gösterme
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
8- Bir üçgende bir köşeden geçen yükseklik, iç açıortay
Sözel dilsel
ve kenar ortay uzunlukları arasında
Doğacı
sıralaması vardır.
ha na va
Sosyal – Kişiler arası
Mantıksal – Matematiksel 9- Bir üçgende kenarlar arasındaki sıralamanın tersi yükseklik,
iç açıortay ve kenar ortaylar arasında vardır.
İçsel bireysel
a b c ha hb hc , a b c v a vb vc ,
Görsel – Uzaysal
a b c na nb nc dir .
Müziksel – Ritmik
10Bedensel - Kinestetik
abc Ç
u
olup
2
2
u ha hb hc 2u
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
u va vb vc 2u
u na nb nc 2u dur.
11- bir üçgenin iç bölgesinde alınacak olan isteksel bir noktanın
üçgenin köşe noktalarına olan uzaklıklarının toplamı, yarı
çevreden
büyük, çevreden küçüktür.
u < x+y+z < 2u
12- bir üçgende iki kenarın orta noktalarını birleştiren doğru
parçası,
üçüncü kenara paralel ve yarısına eşittir.
[DE] // [BC] ve
DE
BC
2
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
Atl11/A
ÜÇGENLER
Üçgende açıortay özellikleri
40+40 dk
5/52011
BÖLÜM2
Açıortaya ait özellikleri söyleme ve yazma
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
ÜÇGENDE AÇIORTAY
Sözel dilsel
1Bir
üçgende
tüm
iç açıortaylar daima bir noktada bir noktada
Doğacı
kesişir.
Sosyal – Kişiler arası
Kesim noktası üçgenin kenarlarına içten teğet olan iç teğet
Mantıksal – Matematiksel
[ AD] na
çemberin merkezidir.
İçsel bireysel
[ BE ] nb iç açıortayla r
Görsel – Uzaysal
[CF ] nc
Müziksel – Ritmik
2- Açıortay üzerindeki her nokta, açının kollarından eşit
uzaklıktadır.
Bedensel - Kinestetik
PH PH ı
KT KT ı
dir .
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
3- İÇ AÇIORTAY TEOREMİ : Bir üçgende iç açıortay kestiği
kenarı komşu oranında böler.
m
b
ve
tir.
NC
AC
NB
4-
AB
n
c
na AN b.c m.n dir.
5- D,E,F iç teğet çemberin kenarlara olan değme noktaları ve
ID IE IF r
i ) A( ABC ) u.r dir .
ise, ii )
AE AF u a
BD BF u b
CD CE u c
dir .
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
ATL10/A
ÜÇGENLER
Üçgende açıortay özellikleri
dk
12/5/2011
BÖLÜM2
Açıortaya ait özellikleri söyleme ve yazma
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
Sözel dilsel
A( ANC) b
6 dir .
Doğacı
A( ANB) c
Sosyal – Kişiler arası
S3
S1
S2
ise;
Mantıksal – Matematiksel 7- a b c k
S1 a.k , S 2 b.k , S3 c.k
İçsel bireysel
8DIŞ
AÇIORTAY TEOREMİ:
Görsel – Uzaysal
Bir dış açıortay karşı kenarı komşu kenarlarla orantılı parçalara
Müziksel – Ritmik
ayırır.
Bedensel - Kinestetik
N ıC
b
x
b
N ıB
9-
c
xa
c
dir .
ı
nA AN ı x.( x a) b.c
2 2 90 90
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
Aynı köşeden geçen iç ve dış
10-
açıortay birbirleri ne diktirler .
m b
1
m
x
n
c
dir .
1 ve 2 den
x
b
n
xa
2
xa c
11- I, içteğet çemberin merkezi [DE]//[BC]
[IT]//[AB] , [IK]//[AC] ise;
i ) DE BD EC
ii ) Ç ( ADE ) b c
iii ) Ç ( ITK ) a dır .
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
GEOMETRİ
Sınıfı
10
Ünitenin Adı / No ÜÇGENLER
Konu
Kenarortaya ait özellikler
Önerilen Süre
dk
BÖLÜM2
Kenarortaya ait özellikleri söyleme ve yazma
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
ÜÇGENDE KENARORTAY
Sözel dilsel
AD
v
Doğacı
a
Sosyal – Kişiler arası
BE vb kenarortaylar
Mantıksal –
CF vc
Matematiksel
1- Bir üçgende tüm kenarortaylar daima bir noktada kesişir. Bu
İçsel bireysel
nokta üçgende ağırlık merkezidir.
Görsel – Uzaysal
2- Bir üçgende kenarortaylar kenardan itibaren 1 , köşeden
Müziksel – Ritmik
3
Bedensel - Kinestetik
itibaren 2 oranında ağırlık merkezinde kesişirler. [BE]//[DF] ise
3
2 CF 2 FE EA
DG
DA
1
3
ve
AG
AD
2
3
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
3- AK 3x , KG x ve DG 2 x dir.
Bir kenarortayın orta noktasının, ağırlık Merkezine olan uzaklığı, o
kenarortayın
1
KG 1
sıdır.
dır .
6
AD 6
4- Kenarortay teoremi:
a2
2
b2
2
c2
2
2v a
2
b2 c2
2vb
2
a2 c2
2vc
2
a2 b2
5- Kenarortay teoremindeki bağıntılar taraf tarafa toplanır ve
düzenlenirse;
3
2
2
2
va vb vc ( a 2 b 2 c 2 ) elde edilir.
4
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
Kenarortaya ait özellikler
dk
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Kenarortaya ait özellikleri söyleme ve yazma
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
6- [AH] yükseklik, [AD] kenarortay,
Sözel dilsel
Doğacı
HD x ise , 2ax b 2 c 2
Sosyal – Kişiler arası
7- Bir dik üçgende hipotenüse ait kenarortay,
Mantıksal – Matematiksel hipotenüsün yarısına eşittir.
İçsel bireysel
BC
AD
dir .
Görsel – Uzaysal
2
Müziksel – Ritmik
5 2
2
2
2
8- Bir dik üçgende 5va vb vc a dir .
Bedensel - Kinestetik
4
9- Bir üçgende iki kenarortay birbirine dik ise,
va vb vc
2
2
2
ve
5a 2 b 2 c 2 dir .
10- bir üçgende bir kenar uzunluğu büyüdükçe bu kenara ait
kenarortay uzunluğu küçülür, kenar uzunluğu küçüldükçe kenara
ait kenarortay uzunluğu büyür.
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
Kenarortaya ait özellikler
dk
BÖLÜM2
Kenarortaya ait özellikleri söyleme ve yazma
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
11- G noktası, ABC ile DEF üçgenlerinin
Sözel dilsel
ağırlık merkezi ise;
Doğacı
Sosyal – Kişiler arası
12- [AD] kenarortay, E [AD] nin
Mantıksal – Matematiksel orta noktası ve [BF]// [DK] ise
İçsel bireysel
CF 2 AF dir.
Görsel – Uzaysal
Müziksel – Ritmik
13- Bir ABC üçgeninin kenarları a,b,c ve bu kenarlara ait
Bedensel - Kinestetik
kenarortaylar, sırası ile va , vb , vc olmak üzere;
a b c va vb vc dir .
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
14-
u va vb vc 2u
15- Bir dik üçgende, dik açı köşesine ait açı ortay,
aynı zamanda hipotenüse ait yükseklik ile kenarortay
arasında kalan açının da açıortayıdır.
[ AH ] [ BC ] , BD DC ve
m( BAE ) m( EAC ) ise
m( HAE ) m( DAE )
m( B) m(C )
2
dir .
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
Kenarortaya ait özellikler
dk
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Kenarortaya ait özellikleri söyleme ve yazma
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
16- G ağırlık merkezi,
Sözel dilsel
BT TG ve
Doğacı
ETKD dörtgeni bir paralelkenardır.
Sosyal – Kişiler arası
CK KG ise ,
Mantıksal – Matematiksel
17- G ağırlık merkezi, [GE]//[BC],[GD]//[AB] ve [GF]//[AC]ise,
İçsel bireysel
AB AC BC
Görsel – Uzaysal
GD GE GF
dür. 18-i Bir
3
Müziksel – Ritmik
üçgende kenarortay, üçgenin alanını iki eşit alana böler.
Bedensel - Kinestetik
ii G ağırlık merkezini köşelere birleştiren doğru parçaları,
üçgenin alanını üç eşit alana böler.
iii Üç kenarortay, üçgenin alanını 6 eşit alana böler.
iv Kenarların orta noktalarını ikişer ikişer birleştiren doğru
parçaları, üçgenin alanını 4 eşit alana böler.
19- d, ağırlık merkezinden geçen bir doğru
olmak üzere köşelerden bu doğruya inilen
dikme uzunlukları
AAı x, BB ı y, CC ı z ise ,
x y z dir .
20- G ağırlık merkezi ve d doğrusu
üçgenin dış bölgesinde ise;
AAı BB ı CC ı 3 GG ı dir .
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdür
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
Üçgende kesen teoremleri
dk
BÖLÜM2
Kesen teoremlerini kavrayabilme
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
ÜÇGENDE KESEN TEOREMLERİ
Sözel dilsel
STEWART
TEOREMİ:
Doğacı
ABC üçgeninde D noktası [BC] kenarı üzerinde herhangi bir
Sosyal – Kişiler arası
b 2 . p c 2 .q a.x 2 a. p.q
Mantıksal – Matematiksel
b 2 . p c 2 .q a ( x 2 p.q )
nokta ise
İçsel bireysel
b 2 . p c 2 .q
x 2 p.q
Görsel – Uzaysal
a
2
2
Müziksel – Ritmik
2
b . p c .q
p.q
dur .
x
Bedensel - Kinestetik
pq
SEVA TEOREMİ:
Bir üçgenin iç bölgesinde alınacak olan isteksel bir noktayı
üçgenin köşe koordinatlarına birleştiren doğru parçalarının
uzantıları, kenarları sırasıyla D,E,F noktalarında kesiyorsa;
DB
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
DC
EC
EA
FA
FB
1
MENELAUS TEOREMİ:
Bir üçgenin kenarları bir d doğrusu tarafından D,E ve F gibi üç
noktada kesildiğinde;
DB
DC
.
CF
.
EA
FA EB
1
CARNOT TEOREMİ:
Bir üçgenin iç bölgesinde alınacak olan isteksel
bir noktadan kenarlara inilen dikmelerin kenarlar
üzerinde ayırmış olduğu doğru parçalarının uzunlukça
birer atlanarak kareleri toplamı aralarında eşittir.
BD CE AF
2
2
2
DC
2
EA FB
2
x 2 z 2 p 2 y 2 t 2 q 2 dir .
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
2
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
Atl10/A
ÜÇGENLER
Üçgende kesen teoremleri
40+40dk
13/5/2011
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Kesen teoremlerini kavrayabilme
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
COSİNÜS TEOREMİ:
Sözel dilsel
ABC üçgeninde;
Doğacı
a 2 b 2 c 2 2bcCosA
Sosyal – Kişiler arası
Mantıksal – Matematiksel b 2 a 2 c 2 2acCosB
İçsel bireysel
c 2 a 2 b 2 2abCosC dir .
Görsel – Uzaysal
SİNÜS TEOREMİ:
m(ADC)=m(ABC)=θ
Müziksel – Ritmik
(Aynı yayı gören çevre açılar eşittir.)
Bedensel - Kinestetik
ADC üçgeninde
sin
b
b
2R
olur .
2R
sin
Diğer Kenarlar içinde aynı oran bulunursa;
a
b
c
2 R elde edilir.
sin A
sin B
sin C
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
Atl10/A
ÜÇGENLER
Üçgende metrik bağıntılar
40+40 dk
13/5/2011
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Pisagor ve öklitin özelliklerini söyleme ve yazma
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
DİK ÜÇGEN
Sözel dilsel
Herhangi iki kenarı dik kesişen yada bir açısı dik açı olan üçgene
Doğacı
dik üçgen denir. Dik üçgenin diklik merkezi A noktasıdır.
Sosyal – Kişiler arası
Şekilde a kenarı hipotenüs, b ve c ise dik kenarlardır.
Mantıksal – Matematiksel 1-PİSAGOR TEOREMİ:
Bir dik üçgende dik kenarların kareleri toplamı hipotenüsün
İçsel bireysel
2
2
2
karesine eşittir. a b c
Görsel – Uzaysal
2- ÖKLİD BAĞINTILARI:
Müziksel – Ritmik
i ) h 2 p.k
Bedensel - Kinestetik
ii ) b 2 p.a
iii ) c 2 k .a
1
1 1
3- 2 2 2
h
b
c
4- A( ABC )
a.h b.c
olup buradan a.h b.c dir .
2
2
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
Üçgende metrik bağıntılar
dk
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Pisagor ve öklitin özelliklerini söyleme ve yazma
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
Sözel dilsel
5- i ) A( ABC ) u.r
Doğacı
abc
ii ) A( ABC ) u (u a )
u
Sosyal – Kişiler arası
2
Mantıksal – Matematiksel iii ) A( ABC ) (u b)(u c) iv ) A( ABC ) m.n dir .
İçsel bireysel
6- Dik üçgende hipotenüse ait kenarortay hipotenüsün yarısına
Görsel – Uzaysal
eşittir. AD BD DC dir .
Müziksel – Ritmik
2
2
2
5va vb vc
Bedensel - Kinestetik
7- ABC dik üçgeninde
5
2
5va a 2 dir .
4
8- Bir dik üçgende 30 nin karşısı hipotenüsün yarısına, 60 nin
karşısı 30 nin karşısının
3 katına eşittir.
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
Üçgende metrik bağıntılar
dk
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Pisagor ve öklitin özelliklerini söyleme ve yazma
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
Sözel dilsel
9- İkizkenar dik üçgende hipotenüs bir dik kenarın 2 katıdır.
Doğacı
10- Bir dar açısı 15 olan dik üçgende hipotenüse ait yükseklik
Sosyal – Kişiler arası
1
BC
hipotenüsün
üne eşittir. AH
ve A( ABC ) 2a 2 dir .
Mantıksal – Matematiksel
4
4
İçsel bireysel
11- ABC üçgeninde,
Görsel – Uzaysal
[ AH ] [ BC ]
Müziksel – Ritmik
AC b , AB c
Bedensel - Kinestetik
BK x , CK y
olmak üzere
c y b x
dir .
12- Kenar uzunlukları3,4,5 ile orantılı olan her üçgen daima dik
üçgendir. Karşıtı daima doğru değildir.
13- ÖZEL DİK ÜÇGENLGER: x ve y pozitif tam sayıları için
bir dik üçgenin kenarları arasında şekildeki bağıntı varsa
kenarları tamsayıdır.
2
2
2
2
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
Üçgende metrik bağıntılar
dk
BÖLÜM2
Pisagor ve öklitin özelliklerini söyleme ve yazma
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
0
0
Sözel dilsel
14- 15 ve 75 nin trigonometrik oranları ;
Doğacı
1
cos 75 sin 15
6 2
Sosyal – Kişiler arası
32
Mantıksal – Matematiksel
sin 75 cos 15
6 2
İçsel bireysel
olarak bulunur .
Görsel – Uzaysal
Müziksel – Ritmik
15- 22,5 ve 67,5 nin trigonometrik oranları ;
Bedensel - Kinestetik
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
cos 67,5 sin 22,5
sin 67,5 cos 22,5
1
42 2
2 1
42 2
olarak bulunur .
16- UYARI: İki kenarı bilinen bir üçgenin alanı, bu kenarları
dik olduğunda en büyük olur.
17- Bir dik üçgende dik açıya ait açıortay aynı zamanda hipotenüse ait yükseklik ile kenarortay arasında kalan açının da
açıortayıdır.
[AE], BAC ile HAD açılarının açıortayıdır.
[AD], ABC üçgeninin [BC] kenarına ait kenarortayıdır.
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
İkizkenar ve eşkenar üçgen
dk
13/5/2011
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
İKİZKENAR VE EŞKENAR ÜÇGEN
Sözel dilsel
İKİZKENAR
ÜÇGEN: İki kenar uzunluğu yada iki açısının
Doğacı
ölçüsü birbirine eşit olan üçgene ikizkenar üçgen denir. İkizSosyal – Kişiler arası
kenar bir üçgende farklı kenar uzunluğuna taban, farklı olan
Mantıksal – Matematiksel açıya tepe açısı, eşit açılara da taban açıları denir.
1- Taban açıları eşittir. m(B)=m(C)
İçsel bireysel
2- İkizkenar bir üçgende tabana ait yükseklik
Görsel – Uzaysal
aynı zamanda açıortay ve kenar ortaydır.
Müziksel – Ritmik
AB AC ve [ AH ] [ BC ] ise
Bedensel - Kinestetik
BH HC ve m( BAH ) m(CAH ) dir .
Tepeye ait yardımcı elemanlar çakışıktır.
ha na v
a
dır .
3-Eşit kenarlara ait yükseklikler birbirine eşittir.
hb hc dir.
4-Eşit olan taban açılarının iç açıortay uzunlukları birbirine
eşittir. nb nc dir .
5-Eşit kenarlara ait kenarortay uzunlukları birbirine eşittir.
vb vc dir .
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
dk
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
6-Tepeye ait dış açıortay tabana paraleldir.[BC] // [AD dir.
Sözel dilsel
Doğacı
7-Taban üzerindeki bir P noktasından eşit kenarlara paralel
Sosyal – Kişiler arası
çizilirse; PD PE x y b c dir .
Mantıksal – Matematiksel
İçsel bireysel
8-Taban üzerindeki bir noktadan eşit kenarlara dikme inilirse;
Görsel – Uzaysal
PD PE h1 h2 hb hc dir.
Müziksel – Ritmik
Bedensel - Kinestetik
9-Taban uzantısındaki bir noktadan eşit kenarlara dikme inilirse;
PD PE h1 h2 hb hc dir.
AB AC
[ AH ] [ BC ] ve
[ DF ] [ BC ] ise
10-
FE FD 2 AH
2 x y 2ha dır .
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
dk
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
EŞKENAR ÜÇGEN:
Sözel dilsel
Bütün kenar uzunlukları, iç açılarının ölçüleri, dış açılarının ölçüleri
Doğacı
eşit olan üçgene eşkenar üçgen denir.
Ç=3a dır.
Sosyal – Kişiler arası
Mantıksal – Matematiksel 1-Bir eşkenar üçgende her köşeye ait yardımcı elemanlar çakışık
olup, tüm yardımcı elemanlar uzunlukça eşittir.
İçsel bireysel
Görsel – Uzaysal
a 3
ha hb hc na nb nc va vb vc
dir .
Müziksel – Ritmik
2
Bedensel - Kinestetik
2- i ) h a 3
2
a2 3
4
h2
h2 3
iii ) A( ABC )
dür.
3
3
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
ii ) A( ABC )
3-P, eşkenar üçgenin içinde herhangi
bir nokta,
[PE] // [BC]
[PD] // [AB]
[PF] // [AC] ise
PE PD PF x y z a dır.
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
dk
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
4-P, eşkenar üçgenin içinde herhangi bir nokta,
Sözel dilsel
[AH] ┴ [BC] , [PD] ┴ [BC] , [PE] ┴ [AC]
Doğacı
ve [PF] ┴ [AB] ise
Sosyal – Kişiler arası
a 3
PD PE PF h1 h2 h3 h
dir .
Mantıksal – Matematiksel
2
İçsel bireysel
5-ABC eşkenar üçgen,
[PF] ┴ [BC] [PD] ┴ [AB] ve [PE] ┴ [AC] ise
Görsel – Uzaysal
a 3
Müziksel – Ritmik
PD PE PF h
dir .
2
Bedensel - Kinestetik
6-ABC eşkenar üçgen
[PE] // [BC] , [PD] // [AC] ve [PF] // [AB] ise
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
PD PE PF a dır.
7-Bir eşkenar üçgende
i ) Yüksekliklerin kesim noktası, yani diklik merkezi;
ii ) Kenarortayların kesim noktası, yani ağırlık merkezi;
iii ) İç açıortayların kesim noktası, iç teğet çemberin merkezi
iv) Kenar orta dikmelerin kesim noktası, yani çevrel çemberin
merkezi aynı olup, çakışık olup ağırlık merkezidir, bundan
dolayı;
a 3
R 2r ise
R r 2r r 3r h
2
h a 3
2h a 3
r
ve R 2r
dür.
3
6
3
3
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
dk
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış
Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve
Ders Kitabı
kaynakça
Öğretmen
Öğrenci
ÜÇGENDE BENZERLİK
Sözel dilsel
ÜÇGENDE
BENZERLİK
Doğacı
İki üçgenin karşılıklı elemanları orantılı veya karşılıklı eleman-ları eş ise bu
Sosyal – Kişiler
üçgenlere benzer üçgenler denir.
arası
Mantıksal –
BC
AC
AB
k , k R k `ye iki üçgenin benzerlik oranı denir.
Matematiksel
EF
DF
DE
İçsel bireysel
Eğer k=1 ise ABC ve DEF üçgenlerine eş üçgenler denir.
Görsel – Uzaysal BENZERLİK TEOREMLERİ:
Müziksel – Ritmik i)(AA) Teoremi: İkişer açılarının ölçüleri eş olan üçgenler benzerdir.
ii)(KAK) Teoremi: İki üçgenin ikişer kenarları orantılı ve bu kenarlar arasındaki
Bedensel açıları eş ise üçgenler benzerdir.
Kinestetik
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
iii)(KKK) Teoremi: İki üçgenin karşılıklı kenarları orantılı ise üçgenler benzerdir.
1- Benzer üçgenlerin karşılıklı bütün elemanları uzunlukça orantılıdır.
ha
va
na 2u
ra
a
b
c
u
r
R
ı k dir .
ı
ı
ı
ı
ı
ı
ha ı v a ı na ı 2u
ra ı R
a
b
c
u
r
2- Benzer üçgenlerin alanlarının oranı benzerlik oranının karesine eşittir.
)
Aı BıC ı ve benzerlik oranı k ise A( ABC
k 2 dir .
ı ı
ı
ABC
A( A B C )
3-TEMEL ORANTI TEOREMİ: Bir üçgenin iki kenarını kesen ve üçüncü kenara
paralel olan bir doğru, bu kenarlar üzerinde orantılı parçalar meydana getirir.
AD
DB
AE
EC
,
AD
AB
AE
AC
dir . Teoremin karşıtı da doğrudur.
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
dk
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
4-TALES TEOREMİ
Sözel dilsel
d1 // d 2 // d 3 ise
Doğacı
AC
BD
AC
BD
Sosyal – Kişiler arası
dir .
Mantıksal – Matematiksel
CE
DF
AE
BF
İçsel bireysel
Görsel – Uzaysal
1 1 1
5-[AB] // [CD] // [EF] ise,
dir .
Müziksel – Ritmik
y x z
Bedensel - Kinestetik
6-[EF] // [AC] , [FD] // [AB] ise
EF
FD
1 dir .
AC
AB
7-ABC bir dik üçgen ve EFDA kare ise,
AC b, AB c ve EF x
b.c
dir
bc
AE
DF
yx
dir .
8-[AD] // [EF] // [BC]
EB
FC z y
olmak üzere karenin bir kenar uzunluğu; x
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
dk
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış
Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve Ders Kitabı
kaynakça
Öğretmen
Öğrenci
ÜÇGENDE ALAN
Sözel dilsel
ÜÇGENDE
ALAN
Doğacı
1- Bir üçgenin alanı, herhangi bir kenar uzunluğu ile o kenara ait yükseklik
Sosyal – Kişiler
uzunluğu çarpımının yarısına eşittir.
arası
a.ha
b.h
A( ABC )
A( ABC ) b
Mantıksal –
2
2
Matematiksel
c.h
İçsel bireysel
A( ABC ) c a.ha b.hb c.hc dir .
2
Görsel – Uzaysal
Müziksel –
2- İki kenar uzunluğu ile kenarlar arasındaki açı belli ise;
Ritmik
b.c. sin A
a.c. sin B
a.b. sin C
A( ABC )
A( ABC )
A( ABC )
dir .
Bedensel 2
2
2
Kinestetik
Açı 90 ise ABC üçgeninin alanı en büyük değerini alır.
3- Kenar uzunlukları bilinen üçgenin alanı;
abc
2
A( ABC ) u (u a )(u b)(u c)
2u a b c u
dir.
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
dk
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
4-İç teğet çemberinin yarıçapı r ve çevresi 2u olan üçgenin alanı;
Sözel dilsel
2u a b c
Doğacı
abc
Sosyal – Kişiler arası
u
olmak üzere;
2
Mantıksal – Matematiksel
A( ABC ) u.r
dir .
İçsel bireysel
Görsel – Uzaysal
5-Çevrel çemberin yarıçapı R olan üçgenin alanı;
Müziksel – Ritmik
a.b.c
A( ABC )
dir .
Bedensel - Kinestetik
4R
6-Dış teğet çemberlerinin yarıçapları
ra , rb , rc
olan üçgenin
alanı;
A( ABC ) (u a).ra
A( ABC ) (u b).rb
A( ABC ) (u c).rc dir .
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
dk
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
r, iç teğet çemberinin yarıçapı, dış teğet çemberlerinin
Sözel dilsel
yarıçapları olan üçgenin alanı;
Doğacı
Sosyal – Kişiler arası
SONUÇLAR:
Mantıksal – Matematiksel 1) Yükseklikleri ve taban uzunlukları eşit olan üçgenlerin alanİçsel bireysel
ları eşittir. d1 // d 2 ise A( ABC ) A( ABD) dir.
Görsel – Uzaysal
2)Yükseklikleri eşit olan üçgenlerin alanları oranı, o yüksekliğe
ait taban uzunlukları oranına eşittir.
Müziksel – Ritmik
A( ABD )
m
Bedensel - Kinestetik
dir .
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
A( ADC )
n
3) Tabanları eşit olan üçgenlerin alanları oranı, o tabana ait
yüksekliklerinin uzunlukları oranına eşittir.
A( ABC )
h1
A( DBC ) h2 dir .
4)
A( ADE )
a.d
dir .
A( ABC ) (a b).(c d )
5) A( ABDC )
BC . AD
2
dir .
6) Benzer üçgenlerin alanları oranı, benzerlik oranının karesine
eşittir.
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü
DERS PLANI
BÖLÜM1
Dersin Adı
Sınıfı
Ünitenin Adı / No
Konu
Önerilen Süre
GEOMETRİ
10
ÜÇGENLER
dk
ÖĞRETME – ÖĞRENME
ETKİNLİKLERİ
BÖLÜM2
Öğrenci kazanımları / Hedef ve Davranışlar
Ünite kavramları ve sembolleri / Davranış Örüntüsü
Güvenlik Önlemleri(varsa)
Öğretme-öğrenme-yöntem ve teknikleri
Anlatım
Kullanılan eğitim teknolojileri-Araç,gereç ve kaynakça Ders Kitabı
Öğretmen
Öğrenci
Sözel dilsel
A( DEF ) x.z.m y.t.n
7)
dir .
Doğacı
A( ABC )
a.b.c
Sosyal – Kişiler arası
Mantıksal – Matematiksel 8) O noktasından kenarlara çizilen paralellerin
oluşturduğu üçgenler için;
İçsel bireysel
A( ABC ) ( S1 S2 S3 ) 2 dir .
Görsel – Uzaysal
Müziksel – Ritmik
Bedensel - Kinestetik
A( ABC )
(a b c)( d e f )
9)
dir .
A( DEFG)
b(e f ) a.e
10) ABC üçgeninde [AN] açıortay ise
NK NH olacağında n;
A( ABN ) c m
dir .
A( ACN ) b n
11) Bir kenarortay üçgenin alanını 2 eş alana, üç kenarortay ise
6 eş alana ayırır.
12) Kenarların orta noktalarını ikişer ikişer birleştiren doğru
parçaları üçgenin alanını 4 eş alana ayırır.
BÖLÜM III
Ölçme ve değerlendirme
Bireysel öğrenme etkinliklerine yönelik ölçme değerlendirme
Grupla öğrenme etkinliklerine yönelik ölçme değerlendirme
Öğrenme güçlüğü olan öğrenciler ve ileri düzeyde öğrenme hızında
olan öğrenciler için ek ölçme değerlendirme etkinlikleri
Dersin diğer derslerle ilişkisi
BÖLÜM IV
Planın uygulanmasına ilişkin açıklamalar
Çağın DALDİKLER
Ders Öğretmeni
Okul Müdürü