TOPOLOJİK TEMEL KAVRAMLAR 1.1. Kümeler ve Fonksiyonlar A

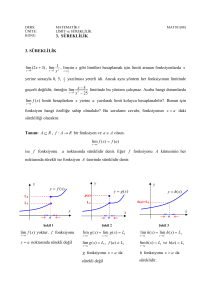
TOPOLOJİK TEMEL KAVRAMLAR
1.1. Kümeler ve Fonksiyonlar
A’nın bir elemanına B’nin yalnız bir elemanını eşleyen bağıntıya bir fonksiyon denir.
f : A → B , Domf = U ⊂ A ve rangef ⊂ B ’dir.
Tanım 1.1.1. f : A → B fonksiyonu için V ⊂ A olsun. U ∩ V ≠ ∅ olmak üzere;
f
V
: U ∩ V → B,
şeklinde tanımlı f
V
f
V
(a) = f (a)
fonksiyonuna f nin V üzerine kısıtlaması denir.
Tanım 1.1.2. f : A → B bir fonksiyon olsun. Domf =A ise f fonksiyonuna A’ya göre global
fonksiyon denir.
Tanım 1.1.3. f : A → B ve g : B → C iki fonksiyon olsun. ( Rangef ) ∩ Domg ≠ ∅ olmak
üzere;
gο f : A → C ,
( gο f )( a ) = g ( f ( a ) )
şeklinde tanımlı fonksiyona g ile f’nin bileşkesi denir ve gο f , g ( f ) şeklinde gösterilir.
Tanım 1.1.4. f : A → B bir fonksiyon olsun. Rangef = B ise f fonksiyonuna örten fonksiyon
denir.
Tanım 1.1.5. f : A → B bir fonksiyon olsun. ∀a1 , a2 ∈ A için f ( a1 ) = f ( a2 ) ⇒ a1 = a2
oluyorsa f’ye 1-1 fonksiyon (injection) denir.
Tanım 1.1.6. 1-1 örten fonksiyonlara bijeksiyon (bijection) denir.
Tanım 1.1.7. f : A → B 1-1 ve örten fonksiyon olsun. f ο g = I f ( A) ve gof = I f −1 ( B ) olacak
şekildeki g fonksiyonuna f nin tersi denir ve g = f −1 şeklinde gösterilir. Bu tanımdan da
anlaşıldığı gibi f −1of fonksiyonu yerine özdeşlik dönüşümünü bir bileşke işleminde yerine
yazarken dikkatli olmalıyız. poh ile pof −1ofoh fonksiyonları aynı fonksiyonlar değildir.
pof −1ofoh fonksiyonu poh fonksiyonunun bir kısıtlamasıdır.
Teorem 1.1.1. f : A → B ve g : B → A , fog ve gof fonksiyonları B ve A üzerinde özdeşlik
fonksiyonları olacak şekilde iki fonksiyon ise f , 1-1, örten ve g = f −1 dir.
Tanım 1.1.8. A1 ve A2 iki küme
p i : A1 × A2 → Ai ,
i = 1, 2
pi ( a1 , a2 ) = ai
şeklinde tanımlı fonksiyonlara izdüşüm fonksiyonları denir.
Tanım 1.1.8. f : A → A1 , g : B → B1 şeklinde verilen iki fonksiyon için
f × g : A × B → A1 × B1
( f × g )( a, b ) = ( f ( a ) , g ( b ) )
şeklinde
tanımlı
fonksiyona
f
ile
g
nin
kartezyen
çarpım
fonksiyonu
denir.
Dom ( f × g ) = ( Domf ) × ( Domg )
Tanım 1.1.9. Eğer önceki tanımda f : A → A1 , g : A → B1 şeklinde özel halini göz önüne
alırsak;
( f , g )( a ) = ( f ( a ) , g ( a ) )
Dom ( f , g ) = Domf ∩ Domg
Bu tanımları herhangi sonlu sayıdaki küme ve fonksiyonlar üzerine taşıyabiliriz.
Tanım 1.1.10. pi : A1 × ... × An → Ai ,
fi : Ai → Ci ,
pi ( a1 ,..., an ) = ai
i = 1, 2,..., n
f1 × f 2 × ... × f n : A1 × A2 × ... × An → C1 × C2 × ... × Cn
( f1 × f 2 × ... × f n )( a1 , a2 ,..., an ) → ( f1 ( a1 ) , f 2 ( a2 ) ,..., f n ( an ) )
Dom ( f1 × f 2 × ... × f n ) = ( Domf1 ) × ( Domf 2 ) × ... × ( Domf n )
fi : A → Ci ,
i = 1, 2,..., n
( f1 , f 2 ,..., f n )( a ) → ( f1 ( a ) , f 2 ( a ) ,..., f n ( a ) )
Dom ( f1 , f 2 ,..., f n ) = ( Domf1 ) ∩ ( Domf 2 ) ∩ ... ∩ ( Domf n )
A1 × A2 × ... × An
f: A
pi
f i = pi of
Ai
olmak üzere f i i = 1, 2,..., n fonksiyonlarına f nin bileşenleri denir.
Problemler 1.1.
1.
f : A → A1 , g : B → B1 , h : A1 → A2
ve
k : B1 → B2
fonksiyonları
verildiğine
göre
( h × k ) o ( f × g ) = ( hof ) × ( kog ) olduğunu gösteriniz.
2. f : A → A, g : B → B fonksiyonları verildiğine göre, p : A × B → A, p ( a, b ) = a olmak
üzere po ( f × g ) = fop olduğunu gösteriniz.
3.
f : A → B, g : C → D
( f × g)
−1
1-1 fonksiyonlar ise
f ×g
nin de 1-1 olduğunu ve
= f −1 × g −1 olduğunu gösteriniz.
4. f : A → B, g : A → C , h : B → B1 , k : B → B2 ve q : C → C1 fonksiyonları verildiğine
göre
i)
( h, k ) of = ( hof , kof )
ii) ( h × q ) o ( f , g ) = ( hof , qog )
olduğunu gösteriniz.
2.1. FONKSİYONLAR VE SÜREKLİLİK
Bu kısımda Öklid Uzayları arasındaki fonksiyonların özelliklerini gözden geçireceğiz.
Dom ( f ) ⊂ R n den R m ye tanımlanan f : Dom ( f ) → R m fonksiyonu; ∀x ∈ Dom ( f ) ⊂ R n
elemanına bir tek y ∈ R m noktası karşılık getiren kural olarak tanımlanır. x in f altındaki
resmini y = f ( x ) yazarak belirteceğiz. f : A → R m den kastımız f fonksiyonunun tanım
kümesinin A olmasıdır. Yani A daki her x elamanı için f ( x ) iyi tanımlıdır. A nın dışındaki
elemanlar içinde f ( x ) iyi tanımlı olabilir, A nın f için maksimal tanım küme olmasında ısrar
etmiyoruz.
f
A
pi of = fi
Rm
p
R
f i : A → R,
1 ≤ i ≤ m , fi ( x ) = yi şeklinde tanımlı fonksiyonlara f nin bileşen fonksiyonları
ya da kısaca bileşenleri denir. O zaman f ( x ) = ( f1 ( x ) ,..., f m ( x ) ) veya daha kısaca olarak
f = ( f1 ,..., f m ) şeklinde belirteceğiz.
Örnek:
a) f : R 2 → R 3 ,
f ( x , y ) = ( y , x, x + y )
b) f : R 3 → R,
f ( x, y, z ) = xyz
c) f : [ 0, ∞ ) → R 3 ,
d) f : R 4 → R 4 ,
(
f ( x , y , z ) = x , x, x
)
f ( x1 , x2 , x3 , x4 ) = ( x1 + x2 , x3 + x4 , x1 x2 , x3 x4 )
f1 ( x1 , x2 , x3 , x4 ) = x1 + x2 , f 2 ( x1 , x2 , x3 , x4 ) = x3 + x4 ,
f3 ( x1 , x2 , x3 , x4 ) = x1 x2 , f 4 ( x1 , x2 , x3 , x4 ) = x3 x4
olur.
Bu örneklerde fonksiyonlar formül yoluyla tanımlandı. Bununla beraber fonksiyonların kısıtlı
şekilde tanımlayacağını da belirtelim. Mesela; f : [1, ∞ ) → R , kuralı “f(x)” i
denkleminin çözümü şeklinde tanımlayabiliriz.
(y
2
(y
2
+ 1) e y = x
+ 1) e y ; y ye göre artan olduğundan
denklem bir tek çözüme sahiptir. Fakat f(x) için herhangi formül yoktur. Bu bir fonksiyonuna
ters fonksiyonuna örnektir. Bu konu 4. bölümde incelenecektir. O halde yukarıdaki ham
fonksiyon tanımındaki geçerli kuralı tam olarak oluşturmak için ne yapmalıyız sorusunu
sorabiliriz. Bu kesin tanım bir fonksiyonunun grafiğini tanımını verdikten sonra verilebilir.
f : A ⊆ R n → R m bir fonksiyon ise G grafiği de R n × R m nin G =
{( x, f ( x ) ) x ∈ A}
alt
kümesidir. ( x, y ) ∈ R n × R m için ( x, y ) ∈ G ⇔ x ∈ A ve y = f ( x ) dir.
Bir fonksiyonun grafiği hakkındaki bilgi f hakkındaki her şeyi söylediğinden f fonksiyonu G
grafiği ile özdeşlenir. O halde bir fonksiyonu kesin olarak tanımlamak için bu fonksiyonun
grafiğindeki sıralı ikili kümesini özelleştirmek gerekir. Hangi sıralı ikililerin kümesi bir
fonksiyonun grafiğidir? H, R n × R m nin herhangi sıralı ikililerinin kümesi olsun. H nın en az
bir fonksiyonunun grafiği olması için gerek ve yeter şart her ( x, y ) ∈ H , ( x, z ) ∈ H ⇒ y = z
olmasıdır.
Tanım 2.2. Bir f fonksiyonu
sıralı
çiftlerin
{
( x, y ) ∈ G
kümesidir.
Bu
Dom ( f ) = x ∈ R n ( x, y ) ∈ G, ∃y ∈ R m
}
ve
( x, z ) ∈ G ⇒ y = z
durumda
özelliğindeki G ⊆ R n × R m
nin
f
şeklinde tanımlanır ve
tanım
kümesi
de
y = f ( x ) ⇔ ( x, y ) ∈ G
şeklinde yazılır. Dönüşüm(Map) ve fonksiyon aynı anlamdadır.
f : A → R m bir fonksiyon ve A1 ⊆ A için f1 : A1 → R m , ∀x ∈ A1 için f1 ( x ) = f ( x ) şeklinde
tanımlı f1 fonksiyonuna f nin A1 ’e kısıtlaması denir ve f
A1
şeklinde yazılır. Benzer olarak
A ⊂ A2 , g : A2 → R m ve ∀x ∈ A için g ( x ) = f ( x ) ise f nin genişlemesi denir. Böyle g nin
tek olmadığı da bir gerçektir.
G = {( x, y )} şeklinde verilen sıralı çiftlerin cümlesi için G = {( y, x )} sıralı çiftlerin cümlesi
de
bir
fonksiyonun
grafiği
( y, x1 ) ∈ G, ( y, x2 ) ∈ G ⇒ x1 = x2
olma
özelliğini
gösterebilir.
Bunun
için
olması gerekir. Eğer G bir f fonksiyonun grafiği ise f nin 1-1
olması x1 ≠ x2 ⇒ f ( x1 ) ≠ f ( x2 ) olması ile tanımlanır. f 1-1 iken G da kesin olarak bir
fonksiyonun grafiğidir. Bu fonksiyona f nin tersi diyerek f −1 şeklinde belirteceğiz. Kısaca
x = f −1 ( y ) ⇔ y = f ( x ) dir.
Eğer f : A → S için S = f ( A ) oluyorsa f ye örten fonksiyon(veya A yı S üzerine dönüştüren
dönüşüm) denir. f : A → S 1-1 ve üzerine ise f ye bijection denir. f bijection ise f −1 : S → A
da bijectivedir. Reel değerli fonksiyonun tersinin olmadığını belirlemek basit bir konudur.
Reel değerli tanım kümesinde artan ve azalan fonksiyonlar bu aralıklarda 1-1 dir. Bu türevin
işaretinden bulunur. 4.Bölümde invers fonksiyonun varlığını göz önüne alarak türevinin
invers bulmada kullanılıp kullanılamayacağını göreceğiz. Şimdi önemli kavram olan
sürekliliğe dönelim.
Tanım 2.3. f : A ⊂ R n → R m bir fonksiyon olsun. a ∈ A olmak üzere; ∀ε > 0 için x ∈ A ve
x − a < δ ⇒ f ( x ) − f ( a ) < ε olacak şekilde δ > 0 sayısı bulunabiliyorsa f ye a da
süreklidir
denir.
Yada
kısaca
∀ε > 0, ∃δ > 0
vardır.
Öyle
ki
x∈ A
ve
x − a < δ ⇒ f ( x ) − f ( a ) < ε şeklinde gösterilir. Eğer ∀a ∈ A için f sürekli ise f ye A da
süreklidir denir. Bu yönteme ε − δ şartı diyeceğiz. δ , ε a bağlı olduğu kadar a noktasına da
bağlı olabilir.
Komşuluklara bağlı olarak; a ∈ A olmak üzere f ( a ) noktasının herhangi ε komşuluğuna
karşılık; f ( A ∩ B ( a, δ ) ) ⊆ B ( f ( a ) , ε ) olacak şekilde a nın bir δ komşuluğu varsa f ye a da
süreklidir denir. Bu sezgisel olan x noktaları a ya yaklaşırken f ( x ) noktaları da f ( a ) ya
yaklaşır şeklindeki tanıma kesinlik kazandırır. Eğer x in a ya yaklaştığını gözlemlediğimizde
f ( x ) de f ( a ) ya yaklaşmalıdır. Ne şekilde olursa olsun x in a ya yaklaşması esnasında x in
A içinde kalması çok önemlidir.
Bir a noktasındaki süreklilik lokal özellik olup, a nın komşuluğunda f nin davranışına
bağlıdır.
Eğer a, A nın yalnız (izole) noktasıysa δ yı öyle küçük seçebiliriz ki x − a < δ olacak
şekilde x ∈ A şeklindeki bir tek nokta a nın kendisi olur. O zaman tanım sağlanır ve f
fonksiyonu yalnız(izole) noktada otomatikman süreklidir. Bununla birlikte yalnız
noktalardaki sürekliliğin önemi azdır.
.a
δ
.x
Örnek 2.4. f : R n → R, f ( x ) = x ile tanımlansın o zaman f, R n üzerinde süreklidir. Yani
norm fonksiyonu R n de süreklidir.
Çözüm:
f ( x) − f ( y) = x − y ≤ x − y
eşitsizliğinden
x− y <δ =ε ⇒
f ( x ) − f ( y ) < ε olacak şekilde δ > 0 sayısı vardır. O halde f her y ∈ R n de süreklidir.
Örnek 2.5. pi : R n → R, pi ( x ) = xi i-yinci izdüşüm fonksiyonu süreklidir.
Çözüm:
pi ( x ) − pi ( y ) = xi − yi ≤ x − y
eşitsizliğinden;
x − y < δ = ε ⇒ pi ( x ) − pi ( y ) < ε olduğundan pi fonksiyonu süreklidir.
Teorem 2.6. f : A ⊆ R n → R m olsun. Aşağıdaki ifadeler denktir.
a) f, a ∈ A noktasında süreklidir.
{ }
( )
b) A daki herhangi x( k ) dizisi için x( k ) → a ⇒ f x( k ) → f ( a )
olur.
İspat: (Functions Several Real Variable p.39)
∀ε > 0
için
Teorem 2.7. f : A → R m ,
f = ( f1 ,..., f m ) ise f , a ∈ A da süreklidir ⇔ Her bir fi a da
süreklidir.
Teorem 2.8. f , g : A ⊆ R n → R m , a ∈ A da sürekli fonksiyonlar ve α ∈ R için α . f , f + g ve
m = 1 halinde f .g fonksiyonları da a ∈ A da süreklidir.
İspat: h = α . f olsun. f sürekli olduğundan ∀ε > 0 için
x − a < δ ⇒ f ( x) − f (a) < ε
olacak şekilde δ > 0 sayısı vardır. O zaman; ∀ε > 0 için
x − a < δ ⇒ h ( x) − h (a) = α f ( x) − f (a) < α ε
olacak şekilde δ > 0 sayısı vardır. O halde h = α . f fonksiyonu a ∈ A da süreklidir.
F = f +g
olsun.
f,
g
a∈ A
da
sürekli
olduğundan;
∀ε1 > 0
için
x − a < δ1 ⇒ f ( x ) − f ( a ) < ε1 olacak şekilde ∃δ1 > 0 sayısı vardır. Benzer şekilde g a ∈ A
da sürekli olduğundan ∀ε 2 > 0 için x − a < δ 2 ⇒ g ( x ) − g ( a ) < ε 2 olacak şekilde ∃δ 2 > 0
sayısı vardır. O zaman ∀ε = ε1 + ε 2 > 0 için
x − a < min {δ1 , δ 2 } = δ ⇒
F ( x) − F (a) =
≤
( f ( x ) − f ( a )) + ( g ( x ) − g ( a ))
( f ( x ) − f ( a )) + ( g ( x) − g ( a ))
⇒ F ( x ) − F ( a ) < ε1 + ε 2 = ε
olacak şekilde δ > 0 sayısı vardır. O halde F = f + g fonksiyonu a ∈ A da süreklidir.
m = 1 halinde ( f .g )( x ) = f ( x ) g ( x ) olmak üzere;
f ( x) g ( x) − f (a) g (a) = f ( x) g ( x) − f (a) g ( x) + f (a) g ( x) − f (a) g (a)
= ( f ( x) − f ( a )) g ( x) + f ( a ) ( g ( x) − g ( a ))
≤ f ( x) − f (a) g ( x) + f (a) g ( x) − g (a)
eşitsizliği vardır. M = 1 + f ( a ) + g ( a ) olsun. f a ∈ A da sürekli olduğundan ∀ε > 0 için
x − a < δ ⇒ f ( x) − f (a) <
ε
M
olacak şekilde δ > 0 sayısı vardır. Benzer şekilde ∀ε > 0 için
x − a < δ ⇒ g ( x) − g (a) <
ε
M
olacak şekilde δ > 0 sayısı vardır. O zaman
g ( x) = g ( x) − g (a) + g (a)
≤ g ( x) − g (a) + g (a)
<
olduğundan; ∀ε > 0 için;
ε
M
+ g (a) < 1+ g (a)
x − a < δ ⇒ f ( x) g ( x) − f (a) g (a) ≤ f ( x) − f (a) g ( x) + f (a) g ( x) − g (a)
⇒ f ( x) g ( x) − f (a) g (a) < g ( x)
(
ε
+ f (a)
M
) Mε +
< g (a) +1
<
(1 +
olacak şekilde δ > 0 sayısı vardır.
Örnek 2.9. f : R 2 → R,
f ( x, y ) = xy R 2 üzerinde süreklidir.
M
f (a)
f (a) + g (a)
M
ε
ε
M
)ε =ε
Çözüm : f , p1 ( x, y ) = x, p2 ( x, y ) = y izdüşüm fonksiyonlarının çarpımı olduğundan ve
izdüşüm fonksiyonları da R 2 üzerinde sürekli olduğundan Teorem 2.8’in son halinden f R 2
üzerinde süreklidir.
Fonksiyonları birleştirmenin başka bir yolu da bileşke almaktır. Bunun anlamı bir f
fonksiyonunu x noktasına uygulayarak elde ettiğimiz
f ( x ) görüntüsüne başka bir g
fonksiyonu uygulayarak g ( f ( x ) ) görüntüsünü elde etmektir. Bununla birlikte; her f ( x ) , g
nin tanım kümesine ait ise bu bileşke tanımlıdır. Bu nedenle;
f : A ⊆ R n → R p ve
g : B ⊆ R p → R m , f ( A ) ⊆ B ise gof : A ⊆ R n → R m , x ∈ A, ( gof )( x ) = g ( f ( x ) ) şeklinde
bileşke fonksiyon tanımlanır.
Teorem 2.10. f : A ⊆ R n → R p , g : B ⊆ R p → R m ve f ( A ) ⊆ B olsun. f nin a ∈ A da ve g
nin b = f ( a ) ∈ B de sürekli olduğunu kabul edelim. O zaman gof de a da süreklidir.
İspat: g, f ( a ) da sürekli olduğundan y ∈ B ve ε > 0 için
y − f ( a ) < ξ olur olmaz
g ( y ) − g ( f ( a ) ) < ε olacak şekilde ξ > 0 sayısı vardır. f, a da sürekli olduğundan ∀ξ > 0
için x ∈ A ve x − a < δ olur olmaz f ( x ) − f ( a ) < ξ olacak şekilde δ > 0 sayısı vardır. O
halde ∀ε > 0 için x − a < δ olur olmaz g ( f ( x ) ) − g ( f ( a ) ) < ε olacak şekilde δ > 0
sayısı vardır. O halde gof fonksiyonu a ∈ A da süreklidir.
Sonuç 2.11. g : A ⊆ R n → R
( m = 1)
a ∈ A da sürekli ve g ( a ) ≠ 0 olduğunu kabul edelim.
⎛1⎞
1
O zaman ⎜ ⎟ ( x ) =
fonksiyonu da a ∈ A da süreklidir.
g ( x)
⎝g⎠
İspat: h : R − {0} → R , h ( u ) =
1
şeklinde tanımlı fonksiyon olsun. h tanım kümesinde
u
süreklidir. g de a ∈ A da sürekli, g ( a ) ≠ 0 olduğundan B ( a, δ ) üzerinde g ( a ) ≠ 0 özellikli
B ( a, δ )
komşuluğu vardır. O zaman
x ∈ B ( a, δ )
⎛1⎞
için ⎜ ⎟ ( x ) = h ( g ( x ) )
⎝g⎠
fonksiyonların bileşkesi olur. O halde g, g ( a ) ≠ 0 ve a ∈ A da sürekli ise
süreklidir. f , g : R n → R , g ( a ) ≠ 0 özelliğinde a da sürekli iki fonksiyon iken
sürekli
1
de a da
g
f
1
= f.
g
g
fonksiyonu da Teorem 2.8 den a da süreklidir.
y ⎞
⎛
fonksiyonu R 2 üzerinde süreklidir.
Örnek 2.12. f : R 2 → R 2 , f ( x, y ) = ⎜ x 2 y,
2 ⎟
x
+
1
⎝
⎠
Çözüm: f1 ( x, y ) = x 2 y koordinat fonksiyonlarının çarpımı olduğundan ve f 2 ( x, y ) =
de g ( x, y ) =
y
1 + x2
1
sürekli fonksiyonu ile y nin çarpımından oluştuğundan süreklidir. O halde
1 + x2
Teorem 2.7. den f R 2 üzerinde süreklidir.
⎧ xy
,
⎪ 2
2
Örnek 2.13. f : R → R , f ( x, y ) = ⎨ x + y
⎪ 0
,
⎩
2
( x, y ) ≠ ( 0, 0 )
( x, y ) = ( 0, 0 )
fonksiyonunun sürekliliğini
araştırınız.
Çözüm: ( 0, 0 ) noktası hariç diğer bütün noktalarda f nin sürekli olduğu yukarıdaki çarpım ve
resiprokaller üzerine verilen sonuçlardan görebiliriz. ( 0, 0 ) da ( 0, 0 ) ’ın δ komşuluğundaki
( x, y )
ler için f ( x, y ) − f ( 0, 0 ) =
xy
< ε olup olmadığını araştıracağız. x ≠ 0 ve y = 0
x + y2
2
için f ( x, 0 ) = 0 ve bu nedenle ε − δ şartı sağlanır. Benzer şekilde ( 0, y ) , y ≠ 0 şeklindeki
noktalar için de sağlanır. x ≠ 0 , y = x doğrusu boyunca f ( x, x ) =
için f ( x, x ) − f ( 0, 0 ) =
1
ve bu nedenle ∀x ≠ 0
2
1
1
olur. O halde ε < için ε − δ şartı sağlanmaz. Bu nedenle de f,
2
2
( 0, 0 )
f (a)
da sürekli değildir. a ya yaklaşan x noktalarını göz önüne alarak f ( x ) noktalarının
ya
yaklaşıp
yaklaşmadığını
düşünmek
uygun
olur.
Şimdi
bu
düşünceyi
olgunlaştıracağız.
{
Tanım 2.14. B′ ( a, ε ) = x ∈ R n 0 < x − a < ε
} cümlesine a ∈ R
n
nin delinmiş ε -komşuluğu
denir ve B′ ( a, ε ) = B ( a, ε ) − {a} delinmiş açık yuvardır.
Tanım 2.15. f : A ⊆ R n → R m olsun. a, A nın limit noktası ise (yani ( A − {a} ) ∩ B ( a, δ ) ≠ ∅
ise) x, a ya giderken f ( x ) in limiti b ∈ R n ye eşit olması için gerek yeter şart her ε > 0 için
x ∈ B′ ( a, δ ) ∩ A ⇒ f ( x ) ∈ B ( b, ε ) olacak şekilde δ > 0 sayısının var olmasıdır.
Bu tanımda a noktasının A kümesinin bir limit noktası olmasına ihtiyacımız vardır. Yani
B′ ( a, δ ) ∩ A , her δ > 0 için en az bir nokta kapsamalıdır. Bununla birlikte a noktası A
kümesinin elemanı olmak zorunda değildir. Bu tanıma denk olan ve dizileri kapsayan önerme
olarak vereceğimiz bir tanım daha vardır.
Önerme 2.16. a, A ⊆ R n nin bir limit noktası ve f : A → R m bir fonksiyon olsun. O zaman
{ ) } ⊆ A, x( ) ≠ a, k ∈ N
lim f ( x ) = b ⇔ ∀ x (
x →a
( )
k
için x( k ) → a iken f x( k ) → b dir.
k
Tabii ki f, a da bir b limitine sahip olması için gerek ve yeter şart f nin her bir fi bileşeninin a
daki limitinin b nin bi bileşenine eşit olmasıdır.
Önerme 2.17. f , g : A ⊂ R n → R m ve lim f ( x ) = b ve lim g ( x ) = c olsun. O zaman;
x→a
x →a
a) lim ⎡⎣ f ( x ) ∓ g ( x ) ⎤⎦ = b ∓ c
x→a
b) lim (α . f )( x ) = α lim f ( x ) = α .b,
x →a
x→a
α ∈R
c) m = 1 için lim f ( x ) g ( x ) = ⎡ lim f ( x ) ⎤ ⎡ lim g ( x ) ⎤ = b.c
x→a
⎣ x→a
⎦ ⎣ x→a
⎦
***
A herhangi bir iç noktaya sahip değilken bu yapı bazı yanlışlıklara yol açar. Mesela,
{
}
A = x ∈ [ 0,1] x rasyonel sayı ve f : A → R , f ( x ) = 1 olsun. f nin A üzerinde sürekli olduğu
⎧1, x ∈ A
şeklinde tanımlı g
kesindir. Bununla birlikte f yi g : [ 0,1] → [ 0,1] , g ( x ) = ⎨
⎩0, x ∉ A
fonksiyonunun A üzerine kısıtlanmışı olarak göz önüne alabiliriz. g fonksiyonu [ 0,1] in
herhangi bir noktasında sürekli değildir. g
A
kısıtlaması A üzerinde sürekli olduğu halde g nin
kendisi A nın herhangi bir noktasında süreksizdir. Bir fonksiyon sürekli ise bu fonksiyonun
herhangi kısıtlaması da süreklidir. Yukarıdaki örnekten de görüleceği gibi bir fonksiyon
sürekli iken bu fonksiyonun genişletilmesi sürekli olmak zorunda değildir.
Daha önceden de belirttiğimiz gibi x → a iken limite sahip olan f ( x ) için a ya herhangi
tarzda yaklaşılabilir. Özel olarak a ya bütün doğrular boyunca yaklaşmakta aynı cevabı
verecektir. R n de a dan geçen ve doğrultusu u olan doğrunun
{ x = a + tu t ∈ R}
olduğunu biliyoruz. u yu doğrultu aldığımızda daima birim alacağız.
kümesi
Önerme 2.18. f : A ⊆ R n → R n , a ∈ int ( A ) olsun. lim f ( x ) = b olması her u doğrultusu için
x→a
lim f ( a + tu ) = b olmasını gerektirir.
t →0
İspat: lim f ( x ) = b ise ∀ε > 0 için x ≠ a,
x→a
x − a < δ ⇒ f ( x ) − b < ε olacak şekilde δ > 0
sayısı vardır. x = a + tu ∈ B′ ( a, δ ) , 0 < t < δ ⇒ f ( x ) = f ( a + tu ) ∈ B ( b, ε ) olur. O zaman
0 < t < δ ⇒ f ( a + tu ) − b < ε olacak şekilde δ > 0 sayısı vardır. Yani lim f ( a + tu ) = b dir.
t →0
Bu önermenin tersi doğru değildir. f doğrular boyunca limite sahip olabilir, fakat f nin limite
sahip olması gerekmez.
2.2. Süreklilik ve Kompaktlık
Sürekli fonksiyonların bir önemli özelliği de kompakt kümeleri kompakt kümelere
dönüştürmeleridir. R n nin altkümesinin kompaktlığından bu alt kümenin R n de kapalı ve
sınırlı olmasını kastedeceğiz.
Teorem 2.19. K, R n nin kompakt bir altkümesi ve f : K → R m K üzerinde sürekli fonksiyon
olsun. O zaman f ( K ) da R m nin kompakt altkümesidir.
İspat: (Functions of Several Real Variables p.44)
Sürekli fonksiyonlar altında ne kapalı bir kümenin görüntüsünün kapalı olması nede sınırlı bir
kümenin görüntüsünün sınırlı olması gerekir.
Örnek 2.20.
x2
a) f : R → R, f ( x ) =
olsun. f ( R ) = [ 0,1) olup R de ne açık ne de kapalıdır. Bu ayrıca
1 + x2
açık bir kümenin görüntüsünün de açık olmak zorunda olmadığını gösterir bir örnektir.
b) f : ( 0,1) → R, f ( x ) =
1
olsun. O zaman f
x
( ( 0,1) ) = (1, ∞ )
Teorem 2.19 dakine benzer düşünceleri kullanarak sürekli fonksiyonların sürekliliğini konu
edinen aşağıdaki teoremi verebiliriz.
Teorem 2.21. K, R n nin kompakt altkümesi ve f : K → R m de K üzerinde sürekli 1-1
fonksiyon olsun. O zaman f −1 : f ( K ) → K fonksiyonu süreklidir.
İspat: (Functions of Several Real Variables )
Bu teorem K kompakt olmadığı zaman doğru olmayabilir. Görüntü kümesi R de yattığında
fonksiyonların maksimum minimumları tartışılabilir.
Tanım 2.22.
f : A ⊆ R n → R fonksiyonu verilsin. a ∈ A olmak üzere ∀x ∈ A için
f ( x ) ≤ f ( a ) oluyorsa f, A üzerindeki a noktasında (global) maksimuma sahiptir denir. Bir
a ∈ A noktasının B ( a, δ ) komşuluğundaki bütün x ler için f ( x ) ≤ f ( a ) olacak şekilde δ -
komşuluğu varsa f fonksiyonu a noktasında (lokal) maksimuma sahiptir denir. Eğer bu
eşitsizliklerde sadece eşitsizlik var ise tam (strict) global maksimum ve tam lokal maksimum
terimleri kullanılır. Bu tanımlarda ≤ yerine ≥ alarak global minimum, lokal minimum
tanımları verilebilir. Maksimum ve minimum tanımlarını çalışmak analizdekine benzer olup
analizdeki teknikleri kullanacağız.
Teorem 2.23. f : K ⊆ R n → R dif.bilir, K ≠ ∅ ve K kompakt olsun. O zaman f, K üzerinde
bir global maksimum bir de global minimuma sahiptir.
{
}
İspat: M = Sup f ( x ) x ∈ K , f ( K ) nın üst sınırlarının en küçüğü olsun. Her boştan farklı
reel sayıların sınırlı cümlesi bir supremuma sahip olduğundan M vardır ve sonludur. Açık
olarak f ( x ) ≤ M , ∀x ∈ K ve M bu özellikteki en küçük sayıdır. M nin kompakt f ( K )
kümesine ait olduğunu gösterelim. Eğer M ∉ f ( K ) ise M ∈ ⎡⎣ f ( K ) ⎤⎦ ve ⎡⎣ f ( K ) ⎤⎦ açık
c
c
olur. O zaman M nin ( M − ε , M + ε ) şeklinde bir ε komşuluğu vardır ve bu f ( K ) nın
noktalarını kapsamaz. O halde ∀x ∈ K için f ( x ) ≤ M − ε olup M − ε bir üst sınırdır. Bu m
nin üst sınırların en küçüğü olması ile çelişir. O halde kabulümüz yanlış yani M ∈ f ( K )
olmak zorundadır. Yani; f ( x ) ∈ M özellikli x ∈ K vardır. Minimum için de ispat benzer
şekilde yapılır.
Yukarıdaki teoremden bir kompakt küme üzerindeki sürekli fonksiyon kendi sınırlarını
oluşturur.
Örnek 2.24.
Rn
üzerindeki her norm Öklidyen norma
α x 1 ≤ x 2 ≤ β x 1 anlamında denktir.
∀x ∈ R n , α , β ∈ R +
için
Çözüm: {ei i = 1,..., n} , R n nin standart bazı ve M = maks {ei i = 1,..., n} olsun. ∀x ∈ R n için
n
x = ∑ xi ei olup üçgen eşitsizliğinden;
i =1
x 1 ≤ x1 e1 + ... + xn en
≤ M ( x1 + ... + xn
≤M n x
α=
1
M n
2
alınarak
α x1≤ x
2
…(1)
)
elde edilir. Ayrıca ∀x, y ∈ R n için
x− y 1 ≤ M n ≤ x− y
fonksiyonunun sürekli olduğu gösterilir. O halde
.
1
2
eşitsizliği kullanılarak
.
{
1
}
fonksiyonu S = x ∈ R n x 2 = 1
kompakt kümesi üzerinde kendi m en küçük alt sınırını oluşturur. z ≠ 0 olduğundan
m = z 1 > 0 ile gösterelim. ∀z ≠ 0 için x = x
olup β =
1
alarak;
m
x2≤
1
x …(2)
m 1
bulunur. (1) ve (2) eşitliklerinden
2
x
yazabiliriz. x 1 = x
x2
2
x
x2
≥m x
1
2
1
M n
x1≤ x2≤
1
x
m 1
eşitsizliği bulunur. O halde .
1
ve .
2
bu anlamda denktirler.
Bir x noktasının bir A kümesine uzaklığı dist ( x, A ) = inf
{ x−a
}
a ∈ A şeklinde tanımlanır.
Genel olarak; infimumu oluşturacak şekilde a ∈ A noktası bulunmayabilir. Bununla birlikte
eğer A kompakt ise infimumu daima vardır. Bu norm fonksiyonunun sürekli olmasının bir
sonucudur ve Örnek 2.24. nedeniyle normla nerede çalışılırsa orada daima sağlanır. x in
yakınında a ∈ A noktası var olduğunda bu a tek olmak zorunda değildir. Mesela; x = 0
elemanı ve A = {a a = 1} kümesini göz önüne alırsak a tek değildir. A nın şeklini oyunun bir
parçası olarak görebiliriz. Buna ait önemli bir düşünce de A nın konveksliğidir.
Tanım 2.25. C, R n nin bir altkümesi ∀x, y ∈ C için x’i y’ye birleştiren
{(1 − t ) x + ty 0 ≤ t ≤ 1}
doğru parçası daima C de kalıyorsa C ye R n nin konveks altkümesi denir.
***
Bu geometrik yaklaşım C nin sınırı C nin içinden dışa doğru köşelenmiş ve kenarlar
oyulmamıştır. Düz doğru parçalarının oluşmasına müsaade edilmiştir.
Örnek 2.26. Açık ve kapalı yuvarlar konvekstir.
Çözüm: C = B ( z , r ) ve x, y ∈ C olsun. O zaman
eşitsizliğinden 0 ≤ t ≤ 1 için
x−z <r ,
y − z < r ve üçgen
(1 − t ) x + ty − z
= (1 − t ) x − (1 − t ) z + ty − tz
= (1 − t )( x − z ) + t ( y − z )
≤ (1 − t ) ( x − z ) + t ( y − z )
≤ (1 − t ) r + tr = r
olur. O halde x, y ∈ C ile sınırlı doğru parçası C nin içinde kalır. Kapalı yuvarlar içinde ispat
benzer şekilde yapılır.
Önerme 2.27. C, R n de kapalı konveks küme olsun. O zaman minimum normlu bir tek c ∈ C
noktası vardır. Yani; 0 a yakın bir tek c ∈ C noktası vardır.
İspat: d = inf
{y
}
y ∈ C olsun. O zaman d = 0 ise 0 ∈ C ve ispatlanacak bir şey yoktur. O
halde 0 ∉ C olsun. c = d olacak şekilde tam bir tane c ∈ C nin var olduğunu göstermek
istiyoruz. Eğer C sınırlı olsaydı böyle c nin varlığı garanti olacaktı çünkü sürekli fonksiyonun
kompakt küme üzerinde infimumuna ulaşır. Bununla birlikte C burada sınırlı olmak zorunda
olmamasına rağmen
C ′ = C ∩ B ( 0, d + 1)
i göz önüne alarak bu yapıyı bu hale
indirgeyebiliriz. O zaman C ′ kompakt ve minimal normlu c′ ∈ C ′ var ve bu C nin minimal
normlu bir noktasıdır. Böylece herhangi norm için minimum normlu noktanın varlığı
gösterilmiş olur. Teklik sadece C nin konveksliğine bağlı değil aynı zamanda komşuluklar
Öklidyen normun tam konvekslik özelliği dediğimiz aşağıdaki özelliğe sahip olmasına
bağlıdır.
x = y =d
Eğer
2
2
ve
2
x≠ y
x+ y + x− y = 2 x +2 y
tekliği gösterelim.
2
ise
x+ y
<r
2
oluyorsa tam konvekstir denir. Bu
şeklindeki paralel kenar kuralından hemen görülür. Şimdi
x = y = d ve x ≠ y olduğunu kabul edelim. O zaman normun tam konvekslik özelliğinden
x+ y
x+ y
< d ve C konveks olduğundan
∈ C ve bunun normu d den daha küçük olamaz.
2
2
O halde x = y olmak zorundadır. Bu ise tekliğin ispatıdır.
Hatırlatma: Öklidyen norm kullanıldığında varlık için kompaktlık gerekli değildir.
a noktasında ε − δ şartı ∀ε > 0 için x − a < δ ⇒ f ( x ) − f ( a ) < ε olacak şekilde bir δ (a
ve ε na bağlı) sayısının var olduğunu söyler. Özel bir ε için aynı δ her a ∈ A için
çalışabilir. Bu güçlü özelliğe düzgün süreklilik denir ve bu özellik f nin bir global özelliğidir.
Teorem 2.28. f : A ⊆ R n → R m fonksiyonunu göz önüne alalım. ∀ε > 0 için x, y ∈ A ve
x − a < δ ⇒ f ( x ) − f ( a ) < ε olacak şekilde sadece ε a bağlı bir δ sayısı varsa f ye A
üzerinde düzgün süreklidir denir.
Yukarıdaki Örnek 2.24. herhangi norm fonksiyonun düzgün sürekli olduğunu gösterir. Bu bir
fonksiyonun A üzerinde düzgün sürekli olması A nın her bir noktasında sürekli olmasını
gerektirdiğinden açıktır. Bunun tersi her zaman doğru değildir. Buna basit bir örnek;
f : ( 0, 2 ) → R, f ( x ) =
1
x
fonksiyonudur. Herhangi 0 < δ < 1 özelliğindeki δ için x = δ , y = 2δ alırsak;
f ( x) − f ( y) =
1
δ
−
1
1 1
=
>
2δ 2δ 2
olur. Bu ise f nin düzgün süreklilik şartlarının sağlanması için mümkün değildir. Bu fonksiyon
bölüm kuralı gereğince her a > 0 noktasında süreklidir. Fakat δ , a ya bağlıdır. Bununla
birlikte f nin tanım kümesi kompakt olduğunda süreklilik düzgün sürekliliğe denktir.
Teorem 2.29. f : K ⊆ R n → R m , kompakt K kümesi üzerinde sürekli olsun. O zaman f, K
üzerinde düzgün süreklidir.
İspat: (Functions of Several Real Variables p.49)
2.6. Topolojik Kavram Olarak Süreklilik
Açık(kapalı) kümelerin sürekli dönüşümler altındaki görüntülerinin açık(kapalı) olmasının
gerekmediğini
görmüştük.
Bununla
beraber
ters
görüntüleri
daha
iyi
olur.
f : A ⊆ R n → B ⊆ R m bir fonksiyon ve T de B nin bir alt kümesi olsun. T nin f altındaki ters
görüntüsü f −1 (T ) şeklinde gösterilir ve f −1 (T ) = { x ∈ A f ( x ) ∈ T } kümesidir. Yani bu, f
altındaki görüntüleri T de yatan A nın elemanlarının cümlesidir. Eğer f, 1-1 ise ( f −1 var) ve
T, f ( A ) da kapsanır ve f −1 (T ) de f −1 altında T nin görüntüsüyle çakışır.
Lemma 2.59. f : A ⊆ R n → R m bir fonksiyon ve S ⊆ A, T ⊆ R m olsun. O zaman;
a) S = f −1 (T ) ⇒ f ( S ) ⊆ T , yani f ( f −1 (T ) ) ⊆ T
b) T = f ( S ) ⇒ S ⊆ f −1 (T ) , yani S ⊆ f −1 ( f ( S ) ) .
İspat:
a) ∃x ∈ f −1 (T ) için y = f ( x ) olacak şekilde y ∈ f ( f −1 (T ) ) alalım. f −1 (T ) nin tanımından
bu x ∈ A ve f ( x ) ∈ T dir. Yani y ∈ T dir.
b) S ⊆ A olduğunu göz önüne alalım. x ∈ S ise f ( x ) ∈ f ( S ) ve böylece tanımdan
x ∈ f −1 ( f ( S ) ) .
(a) ve (b) de eşitlik, genel anlamda sağlanmaz. Bunu (a) için görmek istersek; T ⊆ f ( A )
yani f örten olmalıdır. (b) için f : R → R, f ( x ) = x 2 fonksiyonunu göz önüne alalım. O
zaman [ 0,1] = T = f
([0,1]) fakat
f −1 ([ 0,1]) = [ −1,1] olur. (b) de eşitliğin sağlanması için f nin
1-1 olmasıyla mümkündür.
Topoloji dersinde bir küme üzerinde sürekliliğin tanımı genellikle “Her açık kümenin ters
görüntüsü de açıktır.” Şeklinde özetlenir. f nin tanım kümesi üzerindeki topoloji R n
uzayından ortaya çıkar. Bu nedenle A üzerindeki rölatif topolojidir. Şimdi bu kavramları
açıklayalım.