Ders: Matematik Sınıf: 12.Sınıf Öğrenme alanı: Temel Matematik Alt

Ders: Matematik
Sınıf: 12.Sınıf
Öğrenme alanı: Temel Matematik
Alt Öğrenme Alanı: Belirsiz İntegral
Kazanım: Bir fonksiyonun belirsiz integralini açıklar.
Beceriler: Matematiksel düşünme, Akıl yürütme, Problem çözme, İlişkilendirme, İletişim kurma, Matematiksel
modelleme
Gerekli Ön Bilgiler(Hazır bulunuşluk): Fonksiyonlar, Türev, Belirli İntegral, Geogebra programı kullanımı
Amaç: Öğrencilerin, belirsiz integral anlaması ve açıklayabilmesi amaçlanır.
Araç ve Gereçler: Kâğıt, kalem, bilgisayar
Sınıf Mevcudu:24
Çalışma Yapılacak Grup: 4kişilik gruplar halinde yapılacaktır.
Süre: 1 ders saati
Kaynaklar: Ortaöğretim matematik (9, 10, 11 ve 12. sınıflar) dersi öğretim programı,
Wikipedia Türkiye…
Adım 1: Matematiksel Not
(Belirsiz İntegral Kavramı)
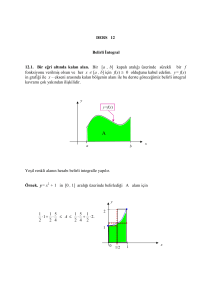
[a,b] I aralığını göstermek üzere, f fonksiyonu I aralığında süreklidir.
𝑏
1- F(x)=∫𝑎 𝑓(𝑡)𝑑𝑡 fonksiyonu I aralığında süreklidir. Bu fonksiyon türevlenebilirdir üstelik F’(x)=f(x) dir.
2- f,g fonksiyonları I aralığında süreklidir. Bu fonksiyonlar türevlenebilirdir. ∀𝑥 ∈ (𝑎, 𝑏) için f’(x)=g’(x) olur.
Buradan f(x)=g(x)+c olacak şekilde bir 𝑐 ∈ 𝑅 vardır.
Adım 2:Aşağıdaki tabloyu verilen örneğe göre doldurunuz. Bulduğunuz verileri karşılaştırarak aralarındaki ilişkiyi
matematiksel bir biçimde ifade ediniz.
𝒚 = 𝒇(𝒙)
f(x)= x
d 3
x  3x 2
dx
3
1
2
f(x)= x2+x-1
3
f(x)=
3
x2
2
𝑥
f(x)= 3x2+
4
𝒅𝒇(𝒙)
𝒅𝒙
∫ 𝒇(𝒙)𝒅𝒙
∫ 𝑥 3 𝑑𝑥 =
𝑥4
4
𝒅𝒇(𝒙)
∫[
] 𝒅𝒙
𝒅𝒙
𝒅
[∫ 𝒇(𝒙)𝒅𝒙]
𝒅𝒙
∫ 3𝑥 2 𝑑𝑥 = 𝑥 3
d x4
[ ] = x3
dx 4
𝑥 2 −3
5
f(x)= 𝑥 3 −9𝑥+6
6
f(x)= 2√𝑥
7
f(x)= √16 − 𝑥 2
8
9
10
11
12
13
14
15
16
17
18
f(x)= sinx
f(x)= tanx
f(x)= sinx+cos2x
f(x)= √1 − 𝑠𝑖𝑛2 𝑥
f(x)= sinx.cos2x
f(x)=
tan2 (tanx)
𝑐𝑜𝑠2 𝑥
𝑐𝑜𝑠2 𝑥+𝑠𝑖𝑛2𝑥
cos 𝑥
f(x)=
f(x)= ln 𝑥
f(x)=
lnx
𝑥
f(x)= ex
f(x)=ln 𝑒 𝑥
Bu şartlar altında ;
𝑥
[a,x] aralığında ∫𝑎 𝑓(𝑡)𝑑𝑡 = F(x) +c f fonksiyonun I aralığındaki belirsiz integrali denir.