(Microsoft PowerPoint - \307EMBER\335N ANAL

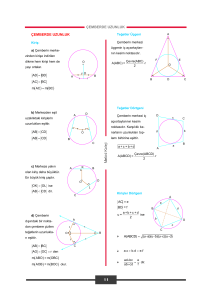
ÇEMBERİN ANALİTİK İNCELENMESİ HAKKINDA GENEL HATIRLATMALAR
ÇEMBER DENKLEMİ
PRATİ
PRATİK Bİ
BİLGİ
LGİ
x2 + y2 = r2 çemberine üzerindeki P(c, d) noktasından
y
P(x, y)
çizilen teğetin denklemi cx + dy = r2
r
b
M(a, b)
PRATİ
PRATİK Bİ
BİLGİ
LGİ
(x – a)2 + (y – b)2 = r2 çemberine üzerindeki P(c, d)
noktasından çizilen teğetin denklemi
x
a
(x – a)(c – a) + (y – b)(d – b) = r2
MERKEZİL ÇEMBER
Merkezi M(a, b) ve yarıçapı r olan çemberin denklemi
PRATİ
PRATİK Bİ
BİLGİ
LGİ
iki nokta arası uzaklık formülünden
x2 + y2 + Dx + Ey + F = 0 çemberine üzerindeki P(c, d)
(x – a)2 + (y – b)2 = r2 dir.
noktasından çizilen teğetin denklemi
E
D
cx + dy + (x+c) + (y+d) + F = 0
2
2
Merkezi M(0, 0) ve yarıçapı r birim olan çemberin denklemi
x2 + y2 = r2 dir
ÇEMBERE DIŞINDAKİ BİR NOKTADAN ÇİZİLEN
TEĞETİN DENKLEMLERİ
Bu çembere merkezil (merkezcil) çember denir.
normal
ÇEMBERİN GENEL DENKLEMİ
2ax – 2by +
a2
+
b2
–
r2
= 0 şeklinde de yazılabilir.
–2a = D, – 2b = E ve a2 + b2 – r2 = F alınırsa,
x2 + y2 + Dx + Ey + F = 0
r
.
P(
c,
d)
ru
su
+
y2 –
Teğet doğrusu
α ..
α
M(a,b)
do
ğ
x2
.
Te
ğe
t
(x – a)2 + (y – b)2 = r2 çember denklemi,
eks TR em yayınları
mMP
m1
genel çember denklemi elde edilir.
|MP| uzunluğu iki nokta arasındaki uzaklık ile bulunur.
r de belli olduğu için tanα bulunabilir.
Bu yazılışa göre çemberin merkezinin koordinatları
a=–
D
, b=–
2
E
2
ve r =
1
2
2
tanα =
2
D + E – 4F
m1 − mMP
1 + m1.mMP
Formülünden mmp bulunarak eğimi (mmp) ve geçtiği bir
ÇEMBERE ÜZERİNDEKİ BİR NOKTADAN ÇİZİLEN
TEĞETİN VE NORMALİN DENKLEMLERİ
normal
. P(c, d)
mnormal
noktası (P(c, d)) bilinen doğru denklemi yazılabilir.
Bir noktanın çemberin neresinde? (İçinde mi,üzerinde mi
d−b
=
c −a
mnormal =
yoksa dışında mı?) olduğunu anlamak için bu noktanın
−1
mteğet
koordinatları sıfıra eşitlenmiş çember denkleminde yerine
yazılır, bulunan sayının işaretine bakılır. Buna göre;
M(a,b)
Teğet doğrusu
– Eğer bu sayı pozitif ise nokta çemberin dışındadır.
– Eğer bu sayı negatif ise nokta çemberin içindedir.
P(c, d) noktası teğet ve normal doğrularının geçtiği noktadır.
– Eğer bu sayı sıfır ise nokta çemberin üzerindedir.
Eğimi ve bir noktası bilinen doğru denkleminden denklemler
Kısaca kuvvet almak noktanın çembere göre durumunu
kolayca bulunabilir.(ya da aşağıdaki yöntemler uygulanabilir.)
tespit eder…
229
[email protected]
Çemberin analitik incelenmesi hakkında genel hatırlatmalar
ÇEMBERDE KUVVET
PRATİ
PRATİK Bİ
BİLGİ
LGİ
T
x2 + y2 = r2 çemberinde orta noktası P(c, d) olan kirişin
uzunluğu: [Bu kiriş P den geçen en kısa kiriştir.]
P(m, n)
A
d)
.
P(
c,
B
| AB |= 2 | c 2 + d2 − r 2 |
P noktasının çembere göre kuvveti: |PT|2 dir.
PRATİ
PRATİK Bİ
BİLGİ
LGİ
P(m, n)
T
K
(x – a)2 + (y – b)2 = r2 çemberinde orta noktası P(c, d) olan
kirişin uzunluğu: [Bu kiriş P den geçen en kısa kiriştir.]
P noktasının çembere göre kuvveti: |PT|.|PK| dir.
A
.)
P(
T
c,d
B
| AB |= 2 | (c − a)2 + (d − b)2 − r 2 |
P(m,n)
K
P noktasının çembere göre kuvveti: – |PK|.|PT| dir.
PRATİ
PRATİK Bİ
BİLGİ
LGİ
KUVVET EKSENİ
.
O2
O1
Eğer çemberler kesişiyorsa, denklemlerdeki x2 , y2 li terimler
x2 + y2 + Dx + Ey + F = 0 çemberinde orta noktası P(c, d)
eks TR em yayınları
Kuvvet ekseni
Kuvvet ekseni
olan kirişin uzunluğu: [Bu kiriş P den geçen en kısa kiriştir.]
A
.
P(c,d
)
B
| AB |= 2 | c 2 + d2 + Dc + Ed + F |
Demek ki herhangi bir noktanın koordinatlarını bir çember
yok edilerek kuvvet ekseninin denklemi elde edilmiş olur.
denkleminde yerine yazdığımızda elde edilen sayı bir şeylerin
uzunluğunu veriyormuş!!!!
(x – a)2 + (y – b)2 = r2
Eğer sayı pozitif ise bu bize noktanın çemberin dışında
T
r
P(m, n)
noktadan çembere çizilen teğet uzunluğudur.
Eğer sayı negatif ise bu bize noktanın çemberin içinde
Ye
rin
e
ya
za
lım
M(a,b)
seçilmiş olduğunu gösterir ve bu sayının karekökü de
(x – a)2 + (y – b)2 – r2 = 0
| PT |= (m − a)2 + (n − b)2 − r 2
P noktasının çembere göre kuvveti = |PT|2 (Tanım)
seçilmiş olduğunu gösterir ve sayının mutlak değerce
karekökünün iki katı da bu noktadan geçen en kısa kirişin
uzunluğudur.
|PT| uzunluğunu bulmak için P noktasının
koordinatları sıfıra eşitlenmiş çember denkleminde
Eğer sayı sıfır ise bu bize noktanın çember yayı
üzerinde seçilmiş olduğunu gösterir.
yerine yazar ve bulunan değerin karekökünü alırız.
230
[email protected]
Çemberin analitik incelenmesi hakkında genel hatırlatmalar
EKSENLERE TEĞET ÇEMBERLER
y
YARIM ÇEMBER DENKLEMLERİ
y
y
y
r
M(– r,r)
r
r
r
M(r,r)
r
–r
O
r
–r
x
(x – r)2 + (y – r)2 = r2
r
O
(x + r)2 + (y – r)2 = r2
y
.
–r
x
x
.– r
x
y = − r 2 − x2
y = r 2 − x2
y
–r
r
x
y
x
y
r
–r
M(– r, – r)
–r
M( r, – r)
r
.
(x + r)2 + (y + r)2 = r2
.
–r
r
O
O
x
x
(x – r)2 + (y + r)2 = r2
–r
–r
y
y
x = r 2 − y2
r=a
b
M
r=b
b
Bir çemberin simetrisi alınırken merkezinin
koordinatlarının simetrisi alınır, yarıçap korunur.
a
x
eks TR em yayınları
M
a
x
(x – a)2 + (y – b)2 = a2
(x – a)2 + (y – b)2 = b2
MERKEZİ EKSENLER ÜZERİNDE BULUNAN
y
ÇEMBERLER
Bir A(x0 , y0) noktası
noktasının y = mx + n doğ
doğruları
rularına gö
göre
simetriklerinin geometrik yerinin denklemi:
Merkezi M(0 , n) ve yarı
yarıçap uzunluğ
uzunluğu çemberin
merkezi ile A(x0 , y0) arası
arasındaki uzaklı
uzaklık olan bir
çemberdir.
y
b
Bir A(x0 , y0) noktası
noktasının y = mx doğ
doğruları
rularına gö
göre
r
simetriklerinin geometrik yerinin denklemi:
r
a
x = − r2 − y2
x
Merkezi M(0 , 0) ve yarı
yarıçap uzunluğ
uzunluğu
x
x 02 + y02 birim
olan bir merkezcil çemberdir.
(x – a)2 + y2 = r2
x2 + (y – b)2 = r2
ÇEMBERİN DÜZLEMDE AYIRDIĞI BÖLGELER
BİR NOKTANIN BİR ÇEMBERE UZAKLIĞI
DIŞ BÖLGE
A noktasının çembere
|AB| = |MA| – r
en kısa uzaklığı
C
r
İÇ BÖLGE
M r B
A
A noktasının çembere
|AC| = |MA| + r
en uzak uzaklığı
İç Bölge: (x – a)2 + (y – b)2 < r2
İKİ ÇEMBER ARASI UZAKLIK
Dış Bölge: (x – a)2 + (y – b)2 > r2
Çemberler arası
en kısa uzaklık
A
r1
M1
A
C r2 M2
B
KUTUP DOĞRUSU
|BC| = |M1M2| – (r1+r2)
D
P(a, b)
AB: ax + by = r2
Çemberler arası
en uzun uzaklık
B
|AD| = |M1M2| + (r1+r2)
231
x2
+
y2
=
r2
AB: kutup doğrusu
[email protected]