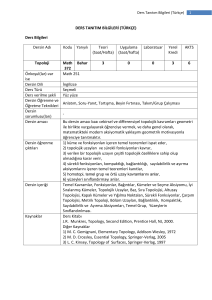
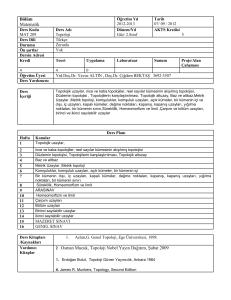
Topoloji Kavramı
Bunları anlatmadan önce Öğrenmenime CBS kitabındaki tüm uygulamaları (ya da en azından 231. sayfaya kadar olan uygulamaları yapmış ol.)
Literatürde nokta, çizgi ve alan verisi için aşağıdaki bilgi verilir.
Peki bu yapıları konumsal veritabanında nasıl
modelleriz?
Noktalar
Çizgiler
1. yol:
Çizgiler
2. yol:
Yakalama yapılmamışsa
yüzbinde birlik bir fark bile farklı
nokta gibi algılanmaya sebep
olabilir. Nokta koordinatları aynı
bile olsa topoloji yok, bğlantılılık
bilgisini elde etmek ağ analizi
yapmak mümkün değil ya da çok
zor
Alanlar
1. yol:
Alanlar
2. yol:
Topoloji Kavramı
Topoloji Kavramı
20 / 67
Şekil 1
Şekil 2
İlişkiselliği saklamak gerekir:
TOPOLOJİ
Nedir Şu Topoloji Dedikleri
/ Matematiksel Olarak Topoloji
/ Konumdan bağımsız olarak Topoloji
İzomorfizm
20 / 65
Peki bu ilişkiselliği konumsal
veritabanlarında nasıl modelleyebiliriz:
Üç Temel Topolojik Yaklaşımla:
1. Hat Düğüm Topolojisi
2. Poligon Hat Topolojisi
3. Sağ-Sol Topolojisi
1
2
Topoloji Kavramı
19 / 67
Topoloji Kavramı
20 / 67
Vector Spatial Analysis
• Map Overlay
– Union, Intersect, Identity, Erase, update, Clip, Select,
Split, Symmetrical Difference, Update Extract, Append,
Dissolve, Merge,
– Table Select
– Point in Polygon, Line in Polygon, Polygon on Polygon
• Proximity
– Buffer, Multiple Ring Buffer, Near, Point Distance
• Statistics
– Frequency, Summary Statistics
İntersect, union filan… her birinin çok farklı özellikleri var, okumakla öğrenmek zor.
Yaparak öğrenmek lazım. Arcgisi kurup tek tek benzer veriler üzerinde çalıştırıp
topolojik olarak ne oluyor görüp öyle öğrenmek lazım.
Dolayısı ile topolojiyi anlatırken hepsini anlatmak zor. Gerek de yok. Ama bir
tanesini seçip (clip, union vb mesela…) topolojik olarak olabilecekleri anlatmak
lazım. Kenarlaştırmadaki problemleri anlatmak lazım mesela… iki resmin
birleşmesi gibi basit bir birleştirme olmadığını geri planda veritabanında bir çok
işlemin meydana geldiğini, topolojik olarak veri yapılarında bir çok değişiklik
olduğunu belirtmek lazım.
Diğerlerinin de genel olarak yaptıklarından bahsedip her birinde çok ince detaylar
olduğundan, bu detaylar sebebi ile birbirlerinden ayrıştıklarından bahsetmek lazım.
Her birinde topolojik olarak çok farklı işlermler meydana geldiğinden bahsetmek
lazım.
Poligon: iki kural
Poligonlar arasındaki geçişler
38
İki poligon katmanı: beş kural
İlk katmanın elemanları, ikinci katmanın
bir elemanının içinde kalmalı
39
Çizgi: sekiz kural
İki farklı çizginin çakışık parçaları
40
İki çizgi katmanı: iki kural vd
İki çizgi çakışmamalı
41
Topological models and frameworks for 3D spatial objects Siyka Zlatanovaa,*, Alias Abdul Rahmanb, Wenzhong Shic
Topological models and frameworks for 3D spatial objects Siyka Zlatanovaa,*, Alias Abdul Rahmanb, Wenzhong Shic
MJEJRH-SDH1990.pdf
MJEJRH-SDH1990.pdf
Paper_Billen_Zlatanova.pdf
Paper_Billen_Zlatanova.pdf
Paper_Billen_Zlatanova.pdf
Paper_Billen_Zlatanova.pdf
Paper_Billen_Zlatanova.pdf
Paper_Billen_Zlatanova.pdf
Paper_Billen_Zlatanova.pdf
Paper_Billen_Zlatanova.pdf
Paper_Billen_Zlatanova.pdf