Uploaded by
common.user5370
AyrikKontrol.ipynb - Colaboratory
Ayrık Kontrol Sistemleri Ders Notu
Hazırlayan: Dr.Öğr. Üyesi Musa Nurullah Yazar
İÇERİK
1. Ayrık Zaman Sistemler ve Matematiksel Temeller
2. Ayrık Zaman Sistemlerin Analizi
3. Ayrık Zaman Açık Çevrim, Kapalı Çevrim Kontrol Sistemleri
4. Ayrık Zaman Kontrolör Tasarımı
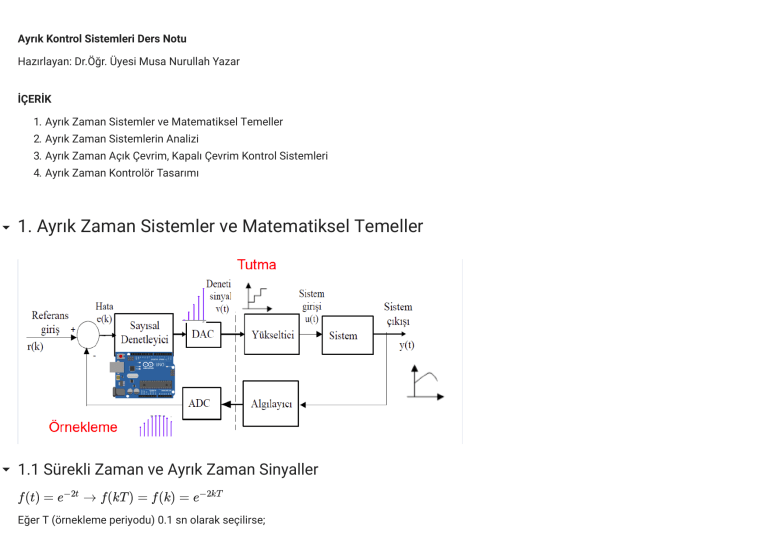
1. Ayrık Zaman Sistemler ve Matematiksel Temeller
1.1 Sürekli Zaman ve Ayrık Zaman Sinyaller
−2t
f (t) = e
−2kT
→ f (kT ) = f (k) = e
Eğer T (örnekleme periyodu) 0.1 sn olarak seçilirse;
/
−0.2k
f (k) = e
1.2 Ayrık Zamanda Temel Test Sinyalleri
1.3 Sürekli Zaman Sistemlerden Ayrık Zaman Sistemlere Geçiş
Sürekli Zaman Sistemler:
/
Doğrusal / Doğrusal Olmayan
Zamanla Değişmeyen / Zamanla Değişen
1.3.1 Birinci Dereceden Fark Denklemleri
Doğrusal zamanla değişmeyen birinci dereceden bir sistem örneğini ele alalım
dy(t)
+ 2y(t) = 3u(t)
dt
Transfer Fonksiyonu:
U (s) →
G(s)
→ Y (s)
Burada G(s)'i bulmak için diferansiyel denkleme Laplace dönüşümü uygulanırsa:
Y (s)
sY (s) + 2Y (s) = 3U (s) → G(s) =
3
=
s + 2
U (s)
Sistemin Ayrık Zaman Modeli elde edilirken diferansiyel denklemdeki türev ifadeleri İleri Fark Yöntemi, Geri Fark Yöntemi veya Merkezi Fark
Yöntemi (Bilineer Dönüşüm-Tustin Algoritması yöntemlerinden biri seçilerek fark denklemine dönüştürülür.
Eğer İleri Fark Yöntemini kullanırsak
dy(t)
y[(k + 1)T ] − y(kT )
|
dt
t=kT
≅
y(k + 1) − y(k)
=
T
T
Bulduğumuz ifadeyi denklemde yerine koyup düzenlersek
y(k + 1) = (1 − 2T )y(k) + 3T u(k) → k = 0, 1, 2, . . .
Elde ettiğimiz fark denklemindeki çıkış sinyalini python ortamında çizdirebiliriz.
import numpy as np
import matplotlib.pyplot as plt
T=0.3 # örnekleme zamanı
k=50
u=np.ones(k) # giriş işareti; birim basamak fonksiyonu
y=np.zeros(k) # çıkış işareti ilk değer atama
print(y[49])
for i in range(k-1):
y[i+1] = (1-2*T)*y[i] + 3*T*u[i]
/
y[i+1]
(1 2 T) y[i] + 3 T u[i]
plt.plot(y)
plt.xlabel('k')
plt.ylabel('y(k)')
plt.show
0.0
<function matplotlib.pyplot.show>
1.3.2 İkinci Dereceden Fark Denklemleri
d
2
y(t)
dy(t)
+ 2ξωn
dt
dy(t)
= q(k)
dt
2
T
y(t)
dq(k)
≅
dt
2
y(k + 1) − y(k)
≅
d
2
+ ωn y(t) = ωn u(t)
dt
q(k + 1) − q(k)
=
dt
T
/
d
2
y(t)
y(k + 2) − 2y(k + 1) + y(k)
≅
dt
T
2
Elde ettiğimiz türev ifadelerini denklemde yerine koyup düzenlersek
2
y(k + 2) = (2 − 2ξωn T )y(k + 1) + (2ξωn T − 1 − ωn T
2
2
)y(k) + ωn T
2
u(k)
Denklemdeki ξ modellenen sistemin sönüm oranını, ωn ise doğal frekansını verir.
u(k) birim basamak fonksiyonu, y(0)=0, T=0.1, xi =0.5, w_n=1 olmak üzere y fonksiyonunu çizdirin.
Nasıl bir y sinyali tahmin ediyorsunuz?
Farklı örnekleme zamanları (T=0.4, T=1, T=5) ile sonuçları elde ediniz
Farklı örneklme zamanlarında sonuç nasıl değişti, yorumlayın
import numpy as np
import matplotlib.pyplot as plt
# İkinci dereceden fark denklemi
# y(k+2) = (2-2*xi*w_n*T)*y(k+1)+(2*xi*w_n*T-1-w_n^2*T^2)*y(k)+w_n^2*T^2*u(k)
# u(kT)=u(k) birim basamak fonksiyonu u(k)=1, k=0,1,2,..
# T: örnekleme periyodu
T=1
k=200
u=np.ones(k)
y=np.zeros(k)
xi = 0.4 #sönüm oranı
w_n = 0.2 #doğal frekans
# python'da bir sayının n. dereceden kuvveti x**n ile hesaplanır
# veya math kütüphanesi "import" edilip math.pow(x,n) ile de hesaplanabilir.
for i in range(k-2):
'''KODU TAMAMLA !'''
plt.plot(y)
plt.xlabel('k')
plt ylabel('y(k)')
/
plt.ylabel('y(k)')
plt.show
<function matplotlib.pyplot.show>
1.4 Matematiksel Temeller (Z-Dönüşümü)
1.4.1 Z-Dönüşümü
1.4.2 Z-Dönüşümü Özellik ve Teoremleri
1.4.3 Ters Z Dönüşümü
1.4.4 Fark Denklemlerinin Z-Dönüşümü ile Çözümü
1.4.5 Ayrık Zaman Transfer Fonksiyonu
1.4.1 Z-Dönüşümü
Sürekli zamanda doğrusal diferansiyel denklemlerin çözümünde Laplace dönüşümü kullanılırken, ayrık zamanda fark denklemlerinin
çözümünde Z-Dönüşümü kullanılır. Z-dönüşümü fark denklemlerini cebirsel hale getirir. Ayrık zaman bir sinyalin, y(k), tek yönlü (0
→ ∞
)Z
Dönüşümü sürekli zaman sinyalinin Laplace dönüşümünün örneklemiş ifadesinden elde edilir.
∞
Y
∗
−skT
(s) = ∑ y(k)e
k=0
/
Burada
sT
z = e
olarak tanımlanır ve kompleks bir değişkendir. Ayrık bir sinyalin Z dönüşümü aşağıdaki gibi elde edilir.
∞
Z {Y (k)} = Y (z) = ∑ y(k)z
−k
k=0
Yukarıdaki denklem sonsuza giden bir seriyi ifade eder ve seriler belirli koşullarda bir değere yakınsar. Çoğu seri aşağıdaki açılımla ifade
edilebilinir.
∞
∑q
n
= 1 + q + q
2
+ q
3
+ ⋯ + q
n
1
=
, |q| < 1
1 − q
n=0
Yukarıdaki denklem her iki taraftan q ile çarpılırsa;
∞
q∑q
n
= q + q
2
+ q
3
+ ⋯ + q
n+1
n=0
Elde ettiğimiz denklemi bir öncekinden çıkarırsak;
∞
∞
∑q
n
− q∑q
n=0
∑q
n
1 − q
n+1
n+1
=
1 − q
n=0
< 1
= 1 − q
n=0
∞
Eğer |q|
n
ise bu seri
∞
∑q
n=0
n
1
=
1 − q
'e yakınsar.
Örnek 1.4.1: Birim basamak fonksiyonunun Z dönüşümü:
u(kT ) = u(k) = (1)
k
/
∞
U (z) = Z {u(kT )} = ∑ u(k)z
−k
= u(0)z
0
+ u(1)z
−1
+ u(2)z
−2
+ …
k=0
∞
U (z) = ∑(z
−1
)
k
= 1 + z
−1
+ z
−2
+ z
−3
+ …
k=0
|z
−1
1
| < 1 → U (z) =
1 − z
Örnek 1.4.2: y(t)
−at
= e
z
=
−1
z − 1
Eksponensiyel Fonksiyon'un Z dönüşümü
∞
−at
Y (z) = Z {e
∞
−akT
} = ∑e
z
−k
−aT
= ∑(e
k=0
|e
z
−1
−aT
| < 1 → ∑(e
z
−1
−1
)
k
k=0
∞
−aT
z
)
k
1
=
−aT
1 − e
k=0
z
−1
z
=
−aT
z − e
1.4.2 Z Dömüşümü Özellikleri ve Teoremleri
Teorem 1: Doğrusallık
Z {ay 1 (kT ) ± by 2 (kT )} = aY1 (z) ± bY2 (z)
Teorem 2: Zamanda Gecikme (Sağa Kaydırma)
Z {y(kT − n)} = z
−n
Y (z)
∞
∞
Z {y(kT − n)} = Z {y(k − n)} = ∑ y(k − n)z
−k
= z
−n
k=0
∑ y(k − n)z
−(k−n)
k=0
∞
q = k − n → z
−n
∑ y(q)z
−(q)
= z
−n
Y (z)
k=0
başlangıç değerleri sıfırdan farklı ise
/
−n
Z {y(k + n)} = z
−n
[Y (z) + ∑ y(k)z
−k
]
k=−1
Teorem 3: Zamanda Öngörü (Sola Kaydırma)
n
Z {y(k + n)} = z
Y (z)
başlangıç değerleri sıfırdan farklı ise
n−1
Z {y(k + n)} = z
n
[Y (z) − ∑ y(k)z
−k
]
k=0
Teorem 4: Son Değer Teoremi
y(∞) = limz→1 (z − 1)Y (z)
Teorem 5: Kompleks Türev (t ile çarpma)
d
Z {ty(t)} = −T z
F (z)
dz
Teorem 6: Kompleks İntegral (t'ye bölme)
y(t)
Z{
Y (z)
1
} = −
t
∫
T
z
Örnek 1.4.3: Rampa fonksiyonunun Z dönüşümü
r(t) = tu(t)
Teorem 5'i kullanırsak
Z {tu(t)} = −T z
d
U (z)
dz
U (z)
'i önceki örnekte bulmuştuk
U (z) =
z
z − 1
d
−1
U (z) =
dz
(z − 1)
2
/
Tz
R(z) = Z {tu(t)} =
(z − 1)
2
olarak bulunur.
Çok Kullanılan Ayrık Zaman Sinyallerin Z Dönüşümü
Analog Fonksiyon
Örneklenmiş Fonksiyon
Z-Dönüşümü
u(t)
u(kT)
z−1
r(t)
tu(kT)
e
e
e
−at
e
sin(wkT)
cos(wt)
cos(wkT)
−at
−akT
sin(wt)
e
cos(wt)
e
−akT
k
Tz
(z−1)
z−e
z
2
−2zcos(wT )+1
z(z−cos(wT ))
z
2
z
2
−2zcos(wT )+1
−2ze
2
−aT
−aT
−ze
−2ze
sin(wT )
cos(wT )+e
−aT
−aT
−2aT
cos(wT )
cos(wT )+e
−2aT
z
k
a u(t)
2
z
cos(wkT )
−aT
zsin(wT )
z
ze
sin(wkT )
2
z
−akT
sin(wt)
−at
z
a u(kT )
z−a
Fark denklemlerinin z-dönüşümünü alma
Örnek 1.4.4:
y(k) − 1.6y(k − 1) + 0.64y(k − 2) = u(k)
y(−1) = 1, y(−2) = 0
ve u(k)
= (0.5)
k
olmak üzere verilen fark denkleminin çözümünü z-dönüşümü kullanarak inceleyiniz.
Başlangıç koşulları dikkate alınmadığında;
Y (z) − 1.6z
u(k)
−1
Y (z) + 0.64z
−2
Y (z) = U (z)
'nın z-dönüşümü:
/
z
U (z) =
z − 5
z
3
Y (z) =
(z − 0.5)(z − 0.8)
2
Başlangıç koşulları dikkate alındığında ise;
Y (z) − 1.6[z
−1
Y (z) + y(−1)] + 0.64[z
−2
Y (z) + z
−1
z
y(−1) + y(−2)] =
z − 0.5
z
Y (z) =
3
(z − 0.5)(z − 0.8)
2
1.6z
+
2
− 0.64z
(z − 0.8)
2
1.4.3 Ters Z Dönüşümü
Ters z-dönüşümü kuvvet serisine açma, kısmi kesirlere ayırma ve rezidü yöntemleri ile hesaplanabilir.
Kuvvet Serisi Yöntemi Bölme işlemi yapılır ve negatif z kuvvetlerinden oluşan bir seri elde edilir.
Örnek 1.4.5:
z
Y (z) =
z
Y (z) = z
−1
+ 3z
−2
2
− 3z + 2
+ 7z
−3
+ 15z
−4
+ …
∞
Y (z) = ∑ y(k)z
−k
k=1
y(k) = 2
k
− 1
Kısmi Kesirlere Ayırma Yöntemi: Verilen ifade basit kesirlere ayrılır, her basit kesrin z-dönüşümü ayru ayrı bulunur. Ancak z dönüşüm tablosuna
bakıldığında z-dönüşümlerinin payında her zaman z çarpanı vardır. Bu nedenle verilen ifade öncelikle z'ye bölünerek kısmi kesirlere ayrılır.
Örnek 1.4.6:
−aT
(1 − e
Y (z) =
)z
−aT
(z − 1)(z − e
)
/
−aT
Y (z)
1 − e
=
z
1
−aT
(z − 1)(z − e
1
=
−
−aT
z − 1
)
z − e
−akT
y(k) = 1 − e
Örnek 1.4.7:
1
Y (z) =
(z − 1)(z − 2)
Y (z)
1
=
z
0.5
=
1
−
z
z(z − 1)(z − 2)
+
z − 1
y(k) = 0.5δ(k) − u(k) + 0.52
0.5
z − 2
k
Örnek 1.4.8:
2z
3
Y (z) =
+ z
2
(z − 2) (z − 1)
Payda kökleri reel ve çakışık olduğundan
Y (z)
2z
=
z
2
+ 1
A
B
=
2
+
z − 1
(z − 2) (z − 1)
2z
2
A = (z − 1)
(z − 2)
+ 1
2
(z − 2) (z − 1)
B = (z − 2)
2z
2
2
∣
∣
+ 1
2
(z − 2) (z − 1)
1
d
C =
[(z − 2)
1! dz
2
2z
2
∣
∣
2
y(k) = 3u(k) + 4.5k2
k
]∣
∣
− 2
z − 2
= 9
z=2
(z − 2) (z − 1)
2
= 3
z=1
+ 1
C
+
z=2
= −1
k
1.4.4 Fark Denklemlerinin Z-Dönüşümü ile Çözümü
/
Örnek 1.4.9: Başlangıç koşulları verilen aşağıdaki fark denklemini z dönüşümü ile çözünüz
y(k + 2) + 3y(k + 1) + 2y(k) = 0,
2
y(0) = 0, y(1) = 1
2
z Y (z) − z Y (0) − zY (1) + 3zY (z) − 3zY (0) + 2Y (z) = 0
z
Y (z) =
z
2
z
=
z
−
z + 1
+ 3z + 2
y(k) = (−1)
k
− (−2)
z + 2
k
1.4.5 Ayrık Zaman Transfer Fonksiyonu
Başlangıç koşullarının sıfır olduğu durumda çıkışın girişe bölünmesiyle transfer fonksiyonu elde edilir.
y(k) + a1 y(k − 1) + … an y(k − n) = b0 u(k) + ⋯ + bm u(k − m)
Y (z) + a1 z
−1
Y (z) + ⋯ + an z
G(z) =
−n
Y (z) = b0 U (z) + ⋯ + bm z
b0 + b1 z
−1
+ ⋯ + bm z
1 + a1 z
−1
+ ⋯ + an z
−m
U (z)
m
n
¯¯
¯¯¯¯¯¯¯
¯
U (z) → ∣
∣G(z) ∣
∣ → Y (z)
–––––
Örnek 1.4.10: Aşağıda verilen fark denklemini kullanarak transfer fonksiyonunu bulunuz.
y(k + 1) + 4y(k) + 3y(k − 1) = u(k) − 2u(k − 1)
zY (z) + 4Y (z) + 3z
−1
Y (z) = U (z) − z
z
=
z+5
(z+2)(z−3)
U (z)
z − 1
G(z) =
Örnek 1.4.11: Transfer fonksiyonu G(z)
−1
2
+ 4z + 3
ile verilen sistemin birim basamak cevabını bulunuz.
z
z + 5
Y (z) = U (z)G(z) =
z − 1 (z + 2)(z − 3)
/
Y (z)
z + 5
A
=
z
B
=
+
z − 1
(z − 1)(z + 2)(z − 3)
C
+
z + 2
z − 3
A = −1, B = 0.2, C = 0.8
y(k) = (−1)
k
+ 0.2(−2)
2. Ayrık Zaman Sistemlerin Analizi
k
+ 0.8(3)
k
2.1 Ayrıklaştırma Yöntemlerinin Laplace Karşılığı ve Kararlılık Analizi
x(k + 1) − x(k)
ẋ(t) =
T
Laplace ve z dönüşümleri uygulanırsa;
zX(z) − X(z)
sX(s) =
z − 1
→ sX(s) =
T
X(z)
T
Buradan ileri fark yöntemi ile ayrıklaştırma yapıldığında s ve z düzlemi arasındaki ilişki
s =
z−1
T
veya z
= 1 + sT
olarak bulunur.
İleri fark yöntemi ile ayrıklaştırılan bir sistemin kararlılığı Laplace domeninden yola çıkılarak bulunabilir. Laplace domeninde kararlılık Re(s)
olduğunda göre z domeninde Re(
z−1
T
) < 0
, z değişkeninin karmaşık bir değişken olduğunu hatırlarsak z
x + jy − 1
Re(
x − 1
) < 0 → Re(
T
kararlı bölge
y
+ j
T
= x + jy
< 0
)
T
x − 1
< 0 → x < 1
T
/
Bilineer Dönüşüm (Yamuk Kuralı) ile Ayrıklaştırma:
Bir sinyalin herhangi bir andaki integrali sürekli zamanda sinyalin o ana kadar taradığı alanın toplamıdır. Matematiksel olarak;
t
y(t) = ∫
x(t)dt + y(t0 )
t0
ifade edilir. Laplace dönüşümü ise:
1
Y (s) =
X(s)
s
dir.
/
Ayrık zamanda bir sinyalin t anındaki taradığı alanı yamuk kuralı ile yaklaşık olarak bulunabilir.
T
y(k) = y(k − 1) +
(x(k) + x(k − 1))
2
Z dönüşümünü uygularsak
Y (z) = z
−1
T
Y (z) +
(X(z) + z
−1
X(z))
2
Y (z) =
T 1 + z
−1
2 1 − z
−1
Dolayısıyla s ve z düzlemleri arasındaki ilişki
2 z − 1
s =
T z + 1
olarak bulunur.
Re(
2 z − 1
2 x + jy − 1
) < 0 → Re(
T z + 1
)
T x + jy + 1
2
x
+ y
2
< 1
/
Örnek:
G(s) =
s+1
s+3
transfer fonksiyonunu bilineer dönüşümü kullanarak ayrık zaman transfer fonksiyonuna dönüşütürüp kararlılık analizini yapın
2(z − 1) + T (z + 1)
G(z) =
(T + 2)z + T − 2
=
2(z − 1) + 3T (z + 1)
(3T + 2)z + 3T − 2
2.2 Ayrık Zaman Kontrol Sistemlerinde Kararlılık Analizi
Bilineer dönüşümü ile sürekli zamandaki kararlılık bölgesi (sol-yarı düzlem) ayrık zamanda birim çember içine dönüşür. Ayrık zaman bir sistemin
kararlı olabilmesi için kutuplarının birim çember içinde olması gerekmektedir.
Yüksek dereceden sistemlerin kararlılığı Jury kriterleri kullanılarak belirlenebilir.
Jury Kriteri ile Kararlılık Analizi
Sistemin karakteristik denklemi
P (z) = a0 z
n
+ a1 z
n−1
+ ⋯ + an−1 z + an = 0
şeklinde verilsin.
Jury testi ile sistemin birim çember dışında kutbunun olup olmadığı belirlenir.
/
Kural 1: P (1)
Kural 2: (−1)
Kural 3: |an |
> 0
n
P (−1) > 0
< a0
Eğer üç kural da sağlanıyorsa jury tablosu oluşturulur.
Örnek(b ve c'lerin hesaplanması)
b0 = an a1 − a0 an−1
b1 = an a2 − a0 an−2
b2 = an a3 − a0 an−3
⋮
c0 = bn−1 b1 − b0 bn−2
c1 = bn−1 b2 − b0 bn−3
c2 = bn−1 b3 − b0 bn−4
⋮
Kural 4:
|bn−1 | > |b0 |
/
|cn−2 | > |c0 |
|dn−3 | > |d0 |
⋮
Son satıra kadar devam eder. Tablodaki satır sayısı 2 ∗ n − 3 (veya bir satırda üç katsayı olana kadar ) tür. Eğer bu 4 kural sağlanıyorsa
sistem kararlıdır.
P (−1) = 0
veya P (1)
= 0
olduğunda diğer şartlar sağlanıyorsa marjinal kararlıdır ( yani z=1'de sistemin kutbu vardır), aksi halde kararsızdır.
Örnek
P (z) = z
4
− 1.2z
3
+ 0.07z
2
+ 0.3z − 0.08
a0 = 1, a1 = −1.2, … a4 = −0.08
P (1) = 0.09 > 0
4
(−1) P (−1) = 1.89 > 0
| − 0.08| < 1
a4
a3
a2
a1
a0
a0
a1
a2
a3
a4
b3
b2
b1
b0
b0
b1
b2
b3
c2
c1
c0
b0 = a4 a1 − a0 a3 = −0.204
b1 = a4 a2 − a0 a2 = −0.075
b2 = a4 a3 − a0 a1 = 1.176
b3 = a4 a4 − a0 a0 = −0.994
|b3 | > |b0 |
c0 = b3 b1 − b0 b2 = 0.315
c2 = b3 b3 − b0 b0 = 0.94
|c2 | > |c0 |
/
Sistem kararlıdır.
Örnek
P (z) = z
3
− 1.1z
2
− 0.1z + 0.2
a0 = 1, a1 = −1.1, a2 = −0.1, a3 = 0.2
P (1) = 0!
(kritik kararlı olabilir)
3
(−1) P (−1) = 1.8 > 0
|a3 | < a0 → |0.2| < 1
a3
a2
a1
a0
a0
a1
a2
a3
b2
b1
b0
b2 = a3 a3 − a0 a0 = −0.12 → |b2 | > |b0 |
Sistem marjinal kararlıdır.
Örnek
P (z) = z
2
− 1.2z + 0.6
P (1) = 0.4 > 0
n
(−1) P (−1) = 2.8 > 0
|a2 | < an → |0.6| < 1
Sistem kararlıdır.
/
Uygulama Problemleri
Problem 1 Ayrık sistem transfer fonksiyonu;
C (z)
G(z) =
0.125z
=
R(z)
z
2
− 1.375z + 0.5
ile verilen bir sistemin birim basamak cevabını bulunuz.
Çözüm
Y (z) = R(z)G(z)
ayrık zamanda birim basamak fonksiyonu R(z)
z
=
z−1
dolayısıyla
0.125z
Y (z) =
(z − 1)(z
Ters Z dönüşümünü bulabilmek için kısmi kesirlere ayırırsak;
2
2
− 1.375z + 0.5)
/
Y (z)
A
Bz + D
=
+
z
z − 1
z
2
− 1.375z + 0.5
A = limz→1 (z − 1)Y (z) = 1
A bilindiği durumda yukarıdaki ifadede payda eşitleme yaparsak
0.125z = A(z
2
− 1.375z + 0.5) + (Bz + D)(z − 1)
0.125z = (A + B)z
Dolayısıyla A
,
,
= 1 B = −1 D = 0.5
2
+ (D − B − 1.375)z + 0.5 − D
olarak bulunur.
z
z
Y (z) =
−
z − 1
sağdaki ifadenin paydasında yer alan polinomun kökleri b2
−at
e
sin(wt)
z
−2aT
= 0.5
2
− 0.5z
− 1.375z + 0.5
olduğundan kompleks eşleniktir. Ve Z dönüşümleri e−at cos(wt) ile
'nin z dönüşümlerinden faydalanılarak bulunur;
z
e
− 4ac < 0
z
2
2
2
=
− 1.375z + 0.5
ve 2e−aT cos(wT )
,
aT = 0.35 wT = 0.24
z
− 0.5z
ve B
z
2
2
−aT
− ze
−aT
− 2ze
−aT
cos(wT )
ze
−2aT
cos(wT ) + e
+ B
z
2
−aT
− 2ze
sin(wT )
−2aT
cos(wT ) + e
= 1.375
= 1.1338
olarak bulunur. Dolayısıyla
−0.35k
y(k) = 1 − e
(cos(0.24k) + 1.1338sin(0.24k)) |k = 0, 1, 2, …
Python Ayrık Kontrol Sistem Uygulaması
!pip install control
import control
import numpy as np
import matplotlib.pyplot as plt
/
z = control.TransferFunction.z
Gz = (0.125*z)/(z**2-1.375*z+0.5)
control.pzmap(Gz) # pzmap sistemin kutup ve sıfırlarını gösterir.
plt.figure()
time = np.linspace(0,1,101)
T, y = control.step_response(Gz,time)
plt.plot(T, y)
/
[<matplotlib.lines.Line2D at 0x7f8edbb9a358>]
Problem 2
y
′′
′
(t) + 14y (t) + 100y(t) = 100x(t)
ile verilen diferansiyel denklemi ileri fark yöntemini kullanarak fark denklemine
dönüştürün
Problem 3
k
y(k + 1) − y(k) = (1 + 2 )x(k)
olmak üzere
Y (z)
X(z)
transfer fonksiyonunu bulup, başlangıç koşullarının sıfır olması durumunda
birim basamak cevabını elde ediniz.
Çözüm Fark denklemine Z dönüşümü uygulanırsa;
z
z
zY (z) − Y (z) = (
+
)X(z)
z − 1
2z
2
z − 2
Y (z)
− 3z
Y (z) =
X(z) → G(z) =
birim basamak fonksiyonu olursa X(z)
=
2
− 3z
=
(z − 1)(z − 2)
X(z)
2z
X(z)
(z − 1)(z − 2)
z
z−1
2z
3
− 3z
Y (z) =
2
2
(z − 1) (z − 2)
elde edilir.
Birim basamak cevabının fark denklemini elde etmek için ifadenin rezidüsünü alıp ters Z dönüşümü uygulanırsa
Y (z)
2z − 2
=
z
,
,
A = −2 B = 0 C = 2
A
B
=
2
(z − 1) (z − 2)
(z − 1)
2
+
C
+
z − 1
z − 2
olarak bulunur.
−2z
Y (z) =
(z − 1)
Y (k) = −2k + 22
Problem 4 Ayrık zaman transfer fonksiyonu G(z)
import control
import numpy as np
import matplotlib pyplot as plt
k
2z
2
z +0.5+1
5
4
3
2
z − 2
= −2k + 2
2
=
+
6z +2z −3z +5z +8z+3
k+1
olan sistemin kararlılığını Jury Testini kullanarak belirleyiniz.
/
import matplotlib.pyplot as plt
z = control.TransferFunction.z
G1= (z**2+0.5*z+1)/(6*z**5+2*z**4-3*z**3+5*z**2+8*z+3)
control.pzmap(G1)
plt.figure()
time = np.linspace(0,1,101)
T, y = control.step_response(G1,time)
plt.plot(T, y)
plt.figure()
control.root_locus(G1)
3. Ayrık Zaman Açık Çevrim ve Kapalı Çevrim Kontrol Sistemleri
Yukarıda verilen blok şemasındaki örnekleme ve tutma işlemleri ayrık zaman kontrol sistemlerinin analiz ve tasarımında oldukça önemlidir.
Sürekli zaman bir sinyalin T örnekleme periyodu ile örneklenip (Analog Dijital Çevirici ile), sıfırıncı dereceden bir tutma devresi ile sürekli zamana
¯
¯
geri dönüştürülmesi (Dijital Analog Çevirici) örneği aşağıdaki şekilde verilmiştir. Resimdeki notasyonda x∗ (t) örneklenmiş sinyali, x̄
(t) ise
tutucu ile elde edilmiş sürekli zaman sinyalini ifade eder.
/
¯
¯
x̄(t) = x(0)[u(t) − u(t − T )] + x(T )[u(t − T ) − u(t − 2T ] + …
Laplace Dönüşümü uygulanırsa;
1
¯¯¯
¯
X (s) = x(0)[
1
−
−T s
e
s
1
] + x(T )[
s
X (s) = [
1
−
s
1
¯¯¯
¯
−T s
e
1
−
s
−2T s
e
] + …
s
∞
−T s
e
−kT s
][ ∑ x(kT )e
s
]
k=0
Burada
∞
X
∗
−kT s
(s) = ∑ x(kT )e
k=0
örnekleme işlemini ifade eder. Örneklenmiş sinyalin z-dönüşümü, z
ile daha önceki bölümde elde edilmişti.
sT
= e
∞
X(z) = ∑ x(kT )z
−k
k=0
[
1
s
−
1
−T s
e
]
s
ise sürekli zamana geçişte tutma işlemini ifade eder ve bu ifadeye sıfırıncı dereceden tutma denilir.
Sonuç olarak örnekleme ve sıfırıncı dereceden tutma aşağıdaki gibi blok şema ile gösterilebilir.
/
s ve z Düzlemleri Arasındaki Dönüşüm ( Zaman Domeni Kriterleri Karşılıkları)
s düzleminde s1,2
z1,2
= −α ± jw
olarak verilen karmaşık değişkenin z düzlemindeki yeri z
sT
= e
olduğundan, z1,2
(−α±jw)T
= e
−αT
= e
±jwT
e
'yi kutupsal olarak ifade edersek:
±jθ
z1,2 = re
Burada r
−αT
= e
z düzleminde z1,2
,θ
= ωT
olarak elde edilir.
= a ± jb
olarak verildiğinde ise z
±jθ
= re
Burada, r
−αT
r = e
−
−
−
−
−
−
2
2
= √a + b
ve θ
= tan
−1
(
b
a
)
Buradan,
1
→ α = −
lnr
T
1
θ = ωT → ω =
1
θ =
tan
T
T
−1
b
(
)
a
Bu eşitliklerden yararlanılarak sürekli zaman domeni kriterlerini ifade ederken kullandığımız sönüm oranı ve doğal frekansı ayrık zamana
dönüştürebiliriz. Sürekli zamanda baskın kutupların reel kısmı sönüm oranı ve doğal frekansın çarpımına eşit olduğu göz önüne alınırsa;
1
α = ξωn = −
lnr
T
−
−
−
−
−
ω = ωn √ 1 − ξ
2
θ
=
T
lnr
ξ =
−
−
−
−
−
−
−
−
−
2
2
√ (lnr) + θ
1
ωn =
Örnek s1,2
= −2 ± j2
Örnek z1,2
= 0.2 + j0.2
T
−
−
−
−
−
−
−
−
−
√ (lnr)
2
2
+ θ
kutuplarının z-düzlemindeki yerini bulunuz. T = 0.1 s
kutuplarının s-düzlemindeki yerini T = 0.5 s için bulunuz.
/
3.1 Açık Çevrim Ayrık Zaman Kontrol Sistemleri
Belirli periyotta örnekleme işlemi yapılarak sürekli zamandan ayrık zamana geçişi ifade eden ve * ile gösterdiğimiz yıldızlı dönüşüm alınırken
dikkat edilmesi gereken bazı özellikler aşağıda verilmiştir.
∗
(A (s))
∗
∗
= A (s)
∗
(A(s). B (s))
(A(s). B(s))
∗
∗
∗
∗
= A (s). B (s)
∗
∗
¯
¯¯¯¯
¯¯¯¯
¯
∗
≠ A (s). B (s) = A. B (s)
Z [A(s). B(s)] ≠ A(z). B(z)
Örnek Transfer fonksiyonu Gp (s)
=
1
s+1
olan bir sistemin
a) Sürekli zamanda birim basamak cevabını bulunuz
/
b) Örnekleme ve tutma ile ayrıklaştırarak T = 0.1 s için birim basamak cevabını bulunuz
a) U (s)
=
1
s
birim basamak girişi için
1
Y (s) = U (s)Gp (s) =
1
1
1
=
s s + 1
−t
−
s
→ y(t) = 1 − e
s + 1
b)
−sT
1 − e
G(s) = Gh (s)Gp (s) =
1
1
−sT
= 1 − e
s
s + 1
∗
s(s + 1)
−sT
A (s) = 1 − e
1
B(s) =
s(s + 1)
∗
G(s) = A (s). B(s)
∗
∗
∗
G (s) = A (s). B (s)
z − 1
G(z) = A(z) ∗ B(z) =
z
z
G(z)
−T
z
(
−
z − 1
1 − e
−T
) =
z − e
−T
z − e
bulunduktan sonra birim basamak cevabı kolayca bulunabilir. Birim basamak işaretinin Z dönüşümü:
z
U (z) =
z − 1
z
Y (z) = U (z)G(z) =
−T
1 − e
z − 1 z − e−T
z
=
z
−
z − 1
−T
z − e
Ters Z dönüşümünü alırsak
−kT
y(k) = 1 − e
3.2 Kapalı Çevrim Ayrık Zaman Kontrol Sistemleri
Kapalı çevrimde yer alan her bir örnekleyicinin çıkışı * ile gösterilerek ayrık zamana geçiş belirtilir.
Örnek Aşağıda verilen kapalı çevrim kontrol sisteminde hata örneklenmiştir. Giriş ve çıkış arasındaki transfer fonksiyonunu elde ediniz.
/
∗
E (s) = R(s) − G(s)H (s)E (s)
∗
∗
E (s) = R (s) − GH
∗
∗
(s)E (s)
∗
R (s)
∗
E (s) =
1 + GH
∗
(s)
∗
Y (s) = G(s)E (s)
Y
Y
∗
∗
∗
∗
(s) = G (s)E (s)
∗
(s)
R (s)
∗
G (s)
=
1 + GH
∗
G(z)
=
(s)
1 + GH (z)
Örnek
/
∗
G(s) = Gh (s)Gp (s) = A (s)B(s)
∗
−sT
A (s) = 1 − e
4
B(s) =
s(s + 2)
∗
∗
∗
G (s) = A (s). B (s)
G(z) = A(z). B(z)
A(z) = 1 − z
z − 1
−1
=
z
4
2
B(z) = Z [
] = Z[
s
s(s + 2)
2
z
−
] = 2(
s + 2
z
−
z − 1
−2T
)
z − e
T=0.1 için
z − 1
0.36
G(z) = 2 − 2
=
z − 0.820
z − 0.82
G(z)
0.36
T (z) =
=
1 + G(z)
z − 0.46
Girişin birim basamak olması durumunda
z
0.36
Y (z) = U (z). T (z) =
z − 1 z − 0.46
Y (z) =
0.67z
z − 1
−
0.67z
z − 0.46
/
ters Z dönüşümü uygulanırsa;
k
y(k) = 0.67(1 − 0.46 )
4. Ayrık Zaman Kontrolör Tasarımı
Ayrık zaman sistemler için kontrolör tasarımında temelde iki yöntem kullanılır.
Sürekli zamanda kontrolör tasarlanır ve tasarlanan kontrolör transfer fonksiyonu ayrık zamana dönüştürülerek yazılımsal olarak
gerçeklenir ( gömülü sistem kod yazma).
Kontrolör ayrık zamanda tasarlanarak yazılımsal olarak gerçeklenir.
Örnek Aşağıda verilen kapalı çevrim sistemin sönümsüz doğal frekansını ωn
= 10 rad/s
kontrolörü tasarlayarak ayrık zaman dönüşümünü T = 0.1 s için hesaplayınız. Gp (s)
=
10 ve sönüm oranının ξ
= 0.8
olmasını sağlayan PI
1
s+2
Sürekli zamanda polinom istenen karakteristiğe ait polinom ile karakteristik polinomun katsayıları eşitlenerek çözüme gidilir. PI Kontrolör yapısı:
Ki
Gc (s) = K p +
Gc (s)Gp (s)
T (s) =
=
1 + Gc (s)Gp (s)
s
Kp s + K i
2
s
+ (2 + K p)s + K i
kontrolörün sağlaması gerektiği isterlerin polinomu ise
2
P d (s) = s
ξ = 0.8
ve wn
= 10
2
+ 2ξwn s + wn
olduğundan
/
2
P d (s) = s
2
P c (s) = s
+ 16s + 100
+ (2 + K p)s + K i
olduğundan
Kp = 14, Ki = 100 olarak bulunur.
Sürekli zaman domeni kriterlerini sağlayan PI kontrolör olarak bulunur.
14(s + 7.14)
100
Gc (s) = 14 +
Tasarlanan süreli zaman kontrolör bilineer dönüşüm ile T
14(s + 7.14)
Gc (z) =
s
= 0.1
=
s
s
için ayrıklaştırılırsa
14(20
∣
∣
s=
2
z−1
T
z+1
=
z−1
z+1
20
+ 7.14)
z−1
19(z − 0.474)
=
z − 1
z+1
Doğrudan Ayrık Zamanda Kontrolör Tasarımı
Kontrol edilecek sistemin transfer fonksiyonun ayrık zaman karşılığı bulunur
Kapalı çevrim sistem çıkışı için istenen zaman domeni kriterlerine (sönüm oranı, doğal frekans, yerleşme zamanı, vb.) göre sürekli
zamandaki baskın kutuplara ilişkin polinom (P d (s) ) elde edilir ve Z dönüşümü uygulanır.
Kriterleri karşılayacak kontrolör parametreleri hesaplanır.
Örnek: Önceki örnekte verilen sistem içim doğrudan sayısal bölgede aşağıdaki gibi PI tasarımı yapılır.
Kontrol edilecek sistemin ayrık zaman transfer fonksiyonu bulunur
/
T = 0.1s
1
Gp (s) =
s + 2
∗
−T s
G(s) = Gh (s)Gp (s) = A (s). B(s) = (1 − e
z − 1
G(z) = A(z). B(z) =
s(s + 2)
−2T
0.5(1 − e
1
Z[
z
1
).
] =
)
−2T
s(s + 2)
z − e
0.09
=
z − 0.8187
PI Kontrolörün azrık zaman transfer fonksiyonu
Ki
Gc (s) = K p +
Burada K
= Kp − Ki
ve a
=
z
→ Gc (z) = K p + K i
s
=
(K p − K i )z − K p
z − 1
z − 1
K (z − a)
=
z − 1
Kp
K p −K i
Gc (z)G(z)
T (z) =
1 + Gc (z)G(z)
karakteristik denklem
z
2
− z(1.8187 − 0.09K ) + (0.8187 − 0.09K a)
Sürekli zamanda verilen kontrol kriterleri wn
= 10rad/s
ve ξ
= 0.8
2
P d (s) = s
+ 16s + 100
s1,2 = −8 ± j6
z domenindeki karşılıkları z
sT
= e
olduğuna göre
z1,2 = 0.371 ± j0.254
Dolayısıyla
P d (z) = z
2
− 0.74z + 0.1994
Karakteristik denklem ile katsayılar eşitlenirse
1.8187 − 0.09K = −0.74
0.8187 − 0.09K a = 0.1994
K = 28
ve a
= 0.2775
olarak bulunur.,
/
28(z − 0.2775)
Gc (z) =
z − 1
Ayrık Kontrolörlerin Mikrodenetleyicilerde Gerçeklenmesi
Sürekli zamanda PID yapısında olan kontrolörün transfer fonksiyonunu ele alalım.
U (s)
Gc (s) =
E (S )
= Kp +
U (z)
Gc (z) =
E (z)
= Kp +
Ki
+ K d s.
s
Ki T z
z − 1
z − 1
+ Kd
Tz
Fark denklemine dönüştürürsek
u(k) = K p e(k) + K i [u(k − 1) + T e(k)] +
= [K p + K i T +
Kd
]e(k) −
T
Kd
T
Kd
[e(k) − e(k − 1)]
T
e(k − 1) + K i u(k − 1)
Örnekleme Frekansının Belirlenmesi
Pratikte örnekleme frekansı (ωs ) sistemin sönümlü doğal frekansın (ωd ) 35 ile 70 katı arasında seçilir.
−
−
−
−
−
ωd = ωn √ 1 − ξ
2
ωs = kωd , → 35 ≤ k ≤ 70
Örnek Kapalı çevrim bir sistem sürekli zamanda %5 aşımı geçmeyecek, sönüm oranı 0.7 ve sönümlü frekansı 10 rad/s olacak şekilde
tasarlanmıştır. Uygun örnekleme zamanını belirleyiniz.
−
−
−
−
−
ωd = ωn √ 1 − ξ
2
−
−
−
−
−
−
−
= 10√1 − 0.49 = 7.14
/
ωs ≥ 35 ∗ ωd = 249.95rad/s
örnekleme periyodu
2 ∗ π
≥ 249.95 → T ≤ 0.025s = 25ms
T
örnekleme periyodu en fazla 25ms seçilebilinir
Genel Uygulama Soruları
1- Y (z)
=
z
2
z −4z+1
,
transfer fonksiyonuna ait fark denklemini elde ediniz y(kT) (k=0,1,2,3,4,5)
,
,
y(0) = 0 y(T ) = 1 y(2T ) = 4 y(3T ) = 15
2- Y (z)
=
z+1
2
z +0.3z+0.02
, y(4T)=56
ters z dönüşümünü kullanarak y(k) ifadesini bulunuz.
Y (z)
z + 1
=
z
z(z
2
A
50z
+
z
+ 0.3z + 0.02)
Y (z) =
z + 0.2
40z
+
z + 0.1
y(k) = 50δ(k) − 90(−0.1)
z + 0.2
k
2
=
C
+
z + 0.1
90z
−
z
3- Ayrık zaman kapalı çevrim transfer fonksiyonu T (z)
B
=
K (z +2z)
2
(1+K )z +(0.2+K )z−0.5
+ 40(−0.2)
k
olan sistemin K'ya bağlı kararlılık aralığını belirleyiniz.
karakteristik polinom:
P (z) = (1 + K )z
2
+ (0.2 + K )z − 0.5
Jury kararlılık kriterlerini uygularsak
P (1) > 2K + 0.7 > 0 → K > −0.35
/
n
(−1) P (−1) > 0 → 0.3 > 0
(n = 2, karakteristik denklem 2. dereceden)
1 + K > | − 0.5| → K > −0.5
Dolayısıyla kararlılık aralığı
∞ > K > −0.5
4- Karakteristik polinomu
P (z) = z
5
+ 0.2z
4
− 0.8z
3
− 0.106z
2
+ 0.1375z + 0.014
olan sistemin kararlılığını Jury tablosunu oluşturarak inceleyiniz.
P(1) = 0.4455 > 0
(-1)^5 P(-1) = 0.2295 >0
z
0
z
1
z
2
z
3
z
4
z
5
a5
a4
a3
a2
a1
a0
a0
a1
a2
a3
a4
a5
b4
b3
b2
b1
b0
b0
b1
b2
b3
b4
c3
c2
c1
c0
c0
c1
c2
c3
d2
d1
d0
b0 = a5 a1 − a0 a4 = −0.1347
b1 = a5 a2 − a0 a3 = 0.0948
b2 = a5 a3 − a0 a2 = 0.7985
b3 = a5 a4 − a0 a1 = −0.1981
b4 = a5 a5 − a0 a0 = −0.9998
|b4 | > |b0 |
c0 = b4 b1 − b0 b3 = −0.1215
/
c1 = b4 b2 − b0 b2 = −0.6908
c2 = b4 b3 − b0 b1 = 0.1714
c3 = b4 b4 − b0 b0 = 0.9815
|c3 | > |c0 |
d0 = c3 c1 − c0 c2 = −0.6524
d2 = c3 c3 − c0 c0 = 0.9485
|d3 | > |d0 |
sistem kararlıdır.
5- Açık çevrim transfer fonksiyonu G(s)
=
4
(s+2)(s+3)
olan bir sistem birim geri-beslemeli yapıda kontrol edilmek istenmektedir. Kapalı çevrim
sisteme birim basamak işareti uygulandığında yerleşme zamanının 4 saniye ve sönüm oranının 0.707 olmasını sağlayan PD kontrolörü belirleyip
kontrolörün ayrık zaman karşılığını sistem için uygun olabilecek en büyük örnekleme periyodu ile bulunuz.
Gc (s) = K p + K d s
4(K p + K d s)
T (s) =
2
s
+ (5 + 4K d )s + (6 + 4K p )
karakteristik denklem:
2
P c (s) = s
+ (5 + 4K d )s + (6 + 4K p )
kapalı çevrim sistemden istenen kriterlere ait karakteristik polinomu belirlemek için:
4
Ts =
ξωn
= 4 → ξωn = 1
–
ξ = 0.707 → ωn = √2
2
P d (s) = s
+ 2s + 2
polinom katsayıları eşitlenirse
(5 + 4K d ) = 2 → K d = −0.75
/
(6 + 4K p ) → K p = −1
Gc (s) = −1 − 0.75s
Örnekleme zamanının seçimi:
Kapalı çevrim sistemin sönümlü doğal frekansı:
−
−
−
−
−
ωd = ωn √ 1 − ξ
2
−
−
1
–
= √2√
= 1
2
Örnekleme frekansı sönümlü doğal frekansın 35 ila 70 katı arasında seçilebilinir. Olabilecek en büyük örnekleme periyodu olabilecek minimum
örnekleme frekansı ile sağlanır.
ωs ≥ 35ωd ≥ 35
2π
T ≤
= 0.18s
ωs
Örnekleme zamanı en fazla T
= 0.18s
olabilir. Bu durumda bilineer dönüşüm kullanarak tasarlanan kontrolörü bulabiliriz.
−16.8z + 13.2
Gc (z) = −1 − 0.75s|
s=
2
z−1
0.18
z+1
=
1.8z + 1.8
/
/









