Devre Analizi Ders Notları
Devre Analiz Teknikleri
DEVRE ANALĐZ TEKNĐKLERĐ
Bu zamana kadar kullandığımız Kirchoffun kanunları ve Ohm kanunu devre problemlerini
çözmek için gerekli ve yeterli olan eşitlikleri sağladılar. Fakat bu kanunları kullanarak
şimdiye kadar izlediğimiz yöntemler biraz daha metodik ve algoritmiktir. Bu metodlarla
herhangi bir devredeki akım ve gerilim hesabı oldukça kolaylaşmış olmaktadır.
Çözüm metotlarına girmeden önce, bu yöntemleri anlatırken kullanacağımız terimlerin ne
manaya gediğini inceleyelim.
Düğüm: Đki veya daha fazla devre elemanının uçlarının birleştiği noktalar düğüm olarak
adlandırılır. Şekil.DT.1 için a, b, c, d, e, f, g, h, i, j noktalarının hepsi düğümdür.
Temel Düğüm: Üç veya daha fazla devre elemanın birleştiği düğüm temel düğüm olarak
adlandırılır. Şekil.DT.1’deki düğümler içerisinde yalnızca c, d, e, f, i, j temel düğümdür.
Yol: Hiçbir devre elemanının iki defa olmamak üzere, temel devre elemanlarının yan yana
olanları üzerinden gidilerek izlenen sıraya yol adı verilir. Şekil.DT.1’deki V2 , R4 , i1 , R6 bir
+
yol oluşturmaktadır. Yine i2 , R7 , V3 , de bir yol oluşturmaktadır.
Şekil.DT.1. Temel terimlerin incelenmesi için örnek devre
Kol: Đki düğümü birleştiren yola kol adı verilir. Örneğin a ve b düğümünü birleştiren R1
direnci bir kol oluşturmaktadır. Yine V4 gerilim kaynağının olduğu yol, i2 akım kaynağının
olduğu yol bir koldur.
Temel Kol: Başka bir temel düğümden geçmeden iki temel düğümü birleştiren yola temel kol
denir. Şekil.DT.1’deki V1 , R1 , R2 yolu i2 yolu, V4 , R8 yolu, R3 yolu, R6 yolu, i1 i1 yolu, R4
yolu ve V2 , R5 yolu temel kol örnekleridir.
Halka: Bir düğümden başlayarak, yine aynı düğüme geri dönen yola halka ismi verilir.
Şekil.DT.1’ deki halka örnekleri ise aşağıdaki gibidir;
R3 − V4 − R8 − R7 , R7 − R6 − i1 − V3 , V2 − V1 − R1 − i2 − R6 − R5
© Uğur TAŞKIRAN 2007
1
Devre Analizi Ders Notları
Devre Analiz Teknikleri
Çevre: Đçinde başka bir halka olmayan halkaya çevre adı verilir. Şekil DT.1. için
R4 − V1 − R1 − R2 − R3 − V3 halkası, V2 − R4 − i1 − R5 halkası, i1 − V3 − R7 − R6 halkası,
R7 − R3 − V4 − R8 halkası, R8 − V4 − i2 halkası aynı zamanda birer çerçevedirler.
Düzlemsel Devre: Birbiri üzerinden atlama yapmadan bir düzlem üzerine (örneğin kağıda)
çizilebilen devrelere düzlemsel devre ismi verilir. Üzerinden atlama yapılmış devreler illaki
düzlemsel olmayan devre olmayabilirler. Bu devrelerin bir kısmı düzlemsel olarak çizilebilir.
Örneğin şekil DT.2’deki devre, şekil DT.3’teki gibi tekrar çizilebilir.
Şekil.DT.2 Örnek düzlemsel Devre
Şekil.DT.3. Şekil.DT.2’deki devrenin
düzeltilmiş hali
Yine de bazı devreler vardır ki düzeltmeler sonucunda dahi atlamasız çizilmez. Bu durumdaki
bir devreye düzlemsel olmayan devre adı verilir. Şekil DT.4’deki devre böyle bir devredir.
R1
R2
R5
V1
+
-
R4
R3
R6
R7
R8
R9
Şekil.DT.2 Düzlemsel Olmayan Devre
Göreceğimiz metodlar içerisinde çevre akımları yöntemi yalnızca düzlemsel devrelere
uygulanabilirken, düğüm gerilimleri yöntemi hem düzlemsel hem düzlemsel olmayan
devrelere uygulanabilir.
Düğüm gerilimleri yönteminde, her düğüme bir gerilim atanarak, Kirchoffun akım kanunu
vasıtasıyla denklemler elde edilir. Fakat bizim için gerekli olan ise temel düğüm sayısının bir
eksiği kadar denklemdir. Yani Düğüm gerilimleri yönteminde toplam denklem sayısı;
ds1 = ne − 1
burada ne , temel düğümlerin sayısıdır.
© Uğur TAŞKIRAN 2007
2
Devre Analizi Ders Notları
Devre Analiz Teknikleri
Çevre akımları yönteminde ise Kirchoff’un gerilim kanunu, toplam çevre sayısı dolayısıyla
denklem sayısı ds2 ise;
ds2 = be − (ne − 1)
formülünden hesaplanır. Burada be toplam temel kol sayısıdır.
Düğüm Gerilimleri Metodu
Düğüm gerilimleri metodu temelde, temel düğümlere bir gerilim atanarak ve her düğüm için
Kirchoff’un akım kanunun yazılmasını temel alan bir yöntemdir. Bu yöntemle bütün temel
düğümlerdeki gerilimler hesaplanır. Bu değerler devrenin diğer noktaları için bir referans
özelliği taşır. Bu değerler vasıtasıyla devrenin herhangi bir noktasından geçen akımı veya
herhangi iki nokta arasındaki gerilimi hesap etmek mümkündür.
Aşağıdaki örnekle birlikte, düğüm gerilimleri yöntemi ile devre çözümünü inceleyeceğiz.
Gerekli olan denklem sayası ds1 = 3 − 1 = 2 .
Şekil.DT.5 Düğüm Gerilimleri Yöntemi Đçin Örnek Devre
Đlk olarak yapılacak iş devredeki düğümlerin tespitidir. Buradaki örnek için 1, 2, 3, ve 4
düğümdür. Fakat esas kullanacaklarımız ise temel düğümlerdir, yani 1, 2 ve 4 tür. Temel
düğümlerin bir tanesi toprak düğümü, yani sıfır volt noktası olarak seçilir ve (
veya
veya
) işaretleriyle gösterilir. Bu sıfır noktası olarak seçilen düğüm genellikle en çok
devre elemanının bağlı olduğu düğüm olur. Bu kesin bir kural olmamakla beraber genel bir
kabul olmuştur. Bazı durumlarda sıfır noktası diğer düğümler arasından seçilebilir. Bundan
sonraki adım geriye kalan temel düğümlere gerilim atamak yani her bir düğümdeki gerilimleri
V1 , V2 ,......, Vne −1 gibi işaretlenir. Burada bir 1 düğümü için V1 ve 2 düğümü için V2 işaretini
kullanalım.
Bundan sonraki aşamada her bir işaretlenen düğüm için, sıfır noktası hariç Kirchoffun akım
kanunu yazılır. 1 düğümü için;
ia + ib + ic = 0
Burada ia , ib ve ic yönlerine dikkat edilerek ve Ohm kanunundan eşitlikler yazılır yani;
V −V
V −V
V −0
ia = 1 k , ic = 1 2 ve ib = 1
R1
R3
R2
V1 − Vk V1 V1 − V2
+
+
=0
R1
R2
R3
© Uğur TAŞKIRAN 2007
3
Devre Analizi Ders Notları
Devre Analiz Teknikleri
Görüldüğü üzere ia , Ri ’nin bulunduğu koldan geçen akımdır ve denklemi ona göre
yazılmıştır. ib ve ic de ona göre yazılmış ve en sonunda ise en başta yazılan denklemde yerine
konmuştur.
2 düğümü için denklemi yazalım.
id + ie + i f = 0
V2 − V1
; yönü ic ’ye terstir, o yüzden bu şeklide yazılmıştır.
R3
V −0
ie = 2
ve i f = −ik akım kaynağının yönü i f ’ye terstir.
R4
Dolayısıyla ikinci denklem
V2 − V1 V2
+
− ik = 0
R3
R4
şeklinde yazılabilir. Böylelikle iki bilinmeyenli iki denklem bulunmuş olur. Diğer değerler; R
dirençler ve kaynak değerleri devrede verilmiş olmalıdır. Đki bilinmeyenli iki denklem ise
doğrusal cebir vasıtasıyla kolaylıkla çözülebilir. Aşağıda verilen örnekle durum daha açık bir
şekilde anlaşılabilir.
id =
Örnek.DT.1: Şekil.DT.5 teki devrede R1 =8 Ω , R2 =3Ω , R3 = 4Ω ve R4 = 12Ω dur.
Vk = 20v ve ik = 5 A ise, R4 üzerinden geçen akımı hesap ediniz.
Sayısal değerleri yukarıda bulduğumuz denklemlerde yerine yazınız.
V1 − 20 V1 V1 − V2
+ +
=0
⇒
17V1 − 6V2 = 60 x 2
8
3
4
V2 − V1 V2
+ −5 = 0
⇒
−3V1 + 4V2 = 60 x3
4
12
34V1 − 12V2 = 120
−9V1 + 12V2 = 180
25V1 = 300
300
V1 =
= 12v
25
60 + V1 60 + 36 96
V2 =
=
=
= 24v
4
4
4
V
24
iR4 = 2 =
= 2A
R4 12
Düğüm Gerilimleri Yöntemi Özel Durumlar
Bağımlı Kaynaklar: Düğüm gerilimleri yönteminde, düğüm gerilimleri devrenin herhangi
bir yerindeki gerilimin ve akımın hesap edilmesi için yeterlidir. Bu yüzden bağımlı
kaynakların olması durumu değiştirmez. Bağımlı kaynakların kontrolleri ise düğüm
gerilimleri değişkenlerinden faydalanarak hesaplanır. Aşağıdaki örneği inceleyelim.
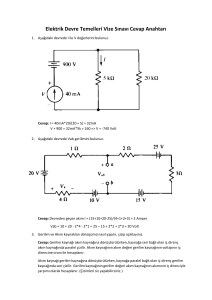
Örnek.DT.2: Aşağıdaki devrede işaretli düğüm gerilimlerini çözünüz.
© Uğur TAŞKIRAN 2007
4
Devre Analizi Ders Notları
Devre Analiz Teknikleri
Devreyi dikkatle incelediğimizde
işaretli olan düğüm gerilimlerinin
birinin daha çözüme başlamadan belli
olduğunu görürüz. Bu V2 dir.
Görüldüğü üzere 25v’luk gerilim
kaynağı V2 ’nin düğümü ile toprak
arasına bağlıdır. Dolayısıyla V2 =25v
olur.
V1 için:
V1
V −V
−1 + 1 2 = 0
10
20
2V1 − 20 + V1 − 25 = 0
⇒
V1
V − 25
−1 + 1
=0
10
20
45
V1 =
V1 = 15v
3
Süper Düğüm: Eğer iki düğüm arasına bir gerilim kaynağı bağlanmış ise kollardan geçen
akımı direk yazamayız. Fakat dolaylı yollardan düğüm gerilimlerini yazabiliriz. Aşağıdaki
örneği inceleyelim.
Örnek.DT.3
V1 V1
+ + ix = 0
10 50
ix : gerilim kaynağı üzerinden
geçen akımı direk
bilemediğimizden gerilim
kaynağı üzerinden geçen bir
akım tanımlandı:
V1 düğümü için
V2 düğümü için
V
−ix + 2 + 2 = 0
10
Bu iki denklemi toplarsak ix terimleri yok olur.
V1 V1
V
+ + 2 + 2 = 0 elde edilir. (Denklem 1*)
10 50
10
Fakat eksik olan bir denklem daha bulunmalıdır. Çünkü 2 bilinmeyenli denklemleri çözmek
için en az iki adet denklem lazımdır. Bu ise kontrollü gerilim kaynağını yerine yazarak
bulunur.
V
V
V1 − V2 = 50i ⇒ i = 1 ⇒ V1 − V2 = 50 1
10
10
−4V1 − V2 = 0
Böylece ikinci denklem elde edilmiş oldu. Denklemler çözülürse:
© Uğur TAŞKIRAN 2007
5
Devre Analizi Ders Notları
5V1 + V1 + 100 + 5V2 = 0
−4V1 − V2 = 0
Devre Analiz Teknikleri
6V1 + 5V2 = −100
⇒
X (5)
−20V1 − 5V2 = 0
−14V1 = −100
100
= 7.142v
4
V2 = −28.57v
V1 =
Denklem (1*) kısaca yazabilmek için süper düğüm yöntemi adı verilen bir yöntem
uygulanabilir. Bu yöntem gerilim kaynaklarının arasına bağlı olduğu her düğüm için
uygulanabilir. Eğer süper düğüm için Kirchoff’un akım kanununu yazarsak:
V1 V1
V
+ +2+ 2 = 0
10 50
10
Denklem (1*)elde ederiz.
Çevre Akımları Metodu
Çevre akımları metodunda temel olan çevrelerin tespit edilerek çevreler içerisinde akımlar
dolaştığının varsayılmasından ibarettir. Daha sonra çevre için Kirchoff’un gerilim kanunu
yazılır. Sonuç olarak be − (ne − 1) adet denklem elde edilir. Bu denklemlerle çevre akımları
hesaplanır. Yine düğüm gerilimlerinde olduğu gibi çevre akımları devrenin herhangi bir
yerindeki gerilim ve akımların hesaplanması için yeterlidir. Şekil.DT.6’yı ele alalım.
+ VR 12
R1
+
Vk1
+
-
i2
R2
VR 22
VR 21
+
-
-
+
+
VR 41
i1
-
R3
VR 32
VR 33
+
-
R4
VR 43
i3
Vk 2
+
-
+
Şekil.DT.6 Çevre Akımları Yönteminin Uygulanması
© Uğur TAŞKIRAN 2007
6
Devre Analizi Ders Notları
Devre Analiz Teknikleri
Şekil.DT.6’daki devrede üç adet çevre olduğu görülmektedir. Devrede dört adette temel
düğüm bulunmaktadır. Devrede altı adette temel kol vardır. Gerekli olan denklem sayısı
be = 6 ve ne = 4 için be − (ne − 1) = 6 − (4 − 1) = 7 − 4 = 3 ’tür. Bu sayı ise çevre sayısına eşittir.
Çevreler tespit edildikten sonra her çevre için çevre içinde dolanarak devresini tamamlayan
çevre akımları tespit edilir. Bu akımların yönleri ya hepsi saat yönünde, ya da saat yönünün
tersi yönde tespit edilir. Burada ve ilerde hep saat yönü tercih edilecektir. Bundan sonra ise
çevre akımının yönü referans alınarak Kirchoff’un gerilim kanunu yazılır. i1 halkası için bunu
yazalım.
−Vk1 + VR21 + VR41 = 0 Burada VR21 ve VR41 , i1 akımına göre pozitif kabul edilir.
−Vk1 + V21 + VR41 = 0 V21 gerilimi bir sonraki aşama için dikkatle seçildi.
Eğer VR21 ve VR41 , i1 akımına göre seçilmişse denklemi yeniden yazarsak;
−Vk1 + (i1 − i2 ) R2 + (i1 − i3 ) R4 = 0
R2 üzerinden geçen akımın (i1 − i2 ) olduğuna ve R4 üzerinden geçen akımın (i1 − i3 )
olduğuna ve kabul edilen referans gerilim yönlerine dikkat ediniz.
i2 halkası için ise
+VR22 + VR12 + VR32 = 0
denklemi yazılıp, değerleri yerine konursa
R2 (i2 − i1 ) + R1i2 + (i2 − i3 ) R3 = 0
Burada VR22 = −VR21 olduğuna ve bunların i1 ve i2 akım yönlerine göre alındığına dikkat ediniz.
i3 halkası için ise
VR43 + VR33 + VRk 2 = 0 ⇒ R4 (i3 − i1 ) + R3 (i3 − i2 ) + Vk 2 = 0
Bu şekilde denklemler bulunmuş olur. Sonuç denklem sistemini çözerek elde edilir.
Örnek.DT.4: Şekil.DT.6’daki devrede Vk1 = 35v, R1 = 50Ω, Vk2 = 25v, R2 = 250Ω,
R3 = 50Ω ve R4 = 25Ω ise i1 , i2 ve i3 çevre akımları kaçtır?
Denklemlerde değerleri yerlerine yazalım.
−35 + (i1 − i2 )250 + (i1 − i3 )25 = 0 ⇒ 275i1 − 250i2 − 25i3 = 35
250(i2 − i1 ) + 50i2 + (i2 − i3 )50 = 0 ⇒ − 250i1 − 350i2 − 50i3 = 0
25(i3 − i1 ) + 50(i3 − i2 ) + 25 = 0 ⇒ − 25i1 − 50i2 + 75i3 = −25
Denklem sistemini çözelim
275 −250 −25
∆ = −250 350 −50 = 1000000 = 106
−25 −50 75
35 −250 −25
∆1 = 0 350 −50 = 300000
−25 −50 75
© Uğur TAŞKIRAN 2007
i1 = ∆1 / ∆ = 0, 3 A
7
Devre Analizi Ders Notları
Devre Analiz Teknikleri
275 35 −25
∆ 2 = −250 0 −50 = 200000
−25 −25 75
i2 = ∆ 2 / ∆ = 0, 2 A
275 −250 35
∆ 3 = −250 350 0 = −100000
−25 −50 −25
i3 = ∆ 3 / ∆ = −0,1A
Çevre Akımları Yöntemi Özel Durumlar
Bağımlı kaynakların devrede bulunması çevre akımları yöntemini değiştirmez çünkü çevre
akımları devrenin herhangibir yerindeki gerilim ve akımını belirlediği için küçük
değişikliklerle devre çözülebilir. Bunun için Örnek.DT.5’i inceleyelim.
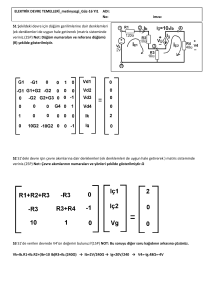
Örnek.DT.5: Çevre akımları yöntemi kullanarak 20Ω’luk direnç üzerinden geçen akımı
hesaplayınız.
2A
i2
10 ohm
20 ohm
Đx
+
-
25 ix
i1
i
+
Vx
5A
i3
80 v
+
-
Şekle bakıldığında iki adet akım kaynağı
Kirchoff’un gerilim kanunu yazmak için
bir problem oluşturur gibi gözükmektedir.
Fakat dikkatli bir incelemeyle i2 = 2 A
olduğunu kolaylıkla bulabiliriz. Böylece
bilinmeyen sayısı bir adet azılmış olur. i1
halkası için denklemi yazalım. 5A lık akım
kaynağı üzerindeki gerilime Vx diyelim.
-
−25ix + (i1 + i2 )10 + Vx = 0
i3 halkası için yazalım
−Vx + (i3 + i2 )20 + 80 = 0
Bu iki denklemi toplarsak,
−25ix + (i1 + i2 )10 + (i3 + i2 )20 + 80 = 0 elde edilir.
Fakat bu denklem Vx değerleri yazmadan da çizikli yol izlenerek de Kirchoff’un gerilim
kanunundan yazılabilir. Böylece akım kaynağı kaldırılarak elde edilen çerçeveye süper çevre
ismi verilir. Bu şekilde yazılan denklem bir denklemi yok ettiği için fazladan bir denklem
daha yazmak gerekir. Bu ise akım kaynağının bağlı olduğu koldan geçen akımı yazarak
bulunur.
i3 − i2 = 5 A (akım kaynağının yönü i1 ile aynı yönde)
Denklemlerdeki fazladan bilinmeyen ix ise i1 − i2 ’ye eşittir.
Tüm değerler yerine yazılırsa;
−25(i1 − 2) + 10(i1 − 2) + 20(i3 − 2) + 80 = 0
−15i1 + 20i3 + 50 − 20 − 40 + 80 = 0
© Uğur TAŞKIRAN 2007
8
Devre Analizi Ders Notları
− 15i1 + 20i3 = −70
15 /
i1 − i3 = 5
Devre Analiz Teknikleri
− 15i1 + 20i3 = −70
⇒
15 i1 − 15i3 = 75
− 5i3 = 5
i3 = 1A
i1 − i3 = 5 ⇒ i1 − 1 = 5 ⇒ i1 = 6 A
i20 Ω = i3 − i2 = 1 − 2 = −1A
Düğüm gerilimleri yöntemi genelde çevre akımları yöntemine göre avantajlıdır. Fakat bazı
durumlarda devre daha bilinmeyenli denklem sistemine dönüştürülebiliyorsa daha az
bilinmeyenli denklem sistemi tercih edilir. Bu arada düzlemsel olmaya devrelere yalnızca
düğüm gerilimlerinin uygulanabildiğini unutmayınız.
Kaynak Dönüşümü
Bazı durumlarda Gerilim kaynağına seri bağlı direnç, akım kaynağına paralel bağlı bir dirence
dönüştürüldüğünde devrede bazı sadeleşmeler olur. Eğer gerilim kaynağına seri bağlı direnci
akım kaynağına paralel bağlı dirence dönüştürülebilecek bir yöntem bulunursa bu
uygulanabilir.
Şekil.DT.7’deki dönüşümü yapabilmek için RL yük direnci üzerinden geçen akımların ve RL
üzerinde düşen gerilimlerin eşit olması gerekir.
Rs
il
il
+
Vk
+
-
VL
+
RL
-
ik
Rp VL
RL
-
Soldaki devre için
Vk
V .R
iL =
ve VL = k L
RS + RL
RS + RL
Sağdaki devre için
ik .R p
iL =
RP + RL
RL =0 için iL = Vk / RS ve iL = ik olmalıdır.
Dolayısıyla ik = Vk / RS olur.
RL = ∞ için VL = Vk ve VL = ik .R p olur.
Eğer Vk ’yı ilk denkleminde yerine yazarsak;
ik = ik .R p / RS ⇒ R p = RS
Sonuç olarak kaynak dönüşümü için gerekli formüller bulunmuş olur. Kaynak dönüşümler
çift taraflıdır.
© Uğur TAŞKIRAN 2007
9
Devre Analizi Ders Notları
Devre Analiz Teknikleri
Örnek.DT.6:
Kaynak dönüşümünü kullanarak ix akımını
hesap ediniz. 11v’luk gerilim kaynağının
güç üretip üretmediğini bulunuz
3 ohm
5 ohm
ix
11 V
+
-
21 ohm
10 ohm
6A
6A’lik 10Ω devre elemanlarına kaynak dönüşümünü uygulayalım.
Vk1 = 6.10 = 60v
RS = 10Ω
Devreyi tekrar çizelim
.
10Ω’luk ve 3Ω’luk dirençler seri hale gelir
ve 13Ω’luk bir dirençle değiştirilebilir
60v’luk gerilim kaynağı 13 Ω’luk dirence
tekrar kaynak dönüşümü uygulayalım.
ik1 = 60v /13Ω = 4, 615 A
RP1 = 13Ω
21 Ω ve 13 Ω’luk direnç paralel
21.13
olduğundan: RP2 =
= 8, 029
21 + 13
© Uğur TAŞKIRAN 2007
10
Devre Analizi Ders Notları
Devre Analiz Teknikleri
4,615’lik akım kaynağı ve 8,029’luk
dirence tekrar kaynak dönüşümünü
uygularsak
Vk2 = 4, 615 . 8, 029 = 37, 058v
RP2 = 8, 029Ω
Devrenin bu haliyle ix ’i hesaplayalım.
11 − 37, 058
ix =
= −2 Amper
5 + 8, 029
Dolayısıyla ix ters yöndedir. Bu durumda 11 v’luk gerilim kaynağı güç tüketir.
Gerilim kaynağına paralel direnç dönüştürülürken yalnızca gerilim kaynağı ve akım
kaynağına seri direnç dönüştürülürken yalnızca akım kaynağı seçilir.
Rs
Vk
+
-
Rp
Vk
+
-
ve
ik
ik
Thevenin ve Norton Eşdeğer Devreleri
veya
=
Đki Uçlu Karmaşık Devre
Thevenin Eşdeğeri
Norton Eşdeğeri
Herhangi bir devre, devre üzerinde belirlenmiş iki noktadan doğru bakıldığında bir gerilim
kaynağı ve bir seri direnç olarak sadeleştirilebilir. Bu sadeleştirmeye Thevenin eşdeğeri’nin
bulunması denir. Aynı şekilde bu sadeleştirme bir akım kaynağı ve buna paralel bağlı direnç
olarak yapılırsa Norton eşdeğeri bulunmuş olur.
Bazı durumlarda devrenin içinden çok uçları arasındaki davranış ile ilgileniyorsak Thevenin
ve Norton eşdeğeri sıkça kullanılır. Bunu yaparken uygulanan yöntem uçlar arasındaki
© Uğur TAŞKIRAN 2007
11
Devre Analizi Ders Notları
Devre Analiz Teknikleri
gerilimi hesaplamaktan başlar. Bu uçlara herhangi bir şey bağlı değilken yapılan gerilim
hesabı Thevenin eşdeğer gerilimini verir. Bu iki uç kısa devre edilerek kısa devre üzerinden
geçen akım hesaplanırsa buna da Norton eşdeğer akımı denir. Bu belirlenen uçlara sırayla
voltmetre ve ampermetre bağlanması gibidir.
Kaynak dönüşümünden,
Vth = I N .RN ve I N = Vth / Rth ⇒ RN = Rth
değerleri hesap edilebilir. Thevenin ve Norton eşdeğerinin bulunmasını standart yöntemle
aşağıdaki örnekle inceleyelim.
Örnek.DT.7: a ve b uçları arasındaki eşdeğer Thevenin devresinin bulunuz. (standart yöntemi
kullanarak)
5 ohm
a
25 V
+
-
2 ohm
5A
b
a ve b uçları arasındaki gerilimi V1 hesap ederek bulalım. Düğüm gerilimleri için V1 yeterlidir
ve V1 = Vab = Vth dir.
V1 − 25 V1
+ −5 = 0
⇒
V1 − 25 + 2V1 − 20 = 0
4
2
3V1 = 45
V1 = 45 / 3
V1 = 45 / 3 = 15v = Vth
a ve b uçları kısa devre edildiğinde geçen akım ise
25v − 0
IN =
+ 5 = 6, 25 + 5 = 11, 25 A
4
V
Rth = th = 1.333Ω
IN
Örnek.DT.8: a ve b uçları arasındaki eşdeğer Norton devresini hesaplayınız.
I N = 11, 25 ve RN = Rth = 1,333Ω
Örnek.DT.9: Kaynak dönüşümünü kullanarak a ve b uçları arasındaki Norton ve Thevenin
eşdeğerini hesaplayınız.
25v’luk gerilim kaynağı ile 4 Ω’luk direnci dönüştürelim.
ik = 25v / 4 = 6, 25 A ve RP = 4Ω
a
6,25 A
4 ohm
2 ohm 6 A
Bu devre akım kaynakları toplanarak ve 4
Ω ve 2 Ω’luk dirençlerin eşdeğerleri
bulunarak hesaplanır.
b
© Uğur TAŞKIRAN 2007
12
Devre Analizi Ders Notları
Devre Analiz Teknikleri
Rth
1,33 ohm
a
Vth
15 V
+
b
Bu devre zaten Norton eşdeğeridir. Thevenin eşdeğeri kaynak dönüşümünden
Vth = I N − RN = 15v ve Vth = RN = 1,33Ω
Not: Thevenin veya Norton eşdeğerini bulurken bazen kaynak dönüşümü kullanılamayabilir.
Bu durumda standart yönteme geri dönülür.
Örnek.DT.10: Aşağıdaki transistörlü yükselteç, eşdeğerinin a ve b uçları arasındaki Thevenin
eşdeğerini bulunuz.
a ve b uçları açıkken Vab = −100.2 Ki olur
10mV − 10−4 v
⇒ V bilinmediğinde v yerine yazılmalıdır.
100
V = Vab ’dir dolayısıyla yerine yazalım;
i ise i =
10mV − 10−4 vab
100
i tekrar yerine konursa
10mV − 10−4 vab
Vab = −100.2 K
= (−10mV + 10 −4 vab )2000
100
−3
0.5vab x 10 = −10mV + 10−4 vab (5vab − vab ) x10 −4 = −10mV
i=
−10 x 10−3
4vab =
= −100
10 −4
vab = −25v = Vth
a ve b uçları kısa devre edilirse
10mV − 10−4 v
I N = −100i olur. i ise i =
v = 0 = vab olduğundan
100
10mV 10 x 10 −3
i=
=
= 10 −4 ⇒
I N = −100.10−4 = 10−2 A
100
10 2
−25v
Rth = Vth / I N =
= 2500Ω
−10 −2
Bazı durumlarda Rth direkt olarak hesaplanabilir. Bunun için şart ise devrenin tamamen direç
ve bağımsız kaynaklardan oluşması gerekir. Bu durumda gerilim kaynakları kısa devre ve
© Uğur TAŞKIRAN 2007
13
Devre Analizi Ders Notları
Devre Analiz Teknikleri
akım kaynakları açık devre yapılarak devre yeniden çizilir ve eşdeğer devre direnci
hesaplanır.
Örnek.DT.11: Örnek.DT.7’deki Rth direncini gerilim kaynaklarını kısa devre ve akım
kaynaklarını açık devre yaparak hesaplayınız.
Devreyi tekrar çizelim:(Gerilim kaynakları kısa, akım kaynakları açık)
Rab =
4Ω .2Ω 8
= = 1,333Ω
4Ω + 2Ω 6
Eğer devrede kontrollü kaynaklar varsa, yine bağımsız kaynaklar yukarıdaki gibi kısa devre
ya da açık devre yapılır. Fakat bu işlem kontrollü kaynaklara uygulanmaz. Onun yerine a ve b
uçları ara sıra test gerilimi uygulanır ve sonuç bu şekilde hesaplanır
Örnek.DT.12: Örnek.DT10’daki devrede Rth direncini test gerilimi yöntemi ile bulunuz.
Girişteki bağımsız gerilim kaynağını kısa devre edelim.
+
V
VT
V
iT = ab + 100i iT = T + 100i
iT
2K
2K
i bu sefer şu şekilde hesaplanır.
−10−4
i=
v değerin negatif olduğuna dikkat ediniz. V = VT olduğundan
100
−10−4
i=
vT yerine yazarsak
100
1
(−10 − 4)
iT =
+ 100
vT
100
2K
−4
iT
iT = (0, 5 x 10−3 − 10 )vT
vt =
4 x 10 −4
Rth =
VT iT / 4 x 10−4 10000
Rth =
=
=
= 2500Ω
4
iT
iT
Maksimum Güç Transferi
Güç transferi olayı elektrik açısından iki şekilde incelenir. Đlk kısım için öretilen gücün ne
kadarının verimli bir şekilde transfer edildiğidir. Güç üretim istasyonlarından, yüke transfer
edilen güç yüzdesi ne kadar büyükse o kadar verimlidir denir. Đkincisi ise transfer edilen
© Uğur TAŞKIRAN 2007
14
Devre Analizi Ders Notları
Devre Analiz Teknikleri
gücün büyüklüğüyle ilgilidir. Bu tip sistemlerde üretilen güç çok sınırlı ve küçük olduğundan
üretilen gücün maksimum değeri yüke transfer edilmek ister. Bu durumda maksimum güç
transferi kuralları uyarlanır. Herhangi bir devre Thevenin eşdeğeri olarak yazılabildiğinden
karmaşık devre bir Thevenin eşdeğeri ile yer değiştirilir.
a
i
Rth
≡
RL
+
-
a
RL
Vth
b
i
b
Şekil.DT.10 Maksimum Güç Transferi
Yük direnci üzerinde harcanan gücü yazarsak.
2
Vth
PL = i .RL =
.RL
Rth + RL
Gücün RL ’ye göre türevini aldığımızda ve sıfıra eşitlediğimizde maksimum güç transferi için
2
gerekli olan RL değerini hesaplayabiliriz.
( Rth + RL ) 2 − RL 2( Rth + RL )
dP
2
= Vth
=0
d RL
( Rth + RL )4
Vth sıfır olamayacağından köşeli parantezin içi dolayısıyla;
( Rth + RL ) 2 − RL 2( Rth + RL ) = 0
Rth 2 + 2 Rth RL + RL 2 − 2 RL Rth − 2 RL 2 = 0
Rth 2 − RL 2 = 0 ⇒
Rth2 = RL2
⇒
Rth = RL
Sonuç olarak RL yük direnci maksimum güç transferi için Rth ’ye eşit olmalıdır.
Örnek.DT.13: Aşağıdaki devrede maksimum güç transferi için RL ne olmalıdır. PR L ne
olmalıdır ( Pmax ) ve üretilen gücün ne kadarı yüke transfer edilmektedir.
Vab = Vth ( RL bağlı değilken)
30.40
Vab =
= 24v
30 + 20
20.30
Rth =
(40v’luk bir gerilim kaynağı
30 + 20
kısa devre edilirse)
Rth = 12Ω
Dolayısıyla maksimum güç transferi için RL = Rth = 12Ω olmalıdır. RL devreye bağlı iken;
© Uğur TAŞKIRAN 2007
15
Devre Analizi Ders Notları
2
RPL = Pmax
Devre Analiz Teknikleri
2
2
Vth
24
24
=
.RL =
.12 = .12 = 12W
12 + 12
24
Rth + RL
40v’luk gerilim kaynağınca üretilen güç ise: ( RL bağlı iken)
V
RL
12
Vab =
.Vth = 12volt
⇒ i30 Ω = ab =
= 0, 4 A
RL + Rth
30 30
V
12
iRL = ab =
= 1A
12 12
Bu durumda kaynaktan çekilen akım i = i20 Ω = i30 Ω + iRL = 1, 4 A
Üretilen güç ise Pü = v.i = 40v.1A = 56W
PL
12W
Transfer edilen güç yüzdesi = %
x100 = %
x100 = %21,43
Pü
56W
Süperpozisyon Metodu
Bir doğrusal sistemde birden fazla kaynak tarafından besleniyorsa sistemin doğal tepkimesi
her bir kaynak için diğer kaynaklar izole edilerek hesaplanan tepkilerin toplamına eşittir.
Sistemin doğrusal olması yeterli şarttır.
Ohm Kanunu; grafiksel ifade ve bağımsız kaynakların iç direnci
Bir direnç üzerinden geçen akımın, gerilime olan grafiği çizilirse, bu Ohm kanununun
grafiksel ifadesi olur. Grafik bir doğrudan oluşur ve eğimi direncin ters değerini verir. Bunun
nasıl olduğunu görelim.
i
Bir doğrunun eğimi: m =
y2 − y1
x2 − x1
i −i
Şekil.DT.11’deki doğrunun eğimi ise m = 2 1 olur
v2 − v1
i − 0 i2 1
eğer v1 = 0 ise , i1 = 0 olduğundan m = 2
= =
v2 − 0 v2 R
1
v −v
m = ise R = 2 1 şeklinde yazılabilir.
R
i2 − i1
i2
i1
V
V1 V2
Şekil.DT.11. Direncin
akım-gerilim grafiği
Şekil.DT.12’de akım ve gerilim kaynağının grafiği görülmektedir. Grafiklerin eğimlerinden
faydalanarak akım ve gerilim kaynağının dirençlerini hesaplayalım.
© Uğur TAŞKIRAN 2007
16
Devre Analizi Ders Notları
i
Devre Analiz Teknikleri
Şekil.DT.12
Gerilim ve
Akım
Kaynağının
Gerilim
Akım
Grafikleri
V
i
ik
V
Vk
Gerilim Kaynağının Grafiği
Akım Kaynağının Grafiği
Gerilim kaynağı için içi direnç hesabı:
v −v
R= 2 1
v2 − v1 = vk − vk = 0
⇒
i2 − i1
0
R=
= 0Ω
i2 − i1
Akım kaynağı için iç direnç hesabı
v −v
⇒
R= 2 1
i2 − i1 = ik − ik = 0
i2 − i1
v −v
R = 2 1 = ∞Ω
0
Sonuç olarak gerilim kaynağının iç direnci sıfır, akım kaynağının iç direnci sonsuzdur.
Tekrar süperpozisyon yöntemine dönersek, devrenin çözümü için başta bir kaynak seçilir ve
diğer bağımsız kaynaklar gerilim kaynağı ise iç direnci sıfır olduğundan kısa devre ve akım
kaynağı ise iç direnci sonsuz olduğundan açık devre yapılır. Devre tek kaynak için çözülür.
Daha sonra bir başka kaynağa geçilir. Çözüm bu kaynak içinde tekrarlanır. Bu işlem bütün
kaynaklar için tekrarlanır. En son çözüm her bir kaynak için bulunan çözümlerin toplamıdır.
Örnek.DT.14: Örnek.DT.6’daki devreyi ve 21Ω’uk direnç üzerinden geçen i akımı
süperpozisyon yöntemi ile çözünüz.
Yalnızca 11v’luk gerilim kaynağı için;
RS1 = 3 + 10 = 13Ω
RP1 =
ix1 =
3+ 2
= 8, 03Ω
11v
= 0.844 A
5 + RP1
i211 =
© Uğur TAŞKIRAN 2007
3.2
8, 03 11v
.
= 0.322 A
5 + 8, 03 21
17
Devre Analizi Ders Notları
Devre Analiz Teknikleri
Yalnızca 6A’lik akım kaynağı için;
5.21
= 4, 038Ω
5 + 21
RS1 = 3 + RP1 = 7, 038Ω
RP1 =
RP2 = 4,131Ω
V2 = 6.RP2 = 24, 785v ⇒
i3 =
V2
= 3, 521A
RS1
V1 = V2 − i3 .3 = 24, 785v − 3.3,521 = 14, 22v
V −14, 22
V
ix2 = − 1 =
= −2,844 = −2 A
i212 = 1 = 0, 677 A
5
5
21
ix = ix1 + ix2 = 0,844 − 2,844 = −2 A ve i21 = i211 + i212 = 0, 0** A
Örnek.DT.15: Aşağıdaki devrede ix akımını süper pozisyon yöntemi ile hesaplayınız.
2A
10 ohm
20 ohm
ix
+
5A
-
100 ix
80 v
+
-
Yalnızca 2A’lik akım kaynağı için;
2A
i1 + ix1 = 2 A ve i =
10 ohm
20 ohm
-
© Uğur TAŞKIRAN 2007
30
−
100ix1
30
+ ix1 = 2 A
−100ix1 + 30ix1 = 60
i1
ix1
100 ix1
−100ix1
ix1 =
60
= −0,857143 A
−70
18
Devre Analizi Ders Notları
Devre Analiz Teknikleri
Yalnızca 5A’lik akım kaynağı için;
i2
10 ohm
i2 = 5 + ix2
20 ohm
ix2
5A
-
100 ix2
100ix2 = i210 + 20ix2
i2 =
80ix2
10
5 + ix2 =
80ix2
10
50 + 10ix2 = 80ix2
ix =
50
= 0, 714 A
70
Yalnızca 80 voltluk gerilim kaynağı için;
10 ohm
20 ohm
ix3
-
100 ix3
80 V +
-
ix3 =
100ix3 − 80
30
30ix3 = 100ix3 − 80
80
= 1,14 A
70
ix = ix1 + ix2 + ix3 = 1 Amper
ix3 =
© Uğur TAŞKIRAN 2007
19