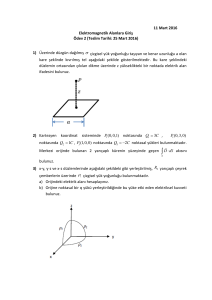
T.C. SAKARYA ÜNİVERSİTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ DERSİ YAZ OKULU ARA SINAVI (Doç.Dr. Tahsin ENGİN – Yrd.Doç.Dr. Zekeriya PARLAK) SORU #1 Şekilde gösterildiği gibi yoğunluğu 900 kg/m3 olan bir sıvı 90o lik bir dirsekten geçerek, 𝐿 = 0,5 m uzunluğundaki ve 𝑏 = 0,01 m genişliğindeki delikten 0 m/s hızdan 2 m/s’ye lineer olarak değişecek şekilde yatay olarak çıkıyor (𝑉 = 4𝑦). 𝑅 = 1 m olduğuna, akış daimi ve ağırlıklar ihmal edildiğine göre O noktasını desteklemek için gerekli olan momenti bulunuz? ÇÖZÜM #1 𝑑 �⃗ � 𝜌 𝑑∀ + � �𝑟⃗ × 𝑉 �⃗ � 𝜌�𝑉 �⃗ ∙ 𝑛�⃗� 𝑑𝐴 � �𝑟⃗ × 𝑉 𝑑𝑡 𝐾𝐻 𝐾𝑌 Akış daimi, meydana gelen kuvvetler ile momentum akışı aynı düzlemdedir ve çıkıştaki birin vektör ile hız vektörü aynı yöndedir. Sadece çıkış akışı O noktası üzerinde saat yönünde bir moment meydana getirecektir ��⃗ = �𝑀 � 𝑀 = � (𝑟 𝑉) 𝜌(𝑉) 𝑑𝐴 𝐾𝑌 Alternatif olarak çıkan akışkanın O noktasından geçen eksene göre yaptığı moment: d𝑀 = d𝐹 ∙ 𝑟, d𝐹 = d𝑚̇ 𝑉, d𝑚̇ = 𝜌𝑉d𝐴 d𝐹 = 𝜌𝑏𝑉 2 d𝑌 d𝐴 = 𝑏 d𝑌 d𝑀 = 𝜌𝑏(𝑅 + 𝑌)𝑉 2 d𝑌 𝐿 M = � 𝜌𝑏 (4𝑌)2 (𝑅 + 𝑌)d𝑌 0 𝐿 𝑀 = 16𝜌𝑏 � (𝑅𝑌 2 + 𝑌 3 ) 𝑑𝑌 0 𝐿 𝑅𝑌 3 𝑌 4 𝑅𝐿3 𝐿4 𝑀 = 16𝜌𝑏 � + � = 𝜌𝑏 � + � 3 4 0 3 4 1∙0,53 𝑀 = 16 ∙ 900 ∙ 0,01 � 3 + 0,54 4 � = 8.25 𝑁. 𝑚 � 𝑀 = � 𝑟𝑚̇𝑉 − � 𝑟𝑚̇𝑉 ç𝚤𝑘𝑎𝑛 ç𝚤𝑘𝑎𝑛 𝑇 = −8.25 𝑁. 𝑚 Moment saat ibresi yönünde meydana geleceğinden Borunun O noktasındaki saat ibresi yönünde uygulanan 8.25 𝑁. 𝑚 momente karşı koyacak, saat yönünün tersinde bir moment ile desteklenmesi gerekmektedir. SORU #2 Değişken kesitli bir borudan hava şekilde gösterildiği gibi daimi olarak akmaktadır. Viskoz ve sıkışabilirlik etkileri ile birlikte kayıpları da ihmal ederek hacimsel debiyi bulunuz? (𝜌ℎ𝑎𝑣𝑎 = 1.2 kg⁄m3 , 𝜌𝑠𝑢 = 1000 kg⁄m3 ) ÇÖZÜM #2 1 ve 2 nokatalarını şekildeki gibi seçerek, Bu iki nokta arasında Bernoulli eşitliğini uygularsak; 𝑃1 𝑉12 𝑃2 𝑉22 + + 𝑧1 = + + 𝑧2 𝜌ℎ 𝑔 2𝑔 𝜌ℎ 𝑔 2𝑔 𝑉2 = 0 (durma noktası), 𝑧2 = 𝑧1 𝜌ℎ 𝑉12 𝑃2 − 𝑃1 = 2 1 ve 2 noktaları arasında basınç taraması yaparsak; 𝑃1 + 𝜌ℎ 𝑔𝑥 + 𝜌𝑠 𝑔ℎ − 𝜌ℎ 𝑔ℎ − 𝜌ℎ 𝑔𝑥 = 𝑃2 𝑃2 − 𝑃1 = 𝑔ℎ(𝜌𝑠 − 𝜌ℎ ) 𝜌ℎ 𝑉12 = 𝑔ℎ(𝜌𝑠 − 𝜌ℎ ) 2 𝜌𝑠 1000 𝑉1 = �2𝑔ℎ � − 1� = �2 ∙ 9,81 ∙ 0,2 � − 1� = 57,15 m/s 𝜌ℎ 1,2 ∀̇= 𝜋0,32 57,15 = 4.03 m3 ⁄s 4 SORU #3 Bir gölden saniyede 0,05 m3 su, 900 m uzunluğunda 10 cm çapında ticari çelik borudan oluşan borulama sistemiyle 100 m yukarıdaki bir depoya taşınmaktadır. Borulama sisteminde beş adet 90o lik, iki adet ise 45 o lik derecelik dirsek bir tam sürgülü açık vana, bir iyi yuvarlatılmış giriş, bir keskin kenarlı çıkış vardır. Pompa-motor gurubunun verimi %70 olduğuna göre suyu yukarı taşımak için gerekli olan elektrik gücünü belirleyiniz? (𝜌 = 1000 kg/m3 , µ = 10−3 Pa. s) ÇÖZÜM #3 1 noktasını göl yüzeyinde 2 noktasını depo sıvı yüzeyinde seçiyoruz. 𝑃1 𝑉12 𝑃2 𝑉22 + + 𝑧1 + ℎ𝑝𝑜𝑚𝑝𝑎,𝑓 = + + 𝑧2 + ℎ𝑘 𝜌𝑔 2𝑔 𝜌𝑔 2𝑔 𝑃1 = 𝑃2 = 𝑃𝑎𝑡𝑚 = 0, 𝑉1 ≅ 𝑉2 ≅ 0, 𝑧1 = 0 , 𝑧2 = 100𝑚 𝑅𝑒 = 𝑉= 𝜌𝑉𝐷 𝜇 = ℎ𝑝𝑜𝑚𝑝𝑎,𝑓 = 𝑧2 + ℎ𝑘 0,05 ∀̇ = = 6,37 m/s 2 𝜋𝐷 ⁄4 𝜋0,12 ⁄4 1000∙6,37∙0,1 10−3 𝜀 0,045 = = 4,5 ∙ 10−4 𝐷 100 1,11 6,9 𝜀 ⁄𝐷 ≅ −1,8 log � +� � 𝑅𝑒 3,7 �𝑓 1 = 637000 akış türbülanslıdır 1,11 6,9 4,5 ∙ 10−4 � = −1,8 log � +� � 3,7 637000 𝑓 = 0,017 ℎ𝑘 = �𝑓 � = 7,65 𝐿 𝑉2 + � 𝐾𝐾 � 2𝑔 𝐷 � 𝐾𝐾 = 5 ∙ 𝐾𝑑𝑖𝑟𝑠𝑒𝑘(90𝑜 ) + 2 ∙ 𝐾𝑑𝑖𝑟𝑠𝑒𝑘(45𝑜 ) + 𝐾𝑔𝑖𝑟𝑖ş + 𝐾ç𝚤𝑘𝚤ş + 𝐾𝑣𝑎𝑛𝑎 � 𝐾𝐾 = 5 ∙ 0,9 + 2 ∙ 0,4 + 0,03 + 1 + 10 = 16,33 ℎ𝑘 = �0,017 900 6,372 + 16,33� = 350,17 m 2 ∙ 9,81 0,1 ℎ𝑝𝑜𝑚𝑝𝑎,𝑓 = 𝑧2 + ℎ𝑘 = 100 + 350,17 = 450,17 m 𝑊̇𝑝𝑜𝑚𝑝𝑎,𝑓 = 𝑚̇ 𝑔 ℎ𝑝𝑜𝑚𝑝𝑎,𝑓 = 1000 ∙ 0,05 ∙ 9,81 ∙ 450,17 = 220808 W 𝑊̇𝑒𝑙𝑒𝑘𝑡𝑟𝑖𝑘 = 𝑊̇𝑝𝑜𝑚𝑝𝑎,𝑓 𝜂𝑝𝑜𝑚𝑝𝑎−𝑚𝑜𝑡𝑜𝑟 = 220808 0,7 = 315440 W ≅ 316 kW SORU #4 Dakikada 1,8 m3 temiz hava ihtiyacı olan bir odayı havalandırmak üzere bir fan seçilecektir. Fan çıkışından hava hızının 10 m⁄s’yi geçmemesi istenmektedir. Kullanılacak fan-motor grubu 3,6 W elektrik tükettiğine göre (a) fanın dış çapını bulunuz? (b) fan-motor grubunun verimini bulunuz (𝜌ℎ = 1.2 kg⁄m3 ) ÇÖZÜM #4 (a) 𝐷=� (b) ∀̇ 1,8/60 = = 0,061 m (𝜋 𝑉)⁄4 (𝜋 ∙ 10)⁄4 1 noktasını fanın girişinden uzak bir noktada ve 2 noktasını fan çıkışında belirlenir., 1 noktası fandan yeteri kadar uzak olduğundan 𝑃1 = 𝑃𝑎𝑡𝑚 ve buradaki akış hızı önemsizdir 𝑉1 ≅ 0. Aynı şekilde 𝑃2 = 𝑃𝑎𝑡𝑚 olacaktır. 1 ve 2 noktası arasındaki bu kontrol hacmi için enerji denklemini yazarsak; 𝑚̇ � 𝑃2 𝑉22 𝑃1 𝑉12 + + 𝑔𝑧1 � + 𝑊̇ 𝑓𝑎𝑛 = 𝑚̇ � + + 𝑔𝑧2 � + 𝐸̇ 𝑚𝑒𝑘,𝑘𝑎𝑦𝚤𝑝 𝜌 2 𝜌 2 𝐸̇𝑚𝑒𝑘,𝑘𝑎𝑦𝚤𝑝 = 𝐸̇𝑚𝑒𝑘,𝑘𝑎𝑦𝚤𝑝,𝑓𝑎𝑛 dır. Böylece 𝑊̇𝑓𝑎𝑛,𝑓 = 𝑊̇𝑓𝑎𝑛 − 𝐸̇𝑚𝑒𝑘,𝑘𝑎𝑦𝚤𝑝,𝑓𝑎𝑛 𝑊̇𝑓𝑎𝑛,𝑓 = 𝑚̇ %50 verimle çalışmaktadır. 𝑉22 2 𝜂𝑓𝑎𝑛−𝑚𝑜𝑡𝑜𝑟 = 1,8 102 = 1,2 ∙ � 60 � 2 1,8 = 1,8 𝑊 𝑊̇𝑓𝑎𝑛,𝑓 = = 0,5 𝑊̇𝑒𝑙𝑒𝑘𝑡𝑟𝑖𝑘 3,6
