özel tanımlı fonksiyonlar

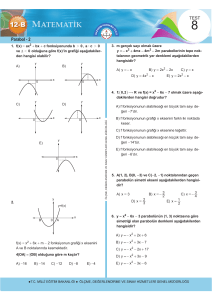
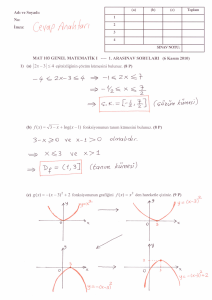
ÖZEL TANIMLI FONKSİYONLAR
A. Bir Fonksiyonun Tanım Kümesi
sağlayan x değerleri için tanımsızdır.
Kuralı verilmiş bir fonksiyonun tanımlı olduğu en geniş reel
sayı kümesine o fonksiyonun tanım kümesi (tanım aralığı)
denir
Buna göre,
1.
3
2
x  4 x  0  x.( x  4)  0  x.( x  2).( x  2)  0
 x  0 veya x  -2 veya x  2 dir.
Polinom Fonksiyonunun Tanım Kümesi
n
n1
f ( x )  a n .x  a n1 .x
 ...  a1 .x  a 0
3
x  4 x  0 denkleminin çözüm kümesi Ç  { 2,0,2}
olduğuna göre f ( x ) fonksiyonunun en geniş tanım kümesi,
şeklindeki reel katsayılı polinom fonksiyonları bütün reel
sayılar için tanımlıdır.
R  { 2,0,2} dir.
Tanım kümesi A ile gösterilirse, polinom fonksiyonlarının
tanım kümesi A  R olur.
3.
Çift Dereceden Köklü Fonksiyonların Tanım
Kümesi
Örnek:
n pozitif tam sayı olmak üzere, f ( x )  2n g( x ) şeklindeki
2
f ( x )  x  8 x  5 fonksiyonunun en geniş tanım aralığını
fonksiyonlar g( x )  0 için tanımlıdır. g( x )  0 eşitsizliğinin
çözüm kümesi Ç= B ise f ( x ) fonksiyonunun en geniş tanım
kümesi (tanım aralığı) A  B olur.
bulalım.
Çözüm:
Örnek:
2
f ( x )  x  8 x  5 bir polinom fonksiyonudur. Polinom
fonksiyonlarının en geniş tanım kümesi reel sayılar kümesi
olduğuna göre, A  R dir.
2.
f ( x) 
bulalım.
Çözüm:
Rasyonel Fonksiyonların Tanım Kümesi
f ( x) 
P( x )
Q( x )
x2  x  12 fonksiyonunun en geniş tanım aralığını
f ( x) 
şeklindeki rasyonel fonksiyonlar
x2  x  12 fonksiyonunun en geniş tanım aralığı
2
x  x  12  0 eşitsizliğinin çözüm kümesidir. Buna göre,
Q( x )  0 için tanımsızdır. Q( x )  0 denkleminin çözüm
kümesi Ç = B ise f ( x ) fonksiyonunun en geniş tanım
kümesi (tanım aralığı) A  R  B olur.
2
x  x  12  0  x  3 veya x  4 tür.
Örnek:
f ( x) 
x3  4 x
x3  4 x
2
x  x  12  0 eşitsizliğinin çözüm kümesi,
fonksiyonunun en geniş tanım kümesini
bulalım.

  


Ç   ,3  4,   R   3,4 olduğuna göre,
Çözüm:


f ( x ) fonksiyonunun en geniş tanım Ç  R   3,4 tür.
3
Verilen f ( x ) fonksiyonu x  4 x  0 denklemini
1
Örnek:
f ( x) 
Örnek:
1
4 2
x 9 
x

1
x4
f ( x) 
fonksiyonunun en geniş
3
4  x fonksiyonunun en geniş tanım aralığını
bulalım.
tanım aralığını bulalım.
Çözüm:
Çözüm:
Kökün derecesi tek sayı olduğu için, f ( x ) in tanım kümesi
4  x in tanım kümesiyle aynıdır. 4  x in tanım aralığı reel
sayılar kümesi olduğundan f ( x ) in tanım aralığı A  R dir.
f ( x ) fonksiyonunun en geniş tanım aralığı
4 2
x  9 ile
1
x

1
x4
nin tanımlı olduğu aralıkların
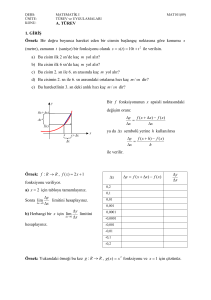
B. Parçalı Fonksiyonlar
kesişim kümesidir.
Tanım kümesinin alt aralıklarında farklı birer kuralla
tanımlanan fonksiyonlara parçalı fonksiyonlar adı verilir.
4 2
2
x  9 un tanım kümesi x  9  0 eşitsizliğinin çözüm
kümesidir.
Örnek:
2
x  9  0 ise x  3 veya x  3 tür.
  

f ( x) 
Ç   ,3  3,  dur.
1
1
x

1
x4
nin tanım aralığı
1
x

1
x4
Örnek:
 0 eşitsizliğinin
x 1
2 x  1 ,

f ( x )   x2 , - 1  x  1 fonksiyonu parçalı fonksiyondur.
0 ,
x  -1

çözüm kümesidir.
1
x
Ç

2
1
x4
0
4
x.( x  4)
 0  0  x  4 tür.
 
 0,4 tür.
Örnek:
Buna göre f ( x ) fonksiyonunun en geniş tanım aralığı,
f ve g fonksiyonları R den R ye tanımlıdır.
 
Ç  Ç  Ç  3,4 tür.
1
2
4.
x , x  0
fonksiyonu parçalı fonksiyondur.

 x , x  0
f ( x) 
Tek Dereceden Köklü Fonksiyonların Tanım
Kümesi
4 x , x  2
ve

1  x , x  2
g( x ) 

x2 , x  0
olduğuna


x

1
,
x

0

göre, f (5)  g( 5)  ( f  g)(1) değerini bulalım.
n pozitif tam sayı olmak üzere, f ( x )  2n  1 g( x )
Çözüm:
fonksiyonu, g( x ) in tanımlı olduğu her yerde tanımlıdır.
g( x ) in tanım kümesi B ise f ( x ) fonksiyonunun en geniş
tanım kümesi (tanım aralığı) A  B dir.
5  2 olduğuna göre, f ( 5)  4.5  20 dir.
 5  0 olduğuna göre, g( 5)  5  1  4 tür.
2
( f  g)(1)  f (1)  g(1)  (1  1)  1  1 dir.
2
Buna göre, f (5)  g(5)  (f  g)(1)  20  4  1  17 dir.
Örnek:
Örnek:
g( x ) 
f ve g fonksiyonları R den R ye tanımlıdır.
f ( x) 
4 x , x  2
ve

1  x , x  2
g( x ) 

x2 , x  0
fonksiyonunun grafiğini çizelim.


x  1 , x  0
Çözüm:
x2 , x  0
olduğuna

x  1, x  0
göre, ( f  g)( x ) fonksiyonunu bulalım.
Çözüm:
x2
4 x ,
4 x , x  2 
f ( x)  
 1  x , 0  x  2
1  x , x  2 
x0
1  x ,
C. Mutlak Değer Fonksiyonu
x2 , x  2
x2 , x  0  2
g( x )  
 x , 0  x  2
x  1 , x  0 
x  1, x  0

f : A  B reel değerli fonksiyon olsun.
f ( x)  f ( x) 
 x2  4x ,
x2


( f  g)( x )   x2 - x  1 , 0  x  2
 2 x ,
x0

f ( x ) , f(x )  0

- f(x ) , f(x )  0
şeklinde tanımlanan f fonksiyonuna mutlak değer
fonksiyonu denir.
Örnek:
f : R  R , f ( x )  x  2 olduğuna göre f ( x ) fonksiyonunu
Örnek:
f ( x) 
bulalım.
4 x , x  2
fonksiyonunun grafiğini çizelim.

1  x , x  2
Çözüm:
f ( x)  x  2 
Çözüm:
x  2 , x - 2  0 x  2 , x  2


- (x - 2) , x - 2  0  x  2 , x  2
Örnek:
f : R  R , f ( x )  x  1 olduğuna göre f ( x ) fonksiyonunu
grafiğini çizelim.
3
Çözüm:
Buna göre f ( x )  x2  4 fonksiyonunun grafiği aşağıda
f ( x)  x  1 
x  1 , x  1

1  x , x  1
çizilmiştir.
2.Yol
Kural
Mutlak değerin tanımını ve yukarıdaki grafiği göz önüne
alalım. f ( x ) in negatif olmadığı yerde f ( x ) in grafiği
f ( x ) in
aynısıdır. f ( x ) in negatif olduğu yerde f ( x ) in grafiği f ( x )
in grafiğinin Ox eksenine göre simetriğidir.
Bu durumda y  f ( x ) in grafiğini iki adımda çizebiliriz.
1.Adım: y  f ( x ) in grafiği çizilir.
2.Adım: Ox ekseninin üst tarafında kalan eğri aynen
bırakılır. Ox ekseninin altında kalan kısmın Ox
eksenine göre simetriği alınır.
Örnek:
f : R  R , y  f ( x)
fonksiyonunun grafiği
yanda verilmiştir. Buna
göre y  f ( x ) in
Örnek:
grafiğini çizelim.
2
f : R  R , f ( x )  x  4 olduğuna göre f ( x )
fonksiyonunu grafiğini çizelim.
Çözüm:
Çözüm:
2
f ( x )  x  4 fonksiyonunun işaretini inceleyelim.
f ( x ) fonksiyonu  6  x  0 aralığında negatif değerler,
diğer yerlerde negatif olmayan değerler almıştır.
Buna göre  6  x  0 aralığındaki ( x ekseni altındaki)
görüntünün x eksenine göre simetriği alınarak y  f ( x )
2
f ( x)  x  4

x2  4 , x  2 ve

2

4  x , - 2  x  2
fonksiyonunun grafiğini çizilmiş olur.
x2
olur.
y  f ( x ) fonksiyonunun grafiği aşağıda verilmiştir.
4
3. bölgede x  0 ve y  0 olduğundan  x  y  2 olup
bu doğrunun 3. bölgede kalan kısmı alınır.
4. bölgede x  0 ve y  0 olduğundan x  y  2 olup bu
doğrunun 4. bölgede kalan kısmı alınır.
Buna göre, istenen grafik aşağıdaki gibi olur.
Örnek:
f : R  R , f ( x )  x  x  1 fonksiyonunun grafiğini
çizelim.
Çözüm:
Örnek:
y  x  1 fonksiyonunun grafiğini çizelim.
Çözüm:
y  x  1 olduğuna göre,
x  1
 2 x  1 ,

f ( x )  1 ,
- 1  x  0 olur.
2 x  1 ,
x0

y  0 için y  x  1 olur.
y  0 için  y  x  1  y  1  x olur.
Örnek:
Örnek:
x  y  2 fonksiyonunun grafiğini çizelim.
 
f :  1,2  R , f ( x )  x  x  1 fonksiyonunun grafiğini
Çözüm:
çizelim.
Koordinat düzleminin 1. bölgesinde x  0 ve y  0
olduğundan x  y  2 olup bu doğrunun 1. bölgede kalan
kısmı alınır.
Çözüm:
f ( x)  x  x  1 
2. bölgede x  0 ve y  0 olduğundan y  x  2 olup bu
doğrunun 2. bölgede kalan kısmı alınır.
5
0x2
1 ,

- 2x  1 , - 1  x  0
 
sgn f ( x )  f ( x )
1 , f(x )  0

 0 , f(x )  0 şeklinde tanımlanan
- 1, f(x )  0

fonksiyona f nin işaret fonksiyonu denir.
Örnek:
Örnek:


sgn 1  1

f :  2,2  R , f ( x )  cos x  cos x  1 fonksiyonunun
Çözüm:
2


2

2
3
3
2
2
x
x
x



2
sgn 
 2  x  
 3

sgn  101  1
grafiğini çizelim.

2
3
2

2
 cos x  0  f ( x )  2. cos x  1 dir.
1
  1
Örnek:

 cos x  0  f ( x )  1 dir.

sgn x3  x2  12 x  0 denkleminin çözüm kümesini
bulalım.
 cos x  0  f ( x )  2. cos x  1 dir.
Çözüm:


3
2
sgn x3  x2  12 x  0  x  x  12 x  0
 cos x  0  f ( x )  1 dir.
2
 x.( x  x  12)  0
 x  2  cos x  0  f ( x )  2. cos x  1 dir.
 x.( x  4).( x  3)  0
Bu durumda y  cos x  cos x  1 fonksiyonunun grafiği

aşağıdaki gibi olur.

Ç.K.   3, 0, 4 olur.
Örnek:
 
sgn x2  9  1 denkleminin çözüm kümesini bulalım.
Çözüm:
 
2
2
sgn x2  9  1  x  9  0  x  9  3  x  3


 Ç.K.   3,3 olur.
D. İşaret Fonksiyonu
Örnek:
f : A  R  R bir fonksiyon olmak üzere,


f ( x )  sgn x  1 fonksiyonunun grafiğini çizelim.
6
Çözüm:
1 , x  3 veya

sgnf ( x )   0 , x  3 veya
 1 , - 3  x  1

1 , x  1  0 1 , x  1


sgnx  1  0 , x  1  0  0 , x  1 olur.
 1 , x  1  0  1 , x  1



x 1
x  1 olur.
 
y  sgn f ( x ) fonksiyonunun grafiği aşağıda verilmiştir.

y  sgn x  1 fonksiyonunun grafiği aşağıda verilmiştir.
Örnek:


f : R  R , f ( x )  sgn 2  x fonksiyonunun grafiğini
Örnek:
çizelim.
 
Çözüm:
2
f : R  R , f ( x )  x  x  6 olmak üzere sgn f ( x )
ifadesinin eşitini bulalım.
2  x  0  x  2  x  2 dir.
Çözüm:
2  x  0  x  2  2  x  2 dir.
2
f ( x )  x  x  6  0 için,
2  x  0  x  2  x  2 veya x  2 dir.
2
a  1  0 ve   b  4ac  23  0 olup f ( x )  0 dır.

Buna göre sgnf ( x )   1 dir.
f ( x )  sgn 2 
Örnek:

1 ,  2  x  2

x   0 , x  2 veya x  2 olur.
 1 , x  2 veya x  2


y  sgn 2  x fonksiyonunun grafiği aşağıda verilmiştir.
 
2
f : R  R , f ( x )  x  2 x  3 olmak üzere sgn f ( x )
fonksiyonunun grafiğini çizelim.
Çözüm:
7
Örnek:
0  x    sin x  0  f ( x)  sgn(sin(x))  1 dir.
f : R  R , y  f ( x)
fonksiyonunun grafiği
yanda verilmiştir. Buna
göre y  sgn f ( x) in
grafiğini çizelim.
x    f ( )  sgn(sin())  sgn(0)  0 dır.
  x  2  sin x  0  f ( x)  sgn(sin(x))  1 dir.
x  2  f ( 2)  sgn(sin(2))  sgn(0)  0 dır.
Bu durumda y  f ( x ) fonksiyonunun grafiği aşağıdaki gibi
olur.
Çözüm:
y  f ( x ) fonksiyonu x  4 , x  1 ve x  4 için sıfıra eşit
olmaktadır.
Bu nedenle, bu değerler için sgn f ( x)  0 olur.
x  4 ve 1  x  4 için y  f ( x ) fonksiyonu negatif
değerler almaktadır.
Bu nedenle, x  4 ve 1  x  4 için sgn f ( x)  1 olur.
 4  x  1 ve x  4 için y  f ( x ) fonksiyonu pozitif
değerler almaktadır.
E.
Tam Değer Fonksiyonu
Bu nedenle,  4  x  1 ve x  4 için sgn f ( x)  1 olur.
1.
Tam Değer Kavramı
x bir reel sayı olmak üzere, x ten büyük olmayan en büyük
tam sayıya x in tam değeri denir ve x ile gösterilir.
x bir reel sayı olmak üzere, x ten küçük olan en büyük tam
sayı t ise,
Örnek:

f : R  Z , f ( x)  x 

f :  2,2  R , f ( x)  sgn(sin x) fonksiyonunun
grafiğini çizelim.
x ,

t ,
xZ


xZ
olur.
Örnek:
Çözüm:
8 8
x  2  f ( 2)  sgn(sin(2))  sgn(0)  0 dır.
8,15  8
 2  x    sin x  0  f ( x)  sgn(sin(x))  1 dir.
 8,15  9
x    f ( )  sgn(sin())  sgn(0)  0 dır.
   x  0  sin x  0  f ( x)  sgn(sin(x))  1 dir.
Kural
x  0  f ( 0)  sgn(sin(0))  sgn(0)  0 dır.
x  a  a  x  a  1 , a  Z dir.
8
Örnek:
x2
3
Buna göre x in alabileceği tamsayı değerlerinin toplamı; 2+2 = 0 dır.
 4 eşitliğini sağlayan x değerinin çözüm aralığını
Örnek:
bulalım.
2
x  4  5 denkleminin çözüm aralığını bulalım.
Çözüm:
x2
3
44
x2
3
Çözüm:
 4  1  12  x  2  15
2
2
x  4  5  x2  4  5  x2  9  9  x  10
 14  x  17 olur.
  10  x  3 veya 3  x  10 olur.
2.
Tam Değer ile İlgili Özellikler
Örnek:
a) Her x  R ve a  Z için, x  a  x  a dır.
x  2  x  2  4 denkleminin çözüm aralığını bulalım.
Çözüm:
b) Her x, y  R için x  y  x  y dir.
x2  x2  4  x 2 x 2  4
Örnek:
 2. x  4  x  2
x  3. x
 8 denkleminin çözüm kümesini bulalım.
 2  x  3 olur.
Çözüm:
x  3. x
Örnek:
 8  x  3. x  8  2. x  8
2. x
 x  4  4  x  4  1
2
 9. x  10  0 denkleminin çözüm aralığını
bulalım.
 4  x  3 olur.
Çözüm:
x  a olsun. Buna göre,
Örnek:
2 x
 0 denklemini sağlayan tam sayıların toplamı
2. x
kaçtır?
2
 9. x  10  0  2a  9a  10  0
 ( a  2).( 2a  5)  0
Çözüm:
2 x
2
 02 - x
0
- x
 2
 a  2 veya a 
 2   x  1  1  x  2
x  a  x  2 veya x 
 1  x  2 veya - 2  x  -1 olur.
9
5
2
dir.
5
2
dir.
x 
5
2
olamaz. Çünkü x  Z dir.
x  2  2  x  2  1  2  x  3 olur.
Örnek:
 
f :  1,2  R , f ( x )  x  x fonksiyonunun grafiğini
çizelim.
Çözüm:
Örnek:
 1  x  0  x  1  f ( x )  x  1
2 x  3  11 eşitsizliğini sağlayan en büyük tam sayı
değeri kaçtır?
0  x  1  x  0  f ( x)  x
Çözüm:
1  x  2  x  1  f ( x)  x  1
2x  3  11  2. x  3  11  2. x  8  x  4 tür.
Bu koşula uygun en büyük tam sayı 3 tür.
3.
x  2  x  2  f ( x)  2  2  0 olur.
Bu durumda f ( x ) fonksiyonunun grafiği aşağıdaki gibi olur.
Tam Değer Fonksiyonu
f : A  R  R , f ( x )  x şeklinde tanımlanan fonksiyona
tam değer fonksiyonu denir.
Örnek:
Örnek:
 


f :  2,2  R , f ( x )  x . x . sgn( x ) fonksiyonunun
f :  2,1  R , f ( x )  x fonksiyonunun grafiğini çizelim.
grafiğini çizelim.
Çözüm:
Çözüm:
 2  x  1  x  2
 2  x  1 ise; x   x , x  2 ve sgn( x)  1
olup f ( x)  (  x).( 2).( 1)  2x tir.
 1  x  0  x  1
0  x 1 x  0
 1  x  0 ise; x   x , x  1 ve sgn( x)  1
olup f ( x)  ( x).( 1).( 1)   x tir.
x 1 x 1
x  0 ise; x  0 , x  0 ve sgn( x )  0 olup
f ( x)  0.0.0  0 dır.
0  x  1 ise; x  x , x  0 ve sgn( x )  1
olup f ( x)  x.0.1  0 dır.
10

1  x  2 ise; x  x , x  1 ve sgn( x )  1
2
 x   ise 0  sin x  1  f ( x )  sin x  0
olup f ( x)  x.1.1  x tir.
  x  2 ise  1  sin x  0  f ( x)  sin x  1
x  2 ise; x  2 , x  2 ve sgn( x )  1
x  2 ise f ( 2)  sin 2  0
olup f ( x)  2.2.1  4 tür.
Buna göre fonksiyonun grafiği aşağıdaki gibidir.
Bu durumda fonksiyonun grafiği aşağıdaki gibi olur.
Örnek:
A  { (x ,y)  R  R : x . y  2 } bağıntısının grafiğini
çizelim.
Örnek:


f :  2,2  R , f ( x )  sinx fonksiyonunun grafiğini
Çözüm:
çizelim.
x  Z ve y  Z dir.
x . y  2 ise,
Çözüm:
x
 1 , y  2 veya
x  2 ise f ( 2)  sin(-2 )  0  0
x
 1 , y  2 veya
 2  x  
3
2
ise 0  sin x  1  f ( x)  sin x  0

x
 2 , y  1 veya


x
 2 , y  1 dir.

Öncelikle x  1 , y  2 koşulunu sağlayan noktaları
düzlemde gösterelim.
x

 3
2
3
2
ise f ( 
3
2
)  sin(-
3
2
)  1 1
x  1  1  x  2 dir.
 x    ise 0  sin x  1  f ( x )  sin x  0
y  2  2  x  1 dir.
   x  0 ise  1  sin x  0  f ( x )  sin x  1
0x
x

2

2
Şimdi bütün noktaları gösterelim.
ise 0  sin x  1  f ( x)  sin x  0


2
2
x  2  2  x  3,
y  1  1  y  0 dır.
x  -1  -1  x  0 ,
y  2  2  y  3 tür.
ise f ( )  sin( )  1  1
x  2  2  x  -1 ,
11
y  1  1  y  2 dir.
2.
log( 4  x )
f ( x) 
x2  4
fonksiyonunun en geniş tanım
aralığını bulunuz.
Çözüm:
2
4  x  0 ve x  4  0 olmalıdır. Bu durumda,
x  4 ve x  2 dir.
Buna göre f fonksiyonunun en geniş tanım aralığı
Örnek:
 ,4   2,2 olur.
A  { (x ,y)  R  R : x - y  2 } bağıntısının grafiğini
çizelim.
3.
Çözüm:
x
f ( x) 
1  sgn( x )
fonksiyonunun en geniş tanım
aralığını bulunuz.
x - y  2  2  x - y  1 olur.
Çözüm
Paydayı sıfır yapan x değerleri için f fonksiyonu tanımsızdır.
Buna göre,
1  sgn( x)  0  sgn x  1  x  0 olur.
x  0 için f fonksiyonu tanımsızdır. Buna göre f
fonksiyonunun en geniş tanım aralığı, 0,  olur.
4.
Çözümlü Sorular
1.
f ( x) 
7  2 x  1 fonksiyonunun en geniş tanım
aralığını bulunuz.
f : R  R , f ( x )  x  x  sgn( x ) fonksiyonunun
 5,4  aralığındaki ifadesini bulunuz.
Çözüm




x   5,4 ise, x   x , x  5 , sgn( x)  1 dir.
x   5,4 ise, f ( x)   x  5  1   x  6 olur.
Çözüm:
f ( x) 
7  2 x  1 fonksiyonunun en geniş tanım aralığı
5.
7  2 x  1  0 eşitsizliğinin çözüm kümesidir.
x
5
 1  6 denklemini sağlayan kaç tane x tam sayısı
vardır?
7  2 x  1  0  2x  1  7  7  2x  1  7
 8  2x  6  4  x  3 olur.
12
Çözüm
x
5
1  6  6 
7.
x
5
1 6 1 7 
x
5
8
 35  x  40 olur.
f ( x)  5 
f (12)  5 
8.
Yandaki şekilde y  f ( x )
fonksiyonunun grafiği
verilmiştir. g( x )  f ( x )  f ( x )
olduğuna göre f (12) kaçtır?
Çözüm
12
Buna göre, verilen denklemi sağlayan tam sayılar 35, 36,
37, 38, 39 olmak üzere, 5 tanedir.
6.
x
5
5
x x
 5  2,4  5  2  3 tür.
 6 denkleminin çözüm kümesini bulunuz.
Çözüm
x  Z olduğundan x  x
6 x  x 6
olduğuna göre y  g( x )
fonksiyonunun grafiğini
çiziniz.
 2. x  x  3
 3  x  4 tür.
Çözüm
Verilen grafiğe göre,
9.
 2 denkleminin çözüm aralığını
bulunuz.
x  2  f ( x )  0  f ( x )  f ( x ) olup,
g( x)  f ( x)  f ( x)  0 dır.
x  3. x  2
Çözüm
x  2  Z olduğu için,
x  2  f ( x )  0  f ( x )  f ( x ) olup,
x  3. x  2
g( x)  f ( x)  f ( x)  0 dır.
 2  x  3. x  2  2


 x  3. x  2  2
 2  x  2  f ( x )  0  f ( x )  f ( x) olup,
 4. x  6  2
g( x)  f ( x)  f ( x)  2.f ( x) tir.
 4. x  8  x  2
 2  x  1 olur.
10. sgn( x  3)  x  3 denkleminin çözüm kümesini
bulunuz.
13
Çözüm
12. f ( x )  x  1  x fonksiyonunun grafiğini çiziniz.
x  3 için sgn(3  3)  3  3  sgn(0)  3  3
Çözüm
0  3  3 olup denklemi sağlamaz.
f ( x) 
x  3 için sgn( x  3)  1 dir. Buna göre,
x  1  0 , x  1 - x

x  1  0 , - x - 1 - x

x  1 ,

x  - 1 ,
1
- 2x - 1
sgn( x  3)  x  3  1  x  3  x  2
olup denklemi sağlar.
x  3 için sgn( x  3)  1 dir. Buna göre,
sgn( x  3)  x  3  1  x  3  x  4
olup x  3 olduğundan denklemi
sağlamaz.
13. 2. 2.x
2
 2.x  6  0 denkleminin çözüm aralığını
bulunuz.
Buna göre denklemin çözüm kümesi Ç={2} dir.
Çözüm
x
11. x  2,3  olmak üzere x .x
denkleminin kökleri x ve x olduğuna göre,
1
2.x  a olsun.
 9.x  5. x  0
2
2. 2.x
2
2
 2.x  6  0  2a  a  6  0
sgn( x  1)  sgn( x  3) değeri kaçtır?
1
2
 ( a  2).( 2a  3)  0  a  2 veya a 
Çözüm
 
x  2,3 ise x  2 dir. Buna göre,
x .x
x
3
2
 2.x  2  2  2 x  1  1  x  
Z
1
2
olur.
2
 9.x  5. x  0  2 x  9 x  10  0
 ( x  2).( 2x  5)  0
5
 x  2 ve x  dir.
2 2
1
5
sgn( x  1)  sgn( x  3)  sgn(2  1)  sgn(  3)
1
2
2
1
x
14.
4
2
 3  sgn( x  x  4) denklemini sağlayan kaç
tane tam sayı vardır?
Çözüm
a  0 ve   0 olduğundan dolayı her x  R için
2
2
x  x  4  0 olup sgn( x  x  4)  1 dir.
 sgn(3)  sgn(  )
2
x
x
2
 3  sgn( x  x  4) 
31
4
4
 1  1  0 olur.

x
4
 2  2 
Konu Bitmiştir.
14
x
4
 1  8  x  4 tür.
15