A. IS – LM ANALİZİ
A.1. IS Analizi (Mal Piyasası)
IS (Investment – Saving) (Yatırım – Tasarruf) Eğrisi, faiz oranları ile gelir düzeyi arasındaki
ilişkiyi gösterir. Analizin bu kısmında yatırımları I = I0 – bi olarak ifade edeceğiz. I0:Otonom
yatırımları, bi: faize bağımlı yatırımları ifade edecektir. Bunun dışında yatırım harcamaları,
beklentilerin bir fonksiyonudur. Böylece toplam harcama fonksiyonu:
AE = A0 + c(1 – t)Y – bi şeklini alacaktır. A0 = C + I + G (+ cTR – cT)
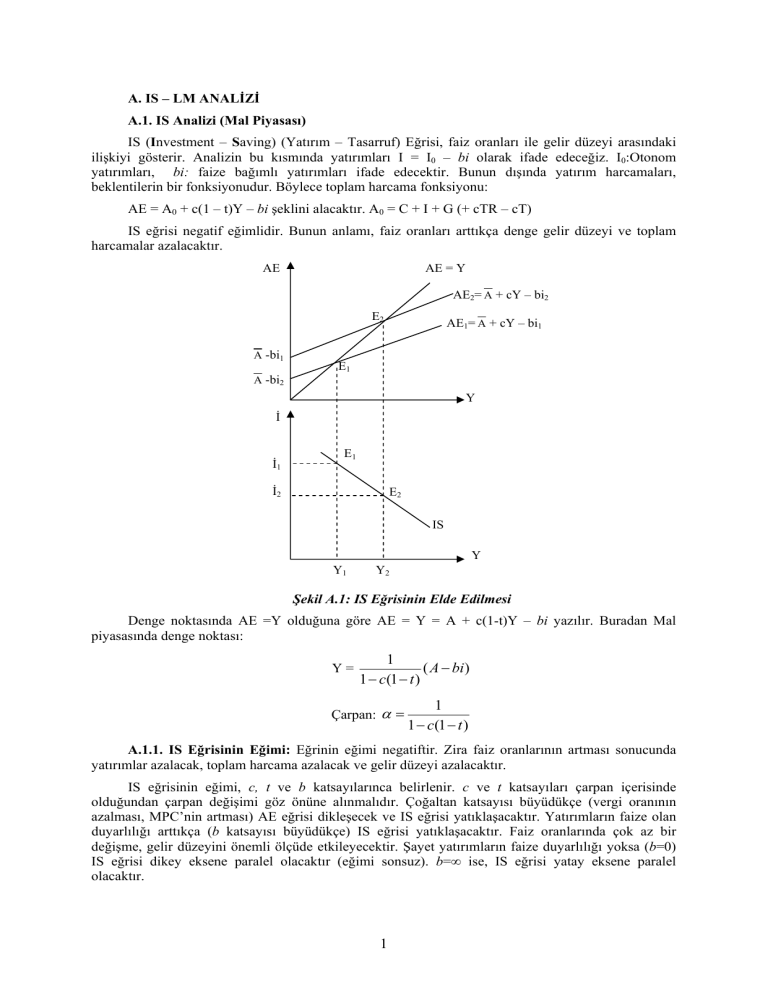
IS eğrisi negatif eğimlidir. Bunun anlamı, faiz oranları arttıkça denge gelir düzeyi ve toplam
harcamalar azalacaktır.
AE
AE = Y
AE2= A + cY – bi2
E2
A -bi1
A -bi2
AE1= A + cY – bi1
E1
Y
İ
İ1
E1
İ2
E2
IS
Y
Y1
Y2
Şekil A.1: IS Eğrisinin Elde Edilmesi
Denge noktasında AE =Y olduğuna göre AE = Y = A + c(1-t)Y – bi yazılır. Buradan Mal
piyasasında denge noktası:
Y=
1
( A − bi )
1 − c(1 − t )
Çarpan: α =
1
1 − c(1 − t )
A.1.1. IS Eğrisinin Eğimi: Eğrinin eğimi negatiftir. Zira faiz oranlarının artması sonucunda
yatırımlar azalacak, toplam harcama azalacak ve gelir düzeyi azalacaktır.
IS eğrisinin eğimi, c, t ve b katsayılarınca belirlenir. c ve t katsayıları çarpan içerisinde
olduğundan çarpan değişimi göz önüne alınmalıdır. Çoğaltan katsayısı büyüdükçe (vergi oranının
azalması, MPC’nin artması) AE eğrisi dikleşecek ve IS eğrisi yatıklaşacaktır. Yatırımların faize olan
duyarlılığı arttıkça (b katsayısı büyüdükçe) IS eğrisi yatıklaşacaktır. Faiz oranlarında çok az bir
değişme, gelir düzeyini önemli ölçüde etkileyecektir. Şayet yatırımların faize duyarlılığı yoksa (b=0)
IS eğrisi dikey eksene paralel olacaktır (eğimi sonsuz). b=∞ ise, IS eğrisi yatay eksene paralel
olacaktır.
1
AE’2= A +cY-b’i2
AE
AE’1= A +cY-b’i1
AE2= A +cY-bi2
AE1= A +cY-bi1
b’ > b
0
İ
İ1
Y1 Y’1 Y2
E1
Y’2
E’1
E’2
İ2
E2
IS1
0
IS2
Y
Şekil A.2: IS Eğrisinin Eğimi
A.1.2. IS Eğrisinin Kayması: Faiz oranlarındaki değişim IS eğrisi üzerinde hareket ettirirken,
otonom harcamalardaki değişim, veri faiz oranında IS eğrisini kaydıracaktır. Kayma çarpan kadar
olacaktır. Zira
ΔY=
1
ΔA − bi
1 − c(1 − t )
A.2. LM Analizi (Para Piyasası)
Para piyasasından hareketle gelir düzeyi ile faiz oranı arasındaki ilişkiyi gösteren eğridir. LM
analizine geçmeden önce para arzı –para talebi kavramlarına açıklık getirelim.
A.2.1. Para Piyasasında Denge:
A.2.1.1. Para Arzı: Keynesyen modelde para arzı dışsaldır. Yani MB tarafından kontrol
edilmektedir. Ekonomideki fiyatlar genel düzeyini de veri kabul edersek para arzını şu şekilde ifade
−
edebiliriz: MS=
M
−
P
A.2.1.2. Para Talebi: Keynes’e göre bireylerin portföyü iki aktiften oluşmaktadır. Bireyler para
ve tahvilden oluşan portföylerini bu iki aktifin getirisine göre ayarlamaktadır. Klasiklerden farklı
olarak Keynesyen para talebi teorisine Likidite Tercihleri Teorisi denmesinin temel nedeni budur.
Zira Keynes, sadece para talebi ile ilgilenmemiş, aynı zamanda para benzeri (likit) nakite çabuk
dönebilme kabiliyeti olan aktiflerle de ilgilenmiştir. Daha sonra başta Tobin olmak üzere birçok
Keynesyen iktisatçı tarafından portföy teorisi geliştirilmiştir.
Likidite Tercihleri Teorisinde para talebini belirleyen etmenler üç tanedir. İlk ikisi yani işlem ve
ihtiyat güdüsü ile para talebi Klasiklerde olduğu gibi gelir ile doğru orantılıdır. Keynes’in katkısı
spekülasyon güdüsü ile para talebi olmuştur. Bireyler, ellerinde her zaman belirli bir miktar nakit
parayı tutarak para piyasasındaki faiz gelişmelerinden faydalanmak isterler. Paranın elde tutulmasının
bir getirisi yoktur. Onun için şayet piyasa faiz oranı, insanların geleceğe dönük beklentilerinden
oluşan normal faiz oranından düşükse, bireyler ileride faiz oranlarının artacağını ve tahvillerin
fiyatlarının düşeceğini beklerler. Dolayısıyla bugün tahvil satıp nakitte beklerler. Ancak piyasa faiz
2
oranı, normal faiz oranından yüksekse, ileride faizlerin düşüp tahvil fiyatlarının değer kazanacağını
düşündüklerinden bugün tahvil alıp ileride fiyatı yükselince kâr etmeyi beklerler. Tahvilin (Konsolun)
ikinci el fiyatı şu şekilde hesaplanır:
PB=
CP
r
PB: Tahvilin fiyatı
CP: Kupon Bedeli (Tahvilin faiz getirisi)
r: faiz oranıdır.
Örneğin 100$ nominal değerli bir tahvil aldık ve yıllık getirisi % 4’ken piyasa faiz oranı % 5’e
çıksın.
4
= 80$ Tahvilin fiyatı olur.
0,05
Böylece para talebini
MD=
M
= L(Y,i) = kY – hi
P
şeklinde yazabiliriz.
Faiz oranları yükseldiği (düştüğü) zaman paranın dolaşım hızı artar (azalır). Para talebi
gelirin pozitif, faiz oranlarının negatif bir fonksiyonudur.
M.V = P. Y ise Keynesyen yaklaşımda para talebi gelir ve faiz oranının bir fonksiyonudur.
Dolayısıyla para talebi yerine likidite tercihi yazılabilir Md = L(Y,i). Paranın dolaşım hızı ise,
V=
P.Y
olur.
L(Y , i )
İ
İ*
İ
M
P
İ1
E
İ
E1
E2
İ2
L(Y,i)
MS
M/P
E2
İ1
E1
İ2
L(Y,i)
M 1S
M S2
M/P
L(Y2,i)
L(Y1,i)
0
MS
Şekil A.3: Para Piyasasında Denge
A.2.2. LM Eğrisinin Türetilmesi: Gelir düzeyi Y1 iken, para talebi L1 ve faiz oranı da i1
kadardır (E1 denge noktası). Gelir düzeyi artınca (Y2) para arzı sabitken para talebinin artması (L2)
sonucunda piyasada bir para talebi fazlası oluşur. Para talebi fazlalıkların anlamı tahvil piyasasına
tahvil bırakılıp para çekilmiştir. Tahvilin arz fazlası olunca fiyatı düşer, faiz oranlarını da arttıracaktır
(i2). Çeşitli gelir düzeyi – faiz oranı arasındaki ilişkileri gösteren eğriye LM eğrisi denilmektedir.
3
M/P
İ
İ
LM
E2
İ2
İ1
>>>
E1
İ2
İ1
L(Y2,i)
L(Y1,i)
MS
Y1
M/P
Y2
Y
Şekil A.4: LM Eğrisinin Elde Edilmesi
A.2.3. LM Eğrisinin Eğimi: LM Eğrisi pozitif eğimlidir. Para talebinin gelire duyarlılığı (k)
büyüdükçe ve faize duyarlılığı (h) düştükçe LM eğrisi dikleşecektir.
A.2.4. LM Eğrisinin Kayması: LM eğrisi, para arzındaki ve para talebindeki otonom
değişimlere bağlı olarak kayacaktır. Örneğin para arzındaki bir artış sonucunda para talebi sabitken
para arzı fazlası oluşur. Bu fazlalık tahvil piyasasına yönlenirse, tahvilin fiyatı artar ancak faizler
düşer. Böylece veri para talebinde LM eğrisi sağa kayacaktır. Bunun yanında para talebinde de
otonom kaymalar LM eğrisini etkileyecektir. Örneğin kredi kartı kullanımının yaygınlaşması ile para
talebi azalacak (L2) ve LM eğrisi de sağa kayacaktır.
NOT: Reel Faiz Oranı = Nominal Faiz Oranı – Beklenen Enflasyon (I. Fisher)
B. PARA POLİTİKASI
B.1. Genişletici Para Politikası: MB para arzını genişletsin (MS↑). IS – LM dengesi E1
noktasında sağlanmışken şimdi denge E2 noktasındadır. Burada para arz fazlası oluşmuş (LM eğrisinin
sağında) ve bu fazla para ile ekonomideki aktörler tahvil talep etmiş, tahvil talebinin artması
sonucunda fiyatları yükselirken, faiz oranı da düşmüştür (i1’den i3’e) (Para Politikasının Likidite
Etkisi). Burada ortaya çıkan etkiye denilmektedir. Faiz oranlarının düşmesi sonucu yatırım harcama
talebi artmış ve IS eğrisinin sol tarafında talep fazlası oluşmuştur. Bireylerin gelirleri artınca para
talepleri de artmaya başlamış, bu da faizlerin artmasına neden olup (para politikasının gelir etkisi)
ekonomi E3 noktasında Y2 kadar gelir ve i2 faiz seviyesinde dengeye gelmiştir.
−
Ms↑ ⇒ LM↓ ⇒ Y1 , M S > M D ⇒ DB ↑, PB ↑ ,i3↓ ⇒ I↑ ⇒ Y2↑ ⇒ Md↑ ⇒ i2↑
B.2. Daraltıcı Para Politikası: MB para arzını kısınca LM eğrisi sola kaymış ve Y1 gelir
seviyesinde para talep fazlası ortaya çıkmıştır. Tahvil arz fazlası oluşmuş, tahvilin fiyatı düşerken faiz
oranları yükselmiştir (i3 seviyesine). Buraya kadar olan kısım, para politikasının likidite etkisidir. Bu
durumda IS eğrisinin sağında yer alındığından toplam üretim toplam harcamadan fazladır yani arz
fazlası söz konusudur. Faiz oranları da i3 seviyesinde olduğundan yatırım talebi azalacak ve
ekonomide milli gelir Y2 seviyesine faizler de i2 seviyesine gerileyecektir (para politikasının hasıla
etkisi).
−
Ms↓ ⇒ LM↑ ⇒ Y1 , M s < M d ⇒ DB ↓, PB ↓, i3↑ ⇒ I↓ ⇒ Y2↓ ⇒ Md↓ ⇒ i2↓
4
LM1
İ
E1
İ1
İ3
0
E2
İ3
LM2
∨
∨
∨
∨
∨ E2
İ2
LM2
İ2
E3
E3
İ1
∧
∧
∧
∧
LM1
E1
IS
IS
Y
Y2
Y1
0
Y2
Y
Y1
Şekil B.1: Genişletici ve Daraltıcı Para Politikasının Denge Faiz ve Gelir Düzeyine Etkisi
B.3. Para Politikasında Özel Durumlar:
B.3.1. Şayet Yatırımlar faize duyarlı değilse (b=0); para politikası ile likidite etkisi ortaya
çıkmaz ve milli gelir ve hasıla düzeyinde bir değişme gözlenmez.
B.3.2. Likidite Tuzağı (para talebinin faize sonsuz duyarlı olması – h=∞); Piyasadaki (reel)
faiz oranları sıfıra yakın bir noktada ise, para arzındaki bir artış, tahvil piyasalarına yönlendirilmez.
Zira insanlar faizin yükseleceğini ve tahvil fiyatlarının düşeceğini beklediklerinden parayı ellerinde
tutarlar. Keynesyenlere göre para politikasının işlememe nedeni likidite tuzağıdır.
İ
IS
İ
LM1
LM2
İ1
LM1 LM
2
E1
İ2
E2
0
İ1
Y
Y
0
Şekil B.2: Yatırımlar Faize Duyarsız (b=0)
Y1
Y
Şekil B.3: Likidite Tuzağı (h=∞)
B.3.3. Para talebi faize duyarsız ise (h=0); L=kY şeklinde olması durumunda LM eğrisi diktir
ve para politikasının genişlemesi sonucunda hasıla düzeyi LM eğrisindeki kayma kadar artacaktır .
Para talebinin faizlerden bağımsız sadece hasıla düzeyi ile belirlendiğini vurgulayan Klasik
iktisatçıların görüşüne yakın olduğundan Klasik Durum adı verilmiştir.
İ
LM1
LM2
E1
İ1
E2
İ2
IS
Y
Y1
Y2
Şekil B.4: Klasik Durum (h=0)
5
C. MALİYE POLİTİKASI:
C.1. Genişletici Maliye Politikası: IS eğrisi içerisinde kamu (maliye) politikası G, TR ve T ile
uygulanabilir. Hatırlanacağı üzere A=C + I + G + cTR – cT şeklinde ifade edilmiştir. IS dengesinde
Y=α(A – bi) olduğuna göre A’daki değişimlerin hem mal piyasasını hem de para piyasasını nasıl
etkilediğini görelim. Hükümet harcamalarının artması ile (ΔG↑) normal Keynesyen modelde çarpan
kadar milli gelirde artış yaşanır (α ΔG) ve şekilde görüldüğü gibi milli gelirin Y1 seviyesinden Y3
seviyesine çıkmasına neden olur. Ancak dikkat edilirse LM analize katılınca milli gelir artışı Y2 kadar
olmuştur. Zira hükümet harcamalarının artması ile mal talebi fazlası oluşmuş, bunun sonucunda milli
gelir artmış, milli gelir artışı sonucunda para talebi de artmıştır. Artan para talebi sonucunda
ellerindeki tahvilleri çıkarıp paraya çevirmeye başlamışlar, tahvilin fiyatı düşerken faiz oranları da
yükselmeye başlamıştır. Faiz oranlarındaki artış ise, belirli bir oranda yatırımların azalmasına ve milli
gelirin düşmesine yol açmıştır. Hükümet harcamalarının artarak faizleri arttırması ve özel yatırımların
azalmasına Engelleme/Dışlama Etkisi denilmektedir.
−
−
G ↑⇒ i , AE ↑, Y3 ↑⇒ M D ↑, M S ⇒ DB ↓, PB ↓, i ↑⇒ I ↓⇒ Y2 ↓
C.2. Daraltıcı Maliye Politikası: Aynı şekilde maliye araçlarının birindeki değişimin
Keynesyen analizde olduğu gibi denge gelir düzeyini fazla etkilemesi beklenmez. Örneğin devlet gelir
vergisi oranlarını arttırsın. Böylece çarpanın değeri azalacak aynı zamanda toplam harcama eğrisi
yatıklaşacaktır. Basit Keynesyen modelde çarpan etkisi kadar harcama düzeyi ve milli gelir düşecektir
[
1
]. IS eğrisi hem içe kayacak hem de eğimi değiştiği için daha dikleşecektir. Ancak denge
1 − c(1 − t )
gelir düzeyi Y3 seviyesine düşmez. Vergi artışı sonucu üretim azalmış (gelir düzeyi azalmış) buna
bağlı olarak toplam harcamalar azalmış ve para talebi düşmüştür. Tahvile yönelen para sonucunda
tahvil fiyatları artmış ve faiz oranları düşmüştür. Faizlerin düşmesi ile yatırım harcamaları artışı milli
gelir düzeyini belirli bir miktarda arttırmıştır (Y2’ye kadar).
−
G ↓⇒ i , AE ↓, Y3 ↓⇒ M D ↓, M D < M S ⇒ DB ↑, PB ↑, i ↓⇒ I ↑⇒ Y2 ↑
İ
LM
İ
LM
E2
İ2
İ1
E1
>>>>
İ1
İ2
<<<
E1
E2
E3
IS1
IS2
IS1
Y1
E3
Y2
Y3
IS2
Y
Y
Y3 Y2
Y1
Şekil C.1: Genişletici ve Daraltıcı Maliye Politikasının Denge Faiz ve Gelir Düzeyine Etkisi
C.3. Maliye Politikasında Özel Durumlar:
C.3.1. Yatırımlar faize duyarsız ise (b=0); kamu harcamaları özel kesim harcamaları üzerinde
daraltıcı bir etki meydana getirmez ve böylece milli gelir ve hasıla düzeyi IS eğrisindeki kayma kadar
artacaktır.
C.3.2. Para talebi faize tam duyarlı ise (Likidite tuzağı varsa h=∞); maliye politikası tam
etkin olacaktır ve gelir düzeyi IS eğrisindeki kayma kadar artacaktır.
6
IS1
İ
IS2
LM
E2
İ2
IS1
İ1
0
Y1
b=0
IS2
İ2
E1
İ1
E1
LM
İ
İ
E2
LM İ1
IS1
Y2
Y
0
Y1
Y2
Y
0
h=∞
Y*
IS2
Y
h=0
Şekil C.2: Maliye Politikasında Özel Durumlar
C.3.3. Klasik Durum (LM eğrisi dik – para talebi faiz haddine hiç duyarlı değil h=0); Bu
durumda maliye politikası hiç etkin olamayacaktır. Yani sadece faizler genel düzeyi artacak, milli gelir
denge düzeyinde bir değişiklik olmayacaktır. Bu durumda tam dışlama söz konusu olacaktır.
7