DERS İÇERİKLERİ
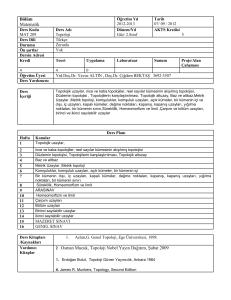
MAT 127 Analiz I
4+2+0
Kümeler; Reel sayılar kümesi; Bağıntılar ve fonksiyonlar; Polinomlar, rasyonel fonksiyonlar;
trigonometrik fonksiyonlar, ters trigonometrik fonksiyonlar; üstel ve logaritmik fonksiyonlar,
hiperbolik fonksiyonlar, tersleri, grafikleri; Reel sayılar dizisi ve limit, Balzona-Weiertstrass
teoremi; Fonksiyonlarda Limit; Sürekli fonksiyonlar ve temel teoremler; Düzgün süreklilik;
Türev kavramı ve türevlenebilir fonksiyonların temel teoremleri; Türevin uygulamaları;
Aradeğer Teoremi, L, Hospital Kuralı, Monotonluk, ekstremumlar, asimtotlar, grafik çizimleri
FİZ 119 ---->FİZİK I
Fiziksel büyüklükler, standartlar, birimler; vektörler; gösterimi, geometrik ve analitik
toplanması, skaler ve vektörel çarpım, birim vektör kavramı, bileşenler; Tek boyutta hareket;
parçacık kinematiği, konum ve yer değistirme vektörü, ortalama hız, ani hız, ortalama ivme,
ani ivme ve türev kavramı; Düzlemsel hareket; sabit ivmeli düzlemsel hareket, eğik atış,
düzgün dairesel hareket, göreceli hız ve ivme, merkezcil ivme; Parçacık dinamiği-I; Kuvvet ,
kütle ve ağırlık kavramları ve Newton kanunları; Parçacık dinamiği –II; Sürtünme kuvvetleri
ve düzgün dairesel hareketin dinamiği; İş ve Enerji ; Sabit ve değişken kuvvetin yaptığı is, iş
ve enerji teoremi ve kinetik enerji kavramı; Enerjinin Korunumu; Korunumlu kuvvetler,
potansiyel enerji, mekanik enerji, kütle ve enerji ilişkisi ve enerjinin korunumu yasası; Parçacık
sistemlerinin dinamiği; kütle merkezi ve hareketi, lineer momentum ve korunumu; Çarpışma;
impuls ve momentum, çarpışmada momentum korunumu, bir, iki ve üç boyutta çarpışma,
tepkimeler ve bozulmalar, tesir kesidi; Dönme Kinematiği; Dönme hareketi ve değişkenleri,
sabit ivmeli dönme, doğrusal ve dairesel kinematik arasındaki bağıntılar; Dönme dinamiği-I;
Tork, açısal momentum, çok parçacık sistemleri,dönme kinetik enerjisi ve moment kavramı;
Dönme dinamiği – II; Katı cisimlerin dönme dinamiği, yuvarlanan cisim hareketi, açısal
momentum korunumu; Katı cisimlerin dengesi; statik denge , çekim merkezi ve denge
örnekleri.
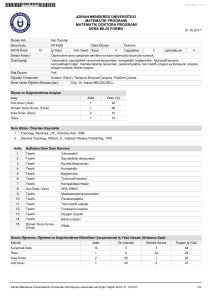
MAT … Soyut Matematik-I 4+0+0
Önermeler;
Kümeler;Bağıntılar;Fonksiyonlar;Cebirsel
yapılara
Tümevarım; Tam sayılar; Rasyonel sayılar; Reel sayıların inşası.
ENF 100 Temel Bilgisayar Teknolojileri Kullanımı 2+1+0
giriş;Doğal
sayılar;
2
AITB 191 ATATÜRK İLKELERİ VE İNKILAP TARİHİ-I 2+0+0
TDB 109 TÜRK DİLİ 2 0 0
YDB 115 English-I 3 0 0
The Mathematical Sciences: What are the Mathematical Sciences?: classifying and defining.
Latin roots: order of events. Pioneers in Mathematical Science: The basic Mathematical
symbols; Fundamental operation of arithmetic; Natural numbers; integer numbers; rational
numbers; reel numbers; basic properties of numbers; absolute value; roots of polynomials;
equations; roots of equations; basic operations in sets and some properties of theirs
MAT 128 Analiz II 4+2+0
Belirsiz integraller ve inregral alma teknikleri; Riemann integrali, İntegrallenebilir fonksiyon
sınıfları, ortalama değer teoremleri, İntegral hesabının temel teoremleri, Riemann integralinin
bazı uygulamaları; Genelleştirilmiş Riemann integrali (tipleri ve yakınsaklık testleri); Reel sayı
serileri ve yakınsaklık; Sonsuz çarpımlar; Fonksiyon dizi ve serileri; Noktasal ve düzgün
yakınsaklık, kuvvet serileri, Taylor serileri, Fourier serileri.
MAT ….Soyut Matematik-II 4+0+0
Sıralama bağıntıları; İyi sıralı kümeler;Sırasal eşyapı dönüşümleri;Kafesler; Seçme
aksiyomu;Eşgüçlü kümeler ve kardinal sayılar;Sonlu ve sonsuz kümeler;Ordinal sayılar.
MATH …. Analytical Geometry 4+0+0
Cartesian coordinates in R2 and R3, Polar, Cylindirical and spherical coordinates, Vectors in R2
and R3, Straight lines in R2 and R3, Rotations and translations in plane, Conics, Special surfaces
in space, Cylinders, Rotational surfaces, Quadratic surfaces
FİZ 118 ---->FİZİK II
Elektrik Alanları, Gauss Kanunu, Elektrik Potansiyeli, Sığa ve Dielektrik, Akım ve Direnç,
Doğru Akım Devreleri, Magnetik Alanlar, Magnetik Alan Kaynakları, Faraday Kanunu,
İndüktans, Alternatif Akım Devreleri.
AITB 192 ATATÜRK İLKELERİ VE İNKILAP TARİHİ-I 2+0+0
TDB 1110 TÜRK DİLİ 2 0 0
3
YDB 116 English-II 2 0 0
Course description: English grammar at elementary level. One, ones, some, any, not any, no,
no one, not anybody, anyone, anything, nobody, no one, nothing, somebody, anything, nowhere
etc., every all, everybody, everything etc., all, most, some, no, none, any both, either, neither,
a lot, much, many, (a) little, (a) few, get, word order, modal auxiliaries, passive,
gerund&infinitives, would like ..?, I’d like ..., indirect speech, asking someone to do something,
purpose, go to, go on, go for, …go-ing, enough, too, and but or so, because, before, after,
during, while, when, adverbs, comparisons, relative (adjective) clauses, if-clauses,
prepositions, preposition+ing, (good at …ing etc.), look at, listen to etc., phrasal verbs.
MATH… Analysis-III 4+2+0
Functions of several real variables, Topology of Rn, Limit, Continuity, Compactness,
Sequences of functions, Series of functions. Series in Rn, Linear operators and matrices.
Derivative, Chain rule. Mean value theorems. Partial derivatives. Implicit and ınverse function
theorems. Maximum and minimum, Lagrange multiplier rule.
MAT… Olasılık ve İstatistik-I 4+0+0
Örnek uzaylar. Olaylar ve üzerinde işlemler. Kesikli olasılık modelleri. Cebir, sigma cebir
kavramları. Borel sigma cebiri. Olasılık aksiyomları. Geometrik olasılık. Koşullu olasılık.
Olayların bağımsızlığı. Tam olasılık ve Bayes formülü. Rasgele değişkenin tanımı, özellikleri,
örnekler, dağılımı ve dağılım fonksiyonu. Dağılım fonksiyonunun temel özellikleri.
Dağılımların sınıflandırılması: sınıfların özellikleri ve örnekler. Rasgele değişkenin
fonksiyonunun dağılımı. Ortak ve marjinal dağılımlar. Sayısal karakteristikler. Beklenen
değerin tanımı. Chebishev eşitsizliği. Yakınsama çeşitleri. Büyük sayılar kanunu. Rasgele
değişkenlerin fonksiyonel karakteristikleri. Momnet çıkaran fonksiyonlar. Karakteristik
fonksiyonlar. Merkezi limit teoremi.
MAT 215 Lineer Cebir I 4+0+0
Vektör uzayları; alt uzaylar ve bölüm uzayları; Lineer bağımlılık; lineer bağımsızlık;taban;
Lineer dönüşümler ve matrisler;Direkt toplamlar;Lineer dönüşümler uzayı ve dual uzaylar;
Rank; Elemanter matris işlemleri; Lineer denklem sistemleri ve çözümleri.
MATH … Differantial Equations-I 4+0+0
First-order equations and various applications; Linear equations of higher order; Solutions of
initial value problems by Laplace transform; Systems of linear differential equations; solutions
by Laplace transform, the eigenvalue method for homogeneous systems; Multiple eigenvalue
solutions; Series solutions of linear equations; Ordinary and regular-singular points.
4
YDB 211 Inglizce Okuma ve Yazma 2+0+0
Bölümle ilgili okuma parçaları; dil bilgisi çalışmaları; kelime ve çeviri aktiviteleri; dinleme
etkinlikleri; bölümle ilgili güncel konular hakkında münazaralar.
MAT 216 Lineer Cebir II 4+0+0
Determinantlar; Özdeğerler ve özvektörler; Kuadratik formlar;İç çarpım uzayları; Öklid ve
üniter uzaylar; Ortogonal ve üniter uzaylar; Karakteristik polinomlar.
MAT…Olasılık ve İstatistik-II
İstatistiğin temel problemlerine giriş. Verilerin düzenlenmesi. İstatistik kavramı.Parametre
tahmini. Tahminlerin özellikleri: tutarlı, yansız, etkinlik ve asimptotik normallik. Tahmin
yöntemleri: Momentler, en büyük olabilirlik yöntemleri. Rao-Cramer eşitsizliği. Aralık
tahminleri. T-student dağılımı. Ki-kare dağılımı. Aralık tahminleri. Fisher dağılımı. Basit
hipotezlerin testi. Regresyon analizi. En küçük kareler tahmini. Doğrusal regresyon. Doğrusal
olmayan regresyon. Korelasyon. Korelasyon katsayısının önemi. Uyum iyiliği testleri.
MATH…. Analysis-IV 4+2+0
Double and triple integrals. Application of double and triple integrals. Change of variables for
double and trible integrals. Integral and uniform convergence. Vectoral analysis. Gradient,
Rotation, Diverjans. Integrals along paths. Surfaces and surface integrals. Green theorem,
Diverjans theorem, Stokes theorem.
MATH … Differantial Equations-II 4+0+0
Boundary value and eigenvalues problems. The method of Green’s functions. Fourier series
and Fourier integrals. Generalized Fourier series. Non-homogeneous boundary value problems.
Fourier integral representations.
YDM 214 Mesleki İngilizce-I 2+0+0
Matematikle ilgili kavramların öğrenilmesi, matematiksel konuların okuma, anlama ve yazma.
MAT 313 Cebir I 4+0+0
Tam sayılar; Bölünenimle; Kongrüanslar; Yarıgruplar ve gruplar;Altgruplar ve yansınıflar;
Devirli gruplar;Üreteçler ve bağıntılar;Normal altgruplar; Bölüm grupları Homomorfiler;
İzomorfi teoremleri; Otomorfiler; Simetrik gruplar.
5
MATH… Differantial Geometry 4+0+0
Vector fields, The Jacobian of a map, Covariant derivative, curves in R3 , Change of parameter,
Frenet formulas, Bertrand’s curves, Surfaces, Shape operator, normal curvatures, Fundamental
forms, Gauss and mean curvatures, Special curves on a surface, Gauss map and geodesics,
Ruled surfaces,
MAT 331 Kompleks Analiz 4+0+0
Kompleks sayılar, elamanter fonksiyonlar, kompleks integral, Cauchy Riemann Denklemleri,
Eğrisel İntegraller. Cauchy Teoremi, Cauchy İntegral Formülü, Basit bağlantılı bölgeler.
Homotopi ve dönme sayısı. Analitik Fonksiyon dizi ve serileri. Analitik Fonksiyonların ayrık
aykırı noktaları, Konfor dönüşümleri. Möbiüs Dönüşümleri. Riemann Dönüşüm Teoremi.
Analitik Devam.
MATH…. Symbolic Analysis With MATLAB 4+0+0
MATLAB; Scalars, vectors, matrices with aritmetic operations, Matrix functions in MATLAB,
Graphics, Symbolic Mathematics Toolbox: Real and complex symbolic variables, Creating
symbolic math functions, Standart symbolic functions, squences, limit, continuity, derivative
with applications, integral with applications, Series, Solution of diferential equations, Symbolic
operations with Graphical User Interface.
YDM 313 Mesleki İngilizce-II 2+0+0
Bilimsel İngilizcenin özellikleri, lisans matematik dersleri ve temel araştırma alanlarının
tanımı. Matematikle ilgili konuların ve literatürün takibi.
MAT 314 Cebir II 4+0+0
Halkalar; Althalkalar ve idealler; İdeallerin toplamı; Maksimal ve asal idealler; Homomorfiler;
İzomorfi teoremleri; Kesir cismi; Polinomlar halkası; Halkalarda aritmetik; Esas ideal
halkaları;Euclid bölgesi; Asal elemanlara parçalanabilir halkalar; İndirgenemezlik kriterleri.
MAT 348 Genel Topoloji 4+0+0
Topolojik uzay tanımı ve temel kavramlar; Taban, komşuluk tabanı ve sayılabilirlik özellikleri;
Sürekli fonksiyonlar, homeomorfizm; Fonksiyonlarla üretilen topolojiler, çarpım ve bölüm
uzayları; Yakınsaklık; Ayırma aksiyomları; Kompaktlık; Bağlantılılık.
MAT … Reel Analiz 4+0+0
Ölçü uzayları; Ölçülebilir fonksiyonlar; Lebesgue ölçüsü ve Lebesgue integrali; Normlu vektör
uzayları ve Hilbert zaylarına giriş.
6
YDM 314 English in Business Life 2+0+0
Çalışma alanlarında, iş ve yöneticilikte kullanılan İngilizceyi paratik yapma, iş imkanları,
lisansüstü programlara giriş, fizik araştırma alanları ve makale yazma, iş hayatındaki
problemler, seçilmiş okuma parçaları ve dinleme.
SEÇMELİ-I
4+0+0
MAT …… Partial Differential Equations
4+0+0
First-order linear, quasilinear and nonlinear partial differential equations; Classification of
second-order linear differential equations. Heat and wave equations with applications; Potantial
equation with Dirichlet and Neumann boundary conditions.
MAT 493 Seminer-I 0+2+0
Seçilmiş konular çerçevesinde bir veya daha çok sayıda öğretim üyesi yönetiminde, öğrenciler
tarafından hazırlanan çalışmaların sunulması ve tartışılması.
SEÇMELİ-I 4+0+0
SEÇMELİ-II 4+0+0
SEÇMELİ-III 4+0+0
MAT 494 Seminer-II 0+2+0
Seçilmiş konular çerçevesinde bir veya daha çok sayıda öğretim üyesi yönetiminde, öğrenciler
tarafından hazırlanan çalışmaların sunulması ve tartışılması.
MAT 400 Bitirme Çalışması 0+6+0
Öğrencinin, verilen bir konu üzerinde, bir öğretim üyesi yönetiminde yaptığı derleme türünde
bir çalışmadır.
MAT … Fonksiyonel Analize Giriş 4+0+0
Önbilgiler: Lebesgue integrasyon teorisi, Tam metrik uzaylar; Normlu vektör uzaylar; Banach
uzayları ve cebirleri; Hahn-Banach teoremi ve sonuçları; Dual uzaylar; Hilbert uzayları.
SEÇMELİ-I 4+0+0
SEÇMELİ-II 4+0+0
7
SEÇMELİ DERS İÇERİKLERİ
VI. Yarıyıl Seçimli Dersleri
SEÇ 302 Sayısal Analiz 4+0+0
Sayısal analiz nedir? Ön bilgiler, Hata analizi, Nonlineer denklemler için sayısal çözüm
yöntemleri, Lineer denklem sistemlerinin sayısal çözümü için doğrudan ve ardışık çözüm
yöntemleri, Nonlineer denklem sistemleri için sayısal yöntemler, Interpolasyon, Yaklaştırma
yöntemleri, Sayısal türev, Sayısal integral yöntemleri, Diferensiyel denklemler için sayısal
çözüm yöntemleri.
SEÇ 304 Sayılar Teorisi 4+0+0
Kongruanslar; 1.dereceden kongruanslar; Yüksek dereceden kongruanslar; Asal modüller;
Kuvvet rezidüleri; Kuadradik rezüdiler; Legendre sembolü; Kuadratik Reciprocity
Teoremi;Jacobi sembolü; Numerik fonksiyonlar; Bazı diofant denklemleri.
SEÇ 308 Dif. Geometriden Seçme Konular 4+0+0
Paralel
yüzeyler;
Sabit
eğrilikli
yüzeyler;
Diferensiyellenebilir
manifoldlar;
Diferensiyellenebilir formlar.
VII. Yarıyıl Seçimli Dersleri
SEÇ 401 Topolojiden Seçme Konular 4+0+0
Tam metrik uzaylar: Baire Kategori Teoremi, Banach sabit nokta teoremi ve uygulamaları; Bir
metrik uzayın tamlaştırılması; Fonksiyon uzayları; Topolojik grupların tanımı ve temel
özellikleri; Homotopi kavramı.
SEÇ 405 Diferensiyel Denklemlerin Sayısal Çözümleri 4+0+0
Başlangıç değer problemi için sayısal yöntemler: Tek-adım yöntemi, çok adım yöntemleri,
kararlılık, yakınsaklık kavramları; Sınır değer problemleri için sayısal yöntemler; Lineer ve
nonlineer denklem sistemlerinin sayısal çözümü. Sonlu elemanlar yöntemine giriş.
SEÇ 409 Soyut Cebir 4+0+0
Cisim genişlemeleri;Cebirsel genişlemeler; Parçalayıcı cisimler ve Normal genişlemeler;
Cebirsel Kapanış; Ayrılabilir genişlemeler; Cebirin esas teoremi; Sonlu cisimler; Galois
cisimleri.
8
SEÇ 415 Kompleks Analizden Seçme Konular 4+0+0
Analitik genişletmeler; Tam fonksiyonlar, Normal aileler C
de analiz; Holomorf
fonksiyonların analizi; Meromorf fonksiyonlar, Mittag-Leffler, Weierstrass teoremleri;
Harmonik ve altharmonik fonksiyonlar.
VIII. Yarıyıl Seçimli Dersleri
SEÇ 404 Ayrık Gruplar 4+0+0
Topolojik gruplar; Topolojik dönüşüm grupları; Örtmeler; PSL (2,R) grubu ve bunun özel alt
grupları; Hiperbolik geometri; Hiperbolik alan; Gauss-Bonet formülü; Fuksiyon gruplar ve
cebirsel özellikleri; Temel bölgeler.
SEÇ 412 Modül Teorisi 4+0+0
Modüller; Alt modüller; Bölüm modülleri;Modüllerin direkt toplamı; Homomorfiler; İzomorfi
teoremleri; Tam indirgenebilir modüller; Serbest modüller;
Zincir koşullar; Artinian ve
notherian modüller.
SEÇ 418 Endüstriyel Matematik 4+0+0
Matematik Modelleme, Boyutsuzlaştırma, Kristalleşme, Atmosfer kalitesi, Lazerle geometrik
oluşumlar, Renkli film negatifi, Araç eksoz gaz konsantrasyonu, Fotokopi makinası
SEÇ …. Gruplar Teo. Seç. Konular 4+0+0
Gruplar; Grup izomorfileri; Eşlenikler ve G-kümeleri; Normal Seriler; Çözülebilir gruplar;
Nilpotent gruplar; Sonlu üretenli abel grupları; Sylow-altgrupları; Sylow-teoremleri; p2, pq
mertebeli gruplar.
SEÇ…. Cebirsel Sayılar Teorisi 4+0+0
Tamlık bölgeleri; Öklid Bölgeleri; Notherian Bölgeler; Tamlık Bölgesi üzerinde cebirsel
elemanlar; Cebirsel genişlemeler; Cebirsel sayı cisimleri; Cebirsel Baz; Dedekind Bölgeleri;
İdeallerin Normu; Reel kuadratik cisimlerin birimleri
Prof. Dr. Funda KARAÇAL
Matematik Bölüm Başkanı