Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon

Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
GÜNEġ VE BENZERĠ YILDIZLARDA
MANYETĠK KONVEKSĠYON
Gülizar GENÇOĞLU, Evrim KIRAN, Rennan PEKÜNLÜ
EGE Üniversitesi, Fen Fakültesi, Astronomi ve Uzay Bilimleri Bölümü, Bornova, 35100, İzmir
[email protected], [email protected], [email protected]
Özet: Güneş ve diğer soğuk yıldızlarda MHD dinamo, manyetik akı depolanması, manyetik akı
tüplerinin konveksiyon bölgesi ve “overshoot” katmanındaki kararlılık özellikleri, üzerinde yoğun
olarak çalışılan konulardır. Konu, çoğunlukla “ince akı tüpü” yaklaşımıyla incelenmekte ve genel
bağıntılar türetilmektedir. Bu yaklaşımda akı tüplerinin mekanik denge durumu, “doğrusal kararlılık”
bağlamında incelenmektedir. Biz MHD I doktora dersinde, yıldızlarda dinamo sürecinin önemli bir
aşaması olan manyetik konveksiyonu değişik kaynaklardan inceledik ve derleme çalışma hazırladık.
1.
GiriĢ
Manyetik alanların varlığı, Güneş‟in tüm katmanlarında önemli sonuçlar içermektedir.
Konveksiyon bölgesi, bir hidromanyetik dinamo mekanizmasının 11 yıllık aktivite çevrimi ve
22 yıllık manyetik çevrim içerisinde Güneş yüzeyindeki aktif bölgelerde meydana çıkan
manyetik akının üretildiği yerdir. Çevrimsel değişim, Güneş leke gruplarının polarite
kuralları, aktivite kuşağının enlemsel göçü gibi tüm düzenlilikleriyle dinamo süreci, çoğu
özelliklerinin halen yeterince anlaşılmadığı çalkantılı plazmanın dikkat çekici bir iç
organizasyonunu temsil etmektedir.
Güneş yüzeyinin dönmesine ilişkin erken dönem çalışmalar yüzeyin diferansiyel döndüğünü
göstermişti. Ayrıntılı helyosismolojik gözlemler bugün Güneş‟in iç bölgelerinin dönmesine
ilişkin değerli bilgiler sunmaktadır. Yıldız evrim modellerinin öngörülerinin tersine, Güneş‟in
ışınımsal iç bölgesi hemen hemen tekdüze dönme gösteriyor. Konvektif bölgenin dönmesi de
önceden düşünülenden oldukça farklı. Önceden, dönme oranının dönme ekseninden olan
uzaklığa bağlı olacağı düşünülüyordu. Helyosismolojik çalışmalar hem konvektif bölgenin
tabanında hem de ışıkkürenin hemen alt bölgelerinde dönme-kesme (rotational shear layers)
katmanların varlığını gösterdi (Şekil 1).
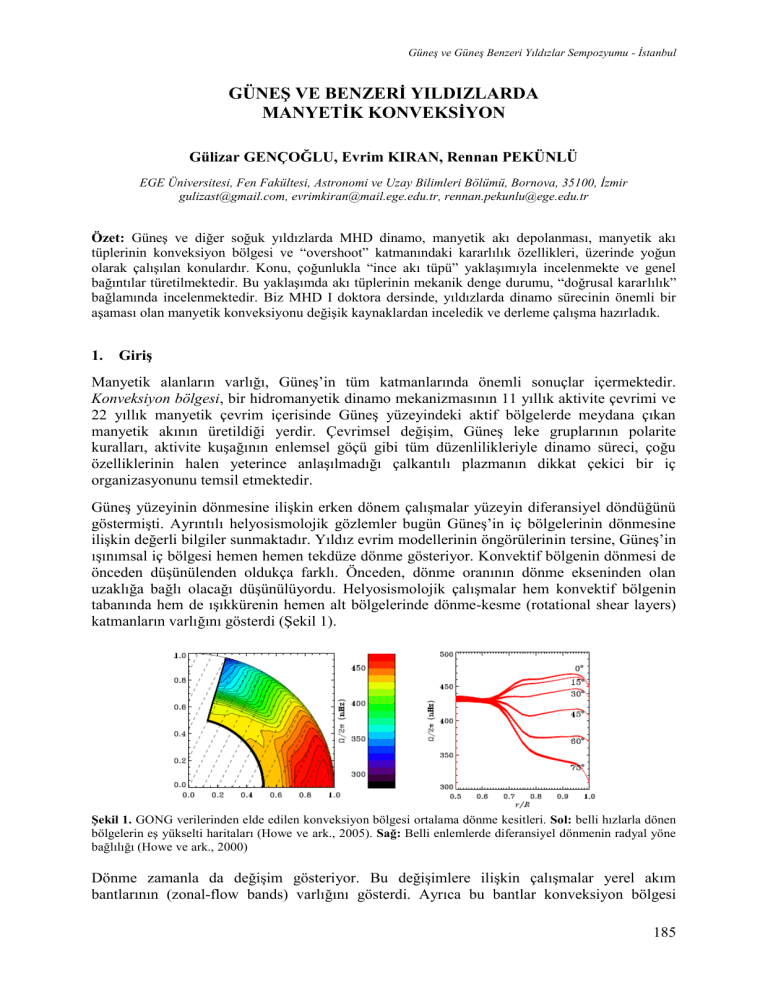
ġekil 1. GONG verilerinden elde edilen konveksiyon bölgesi ortalama dönme kesitleri. Sol: belli hızlarla dönen
bölgelerin eş yükselti haritaları (Howe ve ark., 2005). Sağ: Belli enlemlerde diferansiyel dönmenin radyal yöne
bağlılığı (Howe ve ark., 2000)
Dönme zamanla da değişim gösteriyor. Bu değişimlere ilişkin çalışmalar yerel akım
bantlarının (zonal-flow bands) varlığını gösterdi. Ayrıca bu bantlar konveksiyon bölgesi
185
Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon
boyunca uzanıyor ve aynı bantlar Güneş çevrimi boyunca göçediyor. Dönmenin sergilediği
başka zamansal değişimler de var; bu arada jet benzeri yapılar da görülüyor (Howe, 2009).
Dinamik açıdan en ilginç bölge, diferansiyel dönen konveksiyon bölgesiyle hemen hemen katı
cisim gibi tekdüze dönen ışınımsal iç bölgenin sınırında bulunan ve “tachocline” adı verilen
bölgedir. Helyosismolojik çalışmalar “tachocline”ın kararlı katmanlaşma gösteren iç bölgede
yeraldığını gösteriyor. Özellikle yüksek enlemlerde “tachocline”, fırlatma katmanıyla
(overshoot region) ve konvektif zarfla üst üste çakışmış görünüyor (Şekil 2).
ġekil 2. Diferansiyel dönmeyi temel alarak oluşturulmuş Güneş dönme yapısı. Konveksiyon bölgesinde enlemsel
diferansiyel dönme gösteren bölgeyle katı cisim dönmesi gösteren ışınımsal katman arasındaki geçiş bölgesine
tachocline denir (Rüdiger ve Hollerbach, 2004).
Kararlı katmanlaşma bu bölgenin dinamiği için önemli ipuçları sunuyor. Işınımsal bölgeye de
sızabilen konvektif devinimler ve diferansiyel dönmedeki kararsızlıklar “tachocline”da
çalkantı üretebilir, ancak kaldırma kuvvetleri dik yönde, ışıkküreye doğru olan devinimleri
bastırır. “Tachocline”ın kararlı katmanlaşma göstermesi, fırlatma katmanına yakınlığı ve
güçlü diferansiyel dönme, bu katmanın manyetik akı üretme ve depolamada en ideal yer
olmasını sağlıyor. Manyetik alanın dinamik etkinliği, konvektif zarftan çok “tachocline”da
baskındır. “tachocline”ın bir başka önemli özelliği, çok ince oluşudur: 0,05R (Çizelge 1).
Çizelge 1. Tachocline bölgesinin Güneş özeğinden olan uzaklığı r ve genişliği  (Howe, 2009).
Güneş dinamosunun işlemesi için manyetik akı tüplerinin yükselme zamanı kadar temel olan
bir problem, bir dengenin varlığı ve onun kararlılığıdır. Yani manyetik alanların Güneş
çevriminin yarı dönemiyle kıyaslanabilir sürelerde üretildiği yerde kalıp kalamayacağını
bilmek, önemlidir. Şayet manyetik akı, durağan olarak katmanlaşmış overshoot katmanında
mekanik dengede depolandıysa, sonunda nasıl patlayabileceği ve leke grupları ve aktif
186
Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
bölgeler oluşturabileceği sorusunun yanıtlanması gerekir. Konveksiyon bölgesindeki
manyetik akı tüplerinin kararlılığına ilişkin çalışma, ilk olarak Spruit ve van Ballegooijen
(1982) tarafından gerçekleştirilmiştir. Daha sonra Ferriz-Mas ve Schüssler (1993) manyetik
konveksiyon sürecini en ince ayrıntılara dek çalışmıştır. Şimdi bu çalışmanın önemli
bölümlerine ve sonuçlara değinelim. Bu poster sunumun tamamına yakını Ferriz-Mas ve
Schüssler (1993) çalışmasının kısaltılmış çevirisinden oluşuyor.
2. Temel MHD EĢitlikleri
Bu bölümde diferansiyel dönme ve diğer hız alanlarının varlığında yıldızın konveksiyon
bölgesinde yeralan, yalıtılmış bir ince akı tüpünün devinimini güden temel eşitlikleri
inceleyeceğiz. Yıldız,  e açısal hızıyla dönsün. Açısal hız, konsayıların işlevi olabilir.
Kullanacağımız konsayı düzeneğinin açısal hızı,  olsun. Durgun (stationary) denge
durumunda akı tüpünün dönme oranı,  olarak alınacaktır (Ferraro‟nun “birlikte dönme”
yasası). Ereksel MHD yaklaşımında  sabit açısal hızıyla dönen konsayı düzeneğinde
devinim eşitliği, aşağıdaki gibidir :

Dv
B2


  p 
Dt
8

D

  v  ,
Dt  t
 B .   B
 
  g   Ω  Ω  r   2  v  Ω
4

(2.1)
konvektif türevi simgelemektedir. v, plazmanın akışkan hızı;  , kütle
yoğunluğu; p, basınç; g, çekim ivmesi; B, manyetik alan. Lorentz kuvveti, manyetik basınç
(eşitliğin sağındaki 2. terim) ve manyetik gerilme kuveti (eşitliğin sağındaki 3.terim) olmak
üzere ikiye ayrılmıştır.
Manyetik akı tüpü dışındaki ortamın akı tüpünün devinimi tarafından tedirgin edilmediği
varsayılmıştır (  /  t  0 ). Bu durumda devinim eşitliği, aşağıdaki biçimde yazılır:
e
D ve
  e ve .  ve  pe   e g  Ω  Ω  r   2  e ve  Ω
Dt
(2.2)
Bu bağıntıdaki „e‟ alt indisi, dış ortama (external medium ) gönderi yapmaktadır. ve hızına
katkı, dış ortamın dönme oranının başvuru dizgesinin dönme oranı ‟dan sapması sonucu
gerçekleşmektedir.
İncelemek istediğimiz kararsızlıklar, ince akı tüpünün devinimine ve bozulmasına
(deformation) neden olabilecek kararsızlıklardır. Bu tür kararsızlıklar, akı tüpünün
parçalanmasına neden olmaz. Tüpün parçalanmasıyla sonuçlanacak kararsızlıklara RayleighTaylor ve Kelvin-Helmholtz kararsızlıkları denir. İnce akı tüpünün eğriliğini dikkate alırsak
incelememiz daha da kolaylaşacaktır (Spruit, 1981a, 1981b). Akı tüpüne ilişkin nicelikleri, “i”
alt indisiyle göstereceğiz. Ancak akı tüpü dışındaki ortamı manyetik alandan bağışık
varsaydığımız için B manyetik alanına indis vermemize gerek yoktur. İnce akı tüpü
yaklaşımında akı tüpüne ilişkin nicelikler ( pi , B2 , i , vi ), tüpün kesiti boyunca alınan
ortalamalar olarak düşünülecektir. Bu durumda “ i ” indisli nicelikler, akı tüpü boyunca
ölçülen s yay uzunluğunun ve t zamanının işlevleri olacaktır. Akı tüpünün a(s) yarıçapının
manyetik alanla ilişkisini manyetik akının korunumu ilkesi kurar:
 a 2 B   mag  sabit
(2.3)
187
Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon
İnce akı tüpü yaklaşımının temel varsayımı, daha önce belirtildiği gibi akı tüpüyle onu
çevreleyen ve manyetik alandan bağışık ortamın anlık yatay basınç dengesidir:
B2
pi 
 pe
8
(2.4)
Bu basınç dengesinin geçerli olduğu süre, hızlı manyetik ses dalgasının akı tüpünü
enlemesine geçiş süresine denktir. Eğer akı tüpünün yarıçapı diğer ölçek uzunluklarından da
küçükse bu süre, istenildiği kadar kısa tutulabilir. Akı tüpünü betimleyen eğri, r(s, t) ile
gösterilsin. Tüpün gerilmeye uğraması ve tüp boyunca plazma akışkanının devinimi nedeniyle
belli bir kütle öğesine karşılık gelen yay uzunluğu, zamanla değişecektir. Bu değişikliğin ince
akı tüpü yaklaşımında dikkate alınması gerekmektedir. Bu gerçekten yola çıkarak eğrinin her
bir noktasında Frenet vektör tabanı (Şekil 3) oluşturacağız. Adı geçen vektör tabanının birim
vektörleri, şöyledir:
ġekil 3. Frenet-Serret vektör tabanının birim vektörleri, t (teğet), n (normal) ve b (binormal) olarak adlandırılır.
et 
 r  s, t 
s
; en 
2
1  r  s, t 
; eb  et  e n
  s2
(2.5)
Yukarıdaki bağıntıda    2 r  s, t  /  s 2 , yerel eğriliktir ve daima pozitiftir. Şimdi, (2.1)
eşitliğinin ince akı tüpü yaklaşımındaki çeşitlemesini elde edebilmek için toplam basınç
gradyentini  pT  pi  B 2 / 8  iki terim toplamı olarak yazacağız:
 p
pT   // pT   pT   T
 s

 et   pe

(2.6)
Bu bağıntıdaki ikinci eşitliği oluştururken (2.4) bağıntısı kullanılmıştır. Dikkat edilirse,
toplam iç ve dış basınç gradyentlerini eşitlerken, tüp içi niceliklerin dik yöndeki değişimlerini
Taylor serisine açtık ve yalnızca birinci dereceden terimi aldık. Bu yaklaşım, ancak ince akı
tüpü yaklaşımında geçerlidir (Ferriz-Mas ve Schüssler, 1989). (2.6) eşitliğinin geçerli
olabilmesi için Taylor açılımı, birinci terimden sonra kesilmelidir. (Schüssler, 1990).
Şimdi de (2.6) eşitliğini ve manyetik alanın, manyetik basınç ve manyetik gerilme terimlerine
ayrılma işlemini yaparsak,
188
Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
 B   B 
4
  B2 
B2
e

 en
  t
s  8 
4
(2.7)
Yalnızca toroidal bileşeni olan bir manyetik alan için, yani, B  Bet , momentum eşitliğinin
ince akı tüpü çeşitlemesini elde ederiz:
i
Dvi
p
B2
  i et  e g  Ω   Ω  r    2 e v e  Ω  e  v e   v e 
 en
Dt
s
4
 i g  i Ω   Ω  r   2 i vi  Ω  FD
(2.8)
(2.8) bağıntısındaki dış ortamın dik yöndeki basınç gradyenti, (2.2) eşitliği yardımıyla ortadan
kaldırılabilir. (2.2) bağıntısı, dış ortamın durgun   /  t  0  denge durumunu betimlemektedir.
 pT   pe   e g  Ω  Ω  r   2 e ve  Ω  e ve . ve 
(2.9)
(2.9) numaralı eşitliği (2.8) numaralı momentum eşitliğinde kullanırsak ve Frenet tabanındaki
et , en , eb  izdüşümünü alırsak ince akı tüpünün devinim eşitliklerini elde edebiliriz:
 Dvi
 i Dt

pi

  et   s  i g  et  i Ω   Ω  r   et  2 i  vi  Ω   et

(2.10 a)
 Dvi 
 i Dt   en   i  e  g  en  i Ω   Ω  r    en  2 i  v i  Ω   en


B2
 e  Ω   Ω  r   2 v e  Ω   v e   v e   en 
  FD  en
4
(2.10b)
 Dvi 
 i Dt   eb   i  e  g  en  i Ω   Ω  r   eb  2 i  vi  Ω   eb


(2.10 c)
 e  Ω   Ω  r   2 v e  Ω   v e   v e   eb  FD  eb
(2.10) bağıntılarının önceki çalışmalarla karşılaştırıldığında yeniliği,  e  v e .v e eylemsiz
(inertial) teriminin içerisinde yatmaktadır. Bu terim, dış ortamın denge eşitliğinden gelmekte
ve akı tüpünün devinim eşitliğine yatay basınç denge koşuluyla girmektedir. Akı tüpüne dik
yöndeki akışkan hızının Alfven hızı düzeylerinde olması durumunda (ki bu hız, eşpaylaşım
alanı için konveksiyon hızına eşittir) ve hız ölçek uzunluğunun da basınç ölçek uzunluğu
düzeylerinde olması durumunda eylemsizlik (atıl) teriminin genliği, kaldırma kuvvetininkine
eşit olmaktadır. Bu nedenle tüp dışındaki plazma akışkan hızlarını boşladığımızda yanılgılı
sonuçlara ulaşabiliriz.
Dikkat edilirse, (2.10) eşitliklerinde sürüklenme kuvvetinin tüp boyunca bileşeni yoktur
( FD  et  0 ). Çünkü sürüklenme kuvvetini doğuran neden, devinim içindeki akı tüpünün yukarı
akıntı (upstream) ve aşağı akıntı (downstream) sınırlarındaki basınç farkıdır.
189
Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon
Eşitlikler dizgesinin „kapalı‟ olabilmesi için süreklilik eşitliği, manyetik indüksiyon ve erke
eşitliği ve durum denkleminin de yazılması gerekmektedir. Sonsuz elektriksel iletkenlik
sınırında süreklilik eşitliği ve manyetik indüksiyon eşitliği birleştirilirse,
D B B 
    .   vi
D t  i   i 
(2.11)
elde edilir; bu bağıntının ince akı tüpü çeşitlemesi de aşağıdaki gibidir:
D  i

Dt  B
 i

 B


 s  vi  et    vi  en   0
(2.12)
Erke eşitliği olarak izentropik evrim eşitliği kullanılacaktır; burada S, özgün (specific)
entropidir. Yıldızların konveksiyon bölgelerinin derinliklerinde ortaya çıkan kararsızlıklar
için bu, geçerli bir yaklaşımdır. Çünkü dinamik zaman ölçeği, akı tüpünün çevresiyle
ışınımsal veya ısısal iletkenlik yoluyla erke alış-veriş zaman ölçeğinden çok daha küçüktür
(Moreno-Insertis, 1986). Son olarak, ereksel bir gazın durum denklemini ele alırsak izentropi
eşitliği,
D p  p D

Dt
 Dt
(2.13)
biçiminde ifade edilir.
(2.4) eşitliğiyle verilen basınç denge koşulu ile birlikte (2.10), (2.12) ve (2.13) eşitlikleri,
„kapalı‟ bir eşitlikler dizgesi oluşturmaktadır. Bu dizgenin matematiksel yapısı (dik
düzlemdeki devinimler için), Moreno-Insertis (1984, 1986) tarafından araştırılmıştır.
3. Diferansiyel Dönme ve Toroidal Akı Tüpü
Denge durumundaki yapısı halka biçiminde olan ve yıldızın eşlek düzleminde yeralan, eksen
bakışıklığına sahip toroidal manyetik akı tüpünün kararlılığını incelemek için 2. Bölüm‟de
türetilen eşitlikler kullanılacaktır. Başvuru dizgesi ve akı tüpü,  açısal hızıyla dönerken
ardalandaki plazma ortamının e(r) açısal hızıyla döndüğü varsayılacaktır.
Yıldızın dönmesi ve çekim alanı, soruna yeğlenmiş yönler sunacaktır. Bu nedenle
incelememizde yardımcı konsayı düzenekleri (küresel ve silindirik) kullanacağız. Küresel
konsayılar, (r, , ) biçimindedir. r, yıldızın özeğinden olan uzaklık; , yıldızın dönme
yönüne doğru ölçülen boylam (azimut) ve  da eşlek düzleminden uçlaklara doğru ölçülen
enlemdir. e z , sabit bir dönme ekseni boyunca alınan birim vektör olsun; bu durumda  = 
e z ;e =e(r) e z olur.
Sabit bir eksen çevresinde salt dönme devinimi yapan bir cisimde ortaya çıkabilecek en olası
bakışıklık, eksensel bakışıklıktır ( / 0 ): e( r ) = e (r, ) . Eşlek düzleminde ve hızının
dönen konsayı düzeneğindeki bileşenleri,
ve r  0 ; ve  r  e    ; ve   0
190
(3.1)
Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
3.1. Denge durumu
Dış ortamın denge durumunu, (2.2) bağıntısı belirlemektedir. (3.1) bağıntısını kullanarak
eşlek düzlemindeki eylemsizlik ve dönme terimleri, aşağıdaki gibi yazılır:
2ve  Ω  2r  e    er
(3.2 a)
Ω   Ω  r   r er
(3.2 b)
2
  ve   ve  r  e    er
2
(3.2 c)
Sonuç olarak denge eşitliğinin eşlekteki bileşeni, aşağıdaki gibi yazılır:
pe   e g   e r  e2 r
(3.3)
Bu eşitliği de bileşenleri cinsinden yazabiliriz:
 pe
  e g  r  r  e2    e g  r  e2
r




(3.4)
 pe  pe

0


(3.5)
Yukarıdaki bağıntılarda g = g(r)r olduğu unutulmamalıdır. (3.5) eşitliği, dış katmanlaşmanın
eksensel ve enlemsel bakışıklık gösterdiğine işaret etmektedir.  e r  e2 terimi; Coriolis
kuvveti, merkezkaç kuvveti ve e  ve   ve eylemsizlik terimlerinin birleşimidir.
Şimdi manyetik akı tüpünün denge yapısını inceleyelim. “o” alt indisi, denge yapısının
parametrelerine gönderi yapacaktır. ro(so), düzlemsel bir eğri olarak varsayılan akı tüpü
içindeki akışkan öğesinin denge konumunu göstersin; so da bu akışkan öğesine karşılık gelen
yay uzunluğudur. Toroidal akı tüpü, ro uzaklığında, eksen bakışıklığı gösteren ve eşlek
düzleminde yeralan bir yapı olarak varsayılacaktır. ro uzaklığındaki dış plazma ortamının hızı,
ve0  r0  e0    e 0 ve dönme oranı da eo = e(ro)‟dır. Durgun denge durumunda (2.10a)
ve (2.10c) numaralı momentum eşitliğinin teğet (azimutal) ve enlemsel (binormal) bileşenleri,
sıfır olur ve normal (radyal) bileşen, aşağıdaki gibi bulunur:




Bo2
  eo   io  g o  ro  e2 o   io ro  e2 o   2  0
4  ro
(3.6)
(3.6) eşitliği, manyetik eğrilik (gerilme kuvveti), kaldırma kuvveti ve dönmenin uyarttığı
kuvvetler (Coriolis ve merkezkaç kuvvetleri) arasındaki dengeyi betimlemektedir. Akı
tüpünün denge durumunda çizdiği yol, tüpün çevresidir. Denge durumunda akı tüpü içindeki
plazmayla dış ortamın göreli deviniminin tüpe dik yönde bileşeni olmadığından sürüklenme
(drag) kuvveti, sıfır olur ve (3.6) denge eşitliği, aşağıdaki gibi yeniden yazılır:
2
v2A  e o   ro e o  ro

 1  1 
e2o  2  0

ro go  i o  
go  go


(3.7)
Bu eşitlikte v A  Bo / 4  i o , Alfven hızıdır.
191
Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon
Şimdi boyutsuz bir niceliği sunalım (Spruit ve van Ballegooijen, 1982):
f 
pi o
H

ro g o  io ro
(3.8)
Şimdi diğer boyutsuz parametreleri tanımlayalım:
  8 pi o / B 2o
(3.9 a)
x  ro  2 / g o
(3.9 b)
xe  ro  e2o / g o
(3.9 c)
Kolayca görüldüğü gibi x ve xe, merkezkaç ivmesinin çekimsel ivmeye oranlarıdır; her ikisi
de Güneş ve benzeri geç tür yıldızlarda 10–5 düzeylerinde değerlere sahiptir. ro uzaklığında dış
basınç ölçek uzunluğu,
 e1 
1 pe
pe 0 r

r0
 g  r 2  1  xe
1
 e  g  re2   e 0 0 1  0 e 0  
pe 0
pe 0 
g0 
He
(3.10)
(3.4)
biçiminde yazılır. Burada He = peo / ( goeo), dönmenin dikkate alınmadığı durumda dış basınç
ölçek uzunluğudur. He ile e arasındaki ilişki, aşağıda verilmiştir (bu bağıntıları türetirken iç
ve dış plazma ortamının molar kütlelerinin aynı olduğunu varsayacağız):
T
H
H
1  xe   i o 1  xe   1  2 /   f  x

1  1 /  
e He
Te o
(3.11)
3.2. Tedirgin edilmiĢ akı tüpü geometrisi
Bu alt bölümde, akı tüpünün denge durumuna uygulanan küçük bir ötelemenin tüpün
kararlılığını nasıl etkileyeceğini inceleyeceğiz. Yıldızın dönmesi ve çekim alanı, soruna
„yeğlenmiş yönler‟ sunduğundan tedirginlik niceliklerinin hesaplanmasında küresel ve
silindirik konsayıları da dikkate alacağız. Bu yaklaşım, sorunun incelenmesini basitleştirecektir.
Akı tüpünün ro(so) denge durumundan  ile göstereceğimiz Lagrangian ötelemesine uğradığını düşünelim. Bu durumda başlangıçtaki yay uzunluğu so olan akışkan öğesinin yeni konumu,
r = ro(so)+(so, t)
(3.12)
olacaktır.  ötelenmesini Frenet tabanında  et 0 , en 0 , eb 0  , küresel tabanda  er 0 , e 0 , e 0  ve
silindirik tabanda  er 0 , e 0 , e z 0  betimleyeceğiz:
192
ξ  s0 , t   t et 0  nen 0  beb 0
(3.13 a)
ξ  s0 , t   r er 0   e 0   e 0
(3.13 b)
ξ  s0 , t    ReR 0   e 0   z e z 0
(3.13 c)
Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
3.3. Tedirginlik nicelikleri
Tedirgin edilmiş akı tüpü geometrisinin belirlenmesinden sonra, ince akı tüpü devinim
eşitliklerine giren ve tedirginliğe uğramış fiziksel niceliklerin doğrusal biçimlerini bulmaya
çalışalım. Eşlek düzleminde yeralan bir manyetik akı tüpü için Frenet  et 0 , en 0 , eb 0  ve küresel
e
r0
, e 0 , e 0  vektör tabanlarını kullanmak, yeterli olacaktır. Tüm tedirginlik niceliklerini
küresel konsayılarda betimlenen öteleme cinsinden vereceğiz (r ,  , ).
ro denge durumu değeri, her üç konsayı düzeneğinde de ele alınacaktır. Denge durumundaki
akı tüpü, seçtiğimiz başvuru dizgesinde durgun durumdadır (t = 0 ). Akı tüpüyle birlikte
tedirgin edilmiş olan akışkan öğesinin hızı:
 ξ 
vi      r er 0   e 0   e 0
  t  s0
(3.14)
İvmeyi de benzer yöntemle aşağıdaki gibi elde ederiz:
D vi   vi 

   r er 0   e 0   e 0
D t   t s
0
(3.15)
Devinim eşitliğine giren tüm terimler, denge durumu değerleriyle tedirginlik değerlerinin
toplamı cinsinden yazılacaktır. Denge durumu „o‟ alt indisiyle, tedirginlik değerleri de „1’ alt
indisiyle gösterilecektir: p = po + p1 ; B = Bo + B1 , vb.
Manyetik akı tüpünün ötelenmesi ve dış plazma ortamının katmanlaşmış olması, dış ortam
niceliklerinin (Lagrangian) tedirginliğe uğramalarına neden olmaktadır. Dış basınç
tedirginliği için
pe1    pe
ro
 go 
eo
1  xe  r
(3.16)
yazılabilir. Burada (3.4), (3.5) eşitlikleriyle verilen dış ortam katmanlaşması kullanılmıştır. ro
uzaklığındaki e dış basınç ölçek uzunluğu cinsinden yazarsak pe1 / pe0 =  r /e olur.
Dış yoğunluk tedirginliği,  e1 , dış ortamın logaritmik sıcaklık gradyenti kullanılarak [ ( d
lnTe / d lnpe) r o], pe1 cinsinden bulunabilir:
 e1    e o 1   
r
e
(3.17)
 gradyentinin logaritmik süperadyabatiklik,  =ad , ve özgün ısılar oranı  ile ilişkisi,
aşağıdaki gibidir:
    1
1

(3.18)
Konveksiyon bölgesinin dibinde, ad = ( 1)/ = (dlnTi / dlnpi) varsayımı kullanılmıştır. Bu,
geçerliliği gösterilebilir bir varsayımdır (Schüssler, 1993).
(2.4), (2.12) ve (2.13) eşitliklerini kullanmak suretiyle aşağıdaki bağıntılara ulaşabiliriz.
Denge durumundan küçük genlikli sapınçlar sonucu tedirgin edilmiş terimleri yazıp
193
Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon
linearization (doğrusallaştırma) uygulamalıyız. Buna göre tedirginlik terimlerinin birbiriyle
çarpımı (örn.  1 B 1 ) ve kareleri boşlanacaktır. (2.13) eşitliğinin doğrusallaştırma işlemi
sonucunda aşağıdaki (3.21) eşitliğine kolaylıkla ulaşılır. İzlenen yöntemin diğer adımı ise
(2.4) eşitliğine doğrusallaştırma uygulamaktır. Bulunan eşitlik düzenlenince aradığımız
 i 1 /  i o ve B 1 / Bo oranlarının bulunduğu bir eşitliğe ulaşırız.
B1 cT2    
2 1  x  r 
 2 
 1 

 
Bo v A   so     f  ro 
(3.19)
i 1
c 2  2    4 1  x  r 
  T2 


 
i o
v A     so     f  ro 
(3.20)
pi 1
pi o

 i1
i o
(3.21)
(Schüssler, 1993). Bu bağıntılar yazılırken (3.7) yardımıyla eoio oranı ortadan kaldırılmıştır. Diğer yandan cT ile gösterilen akı tüpü hızını tanımlıyoruz:
cT2 
cs2 v2A
cs2  v 2A
(3.22)
Burada v A  Bo / 4  i o , Alfven hızı ve c s   pi o /  i o de akı içi ortamındaki ses hızıdır.
Toroidal geometriye sahip akı tüpünün eğriliğinden kaynaklanan eğrilik kuvveti (3.23)
eşitliğiyle verilir.
Bo2
B
B2
B2

 o B1  o
4
4  ro 2  ro
4
  r  2 r
 2 
r
 so2
 o




(3.23)
Bu bağıntıda  o 1 / ro ‟dır.
Çekim ivmesinin uzaklığa bağımlılığının kuvvet yasası biçiminde olduğunu varsayıyoruz:

r
g  r    go   er
 ro 
(3.24)
go  g(ro).  değeri, yıldızın içindeki kütle dağılımına bağlıdır; konveksiyon bölgesindeki
kütlenin katkısı, boşlanabilecek denli az ise  = 2 alınır.
r = ro +  tedirgin edilmiş konumunda e açısal hızı,
  e 
e  e  ro   ξ  e r0  eo  r 
  eo  eo r
  r r0
(3.25)
biçiminde bulunur. Diferansiyel dönmenin eşlek düzlemine göre bakışık olduğu varsayılmıştır; diğer bir deyişle  e / = 0 ‟dır.
194
Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
İncelememizde (2.10) eşitliklerinin normal ve binormal bileşenlerinin sağ tarafındaki son
terimler, basite indirgenir:
 2 ve  Ω  Ω   Ω  r    v e .   v e    R e2e R
(3.26)
(3.26) eşitliğinin tedirgin edilmiş biçimi:
2
2
 R e2 eR . en  R e2  ro eo
 eo
 r  2 ro eo eo  r
(3.27a)
 2
 R  e R . eb   r 
 so2
(3.27b)
2
e
2
o
2
eo
olarak bulunur.
3.4. DoğrusallaĢtırılmıĢ denklemler
Tedirginlik nicelikleri, ince akı tüpü devinim eşitlikleri dizgesinde, (2.4), (2.10), (2.12) ve
(2.13), yerlerine yazılıp diğer tüm niceliklerin elenmesiyle (2.10) eşitliğinin bileşenleri, r , ,
 tedirginlik bileşenleri cinsinden yazılabilir. Dahası, toroidal akı tüpü için (so= ro o) so‟a
göre alınmış uzay türevlerini, tedirgin edilmemiş azimut konsayısına göre türeve
dönüştürebiliriz; yani,  /  so   1 / ro  /  o olur ve böylece aşağıdaki eşitlikler dizgesini
elde ederiz.
3.4.1. Teğet (azimutal) bileĢen
 io   
r
1  pi 1  i o g o   r

 i o 2
 2  i o  r
ro   o
ro   o
 o
(3.28)
(3.28) bağıntısında (3.8) numaralı eşitlikle tanımladığımız f  H / r0 parametresini kullanmak
ve biraz cebirsel işlem yapmak suretiyle yeniden yazabiliriz:
2
 g  c 2  2  

1  x  r 

2
f
 4 f  f 


2
2

 o


   o 
  2  r   o  T2
  H  vA
(3.29)
Zaman birimini de aşağıdaki gibi tanımlayalım:
1/ 2
H 
 

 go 
 2
H
vA
(3.30)
Güneş‟in konveksiyon bölgesinin dibindeki katmanlar için H  6  10 9 cm ; g o  5  10 4 cm s 2
ve B  10 4  105 G manyetik alan değerleri için   10 5-10 7 ve   1-10 gün değerleri elde
edilir. (3.29) eşitliğini 2 ile çarpıp denklemi boyutsuz biçime indirgemek suretiyle aşağıdaki
bağıntıyı elde ederiz:
2
cT2 2   
cT2 
1  x  r



f 

   2  r  2 2 f

4
f
2
2 
2     o
vA
 o
vA 
2


(3.31)
195
Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon
3.4.2. Radyal (normal) bileĢen
Devinim eşitliğinin doğrusallaştırılmış normal bileşeni, aşağıdaki gibi bulunur:

 2 r 

  r 
  g o  i o   e o  r
2 
ro
 o 

 g o  i 1   e1    io  2 r  ro  2  i 1  2  i o  
  i o r 
Bo2 B1
B2
 o2
2  ro Bo 4  ro
(3.32)
  e o  e2 o  r  ro  e2 o  e1  2  eo ro  e o e o  r
Teğet bileşen için de aynı yöntemi kullanırsak yeniden düzenlenmiş boyutsuz biçimini elde
ederiz:
 2 r  2     2 f 2
 2r
cT2 
1  x   

4
f
f
 T r

2
2 
2    o
 o
vA 
(3.33)
(3.33) bağıntısındaki T terimi, aşağıdaki gibi bulunmuştur:
T  2 f 2
cT2
v 2A
 eo 
 2 1  x  6 

 1 
1 
   f  


f





 io

 r
cT2  4 f 1  x 
 1  x  2 

   f  eo o 1   1  xe 
vA  

i o  e

(3.34)
 eo

 H eo
 f 
xe  x   2
ro eo eo
 i o

g o i o


3.4.3. Enlemsel (binormal) bileĢen
Akı tüpü içindeki devinimlerin doğurduğu Coriolis kuvvetinin binormal bileşeni sıfır
olduğundan, binormal yönünde etkiyen kuvvetler; kaldırma kuvveti, merkezkaç kuvveti ve dış
dönme kuvvetlerinin kombinasyonudur,  e r e2 eR  eb . Momentum eşitliğinin binormal
bileşeninin doğrusallaştırılmış biçimi de şöyle bulunur:
 
 v2A
v2A  2
1
2
2 

 2  e o     
2
2
2
ro  o
1  ro e o / go  ro





(3.35)
Bu bağıntının boyutsuz biçimi de aşağıdaki gibi bulunur:
 2  2 f 2
 2  2 f 2  f  xe  x 


1  xe
  o2
(3.36)
(3.31), (3.33) ve (3.36) eşitliklerinden görülüyor ki eşlek düzleminde devinim eşitliğinin
binormal bileşeni, diğer bileşenlerden bağımsız (decoupled) oluyor. Diğer bir deyişle, enlem
boyunca olan devinimler, tüpün denge düzlemindeki devinimlerinden bağımsızdır. Bu
nedenle enlemsel devinimler bağımsız olarak incelenebilir.
196
Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
3.5. 
1 KoĢulu için yaklaĢık eĢitlikler
Güneş veya geç tür yıldızların konveksiyon bölgelerinin derin katmanlarında basınç,
61013dyn cm –2 ve manyetik alan yeğinlikleri, Bo = 104–105G denlidir. Bu değerlerle,  
105-107 aralığında değerler alır. Bu özellik, (3.28), (3.32), (3.35) eşitliklerinin
basitleştirilmesinde kullanılabilir. Genliği 1 birim ve  -1 düzeylerinde olan terimleri tutup
diğerlerini boşlarsak birim genlikteki terimlerin birbirini „götürdüğünü‟ görürüz. Sonuçta 2
ile çarpıp boyutsuz duruma getirme işlemi,  ,  x ,  xe gibi terimlerin varlığına götürür.
 1 sınırında elde ettiğimiz eşitlikler, şöyledir:
3.5.1. Teğet (azimutal) bileĢen
 2

1   r



4
f
f


2

 02

  0
(3.37)

 2 r
1   

 4 f  f 
 T r
2
2



 o

 o
(3.38)
 2   2  r   2 f 2
3.5.2. Radyal (normal) bileĢen
 2 r  2     2 f 2
T katsayısının yeni biçimi,
T  2   1 f 2 


21 1
~
~
~ ~
f           1  e2 o   2  2ro  e o e o

  2
4
(3.39)
~
~
olarak bulunur. Burada     ve  e o    eo , boyutsuz açısal hızlardır.
3.5.3. Enlemsel (binormal) bileĢen
 2  2 f 2
 2 
~
~
 2 f 2   e2 o   2  
2
 o


(3.40)
4. Dağılma Bağıntısı ve Kararlılık Ölçütü
(3.31), (3.33) ve (3.36) eşitlikleri sabit katsayılı doğrusal, homojen kısmi diferansiyel
denklemler dizgesidir. Bu denklemlerin çözümü,
  ˆ exp (i t  i m o )
(4.1)
biçiminde bulunur. Burada ˆ , karmaşık genliktir.  , karmaşık frekans ve m tamsayısı da
azimutal dalga sayısıdır. Bu çözüm ile  /  t  i ve  /    im yazabiliriz.  ‟nın sanal
kısmı, denge durumunun kararlılığını belirlemektedir;  i  0 ise tedirginlik zamanla büyür,
 i  0 ise tedirginlik zamanla söner.  ‟nın gerçel kısmı  r , kararsızlığın monoton veya
titreşimsel olduğunu belirtmektedir.
197
Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon
4.1. Enlemsel (binormal ) tedirginlikler
Enlemsel (binormal) tedirginlikler,   , normal ve teğet tedirginliklerden bağımsız
(decoupled) olduğu için bağımsız olarak incelenebilir. (3.30) eşitliğiyle verilen birim zaman
~
~    ve 
tanımına göre karmaşık frekans ve açısal hız, boyutsuz olarak yazılabilir: 
 
Enlemsel tedirginliklerin dağılma bağıntısını elde etmek için (4.1) eşitliği,    1 limiti için
elde edilmiş olan (3.40) eşitliğinde yerine yazılmalıdır:
~
~ 2  2 f 2 m 2  1   e2o   2
~

(4.2)
Dönmenin olmadığı durumda, eksen bakışıklığı gösteren (m = 0) tedirginlikler için ~ 2 <0
olmaktadır. Çözümün negatif sanal kısım vermesi durumunda eşlek düzleminde dengede
bulunan akı tüpü, „uçlaklara doğru kayma‟ kararsızlığına uğrar (Spruit ve van Ballegooijen,
1982; Moreno-Insertis ve ark., 1992).
ġekil 4. Uçlaklara doğru kayma kararsızlığına (poleward slip instability) uğrayan toroidal akı tüpünün
devinimini gösteriyor (Spruit ve van Ballegoijen, 1982).
Spruit ve van Ballegooijen (1982)‟de “uçlaklara doğru kayma” kararsızlığı için kaygan bir
kürenin çevresindeki bir elastik bandın kararsızlığı benzetilmesi kullanılmıştır. Öyleyse akı
tüpü yükselirken bir bütün olarak dönme eksenine uzaklığını azaltarak devinmektedir. Akı
tüpü eşlek düzleminin dışına çıkmaya başladığında değişik yönlere doğru olan temel
kuvvetler, tüpü kararsızlığa uğratır. Manyetik gerilme (eğrilik) kuvveti, dönme eksenine
doğru; kaldırma kuvveti, radyal yönde yıldızın yüzeyine doğrudur. Sonuçta, manyetik gerilme
kuvvetinin enlemsel bileşenini dengeye getirecek kaldırma kuvveti olmadığından ve enlemsel
bileşen uçlaklara doğru yöneldiğinden manyetk akı tüpü, eşlek düzleminden uçlaklara doğru
kalkar.
(4.2) eşitliği, akı tüpü içi ve dışı ortamın dönme oranlarının farklı olmasının uçlaklara kayma
kararsızlığını etkileyeceğine işaret etmektedir: tüp dış plazma ortamından daha yavaş dönerse,
~ ~
~ ~
   eo, kararsızlığın genliği zamanla artar; akı tüpü daha hızlı dönerse ,    e0,
kararsızlık zamanla söner ve tüpün eşlekteki denge durumu, kararlı hale gelir. Bunun nedeni,
~ ~
tıpkı eğrilik kuvvetinin kararsızlık yaratma eğilimi gibidir:    eo için Coriolis kuvveti,
dönme ekseninden dışarıya doğrudur ve eşlek düzlemi dışında, yönü eşleğe doğru olan
enlemsel (latitudinal) bileşeni vardır. Eğer bu bileşen yeterince büyükse, manyetik gerilme
kuvvetinin uçlağa doğru olan enlemsel bileşenini dengeler ve tüpü geriye eşlek düzlemine
doğru sürer.
198
Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
~
~
(4.2) eşitliğinden görülüyor ki,    eo için m  0 koşulunu sağlayan tüm tedirginlik
biçemleri (modları), kararlıdır. Eksen bakışıklığı gösteren (m = 0) biçemlerin kararlı duruma
getirilmesi için ise aşağıdaki bağıntı sağlanmalıdır:
 v

 1  A
 ro e o
e o





2
(4.3)
Güneş‟in konveksiyon bölgesinin dibinde, kararlı denge durumunda bulunan bir akı tüpünün
hızının dış ortamın hızından olan farkını hesaplayabilmek için RO  5105 km ; eo  2,7 106 s 1 ;
  0,2 g cm3 boyutlu nicelikleri (4.3) eşitliğinde kullanılmıştır. Bu değerlerle birlikte
B  10 4  105 G manyetik alan değerleri ve Alfven hızı, v A  60  600 ms 1 olarak bulunur. Bu
değerleri (4.3) eşitliğinde kullanırsak,  / eo 1, 001  1,1 aralığında değerler alır. Açısal hız
farklılığı, akı tüpüyle çevresi arasında doğrusal hız farkı doğurur. Bu fark, B  10 4 G için 1ms-1
ve B  10 5 G için de 100ms-1 denlidir. Kısacası, usa yatkın manyetik alan değerleri
varsayarsak, akı tüpünün Güneş‟in dönme yönünde çevresine göre daha hızlı dönüyor olması,
uçlaklara doğru kayma kararsızlığını bastırabilir. Özellikle belirtmekte yarar var, Alfven
hızından küçük doğrusal hızlar Kelvin-Helmhotz kararsızlığına neden olmazlar
(Chandrasekhar, 1961). Uçlaklara doğru kayma kararsızlığıyla ilgili ayrıntılı inceleme,
Moreno-Insertis ve ark. (1992) makalesinde bulunabilir.
4.2. Dağılma bağıntısı ve kararlılık ölçütü
(4.1) eşitliğini, doğrusallaştırılmış devinim eşitliğinin teğet [(3.31) eşitliği] ve normal [(3.33)
eşitliği] bileşenlerinde kullanalım. Bu eşitlikler eşleşmiş (coupled) olduğundan ˆr ve ˆ ile
gösterilen öteleme genlikleri için doğrusal cebirsel eşitlikler dizgesi elde ederiz. Bu
eşitliklerin matris gösterimi, aşağıdaki gibidir:
2

2
2 2 cT
  2m f 2

vA


2
 2 i   2mf cT  f  1  x  


 
2  
v2A 


cT2 
1  x  
 2 i   2mf 2  f 
 
2   
vA 


2
2 2

  T  2m f


ˆ 
   0 (4.4)
ˆ
 r 
Non-trivial çözümler için matrisin determinantının sıfır olması gerekir. Bu koşul, boyutsuz
~    özdeğer (eigenvalue) probleminin çözümü anlamına gelir.
karmaşık frekansın 
Matrisin çözülmesi sonucu elde edilen dağılma bağıntısı, dördüncü dereceden bir bağıntıdır:
~4  d 
~2  d 
~ d  0

2
1
o
(4.5)
Bu bağıntıda ortaya çıkan katsayılar, şöyledir:

c2 
d 2  T  4 2  2 m2 f 2 1  T2 
 vA 
(4.6a)
199
Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon
d1  16 m f
cT2 
1 x 
f

2 
2 
vA 
(4.6b)
2
cT2 
cT2 
1 x  
2 2
d0  2 m f 2 T  2 m f  8 2  f 
 
2  
vA 
vA 


2
2
(4.6c)
T niceliğini, (3.34) eşitliğiyle tanımlamıştık    1 limitinde d0, d1, d2 katsayıları aşağıdaki
biçimlere bürünürler:
4
21 1
d 2  2 f 2   1  2 m 2  f        

  2
(4.7a)
~2 ~2
~2
~ ~
   1  e o    4  2 ro  e o e ro 





1 ~

d1  16 m f  f 
2  


(4.7b)

4
1
 2

2
2 f   3  m   f       
d o  2m f 
(4.7c)

~
~
~
~
2
2
  1  e o    2ro  e o e ro  


~ teriminin dördüncü
Eşlek düzlemindeki tedirginlikleri betimleyen (4.5) dağılma bağıntısı, 
dereceden bir bağıntısıdır. Bu bağıntı yardımıyla hem eksen bakışıklığı gösteren tedirginlik
biçemi için (m = 0) hem de hızlı dönme limitinde (m  1) kararlılık koşulları belirlenebilir.
~
Aşağıdaki incelemede göreceğiz ki, gelişigüzel alınmış bir  e değeri için (4.5) eşitsizliğini
2
2


çözmeksizin kararlılık ölçütü belirleyebileceğiz. Aşağıdaki alt bölümlerin hepsinde    1
varsayılacaktır.
4.3. Eksen bakıĢıklığı gösteren tedirginlik biçemleri
m = 0 için (4.5) dağılma bağıntısı, aşağıdaki biçimine indirgenir:
~ 2 ( ~ 2  d 2 )  0
(4.8)
Kolayca görüleceği gibi, d2 > 0 ise eksen bakışıklığı gösteren tedirginlik biçemi, kararsızdır.
(4.7a,b,c) eşitliklerini kullanarak bir kararlılık ölçütü elde edebiliriz:
2 1    f 2 
21 1
f         1    e2o  2  42  4 q e2o  0

  2

4

(4.9)
Ferriz-Mas (1996)‟da, Güneş‟e ilişkin beş farklı derinlik için parametre değerleri, Çizelge
2‟de verilmektedir.
(4.9) eşitsizliğinde tanımlanan q,
q
biçimindedir.
200
ro e ro 
2 e o
(4.10)
Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
Eksen bakışıklığı gösteren tedirginlik biçemine manyetize olmamış akışkanlarda gözlenen
kaldırma kuvveti kökenli titreşimler gözüyle bakabiliriz.
Şimdi de Brunt-Väisälä frekansını tanımlayalım:
~MBV  2 1    f 2 
4

f 


21 1
~
~
~
~
       1     e2 o   2  4 2  4 q  e2 o
  2
(4.11)
~ 2  0 ) konvansiyonel biçimini alır. Dönmenin olmadığı
Böylece (4.9) kararsızlık koşulu, ( 
MBV
durumda m = 0 biçemi, tamamen dikinedir (transverse).
Çizelge 2. Beş farklı derinliğe ilişkin parametre değerleri.
ro(km)
δ     ad
peo (dyn cm-2)
5.5910  105
5.3847 105
5.1259 105
5.0734 105
5.0421 105
+2.0014  10-7
1.7809  10-9
4.2325  10-7
9.0713  10-7
2.6155  10-6
1.5019  1013
2.3507  1013
3.8912  1013
4.2833  1013
4.5323  1013
 eo
(g cm-3)
8.1914  10-2
1.0715  10-1
1.4498  10-1
1.5358  10-1
1.5887  10-1
Teo (K)
1.3808  106
1.6497  106
2.0153 106
2.0936  106
2.1411  106

1.6677
1.6672
1.6665
1.6664
1.6663
go (cm s-2)
4.2073  104
4.5190  104
4.9583  104
5.0548  104
5.1136  104
Güneş‟in konveksiyon bölgesinin alt kısımları ve overshoot bölgesinde farklı derinliklerdeki
fiziksel parametrelerin değerleri. ro  5,5910 10 5 km ‟de (1.satır) süperadyabatiklik, pozitif
ancak çok küçüktür. ro  5,3847 10 5 km ‟de (2.satır) süperadyabatiklik, işaret değiştirmektedir;
bu yüksekliğin aşağısında katmanlaşma, subadyabatiktir. Konveksiyon bölgesinin subaydabatik alt kısmı, bu modelde yaklaşık 26.000km‟ye dek uzanmaktadır. Konveksiyon bölgesinin
dibi, ro  5,1259 10 5 km ‟dedir (3.satır). Bu yüksekliğin aşağısında keskin konveksiyon bölgesi
başlar ve aşağıya doğru 10.000km‟ye dek uzanır. Overshoot katmanının ortası, yaklaşık
olarak ro  5,0734 10 5 km ‟de (4.satır) bulunur. ro  5,042110 5 km (5.satır) ışınım bölgesine
geçişin yukarısında yaklaşık 20.000km derinliğine karşılık gelmektedir. Aşağı doğru ışınım
bölgesinin başlangıcına dek tüm subadyabatik katmanın boyutu, bu nedenle 36.000km‟dir
(Ferriz-Mas, 1996).
Eğer dönme de çözümlemeye katılırsa Coriolis kuvveti, boyuna (longitudinal) tedirginlik
dayatmaktadır. Boyuna ve dikine tedirginlikler arasındaki ilişkiyi,
~
 ˆ
ˆ
  2 i ~  r

(4.12)
biçiminde verir. Bo0 ; f 0 (eğriliğin olmadığı durum); 0 ve e 0 koşulları altında
boyutlu frekans, manyetik alan içermeyen bir atmosferin Brunt-Väisälä frekansına eşit
olmaktadır ( N2 = go / H ); burada go , çekim ivmesi; H , atmosferin basınç ölçek
uzunluğudur.
 < 0 ve  < 2 olduğundan (4.9) eşitsizliğinin sol tarafındaki birinci ve üçüncü terimler, daima
pozitif değerlere sahiptir ve bu nedenle manyetik akı tüpünü kararlı kılacak etkide bulunurlar.
~
4 2 terimi de aynı biçimde etki yapar. Tüpün kararlılığının belirlenmesi sorununa
katmanlaşmanın etkisi,  terimiyle girmektedir:  > 0 (süperadyabatik bölge, konveksiyon
bölgesi) için katmanlaşma, kararsızlığa neden olacak biçimde etki yapmaktadır; diğer yandan,
subadyabatik bölge (örneğin overshoot katmanı), tüpün kararlı kalması yönünde etkimektedir.
201
Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon
(4.9) eşitsizliğinin sol tarafındaki beşinci terim, tüp içi ve dışındaki ortamların farklı açısal
hızlarının doğurduğu etkiyi belirler. eo ile  arasında ortaya çıkabilecek olası en büyük farkı,
Alfven hızı belirlemektedir. Çünkü Alfven hızından daha büyük hızlar, Kelvin-Helmholtz
kararsızlığının doğmasına neden olur (Chandrasekhar, 1961). İncelediğimiz modelde bu
kararsızlık, dikkate alınmamıştır; bu kararsızlığın büyüyebilmesi için dış ortamda (Eulerian)
basınç tedirginliğinin ortaya çıkması gerekir ki bu incelemede böylesi bir tedirginlik, dikkate
alınmamıştır.
ro eo 
max
 v A varsayımıyla (3.30) bağıntısından
~ ~
   e o 1   
~
~
 eo  

  2f
~


eo

max
 2 f elde edeceğimizden

koşuluyla


(4.13)
yazabiliriz.
Akı tüpü içindeki plazmanın dış ortamdaki plazmayla ters yönde dönmesini sağlayabilecek
olası bir süreç olmadığından  >1 dir. Güneş‟in konveksiyon bölgesinin dibinde (eo =
2,710 –6 s–1 ; Bo= 104105G; F = 0,114 ) eo  0,37  3,7 değerlerini elde ederiz. eo ‟ın
büyük değerler alabilmesi için Bo ‟ın küçük değerler alması gerekir; bu önermenin tersi de
doğrudur.  parametresinin alabileceği uç değerler, Bo= 104G için  = 0,04 ve Bo= 105G
için  = 0,4 olur. Eğer Bo değeri yeterince büyükse Kelvin – Helmholtz kararsızlığının izin
verdiği açısal hız farkının küçük olması gerekmiyor. Dönme gösteren yıldızda akı tüpü
deviniyorsa, açısal momentumun korunumu gereği böylesi hız farklılıkları ortaya çıkacaktır
(ayrıntılı inceleme için bkz. Moreno-Insertis ve ark., 1992).
(4.13) eşitliğini (4.9) koşulunda yerine yazarsak, kararsızlık koşulunu aşağıdaki biçimiyle
elde etmiş oluruz:
~
~
F  f       2   3    e2o  4 1  q  e2o  0
(4.14)
Yukarıdaki bağıntıda kullanılan F  f  , aşağıdaki gibi tanımlıdır:
F  f   2 1    f 2 
4

f 
21 1
  
   2 
(4.15)
Bu bağıntı, hem dönme hem de manyetik alandan bağımsızdır.
(4.14) eşitsizliğinin sol tarafındaki terimleri Güneş‟in konveksiyon bölgesinin dibindeki bir
akı tüpü için bulmaya çalışalım.  = 5/3; f = 0,1 ; =1,82 için F(f)= 0,08 bulunur. Bunun
anlamı şudur: yıldız dönmüyorsa, süperadyabatik katmanlaşmanın ( > 0) bulunduğu bölgede
yeralan akı tüpü, kararsızdır (Spruit ve van Ballegooijen, 1982). Diğer yandan akı tüpünün
manyetik alan yeğinliği yeterince büyükse (, yeterince küçükse    0,08 olur) bu tüp,
subadyabatik katmanlarda bile kararsızdır.  ve , daima şu aralıklarda bulunmaktadır:
 >1 ;   2. (4.14) eşitsizliğinin solundaki birinci dönme teriminin işareti, ‟nın
işaretiyle belirlenmektedir;  > 0 için (iç bölgenin dönme hızı, dış bölgeninkinden daha
büyük) adı geçen terim, kararlı kılıcı;  < 0 için de kararsızlık ortaya çıkarıcı etkide
bulunmaktadır. Bu davranış, açısal momentumun korunumunu kararlı duruma getirecek etki
yapar. Akı tüpü içindeki plazmanın dönme oranının artması, dönmeyi yavaşlatıcı Coriolis
kuvvetinin artmasına neden olur. Yukarıda verilen parametreler ve ‟nın alabileceği en büyük
202
Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
değerler için [(90) eşitliğinin izin verdiği ölçüde] bu terimin değeri,  > 0 için 0,17–1,45
aralığına; <0 için de (0,11 )  (1,39) aralığına düşmektedir. Göreli hızın etkisi, F  f  den
gelen katkıdan daha büyük olabilir. (4.14) eşitsizliğinin sol tarafındaki son terim,  e ‟nin
radyal gradyentini içerir. Radyal yönde dışarı doğru bir artış (q > 0), akı tüpünü kararlı kılıcı;
dışa doğru bir azalış (q < 0) ise kararsızlık üretici bir etki yapmaktadır. Güneş için q değerleri,
Schou ve ark. (1992) çalışmasından türetilebilir. Bu araştırma grubu, Güneş‟in global p
titreşimlerinin dönmenin etkisiyle nasıl yarıldığını incelemişlerdir. Çalışmada sunulan
grafiklerden konveksiyon bölgesinin dibinde, eşlek bölgesi yakınlarında q = 0,06 olduğu
anlaşılıyor. Özetleyecek olursak, Güneş‟teki diferansiyel dönme, q  1 olduğundan, akı
tüpünü kararlı kılacak bir etki doğurduğu gibi, eksen bakışıklığı gösteren tedirginlikler için de
önemli bir etki değildir. q = 0,06 değeri için (4.14) eşitsizliğinin sol tarafındaki son terimin
değeri, 0,58 58,0 aralığına düşmektedir. 58,0 değeri, manyetik alanın 104 G değerine, 0,58
değeri de manyetik alanın 10 5G değerine karşılık gelmektedir.
ġekil 5. Eksen bakışıklığı gösteren (m=0) biçemlere ilişkin kararlılık çizgesi. Güneş‟in konveksiyon bölgesinin
dibi (  = 5/3,  = - 1,82 , f = 0,11 ,  eo = 2,7  10 – 6s – 1, q = 0,06 )‟nin temsili parametreleri için BO manyetik
alan yeğinliğine karşı  süperadyabatikliği. Her bir eğri, kararsızlık bölgesini (parabolun dışı) kararlılık
bölgesinden (parabolun içi) ayırmaktadır. Sürekli çizgi,  = eo; kesikli çizgi,  < eo ve kesikli nokta
biçimindeki çizgiler de  > eo durumlarına karşılık gelmektedir. Bu durumlarda izin verilebilir en büyük açısal
hız farkının (eo   ) =  vA / r o olduğu varsayılmıştır (Ferriz-Mas ve Schüssler, 1993).
Şekil 5, (4.14) eşitsizliğinden türetilen kararlılık çizgesini göstermektedir. Burada manyetik
alan yeğinliği, dış ortamın süperadyabatikliği ve iç ve dış ortamlar arasındaki dönme hızı
farkının manyetik akı tüpünün kararlılık özelliklerini nasıl etkilediğini inceleyeceğiz. Bu
nedenle  değeri, manyetik alan yeğinliğinin işlevi olarak verilmiştir. Çizgedeki sürekli çizgi,
   eo için; kesikli çizgi ve kesiklinokta biçiminde verilen çizgiler de  eo   v A / ro (izin
verilebilir en büyük açısal hız farkları) içindir. Diğer parametreler (basınç ölçek uzunluğu, dış
ortamın dönme oranı, diferansiyel dönme vb.), Güneş konveksiyon bölgesinin dibine özgü
değerlerdir. Her bir eğrinin üst dışında yeralan ( , Bo) sıralı ikilisi, kararsız akı tüpü; altındaki
sıralı ikililer de kararlı akı tüpü için değerlerdir. Akı tüpü içindeki plazmanın daha hızlı
dönmesi (   0), daima kararlı kılıcı etki yapmaktadır. Ancak kararsızlığa neden olan daha
yavaş iç dönme, Bo  5105G aralığında kararlı kılıcı etkiye dönüşmektedir. Çünkü bu
değerlerde   2 olur ve (4.12) eşitsizliğinin sol tarafındaki üçüncü terim, pozitif değerler
alır. Ancak yukarıda da değinildiği gibi,   1 değerleri, fiziksel gerçeklikle uyuşmamak203
Güneş ve Güneş Benzeri Yıldızlarda Manyetik Konveksiyon
tadır. Çünkü bu aralıktaki  değerleri, akı tüpü içindeki plazmanın ters yöne doğru devinimi
anlamına gelir. Bu nedenle, sürekli çizgiyle kesikli çizgilerin kesişme noktasının fiziksel
anlamı olmayabilir.
Şekil 5‟de manyetik alan yeğinliği 105G değerinin birkaç katı olan akı tüplerinde ortaya çıkan
eksensel bakışık tedirginliklerin, konveksiyon bölgesinin diplerinde (  10 –7 ), iç plazmanın
dönme oranına bağlı olarak kararlı olduğu görülüyor (Spruit, 1977). Konvektif overshoot
katmanı gibisinden subadyabatik katmanlaşma gösteren bölgelerde akı tüpünün kararsız
olabilmesi için manyetik alan yeğinliğinin çok büyük olması gerekmektedir. Diğer yandan,
düşük alan yeğinlikleri için her üç eğri de o  3,410 –6 değerine asimptotik olarak
yaklaşmaktadır. Bu davranışı, (4.14) eşitsizliğine bakarak da anlayabiliriz: F( f )  0,08
~
niceliğiyle birlikte  2   3    e2o terimi de boşlanırsa (Bo 0 için  0 olduğundan
boşlanabilir) tedirginlik biçemlerinin davranışı, (4.14) eşitsizliğinden de görülebilir. (4.14)
eşitsizliğini  ile bölersek,

4  e2 o H
go
1  q 
(4.16)
elde edilir. Bu koşul, dönen, manyetik alandan yoksun ve katmanlaşma gösteren bir ortam
için konvektif kararsızlık koşuludur (van Ballegooijen, 1983).
5. Sonuçlar
Güneş ve diğer soğuk yıldızların overshoot bölgeleri de içerilmek üzere, dış konveksiyon
bölgelerinde manyetik akı depolanma sorununun çözümü için ince akı tüpü yaklaşımında
manyetik yapıların kararlılığı doğrusal tedirginlik bağlamında incelenmiştir.
İlk uygulama olarak, diferansiyel dönme gösteren bir yıldızın eşlek düzleminde yeralan
eksensel bakışık toroidal akı tüpünün kararlılığı incelenmiştir. Dış ortamın plazma akışkan
hızıyla akı tüpü içindeki plazmanın akış hızı farkı herhangi bir koşul koymaksızın dikkate
alınmıştır. Eşlek düzlemine dik yöndeki enlemsel tedirginlikler de incelemeye katılmıştır.
Sonuçlar, şöyle sıralanabilir:
1. Eğer akı tüpü içindeki plazma çevresine göre daha hızlı dönerse, “uçlağa doğru kayma
kararsızlığı” (Spruit ve van Ballegooijen, 1982), bastırılmış olur.
2. Eşlek düzlemindeki tedirginliklerin ortaya çıkardığı eksensel bakışık biçemler, açısal
momentumun korunumu nedeniyle dönmenin etkisiyle güçlü bir biçimde bastırılır.
3. Güneş‟in konveksiyon bölgesinin dibindeki overshoot katmanında geçerli koşullar
altında, 10 5G dek manyetik alan yeğinliğine sahip tüpler, kararlıdır.
4. 10 5G 1,5105G alan değerleri aralığında ikinci bir kararlılık bölgesi bulunmuştur. Bu
bölge, konveksiyon bölgesinin alt kısımlarındaki süperadyabatik katmanlaşma
gösteren kısımlara dek uzanır. İkinci kararlılık bölgesi, değişik biçem eşleşmesinden
kaynaklanan kararsızlık bölgelerini birbirinden ayırır. Yeni kararlılık bölgesinin ortaya
çıktığı B0 ve  değerler aralığı,  (iç–dış ortamların dönme hızları oranı) ve
q(diferansiyel dönme) değerlerine duyarlı bir biçimde bağlıdır.
5. Güneş‟in overshoot katmanındaki diferansiyel dönme, kararlı kılıcı etki taşır ancak
q  1 olduğu için bu etki, eksen bakışıklığı göstermeyen biçemler için önemli değildir.
~2
~2
Gerçekte 4  eo
, 4 qeo
‟den yaklaşık 20 kez büyüktür.
204
Güneş ve Güneş Benzeri Yıldızlar Sempozyumu - İstanbul
6. 104G‟a dek manyetik alan yeğinliğine sahip akı tüplerinin kararlılığı, çoğunlukla
diferansiyel dönme ile belirlenir. Ancak güçlü alanlar (  105G) için kararlılık, sadece
tabakalaşmaya bağlıdır.
Kaynaklar
- Chandrasekhar, S., 1981, Hydrodynamic and Hydromagnetic Stability, Clarendon Press, Oxford,
1961 (Dover ed., 1981)
- Ferriz-Mas, A., Schüssler, M., 1989, Geophys. Astrophys. Fluid Dynamics, Vol. 48, 217
- Ferriz-Mas, A., Schüssler, M., 1993, Geophys. Astrophys. Fluid Dynamics, Vol. 72, 209.
- Ferriz-Mas, A., 1996, ApJ, 458, 802.
- Howe, R., Christensen-Dalsgaard, J., Hill, F., Komm, R.W., Larsen, R.M., Schou, J., Thompson,
M.J., Toomre, J., 2000, Science, 287, 2456
- Howe, R., Christensen-Dalsgaard, J., Hill, F., Komm, R., Schou, J., Thompson, M.J., 2005, ApJ,
634, 1405.
- Howe, R., 2009, Living Rev. Solar Phys., 6, 1
- Moreno-Insertis, F., 1984, Die dynamische Entwicklung von magnetischen Fluröhren in der Konvektionszone der Sonne, Ph.D Thesis, Universitaat München.
- Moreno-Insertis, F., 1986, A&A, 166, 291
- Moreno-Insertis, F., Schüssler, M., Ferriz-Mas, A., 1992, A&A, 264, 686
- Rüdiger, G., Hollerbach, R., 2004, The Magnetic Universe, Wiley-VCH Verlag GmbH & Co.
KgaA., Weinheim
- Schou, J. ve ark., 1992, ApJ, 385, L59
- Schüssler, M., 1990, Comments on the structure and dynamics of magnetic fields in stellar
convection zones, Habilitationsschrift, Universitat Göttingen
- Schüssler, M., 1993, IAUS, 157, 27
- Spruit, H.C., 1981a, A&A, 98, 155
- Spruit, H.C., 1981b, A&A, 102, 129
- Spruit, H.C., van Ballegooijen, A. A., 1982, A&A, 106, 58 (erratum, 1982, A&A, 113, 350)
- van Ballogooijen, A. A., A&A, 1983, 118, 275
205