SAYISAL YÖNTEMLER
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
SAYISAL
YÖNTEMLER
5.HAFTA İÇERİĞİ
Sayısal İntegrasyon
SAYISAL
YÖNTEMLER
analitik olarak hesaplanabilir.
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
Basit
fonksiyonların
(polinom,
üstel
ve
trigonometrik gibi sürekli fks.lar) integrali
Fakat integrali zor olan karmaşık yapıdaki
fonksiyonların analitik olarak hesaplanması ya
zor ya da imkansızdır.
Bu gibi durumlarda
yararlanılır.
sayısal
integralden
Sayısal İntegrasyon
b
a
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
I f ( x ) dx
Sayısal integrasyon yukarda verilen herhangi bir
integralin
değerinin
yaklaşık
olarak
bulunmasıdır.
İntegralin sınırları olan a ve b sayıları sabit ve
fonksiyon bu aralıkta sürekli ise integralin
sonucu sabit bir sayıdır.
SAYISAL
YÖNTEMLER
SAYISAL
YÖNTEMLER
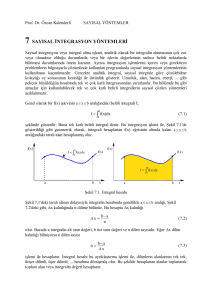
Bu integralin değeri
x=a ve x= b doğruları ile
y=f(x) eğrisinin altında
kalan alana eşittir.
f(x)
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
y
0
a
b
x
Sayısal integrasyon verilen a-b aralığında fonksiyon n
parçaya ayrılarak her bir parçanın alanının bulunması
yöntemlerini içerir. Daha sonra ise toplam alan yani
integralin yaklaşık değeri hesaplanır.
Sayısal İntegrasyon Yöntemleri
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
• Dikdörtgenler Yöntemi
• Yamuk (Trapez) Yöntemi
• Simpson Yöntemi
• Orta Nokta Yöntemi
• Gauss Yöntemi
SAYISAL
YÖNTEMLER
Dikdörtgenler Yöntemi
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
y
f(x)
yo
0
so s1 s2 …
y1 y2 y3 …
h
a=xo x1
h
h …
x2 x3…
yo= f(xo) ve yn= f(xn)
so= h·yo = h· f(xo)
s1= h·y1 = h· f(x1)
.
.
.
Sn-1
yn
h
b=xn
SAYISAL
YÖNTEMLER
x
a ve b arasını n adet
çubuk ile
böldüğümüzde oluşan
dikdörtgenlerin
alanının hesaplanması
amaçlanır.
Sn-1= h·yn-1 = h· f(xn-1)
x n x0
h
n
ÖRNEK
x2
1 x 2 2 dx
SAYISAL
YÖNTEMLER
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
8
İntegralini n= 6 için
dikdörtgenler yöntemini
kullanarak bulunuz.
I. Basamak
xn=8 ve xo=1
x2
f(x) 2
x 2
x n xo 8 1
h
1,16666
n
6
SAYISAL
YÖNTEMLER
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
II. Basamak
k
xk
f(xk)
0
1
1
1
2,16666
0,6224
2
3,3333
0,4068
3
4,5
0,2928
4
5,6667
0,2247
5
6,833
0,1814
6
8
0,1515
Yamuk Yöntemi
SAYISAL
YÖNTEMLER
Bu yöntemde integrasyon n sayıda yamuk kullanılarak
hesaplanır.
I h i fi
y
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
n 1
i 0
f(x)
fi =f(xi)
h
hi =i. dikdörtgenin genişliği
0
xo=a xi
xn=b
x
hi =xi+1 - xi
Eğer dikdörtgenin genişliği sabit ise
h=(b-a)/n
= (xn-xo)/n
SAYISAL
YÖNTEMLER
b
I f ( x ) dx
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
a
İntegralini [a,b] aralığında n eşit
parçaya ayıralım.
y
y=f(x)
G
A
yo
0
C D E
B
F
s1 s2 … …
y1 y2 … …
sn
yn
h …
h
h
h
a=xo x1 x2 …
b=xn x
Her bölme noktasından
dikler çıkılır bu dikler ile
f(x) eğrisinin kesiştiği
noktalar birer doğru ile
birleştirilir. Bu durumda
n adet yamuk elde edilir.
SAYISAL
YÖNTEMLER
y
y=f(x)
xoABx1 yamuğunun alanı
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
G
A
S1=(1/2)·h·(yo+y1)
S2=(1/2)·h·(y1+y2)
…
Sn=(1/2)·h·(yn-1+yn)
yo
0
C D E
B
F
s1 s2 … …
y1 y2 … …
sn
yn
h …
h
h
h
a=xo x1 x2 …
b=xn x
SAYISAL
YÖNTEMLER
Toplam Alan
S=(1/2)·h·(yo+y1)+…+(1/2)·h·(yn-1+yn)
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
S=S1+S2+…+Sn
S=(1/2)·h·(yo+2y1+2y2+…+2yn-1+yn)
S=h·((yo+yn)/2+y1+y2+…+yn-1)
y o y n n 1
S h
yi
i 1
2
xn - xo
h Δx
n
yo=f(xo)
xo=a
yn=f(xn)
xn=b
alarak yeniden düzenlersek
f(x o ) f(x n ) n 1
S Δx
f(x o kx)
2
k 1
olur
Örnek
SAYISAL
YÖNTEMLER
1
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
1
I 2
dx
x 1
0
İntegralini n=4 için yamuk yöntemi
kullanarak hesaplayınız
I. Adım : xo=0 ve xn=1
II. Adım :
xn xo 1 0
x
0.25
n
4
k
xk
f(xk)
0
0
1
1
0,25
0,94187
2
0,50
0,8
3
0,75
0,64
4
1
0,5
SAYISAL
YÖNTEMLER
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
III. Adım :
f(x o ) f(x n ) n 1
S Δx
f(x o kx)
2
k 1
1 0,5
S 0,25
0,94187 0,8 0,64 0,782794
2
Bu fks.için gerçek integral :
1
1
1 1
I 2
d x tg x |0
x 1
0
arctg1 arctg 0
0
4
0 ,785398
I S
t
I
0 ,7853951 0,782794
0 ,7853951
0 ,0033155
SAYISAL
YÖNTEMLER
ÖDEV:
Makina Müh. Bölümü
Yıldız Teknik Üniversitesi
I e x sin 2 x d x
integralinin değerini n=4 için yamuk
0
ve dikdörtgen yöntemleri ile çözünüz.