Bir tekerlek, 3.5 rad/ s2 `lik

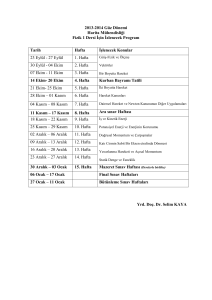
HARRAN ÜNİVERSİTESİ 2016 YILI ZİRAAT FAKÜLTESİ FİNAL SINAVI
SORU ÖRNEKLERİ
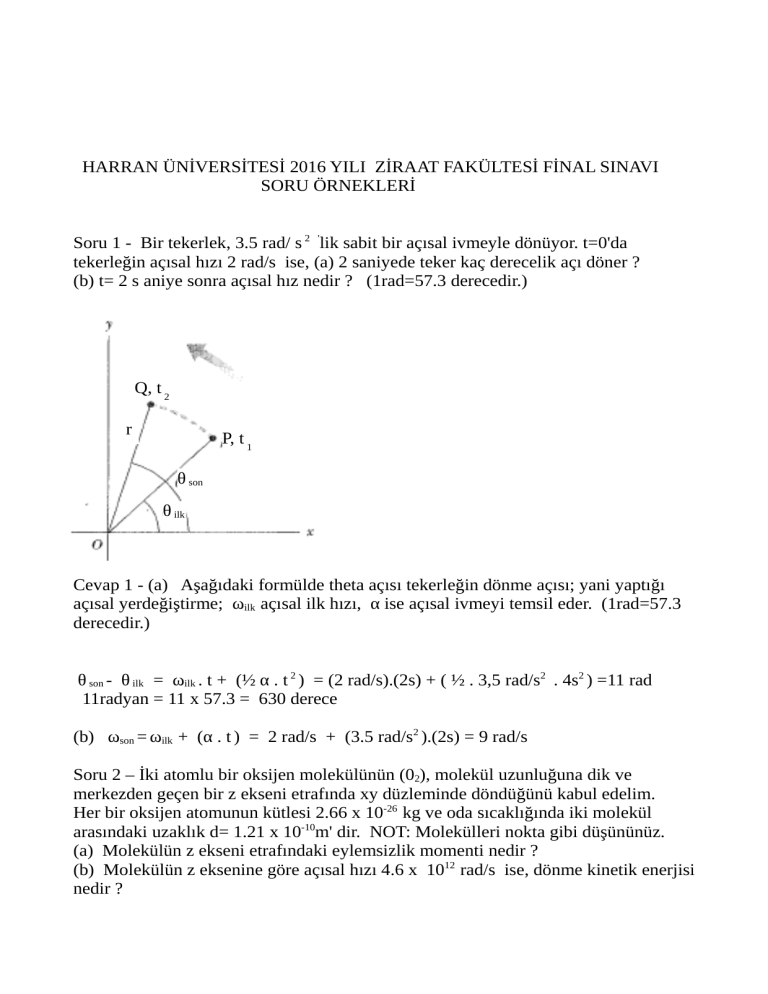
Soru 1 - Bir tekerlek, 3.5 rad/ s 2 'lik sabit bir açısal ivmeyle dönüyor. t=0'da
tekerleğin açısal hızı 2 rad/s ise, (a) 2 saniyede teker kaç derecelik açı döner ?
(b) t= 2 s aniye sonra açısal hız nedir ? (1rad=57.3 derecedir.)
Q, t 2
r
P, t 1
θ son
θ ilk
Cevap 1 - (a) Aşağıdaki formülde theta açısı tekerleğin dönme açısı; yani yaptığı
açısal yerdeğiştirme; ωilk açısal ilk hızı, α ise açısal ivmeyi temsil eder. (1rad=57.3
derecedir.)
θ son - θ ilk = ωilk . t + (½ α . t 2 ) = (2 rad/s).(2s) + ( ½ . 3,5 rad/s2 . 4s2 ) =11 rad
11radyan = 11 x 57.3 = 630 derece
(b) ωson = ωilk + (α . t ) = 2 rad/s + (3.5 rad/s2 ).(2s) = 9 rad/s
Soru 2 – İki atomlu bir oksijen molekülünün (02), molekül uzunluğuna dik ve
merkezden geçen bir z ekseni etrafında xy düzleminde döndüğünü kabul edelim.
Her bir oksijen atomunun kütlesi 2.66 x 10-26 kg ve oda sıcaklığında iki molekül
arasındaki uzaklık d= 1.21 x 10-10m' dir. NOT: Molekülleri nokta gibi düşününüz.
(a) Molekülün z ekseni etrafındaki eylemsizlik momenti nedir ?
(b) Molekülün z eksenine göre açısal hızı 4.6 x 1012 rad/s ise, dönme kinetik enerjisi
nedir ?
Cevap 2- (a) Eylemsizlik momemti = I = Σ mi ri 2 buradaki “i” harfi 1, 2, … gibi
i
sistemde bulunan cisimlerin sayısı karar olan sayılar dizisidir. ri ise her cismin
dönme merkezine uzaklığıdır.
I = Σ mi ri 2 = m1r12 + m2r22 = m. (d/2)2 + m. (d/2)2 = ½ m.d2
i
I= ½ . (2.66 x 10-26 kg).(1.21 x 10-10m)2 = 1.95 x 10-46 kg.m2
(b) Tabiki önce a seçeneği çözülüp, eylemsizlik momenti (I) bulunmalıdır.
Dönme kinetik enerjisi = Tdönme = ½ I. ω2
Tdönme = ½ (1.95 x 10-46 ).(4.6 x 1012 rad/s)2 = 2.06 x x 10-21 joule
Soru 3 - Dört küçük küresel kütle, xy düzleminde kütlesi ihmal edilen bir düzeneğin
uçlarına yerleştirilmiştir. (a) Sistem, ω açısal hızıyla y ekseni etrafında dönerse, bu
eksene göre eylemsizlik momenti ve kinetik enerjisi ne olur ?
(b) Eğer sistem, O noktasından geçen bir z ekseni etrafında dönerse, z eksenine göre
eylemsizlik momenti ve dönme kinetik enerjisi ne olur?
m1=m
m4=M
m3=M
m2=m
Cevap (a) Eylemsizlik momemti = I = Σi mi ri 2 = m1r12 + m2r22 + …
Dönme kinetik enerjisi = Tdönme = ½ I. ω2
ise bunu hareket doğrultusuna göre bileşenlerine ayırmak, izlenecek yol olmalıdır. Y
ekseninde yapılan dönmelerde cisimlerin dönme eksenlerine uzaklığı olan r=0
olacağından, bu cisimlerden eylemsizlik momentine bir katkı gelmez.
Iy = m1r12 + m2r22 + m3r32 +m4r42 = m 02 + m 02 +M.a2 +M.a2 = 2.M.a2
Tdönme = ½ Iy. ω2 = ½ . (2.M.a2). ω2 = M.a2. ω2
(b) Burada formüllerdeki r uzaklığının dönme noktasına dik uzaklık olduğunu
bilmek lazım.
Iz = m1r12 + m2r22 + m3r32 +m4r42 = m.b2 + m.b2 +M.a2 +M.a2 = 2.M.a2 + 2.m.b2
Tdönme = ½ Iz. ω2 = ½ . (2.M.a2 + 2.m.b2). ω2 = (M.a2 + m.b2). ω2
Soru 4 - Yarıçapı R, kütlesi M ve eylemsizlik momenti
I olan bir tekerlek yandaki şekildeki gibi sürtünmesiz yatay bir
milde dönmektedir. Tekerleğin açısal ivmesini ve ipteki T
gerilmesini bulunuz.
Cevap 4 - Öncelikle Tork'un ne olduğu bilinmelidir.
Tork bir kuvvetin bir cismi bir eksen etrafında döndürme
eğilimidir.
τ= F. d şeklinde kuvvet ve bu kuvvetin dönme noktasına dik
uzunluğunun çarpımıyla bulunur. τ= F. d= (F.sinφ) .r şeklinde
de aşağıdaki gibi hesaplanabilir.
Sonuç olarak sorudan hareketle Tork= τ= F. d = T.R olarak yazılır. Tekerleğin
ağırlık merkezi ve milin merkesi hareket ekseninden geçtiği için bunların turku sıfır
olacaktır. Çünkü R=0 'dır.
Σ τ = I. α şeklinde eylemsizlik momenti ve açısal ivme cinsinden de yazılabilir.
Dolayısıyla τ = I. α = T.R ve α = (T.R) / I bulunur. Aşağı yönlü cismin hareketini
pozitif yön olarak alır, hareket yönğnde Newton'un 2. yasasını uygularsak:
Σ Fy = m.g – T = m.a
sonuç olarak çizgisel ivme a = (m.g – T) /m olur.
Cisim ve tekerlek kaymayan bir ipe bağlı olduklarından asılan cismin çizgisel
ivmesi, tekerleğin dış yüzeyindeki bir noktanın çizgisel ivmesine eşittir. Bu yüzden
çizgisel ve açısal ivme arasındaki ilişki şöyledir :
a= R. α olur. Önceden bulduğumuz bağıntılarıda kullanırsak,
a= R. α = R. (T.R / I ) = (m.g – T) /m bulunur. Gerekli ara işlemler yapılırsa
(burayı siz yapacaksınız) ,
T= mg / (1+ mR2/ I) ip gerilmesine ulaşılır.
a = g / (1+ I/ mR2) ve α = a/R = g/ (R+ I/ mR)
Soru 5 - Dönme eksenine göre eylemsizlik momenti I,
yarıçapı R olan bir makara üzerinden geçen bir ipin uçlarına
m1≠ m2 olan iki cisim asılıyor. İp makara sisteminden
kaymamaktadır. Sistem durgunken serbest bırakılıyor.
m2 kütlesi h kadar düşerken m1 yükseliyor. Kütlelerin
çizgisel hızlarını ve açısal hızlarını bulunuz. Sürtünmeleri
ihmal ediniz.
Cevap 5 - Makara ve kütleden oluşan sistemin kinetik
enerjisindeki artış, potansiyel enerjideki azalışa eşit olmalıdır.
Sistem durgunken harekete başladığı için ilk anda sistemin
kinetik enerjisi 0'dır. Sistemin hem öteleme hem de dönme kinetik enerjisi olacaktır.
∆K= kinetik enerji farkı = Kson - Kilk =[ ½ m1 νson2 + ½ m2 νson2 + ½ I. ωson2 ] - 0
Burada aynı ipe bağlı olan kütlelerin hızları eşit alınmıştır. Çizgisel ve açısal hız
arasındaki ilişki ν = R. ω olarak bilinir. Bu üstteki formülde yazılırsa:
∆K= ½ (m1 + m2 + I/R2 ) . νson2 bulunur. Kaybedilen ve kazanılan potansiyel
enerjiler şöyle verilir:
∆U1= m1 .g .h
ve ∆U2= -m2 .g .h olur. Enerjinin korunumu yazılırsa:
∆K + ∆U1 +∆U 2 = ½ (m1 + m2 + I/R2 ) . νson2 + m1 .g .h -m2 .g .h = 0
Sonuç olarak, νson = ( [ 2(m1 – m2).g.h ] / [m1 + m2 + I/R2 ] ) ½
νson = R. ωson olduğundan açısal hız şöyle bulunur:
ωson = (1/R). ( [ 2(m1 – m2).g.h ] / [m1 + m2 + I/R2 ] ) ½
Soru 6 - Şekildeki durgun katı küre için, kütle
merkezinin (KM) eğik düzlemin alt ucundaki hızını
ve kütle merkezinin doğrusal ivmesini hesaplayıp,
sonucu yorumlayınız. (Not: Küre için
eylemsizlik momenti = IKM = 2/5 M.R2)
Cevap 6 – Enerjinin kounumu ilkesini kullanırsak,
eğik düzlemin tepesinde Uilk=M.g.h potansiyel ve
Kilk=0 kinetik enerjisine sahip olan bir kürenin, bu toplam enerjisini sistemin aşağı
ucundada korumasını bekleriz. Bu yüzden,
Eilk = Eson
Kilk + Uilk = Kson + Uson
0+ M.g.h = [ ½.IKM .ω2 + ½ . M.R2 .ω 2 ] + 0
ν= R. ω olduğundan, formül νKM kütle merkezi cinsiden yazılırsa:
M.g.h = ½.[ IKM ./R 2 + M ] .νKM 2
νKM = [ 2gh / (1 + IKM ./MR 2)]1/2=[ 2gh / (1 + [2/5 MR2 ./MR 2] )]1/2 = (10/7 g.h )1/2
Şimdi kütle merkezinin doğrusal ivmesinin hesaplamak için düşey doğrultudaki yer
değiştirmeyi dik üçgende pisagor yöntemiyle h= x .sinθ kullanmak lazım.
Dolayısıyla; νKM 2= (10/7 g. x .sinθ) olurken, νson 2 = νilk 2 + 2 aKM .x formülü
hatırlanak olursa; ilk hızı sıfır (νilk = 0) olan bu cismin ivmesinin
aKM = νson 2 / 2.x = 5/7 .g . sinθ olduğu görülür.
YORUM: Bu sonuçlar, bize kütle merkezinin hız ve ivmesinin kürenin kütle ve
yarıçapından bağımsız olduğu gerçeğini gösterir.
Soru 7 - M kütleli ve L uzunluklu katı bir
çubuk, merkezinden geçen sürtinmesiz bir mile
tutturulmuştur. Bu çubuğun uçlarında m1 ve m2
kütleli iki parçacık bulunmaktadır. (a) Sİstemin
açısal momentum büyüklüğü için bir ifade
bulunuz. (b) Çubuk yatayla θ açısı yaptığında,
sistemin açısal ivmesinin büyüklüğü için bir
ifade bulunuz ve yorumlayınız.
NOT: Merkezinden geçen eksen etrafında
dönen L uzunluklu çubuk için IKM = 1/12 M.L2
Cevap 7- (a) Eğer eylemsizlik momenti bulmada kullanılan paralel eksen teoremi
hatırlacak olursa, I = IKM + m.d2 ifadesinde KM kütle merkezini, d ise kütle
merkezinden geçen eksenden d kadar uzaklığı ifade eder. Böylelikle,
I = I = IKM + m1.d12 + m2.d22 = 1/12 M.L2 +m1.(L/2)2 +m2.(L/2)2
I = (L2 /4). (M/3+m1+m2 ) bulunurken,
açısal momentum = L = I.ω = [ (L2 .ω) /4 ]. (M/3+m1+m2 ) olarak bulunur.
(b) Öncelikle cismlerin dönmesi ve açısal ivmenin olabilmesi için m1≠m2 ve
θ≠ 90 veya -90 derece şartı sağlanmalıdır.
Sonrasında toplam dış tork = τ1 + τ2 = I.α' u bulmalıyız.
τ1 = m1.g.(L/2).cosθ sağ el kuralıyla sayfa düzleminden dışarıyken,
τ2 = - m2.g.(L/2).cosθ torku sayfa süzlemine doğru bir tork oluşturur.
Toplam tork = τ1 + τ2 = m1.g.(L/2).cosθ – m2.g.(L/2).cosθ= ½ . (m1– m2).g.L. cosθ
olur.
m1 > m2 olması durumunda net tork düzlem dışına iken, m1 < m2 durumnda düzleme
doğrudur.
α = τ toplam / I = [ ½ . (m1– m2).g.L. cosθ ] / [ (L2 /4). (M/3+m1+m2 ) ]
α = [2.(m1– m2).g.cosθ ] / [L.(M/3+m1+m2 ) ]
Yukarıdaki formülde açısal ivme α ' nın θ =90 veya -90 derece iken en küçük değeri
sıfırı, θ =0 veya 180 derece iken ise en büyük değerini alacağı görülür.
Soru 8 - Dairesel disk, sürtünmesiz yatay
bir platformda düşey bir mil etrafında
yatay düzlemde dönmektedir. Platform
M=100kg kütleli ve R=2m yarıçapa
sahiptir. m=60kg kütleli bir öğrenci dönen
platformun kenraından merkezine doğru
yavaşça yürümektedir. Öğrenci,
platformun kenarındayken sistemin açısal
hızı 2 rad/s ise, öğrenci merkezden
r= 0.5m uzaklıktaki notaya geldiğinde
açısal hızı ne olur bulunuz ve
yorumlayınız ?
Cevap 8- Eğer Isistem= Iilk= Iplatform+ Iöğrenci
veya kısaca Iilk= Ip+ Iö şeklinde
gösterilirse,
Iilk= ½ .MR2 + mR2 olur. Öğrenci r < R konumuna kadar yürüdüğünde Ison = Ipson+
Iöson = ½ .MR2 + mr2 değerine doğru azalır. Dönen platform ve öğrenci sistemine etki
eden dış dönme momenti olmadığından açısal momentumun korunumu yasası
uygulanabilir.
Iilk ωilk = Isonωson
(½ .MR2 + mR2 ).ωilk = (½ .MR2 + mr2) .ωson
ωson =ωilk .(½ .MR2 + mR2 ) / (½ .MR2 + mr2 )
ωson = [ (200cm+240cm)/ (200cm+15cm) ]. 2rad/s
ωson = 4.1 rad/s beklendiği gibi açısal hız artmıştır.
Soru 9 – Düzgün bir cisim için denge şartını yazınız. Kuvvetlerin eşdeğer olması
nasıl sağlanır ?
Cevap 9- Bir cismin dengede olabilmesi için iki şartın sağlanması gerekir. Bunlar:
1. Cisme etkiyen dış kuvvetlerin bileşkesi sıfır olmalıdır. Yani, ΣF =0 ' dır.
2. Herhangi bir dönme eksenine göre dış torkların bileşkesi yada açısal ivmesi
(α ) sıfır olmalıdır. Yani, Στ = I.α = 0 olmalıdır.
Soru 10 - Yandaki resimde 50N'luk
bir küre yatay olarak tutulmaktadır.
Pazu kaslarının dirsekteki dönme
noktasına uzaklığı d=3cm ve eldeki
kürenin dönme noktasına uzaklığı
L=35cm'dir. Önkolun ağırlığını
ihmal ederek, pazunun önkola
uyguladığı yukarı doğru kuvveti ve
dirsekteki dönme noktasından
üst kola uygulanan aşağı doğru
kuvveti bulunuz.
Cevap 10 - Pazunun yukarı doğru uyguladığı kuvvet F ve R tamda dönme noktasında
olan aşağı yönlü kuvvet ise pozitif y noktasındaki kuvvetlerin bileşkesi denge şartı
için 0 olmalıdır.
ΣFy = F -R – 50 = 0 ise F-R = 50 newton olur.
İkinci denge şartından, bileşke tork O noktasına göre sıfır olmadır.
F.d – m.g.L = 0
F. (3cm) – (50 N).(35cm) = 0 ise F= 583 Newton bulunur.
R= F-50= 533 Newton bulunur.
Derleyen: Öğrt. Gör. Dr. İlker Can Çelik
Fizik Bölümü, Nükleer Fizik A.B.D
Kaynak: Fen ve Mühendislik için Fizik (Serway) Ünite 10,11, 12