Makine Mühendisliği İçin
Elektrik-Elektronik Bilgisi
Ders Notu-3
Doğru Akım Devreleri
Hazırlayan: Yrd. Doç. Dr. Ahmet DUMLU
ELEKTROMOTOR KUVVETİ
Kapalı
bir
devrede
sabit
bir
akımın
oluşturulabilmesi
için
elektromotor kuvvet (emk) adı verilen bir enerji kaynağına ihtiyaç
duyulmaktadır.
Şekilde devreye elektromotor kuvvetini
veren bir batarya ve ona bağlı bir direnç
gösterilmiştir.
negatif
Bataryanın
ucundan
daha
pozitif
ucu,
yüksek
bir
potansiyele sahip olup bataryanın iç
direnci ihmal edildiğinde bataryanın uçları
arasındaki potansiyel fark (yani çıkış
voltajı), bataryanın emk’sına eşittir.
Pratikte her bataryanın bir iç direnci olunduğundan bataryanın çıkış
voltajı bataryanın emk’sı eşit değildir.
Yukarıdaki şekilde gösterildiği gibi 𝜀 emk’ya sahip olan bataryanın
kesikli çizgiler içinde gösterildiği gibi küçük de olsa 𝑟 kadarlık bir iç
direnci bulunmaktadır. Şimdi bu devreyi analiz edelim.
Şekilde kapalı devrede 𝐼 kadarlık bir akımın aktığını ve bataryanın 𝑎 ve
𝑏 noktaları arasında pozitif bir yükün hareket ettiğini düşünelim.
Hareketli yükler bataryanın negatif ucundan pozitif ucuna hareket
ettiğinde, bu yüklerin potansiyeli 𝜀 kadar artar. Fakat yük, 𝑟 direnci
içerisinden geçerken, bu potansiyel 𝐼𝑟 kadar azalır. Bu durumda
bataryanın 𝑎 ve 𝑏 noktaları arasındaki potansiyel fark yani bataryanın
çıkış voltajı (∆𝑉 = 𝑉𝑏 − 𝑉𝑎 ) aşağıdaki gibi ifade edilir.
∆𝑉 = 𝑉𝑏 − 𝑉𝑎 = 𝜀 − 𝐼𝑟
∆𝑉 = 𝑉𝑏 − 𝑉𝑎 = 𝜀 − 𝐼𝑟
Bataryanın bu çıkış voltajı (∆𝑉), kapalı devrenin 𝑐 ve 𝑑 noktaları
arasına bağlanmış olan ve yük direnci olarak ifade edilen 𝑅
direncinin uçları arasındaki potansiyel farka eşit olup bu potansiyel
∆𝑉 = 𝐼𝑅 ‘ye eşittir. Bu durumda bataryanın 𝜀 değeri aşağıdaki gibi
elde tanımlanır.
∆𝑉 = 𝑉𝑏 − 𝑉𝑎 = 𝜀 − 𝐼𝑟 = 𝐼𝑅 → 𝜀 = 𝐼𝑟 + 𝐼𝑅
𝜀 = 𝐼𝑟 + 𝐼𝑅
Bu eşitlikten akımı çözersek;
Bu eşitlikten göre; kapalı devreden geçen akım, hem bataryaya bağlı
dış dirence hem de bataryanın iç direncine bağlıdır. Eğer yük direnci
𝑅
bataryanın iç direncinde
𝑟
çok büyükse çoğu analiz
yöntemlerinde bu iç direnç ihmal edilir.
Eğer emk ifadesi (𝜀 = 𝐼𝑟 + 𝐼𝑅) 𝐼 akımıyla çarpılırsa; emk kaynağının
çıkış gücü aşağıdaki gibi tanımlanır. Dolayısıyla çıkış gücü hem yük
direncinde hem de iç dirençte ısıl güç olarak harcanmaktadır.
Örnek; bir batarya, 12 𝑉’luk emk ve 0,05Ω′ luk iç dirence sahiptir.
Bataryanın uçları 3Ω’luk bir yük direncine bağlanıyor.
A)Devredeki akımı ve bataryanın çıkış voltajını hesaplayınız.
B) Yük direncinde ve bataryanın iç direncinde harcanan gücü
hesaplayınız. Batarya tarafından sağlanan güç ne kadardır.
Devreden akan akım
Yüke düşen potansiyel
Yükün harcadığı güç
Batarya iç direncinin harcadığı güç
Batarya tarafından sağlanan güç
SERİ VE PARALEL BAĞLI DİRENÇLER
İki veya daha fazla direnç, çift başına sadece tek bir ortak noktaya
(Yani Şekildeki b noktası) sahip olacak şekilde birbirine bağlanmışsa,
bu dirençlerin seri bağlı oldukları söylenir. Seri bağlı dirençlerden
geçen akım aynı olup bu dirençlerin uçlarına uygulanan potansiyel
fark dirençler arasında bölünecektir.
Şekildeki seri bağlı devrede, 𝑎 noktası ile 𝑏 noktası arasındaki
potansiyel fark 𝐼𝑅1 ’e eşitken 𝑏 noktası ile 𝑐 noktası arasındaki
potansiyel fark 𝐼𝑅2 eşittir. Bu durumda 𝑎 ile 𝑐 arasındaki potansiyel
farkın değeri kaynak gerilimine eşit olacağından aşağıdaki eşitlik
yazılabilir.
Elde edilen bu eşitliğe göre devrede (𝑅1 + 𝑅2 ) toplamıyla ifade edilen
devre direnci 𝑅𝑒𝑞 eşdeğer direnci ile temsil edilebilir. Yani devreden
𝑅1 ve 𝑅2 direnci çıkarılıp bunların yerine 𝑅𝑒𝑞 eşdeğer direnci
bağlanırsa devreden aynı akım akacaktır. Dolayısıyla seri bağlı
devrelerde eşdeğer direnç aşağıdaki gibi elde edilir.
Şimdi ise şekilde gösterildiği gibi birbirine paralel bağlanmış devreyi
inceleyelim. Bataryadan ayrılan 𝐼 akımı 𝑎 noktasına (Bu noktaya
düğüm noktası denir) vardığında iki kola ayrılmaktadır. İki kola ayrılan
akımlardan birincisi 𝑅1 direncinden gecen 𝐼1 akımı diğeri ise 𝑅2
direncinden gecen 𝐼2 akımıdır.
Devreden akan yük korunumlu olduğundan, 𝑎 noktasına giren 𝐼
akımı, bu noktadan ayrılan toplam akıma eşittir. Bu eşitlik aşağıdaki
gibi ifade edilmektedir.
Paralel bağlı dirençlerde potansiyel fark eşit olacağından aşağıdaki
eşitlik yazılabilir.
Dolasıyla paralel bağlı iki dirence ait eşdeğer direncin değeri
aşağıdaki gibi hesaplanabilmektedir.
İkiden fazla direnç paralel bağlanmış ise
eşdeğer direnç değeri aşağıdaki gibidir.
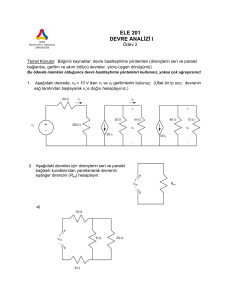
Örnek Şekilde verilen doğru akım devresi için
a) 𝑎 ve 𝑐 arasındaki eşdeğer direnci bulunuz.
b) 𝑎 ve 𝑐 arasına 42 Voltluk bir potansiyel fark uygulanırsa her bir
dirençteki akım ne kadardır.
Örnek Şekildeki paralel bağlı devrede 𝑎 ve 𝑏 noktaları 18 𝑉′luk bir
potansiyel fark uygulanıyor.
a) Her bir dirençteki akımı bulunuz.
b) Her bir dirençte harcanan gücü ve toplam harcana gücü bulunuz.
c) Devrenin eşdeğer direncini bulunuz.
KIRCHHOFF KURALLARI
Çoğu
doğru
akım
devrelerinde
kombinasyonlarına
indirgenerek
basit
seri-paralel
analiz
direnç
gerçekleştirilemez
(Aşağıda devredeki gibi). Bu durumda Kirchoff kurallarından
yararlanır.
Kirchhoff kuralları için tanımlamalar;
1.) Bir devredeki düğüm noktası üç yada daha fazla iletkenin
buluştuğu bir noktadır.
2.) Bir ilmek (döngü veya göz) herhangi bir kapalı iletim yoludur.
İlmek 2
i
i
i
İlmek 1
i
i1
i2
i2
Kirchhoff kuralları
1. Herhangi bir düğüm noktasına gelen akımların toplamı, bu düğüm
noktasından çıkan akımların toplamına eşit olmalıdır.
Bu kural yük korunu ile ilgili olup devredeki
verilen bir noktaya ne kadar akım girerse o
kadar akım bu noktayı terk etmek zorundadır.
Yandaki şekle göre aşağıdaki matematiksel
ifade yazılabilir.
2. Herhangi bir kapalı devre boyunca (herhangi bir ilmek veya göz
boyunca) bütün devre elemanların uçları arasındaki potansiyel
farkların cebirsel toplamı sıfırdır.
Bu kural enerjinin korunu ilkesinden ileri gelmektedir. Çünkü enerji
korunumuna göre, bir devrede kapalı bir ilmek (göz) boyunca
hareket eden herhangi bir yük, başladığı noktaya tekrar geldiğinde,
kazandığı enerjinin toplamı, kaybettiği enerjinin toplamına eşit
olmalıdır.
Kapalı bir ilmek için Kirchhoff’ un ikinci kuralı uygulanması
durumda uyulması gereken kurallar;
1. Kapalı bir ilmek için keyfi bir akım yönü belirleyin (Genellikle
saat yönünde seçilir.).
2. Eğer seçilen yönüne göre, akım emk kaynağının eksi ucuna giriyor
ve artı ucundan çıkıyorsa bu emk kaynağı için potansiyel fark değeri
pozitif alınır.
Tam tersine, seçilen akım yönüne göre, akım emk kaynağının artı
ucuna giriyor ve eksi ucundan çıkıyorsa bu kez emk kaynağı için
potansiyel fark değeri negatif alınır.
3. Seçilen akım yönüne bakılmaksızın bir direncin uçları arasındaki
potansiyel fark her zaman negatif olup değeri −𝐼𝑅 kadardır.
4. Genel olarak belirli bir devre problemini çözmek için ihtiyaç
duyulacak olan bağımsız denklem sayısı, en az bilinmeyen
niceliklerin sayısına eşit olmalıdır.
5. Eğer devreniz aşağıdaki gibi iki veya daha fazla ilmeklerden
oluşuyorsa; Birinci, ikinci, üçüncü ve dördüncü kurallar aynen geçerli
olup, ilmekleri birbirinden ayıran kollardaki dirençlerin potansiyel farkı
için aşağıdaki işlemler yapılır.
Birinci ilmek için eşitlik yazılırken iki
ilmeği
birbirinden
ayıran
koldaki
direncin (bu örnekte 6 ohm’luk direnç)
potansiyel
farkı
−𝑅 ∗ (𝐼1 − 𝐼2 )
yazılırken ikinci ilmek için eşitlik
yazılırken bu direncin potansiyel farklı
− 𝑅 ∗ (𝐼2 − 𝐼1 ) şeklinde yazılır.
6. Seçilen akım yönüne bağlı olarak denklem çözümünde akımlar için
negatif sonuç veya sonuçlar çıkabilir. Bu durumda elde edilen
sonucun büyüklüğü doğru olup sadece analiz sırasında akımın yönü
ters alınmış olacaktır.
Örnek Şekildeki tek ilmekli devre için;
a) Devreden akan akımı bulunuz.
b) Her bir dirençte harcanan gücü bulunuz. 12 voltluk bataryanın
devreye verdiği gücü bulunuz.
Akım saat yönünde seçildi
Akım saat yönünün tersi
yönünde seçildi
Akım saat yönünde seçildi
+𝜀1 − 𝑅1 𝐼 − 𝜀2 − 𝑅2 𝐼 = 0
+6 − 8𝐼 − 12 − 10𝐼 = 0 → −6 − 18I = 0 →
−6
𝐼=
𝐼 = −0,33 𝐴𝑚𝑝𝑒𝑟
18
Sonuç eksi çıktığı için akım yönü ters seçilmiş.
Bu kez akım saat yönünün tersi yönünde seçilirse sonuç nasıl elde edilir.
−𝜀1 − 𝑅2 𝐼 + 𝜀2 − 𝑅1 𝐼 = 0
−6 − 10𝐼 + 12 − 8𝐼 = 0 → +6 − 18I = 0 →
+6
𝐼=
𝐼 = +0,33 𝐴𝑚𝑝𝑒𝑟
18
Sonuç pozitif çıktığı için akım yönü doğru seçilmiştir.
Her bir dirençte harcanan güç;
Dirençler tarafından harcanan toplam güç;
12 voltluk bataryanın devreye verdiği güç;
Geriye kalan 2 Watt’lık güç ise 6 voltluk devreyi şarj etmek için
harcanmaktadır. Dolayısıyla devrelerdeki her emk kaynağı devreye
güç vermeye bilir!
Örnek şekilde gösterilen devredeki 𝐼1 , 𝐼2 ve 𝐼3 akımlarını bulunuz.
Birinci İlmek için;
−4𝐼2 − 14 − 6 𝐼2 − 𝐼3 − 10 = 0
İkinci İlmek için;
−2𝐼3 + 10 − 6 𝐼3 − 𝐼2 = 0
24 + 10𝐼2
Denklem birden 𝐼3 akımı çekilirse; 𝐼3 =
6
𝐼3 akımı denklem ikide yerine yazılırsa 𝐼2 akımı 𝐼2 = −3 𝑎𝑚𝑝𝑒𝑟
bulunur. Bu durumda 𝐼3 akımı 𝐼3 = −1 𝑎𝑚𝑝𝑒𝑟 bulunur.
Düğüm kuralı ile 𝐼1 akımı; 𝐼1 + 𝐼2 = 𝐼3 olduğundan 𝐼1 akımı 𝐼1 =
2 𝑎𝑚𝑝𝑒𝑟 bulunur.
Örnek: Şekilde gösterilen devrenin her bir kolundaki akımı hesaplayınız.
Örnek Kirchoff kurallarını kullanarak şekildeki devrede her bir
dirençteki akımı bulunuz.
Multimetre ile Gerilim, Akım ve Direnç
Ölçümleri
Elektrik akımının şiddetini ölçmeye yarayan aletlere “Ampermetre”,
gerilimin şiddetini ölçmeye yarayan aletlere “Voltmetre” ve direnç
ölçmeye yarayan aletlere “Ohmmetre” denir. Her bir büyüklüğü
ölçmek için farklı alet kullanılabileceği gibi, bir aletle bu üç
büyüklüğün ölçülmesi de mümkündür. Bu tür aletler, ölçtükleri
büyüklüklerin birimlerinin baş harfleri (Amper Volt Ohm) yardımıyla
“AVO metre” olarak adlandırılırlar.
Gerilim Ölçme
Gerilim; tanım gereği bir devrede iki nokta arasındaki potansiyel
farkı olduğuna göre, gerek DC ve gerekse AC gerilim ölçerken
multimetre problarının birbirinden bağımsız olan bu noktalara temas
ettirilmesi gerekir. Bu işleme paralel bağlama denir. Bir iletken
üzerindeki tüm noktalar arasındaki potansiyel farkları yaklaşık sıfır
olacağına göre, bu iletken üzerinde herhangi iki nokta arasındaki
gerilimi ölçmek anlamsız olacaktır.
Şekilde bir kaynak ve bir yükten (direnç veya empedans) oluşan en
basit devre gösteriminde, multimetrenin A-B noktaları arasındaki
gerilimi ölçmek için nasıl kullanılması gerektiği görülmektedir.
Ancak ölçme işleminden önce multimetrenin mutlaka uygun
gerilim ölçme konumuna (AC veya DC) alınması gerekir
Akım Ölçme
Bir devre üzerinde birbirinden bağımsız iki nokta arasında bir
gerilim varsa, bu iki nokta arasında elektrik akımı akacaktır. Bu
akımı ölçebilmek için, multimetrenin doğal olarak akım yolu
üzerine (Şekilde A noktası ile yük arasına veya B noktası ile yük
arasına) yerleştirilmesi gerekir. Bu işleme seri bağlama denir. Ancak
bu işlemden önce, multimetrenin uygun akım ölçme konumuna
(A-mA veya μA) alınması gerekir. Şekilde elektrik akımını
ölçebilmek için multimetrenin örnek kullanım şekli görülmektedir.
Direnç Ölçme
Multimetre ile direnç ölçümü şekil 3’ de gösterildiği gibi
yapılmaktadır. Bu ölçüm yapılırken multimetrenin direnç ölçme
konumu kullanılmalıdır. Eğer ölçülen direnç bir devre üzerindeyse,
ölçüm yapmadan önce, direncin en az bir bacağının devre ile
bağlantısı kesilmelidir.