BÖLÜM.4.A-VERİ DÜZENLEME

VERİLERİN DÜZENLENMESİ
VE ORGANİZASYONU
VERİLERİN DÜZENLENMESİ VE ORGANİZASYONU
İstatistik analizlere başlamadan önce
yapılması gereken ilk iş verilerin
düzenlenmesi olmalıdır.
İstatistiksel çalışmalarda pek çok analizi
uygulayabilmek için verilerin dağılımının
normal ya da normale yakın olması
gerekir.
Bir örnekle gidelim
Tanımlayıcı istatistikler
Ortalama
Güven
aralığı
Ortanca
Standart sapma
Çarpıklık
Basıklık
Mean (Ortalama): Gözlem sonuçlarının toplamının gözlem
sayısına bölümüdür.
Her bir gözlem değerinin ortalamadan sapmalarının
toplamı gözlem sayısına bölünürse ve karekökü alınırsa
Standart Sapma bulunur.
Standart sapmanın karesi varyansı verir.
Tahmini yapılacak büyüklüğün arasında kalacağı alanın
hesaplanmasına Güven Aralığı denir.
Seriyi iki eşit parçaya bölen değer Ortanca (Medyan) dır.
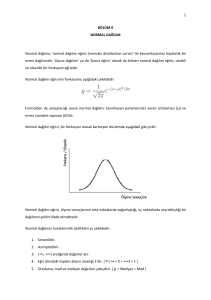
İstatistik çalışmalarında en yaygın kullanılan dağılım
Normal Dağılımdır. Normal dağılım simetriktir. Şekli çan
eğrisine benzer. Simetrik bir dağılımın tepe değeri
(Mod), ortancası (Medyan) ve Ortalaması birbirine
eşittir.
Basıklık (Kurtosis) ve Çarpıklık (Skewness) değerleri
verilerin normal dağılım gösterip göstermediğini ifade
eder.
Çarpıklık veri dağılımının normalden uzaklaşarak sağa ve
ya sola doğru meyleden yamuk bir şekil almasını ifade
eden bir kavramdır. Normal bir dağılımda çarpıklık
katsayısı “sıfır” olacaktır. Çarpıklık arttıkça mod ve
ortalama birbirinden uzaklaşır.
Çarpıklık katsayısı – sonsuz ile + sonsuz arasında
değerler alabilmektedir.
Pozitif ve Negatif olmak üzere iki tip çarpıklıktan söz
edilebilir.
Eğer ortalama medyandan küçük ise dağılım sola
(negatif) çarpık olur.
Eğer ortalama medyandan büyük ise dağılım sağa
(pozitif) çarpık olur.
Çarpıklık ölçüsü ± 3 (±2 de olabilir) aralığında değerler
alması durumunda normal kabul edilmektedir.
Basıklık (Kurtosis) normal dağılım eğrisinin
ne kadar dik ve ya basık olduğunu gösterir.
Tam çan eğrisinin basıklık katsayısı
“sıfır”dır.
Basıklık katsayısı pozitif ise, eğri normale
göre daha diktir.
Negatif ise normale göre daha basıktır.
BAŞARININ ÇAN EĞRİSİ
EKSİK VERİLERİN İNCELENMESİ
Her analizde eksi verilerle karşılaşabiliriz. Bir ankette kişi
soruyu cevapsız bırakabilir… bazı değişkenlerle ilgili
gözlem değerlerine ulaşamayabiliriz…. O halde
Ne yapmamız gerekir?
Bu durumda
 Eksik verilerin gözlemlere rastgele mi
saçıldığı yoksa belirgin bir yapı mı oluşturduğu,
 Eksik verilerin ne kadar sıklıkla karşımıza
çıktığının araştırılması gerekir.
Her zaman eksik veriye yol açan gözlemleri veri grubundan
çıkarma yoluna gitmeyiniz.
Gözlem sayınız önemli derecede etkilenebilir.
O halde ne

yapmalıyız?
Veriye yeni gözlem değerleri eklenebilir,
 Verideki eksik değerler çeşitli
yaklaşımlarla giderilmeye çalışılır.
istatistiksel
Eksik verileri incelemek için
Seçilir
İşaretlenince Missing
Value Analysis
penceresi açılır.
İşaretlenir
Bütün değişkenler Quantitative Variables bölümüne aktarılır.
2.Adım
3.Adım
1. Adım; çünkü gözlem
sayısı eksik gözlem
sayısından daha fazladır.
2. Adım (Patterns)
İşaretlenir
Değişkenler
aktarılır
Seçilir
3. Adım (Descriptives)
Hepsi
işaretlenir
Seçilir
En son pencerede “OK” işaretlendikten sonra analiz
çıktıları ekranı gelir.
Buraya kadar yaptığımız işlemler sonucunda
elde ettiğimiz tablolardan eksik verilerin yapısı,
rastgelelik olup olmadığı, eksik verilerin
toplam verilere etkisi tespit edilebilir.
Separate Variance t Test
Rasgelelik durumu t testi tablosundaki P(2-tail)
Değeri %5 den büyük ise eksik verilerde
rastgelelik vardır.
Missing Patterns (cases with
missing values)
•Eksik veri yapıları tablosundan
eksik verilerin yapısı, sayısı ve
tam gözlem sayısını etkileme
durumunu inceleyebiliriz.
Bunları bir örnek üzerinde görelim
EKSİK VERİLERİN TAMAMLANMASI
Burada eksik verileri çıkartmadan nasıl analize
koyabiliriz? Sorusunun cevabı arayacağız.
Transform / Replace Missing
Values Komutlarını
uygulayınız…..
Method kısmından herhangi bir metod seçilir sonra tüm değişkenler
New Variable(s) kısmına aktarılır. Ve “OK” butonuna basılır.
Eksik değerin altındaki ve
üstündeki tam verilerin
ortalamasını alarak eksik verinin
yerine koyar
Serinin ortalamasını alarak eksik
verilerin yerine koyar
Eksik değerin altındaki
ve üstündeki tam
veriler kullanılır
Eksik değerin altındaki ve
üstündeki tam verilerden
yararlanarak bir medyan değeri
hesaplar eksik verinin yerine
koyar
Mevcut seriler 1’den n’e kadar
ölçeklendirilmiş bir endeks değişkeninde
eksik veriler öngörülen değerlerine göre
yerleştirilir
Eksik veriler tamamlanmadan önceki durum
Eksik veriler tamamlandıktan sonraki durum
NORMALLİK TESTLERİ
SHAPIRO WILK-W TESTİ
KOLMOGOROV SMIRNOV TESTİ
İstatistiksel testler, kabaca "parametrik
testler" ve "parametrik olmayan
testler" olmak üzere ikiye ayrılabilir.
Eldeki bir veri setine, bu testlerden
hangisinin uygun olduğunu belirlemek
için normallik testi yapılmalıdır.
İstatistiksel güven aralıkları
uygulamalarında normallik (normal
dağılıma uygunluk) oldukça önemlidir.
Kullanılan parametrik istatistiksel
tekniklerin geçerli olabilmesi için
populasyon şans değişkeninin normal
dağılıma uyması gerekir.
Veriler normal dağılıma sahip ise
parametrik testler,
Veriler normal dağılıma sahip değil ise
parametrik olmayan testler
uygun olacaktır
UNUTMAYINIZ
• Testlerinde ‘30’ sayısı; istatistiksel teori içinde
anlam taşıdığından önemlidir.
• 30 ve daha büyük örnekli gruplara test gücü
daha fazla olan parametrik testler uygulanır.
• Asıl dayanak dağılımın normal olmasıdır.
• n sayısı 500 de olsa değişken normal
dağılmıyorsa parametrik test seçilemez
Bir örnek verelim
• Bu veri setinde, 4 farklı dersten alınan puanlar verilmiştir.
Bu 4 farklı dersin puanlarının normalliğini test etmek için
öncelikle hipotezler kurulmalıdır.
1. dizayn için hipotezler;
H0: %95 güvenle veriler normal dağılımlıdır.
H1:%95 güvenle veriler normal dağılımlı değildir.
2. dizayn için hipotezler;
H0: %95 güvenle veriler normal dağılımlıdır.
H1:%95 güvenle veriler normal dağılımlı değildir.
3. dizayn için hipotezler;
H0: %95 güvenle veriler normal dağılımlıdır.
H1:%95 güvenle veriler normal dağılımlı değildir.
4. dizayn için hipotezler;
H0: %95 güvenle veriler normal dağılımlıdır.
H1:%95 güvenle veriler normal dağılımlı değildir.
Görüldüğü gibi burada iki farklı test vardır. Bunlardan biri
"Kolmogorov-Smirnov", diğeri ise "Shapiro-Wilk"
testidir. "Shapiro-Wilk" testi daha çok tercih edilir ve
kullanılır. Burada "Shapiro-Wilk" testinin "Sig." değerleri
0.05' den büyük olduğu için tüm gruplar için H0
hipotezleri kabul edilir. Yani tüm gruplar için "%95
güvenle veriler normal dağılımlıdır." denilebilir.