KATI CİSİMLERİN ALANI VE HACİMLERİ
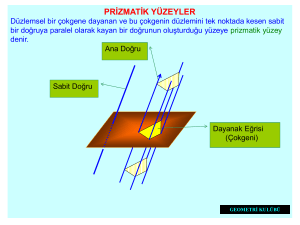
PRİZMATİK YÜZEY
TANIM
Düzlemsel bir çokgen ile bunun düzlemine paralel olmayan bir d doğrusu verilmiş
olsun.
d doğrusuna paralel olan ve çokgenin kenarlarına dayanarak hareket eden l'
doğrusunun oluşturduğu yüzeye, prizmatik yüzey denir (Şekil 1).
Çokgenin köşelerinden d doğrusuna çizilen paralel doğrulara, yan ayrıtlar denir. Ardışık
iki yan ayrıt arasında katan düzlem parçasına,
prizmatik yüzeyin yan yüzleri denir. Çokgen kaç
kenarlı ise o kadar yan yüz vardır.
Bir prizmatik yüzeyin bir düzlemle ara
kesitine, bu prizmatik yüzeyin kesiti denir. Kesit
düzlemi yan ayrıntılara dik ise bu kesite, dik kesit
denir.
TEOREM
Bir
prizmatik
yüzeyin,
paralel
iki
düzlemle kesilmesinden elde edilen iki çokgen
birbirine eştir.
İspat
Şekil 2 de, prizmatik yüzey P ve P' gibi iki
paralel düzlemle kesilmiştir. Böylece elde edilen,
ABCDEF
ve
A'B'C'D'E'F'
çokgenlerinin
eş
olduğunu göstereceğiz.
Bir düzlem paralel iki düzlemle kesildiğinde, ara kesitler paralel olacağından; A'B' //
AB, B'C' // BC, C'D' // CD, D'E' // DE, E'F' // EF, F'A' // FA olur
Uzayda kenarları aynı yönde paralel olan açılar eş olacağından; A'B'C' ABC,
B'C'D' BCD, C'D'E' CDE, D'E'F' DEF, E'F'A' EFA, F'A'B' FAB
Ayrıca; ABB'A', BCC'B', CDD'C', DEE'D', FEE'F', AFF'A' dörtgenleri birer
paralelkenar olduğundan; |AB| = |B'A'|, |BC| = |C'B'|, |CD| = |D'C'|, |DE| = |E'D'|, |EF| = |EF'|,
|AF| = |A'F'| bulunur.
İki çokgen arasında yapılan bire bir eşlemede, karşılıklı kenarlar ve karşılıklı açılar
eş ise bu iki çokgen eş olacağından, ABCDEF - A'B'C'D'E' F' olur.
Sonuç: Bir prizmatik yüzeyin dik kesitleri eştir.
PRİZMALAR
TANIM
Bir prizmatik yüzey ile bunun yan ayrıtlarını kesen paralel iki düzlem tarafından
sınırlanan cisme, prizma denir.
Bir prizmanın tabanlarının dışında kalan yüzeylerine, prizmanın yan yüzeyleri
denir.
Bir prizmada aynı yüzey içinde bulunmayan iki köşeyi birleştiren doğru parçasına,
bu prizmanın köşegeni denir.
Şekil 3 de, bir üçgen prizma görüyorsunuz.
Bu prizmada; ABC üçgenine, alt taban ve A'B'C'
üçgenine, üst taban denir. [AA'], (BB'], [CC'] doğru
parçalarına, bu prizmanın yan ayrıtları denir. [AB],
[BC], [ÇA] doğru parçalarına, alt taban ayrıtları ve
[A'B'], [B'C'], [C'A'] doğru parçalarına, üst taban
ayrıtları denir.
Alt ve üst tabanlar arasındaki uzaklığa, prizmanın yüksekliği denir.
ABB'A', BCC'B', ACC'A' paralelkenarlarına, prizmanın yan yüzleri denir. KLM üçgenine, üçgen prizmanın dik kesiti denir.
Bu bölümde prizma ya da piramitlerin taban ve yan yüzleri için söylenen üçgen,
kare, dikdörtgen, paralelkenar gibi ifadelerden; bunların sınırladığı çokgensel bölgeler
anlaşılacaktır.
TEOREM
Bir prizmanın tabanına paralel kesitleri, tabana eştir.
İspat : Bir prizmatik yüzeyin, paralel iki
düzlemle kesişmesinden elde edilen iki çokgenin,
birbirine eş olduğunu ispatlamıştık. Bu ispattan,
EFGH çokgeninin ABCD çokgenine eş olduğunu
söyleriz (Şekil 4).
Sonuçlar
1. Bir prizmanın yan yüzleri, birer
paralelkenardır.
2. Bir prizmanın dik kesitleri, birbirine eştir.
PRİZMA ÇEŞİTLERİ
TANIM
Yan ayrıtları taban düzlemine dik olan prizmaya, dik prizma denir. Yan ayrıtları
taban düzlemine dik olmayan prizmaya da eğik prizma denir.
Dik prizmaların yan yüzleri birer dikdörtgendir. Yan ayrıtların uzunlukları
yüksekliğin uzunluğuna eşittir.
Eğik prizmaların yan yüzleri birer paralelkenardır.
TANIM
Tabanı düzgün çokgen olan dik prizmaya, düzgün
prizma denir
Bir düzgün prizmanın yan yüzleri birbirine eş dikdörtgenlerdir.
DİKDÖRTGENLER PRİZMASI
TANIM
Tabanları dikdörtgen olan dik prizmaya, dikdörtgenler prizması denir.
Dikdörtgenler prizmasının bütün yüzleri dikdörtgendir.
Dikdörtgenler prizmasında bir köşeden çıkan üç ayrıta, bu dikdörtgenler prizmasının
boyutları denir. Dikdörtgenler prizması özel bir paralelyüz olduğundan, onun tüm özeliklerini taşır. Ayrıca, dikdörtgenler prizmasının cisim köşegenleri eşit uzunluktadır.
TEOREM
Bir dikdörtgenler prizmasında, cisim köşegeninin uzunluğunun karesi, bir köşeden
çıkan üç ayrıtının uzunluklarının karelerinin toplamına eşittir.
İspat
Pisagor
teoreminden,
ABC
dik
üçgeninde, e2 = a2 + b2 dir. A'AC dik üçgeninde,
k2 = e2 + c2 dir. Buradan, k2 = a2 + b2 + c2 bulunur.
Örneğin; ayrıtları 3, 4 ve 12 birim olan
dikdörtgenler
prizmasının
cisim
köşegeninin
uzunluğu,
k=
32 4 2 12 2 = 13 birim olur.
KÜP
Bütün ayrıtları eşit uzunlukta oları dikdörtgenler prizmasına, küp denir.
Küpün bütün yüzleri, birbirine eş karelerdir.
Bir kenarının uzunluğu a birim olan küpün
cisim köşegeninin uzunluğu, a 3 birimdir. Örneğin;
köşegen uzunluğu 10 6 birim olan küpün bir
ayrıtının uzunluğu, a 3 = 10 6 eşitliğinden,
a = 10 2 birim olur.
PRİZMANIN ALANI
TEOREM
Bir eğik prizmanın yanal yüzünün alanı, dik kesit çevresi ile yan ayrıt uzunluğunun
çarpımına eşittir:
İspat ABCDA'B'C'D' prizmasının yan ayrıtının uzunluğu |AA'| = l olsun.
Dik kesiti KLMN dörtgeni olan bir prizma ile bu prizmanın açık şekli, şekilde
belirtilmiştir. Şekildeki ABB'A', BCC'B', CDD'C', DAA'D' dörtgenlerinin birer paralelkenar
olduğunu ispatlamıştık.
|KL|, |LM|, |MN|, |NK| bu paralelkenarların birer yüksekliğidir. Buna göre, şekildeki
prizmanın yanal alanı,
Y = |AA'| . (|KL| + |LM| + |MN| + |NK|)
Y = l . (dik kesit çevresi) olur.
Sonuçlar
1. Bir prizmanın bütün alanı, yanal alanı ile alt ve üst tabanının alanlarının toplamına
eşittir. Alt ve üst tabanları eş olduğu düşünülürse,
S = Y + 2 . G bulunur. Burada G, prizmanın taban alanını göstermektedir.
2. Bir dik prizmanın yanal alanı, taban çevresi ile yüksekliğinin çarpımına eşittir.
Çünkü, dik prizmanın yan yüzü, bir dikdörtgensel bölgedir. Bu dikdörtgensel bölgenin bir kenarının uzunluğu, tabandaki çokgensel bölgenin çevresine eşittir. Diğer kenarının
uzunluğu da dik prizmanın yüksekliğine eşittir.
Örneğin; taban ayrıtlarının uzunlukları 3 cm, 4 cm, 5 cm ve yüksekliği 10 cm olan
üçgen dik prizmanın yanal alanı;
Y = (3+4+5) . 10
Y = 120 cm2 olur.
3. Bir köşeden çıkan ayrıt uzunlukları a, b, c olan dikdörtgenler prizmasının alanı,
S = 2(a.b+b.c+a.c)dir.
Örneğin: boyutları a = 5 cm, b = 3 cm, c = 2 cm olan dikdörtgenler prizmasının bütün alanı, S = 2. (5.3 + 5.2 + 3.2) = 62 cm2 olur.
4. Bir ayrıtının uzunluğu a olan küpün alanı, S = 6 . a2 dir. Çünkü küpte birbirine eş
altı kare vardır.
Örneğin; bir ayrıtının uzunluğu a = 3 birim olan küpün alanı,S = 6 . 32 = 54 br2 olur.
DİKDÖRTGENLER PRİZMASININ HACMİ
TEOREM
Bir dikdörtgenler prizmasının hacmi, bir köşeden geçen üç ayrıtının uzunlukları
çarpımına eşittir.
İspat :
Dikdörtgenler prizmasının boyutları, seçilen bir birim uzunluğunun a,b,c gibi tam
katları olsun
Bu prizmanın tabanına a.b tane birimkare çizilebilir. Her kareye bir birimküp oturtularak, a.b birimküplük bir tabaka (katman) elde edilir. Prizmanın yüksekliği c birim
olduğundan, prizmada bu katmanlardan c tane bulunur. Bu durumda dikdörtgenler
prizmasına, seçilen birimküplerden (a.b).c tane yerleştirilebilir. Öyleyse, dikdörtgenler
prizmasının hacmi, V = a.b.c birimküp olur.
Dikdörtgenler prizmasının boyutları, seçilen birim uzunluğun tam katları değilse,
birim uzunluk a.b.c boyutlarının bir ortak böleni olarak seçilebilir. Böylece aynı ispat, o
durum için de geçerli olur.
Sonuçlar
1. Bir dikdörtgenler prizmasının hacmi, taban alanı ile yüksekliğinin çarpımına
eşittir.
2. Ayrıt uzunluğu, a birim olan küpün hacmi, V = a3 olur.
DİK PRİZMANIN HACMİ
TEOREM
Bir dik prizmanın hacmi, taban alanı ile yüksekliğinin çarpımına eşittir.
İspat
1. durum : Prizmanın tabanı bir dik üçgen olsun.
ABDA'B'D'
dik
üçgen
dik
prizmasının
hacminin
V = A(ABC).h olduğunu göstereceğiz. Verilen dik prizmaya
eş olan, BCDB'C'D' dik üçgen dik prizmasını düşünelim. Bu
iki
dik
prizmanın
DBB'D'
yüzlerini
çakıştırırsak,
ABCDA'B'C'D' dikdörtgenler prizmasını elde ederiz. Bu
prizmanın hacmi, (ABCA'B'C') prizmasının hacminin iki katı
olacaktır.
2V = (|AB|.|AD|).|AA'| olur. Bu durumda, ABDA'B'D' dik üçgen dik prizmasının
hacmi,
V=
1
.(|AB|.|AD|). |AA'|
2
V = taban alanı x yükseklik olur.
2. durum: Dik prizmanın tabanı, herhangi bir ABC üçgeni olsun.
ABC ve A'B'C' tabanlarının, [AH] ve [A'H'] yüksekliklerini çizelim.
A(ABH) = G1 ve A(AHC) = G2 olsun. Birinci
durumdaki ispattan,
V1 = G1.h
V2 = G2.h
+
+
.
V = (G1+G2).h V = G.h bulunur.
3. durum: Taban herhangi bir çokgen olsun.
ABCDEA'B'C'D'E' dik prizması verilmiş olsun. Tabanlara ait [AC], [AD], [A'C'], [A'D'] köşegenlerini çizelim.
[A'C'] ve [AC] köşegenlerinden geçen düzlem ile [A'D']
ve [AD] köşegenlerinden geçen düzlem, bu dik prizmayı bir
takım üçgen prizmalara ayırır. Bu üçgen prizmaların hacimleri
toplamının, çokgen prizmanın hacmini vereceğini düşünürsek,
V = G.h buluruz.
EĞİK PRİZMANIN HACMİ
TEOREM
Bir eğik prizmanın hacmi, dik kesit alanı ile yan ayrıt uzunluğunun çarpımına eşittir.
İspat
Şekilde,
ABCDA'B'C'D'
eğik
prizması
verilmiştir. Bu eğik prizmanın bir dik kesiti EFHK
dörtgenidir. Biz bu eğik prizmanın hacminin, EFHK dik
kesit alanı ile [AA'] yan ayrıtının uzunluğunun
çarpımına eşit olduğunu göstereceğiz. Bunun için dik
prizmanın hacim formülünden yararlanacağız.
Bir an için, eğik prizmayı EFHK dik kesitinden
bir düzlemle kestiğimizi düşünelim. Elde ettiğimiz, EFHKA'B'C'D' cismin A'B'C'D' tabanı,
ABCD tabanı ile çakıştıralım. Eğik prizmaların tabanları eş olduğundan, bu çakıştırma işlemi
yapılabilir. Böylece, ABCDA'B'C' D' eğik prizmasının hacmine eşit olan E'F'H'K'EFHK dik
prizmasını elde ederiz.
Dik prizmanın hacmi = A(E'F'H'K').|K'K| olur. Buradan, eğik prizmanın hacmi =
A(E'F'H'K').|DD'| bulunur.
|KK'| = |DD'| olduğundan, eğik prizmanın hacmi
V = (dik kesit alanı) x (yan ayrıt uzunluğu) olur.
Dik kesit alanı K ve yan ayrıt uzunluğu l ile gösterilirse, V = K.l bulunur.
Örneğin; dik kesit alanı K = 24 cm2 ve yan ayrıt uzunluğu l = 5 cm olan eğik
prizmanın hacmi, V = 24.5 = 120 cm3 olur.
TEOREM
Bir eğik prizmanın hacmi, taban alanı ile yüksekliğinin çarpımına eşittir.
Şekilde, tabanı ABCD dörtgeni olan bir eğik prizma görüyorsunuz. Bu eğik
prizmanın yüksekliği |D'H| = h, yan ayrıt uzunluğu |DD'| = B, taban alanı G, dik kesit alanı
A(EFLM) = K olsun. Dik kesit düzlemi ile
taban düzleminin belirlediği açının ölçüsü de a
olsun. Kenarları birbirine dik olan iki açı eş
olacağından, m(DD'H) = m(EPA) = dır.
EFLM dörtgeni, A'B'C'D' dörtgeninin
dik kesit düzlemi üzerindeki dik iz düşümüdür.
Bu nedenle, A(EFLM) = A(A'B'C'D'). cos olur. Buradan, K = G. cos yazılır.
DD'H dik üçgeninde, cos =
| Dı H |
h
cosα olduğundan, prizmanın hacmi,
ı
l
|D D|
V = K.l
V = (G. cos ).l
V = G.
h
.l
l
V = G.h olarak bulunur.
CAVALİER (KAVALİYE) İLKESİ
KAVALİYE İLKESİ :
Taban alanları ile yükseklikleri eşit olan iki cismin, tabanlarına paralel ve tabandan
aynı uzaklıktaki kesitlerin alanları her zaman birbirine eşit olursa, bu iki cismin hacimleri eşit
olur.
Şekilde, bir top dosya kâğıdının üç farklı konumunu inceleyiniz. Kâğıtların sayısında
bir artma ya da azalma olmadığından, her üç konumda oluşan prizmaların hacimleri eşit
olacaktır.
Şekildeki üç prizmanın taban alanları ve yükseklikleri eşittir. Bu cisimlerin tabandan
eşit uzaklıktaki kesitlerinin alanları da birbirine eşittir. Kavaliye ilkesine göre, bu üç farklı
cismin hacimleri birbirine eşit olmak zorundadır.
Kavaliye ilkesinden yararlanarak, taban alanları ve yükseklikleri eşit olan bir dik
prizma ile bir eğik prizmanın hacimlerinin eşit olacağını söyleyebiliriz. Buradan da eğik
prizmaların hacimleri için, V = G.h formülünün geçerli olduğunu doğrulayabiliriz.
Örneğin; taban ayrıtlarının uzunlukları ve yükseklikleri eşit olan bir küp ile bir kare
eğik prizmanın hacimleri de eşit olur.
PİRAMİTLER
TANIM
Bir düzlemsel çokgen ile bunun düzlemi dışında bir nokta verilsin. Bu noktayı,
çokgenin köşeleriyle birleştirdiğimizde, oluşan üçgensel bölgelerle çokgensel bölgenin
sınırladığı cisme, piramit denir.
Şekilde,
ABCD
çokgenine,
piramidin
tabanı; P noktasına, piramidin tepesi; [PA], [PB],
[PC], [PD] doğru parçalarına, yan ayrıtlar; tepe
noktasından
taban
düzlemine
indirilen
[PH]
dikmesine, piramidin yüksekliği denir.
Şekildeki PAB,PBC,PCD,PDA üçgenlerine,
piramidin yan yüzleri denir. Tepe noktasından bir yan
yüzün tabanına indirilen dikmeye, bu yan yüze ait
yükseklik denir.
Şekilde,
düzlemine
(P,ABCD)
paralel
Q
piramidi
düzlemiyle
taban
kesilmiştir.
Piramidin yan yüzeyi ile Q düzleminin ara kesiti,
A'B'C'D' çokgenidir.
Piramidin
Q
düzlemiyle
ara
kesiti,
A'B'C'D' çokgensel bölgesidir.
Piramitler tabanını oluşturan çokgensel
bölgenin kenar sayısına göre adlandırılırlar: üçgen
piramit, dörtgen piramit, beşgen piramit vs.
PİRAMİT ÇEŞİTLERİ
TANIM
Tabanı düzgün çokgen olan ve yükseklik ayağı taban merkezinde bulunan piramide,
düzgün piramit denir.
TEOREM
Bir düzgün piramitte:
1. Yanal ayrıtların uzunlukları eşittir.
2. Yan yüzler, birbirine eş ikizkenar üçgenlerdir.
3. Yan yüzlere ait yüksekliklerin uzunlukları eşittir.
İspat İspatı kare dik piramit için yapalım. Diğer düzgün piramitler için de benzer
ispatlar yapılabilir:
1. Karede köşegenler birbirini ortaladığından, |AO| = |OB| = |OC| = |OD| dir. [PO]
taban düzlemine dik olduğundan, m(POA) = m(POB) =
m(POC) = m(POD) = 90° K.A.K. eşlik aksiyomundan,
POA POB POC POD olur.
Eş üçgenlerde karşılıklı kenarlar eş olacağından,
|PA| = |PB| = |PC| = |PD| bulunur.
2.
Düzgün
piramidin
taban
ayrıtlarının
uzunlukları eşit olacağından, |AB| = |BC| = |CD| = |DA|
dır.
3. K.K.K. eşlik teoreminden,
PAB PBC PCD PDA olur. Ayrıca, |PA| = |PB| olduğundan, bu üçgenler
ikizkenardır.
4. Eş üçgenlerin karşılıklı yükseklikleri de eş olacağından, yan yüzlere ait
yüksekliklerin uzunlukları eşittir.
DÜZGÜN DÖRTYÜZLÜ
TANIM
Bütün ayrıtları birbirine eş olan üçgen piramide, düzgün dörtyüzlü denir.
Şekilda, bir ayrıtının uzunluğu a olan düzgün
dörtyüzlünün, |TG| yüksekliğini hesaplayalım.
ABC eşkenar üçgeninde, |AH| =
a
3 olur.
2
G noktası ağırlık merkezi olduğundan,
|AG| =
2
2a
a
3
3 = olur.
|AH| |AG| =
3
32
3
TGA dik üçgeninde Pisagor teoremden,
|TA|2 = |AG|2 + |TG|2 a2 = (
a2 =
a
3 )2 + h2
3
2a 2
a 6
a2
h
+ h2 h 2 =
bulunur.
3
3
3
PİRAMİDİN TABANA PARALEL BİR DÜZLEMLE KESİLMESİ
TEOREM
Bir piramit, tabana paralel bir düzlemle kesilirse:
1. Kesit çokgeni tabana benzerdir.
2. Kesit alanının taban alanına oranı,
bunların
tepe
noktasına
olan
uzaklıklarının,
karelerinin oranına eşittir.
İspat
İspatı kare piramit için yapalım
Diğer piramitler için de benzer ispatlar
yapılabilir.
1. (T,ABCD) piramidinin tabana paralel bir kesiti A'B'C'D' olsun. A'B'C'D' çokgeni
ile ABCD çokgeninin karşılıklı kenarları paraleldir.
Tales teoreminden,
| A I Bl | | B I C I | | C I D I | | D I A I |
k, k IR yazılır.
| AB |
| BC |
| CD |
| DA |
ABCD çokgeninin açıları ile A'B'C'D' çokgeninin açıları, kenarları aynı yönde paralel açılar olduğundan, karşılıklı olarak birbirine eştir.
Karşılıklı kenarları orantılı ve karşılıklı açıları eş olan çokgenler benzer olacağından,
ABCD ~ A'B'C'D' olur.
2. Bu iki çokgenin, piramidin tepe noktasına olan uzaklıkları |TG'| = h' ve |TG| = h
olsun. Benzer iki çokgenin alanlarının oranı, benzerlik oranının karesine eşit olacağından,
A(A ı B ı C ı D ı ) | A ı B ı | 2
olur. Ayrıca,
A(ABCD)
| AB | 2
| A ı B ı | | TA ı | | TG ı | h ı
| AB |
| TA | | TG | h
2
2
A(A ı B ı C ı D ı ) h ı
olduğundan,
bulunur.
A(ABCD)
h
PİRAMİDİN HACMİ
Piramitlerin hacimlerinin hesaplanmasında, Cavalier (Kavaliye) ilkesinden yararlanabiliriz. "Taban alanları ve yükseklikleri eşit olan iki cismin, tabanlarına paralel ve
tabandan aynı uzaklıktaki kesitlerinin alanları her zaman eşit olursa, bu iki cismin hacimleri
eşit olur."
Bu ilkeden yararlanarak, şu yargıya ulaşabiliriz:
Taban alanları ve yükseklikleri eşit olan piramitlerin hacimleri eşittir.
TEOREM
Bir piramidin hacmi,
taban alanı ile yüksekliğinin
çarpımının üçte birine eşittir.
İspat
1. Taban üçgen ise
Şekilde, ABC DEF üçgen prizması; EAC, ECF, düzlemleri ile kesilerek üç tane
üçgen piramide ayrılmıştır. Bu piramitlerin hacimlerinin eşit olduğunu gösterelim:
(E,ABC) ve (C,EDF) piramitlerinin tabanları eş üçgenlerdir ve yükseklikleri de
eşittir. Bu nedenle, (E,ABC) ve (C,EDF) piramitleri eştir.
(C,EDF) piramidi, (D,EFC) piramidi olarak ifade edilebilir. Bu piramit, (A,EFC)
piramidine eştir. Çünkü tabanları ortak ve yükseklikleri eşittir. Öyleyse, oluşan bu üçgen
piramitler eştir. Buradan, üçgen piramidin hacmi,V=
1
. G.h bulunur.
3
2. Tabanı bir çokgen ise
Tabanın bir köşesinden çizilen köşegenler ile
tepe noktasının belirttiği düzlemler, çokgen piramidi bir
takım üçgen piramitlere ayırır.
Bu üçgen piramitlerin hacimleri toplamının,
çokgen piramidin hacmini vereceği düşünülürse, V =
1
.G.h olur.
3
DÜZGÜN PİRAMİDİN ALANI
Bir piramidin alanı, taban alanı ile yanal yüzlerinin alanlarının toplamına eşittir.
Tabanı düzgün çokgen olmayan piramidin yanal yüzleri farklı üçgenler olacağından, yanal
alan için belli bir formül söyleyemeyiz. Ancak düzgün piramidin yan yüzleri birbirine eş
ikizkenar üçgenler olduğundan, düzgün piramidin yanal alanı için bir formül bulabiliriz.
TEOREM
Bir düzgün piramidin yanal alanı, taban çevresi ile yanal yüksekliğinin çarpımının
yarısına eşittir.
İspat
İspatı düzgün beşgen piramit için yapalım: Diğer düzgün piramitler için benzer
ispatlar yapılabilir.
PAB PBC PCD PDE PEA olduğunu ispatlamıştık. Öyleyse yanal alan,
1
1
Y = 5. A(PCD) Y = 5. [ . y.a] Y =
y. [5.a]
2
2
Y=
1
y. (taban çevresi) bulunur.
2
Herhangi bir düzgün çokgen için de birbirine eş n tane ikizkenar üçgen olacağından,
1
1
Y = n. A(PCD) Y = n. [ . y.a] Y =
y. [n.a]
2
2
Y=
1
y. (taban çevresi) bulunur.
2
KESİK PİRAMİT
TANIM
Bir piramit, tabana paralel bir düzlemle kesilirse, kesit ile taban arasında kalan
cisme, kesik piramit denir.
Piramidin tabanına, alt taban ve kesit düzlemiyle piramidin ara kesitine, üst taban
denir.
Bir kesik piramitte iki taban arasındaki
uzaklığa,
kesik
piramidin
yüksekliği;
yan
yüzlerindeki yamukların yüksekliğine de yanal
yükseklik denir.
Şekilde, ABCD ve A'B'C'D' benzer
çokgenleri kesik piramidin alt ve üst tabanlarıdır.
ABB'A', BCC'B', CDD'C've DAA'D' yamukları
kesik piramidin yan yüzleridir. |K'K|, BCC'B' yan
yüzüne ait yüksekliktir.|O'O|, kesik piramidin cisim yüksekliğidir.
[AA'],[BB'],[CC'],[DD'] doğru parçaları, kesik piramidin yanal ayrıtlarıdır.
DÜZGÜN KESİK PİRAMİDİN ALANI
TANIM
Düzgün piramidin tabana paralel bir düzlemle kesilmesinden elde edilen kesik
piramide, düzgün kesik piramit denir.
Düzgün kesik piramidin özelikleri
1. Tabanlar birer düzgün çokgendir.
2. Yanal yüzleri birbirine eş olan ikizkenar yamuklardır.
3. Cisim yüksekliği, tabanların ağırlık merkezlerinden geçer.
4. Yanal yüz yükseklikleri birbirine eştir.
TEOREM
Bir düzgün kesik piramidin yanal alanı, alt ve üst taban çevrelerinin toplamıyla,
yanal yüksekliğinin çarpımının yarısına eşittir.
İspat
İspatı düzgün kare kesik piramit için yapalım. Diğer düzgün kesik piramitler için de
benzer ispatlar yapılabilir.
Şekilde, yanal alan, birbirine eş olan dört ikizkenar yamuğun alanlarının toplamına
eşit olacaktır.
(a a ı ). y
2
(4.a 4a ı ). y
Y
2
(Ç Ç ı ). y
Y
olur.
2
Y 4.
Bu durumda; bir düzgün piramidin bütün alanı, yanal alanı ile alt ve üst tabanlarının
alanlarının toplamına eşittir.
S = G+G'+Y olur.
KESİK PİRAMÎDİN HACMİ
TEOREM
Alt ve üst taban alanları G ve G' yüksekliği h olan bir kesik piramidin hacmi,
h
V G G ı G G ı olur.
3
İspat
Şekildeki (P, ABC) piramidinin hacminden,
(P, A'B'C') piramidinin hacmini çıkarırsak,
ABCA'B'C'
buluruz. V =
V=
Ayrıca,
h' =
(h ı ) 2
Gı
Gı
hı
ı
G (h h ı ) 2
G hh
h. G ı
G Gı
kesik
piramidinin
hacmini
1
1
G. (h+h') - G'.h'
3
3
1
[G.h+(G-G').h')] olur.
3
olduğunu ispatlamıştık. Buradan,
bulunur. Bu değer, hacim formülünde yerine yazılırsa,
1
h. G ı
h
V [G.h (G G ı ).
] V [G G ı G.G ı ] elde edilir.
3
3
G Gı
Örneğin; şekilde h = 9 cm, G = 9 cm2 ve G' = 4 cm2 ise,
1
V = . 9 . [9 + 4 + 9.4 ] = 3. (13+6) = 57 cm3 olur.
3
KATI CİSİMLERİN ALANI VE HACİMLERİ
PRİZMATİK YÜZEY
TANIM
Düzlemsel bir çokgen ile bunun düzlemine paralel olmayan bir d doğrusu verilmiş
olsun.
d doğrusuna paralel olan ve çokgenin kenarlarına dayanarak hareket eden l'
doğrusunun oluşturduğu yüzeye, prizmatik yüzey denir (Şekil 1).
Çokgenin köşelerinden d doğrusuna çizilen paralel doğrulara, yan ayrıtlar denir. Ardışık
iki yan ayrıt arasında katan düzlem parçasına,
prizmatik yüzeyin yan yüzleri denir. Çokgen kaç
kenarlı ise o kadar yan yüz vardır.
Bir prizmatik yüzeyin bir düzlemle ara
kesitine, bu prizmatik yüzeyin kesiti denir. Kesit
düzlemi yan ayrıntılara dik ise bu kesite, dik kesit
denir.
TEOREM
Bir
prizmatik
yüzeyin,
paralel
iki
düzlemle kesilmesinden elde edilen iki çokgen
birbirine eştir.
İspat
Şekil 2 de, prizmatik yüzey P ve P' gibi iki
paralel düzlemle kesilmiştir. Böylece elde edilen,
ABCDEF
ve
A'B'C'D'E'F'
çokgenlerinin
eş
olduğunu göstereceğiz.
Bir düzlem paralel iki düzlemle kesildiğinde, ara kesitler paralel olacağından; A'B' //
AB, B'C' // BC, C'D' // CD, D'E' // DE, E'F' // EF, F'A' // FA olur
Uzayda kenarları aynı yönde paralel olan açılar eş olacağından; A'B'C' ABC,
B'C'D' BCD, C'D'E' CDE, D'E'F' DEF, E'F'A' EFA, F'A'B' FAB
Ayrıca; ABB'A', BCC'B', CDD'C', DEE'D', FEE'F', AFF'A' dörtgenleri birer
paralelkenar olduğundan; |AB| = |B'A'|, |BC| = |C'B'|, |CD| = |D'C'|, |DE| = |E'D'|, |EF| = |EF'|,
|AF| = |A'F'| bulunur.
İki çokgen arasında yapılan bire bir eşlemede, karşılıklı kenarlar ve karşılıklı açılar
eş ise bu iki çokgen eş olacağından, ABCDEF - A'B'C'D'E' F' olur.
Sonuç: Bir prizmatik yüzeyin dik kesitleri eştir.
PRİZMALAR
TANIM
Bir prizmatik yüzey ile bunun yan ayrıtlarını kesen paralel iki düzlem tarafından
sınırlanan cisme, prizma denir.
Bir prizmanın tabanlarının dışında kalan yüzeylerine, prizmanın yan yüzeyleri
denir.
Bir prizmada aynı yüzey içinde bulunmayan iki köşeyi birleştiren doğru parçasına,
bu prizmanın köşegeni denir.
Şekil 3 de, bir üçgen prizma görüyorsunuz.
Bu prizmada; ABC üçgenine, alt taban ve A'B'C'
üçgenine, üst taban denir. [AA'], (BB'], [CC'] doğru
parçalarına, bu prizmanın yan ayrıtları denir. [AB],
[BC], [ÇA] doğru parçalarına, alt taban ayrıtları ve
[A'B'], [B'C'], [C'A'] doğru parçalarına, üst taban
ayrıtları denir.
Alt ve üst tabanlar arasındaki uzaklığa, prizmanın yüksekliği denir.
ABB'A', BCC'B', ACC'A' paralelkenarlarına, prizmanın yan yüzleri denir. KLM üçgenine, üçgen prizmanın dik kesiti denir.
Bu bölümde prizma ya da piramitlerin taban ve yan yüzleri için söylenen üçgen,
kare, dikdörtgen, paralelkenar gibi ifadelerden; bunların sınırladığı çokgensel bölgeler
anlaşılacaktır.
TEOREM
Bir prizmanın tabanına paralel kesitleri, tabana eştir.
İspat : Bir prizmatik yüzeyin, paralel iki
düzlemle kesişmesinden elde edilen iki çokgenin,
birbirine eş olduğunu ispatlamıştık. Bu ispattan,
EFGH çokgeninin ABCD çokgenine eş olduğunu
söyleriz (Şekil 4).
Sonuçlar
1. Bir prizmanın yan yüzleri, birer
paralelkenardır.
2. Bir prizmanın dik kesitleri, birbirine eştir.
PRİZMA ÇEŞİTLERİ
TANIM
Yan ayrıtları taban düzlemine dik olan prizmaya, dik prizma denir. Yan ayrıtları
taban düzlemine dik olmayan prizmaya da eğik prizma denir.
Dik prizmaların yan yüzleri birer dikdörtgendir. Yan ayrıtların uzunlukları
yüksekliğin uzunluğuna eşittir.
Eğik prizmaların yan yüzleri birer paralelkenardır.
TANIM
Tabanı düzgün çokgen olan dik prizmaya, düzgün
prizma denir
Bir düzgün prizmanın yan yüzleri birbirine eş dikdörtgenlerdir.
DİKDÖRTGENLER PRİZMASI
TANIM
Tabanları dikdörtgen olan dik prizmaya, dikdörtgenler prizması denir.
Dikdörtgenler prizmasının bütün yüzleri dikdörtgendir.
Dikdörtgenler prizmasında bir köşeden çıkan üç ayrıta, bu dikdörtgenler prizmasının
boyutları denir. Dikdörtgenler prizması özel bir paralelyüz olduğundan, onun tüm özeliklerini taşır. Ayrıca, dikdörtgenler prizmasının cisim köşegenleri eşit uzunluktadır.
TEOREM
Bir dikdörtgenler prizmasında, cisim köşegeninin uzunluğunun karesi, bir köşeden
çıkan üç ayrıtının uzunluklarının karelerinin toplamına eşittir.
İspat
Pisagor
teoreminden,
ABC
dik
üçgeninde, e2 = a2 + b2 dir. A'AC dik üçgeninde,
k2 = e2 + c2 dir. Buradan, k2 = a2 + b2 + c2 bulunur.
Örneğin; ayrıtları 3, 4 ve 12 birim olan
dikdörtgenler
prizmasının
cisim
köşegeninin
uzunluğu,
k=
32 4 2 12 2 = 13 birim olur.
KÜP
Bütün ayrıtları eşit uzunlukta oları dikdörtgenler prizmasına, küp denir.
Küpün bütün yüzleri, birbirine eş karelerdir.
Bir kenarının uzunluğu a birim olan küpün
cisim köşegeninin uzunluğu, a 3 birimdir. Örneğin;
köşegen uzunluğu 10 6 birim olan küpün bir
ayrıtının uzunluğu, a 3 = 10 6 eşitliğinden,
a = 10 2 birim olur.
PRİZMANIN ALANI
TEOREM
Bir eğik prizmanın yanal yüzünün alanı, dik kesit çevresi ile yan ayrıt uzunluğunun
çarpımına eşittir:
İspat ABCDA'B'C'D' prizmasının yan ayrıtının uzunluğu |AA'| = l olsun.
Dik kesiti KLMN dörtgeni olan bir prizma ile bu prizmanın açık şekli, şekilde
belirtilmiştir. Şekildeki ABB'A', BCC'B', CDD'C', DAA'D' dörtgenlerinin birer paralelkenar
olduğunu ispatlamıştık.
|KL|, |LM|, |MN|, |NK| bu paralelkenarların birer yüksekliğidir. Buna göre, şekildeki
prizmanın yanal alanı,
Y = |AA'| . (|KL| + |LM| + |MN| + |NK|)
Y = l . (dik kesit çevresi) olur.
Sonuçlar
1. Bir prizmanın bütün alanı, yanal alanı ile alt ve üst tabanının alanlarının toplamına
eşittir. Alt ve üst tabanları eş olduğu düşünülürse,
S = Y + 2 . G bulunur. Burada G, prizmanın taban alanını göstermektedir.
2. Bir dik prizmanın yanal alanı, taban çevresi ile yüksekliğinin çarpımına eşittir.
Çünkü, dik prizmanın yan yüzü, bir dikdörtgensel bölgedir. Bu dikdörtgensel bölgenin bir kenarının uzunluğu, tabandaki çokgensel bölgenin çevresine eşittir. Diğer kenarının
uzunluğu da dik prizmanın yüksekliğine eşittir.
Örneğin; taban ayrıtlarının uzunlukları 3 cm, 4 cm, 5 cm ve yüksekliği 10 cm olan
üçgen dik prizmanın yanal alanı;
Y = (3+4+5) . 10
Y = 120 cm2 olur.
3. Bir köşeden çıkan ayrıt uzunlukları a, b, c olan dikdörtgenler prizmasının alanı,
S = 2(a.b+b.c+a.c)dir.
Örneğin: boyutları a = 5 cm, b = 3 cm, c = 2 cm olan dikdörtgenler prizmasının bütün alanı, S = 2. (5.3 + 5.2 + 3.2) = 62 cm2 olur.
4. Bir ayrıtının uzunluğu a olan küpün alanı, S = 6 . a2 dir. Çünkü küpte birbirine eş
altı kare vardır.
Örneğin; bir ayrıtının uzunluğu a = 3 birim olan küpün alanı,S = 6 . 32 = 54 br2 olur.
DİKDÖRTGENLER PRİZMASININ HACMİ
TEOREM
Bir dikdörtgenler prizmasının hacmi, bir köşeden geçen üç ayrıtının uzunlukları
çarpımına eşittir.
İspat :
Dikdörtgenler prizmasının boyutları, seçilen bir birim uzunluğunun a,b,c gibi tam
katları olsun
Bu prizmanın tabanına a.b tane birimkare çizilebilir. Her kareye bir birimküp oturtularak, a.b birimküplük bir tabaka (katman) elde edilir. Prizmanın yüksekliği c birim
olduğundan, prizmada bu katmanlardan c tane bulunur. Bu durumda dikdörtgenler
prizmasına, seçilen birimküplerden (a.b).c tane yerleştirilebilir. Öyleyse, dikdörtgenler
prizmasının hacmi, V = a.b.c birimküp olur.
Dikdörtgenler prizmasının boyutları, seçilen birim uzunluğun tam katları değilse,
birim uzunluk a.b.c boyutlarının bir ortak böleni olarak seçilebilir. Böylece aynı ispat, o
durum için de geçerli olur.
Sonuçlar
1. Bir dikdörtgenler prizmasının hacmi, taban alanı ile yüksekliğinin çarpımına
eşittir.
2. Ayrıt uzunluğu, a birim olan küpün hacmi, V = a3 olur.
DİK PRİZMANIN HACMİ
TEOREM
Bir dik prizmanın hacmi, taban alanı ile yüksekliğinin çarpımına eşittir.
İspat
1. durum : Prizmanın tabanı bir dik üçgen olsun.
ABDA'B'D'
dik
üçgen
dik
prizmasının
hacminin
V = A(ABC).h olduğunu göstereceğiz. Verilen dik prizmaya
eş olan, BCDB'C'D' dik üçgen dik prizmasını düşünelim. Bu
iki
dik
prizmanın
DBB'D'
yüzlerini
çakıştırırsak,
ABCDA'B'C'D' dikdörtgenler prizmasını elde ederiz. Bu
prizmanın hacmi, (ABCA'B'C') prizmasının hacminin iki katı
olacaktır.
2V = (|AB|.|AD|).|AA'| olur. Bu durumda, ABDA'B'D' dik üçgen dik prizmasının
hacmi,
V=
1
.(|AB|.|AD|). |AA'|
2
V = taban alanı x yükseklik olur.
2. durum: Dik prizmanın tabanı, herhangi bir ABC üçgeni olsun.
ABC ve A'B'C' tabanlarının, [AH] ve [A'H'] yüksekliklerini çizelim.
A(ABH) = G1 ve A(AHC) = G2 olsun. Birinci
durumdaki ispattan,
V1 = G1.h
V2 = G2.h
+
+
.
V = (G1+G2).h V = G.h bulunur.
3. durum: Taban herhangi bir çokgen olsun.
ABCDEA'B'C'D'E' dik prizması verilmiş olsun. Tabanlara ait [AC], [AD], [A'C'], [A'D'] köşegenlerini çizelim.
[A'C'] ve [AC] köşegenlerinden geçen düzlem ile [A'D']
ve [AD] köşegenlerinden geçen düzlem, bu dik prizmayı bir
takım üçgen prizmalara ayırır. Bu üçgen prizmaların hacimleri
toplamının, çokgen prizmanın hacmini vereceğini düşünürsek,
V = G.h buluruz.
EĞİK PRİZMANIN HACMİ
TEOREM
Bir eğik prizmanın hacmi, dik kesit alanı ile yan ayrıt uzunluğunun çarpımına eşittir.
İspat
Şekilde,
ABCDA'B'C'D'
eğik
prizması
verilmiştir. Bu eğik prizmanın bir dik kesiti EFHK
dörtgenidir. Biz bu eğik prizmanın hacminin, EFHK dik
kesit alanı ile [AA'] yan ayrıtının uzunluğunun
çarpımına eşit olduğunu göstereceğiz. Bunun için dik
prizmanın hacim formülünden yararlanacağız.
Bir an için, eğik prizmayı EFHK dik kesitinden
bir düzlemle kestiğimizi düşünelim. Elde ettiğimiz, EFHKA'B'C'D' cismin A'B'C'D' tabanı,
ABCD tabanı ile çakıştıralım. Eğik prizmaların tabanları eş olduğundan, bu çakıştırma işlemi
yapılabilir. Böylece, ABCDA'B'C' D' eğik prizmasının hacmine eşit olan E'F'H'K'EFHK dik
prizmasını elde ederiz.
Dik prizmanın hacmi = A(E'F'H'K').|K'K| olur. Buradan, eğik prizmanın hacmi =
A(E'F'H'K').|DD'| bulunur.
|KK'| = |DD'| olduğundan, eğik prizmanın hacmi
V = (dik kesit alanı) x (yan ayrıt uzunluğu) olur.
Dik kesit alanı K ve yan ayrıt uzunluğu l ile gösterilirse, V = K.l bulunur.
Örneğin; dik kesit alanı K = 24 cm2 ve yan ayrıt uzunluğu l = 5 cm olan eğik
prizmanın hacmi, V = 24.5 = 120 cm3 olur.
TEOREM
Bir eğik prizmanın hacmi, taban alanı ile yüksekliğinin çarpımına eşittir.
Şekilde, tabanı ABCD dörtgeni olan bir eğik prizma görüyorsunuz. Bu eğik
prizmanın yüksekliği |D'H| = h, yan ayrıt uzunluğu |DD'| = B, taban alanı G, dik kesit alanı
A(EFLM) = K olsun. Dik kesit düzlemi ile
taban düzleminin belirlediği açının ölçüsü de a
olsun. Kenarları birbirine dik olan iki açı eş
olacağından, m(DD'H) = m(EPA) = dır.
EFLM dörtgeni, A'B'C'D' dörtgeninin
dik kesit düzlemi üzerindeki dik iz düşümüdür.
Bu nedenle, A(EFLM) = A(A'B'C'D'). cos olur. Buradan, K = G. cos yazılır.
DD'H dik üçgeninde, cos =
| Dı H |
h
cosα olduğundan, prizmanın hacmi,
ı
l
|D D|
V = K.l
V = (G. cos ).l
V = G.
h
.l
l
V = G.h olarak bulunur.
CAVALİER (KAVALİYE) İLKESİ
KAVALİYE İLKESİ :
Taban alanları ile yükseklikleri eşit olan iki cismin, tabanlarına paralel ve tabandan
aynı uzaklıktaki kesitlerin alanları her zaman birbirine eşit olursa, bu iki cismin hacimleri eşit
olur.
Şekilde, bir top dosya kâğıdının üç farklı konumunu inceleyiniz. Kâğıtların sayısında
bir artma ya da azalma olmadığından, her üç konumda oluşan prizmaların hacimleri eşit
olacaktır.
Şekildeki üç prizmanın taban alanları ve yükseklikleri eşittir. Bu cisimlerin tabandan
eşit uzaklıktaki kesitlerinin alanları da birbirine eşittir. Kavaliye ilkesine göre, bu üç farklı
cismin hacimleri birbirine eşit olmak zorundadır.
Kavaliye ilkesinden yararlanarak, taban alanları ve yükseklikleri eşit olan bir dik
prizma ile bir eğik prizmanın hacimlerinin eşit olacağını söyleyebiliriz. Buradan da eğik
prizmaların hacimleri için, V = G.h formülünün geçerli olduğunu doğrulayabiliriz.
Örneğin; taban ayrıtlarının uzunlukları ve yükseklikleri eşit olan bir küp ile bir kare
eğik prizmanın hacimleri de eşit olur.
PİRAMİTLER
TANIM
Bir düzlemsel çokgen ile bunun düzlemi dışında bir nokta verilsin. Bu noktayı,
çokgenin köşeleriyle birleştirdiğimizde, oluşan üçgensel bölgelerle çokgensel bölgenin
sınırladığı cisme, piramit denir.
Şekilde,
ABCD
çokgenine,
piramidin
tabanı; P noktasına, piramidin tepesi; [PA], [PB],
[PC], [PD] doğru parçalarına, yan ayrıtlar; tepe
noktasından
taban
düzlemine
indirilen
[PH]
dikmesine, piramidin yüksekliği denir.
Şekildeki PAB,PBC,PCD,PDA üçgenlerine,
piramidin yan yüzleri denir. Tepe noktasından bir yan
yüzün tabanına indirilen dikmeye, bu yan yüze ait
yükseklik denir.
Şekilde,
düzlemine
(P,ABCD)
paralel
Q
piramidi
düzlemiyle
taban
kesilmiştir.
Piramidin yan yüzeyi ile Q düzleminin ara kesiti,
A'B'C'D' çokgenidir.
Piramidin
Q
düzlemiyle
ara
kesiti,
A'B'C'D' çokgensel bölgesidir.
Piramitler tabanını oluşturan çokgensel
bölgenin kenar sayısına göre adlandırılırlar: üçgen
piramit, dörtgen piramit, beşgen piramit vs.
PİRAMİT ÇEŞİTLERİ
TANIM
Tabanı düzgün çokgen olan ve yükseklik ayağı taban merkezinde bulunan piramide,
düzgün piramit denir.
TEOREM
Bir düzgün piramitte:
1. Yanal ayrıtların uzunlukları eşittir.
2. Yan yüzler, birbirine eş ikizkenar üçgenlerdir.
3. Yan yüzlere ait yüksekliklerin uzunlukları eşittir.
İspat İspatı kare dik piramit için yapalım. Diğer düzgün piramitler için de benzer
ispatlar yapılabilir:
2. Karede köşegenler birbirini ortaladığından, |AO| = |OB| = |OC| = |OD| dir. [PO]
taban düzlemine dik olduğundan, m(POA) = m(POB) =
m(POC) = m(POD) = 90° K.A.K. eşlik aksiyomundan,
POA POB POC POD olur.
Eş üçgenlerde karşılıklı kenarlar eş olacağından,
|PA| = |PB| = |PC| = |PD| bulunur.
2.
Düzgün
piramidin
taban
ayrıtlarının
uzunlukları eşit olacağından, |AB| = |BC| = |CD| = |DA|
dır.
3. K.K.K. eşlik teoreminden,
PAB PBC PCD PDA olur. Ayrıca, |PA| = |PB| olduğundan, bu üçgenler
ikizkenardır.
4. Eş üçgenlerin karşılıklı yükseklikleri de eş olacağından, yan yüzlere ait
yüksekliklerin uzunlukları eşittir.
DÜZGÜN DÖRTYÜZLÜ
TANIM
Bütün ayrıtları birbirine eş olan üçgen piramide, düzgün dörtyüzlü denir.
Şekilda, bir ayrıtının uzunluğu a olan düzgün
dörtyüzlünün, |TG| yüksekliğini hesaplayalım.
ABC eşkenar üçgeninde, |AH| =
a
3 olur.
2
G noktası ağırlık merkezi olduğundan,
|AG| =
2
2a
a
3
3 = olur.
|AH| |AG| =
3
32
3
TGA dik üçgeninde Pisagor teoremden,
|TA|2 = |AG|2 + |TG|2 a2 = (
a2 =
a
3 )2 + h2
3
2a 2
a 6
a2
h
+ h2 h 2 =
bulunur.
3
3
3
PİRAMİDİN TABANA PARALEL BİR DÜZLEMLE KESİLMESİ
TEOREM
Bir piramit, tabana paralel bir düzlemle kesilirse:
1. Kesit çokgeni tabana benzerdir.
2. Kesit alanının taban alanına oranı,
bunların
tepe
noktasına
olan
uzaklıklarının,
karelerinin oranına eşittir.
İspat
İspatı kare piramit için yapalım
Diğer piramitler için de benzer ispatlar
yapılabilir.
1. (T,ABCD) piramidinin tabana paralel bir kesiti A'B'C'D' olsun. A'B'C'D' çokgeni
ile ABCD çokgeninin karşılıklı kenarları paraleldir.
Tales teoreminden,
| A I Bl | | B I C I | | C I D I | | D I A I |
k, k IR yazılır.
| AB |
| BC |
| CD |
| DA |
ABCD çokgeninin açıları ile A'B'C'D' çokgeninin açıları, kenarları aynı yönde paralel açılar olduğundan, karşılıklı olarak birbirine eştir.
Karşılıklı kenarları orantılı ve karşılıklı açıları eş olan çokgenler benzer olacağından,
ABCD ~ A'B'C'D' olur.
2. Bu iki çokgenin, piramidin tepe noktasına olan uzaklıkları |TG'| = h' ve |TG| = h
olsun. Benzer iki çokgenin alanlarının oranı, benzerlik oranının karesine eşit olacağından,
A(A ı B ı C ı D ı ) | A ı B ı | 2
olur. Ayrıca,
A(ABCD)
| AB | 2
| A ı B ı | | TA ı | | TG ı | h ı
| AB |
| TA | | TG | h
2
2
A(A ı B ı C ı D ı ) h ı
olduğundan,
bulunur.
A(ABCD)
h
PİRAMİDİN HACMİ
Piramitlerin hacimlerinin hesaplanmasında, Cavalier (Kavaliye) ilkesinden yararlanabiliriz. "Taban alanları ve yükseklikleri eşit olan iki cismin, tabanlarına paralel ve
tabandan aynı uzaklıktaki kesitlerinin alanları her zaman eşit olursa, bu iki cismin hacimleri
eşit olur."
Bu ilkeden yararlanarak, şu yargıya ulaşabiliriz:
Taban alanları ve yükseklikleri eşit olan piramitlerin hacimleri eşittir.
TEOREM
Bir piramidin hacmi,
taban alanı ile yüksekliğinin
çarpımının üçte birine eşittir.
İspat
1. Taban üçgen ise
Şekilde, ABC DEF üçgen prizması; EAC, ECF, düzlemleri ile kesilerek üç tane
üçgen piramide ayrılmıştır. Bu piramitlerin hacimlerinin eşit olduğunu gösterelim:
(E,ABC) ve (C,EDF) piramitlerinin tabanları eş üçgenlerdir ve yükseklikleri de
eşittir. Bu nedenle, (E,ABC) ve (C,EDF) piramitleri eştir.
(C,EDF) piramidi, (D,EFC) piramidi olarak ifade edilebilir. Bu piramit, (A,EFC)
piramidine eştir. Çünkü tabanları ortak ve yükseklikleri eşittir. Öyleyse, oluşan bu üçgen
piramitler eştir. Buradan, üçgen piramidin hacmi,V=
1
. G.h bulunur.
3
2. Tabanı bir çokgen ise
Tabanın bir köşesinden çizilen köşegenler ile
tepe noktasının belirttiği düzlemler, çokgen piramidi bir
takım üçgen piramitlere ayırır.
Bu üçgen piramitlerin hacimleri toplamının,
çokgen piramidin hacmini vereceği düşünülürse, V =
1
.G.h olur.
3
DÜZGÜN PİRAMİDİN ALANI
Bir piramidin alanı, taban alanı ile yanal yüzlerinin alanlarının toplamına eşittir.
Tabanı düzgün çokgen olmayan piramidin yanal yüzleri farklı üçgenler olacağından, yanal
alan için belli bir formül söyleyemeyiz. Ancak düzgün piramidin yan yüzleri birbirine eş
ikizkenar üçgenler olduğundan, düzgün piramidin yanal alanı için bir formül bulabiliriz.
TEOREM
Bir düzgün piramidin yanal alanı, taban çevresi ile yanal yüksekliğinin çarpımının
yarısına eşittir.
İspat
İspatı düzgün beşgen piramit için yapalım: Diğer düzgün piramitler için benzer
ispatlar yapılabilir.
PAB PBC PCD PDE PEA olduğunu ispatlamıştık. Öyleyse yanal alan,
1
1
Y = 5. A(PCD) Y = 5. [ . y.a] Y =
y. [5.a]
2
2
Y=
1
y. (taban çevresi) bulunur.
2
Herhangi bir düzgün çokgen için de birbirine eş n tane ikizkenar üçgen olacağından,
1
1
Y = n. A(PCD) Y = n. [ . y.a] Y =
y. [n.a]
2
2
Y=
1
y. (taban çevresi) bulunur.
2
KESİK PİRAMİT
TANIM
Bir piramit, tabana paralel bir düzlemle kesilirse, kesit ile taban arasında kalan
cisme, kesik piramit denir.
Piramidin tabanına, alt taban ve kesit düzlemiyle piramidin ara kesitine, üst taban
denir.
Bir kesik piramitte iki taban arasındaki
uzaklığa,
kesik
piramidin
yüksekliği;
yan
yüzlerindeki yamukların yüksekliğine de yanal
yükseklik denir.
Şekilde, ABCD ve A'B'C'D' benzer
çokgenleri kesik piramidin alt ve üst tabanlarıdır.
ABB'A', BCC'B', CDD'C've DAA'D' yamukları
kesik piramidin yan yüzleridir. |K'K|, BCC'B' yan
yüzüne ait yüksekliktir.|O'O|, kesik piramidin cisim yüksekliğidir.
[AA'],[BB'],[CC'],[DD'] doğru parçaları, kesik piramidin yanal ayrıtlarıdır.
DÜZGÜN KESİK PİRAMİDİN ALANI
TANIM
Düzgün piramidin tabana paralel bir düzlemle kesilmesinden elde edilen kesik
piramide, düzgün kesik piramit denir.
Düzgün kesik piramidin özelikleri
1. Tabanlar birer düzgün çokgendir.
2. Yanal yüzleri birbirine eş olan ikizkenar yamuklardır.
4. Cisim yüksekliği, tabanların ağırlık merkezlerinden geçer.
4. Yanal yüz yükseklikleri birbirine eştir.
TEOREM
Bir düzgün kesik piramidin yanal alanı, alt ve üst taban çevrelerinin toplamıyla,
yanal yüksekliğinin çarpımının yarısına eşittir.
İspat
İspatı düzgün kare kesik piramit için yapalım. Diğer düzgün kesik piramitler için de
benzer ispatlar yapılabilir.
Şekilde, yanal alan, birbirine eş olan dört ikizkenar yamuğun alanlarının toplamına
eşit olacaktır.
(a a ı ). y
2
(4.a 4a ı ). y
Y
2
(Ç Ç ı ). y
Y
olur.
2
Y 4.
Bu durumda; bir düzgün piramidin bütün alanı, yanal alanı ile alt ve üst tabanlarının
alanlarının toplamına eşittir.
S = G+G'+Y olur.
KESİK PİRAMÎDİN HACMİ
TEOREM
Alt ve üst taban alanları G ve G' yüksekliği h olan bir kesik piramidin hacmi,
h
V G G ı G G ı olur.
3
İspat
Şekildeki (P, ABC) piramidinin hacminden,
(P, A'B'C') piramidinin hacmini çıkarırsak,
ABCA'B'C'
buluruz. V =
V=
Ayrıca,
h' =
(h ı ) 2
Gı
Gı
hı
ı
G (h h ı ) 2
G hh
h. G ı
G Gı
kesik
piramidinin
hacmini
1
1
G. (h+h') - G'.h'
3
3
1
[G.h+(G-G').h')] olur.
3
olduğunu ispatlamıştık. Buradan,
bulunur. Bu değer, hacim formülünde yerine yazılırsa,
1
h. G ı
h
V [G.h (G G ı ).
] V [G G ı G.G ı ] elde edilir.
3
3
G Gı
Örneğin; şekilde h = 9 cm, G = 9 cm2 ve G' = 4 cm2 ise,
1
V = . 9 . [9 + 4 + 9.4 ] = 3. (13+6) = 57 cm3 olur.
3