MATH 250 - Mühendisler İçin Doğrusal Cebir ve Türevsel Denklemler

MATH 250 - Mühendisler Ýçin Doðrusal Cebir ve Türevsel Denklemler
DERS TANITIM BÝLGÝLERÝ
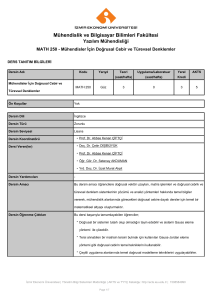
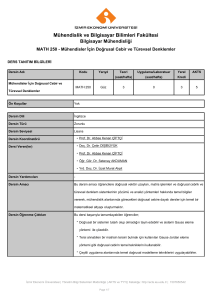
Dersin Adý
Kodu
Yarýyýl
Teori
Uygulama/Laboratuar
Yerel
(saat/hafta)
(saat/hafta)
Kredi
3
0
3
AKTS
Mühendisler Ýçin Doðrusal Cebir ve
MATH 250
Güz/Bahar
5
Türevsel Denklemler
Ön Koþullar
Yok
Dersin Dili
İngilizce
Dersin Türü
Servis Dersi
Dersin Seviyesi
Lisans
Dersin Koordinatörü
* Yrd. Doç. Dr. Özge Sağlam
Dersi Veren(ler)
* Prof. Dr. Mehmet Barış Özerdem
* Yrd. Doç. Dr. Osman Doluca
Dersin Yardýmcýlarý
-
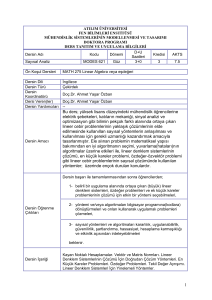
Dersin Amacý
Bu dersin amacı öğrencilere doğrusal vektör uzayları, matris işlemleri ve doğrusal cebrik ve
türevsel denklem sistemlerinin çözümü ve analizi yöntemleri hakkında temel bilgiler
vererek, mühendislik alanlarında görecekleri doğrusal cebire dayalı dersler için temel bir
matematiksel altyapı oluşturmaktır.
Dersin Öðrenme Çýktýlarý
Bu dersi başarıyla tamamlayabilen öğrenciler;
* Doğrusal bir sistemin tutarlı olup olmadığın tayin edebilir ve sistemi Gauss eleme
yöntemi ile çözebilir.
* Tersi alınabilen bir matrisin tersini bulmak için kullanılan Gauss-Jordan eleme
yöntemi gibi doğrusal cebirin temel tekniklerini kullanabilir.
* Çeşitli uygulama alanlarında temel doğrusal modelleme tekniklerini uygulayabilirler.
* Doğrusal vektör uzaylarının ve alt uzayların boyutlarını ve taban vektörler sistemini
bulabilir ve alt uzayları analiz edebilir.
İzmir Ekonomi Üniversitesi | Yönetim Bilgi Sistemleri Müdürlüğü | AKTS ve TYYÇ Kataloğu: http://ects.ieu.edu.tr | 1500378607
Page 1/5
* Karateristik polinomla kare matrislerin özdeğer ve özvektörlerini bulabilir ve
köşegenleşmesi mümkünse martisi köşegenleştirebilir.
Dersin Ýçeriði
Vektör ve matris işlemleri, vektörlerin doğrusal bağımsızlığı ve doğrusal vektör uzayları ve
alt uzaylar, vektör uzaylarının boyutu ve taban vektörleri, doğrusal dönüşümler,
determinantlar, mühendislik uygulamaları ile birlikte doğrusal cebirin, özdeğer-özvektör
analizi ve köşegenleştirme konuları işlenmektedir.
HAFTALIK KONULAR VE ÝLGÝLÝ ÖN HAZIRLIK ÇALIÞMALARI
Hafta
Konular
Ön Hazýrlýk
1
Doğrusal denklem sistemleri. İndirgenmiş satır ve eşelon form.
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition,Section
1.1, 1.2
2
Vektörel denklem. Doğrusal sistemlerin çözüm kümeleri.
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
1.3, 1.5
3
Doğrusal sistemlerin uygulamaları. Doğrusal bağımsızlık.
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
1.6, 1.7
4
Doğrusal dönüşümlere giriş. Doğrusal Modeller.
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
1.8, 1.10
5
Matris işlemleri. Matrisin tersi. Tersinir matrislerin karakterizasyonu
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
2.1, 2.2, 2.3
6
Parçalanmış matrisler Matris çarpanlarına ayırma. Leontief Input-Output Modeli. Ara Linear Algebra and Its Applications,
sınav.
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
2.4, 2.5, 2.6
İzmir Ekonomi Üniversitesi | Yönetim Bilgi Sistemleri Müdürlüğü | AKTS ve TYYÇ Kataloğu: http://ects.ieu.edu.tr | 1500378607
Page 2/5
7
Bilgisayar grafiği uygulamaları. Determinantlara giriş. Determinantların özellikleri.
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
2.7, 3.1, 3.2
8
Cramer kuralı. Vektör uzayları ve alt uzayları. Sıfır uzayları, sütun uzayları ve
Linear Algebra and Its Applications,
doğrusal dönüşümler
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
3.3, 4.1 4.2
9
Doğrusal bağımsız kümeler. Vektör uzayının boyutu. Rank.
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
4.3, 4.5, 4.6
10
Koordinat sistemleri. Taban değiştirme. Fark denklemlerinin uygulamaları
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
4.4, 4.7, 4.8
11
Markov Zinciri. Özvektörler ve özdeğerler. Karakteristik denklemler.
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
4.9, 5.1, 5.2
12
Köşegenleştirme. İç çarpım, uzunluk ve diklik. Ara sınav
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
5.3, 6.1
13
Dik izdüşümler. Dik kümeler.
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
6.2, 6,3
14
Gram-Schmidt süreçleri. En küçük kare problemleri.
Linear Algebra and Its Applications,
David C. Lay, Steven R. Lay, Judi J.
McDonald, Pearson, 5th Edition, Section
6.4, 6.5
İzmir Ekonomi Üniversitesi | Yönetim Bilgi Sistemleri Müdürlüğü | AKTS ve TYYÇ Kataloğu: http://ects.ieu.edu.tr | 1500378607
Page 3/5
15
Tekrar
16
Final sınavı.
KAYNAKLAR
Ders Notu
Linear Algebra and Its Applications, David C. Lay, Steven R. Lay, Judi J. McDonald, Pearson, 5th
Edition.
Diðer Kaynaklar
1) Elementary Linear Algebra, Howard Anton, Chris Rorres, Wiley, 9th Edition.
2) Linear Algebra, Seymour Lipschutz, Shaum's Outline Series, 2nd Edition.
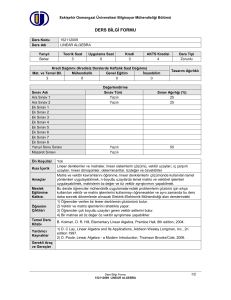
DEÐERLENDÝRME SÝSTEMÝ
Yarýyýl Ýçi Çalýþmalarý
Sayý
Katký Payý
Devam/Katılım
-
-
Laboratuar
-
-
Uygulama
-
-
Arazi Çalışması
-
-
Derse Özgü Staj
-
-
Küçük Sınavlar/Stüdyo Kritiği
-
-
Ödev
-
-
Sunum/Jüri
-
-
Projeler
-
-
Seminer/Workshop
-
-
Ara Sınavlar/Sözlü Sınavlar
1
40
Final/Sözlü Sınav
1
60
Toplam
2
100
YARIYIL ÝÇÝ ÇALIÞMALARININ BAÞARI NOTU KATKISI
1
40
YARIYIL SONU ÇALIÞMALARININ BAÞARI NOTUNA KATKISI
1
60
Toplam
2
100
İzmir Ekonomi Üniversitesi | Yönetim Bilgi Sistemleri Müdürlüğü | AKTS ve TYYÇ Kataloğu: http://ects.ieu.edu.tr | 1500378607
Page 4/5
DERS KATEGORÝSÝ
Ders Kategorisi
Temel Meslek Dersleri
Uzmanlık/Alan Dersleri
Destek Dersleri
İletişim ve Yönetim Becerileri Dersleri
Aktarılabilir Beceri Dersleri
DERSÝN ÖÐRENÝM ÇIKTILARININ PROGRAM YETERLÝLÝKLERÝ ÝLE ÝLÝÞKÝSÝ
#
Program Yeterlilikleri / Çýktýlarý
* Katký Düzeyi
1
2
3
4
5
*1 Lowest, 2 Low, 3 Average, 4 High, 5 Highest
AKTS / ÝÞ YÜKÜ TABLOSU
Aktiviteler
Sayý
Süresi (Saat)
Toplam Ýþ Yükü
Ders saati (Sınav haftası dahildir: 16 x toplam ders saati)
16
3
48
Laboratuvar
-
-
-
Uygulama
-
-
-
Derse Özgü Staj
-
-
-
Arazi Çalışması
-
-
-
Sınıf Dışı Ders Çalışması
16
3
48
Sunum / Seminer
-
-
-
Proje
-
-
-
Ödevler
-
-
-
Küçük Sınavlar
-
-
-
Ara Sınavlar / Sözlü Sınavlar
2
20
40
Final / Sözlü Sınav
1
44
44
Toplam Ýþ Yükü
180
İzmir Ekonomi Üniversitesi | Yönetim Bilgi Sistemleri Müdürlüğü | AKTS ve TYYÇ Kataloğu: http://ects.ieu.edu.tr | 1500378607
Page 5/5