doğru akım devre analizi ö. şenyurt

DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
ONUNCU BÖLÜM: KONDANSATÖRLER VE DOĞRU AKIMDAKİ DAVRANIŞLARI
Anahtar Kelimeler
Kapasitans, kondansatör, kondansatörün dolması, kondansatörün boşalması, dielektrik malzeme,
dielektrik sabiti, elektrostatik alan, RC zaman sabiti
Elektrik devrelerinde sıklıkla kullanılan üç temel devre elemanı direnç, bobin ve kondansatördür.
Kondansatörler bir elektrik alanı sayesinde elektrik enerjisini depolama yeteneğine sahip olan
cihazlardır. Akımın bir manyetik alan oluşturması gibi gerilimde bir elektrik alanı oluşturur. Bu konu ve
kondansatörlerin bazı önemli doğru akım karakteristikleri bu bölümde ele alınacaktır.
Bu bölümde kazandırılacak yeterliklerden sonra öğrenci;
 Kondansatörü, kapasitansı, dielektriği, dielektrik sabitini, elektrik alanını, faradı, RC zaman
sabitini ve kaçak direnci tanımlar.
 Kondansatörlerin dolması ve boşalması olaylarını açıklar.
 Yük, gerilim, kapasitans ve depolanan enerjiyi uygun denklemleri kullanarak hesaplar.
 Seri ve paralel bağlı kondansatörlerin eş değerini belirler.
 Uygun RC zaman sabiti denklemlerini kullanarak devre gerilimlerini hesaplar.
 Kondansatörlerin fiziki ve elektriki özelliklerini tanımlar.
KONDANSATÖRÜN TARİF VE TANIMI
Kondansatörler elektriki elemanlar olup genel olarak kondansatör plakası olarak adlandırılan iki iletken
yüzey ve bu yüzeyleri ayıran iletken olmayan (dielektrik adı verilen) bir malzemeden oluşur.
Şekil 10.1. Kondansatör ve simgeleri
Dielektrik olarak bilinen iletken olmayan malzeme vakum, hava, bal mumlu kağıt, plastik, cam,
seramik, alüminyum-oksit vb olabilir. Kondansatörler uçlarına uygun bir gerilim uygulandığında elektrik
enerjisini depo edebilirler.
ELEKTROSTATİK ALAN
Bildiğiniz gibi aynı yükler birbirini itmekte ve farklı yükler birbirini çekmektedir. Yüklü cisimler
arasındaki elektrostatik alanları göstermek için manyetik kutuplar arasındaki manyetik akıyı göstermek
için kullanılan çizgilere benzeyen çizgiler kullanılır. Elektrostatik alan çizgilerinin yönü genellikle pozitif
yüklü cisimden negatif yüklü cisme doğru gösterilir. Yüklü cisimler arasındaki kuvvet cisimlerdeki yükle
doğru, cisimler arasındaki mesafenin karesi ile ters orantılıdır.
F=k .Q1.Q2 / d2 (kulon kanunu)
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Bunun anlamı belli bir yük için kondansatör plakaları birbirine yaklaştırıldıkça üretilen elektrik alanının
daha güçlü olacağıdır. Ayrıca plakalar arasında depolanan yük arttıkça üretilen alanın gücü de
artacaktır.
Elektrostatik alan depo edilen elektrik enerjisini temsil eder. Bu enerji kaynak tarafından oluşturulur ve
kaynak kaldırıldığında devreye geri aktarılabilir.
Şekil 10.2. Elektrostatik alan
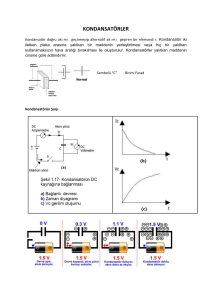
KONDANSATÖRÜN DOLMASI
Aşağıdaki şekil anahtar kapatıldığında kondansatörün kısa bir süre içinde dolması olayını
anlatmaktadır. Anahtar kapatılmadan hemen önce kondansatör plakaları arasında bir gerilim olmadığı
gibi plakaların hiç birinde elektron olarak azlığı veya çokluğu söz konusu değildir. Ayrıca plaklar
arasındaki dielektrik malzeme üzerinde bir elektrik alanı da yoktur.
Şekil 10.3. Kondansatörün dolması
Anahtar kapatılınca devre boyunca bir elektrik akımı başlar, kondansatöre ulaşan elektronlar yarı
iletken malzeme içinden geçemedikleri için kondansatörün bir tarafında toplanırlar. Böylece
kondansatörün bir plakası elektronca zenginleşirken diğer plakadaki elektronlar azalır. Dielektrik
malzemenin atomlarındaki elektron yörüngeleri (vakum durumu hariç) değişir. Çünkü kondansatörün
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
negatif yüklü plakası tarafından
depolanmasını temsil eder.
itilmektedirler.
Bu
değişen
yörüngeler
elektrik
enerjisinin
Şekil 10.4. Bozulan yörüngeler depo edilen elektrik enerjisini temsil eder.
Kondansatörün bir tarafında toplanan elektronlar o plakayı negatif yaptığı gibi aynı anda elektronlar
kondansatörün diğer yanında kaynak tarafından çekilmektedir. Seri devrelerden hatırlayacağınız gibi
akım bütün devre parçalarından aynı değerde geçmektedir.
Sonuç olarak kondansatörün bir plakasında elektron fazlalığı ve diğer plakasında buna eşit miktarda
elektron azlığı oluşacağından plakalar arasında bir gerilim farkı doğacaktır. Eğer yeterli bir dolma
akımı akarsa kondansatörün gerilimi kaynak gerilimine eşit olana kadar artacaktır.
Kondansatörün dolmasına kadar geçen bu sürede kondansatör kısa devre gibi davranır. Bu arada
kondansatör plakaları arasındaki dielektrik ortamda akım akışı olmadığını, bunun yerine
kondansatörün diğer tarafında elektron akışı gerçekleştiği için sanki dielektrik ortamdan da akım
akıyormuş gibi hissedildiğini hatırlatalım. Bu dolma akımı anahtar kapatıldığı anda en büyük
değerindedir ve kondansatörün gerilimi kaynak gerilime eşit olduğu anda sıfıra doğru yaklaşır. Kaynak
gerilimi daha büyük bir değere getirildiğinde kondansatörde depo edilen yük bu yeni seviyeye gelene
kadar artar. Kondansatör kaynak gerilimi ile şarj edildikten sonra açık devre gibi davranır ve doğru
akımı geçirmez.
Özet olarak gerilim ilk uygulandığında en büyük doğma akımı akar. Kondansatör dolarken uçları
arasındaki gerilim kaynak gerilimine doğru artar ve doğma akımı azalır. Kondansatör kaynak gerilimi
ile dolduğunda akım akışı biter. Kondansatör yükünü tutar ve plaklar arasında kaynak gerilimi görülür.
Elektrik enerjisi kondansatörün elektrostatik alanında (dielektrik) depolanmaktadır.
Kondansatör dolduktan sonra aşağıdaki şekilde görüldüğü gibi devre anahtarını açarsak ve dielektrik
malzemenin akıma karşı sonsuz direnç gösterdiğini farz edersek (yani plakalar arasında dielektrik
üzerinden hiçbir kaçak akımın akmadığını varsayarsak), harici bir boşalma yolu kurulmadıkça
kondansatör yüklü olarak kalır.
Şekil 10.5. Kondansatörler harici bir akım yolu sağlanmadıkça yüklü kalırlar.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Dikkat :
Kondansatörler güç kesildiğinde boşaltılmalıdır. Özellikle büyük değerli kondansatör uygulamalarında
boşalma yolu içine giren bir teknik eleman ölmektedir. Çalışmalarda bu tehlike göz ardı edilmemelidir.
Pek çok üretici firma bleeder direnç denilen ve güç kaldırıldığında kondansatörlerin yükünü boşaltan
elemanlar sağlamaktadır. Fakat bu direnç teknik elemanları asla korumaz. Sonuç olarak sistemlerdeki
büyük kondansatörlerin güç kaynağı kapatıldığında boşalacağını sanmayınız.
KONDANSATÖRLERİN BOŞALMASI
Şekil 10.6. Kondansatörün boşalması
Yukarıdaki şekilde kondansatörün boşalması gösterilmiştir. Kondansatör plakaları için harici bir
elektron yolu sağlanmıştır. Bu şekilde plakalar arasındaki yük farkı dengelenir ve potansiyel fark sıfıra
düşer. Bu sağlandığında kondansatör tamamen boşalmış olur.
KAPASİTANSIN BİRİMİ
Buraya kadar anlattıklarımızla kapasitenin kondansatörün elektrik yükünü depolaması ile ilgili
olduğunu anlamışsınızdır. Tahmin edebileceğiniz gibi aynı gerilim değerinde daha fazla yük
depolayabilen kondansatörün kapasitansı daha büyük olacaktır. Kapasitansın birimi faraday’ın anısına
Farad olarak seçilmiştir. 1Farad kondansatör plakaları arasında 1V’luk gerilim oluşturan bir kulonluk
yük söz konusu olduğunda kapasitansın miktarıdır. Farad “F” harfi ile, kapasitans “C” harfi ile gösterilir.
C=Q / V
Burada Q kulon cinsinden yük, V volt cinsinden gerilimdir.
Görüldüğü gibi kondansatörün depo ettiği yük kondansatörün kapasitansı ve gerilimi ile doğru
orantılıdır.
KONDANSATÖRÜN ELEKTROSTATİK ALANINDA DEPOLANAN ENERJİ
Kaynak tarafından sağlanan elektrik enerjisi dolan kondansatörün elektrostatik alanında
depolanmaktadır. Kondansatör boşalırken bu enerji devreye geri verilmektedir. Kondansatörlerde
depo edilen enerji Joule cinsinden aşağıdaki gibi ifade edilebilir.
W=1/2 C.V2
Burada C kondansatörün kapasitansı, V kondansatör plakları arasındaki potansiyel farktır.
KAPASİTANS DEĞERİNİ BELİRLEYEN ETKENLER
Kapasitans değeri birim gerilim için ne kadar yük depolandığı ile ilgilidir. Paralel plakalı kondansatörler
için kapasitans değerini belirleyen fiziki etkenler dielektrik malzemenin kalınlığı türü ve plakaların
örtüşen alanıdır.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 10.7. Kapasitans değerini belirleyen fiziki etkenler
Plakaların örtüşen yüzeyi
Plakaların örtüşen yüzeyi arttıkça depolanan elektronların sayısı ve dolayısıyla yükün miktarı da
artacaktır. Mesela plakaların alanı iki katına çıkartıldığında gerilim sabit kalmak şartıyla kondansatörün
tutacağı yükün miktarı ve kapasitansın değeri iki katına çıkar. SI birim sisteminde m 2 ile gösterilir.
Plakalar arası mesafe veya dielektrik malzemenin kalınlığı
Plakalar arasındaki belirli bir potansiyel fark ve yük olduğunu farz edersek plakalar birbirinden
uzaklaştırıldığında elektrik alanının gücü de azalacaktır. Böylece bu elektrik alanında depolanan
elektrik enerjisi de azalacaktır. Diğer bir ifade ile kapasitans değeri plakalar arasındaki mesafe ile ters
orantılıdır. Plakalar birbirine yaklaştırıldığında, yani daha ince bir dielektrik malzeme kullanıldığında
verilen gerilim için elektrik alanı daha güçlü olacak ve kapasitans değeri artacaktır. SI birim sisteminde
dielektrik malzemenin kalınlığı metre ile gösterilir.
Dielektrik malzemenin türü
Farklı dielektrik malzemelerin elektrik akı çizgilerini toplama yeteneği de farklıdır. Bu özellik ingilizce
adıyla permittivity ve türkçe adıyla dielektrik katsayısı olarak bilinir. İletkenlerin iletkenliklerine
benzediği düşünülebilir. Havanın dielektrik katsayısı 1’dir. Bağıl dielektrik katsayısı, havanın mutlak
dielektrik katsayısının o malzemenin mutlak dielektrik katsayısına oranıdır. Bağıl dielektrik katsayısına
o malzemenin dielektrik sabiti (k) de denir.
k=0 / V
0 dielektrik malzemenin mutlak dielektrik katsayısı, V vakumun mutlak dielektrik katsayısıdır.
Dielektrik sabiti hava için 1, cam için 8, mumlu kağıt için 3,5 mika için 6, seramik için 100 değerindedir.
Bu değerler çevre şartları ve frekansa göre değişebilir. Belirli bir yüzey alanı ve plakalar arası mesafe
için dielektrik sabiti daha yüksek malzemeler kullanıldığında elde edilen elektrik akı çizgilerinin
yoğunluğu da artacaktır. Bu yüzden kapasitans ile dielektrik sabiti doğru orantılıdır. Mesela dielektriği
hava olan bir kondansatörün kapasitesi dielektrik sabiti 5 olan bir malzemenin kullanıldığı
kondansatörün kapasitesinin 5’te 1’idir.
Dielektrik dayanımı
Elektrik alanı yoğunluğu dielektrik üzerindeki gerilim arttırıldıkça artar. Plakalar arasındaki potansiyel
farkı arttırmaya devam edersek erişilen bir noktada dielektrik malzeme içindeki elektronların
yörüngeleri bozulacak ve elektronlar kendi yörüngelerinden ayrılacaktır. Aynı anda dielektrik malzeme
arızalanacak (delinecek) ve iletken haline gelecektir. Eğer bu malzeme hava veya vakum değilse
dielektrik malzeme özelliğini tümüyle kaybedecektir. Dielektrik malzemenin delindiği bu değer dielektrik
dayanımı olarak bilinir. Dielektrik dayanımının uygulamadaki ölçüsü delinme gerilimidir. Delinme
gerilimi malzemenin türüne ve kalınlığına bağlıdır.
Malzemelerin delinme gerilimleri üreticiye ve çalışma frekansına göre değişebilmektedir.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
KAPASİTANS DENKLEMİ
Kapasitansın plakaların birbiri ile örtüşen yüzeyine, plakalar arasındaki malzemenin dielektrik sabitine
ve plakalar arasındaki mesafeye bağlı olduğunu söylemiştik. Buna göre SI birim sisteminde dielektrik
olarak hava veya vakum kullanıldığında kapasitans şu denklemle belirlenir:
C=8,85.10-12 x s / d
Burada C farad cinsinden kapasitans, s metrekare cinsinden örtüşen yüzey alanı ve d metre cinsinden
plakalar arası mesafedir.
Dielektrik malzeme olarak hava veya vakum dışında bir başka malzeme kullanılırsa o malzemenin
dielektrik sabiti (k) yukarıdaki denkleme çarpan olarak gelecektir.
C=8,85.10-12 x k x s / d
Burada k malzemenin dielektrik sabitidir.
SERİ VE PARALEL BAĞLI KONDANSATÖRLERİN EŞ DEĞER KAPASİTANSININ BULUNMASI
Seri bağlı kondansatörlerin eş değer kapasitesi
Şekil 10.8. Seri kondansatörlerin eş değer kapasitesi
Kondansatörlerin seri bağlanması dielektrik malzemenin kalınlığını arttırma etkisi yapacağından eş
değer kapasitansın azalacağını kolayca görebiliriz. Seri bağlı kondansatörlerin eş değer kapasitansı
paralel bağlı dirençlerin eş değer direncinin hesaplanmasında olduğu gibi bulunur.
Seri bağlı kondansatörlerde gerilim dağılımı
Seri devrelerde tek bir akım olabileceği için seri bağlı kondansatörler aynı değerde elektrik yükü
depolarlar. Belirli bir yük için eş değer kondansatörlerin plakaları arasındaki potansiyel fark ta eşit olur.
Fakat farklı değerdeki kondansatörler için plakalar arasındaki potansiyel fark ta farklıdır.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
V=Q / C denkleminden bildiğiniz gibi potansiyel fark yükle doğru, kapasitans ters orantılıdır. Bu durum
Q’nun aynı olmak zorunda olduğu seri devrelerde herhangi bir kondansatörün uçları arasındaki
gerilimin o kondansatörün kapasitansı ile orantılı olduğunu gösterir. Mesela değerleri 5F ve 10F
olan iki kondansatör seri bağlanırsa 5F’lık kondansatör uçlarındaki gerilim 10F’lık kondansatör
uçlarındaki gerilimin iki katı olur.
Şekil 10.9. Seri kondansatörlerde gerilim dağılımı
Değişik değerde kapasitanslar elde etmek için genellikle elektrolitik kondansatörler kullanılır. Fakat
elektrolitik kondansatörlerin toleransları büyük olduğundan hesaplanan ve uygulamada gerçekleşen
gerilim düşümleri tam uymayabilir. Eğer kondansatörün değerleri kesin olarak belli ise gerilim dağılımı
buna uygun olacaktır.
Üç veya daha fazla kondansatör seri bağlandığında gerilimlerin bulunması
Şekil 10.10. Seri kondansatörlerin gerilimlerinin bulunması
Üç veya daha fazla kondansatör seri bağlandığında bunlardan herhangi birinin uçlarındaki gerilimi
bulmak için aşağıdaki denklem kullanılabilir.
VX= VS x CT / CX
Burada VX x kondansatörü uçlarındaki gerilim, VS devrenin doğru akım gerilim kaynağı, CT seri
kondansatörlerin eş değer kapasitesi ve CX x kondansatörünün kapasitans değeridir.
Paralel bağlı kondansatörlerin eş değer kapasitesi
Aşağıdaki şekilde de gösterildiği gibi kondansatörlerin paralel bağlanması alt ve üst plakalarının
elektriki olarak birbirine bağlanması anlamına geleceğinden kondansatör plakalarının örtüşen
yüzeylerinin toplamı kadar bir plaka alanı elde edilecektir. Bu durumda dielektrik kalınlığı
değişmeyecektir. Etkin plaka alanının arttırılması ve dielektrik kalınlığının korunması sonucunda
paralel bağlı kondansatörlerin eş değer kapasitansları her birinin kapasitanslarının toplamı olacaktır.
Kısacası kondansatörlerin paralel bağlanması durumunda eş değer kapasitansın bulunması seri bağlı
dirençlerin eş değerinin bulunması gibidir.
Aşağıdaki şekilde de gösterildiği gibi kondansatörlerin paralel bağlanması alt ve üst plakalarının
elektriki olarak birbirine bağlanması anlamına geleceğinden kondansatör plakalarının örtüşen
yüzeylerinin toplamı kadar bir plaka alanı elde edilecektir. Bu durumda dielektrik kalınlığı
değişmeyecektir. Etkin plaka alanının arttırılması ve dielektrik kalınlığının korunması sonucunda
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
paralel bağlı kondansatörlerin eş değer kapasitansları her birinin kapasitanslarının toplamı olacaktır.
Kısacası kondansatörlerin paralel bağlanması durumunda eş değer kapasitansın bulunması seri bağlı
dirençlerin eş değerinin bulunması gibidir.
Şekil 10.11. Paralel bağlı kondansatörlerin eş değer kapasitesi
Paralel bağlı kondansatörlerde yük dağılımı
Paralel bağlı elemanların gerilimleri aynı olacağından paralel bağlı kondansatörlerin her birinin yükü
kendi kapasitans değeri ile orantılı olacaktır. Yani kapasitansı büyük olan kondansatörün yük de büyük
olacaktır.
Şekil 10.12. Paralel kondansatörlerde yük dağılımı
Mesela değerleri 10F, 20F ve 30F olan üç kondansatör paralel bağlanırsa ve devreye 300V’luk
doğru gerilim uygulanırsa 10F’lık kondansatörün yükü 20F’lık yükünün yarısı ve 30F’lık
kondansatörün yükünün 3’te 1’i olacaktır. Bu durumda devredeki eş değer yük her bir kondansatörün
yüklerinin toplamı olacaktır.
RC ZAMAN SABİTİ
Bölümün başında dediğimiz gibi kondansatörler gerilim değişimine karşı direnirler. Verilen bir
kondansatör için yükün değişimi yük akımı ile doğru orantılıdır. Yani akımın daha yüksek bir değeri için
kondansatörün VS değerine dolması daha çabuk olmaktadır.
Yine bildiğiniz gibi akımın miktarı akım yolu üzerindeki dirençle ters orantılıdır. Bu yüzden
kondansatörün dolma veya boşalma yolu üzerindeki direncin büyümesi kondansatörün dolması veya
boşalması için gereken zamanı arttıracaktır.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Kondansatörün kapasitesi büyütülürse plakaları arasında verilen bir potansiyel farkı sağlamak için
daha fazla yüke ihtiyaç duyulacaktır. Kondansatörler plakaları arasında ani gerilim değişimini
önlediklerinden (dolma veya boşalma yolu üzerinde herhangi bir direnç varsa) kondansatörün kendi
üzerindeki gerilim değişimine karşı koyduğu söylenebilir.
RC zaman sabiti kondansatörün dolması veya boşalması için ihtiyaç duyulan süreyi anlatır.
Kondansatörlerin bir gerilim seviyesinden yeni bir gerilim seviyelerine geçmeleri için 5 RC zaman sabiti
gerekir.
Bir RC zaman sabiti:
 = R.C
 saniye, R ohm, C’ de farad cinsindendir.
Şekil 10.13. RC devresinde gerilimler
Yukarıdaki şekil üzerinde şu açıklamaları yapabiliriz. Direnç ve kondansatör uçlarındaki gerilimlerin
toplamları her zaman eşittir. Kondansatör yüklendiğinde uçlarındaki gerilim kaynağa göre terstir. Bu
yüzden direnç uçlarındaki gerilim herhangi bir anda kaynak geriliminden kondansatör gerilimi
çıkartılarak elde edilen değer kadardır. Buna göre kondansatör VS değerine kadar yüklenirse direnç
uçlarındaki gerilim sıfıra düşer. Yani kondansatör gerilimi ile kaynak gerilimi eşit olur, devreden akım
akışı durur ve direnç üzerine gerilim düşmez. Devredeki anahtar bir an için kapatılırsa kondansatörün
yükü ve gerilimi sıfıra düşer. Bu anda direnç üzerindeki gerilim düşümü kaynak gerilimine eşittir. Aynı
durumda devreden akan akım VR / R ye eşit olur. Bir diğer ifade ile bahsedilen bu anda kondansatör
kısa devre gibi davranır ve akımı sınırlayan tek eleman direnç olur. Yük akımı aktıkça kondansatör
uçlarında ters seri potansiyel fark oluşur ve yük akımı üstel olarak sıfıra doğru azalır. Bu durumda
direnç üzerindeki gerilim düşümü de aynı şekilde azalacaktır. Mesela belirli bir zaman süre sonra
kondansatör kaynak geriliminin yarısı değerinde yüklendiğinde direnç üzerindeki gerilim kaynak
geriliminin diğer yarısı olacaktır. herhangi bir anda kondansatör uçlarındaki gerilimin yüzdesi RC
zaman sabiti ile ilgilidir.
Aşağıdaki şekilde A eğrisi ile gösterildiği gibi bir zaman sabiti sonunda kondansatör gerilimi kaynak
geriliminin %63,2’sine eşittir. Bu değer iki zaman sabiti sonunda %86,5’e, üç zaman sabiti sonunda
%95’e, dört zaman sabiti sonunda %98,5’e ve beş zaman sabiti %99’a ulaşmaktadır. Bu son değerde
kondansatörün tümüyle dolduğu düşünülür.
Aynı şeklin B ile gösterilen eğrisine bakalım. Başlangıçta VR değeri VS’ ye eşittir. Kondansatör
yüklendikçe VR sıfıra doğru azalmaktadır. Direnç gerilimi ve devre akımı kondansatör geriliminin
tersine değişmektedir. Kondansatör gerilimi arttıkça hem devre akımı ve hem de direnç uçlarındaki
gerilim düşümü azalmaktadır.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 10.14. Zaman sabiti ile kondansatörün dolma ve boşalmasının ilişkisi
GERİLİMLERİN BULUNMASINDA ÜSTEL DENKLEMLERİN KULLANILMASI
Yukarıdaki şekilde verilen üstel eğrilerdeki değerlerin bazı basit denklemlerle bulunması mümkündür.
Eğrilerdeki artma veya azalma fonksiyonları doğal logaritma olarak ta bilinen üstel değişim şeklindedir.
Doğal logaritmanın tabanı “e” dir ve değeri 2,710’dir.
Bir RC seri devresinde kondansatör dolarken direnç uçlarındaki gerilim başlangıçta en büyük
değerindedir ve kondansatör yeni gerilim seviyesine doğru dolmakta iken direnç uçlarındaki gerilim
üstel olarak azalır. VR değeri devrenin RC zaman sabitine bağlı olarak kondansatörün dolma süresi
içinde değişir. Yani izin verilen zaman (t) RC zaman sabiti ile bölünür. t 5 veya daha fazla ’a eşit
olduğunda kondansatör tam olarak dolmuştur, devrede akım akışı durur ve V R sıfır olur. t’nin 5’dan
küçük olduğu durumlarda VR’nin değeri aşağıdaki denklemle bulunur.
VR=VS . e- t / 
Burada e=doğal logaritma tabanı veya 2,71028, t saniye cinsinden izin verilen zaman,  ; RC veya bir
zaman sabitidir.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Örnek
Aşağıdaki devrede 10000s sonra VR değeri ne olur?
Aşağıdaki devrede 1,8 zaman sabiti sonra VR değeri ne olur?
Çözüm
Kondansatör gerilimi kaynak gerilimi ile direnç gerilimi arasındaki farka eşittir. Herhangi bir andaki VC
değeri aşağıdaki gibi bulunur:
VC=VS(1-e-t/)
Buna göre ilk örnekte VC değerini hesaplarsak;
VC=50.(1-0,3679)=31,605V
Kontrol etmek için VR ve VC değerlerini toplarsak toplamın 50V’a yani kaynak gerilimine eşit olduğunu
görürüz. Bu hesabımızın doğru olduğunu gösterir.
Aynı şekilde ikinci örnekte VC’yi hesaplayalım.
VC=50(1-0,1653)=41,735V
VR ve VC’yi topladığımızda 50V ettiğini görürüz. Hesabımız yine doğru!
Şekil 10.15. Kondansatörün DA gerilimde davranışı örneği
KONDANSATÖRLERİN TÜRLERİ
Kondansatörler için iki temel sınıflandırma yapılmaktadır. Bunlar sabit ve değişken kondansatörlerdir.
Bu kondansatörlerin tasarımları boyutları ve karakteristikleri oldukça farklı olabilmektedir. Sabit
kondansatörlerin değiştirilemeyen tek bir değeri varken değişken kondansatörlerin değerleri imal
edildikleri aralıkta ayarlanabilmektedir. Bu ayarlamada konumu değiştirilebilen plakanın yerinin
değiştirilmesi ile örtüşen yüzey alanı için farklı değerler elde edilmektedir. Bildiğiniz gibi kapasitans
değeri örtüşen yüzey alanına da bağlıdır. Yani kondansatör plakaları tam olarak örtüştüğünde
kapasitans değeri en büyük hiç örtüşmediğinde ise en küçük değerindedir. Bu tür kondansatörlerde
dielektrik olarak hava kullanılır. Bir diğer değişken kondansatör türü sadece bir tane hareketli plakaya
sahip olan kondansatördür. Üzerindeki vidanın döndürülmesi ile hareketli ve sabit plaka arasındaki
mesafe değiştirilmektedir. Bu mesafe en aza indiğinde kapasitans değeri en büyük mesafe en fazla
miktara çıktığında da en küçük değerine ulaşmaktadır.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Şekil 10.16. Değişken kondansatörler
Kondansatörlerin karakteristikleri
Kondansatörlerin karakteristiklerini belirleyen en önemli unsur kullanılan dielektrik malzemedir. Bazı
çok kullanılan kondansatörler ve özellikleri kısaca şöyle anlatılabilir:
1) Kağıt ve plastik kondansatörlerde çok farklı dielektrik malzemeler kullanılmaktadır. Bunlardan
bazıları plastik türler için polietilen ve kağıt türler için mumlu veya yağlı kağıttır. Genel olarak
plakalar uzun şerit folyolar olup dielektrik malzeme ile ayrılır. Folyo ve dielektrik malzeme çoğu
uygulamada silindirik olarak sarılır. Her plakanın aktif iki yüzeyi vardır. Bunun anlamı bir
plakanın alanı hesaplanırken iki ile çarpılacağıdır. Genellikle 0,001F’tan birkaç F’a kadar
değişen değerlerde imal edilirler. Ses yükselteçleri gibi alçak frekans uygulamalarında çok
kullanılırlar.
Şekil 10.17. Kağıt tipi kondansatör
2) Mika kondansatörlerde dielektrik olarak mika kullanılır. Mikanın delinme gerilimi yüksek ve
kapasitansı düşük olduğundan yüksek gerilim devrelerinde kullanılan yüksek gerilim
kondansatörleri genellikle mikalı yapılırlar. Yapılarında plastik bir çerçeve içine konmuş mika
ve folyo tabakaları birbirini izleyecek şekilde yerleştirildiği görülür. Sıkı, dayanıklı ve nemden
etkilenmeyen yapıdadırlar. Binlerce Volt altında çalışabilirler. Gerilim oranına bağlı olarak 550000pF arasında kapasitans değerlerine sahiptirler
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
3) Seramik kondansatörler küçük boyutlu olup dielektrik dayanımları yüksektir. Disk veya
silindirik yapıda imal edilirler. Neme karşı dayanıklıdırlar. 5-5000pF kapasitans değerlerinde
1000V!a kadar imal edilirler. Daha küçük gerilimler için daha yüksek kapasitans değerleri elde
edilebilir. Hem mika, hem de seramik kondansatörler dielektrik karakteristiklerinin iyi olması
sayesinde birkaç 100MHz’e kadar ses frekans uygulamalarında kullanılmaktadır.
4) Elektrolitik kondansatörler aşağıda sıralanan önemli özelliklere sahiptirler.
a) kapasitans boyut oranı yüksektir.
b) Artı ve eksi uçlu kutupları vardır.
c) Diğer türlere göre daha çok sızıntı akımına izin verirler.
d) Fiyatları düşüktür.
Şekil 10.18. Alüminyum tip Elektrolitik kondansatörler
Yukarıdaki şekilde verilen elektrolitik kondansatör genellikle negatif uç veya elektrot görevini gören
alüminyum bir muhafaza ile çevrelenmiştir. Pozitif elektrot genellikle alüminyum folyo olup amonyumborat veya eş değeri bir elektrolitin içindedir. Eğer bu elektrot bir boraks çözeltisi ise kondansatör ıslak
elektrolitik olarak adlandırılır. Eğer elektrot boraks çözeltisi ile doydurulmuş bir malzeme ise
kondansatöre kuru elektrolitik denir. Dielektriği oluşturmak için kondansatör üzerinden doğru akım
akıtılır. Bunun sonucunda folyo yüzeyinde çok ince (0,1m kadar) bir alüminyum oksit tabakası oluşur.
Bu ince oksit film dielektriktir. Bu tür kondansatörler dielektriğinden sonra adlandırılmazlar. Çünkü
oldukça ince dieletkrik yüzünden birim plaka alanı için kapasitans değeri çok yüksektir. Buna bağlı
olarak delinme gerilimi seviyeleri düşüktür. Dielektriğin çok ince olması bir miktar sızıntı akımına sebep
olur. sızıntı akımının miktarı F başına 1mA kadardır.
Elektrolitik kondansatörlerin devreye bağlarken kutuplara dikkat etmek çok önemlidir. Eğer yanlışlıkla
ters yönde bağlanır ve akım geçirilirse dielektrik tabakada oluşan kimyasal etki tersine dönerek
kondansatörü bozabilir. Bu durumda kondansatör kısa devre edilmiş olur. kondansatör içinde gaz
oluşur ve hatta patlama olabilir. Gerilim değerlerine de bağlı olarak (10V-500V) bu tür kondansatörler
2F’tan birkaç 100F’a kadar değişik kapasite değerlerinde imal edilirler.
Elektrolitik kondansatörlerin ana üstünlüğü birim büyüklük başına fazla kapasitans değerleri elde
edilebilmesidir. Kötü tarafları kutuplanmaları ve yüksek sızıntı akımlarıdır. Bu tür kondansatörler uzun
süre geçtikten sonra özelliklerini kaybedebilirler.
Değişken akım uygulamalarında kullanılan ve kutuplu olmayan özel bazı elektrolitik kondansatörler de
vardır. Bunların önemli bir uygulaması motor başlatma amaçlı kondansatörlerdir. Bu uygulamada
değişken akım ortamında çalışmaya uygun yüksek kapasitans değerlerine ihtiyaç duyulur. Bu tür
kondansatörler iki elektrolitik kondansatörün aynı pakete arka arkaya yerleştirilmesi ile yapılırlar.
Uygun çalışmanın sağlanması için ters seri kutupta bağlanırlar.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Yüksek frekanslarda dielektrik kayıpları yüzünden elektrolitik kondansatör uygulamaları genellikle güç
kaynağı ve ses frekans devreleri ile sınırlanır.
5) Tantal kondansatörler alüminyum yerine tantalın kullanıldığı elektrolitik kondansatörlerdir. Çok
küçük boyutlar için yüksek kapasitans değerlerinde yapılabilmeleri önemli bir özellikleridir.
Ayrıca sızıntı akımları da diğer elektrolitiklerden düşüktür. Üstelik raf ömürleri de daha
uzundur. Düşük gerilimli yarı iletken devre yapıları için üretilen tantal kondansatörler nispeten
daha pahalıdırlar.
Şekil 10.19. Tantal elektrolitik kondansatörler
Kondansatörlerin seçimi
Kondansatörlerin seçimini etkileyen etkenler şunlardır:
1)
2)
3)
4)
5)
6)
7)
Fiziki boyutu ve devreye bağlantı şekli
Kapasitans değeri
Kapasitans toleransı
Çalışma gerilimi
Güvenli çalışma sıcaklığı
Sıcaklık katsayısı
Güç katsayısı (kondansatörde kullanılan dielektriğin kayıplarını ifade eder).
Çizelge 10.1. Kondansatör türleri için önemli karakteristikler
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
KONDANSATÖR KODLARI VE RENK KODLARI
Kondansatör renk kodları için değişik sistemler kullanılmaktadır. Kitabın sonunda mika, seramik disk,
seramik tüp ve kağıt kondansatörler için çok kullanılan bazı renk kodlama yöntemleri verilmiştir. Diğer
renk kodlama sistemlerinde olduğu gibi noktalara veya bantların renkleriyle konumları istenen bilgiyi
ifade etmektedir. Elektrolitik kondansatörler yeterince büyük olduğundan renk kodları yerine bilgilerin
yazılması yöntemi tercih edilir. Birçok seramik kondansatör için de aynı yöntem uygulanmaktadır.
Kondansatörlerin okunması üç grupta toplanabilir:
1.GRUP : Elektrolitik kondansatörlerdir. Bu kondansatörlerin üzerinde kapasite , gerilim değerleri
ve kutupları belirtilmiştir.
2.GRUP : Seramik ve mikalı kondansatörlerin kodlama sistemidir. Örnek kondansatör değerleri
aşağıdaki tabloda verilmiştir.
Çizelge 10.2. Bazı kondansatör kodları ve anlamları
İŞARET
P56
56P
5P6
622
102
n46
DEĞER
0,56pF
56pF
5,6pF
6200pF
1000pF
0,46nF
İŞARET
4n6
46n
.033
.062
1
2,2
DEĞER
4,6nF
46nF
0,033F
0,062F
1F
2,2F
Bu kondansatörlerin üzerinde ayrıca yazılı olan %10 , %20 değerleri toleransı , 60-100-250 DA
kullanma gerilimleridir.
3.GRUP : Kondansatör renk kodlarıdır.
Çizelge 10.3. Kondansatör renk kodları ve anlamları
RENKLER
SİYAH
KAHVERENGİ
KIRMIZI
TURUNCU
SARI
YEŞİL
MAVİ
MOR
GRİ
BEYAZ
KIRMIZI/ MOR
ALTIN
GÜMÜŞ
TAM SAYI ÇARPAN
TOLERANS
0
1
2
3
4
5
6
7
8
9
1
10
100
1000
10000
100000
1000000
10000000
100000000
1000000000
20
1
2
0,1
0,01
5
10
ÇALIŞMA
GERİLİMİ
SICAKLIK
KATSAYISI
NPO
100
250
N150
400
5
630
N750
10
P100
4 renkli; 1. renk sayı , 2. renk sayı , 3. renk çarpan , 4. renk çalışma gerilimi ,
5 renkli; 1. renk sayı , 2. renk sayı , 3. renk çarpan , 4. renk tolerans , 5. renk çalışma gerilimi,
6 renkli; 1. renk sayı , 2. renk sayı , 3. renk çarpan , 4. renk tolerans , 5.renk çalışma gerilimi 6.renk
sıcaklık katsayısıdır.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
KONDANSATÖRLERİN SEÇİMİ
Kondansatör seçimi yapılırken kapasite ve tolerans değerinden önce iki husus göz önünde
bulundurulur.
Çalışma gerilimi : Maksimum gerilimdir. (DC veya Maks. AC)
Sızıntı akımı : Kondansatörlerde kullanılan dielektrik mükemmel bir yalıtkan olamaz ama sızıntı ile
oluşan şarj kayıpları küçük olmalıdır.
Çizelge 10.4. Bazı kondansatör özellikleri
ÖZELLİK
DEĞERLER
TOLERANS
SIZINTI
KULLANIM
YERİ
KUTUPLANMAMIŞ
POLYESTER MİKA
0,01 – 10 F 1Pf – 0,01 F
%20
%1
Küçük
Küçük
Genel
Yüksek frekans
SERAMİK
10pF-1F
-25+50%
Küçük
KUTUPLANMIŞ
ALÜMİNYUM
1-100000F
-10+50%
Büyük
TANTALYUM
0,1-100F
%20
Küçük
Dekuplaj
Düşük frekans
Düşük gerilim
Bu bölümde anlatılanları kısaca özetleyecek olursak;
Kondansatörler elektronik devrelerin çoğunda sıklıkla karşılaşılan oldukça faydalı elemanlardır. Gerilim
değişimine karşı koymak, dolduktan sonra doğru akımı geçirmemek ve elektrik enerjisini depolamak
gibi özellikleri yüzünden çok sayıda uygulamada başvurulan elemanlardır.
Bilmeniz gereken bir diğer konu akım taşıyan iletkenlerin kondansatör etkisi gösterileceğidir. Ayrıca
bobinlerin sarımları arasında da bir kapasitans vardır. Hem bobin sarımları arasındaki, hem de akım
taşıyan iletkenlerin birbirleri veya toprak seviyesi ile aralarındaki kondansatör etkisi bir çok
uygulamada değerlendirilmektedir. Bu etki düşük frekanslarda devre çalışmasını pek etkilemez. Ancak
yüksek frekanslarda hesaba katılması şarttır. Özetle kondansatörler frekansın sıfır olduğu doğru akım
devrelerinde farklı , frekansın sıfırdan farklı olduğu değişken akım devrelerinde çok daha farklı
olmaktadır.
Sonuç olarak kapasitans bir elektrostatik alanda elektrik enerjisini (yükünü) depolandığı için gerilim
değişimine karşı koyma özelliğidir. Birimi Farad olup, 1F’lık kapasitans plakaları arasına 1V
uygulandığında 1Kulonluk yük depolar.
Kondansatör kapasitans özelliğine sahip bir cihazdır. Kapasitans iki iletken plaka ve aralarındaki
iletken olmayan dielektrik ortamla elde edilebileceği gibi kablolarla toprak seviyesi arasında da
oluşabilir.
Kondansatörler çok değişik boyut ve şekillerde ve farklı kapasitans değerleri için imal edilirler.
Kondansatörler yapılarında kullanılan dielektrik malzemeye göre adlandırılırlar. Fakat elektrolitik
kondansatörlerde durum farklıdır.
Kondansatörün kapasitansını belirleyen etkenler örtüşen plaka yüzeyi, dielektriğin kalınlığı ve dielektrik
malzemenin türüdür.
Kondansatörün kapasitans değeri ile geriliminin çarpımı ile elde edilen değer kondansatörün
depoladığı yükü verir.
Dielektrik sabiti farklı malzemelerin depo edebileceği yükü belirtmek için kullanılır.
Kondansatör yüklü iken elektronlar negatif plakada birikir ve pozitif plakada elektron sayısı azalır. Bu
durumda dielektrik malzemenin elektronlarının yörüngeleri bozulur. Kondansatör boşalırken depo
edilen enerji devreye geri döner. Boşalma olayı plakalar arasındaki potansiyel fark sıfır olana kadar
sürer. Bu fark sıfır olduğunda kondansatörün yükü nötr olur.
DOĞRU AKIM DEVRE ANALİZİ
Ö. ŞENYURT - R. AKDAĞ
Sızıntı direnci dielektrik malzemenin akım akışına gösterdiği zorlukla ilgilidir. Eğer dielektrik malzeme
mükemmel bir malzeme ise sızıntı direnci sonsuzdur. Çoğu kondansatör çalışma gerilimleri aşılsa bile
çok yüksek sızıntı dirençleri gösterirler. Elektrolitik kondansatörlerin sızıntı dirençleri diğer türlere göre
daha düşüktür.
Kondansatörler seri bağlandığında eş değer kapasitansları her birinin kapasitanslarından daha
düşüktür. Yani seri bağlı kapasitanslar paralel bağlı dirençler gibidir.
Paralel bağlı kapasitanslar seri bağlı dirençler gibidirler.
Kondansatörlerin dolması ve boşalması için geçen zamanın miktarı dolma ve boşalma akımını
sınırlayan dirence ve yükü depolayan kapasitansın değerine bağlıdır.kondansatörün tam olarak
dolması veya boşalması için 5RC zaman sabitine ihtiyaç vardır.
Kondansatörlerin çok değişik türde renk kodları vardır. Ancak bazı türler için renk kodları yerine
değerler doğrudan gövdeye yazılır.
Dolmuş bir kondansatörün R değeri 100M ya da daha fazladır. Elektrolitik kondansatörler için bu
değer 0,5-1M arasındadır.